Composite synchronization of four exciters driven by induction motors in a vibration system

Abstract

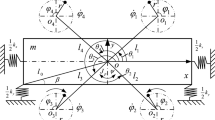
In this paper, a newly composite synchronization scheme is proposed to ensure the straight line vibration form of a linear vibration system driven by four exciters. Composite synchronization is a combination of self-synchronization and controlled synchronization. Firstly, controlled synchronization of two pairs of homodromous coupling exciters with zero phase differences is implemented by using the master–slave control structure and the adaptive sliding mode control algorithm. On basis of controlled synchronization, self-synchronization of two coupling exciters rotating in the opposite directions is studied. Based on the perturbation method, the synchronization and stability conditions of composite synchronization are obtained. The theoretical results indicate that composite synchronization of four exciters with zero phase differences can be implemented with different supply frequencies and the straight line vibration form of the linear vibration system also can be obtained. Some simulations are conducted to verify the feasibility of the proposed composite synchronization scheme. The effects of some structural parameters on composite synchronization of four exciters are discussed. Finally, some experiments are operated to validate the effectiveness of the proposed composite synchronization scheme.

Appendices

Appendix 1: [22]

In our work, we take exciters 1 and 2 as example to explain the controlled synchronization of exciters 1, 2 and 3, 4. From Eq. (7), the equations of motion of exciters 1 and 2 are rewritten as

$$\begin{aligned} & \ddot{\varphi }_{1} = a_{1} \dot{\varphi }_{1} + b_{1} u_{1} + w_{1} T_{L1} \\ & \ddot{\varphi }_{2} = a_{2} \dot{\varphi }_{2} + b_{2} u_{2} + w_{2} T_{L2} , \\ \end{aligned}$$

(27)

where u₁ and u₂ are the torque currents of exciters 1 and 2; a₁, a₂, b₁, b₂, w₁ and w₂ are the corresponding coefficients, a₁ = -f₁/J₁, b₁ = K_T1/J₁, w₁ = -1/J₁, a₂ = -f₂/J₂, b₂ = K_T2/J₂, w₂ = -1/J₂.

The phase tracking error is expressed as

$$e = \varphi_{1} - \varphi_{2} .$$

(28)

From Eqs. (27) and (28), we can obtain

$$\ddot{e} = a_{2} \dot{e} - b_{2} u_{2} + W,$$

(29)

where W is a bounded uncertainty, $W = (a_{1} - a_{2} )\dot{\varphi }_{1} + b_{1} u_{1} + w_{1} T_{L1} - w_{2} T_{L2}$. Here, $\left| W \right| < \rho$ is assumed, where ρ is a positive constant.

The sliding variable is designed as

$$S = \dot{e} + \kappa e + h\int_{0}^{t} {ed\tau } .$$

(30)

where κ and h are two positive constants.

From Eqs. (29) and (30), we can obtain

$$\dot{S} = (a_{2} + \kappa )\dot{e} + he - b_{2} u_{2} + W.$$

(31)

Choosing $\dot{S} = 0$ and ignoring the uncertain term W, the equivalent input is obtained as

$$u_{eq2} = (b_{2} )^{ - 1} [(a_{2} + \kappa )\dot{e} + he].$$

(32)

To reject the parametric perturbations and disturbances, the robust controller is designed

$$u_{sw2} = (b_{2} )^{ - 1} \left[ {\beta \text{sgn} (S)} \right].$$

(33)

where β is a positive constant and sgn($\cdot$) is the sign function

$${\text{sgn}}(S) = \left\{ {\begin{array}{*{20}l} {1,} \hfill &\quad {{\text{ }}S > 0,} \hfill \\ {0,} \hfill &\quad {S = 0,} \hfill \\ { - 1,} \hfill &\quad {{\text{ }}S < 0.} \hfill \\ \end{array} } \right.$$

Thus, the sliding mode controller is obtained as

$$u_{2} = u_{eq2} + u_{sw2} = (b_{2} )^{ - 1} [(a_{2} + \kappa )\dot{e} + he + \beta \text{sgn} (S)].$$

(34)

The adaptive algorithm for the boundary of the uncertainty $\left| W \right|$ is designed as

$$\dot{\beta } = \gamma \left| S \right|,$$

(35)

where γ is the adaptive gain with positive value. According to Eq. (35), the switch gain β is deduced as

$$\beta = \gamma \int_{0}^{t} {\left| {S(\tau )} \right|{\text{d}}\tau } .$$

(36)

The estimated switch gain is defined as $\hat{\beta }$, where $\hat{\beta } > \rho$. Moreover, the estimated error $\hat{\beta }$ can be expressed as

$$\tilde{\beta } = \beta - \hat{\beta }.$$

(37)

By using the modified method [24], the modified adaptive switch gain is obtained as

$$\beta = \gamma \int_{0}^{t} {\left( {\left| {S(\tau )} \right| - p\beta (\tau )} \right){\text{d}}\tau } ,$$

(38)

with

$$\left| {S(t)} \right| = \left\{ {\begin{array}{*{20}l} {\left| {S(t)} \right|,} \hfill & {\left| {S(t)} \right| \ge \delta } \hfill \\ {0,} \hfill & {\left| {S(t)} \right| < \delta } \hfill \\ \end{array} } \right.,$$

where p and δ are two small positive constants.

In order more to reduce the chattering phenomenon, the saturated function ${\text{sat}}( \cdot )$ is employed to replace the sign function $\text{sgn} ( \cdot )$:

$${\text{sat}}(S) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {S > \vartheta } \hfill \\ {\left( {{\text{1/}}\vartheta } \right)S,} \hfill & {\left| S \right| \le \vartheta } \hfill \\ { - 1,} \hfill & {S < - \vartheta } \hfill \\ \end{array} } \right.$$

(39)

where ϑ is a positive constant. Finally, the controller u₂ is expressed as

$$u_{2} = (b_{2} )^{ - 1} [(a_{2} + \kappa )\dot{e} + he + \beta {\text{sat}}(S)] .$$

(40)

Appendix 2: The terms of Eq. (22)

$$\begin{aligned} a_{11} & = \eta_{1}^{2} [\mu_{1} \cos \gamma_{x} + \mu_{2} \cos \gamma_{y} + \mu_{3} r_{l1}^{2} \cos \gamma_{\psi } ]/2 \\ & \quad + \eta_{1} \eta_{2} [\mu_{1} \cos \gamma_{x} + \mu_{2} \cos \gamma_{y} + \mu_{3} r_{l1} r_{l2} \cos (\theta_{2} - \theta_{1} + \gamma_{\psi } )]/2 \\ \end{aligned}$$

(41)

$$\begin{aligned} a_{12} & = \eta_{1} \eta_{4} [\mu_{1} \cos (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \cos (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l4} \cos (2\alpha_{0} - \theta_{1} - \theta_{4} + \gamma_{\psi } )]/2 \\ & \quad + \eta_{1} \eta_{3} [\mu_{1} \cos (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \cos (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l3} \cos (2\alpha_{0} - \theta_{1} - \theta_{3} + \gamma_{\psi } )]/2, \\ \end{aligned}$$

(42)

$$\begin{aligned} a_{21} & = \eta_{4} \eta_{1} [\mu_{1} \cos (2\alpha_{0} - \gamma_{x} ) - \mu_{2} \cos (2\alpha_{0} - \gamma_{y} ) - \mu_{3} r_{l4} r_{l1} \cos (2\alpha_{0} - \theta_{1} - \theta_{4} - \gamma_{\psi } )]/2 \\ & \quad + \eta_{4} \eta_{2} [\mu_{1} \cos (2\alpha_{0} - \gamma_{x} ) - \mu_{2} \cos (2\alpha_{0} - \gamma_{y} ) - \mu_{3} r_{l4} r_{l2} \cos (2\alpha_{0} - \theta_{2} - \theta_{4} - \gamma_{\psi } )]/2, \\ \end{aligned}$$

(43)

$$\begin{aligned} a_{22} & = \eta_{4}^{2} [\mu_{1} \cos \gamma_{x} + \mu_{2} \cos \gamma_{y} + \mu_{3} r_{l4}^{2} \cos \gamma_{\psi } ]/2 \\ & \quad + \eta_{4} \eta_{3} [\mu_{1} \cos \gamma_{x} + \mu_{2} \cos \gamma_{y} + \mu_{3} r_{l4} r_{l3} \cos (\theta_{4} - \theta_{3} + \gamma_{\psi } )]/2, \\ \end{aligned}$$

(44)

$$\begin{aligned} b_{11} & = \eta_{1}^{2} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l1}^{2} \sin \gamma_{\psi } ] \\ & \quad + \eta_{1} \eta_{2} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l1} r_{l2} \sin (\theta_{2} - \theta_{1} + \gamma_{\psi } )], \\ \end{aligned}$$

(45)

$$\begin{aligned} b_{12} & = \eta_{1} \eta_{4} \omega_{0} [\mu_{1} \sin (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \sin (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l4} \sin (2\alpha_{0} - \theta_{1} - \theta_{4} + \gamma_{\psi } )] \\ & \quad + \eta_{1} \eta_{3} \omega_{0} [\mu_{1} \sin (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \sin (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l3} \sin (2\alpha_{0} - \theta_{1} - \theta_{3} + \gamma_{\psi } )], \\ \end{aligned}$$

(46)

$$\begin{aligned} b_{13} & = \eta_{1} \eta_{3} \omega_{0} [\mu_{1} \cos (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \cos (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l3} \cos (2\alpha_{0} - \theta_{1} - \theta_{3} + \gamma_{\psi } )]/2 \\ & \quad + \eta_{1} \eta_{4} \omega_{0} [\mu_{1} \cos (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \cos (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l4} \cos (2\alpha_{0} - \theta_{1} - \theta_{4} + \gamma_{\psi } )]/2, \\ \end{aligned}$$

(47)

$$\begin{aligned} b_{21} & = \eta_{4} \eta_{1} \omega_{0} [ - \mu_{1} \sin (2\alpha_{0} - \gamma_{x} ) + \mu_{2} \sin (2\alpha_{0} - \gamma_{y} ) + \mu_{3} r_{l4} r_{l1} \sin (2\alpha_{0} - \theta_{1} - \theta_{4} - \gamma_{\psi } )] \\ & \quad + \eta_{4} \eta_{2} \omega_{0} [ - \mu_{1} \sin (2\alpha_{0} - \gamma_{x} ) + \mu_{2} \sin (2\alpha_{0} - \gamma_{y} ) + \mu_{3} r_{l4} r_{l2} \sin (2\alpha_{0} - \theta_{2} - \theta_{4} - \gamma_{\psi } )], \\ \end{aligned}$$

(48)

$$\begin{aligned} b_{22} & = \eta_{4}^{2} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l4}^{2} \sin \gamma_{\psi } ] \\ & \quad + \eta_{4} \eta_{3} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l4} r_{l3} \sin (\theta_{4} - \theta_{3} + \gamma_{\psi } )], \\ \end{aligned}$$

(49)

$$\begin{aligned} b_{23} & = \eta_{4} \eta_{1} \omega_{0} [ - \mu_{1} \cos (2\alpha_{0} - \gamma_{x} ) + \mu_{2} \cos (2\alpha_{0} - \gamma_{y} ) + \mu_{3} r_{l4} r_{l1} \cos (2\alpha_{0} - \theta_{1} - \theta_{4} - \gamma_{\psi } )]/2 \\ & \quad + \eta_{4} \eta_{2} \omega_{0} [ - \mu_{1} \cos (2\alpha_{0} - \gamma_{x} ) + \mu_{2} \cos (2\alpha_{0} - \gamma_{y} ) + \mu_{3} r_{l4} r_{l2} \cos (2\alpha_{0} - \theta_{2} - \theta_{4} - \gamma_{\psi } )]/2, \\ \end{aligned}$$

(50)

$$\begin{aligned} c_{1} & = \frac{1}{2}\{ \eta_{1}^{2} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l1}^{2} \sin \gamma_{\psi } ] \\ & \quad + \eta_{1} \eta_{2} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l1} r_{l2} \sin (\theta_{2} - \theta_{1} + \gamma_{\psi } )] \\ & \quad + \eta_{1} \eta_{3} \omega_{0} [\mu_{1} \sin (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \sin (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l3} \sin (2\alpha_{0} - \theta_{1} - \theta_{3} + \gamma_{\psi } )] \\ & \quad + \eta_{1} \eta_{4} \omega_{0} [\mu_{1} \sin (2\alpha_{0} + \gamma_{x} ) - \mu_{2} \sin (2\alpha_{0} + \gamma_{y} ) - \mu_{3} r_{l1} r_{l4} \sin (2\alpha_{0} - \theta_{1} - \theta_{4} + \gamma_{\psi } )]\} , \\ \end{aligned}$$

(51)

$$\begin{aligned} c_{2} & = \frac{1}{2}\{ \eta_{4} \eta_{1} \omega_{0} [ - \mu_{1} \sin (2\alpha_{0} - \gamma_{x} ) + \mu_{2} \sin (2\alpha_{0} - \gamma_{y} ) + \mu_{3} r_{l4} r_{l1} \sin (2\alpha_{0} - \theta_{1} - \theta_{4} - \gamma_{\psi } )] \\ & \quad + \eta_{4} \eta_{2} \omega_{0} [ - \mu_{1} \sin (2\alpha_{0} - \gamma_{x} ) + \mu_{2} \sin (2\alpha_{0} - \gamma_{y} ) + \mu_{3} r_{l4} r_{l2} \sin (2\alpha_{0} - \theta_{2} - \theta_{4} - \gamma_{\psi } )] \\ & \quad + \eta_{4}^{2} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l4}^{2} \sin \gamma_{\psi } ] \\ & \quad + \eta_{4} \eta_{3} \omega_{0} [\mu_{1} \sin \gamma_{x} + \mu_{2} \sin \gamma_{y} + \mu_{3} r_{l4} r_{l3} \sin (\theta_{4} - \theta_{3} + \gamma_{\psi } )]\} , \\ \end{aligned} ,$$

(52)

withª

$$\mu_{1} = r_{m} /\mu_{x}, \quad\mu_{2} = r_{m} /\mu_{y}, \quad \mu_{3} = r_{m} /\mu_{\psi }, \quad \bar{T}_{e1} = T_{e01} - k_{e01} \bar{\varepsilon }_{1}\quad \bar{T}_{e4} = T_{e04} - k_{e04} \bar{\varepsilon }_{2}$$

where T_e01 = T_e1(ω₀), T_e04 = T_e4(ω₀), k_e01 and k_e04 are calculated by substituting parameter values of motors in the flowing equation

$$\begin{aligned} k_{e0} & = \frac{{3n_{p} U_{TH}^{2} R_{r} }}{{(\omega_{e} - n_{p} \omega )^{2} [(R_{s} + R_{r} \omega_{e} /(\omega_{e} - n_{p} \omega ))^{2} + (X_{s} + X_{r} )^{2} ]}} \\ & - \frac{{6n_{p} U_{TH}^{2} R_{r}^{2} (R_{s} + R_{r} \omega_{e} /(\omega_{e} - n_{p} \omega ))\omega_{e} }}{{(\omega_{e} - n_{p} \omega )^{3} [(R_{s} + R_{r} \omega_{e} /(\omega_{e} - n_{p} \omega ))^{2} + (X_{s} + X_{r} )^{2} ]^{2} }} \\ \end{aligned}$$

(53)

Appendix 3: The terms of Eq. (26)

$$d_{1} = \frac{{ - \left( {\eta_{1} + a_{11} } \right)\chi_{22} - a_{12} b_{21} - a_{21} b_{12} - \left( {\eta_{2} + a_{22} } \right)\chi_{11} }}{{\left( {\eta_{1} + a_{11} } \right)\left( {\eta_{2} + a_{22} } \right) - a_{12} a_{21} }}$$

(54)

$$d_{2} = \frac{{ - \left( {\eta_{1} + a_{11} } \right)b_{23} \omega_{0} - a_{12} b_{23} \omega_{0} + a_{21} b_{13} \omega_{0} + \left( {\eta_{2} + a_{22} } \right)b_{13} \omega_{0} + 2\chi_{11} \chi_{22} - 2b_{12} b_{21} }}{{2\left( {\eta_{1} + a_{11} } \right)\left( {\eta_{2} + a_{22} } \right) - 2a_{12} a_{21} }}$$

(55)

$$d_{3} = \frac{{ - \omega_{0} b_{12} b_{23} + \omega_{0} b_{13} b_{21} - \omega_{0} b_{13} \chi_{22} + \omega_{0} b_{23} \chi_{11} }}{{2\left( {\eta_{1} + a_{11} } \right)\left( {\eta_{2} + a_{22} } \right) - 2a_{12} a_{21} }}$$

(56)