Numerical analysis of stress-state-dependent damage and failure behavior of ductile steel based on biaxial experiments

Abstract

The paper deals with a numerical model to investigate the influence of stress state on damage and failure in the ductile steel X5CrNi18-10. The numerical analysis is based on an anisotropic continuum damage model taking into account yield and damage criteria as well as evolution equations for plastic and damage strain rate tensors. Results of numerical simulations of biaxial experiments with the X0- and the H-specimen presented. In the experiments, formation of strain fields are monitored by digital image correlation which can be compared with numerically predicted ones to validate the numerical model. Based on the numerical analysis the strain and stress quantities in selected parts of the specimens are predicted. Analysis of damage strain variables enables prediction of fracture lines observed in the tests. Stress measures are used to explain different stress-state-dependent damage and failure mechanisms on the micro-level visualized on fracture surfaces by scanning electron microscopy.

1 Introduction

During the last years the use of high quality ductile metals has been remarkably increased due to demands and requirements of the customers. For example, reduction in energy consumption, improved cost efficiency and enforced safety pretensions have caused intensive research activities to fulfill environmental, economic and material strength demands. In products of modern engineering disciplines material properties are enhanced to reduce localization of irreversible deformations as well as damage and failure in material samples under various multi-axial loading conditions. Thus, analysis of new engineering materials must be based on accurately predictive and practically applicable constitutive models and corresponding efficient, robust and accurate numerical algorithms.

It has been observed in many experiments and practical applications that loading and deformation of material elements often leads to localized bands of inelastic strains accompanied by damage and fracture processes on the micro-level [3, 4, 29]. Growth of these micro-mechanisms can then produce macro-cracks as a cursor of final failure of structures. These damage and fracture processes acting on the micro-scale depend on the stress state in a material element. For example, tensile loading with high positive stress triaxialities causes growth and coalescence of micro-pores whereas in shear and compressive loading micro-shear-cracks occur. In addition, combination of growth of voids and evolution of micro-shear-cracks are observed for moderate positive stress triaxialities and no damage has been observed in experiments with high negative stress triaxialities [2, 12]. Thus, development of appropriate phenomenological continuum damage models and accurate numerical algorithms must be based on detailed analysis of these stress-state-dependent phenomena on both the micro- and the macro-scale. This demands a sophisticated experimental program and corresponding numerical analyses to reveal the connection between stress states and damage processes.

Various research groups performed during the last decades experiments with different specimens taken from thin metal sheets and corresponding numerical simulations to investigate stress-state-dependent material behavior. Uniaxial tests with specimens with various geometries are used to examine deformation and failure behavior for positive and nearly zero stress triaxialities [1, 2, 5, 11, 18, 20, 22,23,24, 27, 33]. Since only a small range of stress states can be covered in tests with these uniaxially loaded specimens further experiments with biaxially loaded ones have been proposed. For example, details of anisotropic plastic behavior or limit strain at fracture are analyzed by biaxial tests with different cruciform specimens [19, 26, 30, 35]. In addition, further aspects to design geometries of biaxially loaded specimens have been discussed [10, 15, 21] to study stress-state-dependent damage and failure mechanisms.

After the experiments scanning electron microscopy can be used to analyze the fracture surfaces and to reveal stress-state-dependent fracture processes on the micro-scale [10, 15]. However, these pictures only show the final status of fracture and do not deliver information on the damage process during the experiment. An alternative way to investigate formation of damage during the tests is the numerical analysis of differently loaded representative volume elements. For example, numerical studies on the micro-level with three-dimensionally loaded void-containing unit cells have been performed to detect stress-state-dependent damage and fracture mechanisms caused by formation of individual micro-defects and their interactions [6, 12, 13, 16, 17, 25, 34]. The results are used to propose damage criteria and evolution equations for macroscopic damage strain rate tensors.

In the present paper, detailed results of further biaxial experiments and corresponding numerical simulations on specimens taken from thin steel X5CrNi18-10 sheets covering a wide range of stress states are presented and discussed. For motivation, a continuum damage model using damage mode functions based on experiments and numerical calculations on the micro-scale is presented. Results of numerical analysis of biaxial experiments with the recently developed cruciform X0- and H-specimen are discussed with special focus on the effect of stress state on material behavior. Evolution of strain and stress measures in critical regions of the specimen are computed where damage and fracture are expected to occur. They are used to predict damage processes and fracture mechanisms on both the micro- and the macro-level.

2 Continuum damage model

Numerical prediction of inelastic deformation, damage and fracture behavior is based on the phenomenological continuum model [7, 9] taking into account experimental observations [10, 11, 14, 18] and results from numerical investigations on the micro-scale [12, 13, 16]. The theoretical framework is briefly summarized in the present paper to demonstrate the necessity of analysis of multiaxial experiments with various loading conditions to propose and to validate evolution equations for plastic and damage strain rate tensors.

The continuum damage model is based on the introduction of damaged and corresponding fictitious undamaged configurations [31, 32, 36, 37]. In the kinematics, the strain rate tensor is additively decomposed into elastic, ${{\dot{\mathbf{H}}}}^{el}$, effective plastic, ${{\dot{\bar{\mathbf{H}}}}}^{pl}$, and damage parts, ${{ \dot{\mathbf{H}}}}^{da}$. Thus, a kinematic description of damage is proposed and the damage strain rate tensor is taken to be an appropriate damage variable representing the volume fraction of micro-defects as well as taking into account the effect of their current shape and orientation on the macroscopic material behavior.

In the effective undamaged configurations, the effective Kirchhoff stress tensor

$$\begin{aligned} {{\bar{\mathbf{T}}}} = 2 G \; {\mathbf {A}}^{el} + \left( K - \frac{2}{3} G \right) \; \mathrm{tr} \mathbf{A}^{el} \; \mathbf{1} \end{aligned}$$

(1)

is introduced where G and K are the constant shear and bulk modulus of the undamaged matrix material, respectively, and $\mathbf{A}^{el}$ is the elastic part of the strain tensor. In addition, onset of plastic yielding in the matrix material is governed by the yield criterion

$$\begin{aligned} f^{pl} \left( \bar{I}_1, \bar{J}_2 , c\right) \, = \, \sqrt{\bar{J}_2} \, - \, c \, \left( 1 \, - \, \frac{a}{c} \bar{I}_1\right) \, = \, 0, \end{aligned}$$

(2)

with the effective first and second deviatoric stress invariants $\bar{I}_1 = \mathrm{tr} {\bar{\mathbf{T}}}$ and $\bar{J}_2 = \frac{1}{2} \, \mathrm{dev} {{\bar{\mathbf{T}}}} {{\cdot }} \mathrm{dev} {{\bar{\mathbf{T}}}}$, the equivalent yield stress c of the matrix material and the hydrostatic stress coefficient a.

Furthermore, the effective plastic strain rate

$$\begin{aligned} {{\dot{\bar{\mathbf{H}}}}}^{pl} \, = \, \dot{\upgamma } \, {{\bar{\mathbf{N}}}} \; \end{aligned}$$

(3)

describes evolution of plastic deformations where ${{\bar{\mathbf{N}}}} \, = \, \frac{1}{\sqrt{2 \; \bar{J}_2}} \; \mathrm{dev} {{\bar{\mathbf{T}}}}$ denotes the normalized deviatoric stress tensor and $\dot{\upgamma } \, = \, {{\bar{\mathbf{N}}}} \mathbf{\cdot } {{\dot{\bar{\mathbf{H}}}}}^{pl}$ is the equivalent plastic strain rate measure representing the amount of increase of plastic deformations.

Moreover, the damaged configurations are considered to characterize the behavior of the anisotropically damaged ductile metal. The elastic behavior is also influenced by damage [28] and, therefore, the elastic constitutive equation takes into account both the elastic and the damage strain tensors, $\mathbf{A}^{el}$ and $\mathbf{A}^{da}$. Then, the Kirchhoff stress tensor is written in the form

$$\begin{aligned} \mathbf{T} =&2&\left( G + \eta _2 \; \mathrm{tr} \mathbf{A}^{da} \right) \; \mathbf{A}^{el}\nonumber \\+ & {} \left( K - \frac{2}{3} G + 2 \eta _1 \; \mathrm{tr} \mathbf{A}^{da} \right) \mathrm{tr} \mathbf{A}^{el} \; \mathbf{1} \; \nonumber \\+ & {} \eta _3 \; \left( \mathbf{A}^{da} \cdot \mathbf{A}^{el} \right) \; \mathbf{1} \; \nonumber \\+ & {} \eta _3 \; \mathrm{tr} \mathbf{A}^{el} \mathbf{A}^{da} + \eta _4 \; \left( \mathbf{A}^{el} \mathbf{A}^{da} + \mathbf{A}^{da} \mathbf{A}^{el} \right) \, \end{aligned}$$

(4)

with the additional constitutive parameters $\eta _1, \dots , \eta _4$ modeling deterioration of the macroscopic elastic material properties caused by damage and fracture processes on the micro-level. Onset of damage is modeled by the damage criterion

$$\begin{aligned} f^{da} = \alpha I_1 + \beta \sqrt{J_2} - \sigma = 0 \end{aligned}$$

(5)

expressed in terms of the stress invariants ${I}_1 = \mathrm{tr} \mathbf{{T}}$ and ${J}_2 = \frac{1}{2} \, \mathrm{dev} \mathbf{{T}} {\cdot } \mathrm{dev} \mathbf{{T}}$. In Eq. (5) the equivalent damage stress measure $\sigma$ is introduced corresponding to material toughness to micro-defect propagation and the variables $\alpha$ and $\beta$ represent damage mode parameters taking into account the different damage mechanisms acting on the micro-level: void-growth-dominated modes for large positive triaxialities, micro-shear-crack modes for negative stress triaxialities, and mixed modes (simultaneous growth of voids and formation of micro-shear-cracks) for moderate positive stress triaxialities. These damage mode parameters have been identified by micro-mechanical numerical analysis considering void-containing representative volume elements under different three-dimensional loading conditions [12, 13, 16]. They have been expressed in terms of the stress intensity $\sigma _{eq} = \sqrt{3 J_2}$ (von Mises equivalent stress), the stress triaxiality

$$\begin{aligned} \eta = \frac{\sigma _m}{\sigma _{eq}} = \frac{I_1}{3 \sqrt{3 J_2}} \end{aligned}$$

(6)

defined as the ratio of the mean stress $\sigma _m$ and the von Mises equivalent stress $\sigma _{eq}$ as well as on the Lode parameter

$$\begin{aligned} \omega = \frac{2 {T}_2 - {T}_1 - {T}_3}{{T}_1 - {T}_3} \; \; \; \mathrm{with} \; {T}_1 \ge {T}_2 \ge {T}_3 \end{aligned}$$

(7)

here expressed in terms of the principal components of the Kirchhoff stress tensor ${T}_1$, ${T}_2$ and ${T}_3$.

In addition, the damage strain rate tensor is expressed in the form

$$\begin{aligned} {{\dot{\mathbf{H}}}}^{da} \, = \, \dot{\mu } \; \left( \bar{\alpha } \; \frac{1}{\sqrt{3}}\, \mathbf{1} + \bar{\beta } \; \mathbf{N} + \bar{\delta } \; \mathbf{M} \right) \end{aligned}$$

(8)

with the equivalent damage strain rate measure $\dot{\mu }$ describing the amount of increase in irreversible damage strains as well as the normalized stress related deviatoric tensors $\mathbf{N} = \frac{1}{2 \sqrt{J_2}} \, \mathrm{dev}{\tilde{\mathbf{T}}}$ and $\mathbf{M} = \frac{1}{\parallel \mathrm{dev}{\tilde{\mathbf{S}}} \parallel } \, \mathrm{dev}{\tilde{\mathbf{S}}}$ with

$$\begin{aligned} \mathrm{dev}{\tilde{\mathbf{S}}} = \mathrm{dev}{\tilde{\mathbf{T}}} \; \mathrm{dev}{\tilde{\mathbf{T}}} - \frac{2}{3} \; J_2 \; \mathbf{1} \end{aligned}$$

(9)

where ${\tilde{\mathbf{T}}}$ is the stress tensor work-conjugate to the damage strain rate tensor (8). In Eq. (9) the parameters $\bar{\alpha }$, $\bar{\beta }$ and $\bar{\delta }$ are kinematic variables characterizing the portion of volumetric and isochoric damage-based deformations. These parameters are also micro-mechanically motivated and are associated to the different damage and fracture processes on the micro-scale discussed above. They have been determined by numerical calculations on the micro-scale [12, 13, 16].

3 Numerical aspects

The numerical simulations have been performed using the finite element program ANSYS enhanced by a user-defined material subroutine. This subroutine has been developed based on the constitutive equations of the proposed continuum damage model. Integration of the evolution equations of the plastic (3) and damage strains (8) is performed by the inelastic predictor–elastic corrector method [8]. This leads to fast convergence and stability of the numerical algorithm until damage reaches a critical state indicating onset of macro-cracking. The respective specimens have been discretized by eight-node-elements of type Solid185 with linear displacement fields to quantify the three-dimensional strain fields as well as the stresses and the damage quantities in critical regions of the specimens. Geometries of the X0- and H-specimen as well as their finite-element-discretization are shown in Fig. 1. The meshes are based on 86,400 elements for the X0-specimen and 139,320 elements for the H-specimen, respectively, and show remarkable refinement in the notches where high gradients of strain and stress variables are expected to occur. In preliminary studies results with different meshes have been examined and the meshes simulating the localized strain fields in an accurate manner have been chosen. The specimens are simultaneously loaded in direction 1 and 2 and the displacements of the red nodes are computed leading to the relative displacements $\varDelta u_1$ and $\varDelta u_2$ between the red points in axis 1 and 2, respectively.

Fig. 1

Geometry and finite element mesh of the X0- and H-specimen

For the numerical simulation material parameters are needed as input variables for the investigated low carbon steel X5CrNi18-10. Using the load–displacement-curve of a uniaxial tension test the elastic parameters are identified to be Young’s modulus $E =$ 180,000 MPa and Poisson’s ratio $\nu =$ 0.3 whereas the plastic hardening behavior is modeled by the Voce law

$$\begin{aligned} c ( \upgamma ) = c_0 + H_1 \upgamma + H_2 ( 1 - e^{(- n \upgamma )} ) \end{aligned}$$

(10)

with the initial yield strength $c_0 =$ 194 MPa, the hardening parameters $H_1 =$ 477 MPa and $H_2 =$ 184 MPa as well as the hardening exponent $n =$ 5.3. These parameters lead to excellent agreement of the numerical and experimental load–displacement-curves, see Fig. 2.

Fig. 2

Load–displacement-curve of the uniaxial tension test

The damage parameters in Eq. (4) are chosen to be $\eta _i = 150{,}000$ MPa for positive or zero stress triaxialities ($\eta \ge 0$) and $\eta _i = -150{,}000$ MPa for negative ones ($\eta < 0$) to achieve good agreement of numerically predicted and experimental load–displacement curves. The stress-state-dependent parameters in the damage criterion (5) and in the damage rule (8) have been identified by numerical simulations on the micro-level [12]: The damage mode parameter $\alpha$ is given by

$$\begin{aligned} \alpha (\eta ) = \left\{ \begin{array}{ll} 0 &{}\quad \hbox {for} \; \; \frac{-1}{3} \le \eta \le 0 \\ \frac{1}{3} &{}\quad \hbox {for} \; \; \eta > 0 \end{array}\right. \end{aligned}$$

(11)

whereas $\beta$ is taken to be the non-negative function

$$\begin{aligned} \beta (\eta , \, \omega ) = \beta _0 (\eta , \, \omega = 0) + \beta _{\omega } (\omega ) \ge 0, \end{aligned}$$

(12)

with

$$\begin{aligned} \beta _0 (\eta ) = \left\{ \begin{array}{ll} - 0.45 \, \eta + 0.85 &{}\quad \hbox {for} \; \; \frac{-1}{3} \le \eta \le 0 \\ - 1.28 \, \eta + 0.85 &{}\quad \hbox {for} \; \; \eta > 0 \end{array} \right. \end{aligned}$$

(13)

and

$$\begin{aligned} \beta _{\omega } (\omega ) = - 0.017 \, \omega ^3 - 0.065 \, \omega ^2 - 0.078 \, \omega . \end{aligned}$$

(14)

Furthermore, the non-negative parameter ${\bar{\alpha }} \ge 0$ characterizing the amount of volumetric damage strain rates caused by isotropic growth of micro-defects is given by the relation

$$\begin{aligned} {\bar{\alpha }} (\eta ) = \left\{ \begin{array}{ll} 0 &{}\quad \hbox {for} \; \; \eta< 0.09864 \\ - 0.07903 + 0.80117 \, \eta &{}\quad \hbox {for} \; \; 0.09864 \le \eta \le 1 \\ 0.49428 + 0.22786 \, \eta &{}\quad \hbox {for} \; \; 1< \eta \le 2 \\ 0.87500 + 0.03750 \, \eta &{}\quad \hbox {for} \; \; 2 < \eta \le 3.33333 \\ 1 &{}\quad \hbox {for} \; \; \eta > 3.33333. \end{array} \right. \end{aligned}$$

(15)

The parameter ${\bar{\beta }}$ characterizing the amount of anisotropic isochoric damage strain rates caused by evolution of micro-shear-cracks is given by the relation

$$\begin{aligned} {\bar{\beta }} (\eta , \, \omega ) = \left\{ \begin{array}{ll} 0.94840 + 0.11965 \, \eta + \bar{\beta }_{\omega }&{}\quad \hbox {for} \; \; \frac{-1}{3} \le \eta \le \frac{1}{3} \\ 1.14432 - 0.46810 \, \eta + \bar{\beta }_{\omega }&{}\quad \hbox {for} \; \; \frac{1}{3}< \eta \le \frac{2}{3} \\ 1.14432 - 0.46810 \, \eta &{}\quad \hbox {for} \; \; \frac{2}{3}< \eta \le 2 \\ 0.52030 - 0.15609 \, \eta &{}\quad \hbox {for} \; \; 2 < \eta \le \frac{10}{3} \\ 0 &{}\quad \hbox {for} \; \; \eta > \frac{10}{3} \end{array} \right. \end{aligned}$$

(16)

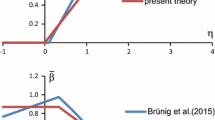
with $\bar{\beta }_{\omega } = ( - 0.0252 + 0.0378 \, \eta ) ( 1 - \omega ^2 )$. In addition, the parameter ${\bar{\delta }}$ also corresponding to the anisotropic damage strain rates caused by the formation of micro-shear-cracks is given by

$$\begin{aligned} {\bar{\delta }} (\eta , \, \omega ) = \left\{ \begin{array}{ll} f_{\delta } ( \eta ) \, {\bar{\delta }}_{\omega } ( \omega ) &{}\quad \hbox {for} \; \; \frac{-1}{3} \le \eta \le \frac{2}{3} \\ 0 &{}\quad \hbox {for} \; \; \eta > \frac{2}{3} \end{array} \right. \end{aligned}$$

(17)

with $f_{\delta } ( \eta ) = - 0.12936 + 0.19404 \, \eta$ and ${\bar{\delta }}_{\omega } ( \omega ) = 1 - \omega ^2$.

4 Numerical analysis of biaxial experiments

The X0-specimen enables analysis of tension dominated stress states with different loading conditions superimposed by small shear effects. On the other hand, with the H-specimen shear dominated stress states occur which can be superimposed with tensile or compressive loads leading to further stress combinations and, therefore, to alternative damage and failure processes on the micro-level. Thus, the proposed experimental-numerical program with different load ratios can be used to study stress-state-dependent behavior in detail.

4.1 X0-specimen

The inelastic deformation as well as damage and failure behavior of the X0-specimen are analyzed for three different loading conditions. For the load ratio $F_1 : F_2 = 1 : 1$ the forces in axis 1 and 2 are simultaneously increased by the same level leading to tensile behavior in the notches of the X0-specimen. For $F_1 : F_2 = 0.5 : 1$ combined tension-shear behavior is expected to occur whereas $F_1 : F_2 = -0.5 : 1$ will lead to more predominant shear behavior in the notched regions.

Fig. 3

Load–displacement-curves of the X0-specimen

The load–displacement-curves $F_1 ( \varDelta u_1)$ for the different load ratios are shown in Fig. 3. For the load ratio $F_1 : F_2 = 1 : 1$ the load maximum of about $F_1 = 12$ kN is reached and the final displacement is $\varDelta u_1 = 2.2$ mm. In the experiment with $F_1 : F_2 = 0.5 : 1$ the load maximum is only about $F_1 = 8$ kN and the displacement only reaches $\varDelta u_1 = -0.5$ mm. For the load ratio $F_1 : F_2 = -0.5 : 1$ the behavior is more ductile with load maximum of about $F_1 = -8$ kN and the displacement reaches $\varDelta u_1 = -8$ mm. In all cases the numerical simulation nicely predicts the experimental load–displacement curves.

Fig. 4

a Maximum and b minimum principal strains of the X0-specimen for (1) $F_1 : F_2 = 1 : 1$, (2) $F_1 : F_2 = 0.5 : 1$, (3) $F_1 : F_2 = -0.5 : 1$ (left: experiment, right: numerical simulation)

Since the load–displacement-curves discussed above only characterize the global behavior of the specimen more detailed analysis is required. For example, strain fields on the surfaces of the notches can be studied in detail based on the experimentally obtained ones by digital image correlation technique. In Fig. 4 experimental (left) and numerically predicted (right) strain fields are shown for the different loading conditions where the maximum and minimum principal strains, $A_{max}$ and $A_{min}$, are monitored at the displacement stage $\frac{2}{3} \varDelta u_1$. In particular, for the load ratio $F_1 : F_2 = 1 : 1$ the maximum principal strain reaches $A_{max} = 0.56$ at the boundary of the notch and a vertical band of localized strains can be seen in Fig. 4a1. This numerically predicted behavior agrees with the experimentally observed one but in the experiment the band is less localized. The minimum principal strain at the notch boundaries is $A_{min} = -0.25$ and the numerically predicted field nicely corresponds to the experimental one, see Fig. 4b1. For the load ratio $F_1 : F_2 = 0.5 : 1$ the maximum principal strain $A_{max}$ reaches 0.6 at the notch boundaries and a localized band with orientation from top left to bottom right can be seen (Fig. 4a2). The numerically predicted distribution agrees well with the experimental one. The minimum principal strain reaches $A_{min} = -0.29$ and also good agreement of experimental and numerical strain field can be seen in Fig. 4b2. For the loading condition $F_1 : F_2 = -0.5 : 1$ the principal strains reach the highest values in the center of the notch surface. The maximum one is 0.74 (Fig. 4a3) and the minimum one reaches $-0.65$ (Fig. 4b3) which are only a bit higher than the experimental ones. In both cases more widespread bands occur with orientation from top right to bottom left. From Fig. 4 it can be concluded that depending on the loading conditions different strain behavior occurs and the numerical simulations well predict the experimental distributions and values of the strain fields. This can be seen as validation of the theoretical and numerical approach presented in this paper.

Fig. 5

Failure behavior: a numerically predicted equivalent damage strain $\mu$ (left: surface, right: cross section), b fracture line for (1) $F_1 : F_2 = 1 : 1$, (2) $F_1 : F_2 = 0.5 : 1$, (3) $F_1 : F_2 = -0.5 : 1$ (X0-specimen)

Fig. 6

a Stress triaxiality $\eta$ and Lode parameter $\omega$, b SEM pictures of the fracture surface for (1) $F_1 : F_2 = 1 : 1$, (2) $F_1 : F_2 = 0.5 : 1$, (3) $F_1 : F_2 = -0.5 : 1$ (X0-specimen)

The equivalent damage strain measure $\mu$ [see Eq. (8)] characterizes the amount of damage in the material. Figure 5 shows the distribution of $\mu$ on the surface of the notch as well as in the cross section shortly before fracture happens and they are compared with photos of the fracture lines of the failed X0-specimen. In particular, for the load ratio $F_1 : F_2 = 1 : 1$ a small band of damaged points can be seen in Fig. 5a1 with maximum values in the center of the notch $\mu =$ 0.11. This indicates that the macro-crack will start in this point and then runs to the surfaces. The fracture line (Fig. 5b1) is vertical corresponding to the distribution of damage. For the loading condition $F_1 : F_2 = 0.5 : 1$ a slightly diagonal band can be seen in Fig. 5a2 with a non-symmetric distribution in the cross section. The maximum value reaches $\mu =$ 0.13. The distribution of $\mu$ also agrees with the fracture line shown in Fig. 5b2. Loading with $F_1 : F_2 = -0.5 : 1$ leads to a diagonal band of the equivalent damage strain $\mu$ from top right to bottom left with the maximum value of $\mu =$ 0.013 in the center of the cross section, see Fig. 5a3. This damage distribution leads to the diagonal fracture line shown in Fig. 5b3. It can be concluded that the distribution of the scalar damage parameter $\mu$ agrees well with the fracture line whose geometry remarkably depends on the loading conditions of the X0-specimen.

It is well known that the stress state affects the damage and failure processes on the micro-level and, therefore, the distribution and amount of the stress triaxiality $\eta$ and the Lode parameter $\omega$ are examined in detail. Figure 6 shows these stress parameters as well as SEM pictures of the fracture surfaces of differently loaded X0-specimens. In particular, for the load ratio $F_1 : F_2 = 1 : 1$ very high stress triaxialities up to $\eta =$ 0.68 are numerically predicted in the center of the notch, see Fig. 6a1. The corresponding Lode parameter is $\omega = -0.5$. These stress parameters are typical for tension dominated stress states caused by simultaneous tensile loading in both axes 1 and 2. For this loading case, in the SEM picture (Fig. 6b1) remarkably large voids can be seen with vertical (out-of-picture) orientation and dimples leading to this typical fracture mode. For the loading condition $F_1 : F_2 = 0.5 : 1$ Fig. 6a2 shows the stress triaxiality $\eta =$ 0.57 and the Lode parameter $\omega = -0.7$ which are numerically predicted in the center of the notch. Thus, the hydrostatic tensile stress is smaller compared to the first load ratio which can also be seen in the SEM picture in Fig. 6b2. The damage mechanism is dominated by small voids which are slightly sheared to the left side. This behavior is typical for tension dominated stress states with small amount of shear which is caused by this load ratio $F_1 : F_2 = 0.5 : 1$ in the center of the X0-specimen. On the other hand, for the load ratio $F_1 : F_2 = -0.5 : 1$ the stress triaxiality is only $\eta =$ 0.2 and the Lode parameter is $\omega = -0.4$ in the center of the notch (Fig 6a3). This shear-dominated stress state leads to formation of some voids which are remarkably sheared as well as to formation of micro-shear-cracks as can be seen in Fig. 6b3. Thus, the predicted stress triaxialities in critical regions of the specimen can be used to predict the damage and fracture processes acting on the micro-level leading to final failure.

4.2 H-specimen

The inelastic deformation as well as damage and failure behavior of the H-specimen are analyzed for three different loading conditions. For the load ratio $F_1 : F_2 = 1 : 0$ only the force in axis 1 is increased leading to tensile behavior in the notches of the H-specimen. For $F_1 : F_2 = 1 : 1$ the forces in axis 1 and 2 are simultaneously increased by the same level leading to combined tension-shear behavior whereas $F_1 : F_2 = -0.5 : 1$ will lead to shear behavior with superimposed compression in the notched regions.

Fig. 7

Load–displacement-curves of the H-specimen

The load–displacement-curves $F_1 ( \varDelta u_1)$ for the different load ratios are shown in Fig. 7. For the load ratio $F_1 : F_2 = 1 : 0$ the load maximum of about $F_1 = 19$ kN is reached and the final displacement is $\varDelta u_1 = 1.9$ mm. In the experiment with $F_1 : F_2 = 1 : 1$ the load maximum is only about $F_1 = 13$ kN and the displacement only reaches $\varDelta u_1 = 0.68$ mm. For the load ratio $F_1 : F_2 = -0.5 : 1$ the load maximum of about $F_1 = -7.5$ kN is reached and the displacement is $\varDelta u_1 = -1.4$ mm. Deviations in the experimental curves for tensile loading in direction 1 can be seen which might be caused by inhomogeneities in material micro-structure especially in the notched regions. However, the numerical simulation is able to predict the global behavior and may be seen as the mean curve of the experimental ones.

Fig. 8

a Maximum and b minimum principal strains of the H-specimen for (1) $F_1 : F_2 = 1 : 0$, (2) $F_1 : F_2 = 1 : 1$, (3) $F_1 : F_2 = -0.5 : 1$ (left: experiment, right: numerical simulation)

In addition, strain fields on the surfaces of the notches can be examined in detail based on the experimentally obtained ones by digital image correlation technique. In Fig. 8 experimental (left) and numerically predicted (right) strain fields are shown for the different loading conditions where the maximum and minimum principal strains, $A_{max}$ and $A_{min}$, are monitored at the displacement stage $\frac{2}{3} \varDelta u_1$. In particular, for the load ratio $F_1 : F_2 = 1 : 0$ the maximum principal strain reaches $A_{max} =$ 0.60 in the notch and a vertical band of localized strains can be seen in Fig. 8a1. This numerically predicted behavior agrees with the experimentally observed one but in the experiment the maxima are slightly smaller and the numerically predicted strain band is more localized. The minimum principal strain at the notch boundaries is $A_{min} = -0.26$ and the field nicely corresponds to the experimental one, see Fig. 8b1. For the load ratio $F_1 : F_2 = 1 : 1$ the maximum principal strain $A_{max}$ reaches 0.78 in the notch center and a localized band with vertical orientation can be seen (Fig. 8a2). The numerically predicted distribution agrees well with the experimental one and the experimental values are only marginally smaller. The minimum principal strain reaches $A_{min} = -0.50$ and also good agreement of experimental and numerical strain fields can be seen in Fig. 8b2. For the loading condition $F_1 : F_2 = -0.5 : 1$ the principal strains reach the highest values in the center of the notch surface. The maximum one is 0.62 (Fig. 8a3) and the minimum one reaches $-0.69$ (Fig. 8b3). In both cases localized bands occur with orientation from top right to bottom left. From Fig. 8 it can be concluded that depending on the loading conditions different strain behavior occurs and the numerical simulations well predict the experimental strain fields. This can be seen as validation of the theoretical and numerical approach presented in this paper.

Fig. 9

Failure behavior: a numerically predicted equivalent damage strain $\mu$ (left: surface, right: cross section), b fracture line for (1) $F_1 : F_2 = 1 : 0$, (2) $F_1 : F_2 = 1 : 1$, (3) $F_1 : F_2 = -0.5 : 1$ (H-specimen)

Fig. 10

a Stress triaxiality $\eta$ and Lode parameter $\omega$, b SEM pictures of the fracture surface for (1) $F_1 : F_2 = 1 : 0$, (2) $F_1 : F_2 = 1 : 1$, (3) $F_1 : F_2 = -0.5 : 1$ (H-specimen)

Figure 9 shows the distribution of the equivalent damage strain measure $\mu$ on the surface of the notch as well as in the cross section shortly before fracture happens and they are compared with the fracture lines of the failed H-specimen. In particular, for the load ratio $F_1 : F_2 = 1 : 0$ a small band of damaged points can be seen in Fig. 9a1 with maximum values at the boundaries of the notch $\mu =$ 0.16. This indicates that the macro-crack will start in these points and then runs through the area. The fracture line (Fig. 9b1) is vertical corresponding to the distribution of damage. For the loading condition $F_1 : F_2 = 1 : 1$ a vertical band can be seen in Fig. 9a2 with non-symmetric distribution in the cross section. The maximum value reaches $\mu = 0.015$. The distribution of $\mu$ also agrees with the fracture line shown in Fig. 9b2. Loading with $F_1 : F_2 = -0.5 : 1$ leads to a diagonal band of the equivalent damage strain $\mu$ from top right to bottom left with maximum of $\mu = 0.014$ at the boundaries of the cross section, see Fig. 9a3. This damage distribution leads to the diagonal fracture line shown in Fig. 9b3. It can again be concluded that the distribution of the scalar damage parameter $\mu$ agrees well with the fracture line whose geometry remarkably depends on the loading conditions of the H-specimen.

Furthermore, the distribution and amount of the stress triaxiality $\eta$ and the Lode parameter $\omega$ are investigated in detail. Figure 10 shows these stress parameters as well as SEM pictures of the fracture surfaces of differently loaded H-specimens. In particular, for the load ratio $F_1 : F_2 = 1 : 0$ very high stress triaxialities up to $\eta =$ 0.68 are numerically predicted in the center of the notch, see Fig. 10a1. The corresponding Lode parameter is $\omega = -0.5$. These stress parameters are typical for tension dominated stress states caused by tensile loading in axis 1 only. For this loading case, in the SEM picture (Fig. 10b1) remarkably large voids can be seen with vertical (out-of-picture) orientation and dimples leading to this typical fracture mode. For the loading condition $F_1 : F_2 = 1 : 1$ Fig. 10a2 shows the maximum stress triaxiality $\eta = 0.4$ with the corresponding Lode parameter $\omega = -1.0$. In the center of the notched region, the stress triaxiality $\eta = 0.3$ and the Lode parameter $\omega = -0.7$ are reached. Thus, the shear stress is dominant which can also be seen in the SEM picture in Fig. 10b2. The damage mechanism is dominated by micro-shear-cracks and only small voids which are sheared to the left side. This behavior is typical for shear-tension stress states. On the other hand, for the load ratio $F_1 : F_2 = -0.5 : 1$ the stress triaxiality is only $\eta = 0.0$ and the Lode parameter is $\omega = -0.2$ in the center of the notch (Fig 10a3). This shear-compression stress state leads to formation of micro-shear-cracks whereas preexisting voids have been compressed and sheared as can be seen in Fig. 10b3. Hence, the predicted stress triaxialities in critical regions of the specimen can be used to predict the damage and fracture processes acting on the micro-level leading to final failure.

5 Conclusions

In the paper a numerical model has been discussed to investigate the influence of stress state on damage and failure in the ductile steel X5CrNi18-10. The numerical analysis is based on a thermodynamically consistent anisotropic continuum damage model taking into account yield and damage criteria as well as evolution equations for plastic and damage strain rate tensors. An efficient and accurate numerical algorithm has been developed and implemented as a user-defined material subroutine in the finite element program ANSYS. Results of numerical simulations of biaxial experiments with the X0- and the H-specimen covering a wide range of stress states have been presented. In the experiments, formation of strain fields are monitored by digital image correlation which can be compared with numerically predicted ones to validate the numerical model. Based on the numerical analysis the strain and stress quantities in selected parts of the specimens have been predicted. Analysis of damage strain variables enables prediction of fracture lines observed in the tests. Numerically predicted stress fields are used to explain different stress-state-dependent damage mechanisms visualized on fracture surfaces by scanning electron microscopy. The paper clearly shows the efficient way to combine experiments and numerical analysis to understand the complex mechanisms of damage and failure in ductile metals on the micro- and the macro-level.