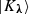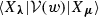Abstract
An explicit formula is obtained for the generalized Macdonald functions on the N-fold Fock tensor spaces, calculating a certain matrix element of a composition of several screened vertex operators. As an application, we prove the factorization property of the arbitrary matrix elements of the multi-valent intertwining operator (or refined topological vertex operator) associated with the Ding–Iohara–Miki algebra (DIM algebra) with respect to the generalized Macdonald functions, which was conjectured by Awata, Feigin, Hoshino, Kanai, Yanagida and one of the authors. Our proof is based on the combinatorial and analytic properties of the asymptotic eigenfunctions of the ordinary Macdonald operator of A-type, and the Euler transformation formula for Kajihara and Noumi’s multiple basic hypergeometric series. That factorization formula provides us with a reasonable algebraic description of the 5D (K-theoretic) Alday-Gaiotto–Tachikawa (AGT) correspondence, and the interpretation of the invariance under the preferred direction from the point of view of the \(SL(2,{\mathbb {Z}})\) duality of the DIM algebra.

Similar content being viewed by others
Notes
As
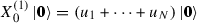 , the vectors
, the vectors 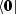 and
and 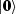 are not the ordinary vacuum states for the algebra \(\mathsf {U}(N)\) but highest weight vectors of highest weight \(\varvec{u}\). Hence, the function
are not the ordinary vacuum states for the algebra \(\mathsf {U}(N)\) but highest weight vectors of highest weight \(\varvec{u}\). Hence, the function  can be regarded as q-analogue of the \((n+2)\)-point conformal block.
can be regarded as q-analogue of the \((n+2)\)-point conformal block.
References
Awata, H., Feigin, B., Hoshino, A., Kanai, M., Shiraishi, J., Yanagida, S.: Notes on Ding–Iohara algebra and AGT conjecture. RIMS kokyuroku 1765, 12–32 (2011). arXiv:1106.4088 [math-ph]
Awata, H., Feigin, B., Hoshino, A., Kanai, M., Shiraishi, J., Yanagida, S.: (unpublished)
Alba, V.A., Fateev, V.A., Litvinov, A.V., Tarnopolskiy, G.M.: On combinatorial expansion of the conformal blocks arising from AGT conjecture. Lett. Math. Phys. 98, 33 (2011). arXiv:1012.1312 [hep-th]
Awata, H., Fujino, H., Ohkubo, Y.: Crystallization of deformed Virasoro algebra, Ding–Iohara–Miki algebra and 5D AGT correspondence. J. Math. Phys. 58(7), 071704 (2017). arXiv:1512.08016 [math-ph]
Awata, H., Feigin, B., Shiraishi, J.: Quantum algebraic approach to refined topological vertex. JHEP 1203, 041 (2012). arXiv:1112.6074 [hep-th]
Alday, L.F., Gaiotto, D., Tachikawa, Y.: Liouville correlation functions from four-dimensional gauge theories. Lett. Math. Phys. 91, 167–197 (2010). arXiv:0906.3219 [hep-th]
Awata, H., Kanno, H.: Instanton counting, Macdonald functions and the moduli space of D-branes. JHEP 0505, 039 (2005). arXiv:hep-th/0502061
Awata, H., Kanno, H.: Refined BPS state counting from Nekrasov’s formula and Macdonald functions. Int. J. Modern Phys. A 24(12), 2253–2306 (2009). arXiv:0805.0191 [hep-th]
Awata, H., Matsuo, Y., Odake, S., Shiraishi, J.: Collective field theory, Calogero–Sutherland model and generalized matrix models. Phys. Lett. B 347, 49 (1995). arXiv:hep-th/9411053
Awata, H., Yamada, Y.: Five-dimensional AGT conjecture and the deformed Virasoro algebra. JHEP 1001, 125 (2010). arXiv:0910.4431 [hep-th]
Awata, H., Yamada, Y.: Five-dimensional AGT relation and the deformed beta-ensemble. Prog. Theor. Phys. 124, 227–262 (2010). arXiv:1004.5122 [hep-th]
Braverman, A., Finkelberg, M., Shiraishi, J.: Macdonald polynomials, Laumon spaces and perverse coherent sheaves, perspectives in representation theory. Contemp. Math 610, 23–41 (2014)
Ding, J., Iohara, K.: Generalization of Drinfeld quantum affine algebras. Lett. Math. Phys. 41(2), 181–193 (1997). arXiv:q-alg/9608002
Feigin, B., Feigin, E., Jimbo, M., Miwa, T., Mukhin, E.: Quantum continuous \(\mathfrak{gl}_\infty \), semi-infinite construction of representations. Kyoto J. Math. 51(2), 337–364 (2011). arXiv:1002.3100 [math.QA]
Feigin, B., Hashizume, K., Hoshino, A., Shiraishi, J., Yanagida, S.: A commutative algebra on degenerate \({\mathbb{CP}}^1\) and Macdonald polynomials. J. Math. Phys. 50(9), 095215 (2009). arXiv:0904.2291 [math.CO]
Feigin, B., Hoshino, A., Shibahara, J., Shiraishi, J., Yanagida, S.: Kernel function and quantum algebra. RIMS kokyuroku 1689, 133–152 (2010). arXiv:1002.2485 [math.QA]
Feigin, B., Tsymbaliuk, A.: Equivariant \(K\)-theory of Hilbert schemes via shuffle algebra. Kyoto J. Math. 51(4), 831–854 (2011). arXiv:1002.2485 [math.QA]
Gasper, G., Rahman, M.: Basic Hypergeometric Series, vol. 96. Cambridge University Press, Cambridge (2004)
Iqbal, A., Kozcaz, C., Vafa, C.: The refined topological vertex. JHEP 0910, 069 (2009). arXiv:hep-th/0701156
Jimbo, M., Lashkevich, M., Miwa, T., Pugai, Y.: Lukyanov’s screening operators for the deformed Virasoro algebra. Phys. Lett. A 229, 285 (1997). arXiv:hep-th/9607177
Kajihara, Y.: Euler transformation formula for multiple basic hypergeometric series of type A and some applications. Adv. Math. 187(1), 53–97 (2004)
Kanno, S., Matsuo, Y., Zhang, H.: Extended conformal symmetry and recursion formulae for Nekrasov partition function. JHEP 08, 028 (2013). arXiv:1306.1523 [hep-th]
Kajihara, Y., Noumi, M.: Multiple elliptic hypergeometric series. An approach from the Cauchy determinant. Indag. Math. 14(3–4), 395–421 (2003). arXiv:math/0306219 [math.CA]
Macdonald, I.G.: Symmetric Functions and Hall polynomials. Oxford University Press, Oxford (1998)
Miki, K.: A \((q,\gamma )\) analogue of the \(W_{1+\infty }\) algebra. J. Math. Phys. 48, 123520 (2007)
Neguţ, A.: Exts and the AGT relations. Lett. Math. Phys. 106(9), 1265–1316 (2016). arXiv:1510.05482 [hep-th]
Neguţ, A.: The q-AGT-W relations via shuffle algebras. Commun. Math. Phys. 358(1), 101–170 (2018). arXiv:1608.08613 [math.RT]
Noumi, M., Shiraishi, J.: A direct approach to the bispectral problem for the Ruijsenaars–Macdonald q-difference operators. arXiv:1206.5364 [math.QA]
Ohkubo, Y.: Kac determinant and singular vector of the level N representation of Ding–Iohara–Miki algebra. Lett. Math. Phys. 109(1), 33 (2019). arXiv:1706.02243 [math-ph]
Shiraishi, J.: A conjecture about raising operators for Macdonald polynomials. Lett. Math. Phys. 73(1), 71–81 (2005). arXiv:math/0503727 [math.QA]
Zenkevich, Y.: Higgsed network calculus. arXiv:1812.11961 [hep-th]
Acknowledgements
The authors would like to thank H. Awata, B. Feigin, A. Hoshino, M. Kanai, H. Kanno, Y. Matsuo, M. Noumi and S. Yanagida for valuable discussions. The research of J.S. is supported by JSPS KAKENHI (Grant Numbers 15K04808 and 16K05186). Y.O. and M.F. are partially supported by Grant-in-Aid for JSPS Research Fellow (Y.O.: 18J00754, M.F.: 17J02745).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Di Francesco.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Construction of Macdonald Symmetric Functions in terms of Topological Vertex
We can obtain Macdonald functions as matrix elements of some compositions of the intertwining operators. The similar derivation and its supersymmetric version are given in [Z]. Set

where the overall factor is chosen for the later convenience. Though the prefactor consisting of the \({\mathcal {G}}\)-factors gives zeros under the restriction of \(\varvec{v}\), but the \({\mathcal {G}}\)-factors which appear from the normal orderings among \(\Phi \)’s and \(\Phi ^*\)’s in \(\mathcal {T}^V\), cancel those zeros, and thus the operator is well-defined. By operator products (C.26) and Lemma C.1, it can be seen that the Young diagrams are restricted to only one row when gluing intertwiners over the vertical representations (Fig. 2), i.e.,

where we put \(m_0 = 0\). Here,  is introduced in Notation 5.7. Then, we have \(\widetilde{{\mathcal {T}}}_1(x)=\Phi ^{(0)}(t^{-1}x)\). Note that the operators \(\Phi ^{(k)}(x)\,\,(k=0,\dots ,N-1)\) in this section slightly differ from those in Sec. 3.2. In this section, \(\Phi ^{(k)}(x)\) is a map \(\mathcal {F}_{t^{-\delta _{k+1}}\cdot {\tilde{\varvec{u}}}} \rightarrow \mathcal {F}_{\varvec{u}}\) with \({\tilde{\varvec{u}}}=(\gamma ^{-1}u_1, \ldots , \gamma ^{-1}u_N)\), that is, the spectral parameter differs by the factor \(\gamma ^{-1}\).
is introduced in Notation 5.7. Then, we have \(\widetilde{{\mathcal {T}}}_1(x)=\Phi ^{(0)}(t^{-1}x)\). Note that the operators \(\Phi ^{(k)}(x)\,\,(k=0,\dots ,N-1)\) in this section slightly differ from those in Sec. 3.2. In this section, \(\Phi ^{(k)}(x)\) is a map \(\mathcal {F}_{t^{-\delta _{k+1}}\cdot {\tilde{\varvec{u}}}} \rightarrow \mathcal {F}_{\varvec{u}}\) with \({\tilde{\varvec{u}}}=(\gamma ^{-1}u_1, \ldots , \gamma ^{-1}u_N)\), that is, the spectral parameter differs by the factor \(\gamma ^{-1}\).
We obtain the expression of Macdonald functions in terms of intertwiners of the DIM algebra. The following proposition says the vacuum expectation value of Fig. 3 gives the Macdonald function of the A type.
Proposition A.1

Proof
The operators \(\widehat{\Phi }_{(m)}(z)\) and \(\widehat{\Phi }^*_{(m)}(z)\) can be decomposed as
where
Then the tensor product of \({\mathcal {A}}(z)\) and \({\mathcal {A}}^*(z)\) corresponds to the screening current (Definition 3.10):
Therefore, we have
Here, we put
As in the proof of Proposition 3.12 (Appendix D.1), \(X^{(1)}(z)\) commutes with \(\widetilde{S}^{(k)}(w)\) up to q-difference:
Further, by the property of the operator products
we obtain
This leads to
By this relation, we get

Thus, the considered matrix elements are eigenfunctions of the difference operator \(D_{N}^1\):

\(\square \)
Remark A.2
By using the expression (A.8), it is shown that the operator \(\widetilde{{\mathcal {T}}}_i(x)\) also represents the screened vertex operator \(\Phi ^{(i-1)}(x)\). Whereas \(\widetilde{{\mathcal {T}}}_i(x)\) is written by a sort of Jackson integrals, \(\Phi ^{(i-1)}(x)\) is introduced by counter integrals. In order to justify the equivalence of the two expressions, see the following argument.
We first note the following deformation of the formal series,
Of course, this series does not converge for arbitrary q and \(\alpha \). However, by the following reason, we can choose some domains for q and \(\alpha \) so that the matrix elements of \(\widetilde{{\mathcal {T}}}_i(x)\) converge there, and thus they are identical to those of \(\Phi ^{(i-1)}(x)\). We discuss the example of the \(i=2\) case. The matrix elements of \(\widetilde{{\mathcal {T}}}_2(x)\) are of the form,

where \(\alpha = u_2/u_1\), and \(\sim \) means the both sides are equal up to some overall factors. The factor  is some finite sum of the monomial of the form \(x^a w^b\) with the maximums and minimums of a’s and b’s depending on \(\varvec{\lambda }\) and \(\varvec{\mu }\). Then, by taking the constant term in w in the above, the running index k is fixed as \(k = n + b \ge b\). Therefore, when we choose the q and \(\alpha \) so that
is some finite sum of the monomial of the form \(x^a w^b\) with the maximums and minimums of a’s and b’s depending on \(\varvec{\lambda }\) and \(\varvec{\mu }\). Then, by taking the constant term in w in the above, the running index k is fixed as \(k = n + b \ge b\). Therefore, when we choose the q and \(\alpha \) so that
the deformation (A.17) is justified by putting \(k< \mathrm {min} (b)\) terms zero, and thus

This discussion can extend to the general i case, and the equivalence between the Jackson integral and contour integral is justified.
Appendix B. Basic Facts for Ordinary Macdonald Functions
In this section, we give the definition and basic facts for ordinary Macdonald functions. Let \(\Lambda _n={\mathbb {C}}[x_1,\ldots ,x_n]^{\mathfrak {S}_n}\) be the ring of symmetric polynomials, and \(\Lambda =\lim _{\leftarrow }\Lambda _n\) be the projective limit in the category of graded rings, i.e., the ring of symmetric functions. \(m_{\lambda }\) denotes the monomial symmetric function. We denote the power sum symmetric functions by \(\mathsf {p}_n=\mathsf {p}_n(x)=\sum _{i \ge 1} x^n_i\). For a partition \(\lambda \), set \(\mathsf {p}_{\lambda }=\prod _{i\ge 1} \mathsf {p}_{\lambda _{i}}\). Macdonald functions are defined as orthogonal functions with respect to the following scalar product.
Definition B.1
Define the bilinear form \(\langle -,- \rangle _{q,t}:\Lambda \otimes \Lambda \rightarrow {\mathbb {C}}\) by
where \(m_i\) is the number of entries in \(\lambda \) equal to i.
Fact B.2
([Ma]) There exists an unique function \(P_{\lambda }\in \Lambda \) such that
The symmetric functions \(P_{\lambda }\) are called Macdonald symmetric functions. It is known that
Here, \(c_{\lambda }\) and \(c'_{\lambda }\) are defined in (3.14). Set \(Q_{\lambda }:=\langle P_{\lambda }, P_{\lambda } \rangle _{q,t}^{-1}\cdot P_{\lambda }\), so that \(\langle P_{\lambda }, Q_{\lambda } \rangle _{q,t}=1\). In this paper, we regard power sum symmetric functions as variables of Macdonald functions and write \(P_{\lambda }=P_{\lambda }(\mathsf {p}_n)\), \(Q_{\lambda }=Q_{\lambda }(\mathsf {p}_n)\). These are abbreviation for \(P_{\lambda }(\mathsf {p}_1,\mathsf {p}_2,\ldots )\) and \(Q_{\lambda }(\mathsf {p}_1,\mathsf {p}_2,\ldots )\). We often substitute the generators \(a_{n}\) in the Heisenberg algebra into Macdonald functions as \(P_{\lambda }(a_{-n})\). Note that this substitution preserves the properties of Macdonald functions as follows. The space of symmetric functions \(\Lambda \) and the Fock space \({\mathcal {F}}\) are isomorphic as graded vector spaces, and they can be identified by

Further, the bilinear form on the Fock spaces preserves the structure of the scalar product \(\langle -, - \rangle _{q,t}\) under this identification, i.e.,

We describe some facts for Macdonald functions that are used in this paper.
1.1 Kernel function
The following function \(\Pi (x,y;q,t)\) is called the kernel function:
This function \(\Pi (x,y;q,t)\) can be expanded in terms of dual bases parametrized by partitions as follows.
Fact B.3
([Ma]) Let \(u_{\lambda }\), \(v_{\lambda } \in \Lambda \) be homogeneous symmetric functions of level \(|\lambda |\) and \(\{u_{\lambda }\}\), \(\{v_{\lambda }\}\) form \({\mathbb {C}}\)-bases on \(\Lambda \). Then, the followings are equivalent:
Note that especially, we have
1.2 Pieri formula
Define the symmetric function \(g_r\in \Lambda \) to be the expansion coefficient of \(y^r\) in the following series:
For a partition \(\lambda \) and a coordinate s, we write
Fact B.4
([Ma]) We have the Pieri rules:
Here, the summation is over the partitions \(\lambda \) such that \(\lambda /\mu \) is a horizontal r-strip, i.e., \(\lambda /\mu \) has at most one box in each column. \(R_{\lambda /\mu }\) (resp. \(C_{\lambda /\mu }\)) is the union of the rows (resp. columns) that intersect \(\lambda -\mu \).
Note that by this formula, we can see that \(Q_{\mu }\) (\(\mu \ngeq \lambda \)) does not appear in the expansion of the product \(\prod _{i \ge 1} g_{\lambda _i}\) in the basis of Macdonald functions.
1.3 Another scalar product
There is another scalar product for which Macdonald functions \(P_{\lambda }\)’s are pairwise orthogonal. Let \(L_r={\mathbb {C}}[x_{1}^{\pm 1},\ldots , x_{r}^{\pm }]\) be the \({\mathbb {C}}\)-algebra of Laurent polynomials in r variables. For \(f(x_1,\ldots , x_r) \in L_r\), we put \({{\bar{f}}}= f(x_1^{-1},\ldots , x_r^{-1})\).
Definition B.5
The scalar product \(\langle -,- \rangle '_r\) on \(L_r\) is defined by
where
Fact B.6
([Ma]) Let \(P_{\lambda }^{(r)}=P_{\lambda } \big |_{x_i \rightarrow 0\, (i>r)}, \, Q_{\lambda }^{(r)}=Q_{\lambda } \big |_{x_i \rightarrow 0\, (i>r)} \in \Lambda _r\) be the Macdonald symmetric polynomials in r variables. Then
where \(\ell (\lambda ), \ell (\mu ) \le r\).
Appendix C. Some Useful Formulas
1.1 C.1 List of operator products
In this subsection, we list some formulas for the normal ordering among the various operators appeared in the main text. We have
and with \({\mathcal {G}}(z) = \prod _{i,j=0}^\infty (1 - z q^i t^{-j})\),
1.2 C.2 On Nekrasov factors
For a partitions \(\lambda \) and non-negative integers \(r, s \in {\mathbb {Z}}_{\ge 0}\), define \({\mathsf {B}}_{r,s}(\lambda )\) to be the partition obtained by removing the 1st to s-th rows and the 1st to r-th columns, i.e.,
For example, if \(\lambda =(5,5,4,4,4,1,1)\), then \({\mathsf {B}}_{2,1}(\lambda )=(3,2,2,2)\). We have the following vanishing condition for the Nekrasov factor.
Lemma C.1
If \(m\ge 0\) and \(n\le 0\), then
If \(m\le -1\) and \(n\ge 1\), then
Note that in particular, \(N_{\emptyset ,\mu }(t)\ne 0\) if and only if \(\mu =(m)\) for some \(m \in {\mathbb {Z}}_{\ge 0}\).
1.3 C.3 Duality of functions \(p_n(x;s|q,t)\) and \(f_n(x;s|q,t)\)
Lemma C.2
Let \(\varvec{\lambda }\) and \(\varvec{\mu }\) satisfy \(\ell (\lambda ^{(i)}), \ell (\mu ^{(i)})\le n_i\).
Here, \(s(\varvec{\lambda })=(s_j(\varvec{\lambda }))_{1\le j\le |\varvec{n}|}\), \(s_{[i,k]_{\varvec{n}}}(\varvec{\lambda })=q^{\lambda ^{(i)}_{k}}t^{1-k}u_i\).
Proof
We denote the LHS by \(F(\varvec{\lambda }|\varvec{\mu })\). Inserting the Macdonald operator \(D_n^1(s;q,q/t)\) and integrating by parts give
where \({\bar{s}}_{[i, k]_{\varvec{n}}} = u_i t^{1-k}\). The LHS gives \(\epsilon _{\varvec{\mu }}F(\varvec{\lambda }|\varvec{\mu })\), and the RHS gives \(\epsilon _{\varvec{\lambda }} F(\varvec{\lambda }|\varvec{\mu })\). Thus we can show \(F(\varvec{\lambda }|\varvec{\mu }) = C(\varvec{\lambda }) \delta _{\varvec{\lambda }, \varvec{\mu }}\) with the coefficient \(C(\varvec{\lambda }) = F(\varvec{\lambda }|\varvec{\lambda })\). We can show \(C(\varvec{\lambda }) = 1\) because both \(f_{|\varvec{n}|}(x;s(\varvec{\lambda })|q,q/t)\) and \(p_{|\varvec{n}|}(x;s(\varvec{\mu })|q,q/t)\) are in \({\mathbb {C}}(s_1,\ldots , s_{|\varvec{n}|})[[x_2/x_1, x_3/x_2,\ldots , x_{|\varvec{n}|}/x_{|\varvec{n}|-1}]]\) and so is their product. \(\quad \square \)
1.4 C.4 Some formulas to prove (4.44)
The coincidence between (4.42) and (4.44) can be identified with the following equation.
Proposition C.3
The following lemmas are formulas for proving (C.34).
Lemma C.4
With \(n = \ell (\lambda )\) and \(m = \ell (\mu )\), the following holds:
where
The equality that we obtain by removing the factors of this type from the both sides of (C.34), can be shown by using following relations.
Lemma C.5
Under the \(\lambda _i \rightarrow \lambda _i+1\) or \(\mu _i \rightarrow \mu _i +1\), we also have the following induction relations,
where
Notation C.6
In what follows in this proof, we set
Definition C.7
We set
Lemma C.8
Under \(\lambda ^{(i)}_k \rightarrow \lambda ^{(i)}_k +1\), that is, \(s_{[i, k]_{\varvec{n}}}\rightarrow qs_{[i, k]_{\varvec{n}}}\), we have
with \(v_{ij} = v_i/v_j\), and
Lemma C.9
Similarly, under \(\mu ^{(i)}_k \rightarrow \mu ^{(i)}_k +1\), that is, \(\sigma _{[i, k]_{\varvec{n}}}\rightarrow q\sigma _{[i, k]_{\varvec{n}}}\), we have
Combining these identities, we complete the proof of (C.34).
Appendix D. Some Proofs of Lemmas and Propositions
1.1 D.1 Proof of Proposition 3.12
By the operator product formulas (C.1)–(C.6), the operator \(\Lambda ^{(j)}(z)\) with \(j\ne i,i+1\) does not contribute in the commutation relation, and it can be shown that
Hence, it is enough to consider the relation only with \(u_i\Lambda ^{(i)}(z)+u_{i+1}\Lambda ^{(i+1)}(z)\).
We have
and
Therefore, by the property \(g_i(qz)=\frac{u_{i+1}}{tu_i}g_i(z)\) with respect to the q-difference, we obtain
\(\square \)
1.2 D.2 Proof of Lemma 3.19
First, we show the relation for \(k=0\). In this proof, we write
for \(i_1<\cdots < i_r\). By the operator products (C.16)–(C.19) and the relation \(:\Phi ^{(0)}(w)\Lambda ^{(1)}(tw):=\Phi ^{(0)}(qw)\Psi ^+(w)\), it can be shown that if \(i_1=1\),
If \(i_1\ge 2\),
Thus, we obtain the relation in the case \(k=0\):
Applying the screening operators to this relation from the right side, we have the case \(k\ne 0\). Indeed, \(\Psi ^+(x)\) commutes with \(S^{(i)}(y)\):
Noting that we have
and by virtue of (D.9) and commutativity of the screening operators, we can establish the relation for general k.
We can show the commutativity of the screening operators as follows. First, it is clear that
By calculating the commutation relation as in the proof of Proposition 3.12, the RHS of (D.11) consists of terms as
Note that \(j_{\ell +2}\ge i+2\). Let us investigate the positions of poles in \(y_i\). Combining the \(\theta \)-functions containing \(y_i\) in \(g(x,y_1,\ldots ,y_k)\) and the operator products among screening currents and \(\Phi ^{(0)}(x)\), there appears the factor
From \(\Phi ^{(0)}(x)\) and \(\Lambda ^{(i)}(ty_1/q)\) in \(\Lambda ^{(j_1,\ldots ,j_{\ell }, i,j_{\ell +2} \ldots , j_r)}\), we have
Noticing that for \(i\ge 2\), the operator product of \(S^{(i-1)}(y_{i-1})\) and \(\Lambda ^{(i)}(ty_i/q)\) are
we have the following set of poles of (D.11) in \(y_i\):
and
If \(r=1\), it gives us the all poles. In general, this list does not exhaust the possible poles. In case \(r\ge 2\), from \(S^{(j)}(y_j)\) and \(\Lambda ^{(j_m)}\) in \(\Lambda ^{(j_1,\ldots ,j_{\ell }, i,j_{\ell +2} \ldots , j_r)}\) with \(m\ne \ell +1\), we have extra poles. From the operator product formulas for them, we have
In addition, from \(\Phi ^{(0)}(x)\) and \(\Lambda ^{(j_m)}\), the following factor arises:
Summarizing these, we can show that the poles in \(y_i\) are in the following positions (Though not all following points are poles, all poles should be in the followings or (D.16)–(D.20)). For \(i\ge 1\),
and for \(i\ge 2\),
For the given integration contour, the poles (D.17), (D.25) and (D.26) are in the disk \(\{z; |z|<|qy_i| \}\). On the other hand, the poles (D.16), (D.18), (D.19), (D.20), (D.23) and (D.24) are in \(\{ z; |z|>|y_i| \}\). Therefore, the change of variable \(y_i \rightarrow q y_i\) is not affected by these poles, and the commutation relation (D.11) becomes zero after the integrals. \(\quad \square \)
1.3 D.3 Proof of Proposition 3.27
By taking the constant terms of  with respect to \(x_i\), the proportional constant \({\mathcal {R}}^{\varvec{n}}_{\varvec{\lambda }}\) is calculated as the expansion coefficient in front of
with respect to \(x_i\), the proportional constant \({\mathcal {R}}^{\varvec{n}}_{\varvec{\lambda }}\) is calculated as the expansion coefficient in front of  in the basis of generalized Macdonald functions. We first consider only the operators that contain the creation operators \(a^{(N)}_{-n}\)’s with respect to the N-th Fock space. That is, we take the constant terms of
in the basis of generalized Macdonald functions. We first consider only the operators that contain the creation operators \(a^{(N)}_{-n}\)’s with respect to the N-th Fock space. That is, we take the constant terms of

Here, we used the expansion formula (3.24), and \(\widetilde{\mathrm {M}}=\mathrm {Mat}(n_N,N-1;{\mathbb {Z}})\) is the set of \(n_N \times (N-1)\) matrices with integral entries. We denote \(x_{[N,i]_{\varvec{n}}}\) by \(y_{i,0}\) in this proof. Further we set
Let \(C(z)=\sum _{k\ge 0} C_k z^k\), \({\widetilde{C}}(z)=\sum _{k\ge 0} {\widetilde{C}}_kz^k\) and \(C^{(\pm )}(z)=\sum _{k\ge 0} C^{(\pm )}_kz^k\) be the formal power series defined by
These series correspond to the operator product formulas among \(\Phi ^{(0)}\) and \(S^{(i)}\)’s. Moreover, we write
for \(e=((e^{(m)}_{i,j})_{i,j=1}^{n_N})_{1\le m\le N-1}, k=((k^{(m)}_{i,j})_{i,j=1}^{n_N})_{1\le m\le N-1} \in M_{n_N}^{N-1}\), and \(\ell =((\ell ^{(m)}_{i,j})_{i,j=1}^{n_N})_{0\le m\le N-2}\in M_{n_N}^{N-1}\). Here \(M_n\) is the set of strictly upper triangular \(n\times n\) matrices with nonnegative integral entries. With these notations, (D.27) can be rewritten as

Here, \( \widetilde{\mathrm {M}}_{\ge 0}=\mathrm {Mat}(n_N, N-1;{\mathbb {Z}}_{\ge 0})\), \(\Phi ^{(0)}(z)=\sum _{n \in {\mathbb {Z}}} \Phi ^{(0)}_{n}z^{-n}\), and \(S^{(i)}(z)=\sum _{n \in {\mathbb {Z}}} S^{(i)}_{n}z^{-n}\). Since the integral gives us the constant terms in \(y_{i,m}\), we have
and
Since \(\sum _{i=1}^{n_N} E^{(m)}_i=0\) and \(\sum _{i=1}^{n_N} (L_i^{(m)} +K_i^{(m)}) =0\), it is shown that
Therefore, \(\sum _{i=1}^{n_N}\mathsf {a}_i^{(N-1)}\) takes its maximum value \(|\lambda ^{(N)}|\) when \(\mathsf {a}^{(m)}_i=0\) for all i and \(m \le N-2\). Since only the operators \(:\prod _{i=1}^{n_N}S^{(N-1)}_{-\mathsf {a}^{(N-1)}_i}:\) have the creation operators acting on the N-th Fock space, it is clear that the maximum degree in the N-th Fock component is \(|\lambda ^{(N)}|\).
Before taking expansion coefficients in the basis of generalized Macdonald functions, we investigate the one in the basis of products of ordinary Macdonald functions  . Consider the terms of level \(|\lambda ^{(N)}|\) with respect to the N-th Fock space. Then, \(\mathsf {a}^{(N-1)}_{i}\) satisfies
. Consider the terms of level \(|\lambda ^{(N)}|\) with respect to the N-th Fock space. Then, \(\mathsf {a}^{(N-1)}_{i}\) satisfies
Furthermore, by the form of \(E^{(m)}_i\), \(K^{(m)}_i\) and \(L^{(m)}_i\), it can be seen that only the following vectors appear:

By the Pieri formula (Fact B.4), we can write the terms of level \(|\lambda ^{(N)}|\) with respect to the N-th Fock space as

Here, \(g^{(N)}_n\) is defined by
Therefore, there appears  only in the case that \(\mu =\lambda ^{(N)}\) on (D.42), i.e., the case that
only in the case that \(\mu =\lambda ^{(N)}\) on (D.42), i.e., the case that
for all i, j, m. Then
for all i, m.
From the above discussion, we have

Here \({\mathcal {O}}\left( P \right) \) expresses the terms  with \(\varvec{\mu }\) satisfying the proposition P. By repeating the similar argument \(N-1\) times, we obtain
with \(\varvec{\mu }\) satisfying the proposition P. By repeating the similar argument \(N-1\) times, we obtain

The existence theorem of generalized Macdonald functions (Fact 3.6) shows that the coefficient in front of  in the basis of generalized Macdonald functions is the same as the one in front of
in the basis of generalized Macdonald functions is the same as the one in front of  in (D.48). \(\quad \square \)
in (D.48). \(\quad \square \)
1.4 D.4 Proof of Lemma 4.11
First, it can be shown that
and

Furthermore, we can see
and
Combining (D.51), (D.52) and (D.53) yields Lemma 4.11. \(\quad \square \)
1.5 D.5 Proof of Lemma 4.13
Set for short
Then \(\phi ^{m,n+m-1}_{\nu }=ABCD\). First, we can get
The first product in (D.58) reproduces the factors in \(d_m((\theta _i); (q^{\mu _i}s_{n+i})|q,t)\), i.e., the first product in (3.36). Next, we have
where
BE reproduces the factors in \(d_m((\theta _i); (q^{\mu _i}s_{n+i})|q,t)\):
This corresponds to the second product in (3.36). The product of \({\mathsf {N}}^{n,m-1}_{\mu }\), D and the remaining factor in (D.58) is
Therefore, Lemma 4.13 follows. \(\quad \square \)
Appendix E. Kac Determinant Revisited
The formula for the Kac determinant with respect to the vectors  has been discussed in [O]. That shows the fact that
has been discussed in [O]. That shows the fact that  form a basis on the Fock space (Fact 2.10). For the sake of reader’s convenience, we revisit the proof, clarifying the choice of the integral cycles. Here, we construct the q-invariance cycles by using the elliptic theta function.
form a basis on the Fock space (Fact 2.10). For the sake of reader’s convenience, we revisit the proof, clarifying the choice of the integral cycles. Here, we construct the q-invariance cycles by using the elliptic theta function.
Definition E.1
Let \(1\le k\le N-1\) and \(u_k=q^s t^{-r} u_{k+1}\) (\(r, s \in {\mathbb {Z}}_{>0}\) ). Define the vector  by the integral
by the integral

Here and hereafter, we use the shorthand notation
where the cycle is the r-dimensional torus \(T: |z_1|=\cdots =|z_r|=1\). Note that \(\varvec{u}\) is the spectral parameter of the codomain of \(S^{(k)}(z_1)\).
Proposition E.2
The vector  does not vanish. In particular, this is of level rs.
does not vanish. In particular, this is of level rs.
Let us prepare a lemma with respect to the symmetrization of theta functions. Set
Lemma E.3
As for the proof of this lemma, see the proof of Lemma 4 in [JLMP].
Proof of Proposition E.2
First, by using the operator products of screening currents and Lemma E.3, we have

Here, \(\Delta (z)\) is defined in (B.15). Note that  can be regarded as the kernel function for the Macdonald functions. Hence, it is expanded in terms of the Macdonald functions (See Fact B.3). Note that \(\prod _{i=1}^rz_i^{-s}\) is the Macdonald polynomial with a rectangular Young diagram in r variables. Therefore, (E.5) can be written as
can be regarded as the kernel function for the Macdonald functions. Hence, it is expanded in terms of the Macdonald functions (See Fact B.3). Note that \(\prod _{i=1}^rz_i^{-s}\) is the Macdonald polynomial with a rectangular Young diagram in r variables. Therefore, (E.5) can be written as

where \(P_{\lambda }^{(r)}(z)\) and \(Q^{(r)}_{\lambda }(z)\) denote the Macdonald polynomials in r variables,
and \(\langle -,- \rangle '_r\) denotes the scalar product defined in Appendix B. Since the Macdonald polynomials are pairwise orthogonal for \(\langle -,- \rangle '_r\) and the inner product \(\langle P^{(r)}_{(s^r)},Q^{(r)}_{(s^r)} \rangle '_r\) can be evaluated (Fact B.6) to be nonvanishing. Thus,  and of level rs. \(\quad \square \)
and of level rs. \(\quad \square \)
We show the following commutativity with the algebra \(\mathsf {U}(N)\). The proof is similar to the case corresponding to the Minimal model, given in [JLMP].
Proposition E.4
Let \(r,s \in {\mathbb {Z}}_{>0}\) and \(k,j \in \{1,\ldots , r\}\). Further we assume \(|t|<|q|\). Then
where the spectral parameter of the codomain of \(S^{(k)}(w_1)\) is \(\varvec{u}\) with \(u_k=q^st^{-r}u_{k+1}\).
Proof
As in the proof of Proposition 3.12, it suffices to consider the relation only with \(\Lambda ^{(k)}(z)+\Lambda ^{(k+1)}(z)\). By (D.4), we have
By symmetrizing the variables \(w_i\)’s, we have
By Lemma E.3, this can be rewritten as
In this expression, we have poles in \(w_l\) at \(w_l=0\), \(w_l=q^nt w_i\) and \(w_l=q^{-n+1}t^{-1}w_i\) (\(i\ne l\), \(n=1,2,\ldots \)). Since \(|t|<|q|\), they do not change the integral while we q-shift the cycle as \(w_l\rightarrow q w_l\). Therefore, the integral (E.11) is zero. \(\quad \square \)
Proposition E.2 and Proposition E.4 show the existence of the singular vectors of the algebra \(\mathsf {U}(N)\).
Corollary E.5
The vector  is a singular vector of level rs, i.e.,
is a singular vector of level rs, i.e.,

for all \(n >0\) and \(i=1,\ldots , N\).
We revisit the proof of the following formula for the Kac determinant  .
.
Proposition E.6
We have
Here \(b_{\lambda }(q) := \prod _{i\ge 1} \prod _{k=1}^{m_i} (1-q^k)\), \(b'_{\lambda }(q) := \prod _{i\ge 1} \prod _{k=1}^{m_i} (-1+q^k)\). \(P^{(N)}(n)\) is the number of N-tuples of Young diagrams of size n, i.e., \(\# \big \{ \varvec{\lambda }=(\lambda ^{(1)}, \ldots , \lambda ^{(N)}) \big | |\varvec{\lambda }| =n\big \}\). In particular, if \(N=1\),
Proof
The inner product  can be calculated by commutation relations of \(X^{(i)}_n\). The parameters \(u_1, \ldots , u_N\) arise from the eigenvalues of \(X^{(i)}_0\). Therefore, it can be seen that
can be calculated by commutation relations of \(X^{(i)}_n\). The parameters \(u_1, \ldots , u_N\) arise from the eigenvalues of \(X^{(i)}_0\). Therefore, it can be seen that  is a polynomial in
is a polynomial in
over \({\mathbb {Q}}(q^{\frac{1}{2}},t^{\frac{1}{2}})\), and thus so does the \(\mathrm {det}_n\). Define the action of the symmetric group \(\mathfrak {S}_N\) (the Weyl group of type \(A_{N-1}\)) on polynomials in \(u_j\) in the usual way. Since \(m_{(1^i)}(u_1,\ldots ,u_N)\) is invariant with respect to this action, \(\mathrm {det}_n\) is also invariant, i.e., a symmetric polynomial in \(u_j\).
Furthermore, let us introduce the new parameters \(u_i'\) and \(u''\) by
Then  can be decomposed as
can be decomposed as

Therefore, \(\mathrm {det}_n\) can be written as
where \(F(u'_1,\ldots , u'_N)\) is some polynomial in \(u'_i\). Note that the maximum degree of \(F(u'_1,\ldots , u'_N)\) with respect to each \(u'_i\) is \(2\sum _{|\varvec{\lambda }|=n}\sum _{k=1}^N \ell (\lambda ^{(k)})\).
By Corollary E.5, it can be seen that for \(r, s \in {\mathbb {Z}}_{>0}\) with \(rs\le n\), the Kac determinant \(\mathrm {det}_n\) has the factors
in the usual way. By the \(\mathfrak {S}_N\) invariance, \(\mathrm {det}_n\) has also the factor
for \(i\ne j\). Noticing the degree of \(F(u'_1,\ldots , u'_N)\), we can see that
Here, \(g_{N,n}(q,t) \in {\mathbb {Q}}(q^{\frac{1}{2}},t^{\frac{1}{2}})\). Thus, we obtained the vanishing loci of the Kac determinant \(\mathrm {det}_n\). The prefactor \(g_{N,n}(q,t)\) has been evaluated in [O]. \(\quad \square \)
As a corollary of Proposition E.6, Fact 2.10 follows.
Appendix F. Examples
1.1 F.1 Examples of 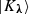
We present examples of the transition matrix  from
from  to the PBW-type basis
to the PBW-type basis  .
.
Examples of \(\alpha ^{(+)}_{\varvec{\lambda },\varvec{\mu }}\) in the case \(N=1\):


Examples of \(\alpha ^{(+)}_{\varvec{\lambda },\varvec{\mu }}\) in the case \(N=2\):


Examples of \(\alpha ^{(-)}_{\varvec{\lambda },\varvec{\mu }}\) in the case \(N=2\):


Examples of \(\alpha ^{(+)}_{\varvec{\lambda },\varvec{\mu }}\) in the case \(N=3\):

Examples of \(\alpha ^{(-)}_{\varvec{\lambda },\varvec{\mu }}\) in the case \(N=3\):

1.2 F.2 Examples of matrix elements 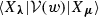
In this section, we demonstrate how to calculate the matrix elements  by the defining relation of \(\mathcal {V}(w)\). Let us first explain it in general case. If \(\varvec{\lambda }\ne (\emptyset ,\ldots , \emptyset )\), let \(j=\min \{i|\lambda ^{(i)}\ne \emptyset \}\). The defining relation gives
by the defining relation of \(\mathcal {V}(w)\). Let us first explain it in general case. If \(\varvec{\lambda }\ne (\emptyset ,\ldots , \emptyset )\), let \(j=\min \{i|\lambda ^{(i)}\ne \emptyset \}\). The defining relation gives

The first term can be rewritten by matrix elements  satisfying \(|\varvec{\nu }|=|\varvec{\lambda }|-1\) (particularly, in the case \(\lambda ^{(j)}_1-1<\lambda ^{(j)}_2\)), and the second term can be expanded by vectors
satisfying \(|\varvec{\nu }|=|\varvec{\lambda }|-1\) (particularly, in the case \(\lambda ^{(j)}_1-1<\lambda ^{(j)}_2\)), and the second term can be expanded by vectors  of level \(|\varvec{\rho }|=|\varvec{\mu }|-\lambda ^{(j)}_{1}\) or \(|\varvec{\mu }|-\lambda ^{(j)}_{1}+1\). (If \(|\varvec{\mu }|-\lambda ^{(j)}_{1},|\varvec{\mu }|-\lambda ^{(j)}_{1}+1<0\), it means just 0 vectors.) If \(\varvec{\lambda }=(\emptyset ,\ldots , \emptyset )\), moving negative modes \(X^{(i)}_{-n}\) to the left side of \(\mathcal {V}(w)\) by the defining relation, we have the expression in terms of Young diagrams of smaller size. In this way, the matrix elements
of level \(|\varvec{\rho }|=|\varvec{\mu }|-\lambda ^{(j)}_{1}\) or \(|\varvec{\mu }|-\lambda ^{(j)}_{1}+1\). (If \(|\varvec{\mu }|-\lambda ^{(j)}_{1},|\varvec{\mu }|-\lambda ^{(j)}_{1}+1<0\), it means just 0 vectors.) If \(\varvec{\lambda }=(\emptyset ,\ldots , \emptyset )\), moving negative modes \(X^{(i)}_{-n}\) to the left side of \(\mathcal {V}(w)\) by the defining relation, we have the expression in terms of Young diagrams of smaller size. In this way, the matrix elements  can be inductively and uniquely determined.
can be inductively and uniquely determined.
The followings are examples.
1.2.1 In \(N=1\) case
First, by the defining relation of \(\mathcal {V}(w)\), we have

By  ,
,  and
and  , we get
, we get

Similarly, it is easily seen that

Moreover, we have

By the direct calculation of the free field expression, we have


By (F.14) and (F.15), we obtain

The matrix element  is already calculated. Since
is already calculated. Since  and
and  in this particular case,
in this particular case,  is factorized and corresponds to the Nekrasov factor (the right hand side of (4.2)):
is factorized and corresponds to the Nekrasov factor (the right hand side of (4.2)):

(F.11), (F.12) and (F.17) are the simplest examples of our main theorem (Theorem 4.4).
We list other cases. Let us first prepare the formula for the action of the algebra \(\mathsf {U}(N)\) on the PBW-type basis  .
.




By using these relation, the matrix elements for larger Young diagrams are inductively determined as follows:












By combining these matrix elements and the examples of transition matrices \(\alpha ^{(\pm )}_{\varvec{\lambda }, \varvec{\mu }}\) from  to
to  in the last subsection, we can check Theorem 4.4.
in the last subsection, we can check Theorem 4.4.
1.2.2 In \(N=2\) case
If there is only one box in all Young diagrams, it is clear that




As in the \(N=1\) case, we prepare the formula for the action of \(X^{(i)}_n\).

where
By these, the matrix elements can be written as





Furthermore, the direct calculation gives


Here,
Thus, we obtain




1.2.3 In \(N=3\) case
Also in the representations of higher level, we can calculate the matrix elements similarly:






List of Notations
1.1 General notations

Especially, in some propositions in Sect. 3, and in Sect. 4, they are specialized as

The Nekrasov factor

Taki’s Flaming factor

1.2 Algebras and representations

PBW-type bases (Definition 2.9)

1.3 Vertex operators associated with generalized Macdonald Functions
Shifted screening currents
Screened vertex operators (Definition 3.14)
Cartan operator arising from the commutation relation between \(\Phi ^{(k)}(x)\) and \(X^{(i)}(z)\) (Lemma 3.19)
Composition of screened vertex operators (Definition 3.25)
1.4 Symmetric functions and vectors in the N-fold tensor Fock spaces

Generalized Macdonald functions (eigenfunctions of \(X^{(1)}_0\)) (Theorem 3.26)

Integral form (Definition 3.37)

Factor arising from the application of Rumanujan’s \({_1}\psi _1\) summation formula (Proposition 3.27)

1.5 Factors in the Macdonald functions and hypergeometric series

The Macdonald functions (Definition 3.21)

Kajihara and Noumi’s multiple basic hypergeometric series (Definition 4.5)

Factors arising in the transformation formula from \(p_{n+m}\) to another series containg \(p_m\) as inner summation (Definition 4.7)

where n, m are nonnegative integers and \(\mu =(\mu _i)_{1\le i \le m} \in {\mathbb {Z}}^m\).
1.6 Mukadé operator and its relatives
The defining relation of the vertex operator \(\mathcal {V}(x) : \mathcal {F}_{\varvec{u}} \rightarrow \mathcal {F}_{\varvec{v}}\) (Definition 4.1)
Realization of \(\mathcal {V}(x)\) for the special case \(v_i=t^{-n_i}u_i\) (Definition 4.14
Mukadé operators connected toward vertical and horizontal directions (Definition 5.8)
Mukadé operator specialized so that Young diagrams are restricted to only one row (Eq. A.8)
Rights and permissions
About this article
Cite this article
Fukuda, M., Ohkubo, Y. & Shiraishi, J. Generalized Macdonald Functions on Fock Tensor Spaces and Duality Formula for Changing Preferred Direction. Commun. Math. Phys. 380, 1–70 (2020). https://doi.org/10.1007/s00220-020-03872-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03872-4



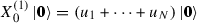 , the vectors
, the vectors  and
and  are not the ordinary vacuum states for the algebra
are not the ordinary vacuum states for the algebra  can be regarded as q-analogue of the
can be regarded as q-analogue of the