The $\psi$-Hilfer fractional calculus of variable order and its applications

Abstract

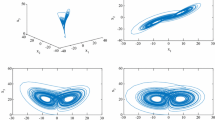
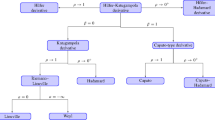
In this paper, we present the $\psi$-Hilfer fractional derivatives of variable order (FDVO) of 3 types I, II and III, versions A and B, as well as their combinations. In addition, we propose approximations and relations between both derivatives, i.e., $\psi$-Hilfer FDVO and $\psi$-Caputo FDVO. With regard to the $\psi$-Hilfer FDVO type II, we discuss the stability of the FVO nonlinear systems 7 solutions by means of one-parameter Mittag-Leffler functions of variable order. Examples 8 involving the FDVO Lü and Chen systems are also presented.

Appendix

From Theorems 11 and 12, we now discuss the operator limitation ${\mathbf {I}}_{a+}^{\alpha \left( x,t\right) ;\psi }\left( \cdot \right)$ and a version of the integration by parts.

Theorem 11

Let $\dfrac{1}{n}<\alpha (x,t)<1$, for all $(x,t)\in \left[ a,b\right] ^{2}$ with a number $n\in {\mathbb {N}}$ greater or equal than two and an increasing function $\psi \in C^{1}([a,b],{\mathbb {R}})$, for $t\in [a,b]$. The $\psi$-Riemann–Liouville FIVO $\alpha (x,t)$,

$$\begin{aligned} {\mathbf {I}}_{a^{+}}^{\alpha (x,t);\psi }:L_{1}(\left[ a,b\right] ,{\mathbb {R}})\longmapsto L_{1}(\left[ a,b\right] ,{\mathbb {R}}) \end{aligned}$$

is a linear and bounded operator.

Proof

First, note that the operator ${\mathbf {I}}_{a^{+}}^{\alpha (x,t);\psi }\left( \cdot \right)$ is linear. Let $\dfrac{1}{n}<\alpha (x,t)<1$ and $f\in L_{1}(\left[ a,b\right] ,{\mathbb {R}})$. We define the following function:

$$\begin{aligned} {\mathbf {H}}(x,t,s):=\left\{ \begin{array}{lcl} \left| \psi ^{\prime }\left( s\right) \left( \psi \left( s\right) -\psi \left( t\right) \right) ^{\alpha (x,t)-1}\right| \left| f(s)\right| , &{} \text { if} &{} s<t, \\ 0, &{} \text {if} &{} t\le s, \end{array} \right. \end{aligned}$$

$\forall (x,t,s)\in \varOmega :=\left[ a,b\right] \times \left[ a,b\right] \times \left[ a,b\right]$.

By hypothesis, $\dfrac{1}{n}< \alpha (x,t) < 1$, and in this sense, for $s+1\le t$ we have $(\psi (t)-\psi (s))^{\alpha (x,t)-1}<1$. On the other hand, for $s< t < s+1$, we have $(\psi (t)-\psi (s))^{\alpha (x,t)-1}<(\psi (t)-\psi (s))^{\frac{1}{n}-1}$.

Therefore, we can write

$$\begin{aligned}&\int _{a}^{b}\left( \int _{a}^{s}{\mathbf {H}}(x,s,t)\,\mathrm{d}t\right) \mathrm{d}s\\&\quad =\int _{a}^{b}\left( \int _{s}^{b}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\right| |f(t)|\right) \,\mathrm{d}s \\&\qquad \int _{a}^{b}|f(t)|\left( \int _{s}^{b}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\right| \,\mathrm{d}t\right) \,\mathrm{d}s \\&\quad =\int _{a}^{b}|f(t)|\left( \begin{array}{c} \displaystyle \int _{s}^{s+1}|\psi ^{\prime }(t)|\left| (\psi (t)-\psi (s))^{\alpha (x,t)-1}\right| \mathrm{d}t \\ +\displaystyle \int _{s+1}^{b}|\psi ^{\prime }(t)|\left| (\psi (t)-\psi (s))^{\alpha (x,t)-1}\right| \mathrm{d}t \end{array} \right) \mathrm{d}s \\&\quad \le \displaystyle \int _{a}^{b}|f(t)|\left( \displaystyle \int _{s}^{s+1}|\psi ^{\prime }(t)|\left| (\psi (t)-\psi (s))^{\frac{1}{n}-1}\right| \mathrm{d}t+\displaystyle \int _{s+1}^{b}|\psi ^{\prime }(t)|\mathrm{d}t\right) \mathrm{d}s \\&\quad =\int _{a}^{b}|f(t)|\left( \int _{s}^{s+1}|\psi ^{\prime }(t)|\left| (\psi (t)-\psi (s))^{\frac{1}{n}-1}\right| \mathrm{d}t+\psi (b)-\psi (s+1)\right) \mathrm{d}s \\&\quad \le \int _{a}^{b}|f(t)|\left\{ n(\psi (s+1)-\psi (s))^{\frac{1}{n}}+\psi (b)-\psi (s+1)\right\} \mathrm{d}s \\&\quad \le \psi (b)\left\| f\right\| \int _{a}^{b}\mathrm{d}s+n\left\| f\right\| \int _{a}^{b}(\psi (s+1)-\psi (s))^{\frac{1}{n}}\mathrm{d}s-\left\| f\right\| \int _{a}^{b}\psi (s+1)\,\mathrm{d}s \\&\quad \le \psi (b)\left\| f\right\| (b-a)+n\left\| f\right\| (b-a)-|\left\| f\right\| \psi (b+1)(b-a) \\&\quad =\left\| f\right\| (b-a)[\psi (b)-\psi (b+1)+n]<\infty . \end{aligned}$$

Remembering the inequality

$$\begin{aligned} \frac{x^{2}+1}{x+1}\le \varGamma (x+1)\le \frac{x^{2}+2}{x+2} \end{aligned}$$

and using the Fubini’s theorem, we have that h is integrable on $\varOmega$ and

$$\begin{aligned} \left\| {\mathbf {I}}_{a^{+}}^{\alpha \left( x,t\right) ;\psi }\left( \cdot \right) \right\|= & {} \int _{a}^{b}\left| \frac{1}{\varGamma (\alpha \left( x,t\right) )} \int _{a}^{t}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha \left( x,t\right) -1}f(s)\,{d} s\right| \,\mathrm{d}t \\\le & {} \int _{a}^{b}\frac{1}{\varGamma (\alpha \left( x,t\right) )} \int _{a}^{t}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha \left( x,t\right) -1}f(s)\right| \,\mathrm{d}s\,\mathrm{d}t \\\le & {} \int _{a}^{b}\left( \frac{\alpha ^{2}(x,t)+\alpha \left( x,t\right) }{ \alpha ^{2}(x,t)+1}\int _{a}^{t}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha \left( x,t\right) -1}f(s)\right| \,\mathrm{d}s\right) \mathrm{d}t \\\le & {} \int _{a}^{b}\left( \int _{a}^{t}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha \left( x,t\right) -1}f(s)\right| \,\mathrm{d}s\right) \mathrm{d}t \\= & {} \int _{a}^{b}\left( \int _{a}^{t}{\mathbf {H}}(x,s,t)\,\mathrm{d}s\right) \,\mathrm{d}t\le (b-a)(\psi (b)-\psi (b+1)+n)\left\| f\right\| <\infty . \end{aligned}$$

Therefore, result

$$\begin{aligned} \left\| {\mathbf {I}}_{a+}^{\alpha \left( x,t\right) ;\psi }\left( \cdot \right) \right\| \le (b-a)(\psi (b)-\psi (b+1)+n)\left\| f\right\| \end{aligned}$$

completes the proof.

Theorem 12

Let $\dfrac{1}{n}<\alpha (x,t)<1$, for all $(x,t)\in \left[ a,b\right] ^{2}$ with a number $n\in {\mathbb {N}}$ greater or equal than two, $f,g\in C([a,b],{\mathbb {R}})$ and $\psi \in C^{1}([a,b],{\mathbb {R}})$ than two an the increasing functions such that $\psi ^{\prime }(\cdot )\ne 0$, for all $t\in [a,b]$. Then

$$\begin{aligned} \int _{a}^{b}g(t){\mathbf {I}}_{a+}^{\alpha (x,t);\psi }f(t)\,\mathrm{d}t=\int _{a}^{b}\psi ^{\prime }(t)f(t){\mathbf {I}}_{b-}^{\alpha (x,t);\psi }\left( \frac{g(t)}{\psi ^{\prime }(t)}\right) \,\mathrm{d}t . \end{aligned}$$

Proof

First, note that the operator ${\mathbf {I}}_{a+}^{\alpha (x,t);\psi }(\cdot )$ is linear. We define the following function

$$\begin{aligned} {\mathbf {H}}(x,t,s):=\left\{ \begin{array}{lcl} \left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}g(t)f(s)\right| , &{} if &{} s<t, \\ 0, &{} if &{} t\le s, \end{array} \right. \end{aligned}$$

$\forall (x,t,s)\in \varOmega :=\left[ a,b\right] \times \left[ a,b\right] \times \left[ a,b\right]$.

As $f,g\in C(\left[ a,b\right] ,{\mathbb {R}})$ and using the Bolzano’s theorem, f and g have maximum and minimum. Therefore, there are constants $c_{1},c_{2}>0$, such that $\left| g\left( t\right) \right| \le c_{1}$ and $\left| f\left( t\right) \right| \le c_{2}$, with $t\in \left[ a,b\right]$.

By hypothesis, $\dfrac{1}{n}<\alpha (x,t)<1$, and, in this sense, for $1\le t-s$, we have $(\psi (t)-\psi (s))^{\alpha (x,t)-1}<1$. On the other hand, for $1>t-s$, we have $\left( \psi (t)-\psi (s)\right) ^{\alpha (x,t)-1}< \left( \psi (t)-\psi (s) \right) ^{\frac{1}{n}-1}$.

We can write

$$\begin{aligned}&\int _{a}^{b}\left( \int _{a}^{t}{\mathbf {H}}(x,s,t)\,\mathrm{d}s\right) \,\mathrm{d}t \\&\quad =\int _{a}^{b}\left( \int _{a}^{t}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}f(s)g(t)\right| \,\mathrm{d}s\right) \,\mathrm{d}t \\&\quad \le \int _{a}^{b}\int _{a}^{t}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\right| \,\left| g(t)\right| \left| f(s)\right| \,\mathrm{d}s\,{\mathrm{d}t} \\&\quad \le c_{1}c_{2}\int _{a}^{b}\int _{a}^{t}\left| \psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\right| \,\mathrm{d}s\,\mathrm{d}t \\&\quad =c_{1}c_{2}\int _{a}^{b}\int _{a}^{t}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\,\mathrm{d}s\,\mathrm{d}t \\&\quad =c_{1}c_{2}\int _{a}^{b}\left( \begin{array}{c} \displaystyle \int _{a}^{t-1}\,\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\,\mathrm{d}s \\ +\displaystyle \int _{t-1}^{t}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\,\mathrm{d}s \end{array} \right) \,\mathrm{d}t \\&\quad<c_{1}c_{2}\int _{a}^{b}\left( \int _{a}^{t-1}\psi ^{\prime }(t)\,\mathrm{d}s+\int _{t-1}^{t}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\frac{1}{n}-1}\,\mathrm{d}s\right) \,\mathrm{d}t \\&\quad =c_{1}c_{2}\int _{a}^{b}\left( \psi (t-1)-\psi (a)+n\left( \psi (t-1)-\psi (t)\right) ^{\frac{1}{n}}\right) \,\mathrm{d}t \\&\quad<c_{1}c_{2}\left( \psi (b-1)-\psi (a)+n\right) \int _{a}^{b}\,\mathrm{d}t \\&\quad =c_{1}c_{2}\left( \psi (b-1)-\psi (a)+n\right) (b-a)<\infty . \end{aligned}$$

On the other hand, knowing the inequality

$$\begin{aligned} \frac{x^{2}+1}{x+1}\le \varGamma (x+1)\le \frac{x^{2}+2}{x+2}, \end{aligned}$$

we can write

$$\begin{aligned}&\int _{a}^{b}g(t){\mathbf {I}}_{a+}^{\alpha (x,t);\psi }f(t)\,\mathrm{d}t\nonumber \\&\quad =\int _{a}^{b}\left( \frac{1}{\varGamma (\alpha (x,t))}\int _{a}^{t}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}g(t)f(s)\,\mathrm{d}s\right) \mathrm{d}t \end{aligned}$$

and using the Fubini’s theorem, we can obtain

$$\begin{aligned}&\int _{a}^{b}g(t){\mathbf {I}}_{a+}^{\alpha (x,t);\psi }f(t)\,\mathrm{d}t\\&\quad =\int _{a}^{b}\left( \frac{1}{\varGamma (\alpha (x,t))}\int _{s}^{b}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}g(t)f(s)\,\mathrm{d}t\right) \,\mathrm{d}s \\&\quad =\int _{a}^{b}\psi ^{\prime }(s)f(s)\left( \frac{1}{\varGamma (\alpha (x,t))} \int _{s}^{b}\psi ^{\prime }\left( s\right) \left( \psi \left( t\right) -\psi \left( s\right) \right) ^{\alpha (x,t)-1}\frac{g(t)}{\psi ^{\prime }(t)}\,{ d}t\right) \,\mathrm{d}s \\&\quad =\int _{a}^{b}\psi ^{\prime }(s)f(s){\mathbf {I}}_{b^{-}}^{\alpha (x,t);\psi }\left( \frac{g(s)}{\psi ^{\prime }(s)}\right) \,\mathrm{d}s\, \end{aligned}$$

which is the desired result.

Theorem 13

(Tavares et al. 2016, 2018; Pooseh et al. 2013; Odzijewicz et al. 2013; Tavares et al. 2017) Assuming the same conditions as Theorem 12 and choosing $\psi \left( t\right) =t$, we have

$$\begin{aligned} \int _{a}^{b}g\left( t\right) {\mathbf {I}}_{a+}^{\alpha \left( x,t\right) }f\left( t\right) \mathrm{d}t=\int _{a}^{b}f\left( t\right) {\mathbf {I}}_{b-}^{\alpha \left( x,t\right) }g\left( t\right) \mathrm{d}t. \end{aligned}$$

Proof

The proof follows directly from Theorem (12).