1 Introduction

Annular swirling jets are met in many technical applications. Gas turbines and aeroengines are examples where annular nozzles are utilised to deliver fuel and oxidiser with a swirl stabilising the flame. In the case of non-premixed combustors mixing processes of the fuel and oxidiser in annular jets are of primary importance for the combustion efficiency and safety. Naturally formed vortical structures in such flows could enhance or deteriorate a mixing intensity. Hence, improved understanding of the annular jets instability could help in the development of new combustion technologies. The swirling jets undergo a vortex breakdown process characterised by spiral-shaped structures. Despite that this phenomenon has been known for many years a mechanism leading to helical structures formation has not been fully understood so far [1]. Theories formulated for the vortex breakdown were categorised into the following underlying concepts:

  1. 1.

    The phenomenon is associated with the concept of critical state or, more generally, with wave phenomena [2,3,4].

  2. 2.

    The phenomenon is analogous to boundary layer separation or flow stagnation [5, 6].

  3. 3.

    The phenomenon is a consequence of the hydrodynamic instability [7,8,9,10].

As was mentioned in [1] the vortex breakdown is highly time dependent phenomenon and the spiral-shaped structures start to precess about the axis of symmetry thus forming the so called precessing vortex core (PVC) [11].

There are many more recent advanced approaches to the vortex breakdown in swirling jets like a sensitivity analysis of Quadri et al. [12] showing that the instability is casued by a combination of Kelvin-Helmholtz mechanism involving conservation of the angular momentum. The Large Eddy Simulations (LES) performed by Garcia-Villalba et al. [13] and Garcia-Villalba and Fröhlich [14] for a turbulent unconfined annular swirling jet showed spiral coherent structures in the near field. Again, the Kelvin–Helmholtz instability was identified as the major source for the generation of the coherent vortices observed in this flow type. However, since the vortex breakdown has been observed in many flow types like circular jets and annular jets with a swirl, it seems that the origin of this phenomenon has not been fully understood so far. As stressed by Vaniershot et al. [15] due to the occurrence of several types of breakdown and the often contradictory results because of a high sensitivity to boundary conditions, there is still no general consensus about the origin of vortex breakdown.

Lehmann et al. [16] carried out experiments on a swirl nozzle with two concentric air jets leaving the nozzle with slightly different swirl. LDA measurements showed that the flow field consisted of a ring jet with a back-flow along the jet axis. The back-flow velocity was about 50% of the maximum jet velocity. The measurements showed that a strong coherent velocity fluctuation of the first azimuthal mode existed close to the nozzle exit. This phenomenon suggested a possibility that the absolute instability was the cause of these fluctuations. The linear stability analysis based on the spatio-temporal stability theory and Briggs/Bers criteria [17, 18] was performed by Michalke [19]. Stability calculations showed presence of the absolutely unstable first azimuthal mode.

Recently one can find many opinions in the literature [20,21,22,23] based on experimental results and stability calculations indicating that the vortex breakdown is actually the manifestation of a self-excited global hydrodynamic instability triggered by absolutely unstable helical modes. The vortex breakdown and the consequent precessing vortex core are very important for controlling the combustion process in gas turbines and in aeroengines. As this phenomenon could be caused by the absolute instability leading to a global helical mode it seems to be important to know the influence of the governing parameters on this phenomenon. Michalke [19] studied the influence of the axial velocity profile, swirl and back-flow on the frequency and temporal growth rate of the absolute first helical mode. Parametric studies with the use of spatio-temporal linear stability analysis were performed by Talamelli and Gavarini [24] for incompressible coaxial jets. However, such studies for annular swirling and non-swirling jets seems to be still lacking.

The present paper is an extension of the Michalke studies including analysis of the shape of axial and tangential velocity profiles. The main goal of the present paper is to apply the linear, local stability analysis to find qualitative dependences of the flow conditions on the helical mode frequency and temporal growth rate. The results of this analysis will be further used to choose properly the flow parameters favourable for the absolute instability for LES of the annular jets. Some of qualitive results shown in the present paper were applied by Wawrzak et al. [25] to establish inlet conditions for an annular non-swirling jet which were favorable for the helical modes generation.

2 Base flow

A schematic view of the annular jet is shown in Fig. 1. The annular jet is characterised by the outer and inner diameters denoted by \(D_o\) and \(D_i\), respectively. Behind the bluff body a central recirculation zone (CRZ) is formed that is surrounded by the inner shear layer. The outer one is formed between the jet and the ambient fluid. Sample axial and tangential velocity profiles in the cross section denoted by the dashed line are also shown. In the case of the local stability analysis it is assumed that the flow is parallel and the velocity field extends infinitely along the jet axis.Thus the base flow of the annular jet is modelled by an axial velocity \(U^d\) and a swirl with circumferential velocity component \(W^d\) (superscript ”d” denotes dimensional variables). In a parallel approximation the radial velocity component \(V^d\) is neglected. The axial velocity component \(U^d \left( r^d \right)\) represents an annular jet with a possible reversed flow on the jet axis with \(U^d \left( r^d=0 \right) =U_0^d<0\). The maximum jet velocity is \(U_{max}\) at \(r^d=R_{Umax}\). All the velocities are normalized by \(U_{max}\) and all lengths by \(R_{Umax}\). The base flow is defined in non-dimensional variables:

$$\begin{aligned} U=\frac{U^d}{U_{max}},\,\,\,U_0=\frac{U_0^d}{U_{max}},\,\,\, W=\frac{W^d}{U_{max}}, \,\,\, r=\frac{r^d}{R_{Umax}} \end{aligned}$$
(1)

Following the work of Michalke [19] we first used the profile proposed by Monkewitz [26] which is given by

$$\begin{aligned} U\left( r\right) =4BF\left( r \right) \left[ 1-BF\left( r \right) \right] \end{aligned}$$
(2)

where \(F\left( r \right)\) is given by Monkewitz and Sohn [27] as:

$$\begin{aligned} F \left( r\right) = \left[ 1+\left( e^{ar^2} -1\right) ^N \right] ^{-1} \end{aligned}$$
(3)

The quantity B depends on \(U_0\)

$$\begin{aligned} B=0.5\left[ 1+\left( 1-U_0 \right) ^{1/2} \right] \end{aligned}$$
(4)

and \(a\left( U_0 \right)\) is determined by the condition \(U\left( 1 \right) =1\). \(N\ge 1\) is a shape factor that controls the thickness of the jet shear layer, i.e. the maximum of dU/dr. To define an axial velocity profile for a given back-flow \(U_0\) and N-parameter it is necessary to solve numerically the following non-linear algebraic equation:

$$\begin{aligned} \Delta \left( a \right) =U \left( 1 \right) -1=4BF\left( 1 \right) \left[ 1-BF\left( 1 \right) \right] -1=0 \end{aligned}$$
(5)

Equation 5 was solved using Newton–Raphson method [28]

Fig. 1
figure 1

Schematic view of the annular swirling jet indicating the central recirculation zone (CRZ) and inner and outer shear layers

Full size image
Fig. 2
figure 2

Annular jet axial velocity profiles described by Eq. (2): a \(N=1\), b \(N=2\)

Full size image
Fig. 3
figure 3

A comparison of model velocity profiles with the experimental data [16]

Full size image

Sample axial velocity profiles for various back-flow velocities and steepness parameters N are shown in Fig. 2. Figure 3 shows three velocity profiles with different steepness parameter compared to the experimental data [16]. It can readily be seen that it is difficult to match a model profile to the experimental data as N-parameter is the only one that controls the velocity profile. Moreover, in real annular nozzles the nozzle walls could be formed in such a way that both shear layers of an annular jet, inner and outer ones, could have different thicknesses. Such velocity profiles features cannot be modelled with the velocity described by Eq.  (2). A new shape of the axial velocity profile in the annular nozzle is a combination of hyperbolic tangent functions. The following function is proposed:

$$\begin{aligned} U \left( r \right)&= U_{in} \tanh \left[ b_{in} \left( r-R_{in} \right) \right] - U_{out} \tanh \left[ b_{out} \left( r-R_{out}\right) \right] \\&\quad +\frac{b_{in}U_{in}}{\cosh ^2\left( -b_{in}R_{in} \right) } \frac{\left[ 1-\tanh \left( b_{in}^0 r \right) \right] }{b_{in}^0} \\&\quad -\frac{b_{out}U_{out}}{\cosh ^2\left( -b_{out}R_{out} \right) } \frac{\left[ 1-\tanh \left( b_{out}^0 r \right) \right] }{b_{out}^0} \\&\quad -U_{in} +U_{out} \end{aligned}$$
(6)

Two terms in the middle lines of Eq. (6) were introduced to satisfy the zero radial gradient at the nozzle axis

$$\begin{aligned} \left. \frac{d U \left( r \right) }{dr} \right| _{r=0}=0 \end{aligned}$$
(7)

If the radius tends to zero then

$$\begin{aligned} \lim _{r \rightarrow 0} U \left( r \right)&=U_{in} \tanh \left( -b_{in}R_{in} \right) -U_{out} \tanh \left( -b_{out}R_{out} \right) \\&\quad + \frac{b_{in}U_{in}}{\cosh ^2 \left( -b_{in}R_{in} \right) b^0_{in} } - \frac{b_{out}U_{out}}{\cosh ^2 \left( -b_{out}R_{out} \right) b^0_{out}} \\&\quad - U_{in}+U_{out}=U_0 \end{aligned}$$
(8)

As \(U_0\) is imposed as a parameter there is a relation between \(U_{in}\) and \(U_{out}\). Assuming a certain value for \(U_{in}\) the parameter \(U_{out}\) is expressed as

$$\begin{aligned} U_{out}=\frac{U_{in} L_{in} -U_0}{L_{out}} \end{aligned}$$
(9)

where

$$\begin{aligned} L_{in}&=\tanh \left( -b_{in}R_{in} \right) +\frac{b_{in}}{\cosh ^2 \left( -b_{in} R_{in}\right) b^0_{in}} -1 \end{aligned}$$
(10)
$$\begin{aligned} L_{out}&= \tanh \left( -b_{out}R_{out} \right) +\frac{b_{out}}{\cosh ^2 \left( -b_{out} R_{out}\right) b^0_{out}} -1 \end{aligned}$$
(11)

If the radius tends to infinity then

$$\begin{aligned} \lim _{r \rightarrow \infty } U \left( r\right) =0 \end{aligned}$$
(12)

Velocity gradients in inner and outer shear layers are controlled by \(b_{in}\) and \(b_{out}\) parameters, respectively. The parameter \(U_{in}\) is chosen in order to get a presumed maximum value of the axial velocity \(U_{max}=1\). Varying \(b_{in}\)-coefficient \(R_{out}\) is kept constant while \(R_{in}\) is calculated to obtain the maximum of the velocity at a chosen radius \(r_{Umax}=1\). Conversely, varying \(b_{out}\) the \(R_{in}\) is fixed while \(R_{out}\) is calculated to obtain the maximum of the velocity at a chosen radius \(r_{Umax}=1\)

Such a model velocity profile is more flexible compared to Eq. (2). Figure 4a shows the model velocity profile with properly chosen parameters compared to the experimental data. It can be seen that the velocity profile with a combination of hyperbolic tangent functions much better agrees with the experiment than the profile used by Michalke [19] as shown in Fig. 3. Using Eq. (6) the velocity gradient in each shear layer can be controlled independently. Sample velocity profiles with various controlling parameters are shown in Fig. 4b.

Fig. 4
figure 4

Model velocity profile based on the hyperbolic tangent functions: a comparison with the experimental data [16], b examples of axial velocity profiles with various parameters

Full size image

To complete the model base flow for a swirling annular jet the azimuthal velocity profile has to be defined. Michalke [19] in his stability calculations applied the swirl velocity as the stationary Hamel-Oseen vortex field given by

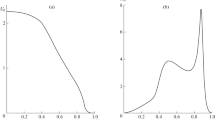
$$\begin{aligned} W \left( r \right) =\frac{A}{r} \left[ \frac{1-\exp \left( -b r^2 \right) }{1-\exp \left( -b \right) }\right] \end{aligned}$$
(13)

where \(A=W_{max}/U_{max}\). Figure 5 shows sample azimuthal velocity profiles compared with the experimental data of Lehmann et al. [16]. It can be seen that there are significant differences and a more flexible azimuthal model velocity profile could bring better results of the linear stability analysis.

Fig. 5
figure 5

Examples of azimuthal velocity profiles compared to the experimental data [16]

Full size image

Quite simple modification of this function could improve the model velocity profile

Fig. 6
figure 6

Azimuthal velocity profiles according to Eq. (14): a tangential velocity profile matching to the experimental data [16], b examples of tangential velocity profiles with varying \(N_W\) parameter

Full size image
$$\begin{aligned} W \left( r \right) =\frac{Ar^{N_W-1}_{W_{max}}}{r^{N_W-1}}\left[ \frac{1-\exp \left( -b r^{N_W} \right) }{1-\exp \left( -b r^{N_W}_{W_{max}}\right) }\right] \end{aligned}$$
(14)

where: \(r_{Wmax}\) denotes the radius for which azimuthal velocity attains its maximum. The exponent \(N_W\) controls the decay rate of the velocity at the vortex periphery while in the vortex core the velocity is still close to the solid body rotation. The parameter b is found from the condition that the function described by Eq. (14) has the maximum at the radius \(r=r_{W_{max}}\). Figure 6a shows the profile matching very well to the experimental data for which \(r_{Wmax}=0.7\), \(A=0.74\) and \(N_W=4.5\). For such parameters the coefficient \(b=1.7634345\). Figure 6b shows sample azimuthal velocity profiles with the swirl number \(A=0.75\), \(r_{W_{max}}=1\) and various \(N_W\) exponents.

3 Stability equations and solution method

The small disturbance of flow parameters is assumed as a wave travelling along axial x and azimuthal \(\varphi\) directions with the amplitude varying along the radial direction r in the following form:

$$\begin{aligned} \left( u',v',w',p'\right) =\left[ {\hat{u}} \left( r \right) ,{\hat{v}} \left( r \right) ,{\hat{w}}\left( r \right) ,{\hat{p}} \left( r \right) \right] \exp {\left[ i \left( \alpha x +m\varphi -\omega t \right) \right] } \end{aligned}$$
(15)

Here \(u',v',w'\) and \(p'\) are axial, radial, azimuthal velocity and pressure disturbances, respectively, \(\alpha\) is the complex wave number and \(\omega\) the complex frequency, m is the azimuthal real wave number. Such disturbances are introduced into the continuity equation and Euler equations in cylindrical coordinates and linearised around the given base flow. As shown by Michalke [19], after eliminating the \({\hat{u}}\) and \({\hat{w}}\) velocities, the stability equations can be written as

$$\begin{aligned} r\sigma \frac{d{\hat{p}}}{dr}&= {} i \left[ 2WZ -r \sigma ^2\right] {\hat{v}}-\frac{2mW}{r}{\hat{p}} \end{aligned}$$
(16)
$$\begin{aligned} \frac{\sigma }{r}\frac{d \left( r{\hat{v}} \right) }{dr}&= {} i \left[ \alpha ^2 +\frac{m^2}{r^2} \right] {\hat{p}} + \left[ \alpha \frac{dU}{dr} +m \frac{Z}{r}\right] {\hat{v}} \end{aligned}$$
(17)

where

$$\begin{aligned} \sigma \left( r \right)&= {} \alpha U - \omega + \frac{W}{r}m \end{aligned}$$
(18)
$$\begin{aligned} Z \left( r\right)&= {} \frac{d W}{dr}+ \frac{W}{r} \end{aligned}$$
(19)

To solve the system of the stability equations (16) and (17) the boundary conditions must be formulated on the jet axis \(r=0\) and for \(r \rightarrow \infty\) using features of the axial and azimuthal velocity profiles of the base flow. The boundary conditions require that \({\hat{v}} \left( r \right)\) and \({\hat{p}} \left( r \right)\) are bounded on the jet axis and both quantities vanish at the jet periphery. The asymptotic behavior for \(r \rightarrow \infty\) can be obtained if one takes into account that

$$\begin{aligned}&\lim _{r \rightarrow \infty } U, \frac{dU}{dr}, Z =0 \\&\lim _{r \rightarrow \infty } \frac{W}{r}=\frac{A_{\infty }}{r^{N_W}} \;\;\;\; \text {where} \;\;\;\; A_{\infty }=\frac{Ar_{W_{max}}^{N_W-1}}{1-\exp \left( -br_{W_{max}}^{N_W-1} \right) } \end{aligned}$$
(20)

Introducing the notation:

$$\begin{aligned} \sigma _{\infty }=\lim _{r \rightarrow \infty } \sigma \left( r \right) =m \frac{A_{\infty }}{r^{N_W}}-\omega \end{aligned}$$
(21)

the stability equations (16) and (17) for \(r \rightarrow \infty\) take the following forms:

$$\begin{aligned} r \sigma _{\infty }\frac{d {\hat{p}}}{dr}&=-i r\sigma ^2_{\infty } {\hat{v}}-2m \frac{A_{\infty }}{r^{N_W}} {\hat{p}} \end{aligned}$$
(22)
$$\begin{aligned} \frac{\sigma _{\infty }}{r} \frac{d\left( r {\hat{v}}\right) }{dr}&=i \left[ \alpha ^2+ \left( \frac{m}{r} \right) ^2 \right] {\hat{p}} \end{aligned}$$
(23)

Introducing the notation \(\Phi =r {\hat{v}}\) Eq. (23) reads as

$$\begin{aligned} \frac{d}{dr} \left[ \frac{r}{m^2+ \left( \alpha r \right) ^2} \frac{d\Phi }{dr} \right] - \frac{\Phi }{r}=0 \end{aligned}$$
(24)

with the decaying solution

$$\begin{aligned} \Phi =rK_m' \left( \alpha r \right) \end{aligned}$$
(25)

where \(K_m\) is the modified Bessel function of the second kind and order m. Hence, \({\hat{v}}\) velocity at the limit \(r \rightarrow \infty\) is

$$\begin{aligned} {\hat{v}} \left( r \right) =K'_m \left( \alpha r \right) \end{aligned}$$
(26)

The asymptotic limit for a pressure perturbation at the jet periphery, with Eq. (22), is

$$\begin{aligned} {\hat{p}} \left( r\right) = - \frac{i}{\alpha } \sigma _\infty K_m \left( \alpha r \right) = - \frac{i}{\alpha } \left( m\frac{A_\infty }{r^{N_W}} -\omega \right) K_m \left( \alpha r \right) \end{aligned}$$
(27)

The boundary conditions for the jet axis, despite a different base flow used in the current analysis, are exactly the same as shown by Michalke [19]. Pressure perturbation at the jet axis is expressed as

$$\begin{aligned} {\hat{p}} \left( r \right) = I_m \left( \beta r \right) \end{aligned}$$
(28)

where \(I_m\) is the modified Bessel function of the first kind and order m, and the velocity

$$\begin{aligned} {\hat{v}} \left( r \right) = \frac{i \alpha }{\sigma _0 \sqrt{1-\mu ^2}} \left[ I_m' \left( \beta r \right) + \frac{ m \mu }{\beta r}I_m \left( \beta r \right) \right] \end{aligned}$$
(29)

The eigenvalue problem now is solved numerically by integrating stability equations (16) and (17) by means of the Runge–Kutta–Fehlberg procedure [29] of \(4{\mathrm{th}}\) order starting with \(r=10^{-6}\) and boundary conditions (28) and (29) up till \(r=1\) yielding \({\hat{p}}_L\left( 1 \right)\) and \({\hat{v}}_L \left( 1 \right)\), and from \(r=\infty\), where the asymptotic solutions (26) and (27) are applied, back to \(r=1\) yielding \({\hat{p}}_R \left( 1\right)\) and \({\hat{v}}_R \left( 1 \right)\). The eigenvalue condition then follows from the matching of these solutions at \(r=1\), requiring:

$$\begin{aligned} G \left( \omega , \alpha \right) = \frac{{\hat{p}}_L}{{\hat{v}}_L}-\frac{{\hat{p}}_R}{{\hat{v}}_R}=0 \end{aligned}$$
(30)

This condition leads, for a given \(\omega\), to a relation \(\alpha \left( \omega \right)\), or, for a given \(\alpha\) to \(\omega \left( \alpha \right)\). The eigenvalue problems can be solved by Newton’s method as

$$\begin{aligned} \omega ^{\left( n+1 \right) }=\omega ^{\left( n \right) } -\frac{G \left( \omega ^{\left( n \right) },\alpha \right) }{ \partial G/ \partial \omega \vert _{\omega ^{\left( n \right) }}} \end{aligned}$$
(31)
$$\begin{aligned} \alpha ^{\left( n+1 \right) }=\alpha ^{\left( n \right) } -\frac{G \left( \omega ,\alpha ^{\left( n \right) } \right) }{\partial G/ \partial \alpha \vert _{\alpha ^{\left( n \right) }}} \end{aligned}$$
(32)

where

$$\begin{aligned} \frac{\partial G}{ \partial \omega }=\frac{1}{{\hat{v}}_L} \left( \frac{\partial {\hat{p}}}{\partial \omega } \right) _L-\frac{1}{{\hat{v}}_R} \left( \frac{\partial {\hat{p}}}{\partial \omega }\right) _R -\frac{{\hat{p}}_L}{{\hat{v}}_L^2} \left( \frac{\partial {\hat{v}}}{\partial \omega } \right) _L+ \frac{{\hat{p}}_R}{{\hat{v}}_R^2}\left( \frac{\partial {\hat{v}}}{\partial \omega }\right) _R \end{aligned}$$
(33)
$$\begin{aligned} \frac{\partial G}{ \partial \alpha }=\frac{1}{{\hat{v}}_L} \left( \frac{\partial {\hat{p}}}{\partial \alpha } \right) _L-\frac{1}{{\hat{v}}_R} \left( \frac{\partial {\hat{p}}}{\partial \alpha }\right) _R -\frac{{\hat{p}}_L}{{\hat{v}}_L^2} \left( \frac{\partial {\hat{v}}}{\partial \alpha } \right) _L+ \frac{{\hat{p}}_R}{{\hat{v}}_R^2}\left( \frac{\partial {\hat{v}}}{\partial \alpha }\right) _R \end{aligned}$$
(34)

In order to use Newton’s method to solve eigenvalue problem one needs information on the derivatives of pressure and velocity perturbations with respect to the complex wave number \(\alpha\) or the complex frequency \(\omega\) respectively. This information can be obtained solving the differential equation obtained from the stability equations (16), (17) and the boundary conditions (26), (27), (28) and (29) differentiated with respect to wave number \(\alpha\) or frequency \(\omega\), respectively.

4 Results

4.1 Non-swirling annular jet

Michalke [19] studied an influence of the back-flow and a shape of the velocity profile on the absolute first azimuthal mode (\(m=1\)). He showed that the temporal absolute growth rate increases when the velocity profile is steeper. However, the steepness of the velocity profile in Eq. (2) used by Michalke [19] is controlled by the exponent N used in Eq. (3). As shown in Fig. 3 the parameter N changes the velocity gradients in both shear layers. An interesting question is how the absolute helical mode depends on the velocity gradient varying independently inner and outer shear layers. Equation (6) proposed in Sect.  2 allows such a control of the axial velocity profile. First an influence of the velocity gradient in the inner shear layer is analysed keeping the steepness of the velocity profile in the outer jet part nearly constant. The parameters of the velocity profiles analysed are gathered in Table 1.

Table 1 The list of the parameters of the velocity profiles controlling velocity gradient in the inner shear layer, back-flow \(U_0=-0.3\)
Full size table
Fig. 7
figure 7

Iso-contours of the imaginary part of the complex frequency \(\omega _{i}\) around a saddle point \(d \omega / d \alpha =0\) in complex wave numbers plane, test case \(In_1BF_{03}\)

Full size image
Fig. 8
figure 8

Influence of the inner shear layer steepness: a axial velocity profiles compared with the profiles used by Michalke, back-flow \(U_0=-0.3\), b complex frequency of the first absolutely unstable helical mode \(\omega _0\)

Full size image

Figure 7 shows iso-contours of the imaginary part of the complex frequency \(\omega _{i}\) around a saddle point \(d \omega / d \alpha =0\) in complex wave numbers plane where pinching condition is satisfied. Having known the \(\omega\) -maps in \(\alpha\)-planes around the saddle point, the precise pairs \((\omega _0,\alpha _0)\), for which \(d\omega /d \alpha = 0\), were found using an iterative procedure presented by Monkewitz and Sohn [27]. Figure 8a shows the velocity profiles of all the test cases gathered in Table 1 compared with the velocity profiles used by Michalke, denoted by thick lines, with the parameter \(N=1\) and 2. Figure 8b shows the complex frequency \(\omega _0\) as a function of the inner shear layer steepness for the case of the back-flow \(U_0=-0.3\). The real part \(\omega _{0,r}\) corresponds to the frequency of the absolute first azimuthal mode. It can be seen that the frequency slightly grows along with the inner shear layer steepness. The imaginary part \(\omega _{0,i}\) expresses an absolute temporal growth rate. The growth rate increases more rapidly along with the parameter \(b_{in}\). Figure 9 shows the eigenfunctions of pressure and velocity perturbations with a varying steepness of the inner shear layer. It can be seen that maximum of both eigenfunctions shift from the jet axis along with the parameter \(b_{in}\). However, for all the cases the perturbations are mainly located in the region of the inner shear layer.

Fig. 9
figure 9

Influence of the inner shear layer steepness on eigenfunctions of the first absolutely unstable helical mode, back-flow \(U_0=-0.3\): a pressure perturbation b velocity perturbation

Full size image

Analogous calculations were performed for a series of the velocity profiles controlling a steepness of the outer shear layer. The parameters of the velocity profiles analysed are presented in Table 2. The velocity profiles compared with the ones used by Michalke [19] with parameter \(N=1\) and 2 are shown in Fig. 10a. The complex frequency \(\omega _0\) of the absolute instability is illustrated in Fig. 10b. By contrast to the test cases shown above, increasing the steepness of the outer shear layer leads to a slight decrease of the absolute mode frequency, while the temporal absolute growth rate remains nearly constant. The influence of the outer shear layer thickness on the eigenfunctions is also weak as shown in Fig. 11.

Table 2 The list of the parameters of the velocity profiles controlling velocity gradient in the outer shear layer, back-flow \(U_0=-0.3\)
Full size table
Fig. 10
figure 10

Influence of the outer shear layer steepness: a axial velocity profiles compared with the profiles used by Michalke, back-flow \(U_0=-0.3\), b complex frequency of the first absolutely unstable helical mode \(\omega _0\)

Full size image
Fig. 11
figure 11

Influence of the outer shear layer steepness on eigenfunctions of the first absolutely unstable helical mode, back-flow \(U_0=-0.3\): a Pressure perturbation b velocity perturbation

Full size image

Then following the research of Michalke [19] the calculations were performed for the test cases controlling steepness of inner and outer shear layers but for a stronger back-flow \(U_0=-0.5\). The parameters of the velocity profiles changing steepness of the inner shear layer are gathered in Table 3, and the velocity profiles are shown in Fig. 12a. Figure 12b shows the complex frequency for these test cases as a function of the inner shear layer steepness parameter \(b_{in}\). The first conclusion is that a stronger back-flow decreases frequency of the absolute first helical mode and increases its growth rate. The conclusions from the present calculations agree with the results of Michalke [19]. The absolute temporal growth rate increases as a function of \(b_{in}\)-parameter in a similar way to the case with a weaker back-flow shown in Fig. 8b. However, frequency of the absolute mode is nearly independent of the inner shear layer thickness. An influence of the inner shear layer thickness on the eigenfunctions in this case, shown in Fig. 13, is very similar to the one observed for a weaker back-flow.

Table 3 The list of the parameters of the velocity profiles controlling velocity gradient in the inner shear layer, back-flow \(U_0=-0.5\)
Full size table
Fig. 12
figure 12

Influence of the inner shear layer steepness: a axial velocity profiles compared with the profiles used by Michalke, back-flow \(U_0=-0.5\), b complex frequency of the first absolutely unstable helical mode \(\omega _0\)

Full size image
Fig. 13
figure 13

Influence of the inner shear layer steepness on eigenfunctions of the first abolutely unstable helical mode, back-flow \(U_0=-0.5\): a pressure perturbation b velocity perturbation

Full size image
Table 4 The list of the parameters of the velocity profiles controlling velocity gradient in the outer shear layer, back-flow \(U_0=-0.5\)
Full size table
Fig. 14
figure 14

Influence of the outer shear layer steepness: a axial velocity profiles compared with the profiles used by Michalke, back-flow \(U_0=-0.5\), b complex frequency of the first absolutely unstable helical mode \(\omega _0\)

Full size image

Finally, the calculations for the back-flow \(U_0=-0.5\) controlling the outer shear layer were carried out. The parameters of the velocity profiles changing steepness of the outer shear layer are gathered in Table 4, the velocity profiles are shown in Fig. 14a. Figure 14b shows the complex frequency for these test cases as a function of the outer shear layer steepness parameter \(b_{out}\). Again, a slight decrease of the frequency is observed with growing the steepness of the outer shear layer while the absolute growth rate is nearly constant. Again, an influence of the outer shear layer thickness on the eigenfunctions, shown in Fig. 15, is rather weak.

Fig. 15
figure 15

Influence of the outer shear layer steepness on eigenfunctions of the first absolutely unstable helical mode, back-flow \(U_0=-0.5\): a pressure perturbation b velocity perturbation

Full size image

The results discussed above showed that changing velocity gradient of the inner shear layer increases temporal growth rate of the first azimuthal absolute mode. In the case of a smaller back-flow \(U_0=-0.3\) a slight increase of the frequency is also observed. For a stronger back-flow \(U_0=-0.5\) an increase of the absolute growth rate as a function of \(b_{in}\) is still observed while frequency remains nearly constant. On the other hand increasing the velocity gradient in the outer shear layer does not change the temporal growth rate but slightly decreases the absolute mode frequency. Conclusions from this part of the non-swirling annular jet stability were utilised by Wawrzak et al. [25] in their LES studies. They showed that helical structures could be triggered by varying the steepness of the inner shear layer while keeping the outer shear layer relatively thick.

In order to compare these results with an influence of the velocity gradients varying in both inner and outer shear layers the calculations with the velocity profiles used by Michalke were repeated with an increased range of the N-parameter. The velocity profiles with the \(N=1-2.5\) and back-flow \(U_0=-0.3\) are shown in Fig. 16a. The influence of the N-parameter on the complex frequency \(\omega _0\) is shown in Fig. 16b. It can be seen that increasing the N-parameter and consequently the velocity gradient in both inner and outer shear layers leads to an increased temporal growth rate and decreased frequency.

Fig. 16
figure 16

Influence of the N-parameter: a axial velocity profiles, back-flow \(U_0=-0.3\), b complex frequency of the first absolutely unstable helical mode \(\omega _0\)

Full size image

Analogous calculations were performed for the back-flow \(U_0=-0.5\) and the results are shown in Fig.17. Influence of the N-parameter on the complex frequency is similar to the influence observed for the back-flow \(U_0=-0.3\), however, the temporal growth rate is higher and frequency is lower for stronger back-flow, as observed also in previous results.

Fig. 17
figure 17

Influence of the N-parameter: a axial velocity profiles, back-flow \(U_0=-0.5\), b complex frequency of the first absolutely unstable helical mode \(\omega _0\)

Full size image

4.2 Swirling annular jet

To control the mixing in annular jets it is interesting to know how the swirl intensity influences the first helical mode frequency as well as the temporal growth rate. Other important parameters are the shape of the azimuthal velocity profile and location of the maximum of the azimuthal velocity profile with respect to the maximum of the axial velocity. In all the results shown in this section the axial velocity profiles were fixed as for the test cases \(In_1BF_{03}\) and \(In_1BF_{05}\) (see Tables 1 and 3) for back-flow velocities \(U_0=-0.3\) and \(U_0=-0.5\), respectively. Two types of azimuthal velocity profiles were applied described by \(N_W=2\) and 5, varying the swirl intensity A. Sample tangential velocity profiles for the swirl number \(A=0.5\) and two different \(N_W\)-parameters associated with the axial velocity profiles with the back-flow velocity \(U_0=-0.3\) are shown in Fig. 18. In the cases shown in this figure maxima of axial and azimuthal velocity coincide.

Figure  19a shows an influence of the swirl number on the complex frequency of the absolutely unstable first helical mode for two different azimuthal velocity profiles. The real part of the complex frequency grows with the swirl intensity for both types of the azimuthal velocity profiles. The absolute temporal growth rate \(\omega _{0,i}\) for both profiles of the azimuthal velocity reveals a maximum value for a certain limited value of the swirl number. For the wider velocity profile with \(N_W=2\) the maximum growth rate is obtained for the swirl number \(A \approx 0.5\) while for the more compact azimuthal velocity with \(N_W=5\) the maximum growth rate is obtained for a higher swirl number \(A \approx 0.6\). However, the maximum values of the growth rates in both cases are very close. These results show that the shape of the tangential velocity profile has quite a limited influence on the absolutely unstable first helical mode. This mode could be promoted by a certain limited value of the swirl that influences both frequency and the growth rate while a shape of the azimuthal velocity profile is of the secondary importance.

Analogous calculations were performed for the axial velocity profile with the back-flow \(U_0=-0.5\). The results are shown in Fig. 19b. As it was already observed for the annular non-swirling jet a higher back-flow causes a decrease of the frequency and increase of the growth rate. The same behaviour can be observed for swirling jet. In this case it is also a certain degree of swirl for which the growth rate attains its maximum. For more compact azimuthal velocity profile \(N_W=5\) this maximum appears for \(A \approx 0.6\) that means at the same swirl number as for the smaller back-flow \(U_0=-0.3\). For a wider azimuthal velocity profile a similar conclusion can be derived as the maximum growth rate is for \(A \approx 0.5\).

Figure 20 shows an influence of the swirl number on the shape of eigenfunctions for the back-flow velocity \(U_0=-0.3\). The maximum of the pressure perturbations shifts to the jet axis along with the growing swirl intensity. An influence of the limited swirl on the velocity perturbation is weak while for the highest swirl number both eigenfunctions change significantly. A similar influence of the swirl number on the eigenfunctions was observed for the stronger back-flow \(U_0=-0.5\) shown in Fig. 21, however, in this case the influence of the swirl intensity is slightly weaker.

Further analysis was devoted to an influence of a certain shift of the maximum azimuthal velocity with respect to the maximum of the axial velocity. As before the axial velocity profiles were fixed and the analysis was carried out for two back-flow velocities \(U_0=-0.3\) and \(U_0=-0.5\). Figure 22 shows all the azimuthal velocity profiles analysed with the axial velocity profile for the back-flow \(U_0=-0.3\). The radius of the maximum of the azimuthal velocity varied in a wide range \(r_{Wmax}=0.5-1.4\). Hence, the swirl could be concentrated close to the jet axis or further in the jet periphery. In practical application this effect could be attained by a design of the guide-vanes producing the swirling motion. The calculations were limited to one swirl number \(A=0.5\) that is close the value leading to the maximum of the growth rate. Only one value of \(N_W=5\) was analysed since this parameter slightly influences the first azimuthal mode. The results for the back-flow \(U_0=-0.3\) are shown in Fig. 23a. Shifting the maximum of the azimuthal velocity with respect to the maximum of the axial velocity in the direction of the jet axis results in a slight increase of the absolute growth rate and frequency. However, decreasing the \(r_{Wmax}\) below 0.6 leads to a certain drop of the growth rate while the frequency is still growing. A shift of the maximum of the azimuthal velocity to the jet periphery results in a monotonic decrease of both the frequency and the growth rate. A slightly different situation was observed in the case of \(U_0=-0.5\) shown in Fig. 23b. In this case concentrating a swirl close to the jet axis leads to an increase of both the frequency and the absolute growth rate.

Finally, to have a complete picture of the flow instability an analysis of the second helical absolutely unstable mode was performed. The calculations were limited to the azimuthal velocity profile with parameter \(N_W=5\) and with the maximum coinciding with the maximum of the axial velocity profile. The results for a varying swirl intensity for both back-flow velocities are shown in Fig. 24. The results for the second mode are compared with the results obtained for the first helical mode with the same base flow. It can be seen that the frequency of the second absolutely unstable helical mode is significantly higher than the frequency of the first mode. The frequency grows along with the swirl intensity. The absolute growth rate varies weakly with the swirl number for both back-flow velocities. In the case of the weaker back-flow the growth rate of the second mode exceeds the growth rate of the first mode for a swirl number \(A>0.9\), while in the case of the stronger back-flow it happens for a slightly higher swirl number. One could expect that for the swirl number for which absolute growth rate of both modes are close each other both modes can appear alternately. Figures 25 and 26 show the eigenfunctions for the second mode for both back-flow velocities. The maxima of the eigenfunctions shift to the jet axis along with the growing swirl number. The shapes of the eigenfunctions for both back-flow velocities are similar.

Fig. 18
figure 18

Sample azimuthal velocity profiles for \(A=0.5\), \(N_W=2\) and \(N_W=5\) associated with the axial velocity profile with the back-flow \(U_0=-0.5\)

Full size image
Fig. 19
figure 19

Influence of the swirl intensity on the complex frequency of the first absolutely unstable azimuthal mode for two different azimuthal velocity profiles: a \(U_0=-0.3\), b \(U_0=-0.5\)

Full size image
Fig. 20
figure 20

Influence of the swirl intensity on eigenfunctions of the first absolutely unstable helical mode, back-flow \(U_0=-0.3\): a pressure perturbation b velocity perturbation

Full size image
Fig. 21
figure 21

Influence of the swirl intensity on eigenfunctions of the first absolutely unstable helical mode, back-flow \(U_0=-0.5\): a pressure perturbation b velocity perturbation

Full size image
Fig. 22
figure 22

Sample azimuthal velocity profiles for \(A=0.5\) and \(N_W=5\), varying \(r_{Wmax}\), associated with the axial velocity profile with the back-flow \(U_0=-0.3\)

Full size image
Fig. 23
figure 23

Influence of the shift of the azimuthal and axial velocity profiles on the complex frequency of the first absolutely unstable helical mode, \(A=0.5\), \(N_W=5\): a \(U_0=-0.3\), b \(U_0=-0.5\)

Full size image
Fig. 24
figure 24

Influence of the swirl intensity on the complex frequency of the second absolutely unstable azimuthal mode for two different azimuthal velocity profiles, compared with the fisrt helical mode, \(N_W=5\): a \(U_0=-0.3\), b \(U_0=-0.5\)

Full size image
Fig. 25
figure 25

Influence of the swirl intensity on eigenfunctions of the second helical mode, back-flow \(U_0=-0.3\), \(N_W=5\): a pressure perturbation b velocity perturbation

Full size image
Fig. 26
figure 26

Influence of the swirl intensity on eigenfunctions of the second helical mode, back-flow \(U_0=-0.5\), \(N_W=5\): a pressure perturbation b velocity perturbation

Full size image

5 Conclusions

The paper presented the spatio-temporal linear local stability analysis of an annular jet without and with a swirl. A new approach was formulated to describe both axial and azimuthal velocity profiles. An axial velocity profile is described by a combination of hyperbolic tangent functions allowing an independent steepness control of the inner and outer shear layers. A modified Hammel–Oseen vortex velocity profile was proposed to control the shape of tangential velocity. The calculations were aimed at an analysis of the influence of the axial velocity radial gradients on the characteristics of the first azimuthal absolute mode. It turned out that increasing a steepness of the inner shear layer promotes absolute instability and the temporal growth rate is increased. A steepness of the inner shear layer has a weak influence on the absolute mode frequency. On the contrary, a steepness of the outer shear layer has no influence on the absolute growth rate while leads to a certain decrease of the oscillations frequency. Increasing a steepness in both inner and outer shear layers leads to, as shown also by Michalke [19], an increased absolute growth rate and a decreased frequency. The calculations performed confirm also conclusion derived by Michalke that a stronger back-flow promotes absolute growth rate and decreases the frequency of the first azimuthal absolute mode. A limited amount of swirl promotes the first helical absolute mode. Swirling increases also frequency of this mode. A shape of the tangential velocity has a certain influence on the instability characteristics. The more compact tangential velocity profile the higher is swirl number with the maximum growth rate. Shifting the maximum of the tangential velocity to the jet axis results in an increase of the absolute mode frequency. The influence of this shift is more pronounced for a higher back-flow. Finally, the second helical absolutely unstable mode was analysed. It was shown that the second mode is characterised by a significantly higher frequency than the first mode. In the case of a stronger swirl intensity the absolute growth rate of the second helical mode is higher than the growth rate of the first one suggesting that in such cases double helical structures can be observed.