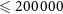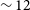1. Introduction
In 2016, the Laser Interferometer Gravitational-Wave Observatory (LIGO) Scientific Collaboration (LSC) announced the first detection of gravitational waves (GWs), produced by a black hole binary (BHB) merger (Abbott et al. Reference Abbott2016c). The detection sparked a new era for astronomy. GW astronomy has been used to measure black hole (BH) properties more accurately than ever before, including spins, masses, and BHB merger rates. At the end of LIGO’s second observing run (O2), there have been 11 reported GW events, 10 from BHB mergers and 1 from a binary neutron star merger (Abbott et al. Reference Abbott2016a, Reference Abbott2016c, Reference Abbott2016d; Abbott et al. Reference Abbott2017a, Reference Abbott2017b; The LIGO Scientific Collaboration et al. 2018; Stoyan, Binnewies, & Friedrich Reference Stoyan, Binnewies and Friedrich2008). With the completion of the O3 run on 2020 March 27, the first few GW BHB detections have been published (Abbott et al. 2020a; 2020b; Reference Abbott2020c), and there will soon be an expanded catalog of BHB merger detections which will allow for detailed comparisons with theoretical models, reportedly including a total of 56 GW detections (LSC 2020).
The origin of merging BHBs is still mostly unknown. There are two broad formation channels: common envelope evolution and dynamical evolution. In the common envelope evolution channel, the BHB progenitors form together in a stellar binary system and co-evolve (Belczynski, Kalogera, & Bulik Reference Belczynski, Kalogera and Bulik2002; Belczynski et al. Reference Belczynski, Holz, Bulik and O’Shaughnessy2016a; Reference Belczynski, Repetto, Holz, O’Shaughnessy, Bulik, Berti, Fryer and Dominik2016b; Dominik et al. Reference Dominik, Belczynski, Fryer, Holz, Berti and Bulik2012; Reference Dominik, Belczynski, Fryer, Holz, Berti and Bulik2013), isolated from gravitational interactions with other stellar objects. In the dynamical evolution channel, the BHB forms via gravitational interactions with other stellar bodies (O’Leary et al. Reference O’Leary, Rasio, Fregeau, Ivanova and O’Shaughnessy2006; O’Leary, O’Shaughnessy, & Rasio Reference O’Leary, O’Shaughnessy and Rasio2007; Banerjee, Baumgardt, & Kroupa Reference Banerjee, Baumgardt and Kroupa2010; Tanikawa Reference Tanikawa2013; Choksi, Gnedin, & Li Reference Choksi, Gnedin and Li2018), with evolution strongly dependent on dynamical processes within dense environments, like young star clusters or globular clusters (GCs) (Baumgardt et al. Reference Baumgardt, Makino, Hut, McMillan and Zwart2003).
In order to better understand the formation of merging BHBs, work has been done to model the evolution of compact binaries based on the current understanding of stellar formation and evolution. Of particular interest is the modelling of dense star clusters through both direct N-body and Monte Carlo (MC) methods (McMillan Reference McMillan2015; Banerjee et al. Reference Banerjee, Baumgardt and Kroupa2010; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017; Rodriguez, Chatterjee, & Rasio Reference Rodriguez, Chatterjee and Rasio2016; Rodriguez et al. Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Giersz et al. Reference Giersz, Askar, Wang, Hypki, Leveque, Spurzem, Bragaglia, Davies, Sills and Vesperini2020; Askar, Arca Sedda, & Giersz Reference Askar, Arca Sedda and Giersz2018; Askar et al. Reference Askar, Giersz, Arca Sedda, Askar, Pasquato, Leveque, Bragaglia, Davies, Sills and Vesperini2020; Hong et al. Reference Hong, Vesperini, Askar, Giersz, Szkudlarek and Bulik2018; Samsing et al. Reference Samsing2018; Arca Sedda et al. Reference Arca Sedda, Mapelli, Spera, Benacquista and Giacobbo2020; Samsing & D’Orazio Reference Samsing and D’Orazio2018; Arca Sedda & Mastrobuono-Battisti Reference Arca Sedda and Mastrobuono-Battisti2019; Kremer et al. 2019; Reference Kremer2020; Rodriguez et al. Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019b; Antonini & Gieles Reference Antonini and Gieles2020). GCs naturally provide the dense stellar environment and low metallicities required to produce high-mass BH mergers through the dynamical evolution channel (Mandel & Farmer Reference Mandel and Farmer2018). Belczynski et al. (Reference Belczynski, Dominik, Bulik, O’Shaughnessy, Fryer and Holz2010) even proposed that low-metallicity massive star progenitors dominate the BHB merger rate. Metallicity effects the progenitor mass and the mass loss rate, as (1) cooling is suppressed in low-metallicity gas clouds, leading to little fragmentation (Stahler & Palla Reference Stahler and Palla2005; Celoria et al. Reference Celoria, Oliveri, Sesana and Mapelli2018) and (2) low-metallicity stars also experience less extreme stellar winds because of their lower opacity, resulting in lower mass loss and heavier stellar remnants (Heger et al. Reference Heger, Fryer, Woosley, Langer and Hartmann2003). Recent work has also focused on modelling BHB mergers in open clusters, which tend to be smaller and younger than GCs (Banerjee 2017; 2018a; 2018b; Reference Banerjee2020a; Rastello et al. Reference Rastello, Amaro-Seoane, Arca-Sedda, Capuzzo-Dolcetta and Fragione2019; Di Carlo et al. Reference Di Carlo, Giacobbo, Mapelli, Pasquato, Spera, Wang and Haardt2019; Reference Di Carlo2020). Banerjee (Reference Banerjee2017) used direct N-body simulations of young, massive open clusters to investigate BHB formation. They found a prevalence for in-cluster mergers mediated by three-body interactions, as opposed to systems merging after ejection from their host cluster.
Separate but related work has focused on nuclear star clusters, dense, luminous star clusters within galactic nuclei. Modelling of dynamical formation of BHBs within nuclear star clusters provides insight into another potential source of GW events (Antonini & Rasio Reference Antonini and Rasio2016; Fragione, Perna, & Loeb Reference Fragione, Perna and Loeb2020a; Hoang et al. Reference Hoang, Naoz, Kocsis, Rasio and Dosopoulou2018; Fragione & Silk Reference Fragione and Silk2020; Davies, Askar, & Church Reference Davies, Askar, Church, Bragaglia, Davies, Sills and Vesperini2020). The unique properties of nuclear star clusters allow for different pathways leading to GW events. For example, Fragione et al. (Reference Fragione, Loeb, Kremer and Rasio2020b) propose a formation channel for intermediate mass BH (IMBH) mergers with stellar BHs through GW capture.
As GCs evolve, heavier stars segregate towards the core in an attempt to establish partial energy equipartition (Trenti & van der Marel Reference Trenti and van der Marel2013), and BHs experience frequent strong dynamical interactions among themselves and with other massive bodies. These include various three- and four-body interactions, such as hardening and exchange, leading to tighter binaries and more mergers. Dynamically formed BHBs differ from isolated binaries in that they can be driven to measurable eccentricities when entering the LIGO frequency band (Rodriguez et al. Reference Rodriguez, Amaro-Seoane, Chatterjee, Kremer, Rasio, Samsing, Ye and Zevin2018). The high central densities of GCs make it also possible to dynamically form hierarchical triplet systems, three-body systems with a tight inner binary and wide companion, with an expectation of one triple every ![]() ${\sim}100$ binaries (Trenti et al. Reference Trenti, Ransom, Hut and Heggie2008). Through Kozai–Lidov oscillations (Lidov Reference Lidov1962; Kozai Reference Kozai1962), angular momentum can be transferred between inner and outer orbits, driving the inner orbit to significant eccentricities at the expense of the outer orbital inclination (Kozai Reference Kozai1962). As a result, a near-circular BHB which otherwise would not merge can be driven to high eccentricities, leading to efficient gravitational radiation, rapid orbital decay, and hence a merger (Celoria et al. Reference Celoria, Oliveri, Sesana and Mapelli2018). If the gravitational radiation cannot effectively circularise the system, then the Kozai–Lidov oscillations can push the binary above the 10 Hz LIGO cut-off with measurable eccentricity (Antonini & Perets Reference Antonini and Perets2012; Seto Reference Seto2013). It is also possible for a single–single or binary–single scattering event to form eccentric binaries that produce eccentric mergers through gravitational capture (Samsing Reference Samsing2018; Samsing et al. Reference Samsing, D’Orazio, Kremer, Rodriguez and Askar2019b).
${\sim}100$ binaries (Trenti et al. Reference Trenti, Ransom, Hut and Heggie2008). Through Kozai–Lidov oscillations (Lidov Reference Lidov1962; Kozai Reference Kozai1962), angular momentum can be transferred between inner and outer orbits, driving the inner orbit to significant eccentricities at the expense of the outer orbital inclination (Kozai Reference Kozai1962). As a result, a near-circular BHB which otherwise would not merge can be driven to high eccentricities, leading to efficient gravitational radiation, rapid orbital decay, and hence a merger (Celoria et al. Reference Celoria, Oliveri, Sesana and Mapelli2018). If the gravitational radiation cannot effectively circularise the system, then the Kozai–Lidov oscillations can push the binary above the 10 Hz LIGO cut-off with measurable eccentricity (Antonini & Perets Reference Antonini and Perets2012; Seto Reference Seto2013). It is also possible for a single–single or binary–single scattering event to form eccentric binaries that produce eccentric mergers through gravitational capture (Samsing Reference Samsing2018; Samsing et al. Reference Samsing, D’Orazio, Kremer, Rodriguez and Askar2019b).
In this paper, we resort to a new large set of direct N-body simulations designed to investigate properties of compact object mergers (de Vita, Trenti, & MacLeod Reference de Vita, Trenti and MacLeod2019; MacLeod, Trenti, & Ramirez-Ruiz Reference MacLeod, Trenti and Ramirez-Ruiz2016) to focus on the formation of BHBs within mid-sized star clusters containing ![]() $5\times 10^4 \leqslant N \leqslant 2\times10^5$ stars, a range that includes the
$5\times 10^4 \leqslant N \leqslant 2\times10^5$ stars, a range that includes the ![]() $8.1\times10^4\,{\rm M}_{\odot}$ median mass for Milky Way GCs (see Heggie & Hut Reference Heggie and Hut2003 Table 1.1) under a typical stellar initial mass function (IMF) even after accounting for mass loss during dynamical evolution. We compare the properties of binaries that merge within a cluster to systems that merge after they are ejected from the cluster, with the goal of understanding how the channels are represented in current and future LIGO observations. Our set of 58 direct N-body simulations explore a range of cluster structure and initial conditions. They are carried out using NBODY6 (Aarseth Reference Aarseth2003) with GPU support (Nitadori & Aarseth Reference Nitadori and Aarseth2012), an efficient code which has been used extensively in the modelling of GCs (Trenti, Vesperini, & Pasquato Reference Trenti, Vesperini and Pasquato2010; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017; Banerjee Reference Banerjee2017). NBODY6 includes subroutines for single stellar evolution (SSE) and binary stellar evolution (BSE), and dynamical interactions are incorporated directly through the equations of motion (see Section 2.1), offering distinct advantages for accuracy over approximate methods such as MC algorithms. The simulations also incorporate advanced prescriptions for relativistic effects.
$8.1\times10^4\,{\rm M}_{\odot}$ median mass for Milky Way GCs (see Heggie & Hut Reference Heggie and Hut2003 Table 1.1) under a typical stellar initial mass function (IMF) even after accounting for mass loss during dynamical evolution. We compare the properties of binaries that merge within a cluster to systems that merge after they are ejected from the cluster, with the goal of understanding how the channels are represented in current and future LIGO observations. Our set of 58 direct N-body simulations explore a range of cluster structure and initial conditions. They are carried out using NBODY6 (Aarseth Reference Aarseth2003) with GPU support (Nitadori & Aarseth Reference Nitadori and Aarseth2012), an efficient code which has been used extensively in the modelling of GCs (Trenti, Vesperini, & Pasquato Reference Trenti, Vesperini and Pasquato2010; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017; Banerjee Reference Banerjee2017). NBODY6 includes subroutines for single stellar evolution (SSE) and binary stellar evolution (BSE), and dynamical interactions are incorporated directly through the equations of motion (see Section 2.1), offering distinct advantages for accuracy over approximate methods such as MC algorithms. The simulations also incorporate advanced prescriptions for relativistic effects.
Table 1. Summary of N-body simulations

For each simulation (identified by a unique ID) we report (from left to right) the initial number of stars; the initial IMBH mass in ![]() ${\rm M}$
ʘ; the velocity dispersion of the natal kick imparted to stellar remnants
${\rm M}$
ʘ; the velocity dispersion of the natal kick imparted to stellar remnants ![]() $\sigma_k$, normalized to the initial cluster velocity dispersion
$\sigma_k$, normalized to the initial cluster velocity dispersion ![]() $\sigma_*$; the fraction of primordial binaries f; the metallicity Z; the number of distinct realizations of the same initial conditions (
$\sigma_*$; the fraction of primordial binaries f; the metallicity Z; the number of distinct realizations of the same initial conditions (![]() $N_{\textrm{sim}}$); the initial half-mass radius
$N_{\textrm{sim}}$); the initial half-mass radius ![]() $r_{\textrm{h,0}}$ in pc; the initial dimensionless potential of the King Model
$r_{\textrm{h,0}}$ in pc; the initial dimensionless potential of the King Model ![]() $W_0$ and the IMF (taken from either Kroupa Reference Kroupa2001 or Salpeter Reference Salpeter1955).
$W_0$ and the IMF (taken from either Kroupa Reference Kroupa2001 or Salpeter Reference Salpeter1955).
1Same as can100k, but with instantaneous stellar evolution
In Section 2, we describe the N-body code used in modelling the GCs, and the specific cluster models and initial conditions. In Section 3, we explore the in-cluster BHB mergers and the distribution of their parameters. In Section 4, we compare and contrast the properties of the in-cluster mergers to the BHBs that merge after being ejected from their host cluster. Finally, in Section 5, we compare our results to the 10 BHB mergers detected during LIGO O1 and O2 and explore the implications for their formation and for future detections.
2. Method
2.1. NBODY6
N-body simulations directly integrate the equations of motion (Heggie & Hut Reference Heggie and Hut2003). Unlike MC methods, they include all gravitational interactions to the desired numerical accuracy (McMillan Reference McMillan2015; Aarseth Reference Aarseth2003), without relying on simplifications of the dynamics (e.g., softening) or specific assumptions for the cross sections of close encounters. Achieving such computational accuracy comes with increased computational cost, so that the particle number we can effectively follow with current hardware in this study is limited to ![]() $N = 50\mbox{K}$,
$N = 50\mbox{K}$, ![]() $100\mbox{K}$, and
$100\mbox{K}$, and ![]() $200\mbox{K}$ stars (where
$200\mbox{K}$ stars (where ![]() $K\equiv 1\,000$). The NBODY series of codes, with NBODY6 (Aarseth Reference Aarseth1999) used in our study, have been specifically designed for the modelling of star clusters. NBODY6 employs block time step schemes and algorithmic regularisation of multi-star systems (Aarseth Reference Aarseth2003; Hut & McWillan Reference Hut and McWillan1986; Makino et al. Reference Makino, Hut, Kaplan and Saygn2006), resulting in significant improvements to the computational efficiency compared to similar direct N-body integrators.
$K\equiv 1\,000$). The NBODY series of codes, with NBODY6 (Aarseth Reference Aarseth1999) used in our study, have been specifically designed for the modelling of star clusters. NBODY6 employs block time step schemes and algorithmic regularisation of multi-star systems (Aarseth Reference Aarseth2003; Hut & McWillan Reference Hut and McWillan1986; Makino et al. Reference Makino, Hut, Kaplan and Saygn2006), resulting in significant improvements to the computational efficiency compared to similar direct N-body integrators.
NBODY6 implements SSE and BSE through SSE and BSE algorithms, respectively (see Hurley, Pols, & Tout Reference Hurley, Pols and Tout2000; Hurley, Tout, & Pols Reference Hurley, Tout and Pols2013), which have been designed to handle complex evolutionary processes, including mass transfer, common envelope evolution, collisions, and supernova kicks. General relativistic effects are also implemented through the Peters orbital evolution equations (Peters & Mathews Reference Peters and Mathews1963) and post-Newtonian terms through BSE. This allows for accurate treatment of close encounters of compact bodies, including gravitational radiation. The version of NBODY6 we use was forked from the official branch in 2015 and customised for increased accuracy in the sphere of influence of a BH (see Trenti et al. Reference Trenti, Vesperini and Pasquato2010 for further details). Note that our version does not include the recently implemented upgrades to some stellar evolution prescriptions for massive stars (stellar wind, mass fallback, and pair-instability supernova) presented in Banerjee et al. (Reference Banerjee, Belczynski, Fryer, Berczik, Hurley, Spurzem and Wang2019). While we do not expect significant changes to our key results as these are relatively minor changes to an already complex code, we plan to run a new set of simulations as a follow-up to this work using the code resulting from the merger of our customisations and the current NBODY version.
For compact binary systems located inside the simulated star cluster, merger times are calculated by the BSE algorithm directly. For BHBs that are ejected from the cluster before merging, inspiral times are calculated in post-processing using the orbit-averaged Peters equation, since NBODY6 stops computing stellar evolution for particles ejected from the system. The inspiral time in these cases can be approximated by the integral (Peters Reference Peters1964b):
 \begin{eqnarray} & & T_{\text{insp}}(a_0,e_0, M_1, M_2) = \frac{12}{19}\frac{{c_0}^4}{\beta} \nonumber \\[3pt] & & \qquad\times \int_0^{e_0}\frac{e^{29/19}\left(1 + \frac{121}{304}e^2\right)^{1\,181/2\,299}}{(1 - e^2)^{3/2}}de,\end{eqnarray}
\begin{eqnarray} & & T_{\text{insp}}(a_0,e_0, M_1, M_2) = \frac{12}{19}\frac{{c_0}^4}{\beta} \nonumber \\[3pt] & & \qquad\times \int_0^{e_0}\frac{e^{29/19}\left(1 + \frac{121}{304}e^2\right)^{1\,181/2\,299}}{(1 - e^2)^{3/2}}de,\end{eqnarray}
with ![]() $\beta = \frac{64}{5}\frac{G^3}{c^5}M_1M_2\left(M_1 + M_2\right)$, where
$\beta = \frac{64}{5}\frac{G^3}{c^5}M_1M_2\left(M_1 + M_2\right)$, where ![]() $M_1$ and
$M_1$ and ![]() $M_2$ are the primary and secondary masses, respectively,
$M_2$ are the primary and secondary masses, respectively, ![]() $a_0$ and
$a_0$ and ![]() $e_0$ are the semi-major axis and eccentricity, respectively, upon ejection from the cluster, and
$e_0$ are the semi-major axis and eccentricity, respectively, upon ejection from the cluster, and ![]() $c_0$ is a constant fixed by
$c_0$ is a constant fixed by ![]() $a_0$ and
$a_0$ and ![]() $e_0$, given by (Peters Reference Peters1964b):
$e_0$, given by (Peters Reference Peters1964b):
2.2. Gravitational recoil
Depending on the orientation of a compact binary and the spins of its components, merger remnants can experience significant recoil due to the asymmetric emission of GWs (Peres Reference Peres1962; Bekenstein Reference Bekenstein1973; Fitchett & Detweiler Reference Fitchett and Detweiler1984). Full calculations for gravitational recoil require numerical relativity. Our simulations do not include recoil kicks to remnants from BH mergers computed on the fly, as this was not implemented in NBODY6 before initial submission of this paper (O’Leary et al. Reference O’Leary, Rasio, Fregeau, Ivanova and O’Shaughnessy2006; Banerjee et al. Reference Banerjee, Baumgardt and Kroupa2010; Bae, Kim, & Lee Reference Bae, Kim and Lee2014; Tanikawa Reference Tanikawa2013; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017).Footnote a A caveat is that numerical modelling has shown that the recoil speed may exceed ![]() $1\,000\,\text{kms}^{-1}$ in special cases (Campanelli et al. Reference Campanelli, Lousto, Zlochower and Merritt2007), and so some of our results may be impacted by the lack of gravitational recoil physics. Future simulations will explore the feasibility of including this additional physics to improve the realism of our numerical modelling.
$1\,000\,\text{kms}^{-1}$ in special cases (Campanelli et al. Reference Campanelli, Lousto, Zlochower and Merritt2007), and so some of our results may be impacted by the lack of gravitational recoil physics. Future simulations will explore the feasibility of including this additional physics to improve the realism of our numerical modelling.
In order to at least partially account for gravitational recoils in our simulations, we apply an approximate treatment of this additional physical ingredient in post-processing. For this, we use an analytic approximation for the recoil velocity, dependent on the symmetric mass ratio presented in Sopuerta, Yunes, & Laguna (Reference Sopuerta, Yunes and Laguna2006):
where ![]() $\eta = \frac{M_1M_2}{(M_1 + M_2)^2}$ is the symmetric mass ratio, and a, b, and c are free parameters. Sopuerta et al. (Reference Sopuerta, Yunes and Laguna2006) presented multiple models to fit the free parameters. We implement a fit in between the lower and upper bound, corresponding to
$\eta = \frac{M_1M_2}{(M_1 + M_2)^2}$ is the symmetric mass ratio, and a, b, and c are free parameters. Sopuerta et al. (Reference Sopuerta, Yunes and Laguna2006) presented multiple models to fit the free parameters. We implement a fit in between the lower and upper bound, corresponding to ![]() $a = 9082$,
$a = 9082$, ![]() $b = -1.43$, and
$b = -1.43$, and ![]() $c = 1.68$. Using this analytic approximation, we calculate the gravitational velocity kick for all in-cluster BHB mergers and determine whether the merger remnant is ejected from its cluster as a result of the kick. Using this information, we construct a refined set of BHB mergers trees which exclude any binaries containing a remnant BH flagged to have been ejected due a previous merger kick. We refer to this set of BHBs as retained in-cluster mergers. Note as a caveat that this analytic model is merely an approximation, and among other aspects does not account for BH spins. Also, the BHs flagged as ejected are retained in the system and more likely to interact with other BHs because of their higher mass; hence, this approach might be too conservative in removing merger events from our analysis, but it nevertheless provides an indication of the likely impact of the recoils on our results. For completeness, we also consider in our analysis the baseline scenario where recoils are ignored.
$c = 1.68$. Using this analytic approximation, we calculate the gravitational velocity kick for all in-cluster BHB mergers and determine whether the merger remnant is ejected from its cluster as a result of the kick. Using this information, we construct a refined set of BHB mergers trees which exclude any binaries containing a remnant BH flagged to have been ejected due a previous merger kick. We refer to this set of BHBs as retained in-cluster mergers. Note as a caveat that this analytic model is merely an approximation, and among other aspects does not account for BH spins. Also, the BHs flagged as ejected are retained in the system and more likely to interact with other BHs because of their higher mass; hence, this approach might be too conservative in removing merger events from our analysis, but it nevertheless provides an indication of the likely impact of the recoils on our results. For completeness, we also consider in our analysis the baseline scenario where recoils are ignored.
2.3. Cluster models
The simulations in this paper are a combination of 33 runs from de Vita et al. (Reference de Vita, Trenti and MacLeod2019), which have been augmented by an additional 25 simulations for a total of 58 realisations, which are summarised in Table 1. In the current paper, we analyse the population of BHB mergers produced by these simulations. We organise the simulations into three main groups based on initial particle number with ![]() $N = 50$K (11 simulations), 100 K (42 simulations), and 200 K (5 simulations). The majority of the simulations are initialised with 100 K particles, as this represents the best compromise between run time and realistic cluster size. Metallicity, primordial binary fraction, stellar remnant natal kick distribution, half-mass radius, IMF, dimensionless potential, and the presence of an IMBH vary across simulations to explore a wide range of parameter space. For some models, multiple independent realisations of the same set of parameters are followed to probe run-to-run variations.
$N = 50$K (11 simulations), 100 K (42 simulations), and 200 K (5 simulations). The majority of the simulations are initialised with 100 K particles, as this represents the best compromise between run time and realistic cluster size. Metallicity, primordial binary fraction, stellar remnant natal kick distribution, half-mass radius, IMF, dimensionless potential, and the presence of an IMBH vary across simulations to explore a wide range of parameter space. For some models, multiple independent realisations of the same set of parameters are followed to probe run-to-run variations.
Three metallicities are considered: ![]() $0.083\,{\rm Z}_{\odot}$,
$0.083\,{\rm Z}_{\odot}$, ![]() $0.16\,{\rm Z}_{\odot}$, and
$0.16\,{\rm Z}_{\odot}$, and ![]() $1.6\,{\rm Z}_{\odot}$. The
$1.6\,{\rm Z}_{\odot}$. The ![]() $0.083\,{\rm Z}_{\odot}$ and
$0.083\,{\rm Z}_{\odot}$ and ![]() $0.16\,{\rm Z}_{\odot}$ models are in the middle to upper range of the Milky Way GC metallicity distribution (Harris Reference Harris1996). The
$0.16\,{\rm Z}_{\odot}$ models are in the middle to upper range of the Milky Way GC metallicity distribution (Harris Reference Harris1996). The ![]() $1.6\,{\rm Z}_{\odot}$ model is more metallic than Milky Way clusters and is only used in one simulation to test the effects of high metallicity on cluster evolution. Although the LIGO GW events do not come from Milky Way clusters, the distribution of extra-galactic GC metallicities is not well constrained, and so we cannot make comparisons to our model metallicities. Exploration of the impact of further reductions in the initial metallicity will be devoted to future work.
$1.6\,{\rm Z}_{\odot}$ model is more metallic than Milky Way clusters and is only used in one simulation to test the effects of high metallicity on cluster evolution. Although the LIGO GW events do not come from Milky Way clusters, the distribution of extra-galactic GC metallicities is not well constrained, and so we cannot make comparisons to our model metallicities. Exploration of the impact of further reductions in the initial metallicity will be devoted to future work.
We consider clusters with initial half-mass radii (![]() $r_h$) of
$r_h$) of ![]() $1.5,2.5,4$, and 6 pc. All models are assumed to be spherically symmetric, with initial conditions drawn from a King (Reference King1966) distribution. The spherical density profile,
$1.5,2.5,4$, and 6 pc. All models are assumed to be spherically symmetric, with initial conditions drawn from a King (Reference King1966) distribution. The spherical density profile, ![]() $\rho(r)$, is characterised by a dimensionless concentration parameter:
$\rho(r)$, is characterised by a dimensionless concentration parameter:
where ![]() $\sigma_o$ is the central velocity dispersion and
$\sigma_o$ is the central velocity dispersion and ![]() $\phi_o$ is the corresponding central potential. We consider systems with
$\phi_o$ is the corresponding central potential. We consider systems with ![]() $W_o = 3,5$, and 7, representing relatively extended systems to relatively concentrated systems (Heggie & Hut Reference Heggie and Hut2003). Most simulations have
$W_o = 3,5$, and 7, representing relatively extended systems to relatively concentrated systems (Heggie & Hut Reference Heggie and Hut2003). Most simulations have ![]() $W_o = 7$ as this is a value close to the long-term concentration of typical simulated star clusters, which is reached after the system relaxes irrespective of the initial concentration (see Trenti, Heggie, & Hut Reference Trenti, Heggie and Hut2007).
$W_o = 7$ as this is a value close to the long-term concentration of typical simulated star clusters, which is reached after the system relaxes irrespective of the initial concentration (see Trenti, Heggie, & Hut Reference Trenti, Heggie and Hut2007).
Particle masses are drawn from either a Kroupa (Reference Kroupa2001) or Salpeter (Reference Salpeter1955) IMF of the form:
with
for the Salpeter IMF, and
 \[ \alpha = \begin{cases} -0.3 & M < 0.08\,{\rm M}_{\odot} \\[3pt] -1.3 & 0.08\,{\rm M}_{\odot}\leq M \leq 0.5\,{\rm M}_{\odot} \\[3pt] -2.3 & 0.5\,{\rm M}_{\odot} \leq M \end{cases}\]
\[ \alpha = \begin{cases} -0.3 & M < 0.08\,{\rm M}_{\odot} \\[3pt] -1.3 & 0.08\,{\rm M}_{\odot}\leq M \leq 0.5\,{\rm M}_{\odot} \\[3pt] -2.3 & 0.5\,{\rm M}_{\odot} \leq M \end{cases}\]
for the Kroupa IMF. Regardless of IMF, we generate particle masses in the range ![]() $ 0.08$–
$ 0.08$–![]() $100\,{\rm M}_{\odot}$. In addition to regular particles drawn from an IMF, a small subset of models contain an IMBH. The IMBHs are generated with a mass of either
$100\,{\rm M}_{\odot}$. In addition to regular particles drawn from an IMF, a small subset of models contain an IMBH. The IMBHs are generated with a mass of either ![]() $100\,{\rm M}_{\odot}$,
$100\,{\rm M}_{\odot}$, ![]() $200\,{\rm M}_{\odot}$, or
$200\,{\rm M}_{\odot}$, or ![]() $400\,{\rm M}_{\odot}$, corresponding to 0.15–0.3% of the initial cluster mass, and hence either begin as or rapidly become the most massive particle in the cluster. We initialise the IMBHs as static (zero kinetic energy) particles in the centre of the potential well and allow them to interact and merge with other particles so that they wander within the host cluster; see MacLeod et al. (Reference MacLeod, Trenti and Ramirez-Ruiz2016) and de Vita, Trenti, & MacLeod (Reference de Vita, Trenti and MacLeod2018) for more details. Although mergers between IMBHs and stellar mass black holes (SMBHs) do occur in the simulations, we do not include them in our analysis and refer instead to MacLeod et al. (Reference MacLeod, Trenti and Ramirez-Ruiz2016).
$400\,{\rm M}_{\odot}$, corresponding to 0.15–0.3% of the initial cluster mass, and hence either begin as or rapidly become the most massive particle in the cluster. We initialise the IMBHs as static (zero kinetic energy) particles in the centre of the potential well and allow them to interact and merge with other particles so that they wander within the host cluster; see MacLeod et al. (Reference MacLeod, Trenti and Ramirez-Ruiz2016) and de Vita, Trenti, & MacLeod (Reference de Vita, Trenti and MacLeod2018) for more details. Although mergers between IMBHs and stellar mass black holes (SMBHs) do occur in the simulations, we do not include them in our analysis and refer instead to MacLeod et al. (Reference MacLeod, Trenti and Ramirez-Ruiz2016).
Natal kicks, drawn from a Maxwellian distribution, are imparted to stellar remnants to account for asymmetry in core-collapse supernova explosions (see de Vita et al. Reference de Vita, Trenti and MacLeod2019 for further explanation). Larger natal kicks can contribute to the disruption of stellar binaries. However, this is not expected to impact the number of BHB mergers significantly, as most BHBs form dynamically.
We initialise some models with a certain fraction of primordial binaries, f, such that there are ![]() $Nf/2$ primordial binaries, and
$Nf/2$ primordial binaries, and ![]() $N(1-f)$ single stars. This is done by randomly selecting
$N(1-f)$ single stars. This is done by randomly selecting ![]() $Nf/2$ particles drawn from the IMF and assigning a companion based on the mass ratio distribution
$Nf/2$ particles drawn from the IMF and assigning a companion based on the mass ratio distribution ![]() $f(q) = 0.6q^{-0.4}$ (Kouwenhoven et al. Reference Kouwenhoven, Brown, Portegies Zwart and Kaper2007). We predict that the primordial binary mass ratio distribution has little effect on the mass ratio of compact body mergers, as binaries are expected to undergo multiple exchange events prior to merger. The eccentricities,
$f(q) = 0.6q^{-0.4}$ (Kouwenhoven et al. Reference Kouwenhoven, Brown, Portegies Zwart and Kaper2007). We predict that the primordial binary mass ratio distribution has little effect on the mass ratio of compact body mergers, as binaries are expected to undergo multiple exchange events prior to merger. The eccentricities, ![]() $0 \leqslant e \leqslant 1$, for primordial binaries are selected from a thermal (i.e., uniform) distribution (Jeans Reference Jeans1919):
$0 \leqslant e \leqslant 1$, for primordial binaries are selected from a thermal (i.e., uniform) distribution (Jeans Reference Jeans1919):
Finally, the initial binary separations are drawn from a uniform distribution in ![]() $\log a_o$ (default NBODY6 choice), with a lower limit of
$\log a_o$ (default NBODY6 choice), with a lower limit of ![]() $a_{\min} = 0.1\,\text{AU}$ and an upper limit of
$a_{\min} = 0.1\,\text{AU}$ and an upper limit of ![]() $a_{\max} = 10\,\text{AU}$ to produce both short- and long-period binaries. This choice ensures a majority of primordial binaries are not disrupted during early stellar evolution (Heggie Reference Heggie1975).
$a_{\max} = 10\,\text{AU}$ to produce both short- and long-period binaries. This choice ensures a majority of primordial binaries are not disrupted during early stellar evolution (Heggie Reference Heggie1975).
The simulations include tidal forces between the cluster and host galaxy. All models are placed in a circular orbit around a point mass galaxy at a galactocentric distance of ![]() $23.3\,\text{kpc}$. Clusters are assumed to under-fill their tidal radius by a factor of three. Clusters are also initialised in dynamical equilibrium, assuming a virial ratio of
$23.3\,\text{kpc}$. Clusters are assumed to under-fill their tidal radius by a factor of three. Clusters are also initialised in dynamical equilibrium, assuming a virial ratio of ![]() $Q = 0.5$ (absolute value of the ratio between gravitational potential energy and kinetic energy).
$Q = 0.5$ (absolute value of the ratio between gravitational potential energy and kinetic energy).
Most of the simulations are run up to a cluster age ![]() $t=12.5$ Gyr or terminated if the particle number reaches
$t=12.5$ Gyr or terminated if the particle number reaches ![]() $0.3\text{N}$ due to tidal dissolution. de Vita et al. (Reference de Vita, Trenti and MacLeod2019) include further details on the initial conditions, as well as on the cluster models used.
$0.3\text{N}$ due to tidal dissolution. de Vita et al. (Reference de Vita, Trenti and MacLeod2019) include further details on the initial conditions, as well as on the cluster models used.
We resort to an extended range of initial conditions to represent the wide range of sizes, masses, concentrations, and metallicities of real-world mid-sized GCs. While in principle the underlying physics of GCs (such as the natal kicks and primordial binary fraction) should remain the same irrespective of other initial conditions for real clusters, the actual values realised in nature for these degrees of freedom remain debated topics in the literature. Therefore, we explore a number of different models to investigate systems that differ in primordial binary fraction and natal kick distribution. See Section 5.2 for a discussion on our model comparison and validation against LIGO results. For an investigation of how varying the binary fraction and natal kicks impact key results, see Appendix A instead.

Figure 1. In-cluster BHB merger rate (orange) and total number of BHs across all clusters (blue) as functions of time. As a cluster ages, the population of BHs evaporates, with the process driven primarily by dynamical ejections.
3. In-cluster BHB mergers
From our 58 simulations, there are 97 stellar BHB mergers within the clusters: 10 from the 11 50 K simulations, 85 from the 42100 K simulations and 7 from the 5 200 K simulations. These merger counts are qualitatively consistent with those reported by other studies with GCs of similar size and parameters (Banerjee et al. Reference Banerjee, Baumgardt and Kroupa2010). For each merger, we record the merger time, component masses, mass ratio, and mass loss. We also track the history of the two components, including information about previous dynamical encounters and initial conditions.
Figure 1 shows the evolution of merger number across all simulations as a function of the age of the star cluster. On average, mergers occur at a higher frequency earlier in the life of a cluster. This is mostly a result of the BH population evaporating due to dynamical ejection. As the number of BHs decreases, it becomes more difficult to form BHBs, and hence mergers become less frequent. We display the evolution of the number of BHs across all simulations as a function of time to show this population evaporation in Figure 1. After the rapid formation of BHs by stellar evolution in the first few tens of Myr (with a substantial fraction ejected by natal kicks), we see a steady decrease over time as the cluster evolves and the BH number changes via dynamical processes (mergers and ejections). Interestingly, the number of mergers roughly follows this steady decrease in BH number (see Section 3.2).
We define the quantity ![]() $N_{\text{retention}}$ as the number of BHs that remain in their host cluster after natal kicks. We also define
$N_{\text{retention}}$ as the number of BHs that remain in their host cluster after natal kicks. We also define ![]() $N_{\text{merger}}$ as the number of in-cluster BHB mergers that occur in a given simulation. Combining these two quantities, we define scaled merger number:
$N_{\text{merger}}$ as the number of in-cluster BHB mergers that occur in a given simulation. Combining these two quantities, we define scaled merger number:
Investigating the relationship between primordial binary fraction, f and ![]() $N_{\text{scaled}}$, we test for a non-parametric correlation using Spearman’s rank-order correlation testFootnote b. We find a correlation coefficient of
$N_{\text{scaled}}$, we test for a non-parametric correlation using Spearman’s rank-order correlation testFootnote b. We find a correlation coefficient of ![]() $\rho = -0.54$ with a p-value of
$\rho = -0.54$ with a p-value of ![]() $0.27$, meaning that there is no statistically significant correlation between f and scaled merger number. When testing for the correlation, we only use canonical simulations (
$0.27$, meaning that there is no statistically significant correlation between f and scaled merger number. When testing for the correlation, we only use canonical simulations (![]() $f = 0$) and simulations with primordial binaries, with all other initial conditions held constant. For example, we use the ‘fb05’ simulation in our correlation test, but not the ‘IMBHfb05’ simulation, as the presence of an IMBH may confound the results. The scaled merger number for
$f = 0$) and simulations with primordial binaries, with all other initial conditions held constant. For example, we use the ‘fb05’ simulation in our correlation test, but not the ‘IMBHfb05’ simulation, as the presence of an IMBH may confound the results. The scaled merger number for ![]() $f = 0$ (canonical) simulations is higher than for any of the
$f = 0$ (canonical) simulations is higher than for any of the ![]() $f \neq 0$ simulations.
$f \neq 0$ simulations.
3.1. Masses
Two parameters of interest for the BHBs that merge within the cluster are the total binary mass and the mass ratio. We define the primary to be the heavier component and the secondary to be the lighter companion. Figure 2 shows the primary and secondary mass distributions as a histogram (top panel) and a cumulative distribution (bottom panel).

Figure 2. Distribution of primary (red) and secondary (blue) masses for the population of BHBs that merge inside their host cluster, derived from all simulations in this study. The top panel shows the histograms for the component masses. The bottom panel shows the corresponding cumulative distribution functions (CDFs).
Both the primary and secondary mass distributions peak around 13–15 ![]() ${\rm M}_{\odot}$, with a mean mass of
${\rm M}_{\odot}$, with a mean mass of ![]() $24.9\,{\rm M}_{\odot}$ and
$24.9\,{\rm M}_{\odot}$ and ![]() $14.5\,{\rm M}_{\odot}$, respectively. The peak corresponds to the peak seen in the overall BH population distribution (which derives from the IMF and stellar evolution assumptions), as we verified by comparing the merging distributions to the mass distribution of a random sample of BHs across all models. It is therefore important to note that this peak is specific to the set of models being simulated, as the minimum progenitor mass is metallicity-dependant.
$14.5\,{\rm M}_{\odot}$, respectively. The peak corresponds to the peak seen in the overall BH population distribution (which derives from the IMF and stellar evolution assumptions), as we verified by comparing the merging distributions to the mass distribution of a random sample of BHs across all models. It is therefore important to note that this peak is specific to the set of models being simulated, as the minimum progenitor mass is metallicity-dependant.
Upon inspection of Figure 2, the distribution of the primary BH masses appears to contain some high-end outliers. Indeed, all five primary masses equal to or greater than ![]() $60\,{\rm M}_{\odot}$ fall outside the range
$60\,{\rm M}_{\odot}$ fall outside the range ![]() $\left[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3-Q_1)\right]$
Footnote c, the standard convention for defining outliers (James et al. Reference James, Witten, Hastie and Tibshirani2014). Further investigation shows that each merger involves the product of the previous merger, that is, the outliers occur when a BH merger product goes on to merge again multiple times. This chain of mergers is the only multi-merger string of its kind present in the simulations. All other BHs merge at most four times in their lifetime, whereas this chain represents seven total mergers. It allows a BH to reach masses above what is achievable through normal stellar evolution. We exclude the chain of seven mergers when comparing the in-cluster mass distributions to the ejected distributions (Section 4.1).
$\left[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3-Q_1)\right]$
Footnote c, the standard convention for defining outliers (James et al. Reference James, Witten, Hastie and Tibshirani2014). Further investigation shows that each merger involves the product of the previous merger, that is, the outliers occur when a BH merger product goes on to merge again multiple times. This chain of mergers is the only multi-merger string of its kind present in the simulations. All other BHs merge at most four times in their lifetime, whereas this chain represents seven total mergers. It allows a BH to reach masses above what is achievable through normal stellar evolution. We exclude the chain of seven mergers when comparing the in-cluster mass distributions to the ejected distributions (Section 4.1).
We do not compare Figure 2 to the output of similar studies in the literature, as the results are model and metallicity-dependent. Many MC studies have utilised models with lower metallicities than the current paper (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017). Expanding our simulation models to these lower metallicities is the subject of future research.
3.2. Mass ratios
We define the mass ratio as ![]() $q = M_2/M_1 \leqslant 1$. Figure 3 displays the cumulative q distribution for merging BHBs (right panel), along with the evolution of q with time (left panel). For
$q = M_2/M_1 \leqslant 1$. Figure 3 displays the cumulative q distribution for merging BHBs (right panel), along with the evolution of q with time (left panel). For ![]() $q \gtrsim 0.1$, the distribution is relatively flat. This result is somewhat surprising. Previous scattering experiments found that BHBs are likely to undergo multiple exchange events, where the lighter of the two binary components is preferentially ejected from the system in favour of the intruder (Sigurdsson & Hernquist Reference Sigurdsson and Hernquist1993). This process serves to systematically increase q, as lower q binaries exchange their relatively light component for masses closer to the primary. The distribution is therefore expected to skew towards higher mass ratios (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017). In the case of the first two studies, the majority of mergers are from ejected BHBs, whereas the third study only considers ejected binaries. We find the mass ratio distribution to vary significantly between in-cluster and ejected BHBs in this paper; see Section 3.
$q \gtrsim 0.1$, the distribution is relatively flat. This result is somewhat surprising. Previous scattering experiments found that BHBs are likely to undergo multiple exchange events, where the lighter of the two binary components is preferentially ejected from the system in favour of the intruder (Sigurdsson & Hernquist Reference Sigurdsson and Hernquist1993). This process serves to systematically increase q, as lower q binaries exchange their relatively light component for masses closer to the primary. The distribution is therefore expected to skew towards higher mass ratios (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017). In the case of the first two studies, the majority of mergers are from ejected BHBs, whereas the third study only considers ejected binaries. We find the mass ratio distribution to vary significantly between in-cluster and ejected BHBs in this paper; see Section 3.

Figure 3. Distribution of mass ratios for BHBs merging within their host cluster. The left panel shows the mass ratio q versus time of merger (in Myr after initialisation). We label mergers according to Table 1; primordial binaries (red), canonical (orange), low metallicity (blue), IMBH (black), large half-mass radius (yellow), high metallicity (pink), large natal kicks (green), and larger king concentrations (purple). The right panel shows the corresponding CDF for the mass ratios of the overall population (dark blue), for binaries that merge in the first 6 Gyr (cyan), and for binaries merging in the last 6 Gyr (pink). The KS statistic comparing the first 6 Gyr to the second 6 Gyr is 0.53, with a p-value of ![]() $3\times10^{-5}$.
$3\times10^{-5}$.
Higher q mergers tend to occur earlier in a cluster’s lifetime. The left panel of Figure 3 displays a breakdown of merger q by simulation type and merger time. All cluster models appear to follow the above trend roughly. We quantify the difference between early and late mergers by performing a Kolmogorov–Smirnov(KS) test, comparing the mass ratio distribution of mergers within the first 6Myr to those in the second 6 Myr. With a KS statistic of 0.53 and a p-value of ![]() $3.03 \times 10^{-5}$, there is strong evidence against the null hypothesis that these two q samples (first 6 Myr data and second 6Myr data) come from the same underlying distribution.
$3.03 \times 10^{-5}$, there is strong evidence against the null hypothesis that these two q samples (first 6 Myr data and second 6Myr data) come from the same underlying distribution.
The result in Figure 3 can be understood as a consequence of BH evaporation. There are no SMBHs present at the beginning of the simulations, but soon after initialisation, stars above a mass of approximately ![]() $20\,{\rm M}_{\odot}$ collapse (Heger et al. Reference Heger, Fryer, Woosley, Langer and Hartmann2003), creating a population of remnant BHs. Once all massive stars have died, the BHs become the most massive bodies in the cluster and migrate to the cluster centre through two-body interactions as the system evolves towards partial energy equipartition (Trenti & van der Marel Reference Trenti and van der Marel2013). This leads to a high density of BHs in the core. Within this dense central population, compact bodies frequently undergo dynamical interactions, exchanging energy and often leading to the ejection of one or more bodies. These interactions and natal kicks reduce the BH population. As the number of BHs decreases, it becomes harder to form high q binaries, because most BHs of similar mass have either already merged or have been ejected from the cluster.
$20\,{\rm M}_{\odot}$ collapse (Heger et al. Reference Heger, Fryer, Woosley, Langer and Hartmann2003), creating a population of remnant BHs. Once all massive stars have died, the BHs become the most massive bodies in the cluster and migrate to the cluster centre through two-body interactions as the system evolves towards partial energy equipartition (Trenti & van der Marel Reference Trenti and van der Marel2013). This leads to a high density of BHs in the core. Within this dense central population, compact bodies frequently undergo dynamical interactions, exchanging energy and often leading to the ejection of one or more bodies. These interactions and natal kicks reduce the BH population. As the number of BHs decreases, it becomes harder to form high q binaries, because most BHs of similar mass have either already merged or have been ejected from the cluster.
4. Ejected BHB mergers
From the total of 58 simulations, there are 239 ejected stellar mass BHBs: 43 from the 50 K simulations, 162 from the 100 K simulations, and 35 from the 200 K simulations. NBODY6 defines the ejection time for a binary as the time after cluster initialisation when the binary satisfies the Jacobi escape criterion; see Ernst et al. (Reference Ernst, Glaschke, Fiestas, Just and Spurzem2007) and Ross, Mennim, & Heggie (Reference Ross, Mennim and Heggie1997). We use Peters’ equations (Peters Reference Peters1964a) for the averaged orbital evolution to calculate the inspiral time of the BHBs upon ejection (Equation (1)). The merger time for escaped BHBs is the sum of the ejection time and this inspiral time. Here, we make the simplifying assumption that all GCs originate at the same epoch, forming at around a redshift of 3.5 (![]() $\sim$12 Gyrs ago), as this age roughly corresponds to the average age for Milky Way clusters. However, this assumption ignores the observed spread in cluster ages and the corresponding metallicity dependence (Forbes & Bridges Reference Forbes and Bridges2010). Using this method, we find that a total of 20 ejected BHBs merge within the age of the Universe: 2 from the 50 K simulations, 10 from the 100 K simulations, 8 from the 200 K simulations, resulting in a total merger number of 117 including the in-cluster mergers. The rest of the 239 do not merge within the age of the Universe, for example, because
$\sim$12 Gyrs ago), as this age roughly corresponds to the average age for Milky Way clusters. However, this assumption ignores the observed spread in cluster ages and the corresponding metallicity dependence (Forbes & Bridges Reference Forbes and Bridges2010). Using this method, we find that a total of 20 ejected BHBs merge within the age of the Universe: 2 from the 50 K simulations, 10 from the 100 K simulations, 8 from the 200 K simulations, resulting in a total merger number of 117 including the in-cluster mergers. The rest of the 239 do not merge within the age of the Universe, for example, because ![]() $a_0$ is too large. For the rest of this paper, we refer to ejected BHBs that merge within the age of the Universe as merging escapers or merging systems. This prevalence for in-cluster over ejected mergers is also seen in N-body simulations of open clusters (Banerjee Reference Banerjee2017; Reference Banerjee2018a;b).
$a_0$ is too large. For the rest of this paper, we refer to ejected BHBs that merge within the age of the Universe as merging escapers or merging systems. This prevalence for in-cluster over ejected mergers is also seen in N-body simulations of open clusters (Banerjee Reference Banerjee2017; Reference Banerjee2018a;b).
BHs that merge within the cluster can go on to form a new binary, so ejected BHBs can contain a BH which is the product of a previous merger. We refer to these as second-generation BHs. Merger chains systematically increase BH mass over generations but are unlikely to affect the orbital parameter distributions for the binaries. This is because all BHB undergo multiple exchange events and dynamical encounters where the orbital parameters are significantly altered, with the specific origin of the component BHs (whether through stellar death or merger) only altering the interaction cross section. We find no statistically significant difference between the orbital parameters of ejected BHBs with second-generation BHs and ejected BHBs with first-generation BHBs. Thirty-two ejected BHBs contain at least one second-generation BHs, with four systems containing a third-generation BH. Only three merging systems contain a second-generation BH and none contain a third-generation BH. In order to test if the observed difference is due to chance, we conduct a Pearson’s chi-squared test (Pearson Reference Pearson1900), a statistical test used on categorical data to determine how likely the observed difference between datasets is purely due to chance. Here, we have data belonging to two categories: whether or not an ejected system contains a second-generation BH, and whether or not a ejected system merges. With a p-value of 0.93, the results are consistent with the null hypothesis that there is no relationship between a system’s ejection status (escape or merging escaper) and whether it contains a second (or higher)-generation BH.
4.1. Masses
In Figure 4, we display the primary and secondary mass distributions for all ejected BHBs, and for the subset that are merging systems. Ejected BHBs exhibit a similar mass peak as in-cluster mergers (Section 3.1). Note that we have excluded the outliers from the in-cluster ![]() $M_1$ data for comparison to the ejected
$M_1$ data for comparison to the ejected ![]() $M_1$ distribution. Unlike their in-cluster counterparts, the ejected systems have no mass outliers. The distribution for
$M_1$ distribution. Unlike their in-cluster counterparts, the ejected systems have no mass outliers. The distribution for ![]() $M_1$ in ejected systems is clearly skewed to lower masses when compared to the in-cluster
$M_1$ in ejected systems is clearly skewed to lower masses when compared to the in-cluster ![]() $M_1$ distribution and statistically different. In fact, a KS test yields a p-value of
$M_1$ distribution and statistically different. In fact, a KS test yields a p-value of ![]() $7.1\times10^{-11}$ for these two distributions. The same cannot be said when comparing the corresponding
$7.1\times10^{-11}$ for these two distributions. The same cannot be said when comparing the corresponding ![]() $M_2$ distributions, with a p-value of 0.39. One possible explanation for the difference in in-cluster and ejected
$M_2$ distributions, with a p-value of 0.39. One possible explanation for the difference in in-cluster and ejected ![]() $M_1$ distributions is that 48% of all in-cluster mergers involve a second- or third-generation BH (on average two or three times more massive than first-generation products of stellar evolution), compared to only 15% for ejected binaries.
$M_1$ distributions is that 48% of all in-cluster mergers involve a second- or third-generation BH (on average two or three times more massive than first-generation products of stellar evolution), compared to only 15% for ejected binaries.

Figure 4. Top panel: Distribution of BHB component masses: primary (red) and secondary (blue) masses of all ejected systems, and the primary (magenta) and secondary (cyan) masses for the subset of ejected systems that merge within the age of the Universe. Bottom panel: Corresponding mass CDFs for the different populations (dashed lines for the ejected systems, dotted lines for the subset that merge). We also include the CDFs for the in-cluster mergers for comparison (solid lines) and the total mass of the systems (![]() $M_t = M_1 + M_2$) (green).
$M_t = M_1 + M_2$) (green).
The mass distributions for merging escapers closely match the ejected mass distributions. For ejected systems, there is no preference for merging based on either primary or secondary mass. This is somewhat surprising, as heavier systems emit more GWs (Equation (1)) than lighter systems with the same orbital parameters. ![]() $\frac{dE_{GW}}{dt}/E_b$ is proportional to
$\frac{dE_{GW}}{dt}/E_b$ is proportional to ![]() $M_1M_2(M_1 + M_2)$, meaning heavier systems merge more rapidly. However, it is more pertinent to instead consider the distribution of binary mass,
$M_1M_2(M_1 + M_2)$, meaning heavier systems merge more rapidly. However, it is more pertinent to instead consider the distribution of binary mass, ![]() $M_t = M_1 + M_2$. When considering
$M_t = M_1 + M_2$. When considering ![]() $M_t$, the set of merging systems appears to be a representative sample of all ejected systems. The orbital parameters (eccentricity and semi-major axis) have a large impact on inspiral time: the integral in Equation (1) varies by several orders of magnitude depending on the initial eccentricity, and ejected systems display a large range in initial separations (see Section 4.4), much larger than the range in BH and binary masses.
$M_t$, the set of merging systems appears to be a representative sample of all ejected systems. The orbital parameters (eccentricity and semi-major axis) have a large impact on inspiral time: the integral in Equation (1) varies by several orders of magnitude depending on the initial eccentricity, and ejected systems display a large range in initial separations (see Section 4.4), much larger than the range in BH and binary masses.
In Figure 5, we display the binary mass for all ejected BHBs as a function of ejection time. Although it appears that higher mass systems are ejected earlier, there is significant clustering around ![]() $28\,{\rm M}_{\odot}$ at early times. We test for non-parametric correlation between binary mass and ejection time using Spearman’s rank-order correlation test. We find a correlation coefficient of
$28\,{\rm M}_{\odot}$ at early times. We test for non-parametric correlation between binary mass and ejection time using Spearman’s rank-order correlation test. We find a correlation coefficient of ![]() $\rho = -0.52$ with a p-value of
$\rho = -0.52$ with a p-value of ![]() $10^{-17}$, indicating strong evidence against statistical independence (
$10^{-17}$, indicating strong evidence against statistical independence (![]() $\rho = 0$). That is, early high-mass ejections are statistically significant.
$\rho = 0$). That is, early high-mass ejections are statistically significant.

Figure 5. Binary mass, ![]() $M_T$, of ejected BHBs as a function of ejection time. The grey points show each ejected BHB. The orange curve shows the trend in the data using a Savitzky–Golay filter. The symmetric 90% confidence interval about the median (green band) is calculated by calculating the corresponding percentiles in 250 Myr bins, smoothed through the Savitzky–Golay filter.
$M_T$, of ejected BHBs as a function of ejection time. The grey points show each ejected BHB. The orange curve shows the trend in the data using a Savitzky–Golay filter. The symmetric 90% confidence interval about the median (green band) is calculated by calculating the corresponding percentiles in 250 Myr bins, smoothed through the Savitzky–Golay filter.
A Savitzky–Golay filter (Savitzky & Golay Reference Savitzky and Golay1964) is used to smooth the data to visualise this general tendency better. We also display the symmetric 90% confidence interval about the median. As the data are discrete, the confidence interval is calculated by first splitting the data into 250 Myr bins and calculating the 5th and 95th percentile in each bin. We apply a Savitzky–Golay filter on the set of percentiles to create smoothed 90% confidence interval, symmetric about the median. These confidence intervals make it clear that higher mass binaries are ejected at earlier times.
Similar trends have been observed in MC simulations of large GCs (Rodriguez et al. Reference Rodriguez, Chatterjee and Rasio2016). This result is slightly counter-intuitive considering the ejection energy required for a binary to escape a cluster is proportional to the binary mass (Heggie & Hut Reference Heggie and Hut2003):
where ![]() $R_h$ is the half-mass radius and
$R_h$ is the half-mass radius and ![]() $M_{GC}$ is the total mass of the cluster. It is therefore easier for lighter binaries to escape a given cluster, as
$M_{GC}$ is the total mass of the cluster. It is therefore easier for lighter binaries to escape a given cluster, as ![]() $E_{ej}$ is lower. Superficially, this means binaries with higher-than-average masses are more easily retained by their host cluster, enabling more dynamic encounters, so that they are more likely to merge before ejection. However, we must consider the mechanisms which lead to ejection. Approximately 80% of all ejected BHBs are ejected after a three-body encounter with another BH. Three-body scattering events harden binaries and can impart significant recoil velocities. Subsequent interactions can build up the centre-of-mass speed (through these recoils), possibly above the escape velocity of the cluster. The cross section for three-body interactions (Celoria et al. Reference Celoria, Oliveri, Sesana and Mapelli2018), under the assumption that the binary is hard, can be approximated by:
$E_{ej}$ is lower. Superficially, this means binaries with higher-than-average masses are more easily retained by their host cluster, enabling more dynamic encounters, so that they are more likely to merge before ejection. However, we must consider the mechanisms which lead to ejection. Approximately 80% of all ejected BHBs are ejected after a three-body encounter with another BH. Three-body scattering events harden binaries and can impart significant recoil velocities. Subsequent interactions can build up the centre-of-mass speed (through these recoils), possibly above the escape velocity of the cluster. The cross section for three-body interactions (Celoria et al. Reference Celoria, Oliveri, Sesana and Mapelli2018), under the assumption that the binary is hard, can be approximated by:
where ![]() $M_1$ and
$M_1$ and ![]() $ M_2$ are the two binary component masses,
$ M_2$ are the two binary component masses, ![]() $m_3$ is the third (single) body mass, a is the binary semi-major axis, and
$m_3$ is the third (single) body mass, a is the binary semi-major axis, and ![]() $\sigma$ is the average stellar velocity within the cluster. With a larger cross section for more massive binaries, heavier BHBs have a higher interaction rate than their lighter counterparts and hence experience a more rapid increase in velocity through successive interaction recoils. The rate of binding energy increase for hard binaries is approximated by:
$\sigma$ is the average stellar velocity within the cluster. With a larger cross section for more massive binaries, heavier BHBs have a higher interaction rate than their lighter counterparts and hence experience a more rapid increase in velocity through successive interaction recoils. The rate of binding energy increase for hard binaries is approximated by:
where ![]() $\rho$ is the mass density in the core and
$\rho$ is the mass density in the core and ![]() $\epsilon$ is a scaling parameter that depends on the specifics of the interaction, with three-body scattering studies finding
$\epsilon$ is a scaling parameter that depends on the specifics of the interaction, with three-body scattering studies finding ![]() $\epsilon \sim 0.2 - 1$ (Mikkola & Valtonen Reference Mikkola and Valtonen1992; Quinlan Reference Quinlan1996). Given
$\epsilon \sim 0.2 - 1$ (Mikkola & Valtonen Reference Mikkola and Valtonen1992; Quinlan Reference Quinlan1996). Given ![]() $E_{ej} \propto (M_1 + M_2)$, and
$E_{ej} \propto (M_1 + M_2)$, and ![]() $ dE_b/dt \propto (M_1M_2)$, heavier binaries are expected to exceed their escape velocity earlier than their lighter counterparts. Heavier BHs are also produced earlier in a cluster’s evolution due to shorter lifespans of high-mass stars and segregate to the dense core more rapidly, enabling quicker binary formation. The exception is second-generation BHs, which form after the cluster has had time to host some mergers.
$ dE_b/dt \propto (M_1M_2)$, heavier binaries are expected to exceed their escape velocity earlier than their lighter counterparts. Heavier BHs are also produced earlier in a cluster’s evolution due to shorter lifespans of high-mass stars and segregate to the dense core more rapidly, enabling quicker binary formation. The exception is second-generation BHs, which form after the cluster has had time to host some mergers.
4.2. Mass ratios
In Figure 6, we show the cumulative q distributions for in-cluster mergers, ejected BHBs, and the subset of ejected systems that merge within the age of the Universe. It is immediately clear that there is a preference for ejecting BHBs with larger mass ratios. Half of all ejected systems possess ![]() $q > 0.86$, because q increases through the exchange of binary components (see Section 3.2). As a result, ejected systems have mass ratios much closer to unity than their in-cluster counterparts. The escaping BHBs and merging escaper distributions are closer to what has been found by Rodriguez et al. (Reference Rodriguez, Chatterjee and Rasio2016, Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a) and Park et al. (Reference Park, Kim, Lee, Bae and Belczynski2017) than the flat distribution of in-cluster mergers. This has important implications when making inferences about formation channels from LIGO data. In Figure 6, we display the 90% confidence interval for the CDF of the 10 LIGO mass ratios measured to date (see Section 5). Taking into account uncertainty in the LIGO masses, there is a clear preference towards higher ratios, with probability
$q > 0.86$, because q increases through the exchange of binary components (see Section 3.2). As a result, ejected systems have mass ratios much closer to unity than their in-cluster counterparts. The escaping BHBs and merging escaper distributions are closer to what has been found by Rodriguez et al. (Reference Rodriguez, Chatterjee and Rasio2016, Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a) and Park et al. (Reference Park, Kim, Lee, Bae and Belczynski2017) than the flat distribution of in-cluster mergers. This has important implications when making inferences about formation channels from LIGO data. In Figure 6, we display the 90% confidence interval for the CDF of the 10 LIGO mass ratios measured to date (see Section 5). Taking into account uncertainty in the LIGO masses, there is a clear preference towards higher ratios, with probability ![]() $\geqslant 0.7$ for
$\geqslant 0.7$ for ![]() $q \geqslant 0.5$ for the 90% confidence interval.
$q \geqslant 0.5$ for the 90% confidence interval.

Figure 6. Cumulative probability distribution for the mass ratios of BHB systems. The blue curve shows the distribution for all BHBs that merge within their host cluster. The orange curve shows the distribution of in-cluster merging BHBs, excluding any BH which is flagged in post-processing as ejected after a previous merger through gravitational recoil (see Section 2.2). The green curve shows the distribution for all ejected BHBs, with the subset which merge within the age of the Universe displayed in red. Slow-merging escapers (purple) are defined as ejected binaries that merge ![]() $ \geqslant 10^4 \ \text{yr}$ after ejection. The distribution of inspiral times is bimodal, with one peak
$ \geqslant 10^4 \ \text{yr}$ after ejection. The distribution of inspiral times is bimodal, with one peak ![]() $ \geqslant 10^4 \ \text{yr}$ and the other peak
$ \geqslant 10^4 \ \text{yr}$ and the other peak ![]() $\leqslant 10^4\ \text{yr}$. The symmetric 90% confidence interval for the mass ratio distribution given by the 10 LIGO events is displayed as a grey band for comparison.
$\leqslant 10^4\ \text{yr}$. The symmetric 90% confidence interval for the mass ratio distribution given by the 10 LIGO events is displayed as a grey band for comparison.
The ejected BHBs that merge display a similarly skewed q distribution to the set of all ejected systems. However, merging escapers have a low-end cut-off (below which there are no BHBs in the population) at ![]() $q = 0.56$, compared to
$q = 0.56$, compared to ![]() $q = 0.18$ for all ejected systems. There is no clear relationship between the mass ratios, eccentricities, or separations for ejected BHBs. The higher cut-off is predominately due to stronger production of gravitational radiation at higher mass ratios for a given binary mass, as
$q = 0.18$ for all ejected systems. There is no clear relationship between the mass ratios, eccentricities, or separations for ejected BHBs. The higher cut-off is predominately due to stronger production of gravitational radiation at higher mass ratios for a given binary mass, as ![]() $T_{\text{insp}} \propto \frac{1}{q}\!\frac{(1+q)^2}{M_T}$ is minimised when
$T_{\text{insp}} \propto \frac{1}{q}\!\frac{(1+q)^2}{M_T}$ is minimised when ![]() $q = 1$.
$q = 1$.
The distribution of inspiral times for ejected mergers displays bimodality. In Figure 6, we display the set of merging escapers that have an inspiral time ![]() $> 10^4\ \text{yr}$ after ejection. We refer to these systems as slow-merging escapers. Merging escapers with
$> 10^4\ \text{yr}$ after ejection. We refer to these systems as slow-merging escapers. Merging escapers with ![]() $ q \geqslant 0.9$ all merge
$ q \geqslant 0.9$ all merge ![]() $\leqslant 10^4\ \text{yr}$ after ejection. Their slower counterparts appear to more closely match the LIGO 90% confidence interval (see Section 5).
$\leqslant 10^4\ \text{yr}$ after ejection. Their slower counterparts appear to more closely match the LIGO 90% confidence interval (see Section 5).
In Figure 6, we also display in orange the set of in-cluster mergers which exclude any system containing a second-generation BH that would have been ejected through gravitational recoil (see Section 2.2). Compared to the full set of in-cluster mergers, this retained population more closely matches the slow-merging escapers, although there is still a significant number of mergers with ![]() $q < 0.5$ not seen in BH pairs merging after dynamical ejection.
$q < 0.5$ not seen in BH pairs merging after dynamical ejection.
4.3. Eccentricities
In Figure 7, we show the cumulative distribution of eccentricities which ejected binary systems possess at the time of their escape from their host cluster. The distribution for all ejected binaries closely matches that of a thermal eccentricity distribution (Equation (7)), with a KS test giving a p-value of 0.15. In simulation models which include primordial binaries, the systems are generated with eccentricities drawn from a thermal distribution, but none of the ejected BHBs are primordial binaries; they form via exchanges or from remnants which are never part of a primordial binary. Although these initial eccentricities may still influence the distribution for binaries formed dynamically, 69% of ejected BHBs come from clusters which did not begin with any primordial binaries. Hence, the result suggests that ejected BHBs have had enough time to thermalise, by interacting with other particles/binaries and exchanging energy many times.

Figure 7. CDF of eccentricities for different subsets of ejected BHBs. The eccentricities are taken at the moment when the binary is ejected from its host cluster. The green curve shows the distribution for all ejected systems, along with a theoretical thermal eccentricity distribution (orange) for comparison. Also shown is the ejected systems that merge within the age of the Universe (red) and the subset of these which which merge ≥ 104 years after ejection. The KS statistic comparing the thermal distribution to all ejected systems is 0.073, with a p value of 0.15.
We also display the cumulative distribution of eccentricities for merging ejected binaries and the slow subset. Higher e systems tend to merge more frequently than ejected BHBs overall. GW emission is stronger at higher eccentricities (Equation (1)), leading to faster inspiral. Ejected systems with high eccentricities progressively circularise after ejection due to gravitational radiation; all the ejected merging systems enter the LIGO frequency band with ![]() $ e \lesssim 10^{-4}$. This can also help explain why we do not see any noticeable preference for higher mass ejected binaries to merge, as eccentricity and separation (see Section 4.4) affect the inspiral time more than mass.
$ e \lesssim 10^{-4}$. This can also help explain why we do not see any noticeable preference for higher mass ejected binaries to merge, as eccentricity and separation (see Section 4.4) affect the inspiral time more than mass.
4.4. Separation
Figure 8 displays a log-scale cumulative distribution for the semi-major axis of ejected BHBs. The green curve shows the distribution for the entire population of ejected binaries, the majority of which are ejected with ![]() $1 \,\text{AU} \leqslant a_0 \leqslant 10\,\text{AU}$. The upper cut-off is partially a result of Heggie’s law (Heggie Reference Heggie1975), a statistical result which states that, on average, hard binaries become harder and soft binaries become softer in three-body encounters. A hard binary has
$1 \,\text{AU} \leqslant a_0 \leqslant 10\,\text{AU}$. The upper cut-off is partially a result of Heggie’s law (Heggie Reference Heggie1975), a statistical result which states that, on average, hard binaries become harder and soft binaries become softer in three-body encounters. A hard binary has ![]() $E_b > 1.2 \Bar{m} \sigma^2$, where
$E_b > 1.2 \Bar{m} \sigma^2$, where ![]() $\sigma$ is the average stellar velocity and
$\sigma$ is the average stellar velocity and ![]() $\Bar{m}$ is the average stellar mass within the cluster. Most of the BHBs are ejected via velocity kicks imparted from subsequent strong three-body hardening. Soft binaries do not receive these hardening kicks and thus can never reach escape velocity, leading to binaries above a certain separation being too soft to be ever ejected.
$\Bar{m}$ is the average stellar mass within the cluster. Most of the BHBs are ejected via velocity kicks imparted from subsequent strong three-body hardening. Soft binaries do not receive these hardening kicks and thus can never reach escape velocity, leading to binaries above a certain separation being too soft to be ever ejected.

Figure 8. CDF for the semi-major axis at the point of ejection on a log scale. The red curve shows the distribution for all ejected BHBs (red), with the merging escapers (green) and slow-merging escapers (purple).
Binaries only have ![]() $a_0 \leqslant$1AU after multiple dynamical interactions (with the number dependent on the nature of the interactions), which in turn take time, leading to few systems with extremely low separations. Close binaries also lose energy to gravitational radiation and quickly merge within the cluster prior to ejection.
$a_0 \leqslant$1AU after multiple dynamical interactions (with the number dependent on the nature of the interactions), which in turn take time, leading to few systems with extremely low separations. Close binaries also lose energy to gravitational radiation and quickly merge within the cluster prior to ejection.
All merging ejected systems come from the low end of the overall ![]() $a_0$ distribution (red curve of Figure 8, as these systems emit GWs more strongly and inspiral more rapidly. For the slow subset that merge at least
$a_0$ distribution (red curve of Figure 8, as these systems emit GWs more strongly and inspiral more rapidly. For the slow subset that merge at least ![]() $10^4\ \text{yr}$ after ejection, there appears to be a preference for larger separations, with all mergers above with
$10^4\ \text{yr}$ after ejection, there appears to be a preference for larger separations, with all mergers above with ![]() $a_0 > 0.1$AU belonging to this subset, as to be expected based on arguments made above. These results, along with those from Sections 3.2 and 4.3, confirm that eccentricity and separation predominately affect whether or not a given ejected system merges within the age of the Universe.
$a_0 > 0.1$AU belonging to this subset, as to be expected based on arguments made above. These results, along with those from Sections 3.2 and 4.3, confirm that eccentricity and separation predominately affect whether or not a given ejected system merges within the age of the Universe.
Although we attribute the prevalence of merging short-period binaries to the low tail (![]() $a \lesssim 1\, \rm{AU}$) of the separation distribution, these extremely short periods are somewhat surprising. To investigate if these short-period binaries originate from a specific subset of initial conditions and/or simulations, we compare the separation data against all other variables (mass, escape time, eccentricity, and mass ratio). Using Spearman’s rank-order correlation test, we find no correlation between variables and find no discernible reason to conclude these short-period binaries are in any way unique, leaving our starting hypothesis of the tail-of-the-distribution origin as the most plausible.
$a \lesssim 1\, \rm{AU}$) of the separation distribution, these extremely short periods are somewhat surprising. To investigate if these short-period binaries originate from a specific subset of initial conditions and/or simulations, we compare the separation data against all other variables (mass, escape time, eccentricity, and mass ratio). Using Spearman’s rank-order correlation test, we find no correlation between variables and find no discernible reason to conclude these short-period binaries are in any way unique, leaving our starting hypothesis of the tail-of-the-distribution origin as the most plausible.
Only 16% of all mergers are from BHBs that are ejected from their host cluster. In contrast, similar studies using MC methods have found ![]() $\gtrsim 50\%$ of mergers from ejected systems (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Askar et al. Reference Askar, Szkudlarek, Gondek-Rosińska, Giersz and Bulik2017). It has been recently suggested that because the current state-of-the-art MC cluster codes, CMC (Joshi et al. Reference Joshi, Rasio and Portegies Zwart2000) and MOCCA (Hypki & Giersz Reference Hypki and Giersz2013), only incorporate strong interactions, the number of in-cluster mergers is being underestimated. Samsing Samsing, Hamers, & Tyles (Reference Samsing, Hamers and Tyles2019a) found that including weak encounters raises the proportion of in-cluster mergers. With weak encounters enabled, the total population of BHB mergers becomes dominated by in-cluster mergers, as we find in our simulations.
$\gtrsim 50\%$ of mergers from ejected systems (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Askar et al. Reference Askar, Szkudlarek, Gondek-Rosińska, Giersz and Bulik2017). It has been recently suggested that because the current state-of-the-art MC cluster codes, CMC (Joshi et al. Reference Joshi, Rasio and Portegies Zwart2000) and MOCCA (Hypki & Giersz Reference Hypki and Giersz2013), only incorporate strong interactions, the number of in-cluster mergers is being underestimated. Samsing Samsing, Hamers, & Tyles (Reference Samsing, Hamers and Tyles2019a) found that including weak encounters raises the proportion of in-cluster mergers. With weak encounters enabled, the total population of BHB mergers becomes dominated by in-cluster mergers, as we find in our simulations.
It is also possible that the initial particle size of our models may impact the number of ejected mergers, as previous work on smaller, less massive open clusters also find that in-cluster mergers dominate (Banerjee Reference Banerjee2017; Reference Banerjee2018a). These results imply that ejected mergers depend superlinearly on the mass of the clusters, as the proportion of ejected to in-cluster mergers appears to increase significantly with cluster mass. This highlights the importance of N-body modelling of smaller clusters such as those presented in this paper, as the majority of MC results focus on high-mass clusters (M ![]() $\sim 10^5-10^6\,{\rm M}_{\odot}$). Given that GCs roughly follow a
$\sim 10^5-10^6\,{\rm M}_{\odot}$). Given that GCs roughly follow a ![]() $1/M^2$ mass distribution, clusters in our mass range better represent the bulk of the population of observed systems.
$1/M^2$ mass distribution, clusters in our mass range better represent the bulk of the population of observed systems.
However, the initial density of the models could be a significant factor contributing to the lower proportion of ejected mergers in the current study. Binary separation upon ejection is primarily determined by the global properties of the cluster (Portegies Zwart & McMillan Reference Portegies Zwart and McMillan2000; Moody & Sigurdsson Reference Moody and Sigurdsson2009), as opposed to the properties of the binary. Physically, this is because denser clusters have higher escape velocities, requiring binaries to harden more to allow for sufficient increase in speed through interaction recoil. Indeed, it can be shown that for ejected systems, one has (Rodriguez et al. Reference Rodriguez, Chatterjee and Rasio2016):
where ![]() $M_{GC}$ is the total cluster mass and
$M_{GC}$ is the total cluster mass and ![]() $\mu = (M_1M_2)/(M_1 + M_2)$ is the reduced binary mass. Equation (12) reinforces the point that smaller, more massive, and thus denser clusters eject tighter binaries, as they have higher escape velocities which allow the binaries to remain in the cluster and thus harden for longer. Our cluster models have similar initial
$\mu = (M_1M_2)/(M_1 + M_2)$ is the reduced binary mass. Equation (12) reinforces the point that smaller, more massive, and thus denser clusters eject tighter binaries, as they have higher escape velocities which allow the binaries to remain in the cluster and thus harden for longer. Our cluster models have similar initial ![]() $r_h$ to the models used in MC studies mentioned above (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Askar et al. Reference Askar, Szkudlarek, Gondek-Rosińska, Giersz and Bulik2017), but lower initial N, and hence lower
$r_h$ to the models used in MC studies mentioned above (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Askar et al. Reference Askar, Szkudlarek, Gondek-Rosińska, Giersz and Bulik2017), but lower initial N, and hence lower ![]() $M_{GC}$. With models that have a higher initial value of
$M_{GC}$. With models that have a higher initial value of ![]() $M_{GC}/r_h$, the mode of distribution of ejection separations,
$M_{GC}/r_h$, the mode of distribution of ejection separations, ![]() $P(a_0)$ (Figure 8), decreases due to Equation (12). In turn, this means that a greater proportion of all ejected binaries can emit sufficient gravitational radiation to merge in the age of the Universe, increasing the proportion of ejected versus in-cluster mergers.
$P(a_0)$ (Figure 8), decreases due to Equation (12). In turn, this means that a greater proportion of all ejected binaries can emit sufficient gravitational radiation to merge in the age of the Universe, increasing the proportion of ejected versus in-cluster mergers.

Figure 9. Scatter plot displaying the relationship between the ratio of the semi-major axis to the reduced mass for each ejected binary, ![]() $a/\mu$, and the ratio of the half-mass radius to cluster mass,
$a/\mu$, and the ratio of the half-mass radius to cluster mass,![]() $R_h/M_{GC}$, at the time each binary is ejected from the cluster. There is a clear positive correlation between the data.
$R_h/M_{GC}$, at the time each binary is ejected from the cluster. There is a clear positive correlation between the data.
We test the validity of Equation (12) to our data by plotting ![]() $a/\mu$ for every ejected binary against
$a/\mu$ for every ejected binary against ![]() $R_h/M_{GC}$ at the time of ejection (Figure 9), finding, as predicted, a clear positive correlation. We quantify the non-parametric correlation between
$R_h/M_{GC}$ at the time of ejection (Figure 9), finding, as predicted, a clear positive correlation. We quantify the non-parametric correlation between ![]() $a/\mu$ and
$a/\mu$ and ![]() $R_h/M_{GC}$ using Spearman’s rank-order correlation test, finding a correlation coefficient
$R_h/M_{GC}$ using Spearman’s rank-order correlation test, finding a correlation coefficient ![]() $\rho = 0.43$ with a p-value of
$\rho = 0.43$ with a p-value of ![]() $10^{-11}$. This indicates strong evidence against statistical independence (
$10^{-11}$. This indicates strong evidence against statistical independence (![]() $\rho = 0$). Thus, our results are consistent with the prediction that denser clusters eject tighter binaries.
$\rho = 0$). Thus, our results are consistent with the prediction that denser clusters eject tighter binaries.
Following Rodriguez et al. (Reference Rodriguez, Chatterjee and Rasio2016), we define
In Figure 10, we show the distribution of ![]() $\kappa$ from all ejected binaries, plotted on a log scale. We fit a log-normal distribution to the data. Figure 10 agrees strongly with the corresponding plot presented in Rodriguez et al. (Reference Rodriguez, Chatterjee and Rasio2016) (Figure 2, top panel), as both data roughly follow a log-normal distribution, with a median
$\kappa$ from all ejected binaries, plotted on a log scale. We fit a log-normal distribution to the data. Figure 10 agrees strongly with the corresponding plot presented in Rodriguez et al. (Reference Rodriguez, Chatterjee and Rasio2016) (Figure 2, top panel), as both data roughly follow a log-normal distribution, with a median ![]() $\log(\kappa)$ value of
$\log(\kappa)$ value of ![]() $\sim 4$.
$\sim 4$.

Figure 10. Probability density of ![]() $\log(\kappa)$ from all ejected binaries (blue). We fit a log-normal distribution to the data (red curve), finding a median value of
$\log(\kappa)$ from all ejected binaries (blue). We fit a log-normal distribution to the data (red curve), finding a median value of ![]() $\sim4$.
$\sim4$.
5. LIGO events
In this section, we compare the results from Sections 3.2 and 4.2 to the 10 BHB mergers observed and published by LIGO to date. We take the LIGO data from the catalog of compact binary mergers observed by LIGO and Virgo during the first and second observing runs, O1 and O2 (The LIGO Scientific Collaboration et al. 2018). In order to incorporate the uncertainties in the LIGO masses, we employ a bootstrapping technique. We draw a random sample from the posterior distributions calculated using Bayesian inference (Vallisneri et al. Reference Vallisneri, Kanner, Williams, Weinstein and Stephens2015). We use combined posterior distributions from two waveform models: an effective precessing spin model, IMRPhenomPv2 (Hannam et al. Reference Hannam, Schmidt, Bohé, Haegel, Husa, Ohme, Pratten and Pürrer2014; Khan et al. Reference Khan, Husa, Hannam, Ohme, Pürrer, Forteza and Bohé2016) and a fully precessing model, SEOBNRv3 (Pan et al. Reference Pan, Buonanno, Taracchini, Kidder, Mroué, Pfeiffer, Scheel and Szilágyi2014; Taracchini et al. Reference Taracchini2014). Parameters are quoted in the source frame.
Although there are now a number of published BHB merger detections from LIGO’s third observing run, we exclude these in our analysis as only one of these events is quoted as a BHB coalescence with reasonable confidence (Abbott et al. Reference Abbott2020a). Moreover, the event mass posteriors required for our rigorous statistical analysis are not publicly available at the time of writing. We plan on including the set of O3 events in a future publication, once the full catalog is released publicly.
5.1. Mass ratio
In Figure 6, we display the simulated cumulative mass ratio distributions, overlaid with the LIGO data. The shaded region represents the 90% confidence bounds for the LIGO distribution, symmetric about the median. We calculate these bounds by sampling from the LIGO primary and secondary mass posteriors. For each of the 10 events, we randomly pair an ![]() $M_1$ value drawn from the posterior with an
$M_1$ value drawn from the posterior with an ![]() $M_2$ value from the secondary mass posterior, without replacement, and this is repeated 10 000 times. This process gives us a q posterior for each detected BHB. Under the convention
$M_2$ value from the secondary mass posterior, without replacement, and this is repeated 10 000 times. This process gives us a q posterior for each detected BHB. Under the convention ![]() $M_1 \geqslant M_2$, these distributions have a sharp cut-off at
$M_1 \geqslant M_2$, these distributions have a sharp cut-off at ![]() $q=1$. We then randomly match each q value from one distribution to one from each of the other nine event posteriors. In effect, we now have a set of 10 000 q samples used to construct CDFs, where each sample has 10 q values, 1 from each event. The 90% confidence intervals for the population distribution are computed by calculating these confidence intervals at each q value. In practice, this means that the confidence bounds for the cumulative distributions contain points from multiple sample CDFs.
$q=1$. We then randomly match each q value from one distribution to one from each of the other nine event posteriors. In effect, we now have a set of 10 000 q samples used to construct CDFs, where each sample has 10 q values, 1 from each event. The 90% confidence intervals for the population distribution are computed by calculating these confidence intervals at each q value. In practice, this means that the confidence bounds for the cumulative distributions contain points from multiple sample CDFs.
An alternative method is to calculate the 5th and 95th percentiles for the 10 events, using our generated q posteriors. Two CDFs are then constructed: 1 from the 10 upper percentiles, and 1 from the 10 lower percentiles. The 90% confidence interval band is the region bound by these two CDFs. However, for this analysis, we only consider the first method discussed.
As can be seen in Figure 6, the LIGO data are skewed towards higher mass ratios. We pair each of the 10 000 bootstrapped LIGO CDFs with the q CDF of a given simulated population (such as the in-cluster mergers) and calculate the corresponding KS statistic (the maximum difference between the cumulative distributions). We then calculate the two-sided critical KS value for a given confidence level. This is the minimum KS statistic that is required to conclude that the differences between the two CDFs are statistically significant, that is, the minimum distance to reject the null hypothesis. The critical value is defined by Fasano & Franceschini (Reference Fasano and Franceschini1987):
where ![]() $\text{K}_{\text{inv}}$ is calculated from the inverse of the Kolmogorov distribution,
$\text{K}_{\text{inv}}$ is calculated from the inverse of the Kolmogorov distribution, ![]() $\alpha$ is the level of significance, and n and m are the number of data points being compared. For the sake of the current analysis, we set the level of significance at
$\alpha$ is the level of significance, and n and m are the number of data points being compared. For the sake of the current analysis, we set the level of significance at ![]() $\alpha = 0.05$. When sampling from the LIGO mass posteriors, we draw 10 000 masses per distribution in order to sample the tails adequately. The proportion of KS statistics above this critical value indicates the proportion of the 10 000 bootstrapped LIGO CDFs that are inconsistent with the null hypothesis, at 95% confidence interval.
$\alpha = 0.05$. When sampling from the LIGO mass posteriors, we draw 10 000 masses per distribution in order to sample the tails adequately. The proportion of KS statistics above this critical value indicates the proportion of the 10 000 bootstrapped LIGO CDFs that are inconsistent with the null hypothesis, at 95% confidence interval.
The above method only allows for comparison with our simulated populations, which we refer to as direct comparison. Alternatively, we wish to determine if our simulated dataset is robust enough to allow us to generalise our comparisons to the overall population of mergers being discussed (i.e., all merging escapers, not just the merging escapers present in our simulations). In effect, we want to know if our simulated data can be treated as a representative sample of the detectable population. We randomly pair each of the 10 000 bootstrapped LIGO CDFs with CDFs constructed from samples drawn, with repetition, from our simulated q distributions (in-cluster, ejected, merging escaper, and slow-merging escaper distributions). Because the critical KS value (Equation (14)) is a function of the size of the two distributions being compared, our new CDFs are constructed from samples which are the same size as the population from which the sample was drawn. For example, when comparing in-cluster mergers to observed events, we randomly draw, with repetition, 97 mass ratios from our distribution of 97 in-cluster mass ratios. In practice, this means these 10 000 sampled distributions are not identical. We refer to this set of comparisons as sampling comparisons.
Table 2 presents the mass ratio comparison between different simulated cluster populations and the LIGO data. We quote comparisons as the probability that the null hypothesis is rejected, at 95% confidence interval. When considering in-cluster and merging escapers without gravitational recoil, the results when sampling from simulated data indicate that the LIGO mass ratios more closely match mergers that occur within the simulated GCs. These results are somewhat surprising; a cursory look at Figure 6 would seem to indicate the opposite. However, the probability of rejecting the null hypothesis (for sampling comparison) only differs by 0.06 between these two simulated populations. Indeed, when compared directly to the simulation distributions, this result is flipped; the LIGO data match the merging escapers better than in-cluster mergers. The mass ratio distribution is approximately flat for in-cluster mergers and skewed to higher ratios for ejected mergers. Thus, these findings offer a dynamical formation pathway for BHB mergers that agrees with the nearly flat/left-skewed mass ratio distribution found by the LIGO Scientific Collaboration (Abbott et al. Reference Abbott2018a). However, the fact that the favoured distribution is different between the direct and sampling comparisons, along with the corresponding differences in rejection probabilities, indicates that our simulated populations for in-cluster and merging escapers are not large enough to be treated as fully representative samples.
Table 2. Comparisons of the mass ratio distributions between LIGO events and various populations of simulation BHBs

The simulation population is being compared and its size is listed, along with the corresponding critical KS value at 95% significance. We also list the probability that the null hypothesis is rejected at 95% confidence interval, corresponding to the proportion of KS statistics above the critical value. Comparison is conducted both directly with our simulated CDFs ![]() $p_{\rm reject}$ [direct] and with a set of CDFs constructed from samples drawn, with repetition, from the simulated distributions
$p_{\rm reject}$ [direct] and with a set of CDFs constructed from samples drawn, with repetition, from the simulated distributions ![]() $p_{\rm reject}$ [sampling]. The in-cluster population consists of all BHBs that merge within their host cluster, the retained population is the subset of in-cluster mergers that takes into account ejection of mergers remnants through gravitational recoil (estimated in post-processing), ejected systems are any BHBs that escape their host cluster, merging escapers are the subset of ejected systems that merge within the age of the Universe, and slow systems are the subset that merge
$p_{\rm reject}$ [sampling]. The in-cluster population consists of all BHBs that merge within their host cluster, the retained population is the subset of in-cluster mergers that takes into account ejection of mergers remnants through gravitational recoil (estimated in post-processing), ejected systems are any BHBs that escape their host cluster, merging escapers are the subset of ejected systems that merge within the age of the Universe, and slow systems are the subset that merge ![]() $\geqslant 10^4\,\textrm{yr}$ after ejection. For all comparisons, the size of the LIGO distribution is 10, corresponding to the 10 BHB mergers detected in O1 and O2.
$\geqslant 10^4\,\textrm{yr}$ after ejection. For all comparisons, the size of the LIGO distribution is 10, corresponding to the 10 BHB mergers detected in O1 and O2.
However, when we take into account gravitational recoil, the in-cluster mergers become a much better match to the LIGO data. Both the sampling and direct comparison for the retained in-cluster mergers have a higher rejection probability than any other population. This is unsurprising, as Figure 6 shows that accounting for gravitational recoil predominately reduces the number of low mass ratio mergers (the majority of which contained a merger remnant BH), producing a similar low q cut-off seen in the LIGO distribution. We note that excluding all in-cluster mergers containing a second-generation BH produces a mass ratio distribution almost identical to the ejected population. This result is very significant, as it implies that the LIGO data cannot be solely from common envelope evolution of field BHBs, as these should contain no second-generation BHs. However, we again note the difference in rejection probabilities between sampling and direct comparisons as an indication that inference from the current sample of events observed is not currently robust enough to draw a firm conclusion.
For ejected systems, the slow-merging escapers match LIGO data the best for both direct and sampling comparison, as expected from the comparison between CDFs in Figure 6. This result has important implications if ejected systems dominate over in-cluster mergers. Ejection times are similar between all ejected mergers and the slow subset (the latter represents approximately half of the total). At design sensitivity, LIGO is limited to a canonical horizon of ![]() $\sim 1640$ Mpc for BHB inspirals with
$\sim 1640$ Mpc for BHB inspirals with ![]() $M_1 = M_2 = 30\,\text{M}_{\odot}$(Abbott et al. Reference Abbott2018b), corresponding to a redshift of 0.39. Assuming that clusters form
$M_1 = M_2 = 30\,\text{M}_{\odot}$(Abbott et al. Reference Abbott2018b), corresponding to a redshift of 0.39. Assuming that clusters form ![]() $\sim 12$ Gyr ago, then the canonical horizon distance corresponds to binaries that merge
$\sim 12$ Gyr ago, then the canonical horizon distance corresponds to binaries that merge ![]() $\geqslant 6$ Gyr after star cluster formation. Slow-merging escapers are thus more likely to be detected than escapers that merge quickly after ejection. As with the other simulated populations, we again point out the difference in direct and sampling rejection probabilities (Table 2) as a caveat that a larger set of N-body runs would be highly beneficial to draw stronger inference. However, the ejected population appears to be sufficiently robust, with the rejection probability changing by 0.01 between sampling and direct comparison. Expanding our datasets to achieve large sample simulated populations to allow for effective comparison will be the subject of future work. We likewise leave a full analysis of the mass dependence (The LIGO Scientific Collaboration & The Virgo Collaboration 2012), and peak GW frequency (Abbott et al. Reference Abbott2016b) to future studies.
$\geqslant 6$ Gyr after star cluster formation. Slow-merging escapers are thus more likely to be detected than escapers that merge quickly after ejection. As with the other simulated populations, we again point out the difference in direct and sampling rejection probabilities (Table 2) as a caveat that a larger set of N-body runs would be highly beneficial to draw stronger inference. However, the ejected population appears to be sufficiently robust, with the rejection probability changing by 0.01 between sampling and direct comparison. Expanding our datasets to achieve large sample simulated populations to allow for effective comparison will be the subject of future work. We likewise leave a full analysis of the mass dependence (The LIGO Scientific Collaboration & The Virgo Collaboration 2012), and peak GW frequency (Abbott et al. Reference Abbott2016b) to future studies.

Figure 11. Breakdown of the number of mergers in each cluster model per mass ratio; primordial binaries (red), canonical (orange), low metallicity (blue), IMBH (black), large half-mass radius (yellow), high metallicity (pink), large natal kicks (green), and larger King concentrations (purple). The left panel displays the mass ratio distribution for all ejected systems and the right panel displays the mass ratio distribution for all in-cluster mergers.
5.2. Data model comparison
It is important to consider how representative our simulations are of actual star clusters that host mergers detectable by LIGO. The models used are not an accurate sample of the real-world GC population in the local Universe. Making such a sample is intrinsically difficult as the underlying distributions for GC parameters are not entirely known, being limited by our ability to observe the clusters. Most of the information pertaining to these distributions come from Milky Way GCs, as extra-galactic clusters are in general too distant. There is no reason to think that these local GCs are representative of all GCs.
Instead, we rely on the relatively wide range of initial conditions to explore the parameter space. When making comparisons to LIGO observations, we must be careful to ensure that the trends we observe are not artefacts of our initial conditions. Figure 11 displays histograms of the in-cluster (right panel) and ejected (left panel) q distributions, separated into each of the eight main models. The overall trends appear to be followed reasonably well by most models. The exception is the ‘high_z’ and ‘W’ models for the in-cluster mergers, all of which have ![]() $q > 0.7$. If these two q distributions were indeed flat, the probability of having five independent mergers above 0.7 is 0.0024. However, as these five mergers only represent
$q > 0.7$. If these two q distributions were indeed flat, the probability of having five independent mergers above 0.7 is 0.0024. However, as these five mergers only represent ![]() ${\sim}5\%$ of in-cluster mergers, their effect on the overall distribution is small and are thus unlikely to significantly confound our results. The same can be said for the presence of two ejected BHBs originating from an IMBH model (black section in Figure 11), both with
${\sim}5\%$ of in-cluster mergers, their effect on the overall distribution is small and are thus unlikely to significantly confound our results. The same can be said for the presence of two ejected BHBs originating from an IMBH model (black section in Figure 11), both with ![]() $q < 0.45$.
$q < 0.45$.
For merging escapers and slow-merging escapers, we display the initial condition information in Table 3. The slow-merging escapers appear to be a representative sample of all merging escapers regarding the proportion of mergers in each model. We also see the relatively large number of ‘can’ and ‘low Z’ ejected BHBs in the merging systems, likely due to the large number of simulations using these models. Only one merging escaper comes from an ‘rh’ model (5%), whereas 45 ejected systems (18%) come from this model. This result is because ‘rh’ models have a larger initial ![]() $r_h$ than other models, leading to wider ejected binaries (Equation (12)). Overall, all these checks do not highlight the presence of significant bias in the analysis introduced by the choice of initial conditions.
$r_h$ than other models, leading to wider ejected binaries (Equation (12)). Overall, all these checks do not highlight the presence of significant bias in the analysis introduced by the choice of initial conditions.
Table 3. Breakdown of the number of mergers in each cluster model, presented for merging escapers and slow-merging escapers

6. Conclusions
In this work, we analyse the mergers of BHBs formed within simulated GCs, comparing the binary parameters of systems which merge inside their host cluster, to systems which merge after being ejected. The analysis is based on a novel set of direct NBODY6 simulations of realistic cluster models spanning a wide range of initial conditions, partially presented previously by de Vita et al. (Reference de Vita, Trenti and MacLeod2019) in the context of structural GC properties. The simulations include SSE and BSE, galactic tides, gravitational radiation, and other relativistic effects, making them an ideal tool to explore BHB mergers and compare with recent LIGO results. The key results are
-
Cluster BH populations evaporate over time through merger and ejection, leading to in-cluster merger frequency decreasing as the GCs age. The number of BHs and the number of BHB mergers are strongly correlated over time with each other.
-
We find no correlation between primordial binary fraction and scaled merger number. This indicates that primordial binaries have little impact on cluster BHB merger rates, likely because merging BHBs are dynamically formed.
-
The in-cluster and ejected mass distributions are relatively similar, except that in-cluster merging BHBs tend to have slightly higher primary masses, as second-generation BHs merge again in the cluster core. Both populations peak in their mass distributions per the overall BH population, resulting from the progenitor cut-off for forming BHs. Higher mass systems tend to be ejected earlier in a cluster’s lifetime because the three-body interaction rate is proportional to binary mass, enabling quicker ejection through successive interaction recoils.
-
The eccentricity distribution for escaping BHBs closely matches a thermal distribution, indicative of multiple three-body interactions. Although primordial binaries (when present) are initialised with eccentricities drawn from a thermal distribution, none of the ejected BHBs are primordial. The subset of ejected BHBs that merge within the age of the Universe has an eccentricity distribution skewed closer to
 $e = 1$ when compared to the thermal distribution, a result of the stronger gravitational radiation production at higher eccentricities.
$e = 1$ when compared to the thermal distribution, a result of the stronger gravitational radiation production at higher eccentricities. -
Only 8% of all ejected BHBs merge within the age of the Universe, corresponding to approximately 16% of mergers when including in-cluster mergers. The ratio of ejected to in-cluster mergers is significantly lower than in previous studies (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a). We attribute this discrepancy to the relatively high stellar densities in the GCs simulated by de Vita et al. (Reference de Vita, Trenti and MacLeod2019).
-
The majority of escaping BHBs are ejected from their host cluster with separations between 1 and 10 AU. However, only systems with separations
 $\lesssim$1 AU produce sufficient gravitational radiation to merge within the age of the Universe.
$\lesssim$1 AU produce sufficient gravitational radiation to merge within the age of the Universe. -
Ejected systems have a mass ratio distribution skewed towards unity, whereas in-cluster systems have an almost flat distribution for
 $q \gtrsim 0.1$. In addition, we observe a bimodality in the inspiral times after escaping the cluster, whereby all extreme mass ratio systems (
$q \gtrsim 0.1$. In addition, we observe a bimodality in the inspiral times after escaping the cluster, whereby all extreme mass ratio systems ( $q > 0.95$) merge within
$q > 0.95$) merge within  $10^4\ \text{yr}$ after ejection.
$10^4\ \text{yr}$ after ejection. -
We compare our simulated mass ratio distributions to the 10 LIGO BHB mergers detected in O1 and O2. Both slow-merging escaping BH pairs and in-cluster mergers that we estimate are not impacted by gravitational recoil match the LIGO O2 data reasonably well. However, the results are affected by low-number uncertainty; therefore, larger samples of observed mergers and a more extensive set of simulations are needed for robust confirmation of this tentative finding and to discriminate between the two possible populations.
-
Finally, we separate our simulations into subtypes based on the initial conditions. We find that the overall trends seen in the mass ratio distributions are mostly also seen in the individual simulation subtypes. We conclude that our selection of initial conditions does not significantly bias the mass ratio distributions.
In a future extension, we plan to run models with lower metallicities to allow for a more comprehensive comparison with similar studies (Rodriguez et al. 2016; Reference Rodriguez, Zevin, Amaro-Seoane, Chatterjee, Kremer, Rasio and Ye2019a; Park et al. Reference Park, Kim, Lee, Bae and Belczynski2017) and to conduct a more systematic investigation into the distribution of real-world GC properties, using the results to expand to a more extensive and realistic simulation database. A full statistical analysis with LIGO O3 Data will also be conducted, incorporating horizon distance calculations to only include simulated BHBs that LIGO can detect. Finally, we will extend our models to different formation epochs, using a cosmological model of GC formation, and incorporate new prescriptions for gravitational recoil in NBODY codes through numerical relativity.
Acknowledgements
We would like to thank Ruggero De Vita, Ilya Mandel, and Marcel Hohmann for useful discussions. Parts of this research are supported by the Australian Re-search Council Centre of Excellence for Gravitational Wave Discovery (OzGrav) (project number CE170100004). This research has made use of data, software, and/or web tools obtained from the Gravitational Wave Open Science Center (https://www.gw-openscience.org), a service of LIGO Laboratory, the LIGO Scientific Collaboration, and the Virgo Collaboration. LIGO is funded by the US National Science Foundation. Virgo is funded by the French Centre National de Recherche Scientifique (CNRS), the Italian Istituto Nazionale della Fisica Nucleare (INFN), and the Dutch Nikhef, with contributions by Polish and Hungarian institutes. Numerical simulations have been performed on HPC clusters at the University of Melbourne (Spartan) and at the Swinburne University (OzSTAR).
Conflicts of interest
None.
A. Primordial binaries and natal kicks
As discussed in Sections 2.3 and 5.2, our models encompass a wide range of initial conditions, reflecting both the variety of masses, concentrations, and ages in the GC population of galaxies, and uncertainties in the input physical ingredients (natal kick distribution and primordial binary fraction). In nature, the latter physical ingredients do not vary from one GC to the next, so it is important to assess if our modelling choices introduce biases in our results. To address this, we split some of our main results by natal kick distribution and primordial binary fraction.
Although we run systems with a number of different primordial binary fractions, due to the small sample size, we only compare clusters without primordial binaries to those with primordial binaries, instead of separating results into the specific primordial binary fraction. For natal kicks, we compare clusters with ![]() $\sigma_k/\sigma_*$ = 1 to those with
$\sigma_k/\sigma_*$ = 1 to those with ![]() $\sigma_k/\sigma_*$ = 2. The key results we compare are in-cluster and ejected masses and mass ratios, along with ejected eccentricities and separations.
$\sigma_k/\sigma_*$ = 2. The key results we compare are in-cluster and ejected masses and mass ratios, along with ejected eccentricities and separations.
When comparing the models with and without primordial binaries using the KS test, only the separation and ejected mass ratio distributions yield strong evidence against the null hypothesis at 95% confidence interval. Figure A.1 shows the ejected BHB mass ratios CDFs for models with and without primordial binaries. Although the difference between these sets of models is statistically significant, they still display the same prevalence of higher mass ratios. This suggests that while the effect of our choice of primordial binary fractions cannot be ruled out, its impact is expected to be modest.

Figure A.1. CDF of the mass ratios for ejected BHBs. The red curve shows the distribution for models without primordial binaries and the blue curve shows the distribution for models with primordial binaries. The KS statistic is 0.26, with a p-value < 0.01.

Figure A.2. CDF of the semi-major axis at the point of ejection plotted on a log scale. The red curve shows the distribution for models without primordial binaries and the blue curve shows the distribution for models with primordial binaries. The KS statistic is 0.22, with a p-value of 0.01.

Figure A.3. CDF of the semi-major axis at the point of ejection plotted on a log scale. The red curve shows the distribution for models with the smaller natal kicks and the blue curve shows the distribution for models with the larger natal kicks. The KS statistic is 0.5, with a p-value of 0.02.
Figure A.2. shows the ejected BHB separation of CDFs for models with and without primordial binaries. Using the KS test to compare ejected separations for the two different kick models, we find evidence against the null hypothesis at 95% confidence interval. Similarly to the mass ratios discussed above, both distributions still display similar trends despite statistically significant differences. All other comparisons of ejected BHB separations for different initial conditions are consistent with the null hypothesis instead.
Figure A.3. displays the CDFs of ejected BHB separations for the two kick models. Although the differences between the distributions are statistically significant, this is unlikely to significantly affect results concerning the entire set of ejected systems due to the small number of ejected BHBs from these high-kick models (9 out of 239). All of these nine escaping binaries are ejected well after the formation of all BHs in their host cluster, meaning none are ejected due to a natal kick.
B. Statistical definitions
-
Savitzky–Golay filter: The Savitzky–Golay filter is a digital filter used to smooth a set of data points, increasing the precision of the data without altering the signal tendency. For each data point, the filter fits a polynomial to a window of adjacent data points by a method of least squares (Savitzky & Golay Reference Savitzky and Golay1964).
-
Outliers: An outlier is any data point that appears to be outside the general pattern of the data. Although outliers can occur in any legitimate dataset, they are unlikely and so usually indicate some sort of error (Moore, McCabe, & Craig Reference Moore, McCabe and Craig1993). There are multiple definitions used to define outliers, with the most common being the so-called ‘Tukey’s fence’: any data 1.5 times the interquartile range above the third quartile or below the first quartile, that is, outside the range
 $\left[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3-Q_1)\right]$ is considered an outlier (Tukey Reference Tukey1977).
$\left[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3-Q_1)\right]$ is considered an outlier (Tukey Reference Tukey1977). -
Pearson’s chi-squared test: Pearson’s chi-squared test is a statistical test used on categorical data to determine how likely the observed difference between datasets is purely due to chance. This is often used on a set of events, each corresponding to an outcome of a categorical variable. For example, one could have a set of dice rolls and test if the six-sided die is fair, where the categories are the outcome of the roll. The test statistic is a
 $\chi^2$ value, which is compared to a
$\chi^2$ value, which is compared to a  $\chi^2$ frequency distribution with the same degrees of freedom as the data. This allows for the null hypothesis (that there is no relation in the frequency of data between categories) to be rejected or supported at a given confidence level (Pearson Reference Pearson1900).
$\chi^2$ frequency distribution with the same degrees of freedom as the data. This allows for the null hypothesis (that there is no relation in the frequency of data between categories) to be rejected or supported at a given confidence level (Pearson Reference Pearson1900). -
KS test: The two-sided KS test is a non-parametric statistical test used to compare two data samples to determine if they differ significantly, with the null hypothesis that they are sampled from the same underlying distribution. The test statistic is simply the maximal distance between the two sample CDFs. The test accounts for the size of each sample and makes no assumption on the distributions (Fasano & Franceschini Reference Fasano and Franceschini1987; Stephens Reference Stephens1974).
-
Spearman’s rank-order correlation test: Spearman’s rank-order correlation test is a non-parametric statistical test used to determine if the correlation between two variables is statistically significant. It assesses both the direction and strength of the monotonic relationship between the two variables and so can be used to test for non-linear correlation (McDonald Reference McDonald2009).