Dynamic analysis of an elastic plate on a cross-anisotropic elastic half-space under a rectangular moving load

Abstract

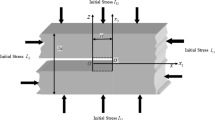
The dynamic response of an elastic thin plate resting on a cross-anisotropic elastic half-space to a rectangular load moving on its surface with constant speed is analytically obtained. The moving load and the plate and soil displacements are expanded in double complex Fourier series involving the two horizontal coordinates x and y as well as the time and the load velocity. Thus, the plate equation of lateral motion reduces to an algebraic equation, while the soil equations of motion reduce to a system of three ordinary differential equations with respect to the vertical coordinate z, which can be easily solved. Compatibility and equilibrium at the plate–soil interface as well as employment of the boundary conditions of the system enable one to determine the solution in terms of displacements of the plate and the half-space soil medium. The solution is first verified by using it to obtain as special cases the solutions for isotropic and cross-anisotropic half-space problems and compare them against existing analytical solutions. Parametric studies are conducted to assess the effects of the degree of cross-anisotropy on the plate and soil responses in conjunction with the effects of other important parameters, such as the speed of the moving load.

Appendices

Appendix A

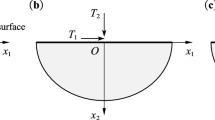
The assumption that the plate extends to infinity along both directions x and y is an approximation for mathematical convenience. The correct solution involves finite plate dimension along the y-direction and can only be obtained by a numerical method. In order to validate the proposed method, elastic dynamic finite element analyses (FEA) have been conducted with the aid of the commercial program ABAQUS [38]. The half-space has been modeled with solid elements assuming a homogeneous isotropic soil with material properties equal to $E=0.5$ GPa, ${v}=0.2$ and $\rho =2000$ kg/m$^{{3}}$. The plate of 5.0 m width has been modeled with shell elements with concrete material properties equal to $E_\mathrm{p}=30$ GPa, ${v}=0.25$ and $\rho =2300$ kg/m$^{{3}}$. The moving load was assumed equal to ${P}=105$ kN acting over an area with length equal to 0.2 m and width equal to 0.2 m. It was modeled in ABAQUS [38] as a prescribed force varying with time, i.e., as a moving force problem, using the DLOAD subroutine and a simple FORTRAN [39] script developed by the authors for this purpose. The infinite half-space soil medium has been modeled as a finite domain and to eliminate reflected waves at the boundaries, viscous boundaries have been used. Half of the domain was considered, as depicted in Fig. 22a due to symmetry. More information about the modeling can be found in [40]. The maximum response values of $w_\mathrm{p}$ and $M_{yy}$ versus the y-direction coming from the above FEA and the present method are compared in Fig. 22b and c, respectively. One can easily see in these figures that the responses coming from the present method are close to the ones obtained by FEA (up to 2.5 m) and that the response of the plate along the y-axis decreases fast as one goes away from the x-axis. Thus, the response obtained for the plate model with a finite dimension (up to 2.5 m) along the y-direction is closely approached by the one corresponding to the infinitely extended plate model along the x- and y-directions.

Fig. 22

Validation of the proposed method with FEA: a the FEA model, b maximum vertical plate displacement $w_\mathrm{p}$ and c maximum bending moment $M_{yy}$ versus y

Appendix B

For ${n}=0$ and ${m}=0$, Eqs. (33)–(36) become

$$\begin{aligned}&{U}_{{{00}}}^{{\prime \prime }}=0,\nonumber \\&{V}_{{{00}}}^{{\prime \prime }}=0,\nonumber \\&{W}_{{{00}}}^{{\prime \prime }}=0,\nonumber \\&{0=}{F}_{{00}}{-}{Q}_{{{00}}}, \end{aligned}$$

(B1)

respectively. The boundary conditions (55), (56), (58) and (61) become

$$\begin{aligned}&{U}_{{{00}}}^{{\prime }}\left( {0} \right) =0,\nonumber \\&{V}_{{{00}}}^{{\prime }}\left( {0} \right) =0,\nonumber \\&{U}_{{{00}}}\left( {H} \right) ={V}_{{{00}}}\left( {H} \right) ={W}_{{{00}}}{(H)=0},\nonumber \\&{c}_{{33}}{W}_{{{00}}}^{{\prime }}\left( {0} \right) =-{F}_{{{00}}}, \end{aligned}$$

(B2)

respectively. Using Eqs. (B1) and (B2), one can easily find the solutions for ${U}_{{{00}}}$, ${V}_{{{00}}}$, ${W}_{{{00}}}$ as

$$\begin{aligned}&{U}_{{{00}}}={V}_{{{00}}}=0,\nonumber \\&{W}_{{{00}}}=\frac{{F}_{{{00}}}}{{c}_{{33}}}\left( {H-z} \right) , H >z. \end{aligned}$$

(B3)

It has been found that a value of ${H}=200$ m approximates well the case where H approaches infinity.

Appendix C

For ${n}=0$ and ${m}> 0$, Eqs. (33)–(35) become

$$\begin{aligned}&{A}_{{{1}}}{U}_{{0m}}^{{\prime \prime }}{{+B}}_{{{1}}}{U}_{{0m}}=0, \end{aligned}$$

(C1)

$$\begin{aligned}&{A}_{{{2}}}{V}_{{0m}}^{{\prime \prime }}+{B}_{{{2}}}{V}_{{0m}}+{D}_{{{2}}}{W}_{{0m}}^{{\prime }}=0, \end{aligned}$$

(C2)

$$\begin{aligned}&{{A}_{{{3}}}{W}_{{0m}}^{{\prime \prime }}{+B}}_{{{3}}}{W}_{{0m}}+{D}_{{{3}}}{V}_{{0m}}^{{\prime }}=0, \end{aligned}$$

(C3)

respectively, where

$$\begin{aligned}&{A}_{{{1}}}={c}_{{{44}}}, \quad {B}_{{{1}}} = -{c}_{{{66}}}\mu _{{m}}^{{2}},\nonumber \\&{A}_{{{2}}}={c}_{{{44}}}, \quad {B}_{{{2}}} = -{c}_{{{11}}}\mu _{{{m}}}^{{2}} \quad {D}_{{{2}}}=\left( {c}_{{{13}}}+{c}_{{{44}}} \right) {i}\mu _{{{m}}},\nonumber \\&{A}_{{{3}}}={c}_{{{33}}}, \quad {B}_{{{3}}} = -{c}_{{{44}}}\mu _{{{m}}}^{{2}}, \quad {D}_{{{3}}}=\left( {c}_{{{13}}}+{c}_{{44}} \right) {i}\mu _{{{m}}}. \end{aligned}$$

(C4)

The boundary conditions (55), (56) and (61) become

$$\begin{aligned}&{U}_{{{0m}}}^{{\prime }}\left( {0} \right) =0, \end{aligned}$$

(C5)

$$\begin{aligned}&{V}_{{{0m}}}^{{\prime }}\left( {0} \right) {+i}\mu _{{{m}}}{W}_{{{0m}}}\left( {0} \right) =0, \end{aligned}$$

(C6)

$$\begin{aligned}&{c}_{{{13}}}{i}\mu _{{{m}}}{V}_{{0m}}\left( {0} \right) +{c}_{{{33}}}{W}_{{0m}}^{{\prime }}\left( {0} \right) {-D}\mu _{{m}}^{{4}}{W}_{{{0m}}}{(0)=-}{F}_{{0m}}, \end{aligned}$$

(C7)

respectively.

Equation (C1) is uncoupled and in conjunction with Eqs. (C5) and (58)$_{{{1}}}$ yields the solution

$$\begin{aligned} {U}_{{{0m}}}{=0 }. \end{aligned}$$

(C8)

For Eqs. (C2) and (C3), a solution of the form

$$\begin{aligned} {V}_{{{0m}}}{=S}{e}^{{qz}}, \quad {W}_{{{0m}}}{=T}{e}^{{qz}}, \end{aligned}$$

(C9)

is assumed. Substituting this solution into Eqs. (C2) and (C3) results in

(C10)

The above equation has non-trivial solution for S and T for those q which are the roots of the equation

$$\begin{aligned} {A}_{{{2}}}{A}_{{3}}{q}^{{4}}+\left( {B}_{{3}}{A}_{{{2}}}+{B}_{{{2}}}{A}_{{3}}{-}{D}_{{{2}}}{D}_{{{3}}} \right) {q}^{{2}}+{B}_{{{2}}}{B}_{{3}}{=0 } \end{aligned}$$

(C11)

By writing Eq. (C11) in the form

$$\begin{aligned} {A}_{{{2}}}{A}_{{{3}}}\bar{{q}}^{{2}}+\left( {B}_{{{3}}}{A}_{{{2}}}+{B}_{{2}}{A}_{{{3}}}{-}{D}_{{2}}{D}_{{{3}}} \right) \bar{{q}}+{B}_{{2}}{B}_{{{3}}}{=0 }. \end{aligned}$$

(C12)

with $\bar{{q}}={q}^{{2}}$ and by taking only ${q=-}\sqrt{\bar{{q}}}$, the boundary conditions (58)$_{{{2,3 }}}$ are automatically satisfied for H approaching infinity. Thus, the solutions (C9) take the form

$$\begin{aligned}&{V}_{{{0m}}}=\sum \limits _{{{k=1}}}^{2} {{S}_{{{0mk}}}{e}^{{q}_{{{k}}}{z}}},\nonumber \\&{W}_{{{0m}}}=\sum \limits _{{{k=1}}}^{2} {{T}_{{{0mk}}}{e}^{{q}_{{{k}}}{z}}}, \end{aligned}$$

(C13)

where ${S}_{{{0mk}}}$ can be obtained in terms of ${T}_{{{0mk}}}$ by using Eq. (C10) and reads

$$\begin{aligned} {S}_{{{0mk}}}{=-}\frac{{D}_{{2}}{q}_{{{k}}}}{{B}_{{{2}}}+{A}_{{2}}{q}_{{{k}}}^{{2}}}{T}_{{{0mk}}}. \end{aligned}$$

(C14)

Replacing ${V}_{{{0m}}}$ and ${W}_{{{0m}}}$ in Eqs. (C6) and (C7) with their expressions (C13), one can rewrite them in the form

$$\begin{aligned}&\sum \limits _{{{k=1}}}^{2} {{q}_{{k}}{S}_{{{0mk}}}} {+i}\mu _{{m}}\sum \limits _{{{k=1}}}^{2} {T}_{{{0mk}}} =0, \end{aligned}$$

(C15)

$$\begin{aligned}&{c}_{{{13}}}{i}\mu _{{{m}}}\sum \limits _{{k=1}}^{2} {S}_{{{0mk}}} +{c}_{{33}}\sum \limits _{{{k=1}}}^{2} {{q}_{{k}}{T}_{{{0mk}}}} {-D}\mu _{{m}}^{{4}}\sum \limits _{{{k=1}}}^{2} {T}_{{0mk}} {=-}{F}_{{{0m}}}. \end{aligned}$$

(C16)

Equations (C15) and (C16) serve to compute the two unknown constants ${T}_{{{0mk }}}(k=1,2)$ since ${S}_{{0mk}}$ have already been expressed in terms of ${T}_{{0mk}}$ by Eq. (C14).

Appendix D

For ${m}=0$ and $n> 0$, Eqs. (33)–(35) become

$$\begin{aligned}&{{A}_{{{1}}}{U}_{{n0}}^{{\prime \prime }}{+B}}_{{{1}}}{U}_{{n0}}+{D}_{{{1}}}{W}_{{n0}}^{{\prime }}=0, \end{aligned}$$

(D1)

$$\begin{aligned}&{A}_{{{2}}}{V}_{{n0}}^{{\prime \prime }}+{B}_{{{2}}}{V}_{{n0}}=0, \end{aligned}$$

(D2)

$$\begin{aligned}&{{A}_{{{3}}}{W}_{{n0}}^{{\prime \prime }}{+B}}_{{{3}}}{W}_{{n0}}+{C}_{{{3}}}{U}_{{n0}}^{{\prime }}=0, \end{aligned}$$

(D3)

respectively, where

$$\begin{aligned}&{A}_{{{1}}}={c}_{{{44}}}, \quad {B}_{{{1}}}=\rho {\lambda }_{{n}}^{{2}}{V}^{{2}}{-}{c}_{{11}}{\lambda }_{{{n}}}^{{2}}, \quad {D}_{{{1}}}=\left( {c}_{{{13}}}+{c}_{{44}} \right) {i}{\lambda }_{{{n}}},\nonumber \\&{A}_{{2}}={c}_{{{44}}}, \quad {B}_{{{2}}}=\rho {\lambda }_{{n}}^{{2}}{V}^{{2}}{-}{c}_{{66}}{\lambda }_{{{n}}}^{{2}},\nonumber \\&{A}_{{3}}={c}_{{{33}}}, \quad {B}_{{{3}}}=\rho {\lambda }_{{n}}^{{2}}{V}^{{2}}{-}{c}_{{44}}{\lambda }_{{{n}}}^{{2}}, \quad {C}_{{{3}}}=\left( {c}_{{{13}}}+{c}_{{44}} \right) {i}{\lambda }_{{{n}}}, \end{aligned}$$

(D4)

The boundary conditions (55), (56) and (61) become

$$\begin{aligned}&{U}_{{{n0}}}^{{\prime }}\left( {0} \right) {+i}{\lambda }_{{{n}}}{W}_{{{n0}}}\left( {0} \right) =0, \end{aligned}$$

(D5)

$$\begin{aligned}&{V}_{{{n0}}}^{{\prime }}\left( {0} \right) =0, \end{aligned}$$

(D6)

$$\begin{aligned}&{c}_{{{13}}}{i}{\lambda }_{{{n}}}{U}_{{n0}}\left( {0} \right) +{c}_{{{33}}}{W}_{{n0}}^{{\prime }}\left( {0} \right) {-}\left[ {D}{\lambda }_{{n}}^{{4}}{-}{c}_\mathrm{p}{i}{\lambda }_{{{n}}}{V-}{m}_\mathrm{p}{\lambda }_{{n}}^{{2}}{V}^{{2}} \right] {W}_{{n0}}{(0)=-}{F}_{{{n0}}}, \end{aligned}$$

(D7)

respectively.

Equation (D2) is uncoupled and in conjunction with Eqs. (D6) and (58)$_{{{2}}}$ yields the solution

$$\begin{aligned} {V}_{{{n0}}}{=0 }, \end{aligned}$$

(D8)

For Eqs. (D1) and (D3), a solution of the form

$$\begin{aligned}&{U}_{{{n0}}}{=R}{e}^{{qz}}, \quad {W}_{{{n0}}}{=T}{e}^{{qz}} \end{aligned}$$

(D9)

is assumed. Substituting this solution into Eqs. (D1) and (D3) results in

(D10)

The above equation has non-trivial solution for R and T for those q which are roots of the equation

$$\begin{aligned} {A}_{{{1}}}{A}_{{3}}{q}^{{4}}+\left( {B}_{{3}}{A}_{{{1}}}+{B}_{{{1}}}{A}_{{3}}{-}{D}_{{{1}}}{C}_{{{3}}} \right) {q}^{{2}}+{B}_{{{1}}}{B}_{{3}}{=0 }. \end{aligned}$$

(D11)

By writing Eq. (D11) in the form

$$\begin{aligned} {A}_{{{1}}}{A}_{{{3}}}\bar{{q}}^{{2}}+\left( {B}_{{{3}}}{A}_{{{1}}}+{B}_{{1}}{A}_{{{3}}}{-}{D}_{{1}}{C}_{{{3}}} \right) \bar{{q}}+{B}_{{1}}{B}_{{{3}}}{=0 } \end{aligned}$$

(D12)

with $\bar{{q}}={q}^{{2}}$ and by taking only ${q=-}\sqrt{\bar{{q}}}$, the boundary conditions (58)$_{{{1,3 }}}$ are automatically satisfied for H approaching infinity. Thus, the solutions (D9) take the form

$$\begin{aligned}&{U}_{{{n0}}}=\sum \limits _{{{k=1}}}^{2} {{R}_{{{n0k}}}{e}^{{q}_{{{k}}}{z}}},\nonumber \\&{W}_{{{n0}}}=\sum \limits _{{{k=1}}}^{2} {{T}_{{{n0k}}}{e}^{{q}_{{{k}}}{z}}}, \end{aligned}$$

(D13)

where ${T}_{{{n0k}}}$ can be obtained in terms of ${R}_{{{n0k}}}$ by using Eq. (D10) and reads

$$\begin{aligned} {T}_{{{n0k}}}{=-}\frac{{B}_{{1}}+{A}_{{{1}}}{q}_{{k}}^{{2}}}{{D}_{{{1}}}{q}_{{k}}}{R}_{{{n0k}}}. \end{aligned}$$

(D14)

Replacing ${U}_{{{n0}}}$ and ${W}_{{{n0}}}$ in Eqs. (D5) and (D7) with their expressions (D13), one can rewrite them in the form

$$\begin{aligned}&\sum \limits _{{{k=1}}}^{2} {{q}_{{k}}{R}_{{{n0k}}}} {+i}{\lambda }_{{n}}\sum \limits _{{{k=1}}}^{2} {T}_{{{n0k}}} =0, \end{aligned}$$

(D15)

$$\begin{aligned}&{c}_{{{13}}}{i}{\lambda }_{{n}}\sum \limits _{{{k=1}}}^{2} {R}_{{{n0k}}} +{c}_{{{33}}}\sum \limits _{{{k=1}}}^{2} {{q}_{{{k}}}{T}_{{{n0k}}}} {-}\left[ {D}{\lambda }_{{n}}^{{4}}{-i}{c}_\mathrm{p}{\lambda }_{{n}}{V-}{m}_\mathrm{p}{\lambda }_{{n}}^{{2}}{V}^{{2}} \right] \sum \limits _{{k=1}}^{2} {T}_{{{n0k}}} {=-}{F}_{{n0}}. \end{aligned}$$

(D16)

Equations (D15) and (D16) serve to compute the two unknown constants ${R}_{{{n0k }}}$ $({k}=1,2)$ since ${T}_{{{n0k}}}$ have already been expressed in terms of ${R}_{{{n0k}}}$ by Eq. (D14).