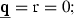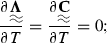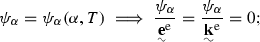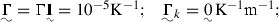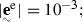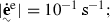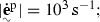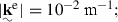Abstract
During most metal manufacturing processes, the medium deforms by generating large quantities of plastic strain at relatively high strain rates, inevitably inducing rises in temperature. Metals characterized by low thermal conductivity properties might locally retain high temperatures, consequently undergoing thermal softening. The classical balance laws governing the continuum equilibrium show severe mesh sensitivity if they were numerically discretized through finite element methods. Furthermore, the plastic deformation tends to localize in narrow areas whose characteristic length is comparable to grain size, thereby requiring the adoption of theories able to predict size-effects. In this manuscript we demonstrate that the Cosserat medium is able to overcome these issues related to manufacturing processes simulation. We first provide a thermodynamically-consistent description of the Cosserat medium, and then we propose a method to calibrate the two additional characteristic lengths introduced by the Cosserat medium description by enriching the model with the TANH stress flow rule under adiabatic conditions.






Similar content being viewed by others
References
Aldakheel, F., Miehe, C.: Coupled thermomechanical response of gradient plasticity. Int. J. Plast. 91, 1–24 (2017). https://doi.org/10.1016/j.ijplas.2017.02.007
Ask, A., Forest, S., Appolaire, B., Ammar, K.: A Cosserat-phase-field theory of crystal plasticity and grain boundary migration at finite deformation. Contin. Mech. Thermodyn. (2018). https://doi.org/10.1007/s00161-018-0727-6
Bauer, S., Dettmer, W.G., Perić, D., Schäfer, M.: Micropolar hyper-elastoplasticity: constitutive model, consistent linearization, and simulation of 3D scale effects. Int. J. Numer. Methods Eng. 91(1), 39–66 (2012). https://doi.org/10.1002/nme.4256
Cahuc, O., Darnis, P., Laheurte, R.: Mechanical and thermal experiments in cutting process for new behaviour law. Int. J. Form. Process. 10(2), 235–269 (2007). https://doi.org/10.3166/ijfp.10.235-269
Calamaz, M., Coupard, D., Girot, F.: A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti–6Al–4V. Int. J. Mach. Tools Manuf. 48(3–4), 275–288 (2008). https://doi.org/10.1016/j.ijmachtools.2007.10.014
Chaboche, J.: Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 5(3), 247–302 (1989). https://doi.org/10.1016/0749-6419(89)90015-6
Chambon, R., Caillerie, D., El Hassan, N.: One-dimensional localisation studied with a second grade model. Eur. J. Mech. A Solids 17(4), 637–656 (1998). https://doi.org/10.1016/S0997-7538(99)80026-6
Chen, G., Ren, C., Yang, X., Jin, X., Guo, T.: Finite element simulation of high-speed machining of titanium alloy (Ti-6Al-4V) based on ductile failure model. Int. J. Adv. Manuf. Technol. 56(9–12), 1027–1038 (2011). https://doi.org/10.1007/s00170-011-3233-6
Cheng, C., Mahnken, R.: A multi-mechanism model for cutting simulations based on the concept of generalized stresses. Comput. Mater. Sci. 100(PB), 144–158 (2015). https://doi.org/10.1016/j.commatsci.2014.12.028
Cosserat, E., Cosserat, F.: Theorie des corps deformables. A. Hermann et fils (1909)
de Borst, R.: Simulation of strain localization: a reappraisal of the Cosserat continuum. Eng. Comput. 8(4), 317–332 (1991). https://doi.org/10.1108/eb023842
de Borst, R.: A generalisation of theory for polar continua. Comput. Methods Appl. Mech. Eng. 103(3), 347–362 (1993). https://doi.org/10.1016/0045-7825(93)90127-J
De Borst, R., Mühlhaus, H.B.: Gradient-dependent plasticity: formulation and algorithmic aspects. Int. J. Numer. Methods Eng. 35(3), 521–539 (1992). https://doi.org/10.1002/nme.1620350307
de Borst, R., Sluys, L.J.: Localisation in a Cosserat continuum under static and dynamic loading conditions. Comput. Methods Appl. Mech. Eng. 90(1–3), 805–827 (1991). https://doi.org/10.1016/0045-7825(91)90185-9
Dong, F., Wang, X., Yang, Q., Liu, H., Xu, D., Sun, Y., Zhang, Y., Xue, R., Krishnaswamy, S.: In-situ measurement of Ti–6Al–4V grain size distribution using laser-ultrasonic technique. Scr. Mater. 154, 40–44 (2018). https://doi.org/10.1016/j.scriptamat.2018.05.009
Fleck, N.A., Hutchinson, J.W.: Strain gradient plasticity. Adv. Appl. Mech. 33(C), 295–361 (1997). https://doi.org/10.1016/S0065-2156(08)70388-0
Forest, S., Barbe, F., Cailletaud, G.: Cosserat modelling of size effects in the mechanical behaviour of polycrystals and multi-phase materials. Int. J. Solids Struct. 37(46–47), 7105–7126 (2000). https://doi.org/10.1016/S0020-7683(99)00330-3
Forest, S., Sievert, R.: Elastoviscoplastic constitutive frameworks for generalized continua. Acta Mech. 160(1–2), 71–111 (2003). https://doi.org/10.1007/s00707-002-0975-0
Forest, S., Sievert, R.: Nonlinear microstrain theories. Int. J. Solids Struct. 43(24), 7224–7245 (2006). https://doi.org/10.1016/j.ijsolstr.2006.05.012
González, D., Alkorta, J., Martínez-Esnaola, J.M., Gil Sevillano, J.: Numerical analysis of the indentation size effect using a strain gradient crystal plasticity model. Comput. Mater. Sci. 82, 314–319 (2014). https://doi.org/10.1016/j.commatsci.2013.10.004
Grammenoudis, P., Tsakmakis, C.: Hardening rules for finite deformation micropolar plasticity: restrictions imposed by the second law of thermodynamics and the postulate of Il’iushin. Contin. Mech. Thermodyn. 13(5), 325–363 (2001). https://doi.org/10.1007/s001610100055
Guo, Y.B., Wen, Q., Woodbury, K.A.: Dynamic material behavior modeling using internal state variable plasticity and its application in hard machining simulations. J. Manuf. Sci. Eng. Trans. ASME 128(3), 749–759 (2006). https://doi.org/10.1115/1.2193549
He, L., Su, H., Xu, J., Zhang, L.: Simulation analysis of the influence of dynamic flow stress behavior on chip formation. Int. J. Adv. Manuf. Technol. 95(5–8), 2301–2313 (2018). https://doi.org/10.1007/s00170-017-1275-0
Hor, A., Morel, F., Lebrun, J.L., Germain, G.: Modelling, identification and application of phenomenological constitutive laws over a large strain rate and temperature range. Mech. Mater. 64, 91–110 (2013). https://doi.org/10.1016/j.mechmat.2013.05.002
Huang, J., Kalaitzidou, K., Sutherland, J.W., Milligan, W.W., Aifantis, E.C., Sievert, R., Forest, S.: Gradient plasticity: implications to chip formation in machining. In: 4th International ESAFORM Conference on Material Forming, pp. 527–530 (2001)
Jebahi, M., Cai, L., Abed-Meraim, F.: Strain gradient crystal plasticity model based on generalized non-quadratic defect energy and uncoupled dissipation. Int. J. Plast. 126(April 2019), 102617 (2019). https://doi.org/10.1016/j.ijplas.2019.10.005
Joshi, S.S., Melkote, S.N.: An explanation for the size-effect in machining using strain gradient plasticity. J. Manuf. Sci. Eng. 126(4), 679 (2004). https://doi.org/10.1115/1.1688375
Khoei, A.R., Yadegari, S., Biabanaki, S.O.: 3D finite element modeling of shear band localization via the micro-polar Cosserat continuum theory. Comput. Mater. Sci. 49(4), 720–733 (2010). https://doi.org/10.1016/j.commatsci.2010.06.015
Koiter, W.T.: Couple stresses in the theory of elasticity, I & II. Philos. Trans. R. Soc. Lond. B 67, 17–44 (1964)
Kratochvíl, J., Labbé, E., Rey, C., Yang, S.: On physically motivated mesoscale Cosserat model of shear band formation. Scr. Mater. 41(7), 761–766 (1999). https://doi.org/10.1016/S1359-6462(99)00214-6
Lele, S.P., Anand, L.: A large-deformation strain-gradient theory for isotropic viscoplastic materials. Int. J. Plast. 25(3), 420–453 (2009). https://doi.org/10.1016/j.ijplas.2008.04.003
Li, J.C., Chen, X.W., Chen, G.: Numerical simulations on adiabatic shear behaviour of 921A steel pure shear hat-shaped specimens. WIT Trans. Built Environ. 113, 323–334 (2010). https://doi.org/10.2495/SU100281
List, G., Sutter, G., Bi, X.F., Molinari, A., Bouthiche, A.: Strain, strain rate and velocity fields determination at very high cutting speed. J. Mater. Process. Technol. 213(5), 693–699 (2013). https://doi.org/10.1016/j.jmatprotec.2012.11.021
Marchand, A., Duffy, J.: An experimental study of the formation process of adiabatic shear bands in a structural steel. J. Mech. Phys. Solids 36(3), 251–283 (1988). https://doi.org/10.1016/0022-5096(88)90012-9
Molinari, A., Soldani, X., Miguélez, M.H.: Adiabatic shear banding and scaling laws in chip formation with application to cutting of Ti-6Al-4V. J. Mech. Phys. Solids 61(11), 2331–2359 (2013). https://doi.org/10.1016/j.jmps.2013.05.006
Mühlhaus, H.B., Vardoulakis, I.: The thickness of shear bands in granular. Géotechnique 37(3), 271–283 (1987). https://doi.org/10.1680/geot.1987.37.3.271
Neff, P.: A finite-strain elastic–plastic Cosserat theory for polycrystals with grain rotations. Int. J. Eng. Sci. 44(8–9), 574–594 (2006). https://doi.org/10.1016/j.ijengsci.2006.04.002
Nguyen, G.D., Korsunsky, A.M., Belnoue, J.P.: A nonlocal coupled damage-plasticity model for the analysis of ductile failure. Int. J. Plast. 64, 56–75 (2015). https://doi.org/10.1016/j.ijplas.2014.08.001
Pamin, J., Wcisło, B., Kowalczyk-Gajewska, K.: Gradient-enhanced large strain thermoplasticity with automatic linearization and localization simulations. J. Mech. Mater. Struct. 12(1), 123–146 (2017). https://doi.org/10.2140/jomms.2017.12.123
Peirs, J., Verleysen, P., Degrieck, J., Coghe, F.: The use of hat-shaped specimens to study the high strain rate shear behaviour of Ti-6Al-4V. Int. J. Impact Eng. 37(6), 703–714 (2010). https://doi.org/10.1016/j.ijimpeng.2009.08.002
Poole, W., Ashby, M., Fleck, N.: Micro-hardness of annealed and work-hardened copper polycrystals. Scr. Mater. 34(4), 559–564 (1996). https://doi.org/10.1016/1359-6462(95)00524-2
Rattez, H., Stefanou, I., Sulem, J., Veveakis, M., Poulet, T.: Numerical analysis of strain localization in rocks with thermo-hydro-mechanical couplings using Cosserat continuum. Rock Mech. Rock Eng. 51(10), 3295–3311 (2018). https://doi.org/10.1007/s00603-018-1529-7
Royer, R., Darnis, P., Laheurte, R., Gérard, A., Cahuc, O.: Finite strain gradient plasticity theory for high speed machining. Procedia Eng. 10, 2312–2317 (2011). https://doi.org/10.1016/j.proeng.2011.04.381
Sabet, S.A., de Borst, R.: Structural softening, mesh dependence, and regularisation in non-associated plastic flow. Int. J. Numer. Anal. Meth. Geomech. 43(13), 2170–2183 (2019). https://doi.org/10.1002/nag.2973
Śloderbach, Z., Paja̧k, J.: Thermodynamic potential of free energy for thermo-elastic–plastic body. Contin. Mech. Thermodyn. 30(1), 221–232 (2018). https://doi.org/10.1007/s00161-017-0597-3
Steinmann, P., William, K.: Localization within the framework of micropolar elasto-plasticity. In: Brüller, O.S., Mannl, V., Najar, J. (eds.) Advances in Continuum Mechanics, pp. 296–313. Springer, Berlin (1991). https://doi.org/10.1007/978-3-642-48890-0_24
Stölken, J., Evans, A.: A microbend test method for measuring the plasticity length scale. Acta Mater. 46(14), 5109–5115 (1998). https://doi.org/10.1016/S1359-6454(98)00153-0
Taylor, G.I., Quinney, H.: The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 143(849), 307–326 (1934). https://doi.org/10.1098/rspa.1934.0004
Tordesillas, A., Peters, J.F., Gardiner, B.S.: Shear band evolution and accumulated microstructural development in Cosserat media. Int. J. Numer. Anal. Meth. Geomech. 28(10), 981–1010 (2004). https://doi.org/10.1002/nag.343
Wang, W.M., Sluys, L.J., De Borst, R.: Viscoplasticity for instabilities due to strain softening and strain-rate softening. Int. J. Numer. Methods Eng. 40(20), 3839–3864 (1997). https://doi.org/10.1002/(SICI)1097-0207(19971030)40:20<3839::AID-NME245>3.0.CO;2-6
Wang, X.B.: Adiabatic shear localization for steels based on Johnson–Cook model and second- and fourth-order gradient plasticity models. J. Iron Steel Res. Int. 14(5), 56–61 (2007). https://doi.org/10.1016/S1006-706X(07)60075-2
Wcisło, B., Pamin, J.: Local and non-local thermomechanical modeling of elastic–plastic materials undergoing large strains. Int. J. Numer. Methods Eng. 109(1), 102–124 (2017). https://doi.org/10.1002/nme.5280
Wu, J., Liu, Z.: Modeling of flow stress in orthogonal micro-cutting process based on strain gradient plasticity theory. Int. J. Adv. Manuf. Technol. 46(1–4), 143–149 (2010). https://doi.org/10.1007/s00170-009-2049-0
Ye, G.G., Chen, Y., Xue, S.F., Dai, L.H.: Critical cutting speed for onset of serrated chip flow in high speed machining. Int. J. Mach. Tools Manuf 86, 18–33 (2014). https://doi.org/10.1016/j.ijmachtools.2014.06.006
Yuan, H., Chen, J.: Identification of the intrinsic material length in gradient plasticity theory from micro-indentation tests. Int. J. Solids Struct. 38(46–47), 8171–8187 (2001). https://doi.org/10.1016/S0020-7683(01)00121-4
Zheng, Q.S.: Theory of representations for tensor functions—a unified invariant approach to constitutive equations. Appl. Mech. Rev. 47(11), 545 (1994). https://doi.org/10.1115/1.3111066
Z-set. non-linear material and structure analysis suite. http://zset-software.com. Accessed 2020-03-02
Acknowledgements
This project has received funding from the European Union’s Marie Skłodowska-Curie Action (MSCA) Innovative Training Network (ITN) H2020-MSCA-ITN-2017 under the grant agreement No 764979.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Emilio Barchiesi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Derivation of \(\dot{T}\)
Derivation of \(\dot{T}\)
The derivation of the temperature rate can be derived starting from the definition of the entropy from Eq. (27) and assuming the Helmholtz free energy function as in Eq. (21):

then, by then taking the time variation of the entropy:

where:



and:

and by plugging them it into the heat Equation Eq. (33), we obtain:

from which the temperature rate can be evaluated as:

The one reported in Eq. (67) is an expression of the temperature rate which contains many terms whose magnitude is well below the magnitude of the larger terms as  for example, therefore assumptions were made on some of the quantities populating Eq. (67) in order to make it usable, and here follows the list of hypotheses:
for example, therefore assumptions were made on some of the quantities populating Eq. (67) in order to make it usable, and here follows the list of hypotheses:
-
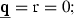
-
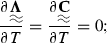
-
\(\dfrac{\partial C_{\varepsilon }}{\partial T}\) = 0;
-
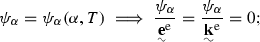
-
T = 500 K ;
-
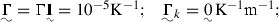
-

-
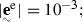
-
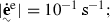
-
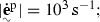
-
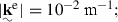
-

-
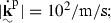
-
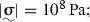
-
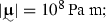
Furthermore, by assuming the material elastic and plastic models to be the ones described in Tables 1 and 2 , the terms in Eq. (67) have the orders of magnitudes listed in Table 3.
From the comparison of the order of magnitudes of the terms in Eq. (67) that are presented in Table 3, the temperature flow rule can assume the following form:

Rights and permissions
About this article
Cite this article
Russo, R., Forest, S. & Girot Mata, F.A. Thermomechanics of Cosserat medium: modeling adiabatic shear bands in metals. Continuum Mech. Thermodyn. 35, 919–938 (2023). https://doi.org/10.1007/s00161-020-00930-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-020-00930-z