1 Introduction

The unification of physical height systems is an essential geodetic application of the Earth’s gravity field. It is important and urgent to have a globally consistent height system within a few centimeters or better, for both scientific and societal reasons (Plag et al. 2009; Sánchez 2012; Ihde et al. 2017). In 2015, the International Association of Geodesy (IAG) introduced the International Height Reference System (IHRS) as the global standard for the determination of physical heights (see Drewes et al. 2016). The IHRS is defined as a geopotential reference system corotating with the Earth. Station coordinates are given by (1) potential values \(W({\varvec{X}})\) (and their changes with time \(\hbox {d}W({\varvec{X}})/\hbox {d}t\)) defined within the Earth’s gravity field and, (2) geocentric Cartesian coordinates \({\varvec{X}}\) (and their changes with time \(\hbox {d}{\varvec{X}}/\hbox {d}t\)) referring to the International Terrestrial Reference System (ITRS, Petit and Luzum 2010). For practical purposes, potential values \(W({\varvec{X}})\) and geocentric positions \({\varvec{X}}\) can be transformed to geopotential numbers \(C_\mathrm{P}\) and ellipsoidal heights h, respectively (Ihde et al. 2017). The determination of potential values as IHRS coordinates may be performed following the strategies applied for the (quasi-) geoid modeling. In the following, we basically determine the disturbing potential \(T({\varvec{X}})\), and after restoring the reference potential \(U({\varvec{X}})\), we can obtain \(W({\varvec{X}})=U({\varvec{X}})+T({\varvec{X}})\). According to Ihde et al. (2017), the target uncertainty of \(W({\varvec{X}})\) should be at the \(10^{-2}\,{\text {m}^2}/{\text {s}^2}\) level (equivalent to around 1 mm for physical heights). However, the reliability of the potential estimation undergoes the same limitations of the precise (quasi-) geoid modeling. Thus, a high-resolution and high-precision (quasi-) geoid model is the key for the realization of the IHRS.

Satellite gravity observation missions such as the Gravity Recovery and Climate Experiment (GRACE, Tapley et al. 2004) and the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE, Rummel et al. 2002) are the main data sources for global geoid modeling. However, the main limitation of satellite gravity models is the spatial resolution, since they lack information about spatial wavelengths below 70–80 km (Pail et al. 2011). This missing high-frequency part of the gravity signal can cause an omission error of 20 to 40 cm in terms of geoid heights (Rummel 2012). This value can be even higher in regions with very rough topography. In contrast, other types of measurements such as airborne, shipborne or terrestrial gravity observations can provide a much higher spatial resolution of a few kilometers. Thus, they can be used in addition to the global models for regional geoid refinement to improve the resolution and accuracy. High-resolution regional gravity modeling is especially inevitable in mountainous areas, since the very short wavelengths are correlated with local topography to a large extent (Bucha et al. 2016).

This study focuses on the computation of height anomalies, geoid heights, and geopotential values (as IHRS coordinates) in Colorado, USA (Fig. 1). These results contribute to the ‘1 cm Geoid Experiment’ (Wang et al. 2020). This study is of great interest and importance for three reasons, namely (1) Colorado is a mountainous area with high elevations and rugged topography, which makes the gravity field modeling challenging, (2) with altogether fourteen contributions worldwide (see Wang et al. 2020 for the list of the participants) involved in this experiment with different methodologies, the comparison of the results should highlight the disparities of each method, (3) we apply an approach based on spherical radial basis functions (SRBFs), which has not been widely studied for modeling the airborne data (Li 2018). According to Sánchez et al. (2020), the calculation of reference stations for the IHRS realization might be distributed worldwide, and the calculation methods have to be verified and documented beforehand. Within the ‘1 cm Geoid Experiment,’ we prove that our SRBF-based (quasi-) geoid model is consistent with thirteen independent results calculated by different methods, and we provide a detailed documentation about our method within this paper.

Wu et al. (2017a) pointed out that it is difficult to combine heterogeneous data using the Stokes/Molodensky integral, since it requires a grid interpolation; and when dealing with large number of point-wise data (which is the case for the ‘Colorado Experiment’), the least-squares collocation (LSC) is numerically inefficient (Wittwer 2009). SRBFs are an appropriate tool for regional gravity field modeling, since they fulfill the Laplace equation such as the spherical harmonics (SHs), due to their relations to the Legendre polynomials. Although SRBFs are thus also global functions, they can be used appropriately for regional applications to consider the heterogeneity of different data types, due to their localizing feature. SRBFs are a good compromise between ideal frequency localization (SHs) and ideal spatial localization (Dirac delta functions) (Freeden et al. 1998). The fundamentals of SRBFs are introduced by Freeden et al. (1998), Freeden and Michel (2004), among many others. They have been applied in gravity field modeling during the last two decades, e.g., by Schmidt et al. (2006), Schmidt et al. (2007) and Klees et al. (2008). The SRBFs are placed on point grids, to which the unknown coefficients are associated. These coefficients can be estimated from the observations, and they reflect the energy of the gravity signal (Naeimi et al. 2015). The modeled gravitational functionals are then computed from these estimated coefficients. Four factors of the SRBFs need to be specified, which influence the modeling accuracy. We discuss in detail (see Sect. 4.2) the choice of (1) the choosing bandwidth, (2) the locations of the SRBFs, (3) the type of the SRBFs, and (4) the extensions of the data zone for reducing edge effects.

Two types of high-resolution data sets, the terrestrial and the airborne gravity measurements, are combined in this study. However, the GRAV-D (Gravity for the Redefinition of the American Vertical Datum) airborne gravity data require additional editing or low-pass filtering before being used (see e.g., GRAV-D Science Team 2018). Various low-pass filtering methods exist and have been applied to the airborne gravity data, such as the spatial Gaussian filter, the fast Fourier transform (FFT, Childers et al. 1999), and the Butterworth filter (Forsberg et al. 2001). Lieb et al. (2015) proposed a low-pass filtering in the spectral domain by SRBFs. Li (2018) demonstrated that the SRBFs show certain de-noising or smoothing properties of the high-frequency noise in the airborne data. In this study, we apply the low-pass filter to the airborne gravity data by using the cubic polynomial (CuP) function, and the smoothing features in this type of SRBFs are used for filtering the high-frequency noise in the airborne data. An advantage of using the CuP function for low-pass filtering is that the filtering process is automatically done when establishing the observation equations, i.e., no extra computation efforts are required. For the terrestrial gravity data, the non-smoothing Shannon function is preferred to avoid the loss of spectral information (Bucha et al. 2016). Schreiner (1999) showed that it is possible to use different types of SRBFs for different types of observations, since the coefficients are independent on the choice of the SRBFs, as long as they cover the same frequency range. Klees et al. (2018) achieved an improvement by applying a truncated SRBF for the terrestrial data but a tapered SRBF for the satellite data, based on simulations. However, to the best of our knowledge, the idea of combining different types of SRBFs for different types of observations has not been applied to real data sets yet. Thus, our results based on real data also indicate the validity of this idea.

We apply the remove–compute–restore (RCR) procedure (e.g., Forsberg and Tscherning 1981; Forsberg 1993), in which a global gravity model (GGM) is usually removed before the computation. In this study, however, not only a GGM, but also a topographic model is removed, due to the high elevation and rugged terrain of the study area. Forsberg and Tscherning (1981) pointed out that the inclusion of the topographic effects is indispensable for regional gravity field modeling in mountainous areas. Hirt (2010) showed that the signal omission error (gravity field components which are omitted by a truncated expansion) can be greatly reduced, and the model accuracy can be significantly improved by including the residual terrain model (RTM) in mountainous areas. After the remove step, the remaining part is then modeled by the combination of the terrestrial and airborne observations. These two types of observations are combined within a parameter estimation procedure (Schmidt et al. 2007). However, the derived least-squares system is in most cases ill-posed or even singular, due to three reasons, namely (1) the number of used basis functions is usually larger as required, (2) the given data gaps as well as (3) the downward continuation of the airborne or satellite measurements to the surface of the Earth. Thus, regularization is necessary to obtain a numerically stable solution. We apply the Tikhonov regularization which can be interpreted as an estimation with prior information (Koch 1990). The relative weight between the two observation types as well as the relative weight between the observations and the prior information, which can be interpreted as the regularization parameter, is determined by the method of variance component estimation (VCE, Koch 1999; Koch and Kusche 2002). Naeimi et al. (2015) demonstrated, however, that VCE does not always give reliable regularization results. Thus, the L-curve method (see e.g., Hansen 1990) or the generalized cross-validation (GCV, see e.g., Golub et al. 1979) could be used instead. We here propose a method which combines VCE for determining the relative weight between the two observation types and the L-curve method for determining the regularization parameter (Liu et al. 2020).

This work is organized as follows: In Sect. 2, we present the study area as well as the available data; also the procedure of data preprocessing is briefly described. Section 3 introduces the fundamental concepts of SRBFs, the spherical convolution, and the parameter estimation procedure. We explain how the observation equations are formulated, how the unknown coefficients are estimated, and how the resulting gravitational functionals are calculated. Section 4 explains the computation procedure: the RCR, the choices of each factors in SRBFs, and the combination of the data sets. Section 5 presents our models as well as the validation of the results. Finally, Sect. 6 provides the conclusions and outlook.

2 Study area and data preprocessing

2.1 Study area and data

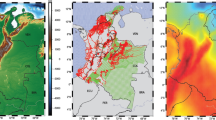
This study is conducted between \(-\,110^\circ \) and \(-\,102^\circ \) longitude and between 35\(^\circ \) and 40\(^\circ \) latitude (Fig. 1a), majorly located in Colorado, USA. It is a mountainous area, with an average elevation of 2017 m. The highest location reaches 4386 m, the lowest 932 m. The eastern part of the study area is more flat than the western and the central part, while it is still higher than 1000 m. The larger the topographic heights are, the worse the accuracy of the geoid becomes (Foroughi et al. 2019). Thus, this is a challenging study area, due to the rugged terrain, high elevation, and varying gravity field.

Fig. 1
figure 1

a Terrain map of the study area; b given terrestrial (blue points) and airborne (green flight tracks) gravity data, GSVS17 benchmarks (223 points of the red line) as well as the model grid area (black rectangle)

Full size image

Two data sets are provided by the National Geodetic Survey (NGS). Figure 1b shows the spatial distribution of these two data sets, projected on the Earth’s surface. The terrestrial gravity data (blue points) have full coverage over the whole study area, but they are not evenly distributed. Comparing Fig. 1a, b, it is clear that this data set has a higher density in the area with higher elevation and a lower density in the low elevation area (eastern part). However, the average point distance reaches approximately 3 km for the whole terrestrial data set. The airborne gravity data (green flight tracks) were collected by the GRAV-D project (GRAV-D Science Team 2017) at a mean flight altitude of 6186 m. They cover most of the study area in the southeastern part, generally between \(-\,109^\circ \) and \(-\,102^\circ \) longitude and between 35\(^\circ \) and 38.5\(^\circ \) latitude. The along-track spatial resolution depends on the aircraft speed, with an average of around 100 m; the cross-track resolution is almost 10 km. We use the data given at their original observation sites, i.e., the observation equations are directly established at the observation points.

We compute two sets of output gravity functionals, and the results will be presented and discussed. The first one is at the Geoid Slope Validation Survey 2017 (GSVS17) benchmarks (red line in Fig. 1b), and the second one is the quasi-geoid and geoid model for the target area from \(-\,109^\circ \) to \(-\,103^\circ \) and 36\(^\circ \) to 39\(^\circ \) (black box in Fig. 1b) with a spatial resolution of \(1'\times 1'\).

2.2 Data preprocessing

In the original terrestrial data (with a total amount of 59,303 points), there are cases that several gravity observations locate at the same position, and we then use only the first of these observations (1090 points deleted). However, in case gravity observations at the same position differ with more than 2mGal from each other, we delete both of them (85 points deleted). Since the measurements are provided in orthometric heights H, we transform them to the ellipsoidal heights h using the geoid model ‘GEOID 12B,’ provided by the National Geodesy Survey (NGS 2012)

$$\begin{aligned} h = H+N_{\textit{Geoid 12B }} . \end{aligned}$$
(1)

The airborne data have a very dense distribution with a total amount of 283,716 observation points, resulting in a design matrix with a size of 55 GB (see Sect. 3.3). To save computation time and to improve the efficiency, we reduce the sampling interval from 1 to 1/8 Hz, i.e., only one observation of an eight-observation block is kept. Thus, an average spatial resolution of approximately 1 km along-track is obtained. The reason that justifies the ‘down sampling’ procedure of the airborne data is that consecutive airborne observations are highly correlated.

Then, for both types of observations, the following data preprocessing steps are performed:

  1. 1.

    Transfer the observations in terms of absolute gravity g to gravity disturbance \(\delta g\) by subtracting the normal gravity \(\gamma \) at the ellipsoidal height h of the observations

    $$\begin{aligned} \delta g_{\text {obs}}=g-\gamma . \end{aligned}$$
    (2)
  2. 2.

    Add the atmospheric correction to the observations

    $$\begin{aligned} \delta g= \delta g_{\text {obs}}+\delta g_{\text {ATM}} , \end{aligned}$$
    (3)

    the atmospheric correction \(\delta g_{\text {ATM}}\) is calculated following Torge (1989) by

    $$\begin{aligned} \delta g_{\text {ATM}}= 0.874-9.9 \cdot 10^{-5}h+3.56 \cdot 10^{-9} h^2 . \end{aligned}$$
    (4)

3 Methodology

3.1 Spherical radial basis function

In general, SRBFs are centered at points \(P_k\) with position vector \({\varvec{x}}_k\) on a sphere \(\varOmega _R\) with radius R. A spherical radial basis function \(B({\varvec{x}},{\varvec{x}}_k)\) can be defined between \(P_k\) and an observation point P by the Legendre series (Freeden et al. 1998; Schmidt et al. 2007),

$$\begin{aligned} B({\varvec{x}},{\varvec{x}}_k) = \sum _{n=0}^{\infty }\frac{2n+1}{4 \pi }\left( \frac{R}{r}\right) ^{(n+1)} B_n P_n ({\varvec{r}}^{T}{\varvec{r}}_k) \end{aligned}$$
(5)

wherein \({\varvec{x}}=r\cdot {\varvec{r}}=r\cdot [\cos \phi \cos \lambda ,\cos \phi \sin \lambda ,\sin \phi ]^\mathrm{T}\) is the position vector of the observation point P, \(\lambda \) is the spherical longitude, \(\phi \) is the spherical latitude, and \(r=R+h'\) with \(h'\) the spherical height of P above the sphere \(\varOmega _R\). The position vector of \(P_k\) reads \({{\varvec{x}}}_k=R \cdot {{\varvec{r}}}_k\), \(P_n\) is the Legendre polynomial of degree n, and \(B_n\) is the Legendre coefficient which contributes to specify the shape of the SRBFs.

A harmonic function \(F({\varvec{x}})\) can be represented as a series expansion of the SRBFs \(B({{\varvec{x}}},{{\varvec{x}}}_k)\)

$$\begin{aligned} F({{\varvec{x}}}) = \sum _{k=1}^{K}d_k B({{\varvec{x}}},{{\varvec{x}}}_k) , \end{aligned}$$
(6)

where K is the number of basis functions, and thus, the number of grid points \(P_k\) and unknown coefficients \(d_k\) as well.

The general expression (Eq. 5) needs to be adapted for describing different gravitational functionals (Lieb et al. 2016). In this study, the observations are given in terms of gravity disturbances \(\delta g\), which can be expressed as the gradient of the disturbing potential T. In spherical approximation, the magnitude of the gravity disturbance can be written as (Heiskanen and Moritz 1967).

$$\begin{aligned} \delta g = -\frac{\partial T}{\partial r}. \end{aligned}$$
(7)

Thus, if T is modeled as in Eq. (6), the adapted spherical basis function for describing \(\delta g({{\varvec{x}}})\) given at an observation site P with position vector \({\varvec{x}}\) is given as

$$\begin{aligned} B_r({{\varvec{x}}},{{\varvec{x}}}_k) = \sum _{n=0}^{\infty }\frac{2n+1}{4 \pi }\left( \frac{n+1}{r}\right) \left( \frac{R}{r}\right) ^{(n+1)}B_n P_n({\varvec{r}}^{T}{\varvec{r}}_k).\nonumber \\ \end{aligned}$$
(8)

A complete list of basis functions adapted to different functionals of the disturbing potential can be found in Koop (1993) or Liu et al. (2020).

3.2 SRBF as a filter

Any SRBF (Eq. 5) can be used as a high-pass, low-pass, or band-pass filter (Schmidt et al. 2007; Lieb 2017), and a harmonic function \(F({{\varvec{x}}})\) can be filtered by it through a spherical convolution. The filtered function \(G({{\varvec{x}}})\) can then be represented by

$$\begin{aligned} G({{\varvec{x}}}) = (B * F)({{\varvec{x}}}). \end{aligned}$$
(9)

In case the SRBF \(B({\varvec{x}},{\varvec{x}}_k)\) in Eq. (6) is chosen as a unique reproducing kernel \(Z({{\varvec{x}}},{{\varvec{x}}}_k)\), in which \(B_n=1\) for \(n=0, \ldots , \infty \), i.e.,

$$\begin{aligned} Z({{\varvec{x}}},{{\varvec{x}}}_k) = \sum _{n=0}^{\infty }\frac{2n+1}{4 \pi }\left( \frac{R}{r}\right) ^{n+1}P_n({\varvec{r}}^{T} {\varvec{r}}_k), \end{aligned}$$
(10)

the filtered function equals the original function

$$\begin{aligned} F({{\varvec{x}}})=(Z*F)({{\varvec{x}}}) = \sum _{k=1}^{K}d_k Z({{\varvec{x}}},{{\varvec{x}}}_k) . \end{aligned}$$
(11)

In case of using a band-limited SRBF, which means setting the Legendre coefficient \(B_n=0\) for all degree \(n>n_\mathrm{max}\), the SRBF acts as a low-pass filter. Schreiner (1999) and Freeden et al. (1998) prove a theorem which shows that the coefficients \(d_k\) are independent on the type of SRBFs as soon as they are band-limited to the same degree.

Theorem In a Hilbert space \(L^2(\varOmega _R)\) of all real square-integrable functions F on \(\varOmega _R\), let \(B({{\varvec{x}}},{{\varvec{x}}}_k)\), Eq. (5), be a band-limited SRBF with

$$\begin{aligned} B_n= \left\{ \begin{array}{ll} \ne 0 &{}\quad \text {for}\ \ n=0,1, \ldots , n_\mathrm{max}\\ = 0&{}\quad \text {for}\ \ n>n_\mathrm{max} \end{array}\right. \end{aligned}$$
(12)

the filtered function \(G_1\, ({\varvec{x}}\)) by the spherical convolution reads

$$\begin{aligned} G_1({{\varvec{x}}})=(B*F)({{\varvec{x}}})=\sum _{k=1}^{K} d_k B({{\varvec{x}}},{{\varvec{x}}}_k) . \end{aligned}$$
(13)

If \(C({{\varvec{x}}},{{\varvec{x}}}_k)=\sum _{n=0}^{\infty }\frac{2n+1}{4 \pi }(\frac{R}{r})^{n+1} C_nP_n({\varvec{r}}^{T} {\varvec{r}}_k)\) has the band limitation \(C_n=0 \ \text {for} \ n>n_\mathrm{max}\), then

$$\begin{aligned} G_2({{\varvec{x}}})=(C*F)({{\varvec{x}}})=\sum _{k=1}^{K} d_k C({{\varvec{x}}},{{\varvec{x}}}_k) \end{aligned}$$
(14)

holds by using the same coefficients \(d_k\), as in Eq. (13). The only condition is that they are band-limited to the same degree \(n_\mathrm{max}\). This theorem makes it possible to use different SRBFs for different data sets and to use different SRBFs in the analysis step (in which the unknown coefficients are estimated) and in the synthesis step (in which the estimated coefficients are used to calculate the output gravitational functionals), respectively.

3.3 Estimation model

As discussed in Sect. 3.1, an observation in terms of gravity disturbance can be represented as

$$\begin{aligned} \delta g({{\varvec{x}}})+e({{\varvec{x}}})=\sum _{k=1}^{K}d_k B_r({{\varvec{x}}},{{\varvec{x}}}_k) , \end{aligned}$$
(15)

where \(e({{\varvec{x}}})\) is the observation error and \(B_r\) is described in Eq. (8). With L observations, we can set up the Gauss–Markov model

$$\begin{aligned} {{\varvec{f}}}+{{\varvec{e}}}={{\varvec{Ad}}}\ \ \text {with} \ \ D({{\varvec{f}}})=\sigma ^2{{\varvec{P}}}^{-1}\ \ \end{aligned}$$
(16)

where \({\varvec{f}}\) is the observation vector, \({\varvec{e}}\) is the error vector, \({\varvec{A}}\) is the design matrix which contains the corresponding basis functions, \({\varvec{d}}\) is the vector of the unknown coefficients, and \(D({{\varvec{f}}})\) is the covariance matrix of the observation vector \({{\varvec{f}}}\), with \(\sigma ^2\) being the unknown variance factor and \({{\varvec{P}}}\) being the given positive definite weight matrix. However, the associated least-squares system is ill-posed or even singular due to the three reasons mentioned in the Introduction. This problem can be solved by introducing the expectation vector \(\varvec{\mu }_d=E({{\varvec{d}}})\) of the coefficient vector \({\varvec{d}}\) as prior information. Then, the additional linear model can be formulated as

$$\begin{aligned} \varvec{\mu }_d+{\varvec{e}}_d={\varvec{d}} \ \ \text {with} \ \ D(\varvec{\mu }_d)=\sigma _d^2{{\varvec{P}}}_d^{-1} , \end{aligned}$$
(17)

where \({{\varvec{e}}}_d\) is the error vector of the prior information. Combining the terrestrial observations \({{\varvec{f}}}_1\) and the airborne observations \({{\varvec{f}}}_2\), as well as the additional linear model, the extended Gauss–Markov model can be set up (see e.g., Schmidt et al. 2007; Liu et al. 2020 for more details). Applying the least-squares method to the extended Gauss–Markov model, the unknown coefficients are estimated as

$$\begin{aligned} \widehat{{{\varvec{d}}}}&= ({{\varvec{A}}}_1^T {{\varvec{P}}}_1 {{\varvec{A}}}_1+\omega {{\varvec{A}}}_2^T {{\varvec{P}}}_2 {{\varvec{A}}}_2+\lambda {{\varvec{P}}}_d)^{-1}\nonumber \\&\quad ({{\varvec{A}}}_1^T {{\varvec{P}}}_1 {{\varvec{f}}}_1+\omega {{\varvec{A}}}_2^T {{\varvec{P}}}_2 {{\varvec{f}}}_2+\lambda {{\varvec{P}}}_d \varvec{\mu }_d) , \end{aligned}$$
(18)

with the covariance matrix:

$$\begin{aligned} D(\widehat{{{\varvec{d}}}}) = \sigma _1^2({{\varvec{A}}}_1^T {{\varvec{P}}}_1 {{\varvec{A}}}_1+\omega {{\varvec{A}}}_2^T {{\varvec{P}}}_2 {{\varvec{A}}}_2+\lambda {{\varvec{P}}}_d)^{-1} . \end{aligned}$$
(19)

\(\omega ={\sigma _1^2}/{\sigma _2^2}\) is the relative weight between the airborne observations \({{\varvec{f}}}_2\) and the terrestrial observations \({{\varvec{f}}}_1\), \(\lambda ={\sigma _1^2}/{\sigma _d^2}\) is the regularization parameter (Koch and Kusche 2002; Schmidt et al. 2007), and the numerical values for the variance factors \(\sigma _1^2\), \(\sigma _2^2\), \(\sigma _d^2\) can be estimated by VCE (see Sect. 4.3). The covariance matrix (19) describes the accuracy of the estimated coefficients. Its main diagonal contains the variances \(v(\widehat{\textit{d}})\), which define the standard deviations of the estimated coefficients as \({\widehat{\sigma }}=\sqrt{v(\widehat{\textit{d}})}\).

3.4 Computation of the resulting gravitational functionals

In the synthesis step, the estimated unknown coefficients are used to determine the disturbing potential T at the computation points \({{\varvec{x}}}_c\)

$$\begin{aligned} \widehat{{{\varvec{T}}}}={{\varvec{B}}}\widehat{{{\varvec{d}}}}, \end{aligned}$$
(20)

where \(\widehat{{{\varvec{T}}}}\) is the vector of the computed disturbing potential and \({{\varvec{B}}}\) is the design matrix, which contains the basis functions between the grid points \(P_k\) and the computation points \(P_\mathrm{c}\).

Applying the error propagation law to Eq. (20), the covariance matrix

$$\begin{aligned} \textit{D}(\widehat{{{\varvec{T}}}})={{\varvec{B}}}{} \textit{D}(\widehat{{{\varvec{d}}}}) {{\varvec{B}}}^T \end{aligned}$$
(21)

is obtained. The estimated standard deviations of the modeled disturbing potential, \({\widehat{\sigma }}_T=\sqrt{v(\widehat{\textit{T}})}\), indicate the accuracy of the resulting gravity model.

The gravity potential values \(W(P_\mathrm{c})\) at computation points \(P_\mathrm{c}\) are then calculated by adding the normal gravity potential \(U(P_\mathrm{c})\) to the disturbing potential \(T(P_\mathrm{c})\), i.e.,

$$\begin{aligned} {\widehat{W}}(P_\mathrm{c})={\widehat{T}}(P_\mathrm{c})+U(P_\mathrm{c}). \end{aligned}$$
(22)

From the disturbing potential, the height anomaly (quasi-geoid) \(\zeta \) at the computation points \(P_\mathrm{c}\) can be calculated following the Bruns’ formula (Heiskanen and Moritz 1967):

$$\begin{aligned} {\widehat{\zeta }}=\frac{{\widehat{T}}}{\gamma } \end{aligned}$$
(23)

where \(\gamma \) is the normal gravity at the normal height of point \(P_\mathrm{c}\). Following Sánchez et al. (2018), we use the ellipsoid GRS80 (Moritz 2000) for the computation of U and \(\gamma \). According to the error propagation law, the standard deviation of the quasi-geoid vector \(\sigma _{\zeta }\) can be calculated by

$$\begin{aligned} {\widehat{\sigma }}_\zeta =\frac{{\widehat{\sigma }}_T}{\gamma }. \end{aligned}$$
(24)

The geoid height N can then be calculated from the quasi-geoid \(\zeta \) following the transformation formula in Heiskanen and Moritz (1967). It is worth mentioning that since the geoid height is obtained from a transformation which includes an approximation, it is expected to be less accurate than the quasi-geoid model. The same transformation formula is also used by most of the other participants in the ‘Colorado Experiment,’ in order to facilitate the comparison between different contributions.

It is worth mentioning that the zero-degree terms \(T_0\) and \(\zeta _0\) (Heiskanen and Moritz 1967) have been added to our final results (see Sánchez et al. 2018), which include the difference between the constant GM values of the GGM (which is the XGM2016 in our case) and the reference ellipsoid GRS80, as well as the difference between the reference potential value \(W_0\) adopted by the IHRS and the potential \(U_0\) on the reference ellipsoid (Sánchez et al. 2016; Sánchez and Sideris 2017),

$$\begin{aligned} T_0= & {} \frac{\text {GM}_{\text {GGM}}-\text {GM}_{\text {GRS80}}}{r_P} \end{aligned}$$
(25)
$$\begin{aligned} \zeta _0= & {} \frac{(\text {GM}_{\text {GGM}}-\text {GM}_{\text {GRS80}})}{r_P \cdot \gamma _Q}-\frac{\varDelta W_0}{\gamma _Q} \end{aligned}$$
(26)

with \(\text {GM}_{\text {GGM}}=3.986004415 \cdot 10^{14}\, {\text {m}^3}/{\text {s}^2}\), \(\text {GM}_{\text {GRS80}}=3.986005 \cdot 10^{14}\, {\text {m}^3}/{\text {s}^2}\), \(\varDelta W_0=-7.45\, {\text {m}^2}/{\text {s}^2}\), and \(r_P\) is the geocentric radial distance of the computation points \(P_\mathrm{c}\).

4 Computation configuration

4.1 Remove–compute–restore procedure

We apply the remove–compute–restore (RCR) procedure (e.g., Forsberg 1993). As is described by its name, the RCR procedure means that a part \(\delta g_R\) of the observations (signal) \(\delta g\) is removed before the computation

$$\begin{aligned} \varDelta \delta g=\delta g - \delta g_R . \end{aligned}$$
(27)

The remaining part \(\varDelta \delta g\) is then processed using the SRBFs to model the gravitational functional \(\varDelta {\widehat{T}}\). Afterward, the removed part is restored in terms of the disturbing potential \(T_R\) as

$$\begin{aligned} T= \varDelta {\widehat{T}} + T_R. \end{aligned}$$
(28)

The removed part \(\delta g_R\) is usually the long-wavelength component from a GGM, since existing global models approximate this part very accurately (Lieb et al. 2016). The RCR procedure also solves the problem that regional gravimetry cannot estimate the long-wavelength parts (Lieb et al. 2016). Beside the GGM, a further improvement in the modeling results can be achieved by additionally including a residual terrain model (RTM) to \(\delta g_R\) in the remove step (Hirt et al. 2010; Sjöberg 2005). The topographic effect plays a key role especially in mountainous areas, since it smoothens the input observations, and this smoothing step is of utmost importance for obtaining a good least-squares fit (Bucha et al. 2016).

Fig. 2
figure 2

a, b The observations (\(\delta g\)); c, d the remaining gravity disturbance after the GGM reduction (\(\delta g\)-\(\delta g_{\text {GGM}}\)); e, f the remaining parts after both the GGM and topographic reduction (\(\delta g\)-\(\delta g_{\text {GGM}}\)-\(\delta g_{\text {Topo}}\)) for the terrestrial data (left column) and the airborne data (right column)

Full size image

In this study, the long-wavelength component is computed from the global gravity model XGM2016 (Pail et al. 2018) up to maximum degree 719 for both the terrestrial and the airborne data. The topographic model dV_ELL_Earth2014 (Rexer et al. 2016) from degree 720 to degree 2159 and a residual terrain model ERTM2160 (Hirt et al. 2014) from degree 2160 to degree \(\sim \) 80,000 (equivalent to a spatial resolution of 250 m) are removed from the terrestrial data; the dV_ELL_Earth2014 from degree 720 to degree 5480 is removed from the airborne data. We use two different topographic models above degree 2160 for the terrestrial and airborne data; this is justifiable due to the fact that the two models (dV_ELL_Earth2014 and ERTM2160) are calculated using the same original data and contain the same signal (Hirt et al. 2014; Rexer et al. 2016). For airborne data, the effect of dV_ELL_Earth2104 from degree 2160 to degree 5480 is equal to the ERTM2160, but the ERTM2160 is only available as a grid on the Earth surface, i.e., not as spherical harmonic coefficients with which the gravity values can be computed at any height.

Figure 2 visualizes the remove step. Comparing the last two rows, it is clear that after the GGM reduction, the gravity field is dominated by the topographic effect, which is very large in this study. This implies the importance of including the topographic effect in the RCR, especially in mountainous areas. After subtracting this topographic effect, the gravity field becomes much smoother, especially in regions with varying elevation (mid part of the study area). As shown by the statistics listed in Table 1, the terrestrial observations are smoothed by 42% in terms of the standard deviation (SD) by subtracting the GGM, and by 82% after including the topographic model. The airborne observations are smoothed by 72% by subtracting the GGM and by 89% after including the topographic model. Such significant smoothing effects enable a better least-squares fit. Including the topographic model gives larger smoothing effects for the terrestrial observations than for the airborne observations. This could be explained by the fact that the high-frequency signal of the gravity field decreases with height, and the airborne gravity measurement is less sensitive to the high-frequency part than the terrestrial gravity measurement. Thus, subtracting the topographic effect affects the terrestrial gravity data more than the airborne gravity data.

Table 1 The statistics of the observations \(\delta g\), the remaining parts after subtracting the GGM, and the remaining parts after subtracting both GGM and the topographic model
Full size table

4.2 Model configuration

4.2.1 Maximum degree of expansion

The maximum degree \(n_\mathrm{max}\) of expansion is related to the spatial resolution (sr) of the observations (Bucha et al. 2016), and their relation reads (Lieb et al. 2016).

$$\begin{aligned} n_\mathrm{max}\le \frac{\pi R}{\text {sr}}. \end{aligned}$$
(29)

Although the observations are distributed unevenly in this study area, the mean spatial resolution counts around 3.5 km for the whole study area. Consequently, \(n_\mathrm{max}=5600\) is chosen as the maximum degree of expansion.

4.2.2 Definition of the target, observation, and computation area

In regional gravity modeling, the extension of the target area \(\partial \varOmega _\mathrm{T}\), the observation area \(\partial \varOmega _\mathrm{O}\), and the computation area \(\partial \varOmega _\mathrm{C}\) needs to be defined carefully. In the border of the observation area \(\partial \varOmega _\mathrm{O}\), the unknown coefficients \(d_k\) cannot be appropriately estimated, due to the lack of fully surrounding observations. This fact provokes edge effects. The observation area \(\partial \varOmega _\mathrm{O}\), where the observations are given, should be larger than the target area \(\partial \varOmega _\mathrm{T}\), in which the final output gravitational functionals are computed. Furthermore, the computation area \(\partial \varOmega _\mathrm{C}\), where the SRBFs are located, should be larger than the observation area \(\partial \varOmega _\mathrm{O}\). The reason for this extension is due to the oscillation of the SRBFs, especially at the boundaries of the computation area \(\partial \varOmega _\mathrm{C}\), where the oscillations cannot overlap and balance with each other (see Naeimi et al. 2015; Lieb et al. 2016 for more details). Thus, \(\partial \varOmega _\mathrm{T}\subset \partial \varOmega _\mathrm{O}\subset \partial \varOmega _\mathrm{C}\).

Fig. 3
figure 3

The different extensions for the areas of computation \(\partial \varOmega _\mathrm{C}\), of observations \(\partial \varOmega _\mathrm{O}\) and of target \(\partial \varOmega _\mathrm{T}\), as well as the location of the observations (grey points) and the location of the grid points (red points)

Full size image

To minimize the edge effects in the computation, margins \(\eta \) need to be defined between the three areas. Usually, the margin size \(\eta _\mathrm{O,T}\) between \(\partial \varOmega _\mathrm{O}\) and \(\partial \varOmega _\mathrm{T}\) and the margin size \(\eta _\mathrm{C,O}\) between \(\partial \varOmega _\mathrm{C}\) and \(\partial \varOmega _\mathrm{O}\) are chosen equally (Bentel et al. 2013a, b). In our case, the target area \(\partial \varOmega _\mathrm{T}\) is given to be between \(-\,109^{\circ }\) to \(-\,103^{\circ }\), and 36\(^{\circ }\) to 39\(^{\circ }\). The observations (grey points in Fig. 3) are mainly located between \(-\,110^{\circ }\) and \(-\,102^{\circ }\) and 35\(^{\circ }\) and 40\(^{\circ }\). So, the margin size \(\eta _\mathrm{O,T}\) between \(\partial \varOmega _\mathrm{O}\) and \(\partial \varOmega _\mathrm{T}\) is fixed to be 1\(^{\circ }\). The determination of the margin size \(\eta _\mathrm{C,O}\) between \(\partial \varOmega _\mathrm{C}\) and \(\partial \varOmega _\mathrm{O}\) follows a method described by Lieb et al. (2016), but it is modified to

$$\begin{aligned} \eta _\mathrm{C,O}=\frac{360^{\circ }}{n_\mathrm{max} \text {cos}(|\phi _\mathrm{max}|)}, \end{aligned}$$
(30)

where \(\phi _\mathrm{max}\) is the maximum latitude value of the target area. The margin size is influenced by the shape of the SRBFs, when the \(n_\mathrm{max}\) is higher, the SRBFs become narrower, and thus, a smaller margin size should be chosen. With \(n_\mathrm{max}=5600\), the value \(\eta _\mathrm{C,O}\approx 0.1^{\circ }\) follows. Figure 3 visualizes the target area, the observation area, the computation area, as well as the margins.

4.2.3 The location of the SRBFs

The location of the SRBFs depends on the type and number of the grid points. Eicker (2008) examined four types of grids, and the results indicate that the Reuter grid and the triangle vertex grid are the most suitable choices for space localizing basis functions. According to Bentel et al. (2013a), different grid types do not have a strong impact on the modeling results, especially comparing to the other three factors listed in the Introduction. In this study, the Reuter grid (Reuter 1982) is chosen. The points of the Reuter grid have a homogeneous coverage on the sphere \(\varOmega _R\). The total number Q of the Reuter grid points on the global sphere is determined following the rule (Lieb et al. 2016),

$$\begin{aligned} (n_\mathrm{max}+1)^2\le Q \le 2+\frac{4}{\pi }(n_\mathrm{max}+1)^2, \end{aligned}$$
(31)

and it amounts to \(Q=31{,}828{,}509\). Then, those Reuter grid points that are distributed in the computation area \(\partial \varOmega _\mathrm{C}\) are used as the locations of the SRBFs (see Fig. 3). In this case, the number of the SRBFs amounts to \(K=26{,}012\).

4.2.4 The type of the SRBFs

Different types of basis functions are introduced and studied in, for example, Schmidt et al. (2007) and Bentel et al. (2013b). Here, the following three types are considered:

  1. 1.

    The Shannon function, and its Legendre coefficients are given by

    $$\begin{aligned} B_n= \left\{ \begin{array}{ll} 1&{}\quad \text {for}\ \ n\ \in \ [0, n_\mathrm{max}]\\ 0&{}\quad \text {else} \end{array}\right. . \end{aligned}$$
    (32)
  2. 2.

    The Blackman function, and its Legendre coefficients are given by

    $$\begin{aligned} B_n=\left\{ \begin{array}{ll} 1&{}\quad \text {for}\ \ n \in [0,n_1)\\ (A(n))^2 &{}\quad \text {for}\ \ n \in [n_1,n_{max}]\\ 0&{}\quad \text {else} \end{array}\right. , \end{aligned}$$
    (33)

    where

    $$\begin{aligned} A(n)= & {} \frac{21}{50}-\frac{1}{2}\text {cos}\left( \frac{2\pi (n-n_\mathrm{max})}{2(n_\mathrm{max}-n_1)}\right) \nonumber \\&+\frac{2}{25}\text {cos}\left( \frac{4\pi (n-n_\mathrm{max})}{2(n_\mathrm{max}-n_1)}\right) . \end{aligned}$$
    (34)
  3. 3.

    The cubic polynomial (CuP) function, and its Legendre coefficients are given by

    $$\begin{aligned} B_n= \left\{ \begin{array}{ll} (1-\frac{n}{n_\mathrm{max}})^2(1+\frac{2n}{n_\mathrm{max}})&{}\quad \text {for}\ \ n\ \in \ [0, n_\mathrm{max}]\\ 0 &{}\quad \text {else} \end{array}.\right. \nonumber \\ \end{aligned}$$
    (35)
Fig. 4
figure 4

Different SRBFs in the spatial domain (top, ordinate values are normed to 1) and the spectral domain (bottom) for \(n_\mathrm{max}=5600\) (\(n_1=3000\) is chosen in the Blackman function)

Full size image

Figure 4 visualizes the characteristics of these three basis functions in the spatial and the spectral domain, correspondingly. The Shannon function has the highest localization in the spectral domain, but it also gets the strongest oscillations in the spatial domain. In contrast, the CuP function has the least oscillations in the spatial domain but has a smoothing decay and extracts the least spectral information in the spectral domain. The Blackman function is regarded as a compromise between these two domains. Usually, the Shannon function is used in the analysis step to avoid the loss of spectral information, and the Blackman function or the CuP function is applied in the synthesis step to reduce erroneous systematic effects (Lieb et al. 2016).

In this study, we apply the CuP function in the synthesis step. In the analysis step, we use the Shannon function for the terrestrial observations; the advantages of using the Shannon function for terrestrial data are explained in Bucha et al. (2016). For the airborne observations, however, we choose the CuP function in the analysis step. This is due to the fact that noise in the high frequencies of the airborne data is large; thus, a low-pass filtering is necessary. Forsberg and Olesen (2010) explained why all types of airborne gravity data need filtering; the filtering is a compensation between the resolution and the accuracy. In the low-frequency part of the airborne data, the gravity signal dominates the noise (Childers et al. 1999); thus, low-pass filters are the most commonly used filters. Bucha et al. (2015) showed that the SRBFs could act as a low-pass filter, and Naeimi (2013) demonstrated that both the Blackman function and the CuP function can be used as build-in low-pass filters, due to their smoothing features. We used the Blackman function and the CuP function for low-pass filtering, and the results (presented in Sect. 5.1) show that both of these two functions can low-pass-filter the airborne observations well. We choose the CuP function for the airborne observations in this study, as it gives slightly better results than the Blackman function does (see Table 2 in Sect. 5.1). And as already discussed in Sect. 3.2, different types of SRBFs can be used for different observation types, in case of the same band limitation.

4.3 Combination of the terrestrial and the airborne data

We combine the terrestrial data and the airborne data using the extended Gauss–Markov model (see Sect. 3.3). Since information about the data quality is not available, we assume that the measurements have the same accuracy and are uncorrelated, and thus, \({{\varvec{P}}}_p={{\varvec{I}}}\), where \({{\varvec{I}}}\) is the identity matrix. The same assumptions are commonly used in existing publications (see e.g., Lieb et al. 2016; Wu et al. 2017b; Slobbe et al. 2019), since it is usually difficult to acquire the realistic full error variance–covariance matrix, and the procedure would become computationally intensive by including it. Moreover, Olesen et al. (2002) showed that for airborne gravity disturbances, noise correlations can be ignored if one aims at a 1-cm quasi-geoid model. Furthermore, we set \({{\varvec{P}}}_d={{\varvec{I}}}\) by assuming that the coefficients are not correlated and have the same accuracy. The models subtracted in the remove step of the RCR procedure serve as the prior information; in this case, we can set the expectation vector \(\varvec{\mu }_d\) to the zero vector (Schmidt et al. 2007). The solution for the estimated coefficients can be obtained from Eq. (18), where two variables need to be determined; one is the relative weight \(\omega \) between the two types of observations, and another is the regularization parameter \(\lambda \).

Table 2 RMS values of the height anomaly results w.r.t the validation data, when using the Shannon function, the Blackman function, and the CuP function for the airborne observations, respectively
Full size table

The relative weight \(\omega \) is determined by VCE, which is an iterative process to estimate the variance factors \(\sigma _1^2, \sigma _2^2, \sigma _d^2\) of different observation types and the prior information. The iteration starts from initial values for \(\sigma _1^2, \sigma _2^2, \sigma _d^2\), and it ends when convergence is reached. The variance factors obtained from VCE read \({\widehat{\sigma }}_1^2=6.13 \times 10^{-10}\), \({\widehat{\sigma }}_2^2=1.61\times 10^{-10}\), and \({\widehat{\sigma }}_d^2=8.17 \times 10^{-14}\). These estimates indicate that the airborne gravity data might have a higher quality than the terrestrial data. It is explainable since the terrestrial observations were gathered during a large time span (since the late 1930s), and thus, their quality may vary regionally. On the other hand, the GRAV-D airborne data were collected in the recent few years. Moreover, the value of \({\widehat{\sigma }}_1\) (2.48 mGal) coincides with Saleh et al. (2013), who estimated the NGS’s terrestrial gravity data to contain error with an RMS of \(\sim 2.2\) mGal. However, it should be noted that the estimated variance factors actually represent the quality of the least-squares fit rather than the accuracy of the data (Bucha et al. 2016).

From the estimated variance factors, the relative weight between the terrestrial data and the airborne data \(\omega ={\widehat{\sigma }}_1^2/{\widehat{\sigma }}_2^2\) and the regularization parameter \(\lambda _{\text {VCE}}={\widehat{\sigma }}_1^2/{\widehat{\sigma }}_d^2\) can be obtained. However, according to Liu et al. (2020), this regularization parameter is not always reliable, so we apply the L-curve method (see e.g., Hansen and O’Leary 1993; Eriksson 2000) to regenerate the regularization parameter \(\lambda \), based on the relative weighting \(\omega \). In this case, the regenerated regularization parameter is \(\lambda =10{,}000\).

5 Results and discussion

As already mentioned in Sect. 2.1, we compute two sets of output gravity functionals. The first one is at the GSVS17 benchmarks, at which thirteen groups worldwide have provided independent height anomaly results as well as geopotential values, and fourteen groups have provided the geoid height results. A list of all participants, as well as an external validation to the leveling-based physical heights, can be found in Wang et al. (2020). Since we do not have access to the leveling-based validation data, we validate various solutions using the mean value of the other groups. Thus, the term ‘validation data’ used in Sects. 5.1–5.2 refers to the mean height anomaly results of the other twelve groups along the GSVS17 benchmarks. We do not include our own results in the evaluation of models to keep the comparison independent; however, the validation of our final results to the mean value of all participants (including ours) is also presented in Sect. 5.4. The second one is a model grid from \(-\,109^\circ \) to \(-\,103^\circ \) and 36\(^\circ \) to 39\(^\circ \) with a resolution of \(1' \times 1'\). Thirteen groups have provided the height anomaly grid models, fourteen groups have provided the geoid height grid model, and the comparison between our models and the mean of all the models are given.

5.1 Evaluation of the low-pass filtering

To test the validity of the low-pass filtering based on the CuP function, we compare this low-pass filtering result to the ones using the Shannon function or the Blackman function for the airborne observations. The height anomaly results at the GSVS17 benchmarks when using these three functions for the airborne data, respectively, are compared with respect to the validation data. (The Shannon function is used for the terrestrial data as already discussed in Sect. 4.2.4.) The statistics are listed in Table 2. The RMS deviations w.r.t the validation data when using the CuP function and the Blackman function for the airborne data are 1.075 cm and 1.080 cm, respectively, which are around 0.5 mm smaller than that when using the Shannon function for both the data sets. It should be noted that when using the Blackman function or the CuP function as low-pass filters, the results improve by 5%, which is not neglectable. These results also indicate the importance of the low-pass filtering for the airborne data. Although the results obtained from the Blackman function and the CuP function are similar, the CuP function still gives a slightly better result (i.e., smaller RMS error) than the Blackman function, and thus, the CuP function is chosen for low-pass filtering the airborne data.

It is worth mentioning that we have also tried to smooth the airborne gravity observations directly by a mean filter, i.e., assign the average value of consecutive observations to the mid observation, and then use the Shannon function. However, the results are worse than those using the CuP function to the original data, which indicates the efficiency of applying the CuP function for smoothing the airborne observations.

Fig. 5
figure 5

Differences between our solutions and the mean value of all the other institutions at the GSVS17 benchmarks

Full size image
Table 3 Comparison between the combined solution and the terrestrial-only, airborne-only, or models-only solution at the GSVS17 benchmarks, w.r.t the validation data
Full size table

5.2 Evaluation of the combined solution comparing to the terrestrial or the airborne-only solution

Shih et al. (2015) demonstrated that the RMS error of their gravity anomaly model drops when an additional data set is incorporated. Jiang and Wang (2016) showed that by adding the GRAV-D airborne data, the agreement to the GPS/leveling data (GSVS11) improves from 1.1 to 0.8 cm in Texas, USA. Forsberg et al. (2012) reported an improvement by the airborne data from 15 to 13 cm in the United Arab Emirates. To assess how much our quasi-geoid model benefits from the regional terrestrial and airborne gravity data, the computation is also conducted to the terrestrial observations and the airborne observations, individually, in the same manner. Each result is compared to the combined solution with respect to the validation data. The differences between our height anomaly results and the validation data when using both data sets, using the terrestrial data only, using the airborne data only, and using no observation data, i.e., only the GGM and the topographic model (models-only solution), are plotted in Fig. 5, respectively. (The ellipsoidal height of the GSVS17 benchmarks is plotted for interpretation reasons.) The statistics are listed in Table 3.

Compared to the validation data, using only the GGM and the topographic model without any observation data gives the worst result, with an RMS error of 4.04 cm; it is improved to 1.76 cm by adding the terrestrial data and further improved to 1.08 cm by including the airborne data. Figure 5 shows that the models-only solution (grey) has the largest variation comparing to the validation data (zero value line), although the models reach a very high harmonic degree. It shows that the topographic models cannot represent the true high-frequency gravity signal accurately, since they usually assume the topographic masses to have constant density (Hirt et al. 2010; Bucha et al. 2016), which is not the case in practice. Thus, regional gravity field refinement with local data is necessary, despite the availability of high-resolution topographic models. From Fig. 5, we can see that the airborne-only solution (blue) has larger oscillations than the terrestrial-only solution (green), and the combined solution (red) benefits from both data sets. The terrestrial-only solution is better than the airborne-only solution, which could be explained by the larger coverage of the terrestrial data as well as the downward continuation of the airborne data. To be more specific, the airborne measurements are collected at an average altitude of 6 km to model the gravity field on the Earth surface, and thus, the modeling results are expected to be less accurate than using the surface gravity data. The improvement in the combined solution is 39% compared to using terrestrial data only and 55% compared to using airborne data only, and it reaches 73% compared to using no gravity observations but only GGM and topographic models. Such significant improvements indicate the validity of our combination model.

Fig. 6
figure 6

a The estimated coefficients \({\widehat{d}}\), b their standard deviations \({\widehat{\sigma }}\), c the histogram of the estimated coefficients, d the test statistic \(|{\widehat{d}}|/{\widehat{\sigma }}\), e the histogram of the test statistic, and f the corresponding significant coefficients when \(p=0.9\) is chosen

Full size image

A significant outcome from Fig. 5 is that the differences between the terrestrial-only solution and the validation data are highly correlated with the variations of the topography (black) at the GSVS17 benchmarks. To be more specific, when the ellipsoidal heights are constant (between around benchmark Nr. 110–180), the terrestrial solution is almost identical to the combined solution; when there are big changes in the ellipsoidal heights (e.g., between around benchmark Nr. 30–90 as well as after benchmark Nr. 180), larger differences between the terrestrial-only solution and the validation data can be observed. Including the airborne data seems to improve the terrestrial-only solution the most in rugged region, which could give some hints about where to place new airborne measurements in mountainous study areas. According to the findings in this study, airborne observations should be taken place in rugged terrain in order to give the maximum benefits, in addition to the local terrestrial data.

5.3 Significance of the estimated coefficients

The estimated coefficients \({\widehat{d}}\) and their standard deviation \({\widehat{\sigma }}\) are plotted in Fig. 6a, b. As we can see, the estimated coefficients inside the observation area \(\partial \varOmega _\mathrm{O}\) (black rectangle) represent the gravitational structures well, i.e., a correlation between Figs. 2e, f and 6a is visible. Larger values in the estimated coefficients (positive and negative) indicate that additional gravity signals with respect to the background model are captured, which shows the physical meaning of the estimated coefficients (Lieb 2017). Outside the observation area \(\partial \varOmega _\mathrm{O}\) (i.e., in the margin between \(\partial \varOmega _\mathrm{O}\) and \(\partial \varOmega _\mathrm{C}\)), the estimated coefficients are close to zero, and their standard deviations are much larger than those inside the observation area. Larger standard deviations also occur in areas with data gaps (referring to Fig. 1b), which is reasonable.

Fig. 7
figure 7

The least-squares residuals of a the terrestrial gravity data, and b the airborne gravity data

Full size image

Theoretically, only the coefficients that are significantly different from zero contribute to the obtained signals and, thus, to model the gravitational functionals. The nonsignificant coefficients then must be removed. To test how many coefficients are significant in our study case, we conduct a t test by the test statistic \(|{\widehat{d}}|\)/\({\widehat{\sigma }}\) (Bentel et al. 2013a). It is worth mentioning that the t test can be applied here because we assumed that the coefficients are not correlated with each other (see Sect. 4.3). The hypothesis statements to test an individual coefficient d are

$$\begin{aligned} H_0 : d=0 \quad \text {vs.} \quad H_1 : d \ne 0 \end{aligned}$$
(36)

The hypothesis \(H_0 : d=0\) will be rejected if its test statistic \(|{\widehat{d}}|/{\widehat{\sigma }}\) (Fig. 6d) is larger than a critical value \(t_{nu,p}\) for the t test. Figure 6e shows the histogram of the test statistic \(|{\hat{d}}|/{\hat{\sigma }}\). In our case, the degree of freedom nu is equal to \(90{,}236-26{,}012 = 64{,}224\), where 90,236 is the number of observations and 26,012 is the number of unknown coefficients. The confidence level \(p=0.9\) is chosen, then \(t_{64224,0.9}=1.282\). It means that if the test statistic \(|{\widehat{d}}|/{\widehat{\sigma }}\) is larger than 1.282, then this coefficient is significantly different from zero with 90% confidence, and the corresponding coefficients are considered. The corresponding significant coefficients are plotted in Fig. 6f.

5.4 Final results and validation

5.4.1 Least-squares residuals of our estimated model

Figure 7 displays the residuals of the least-squares adjustment for the terrestrial gravity observations (Fig. 7a) and the airborne gravity observations (Fig. 7b). The residuals of the terrestrial observations have a mean value of − 0.19 mGal, with a SD of 2.13 mGal, and the residuals of the airborne data have a mean value of − 0.15 mGal, with a SD of 1.25 mGal. The functional model fits the airborne data better than the terrestrial data, which could be explained by the fact that the airborne data get a higher weight than the terrestrial data during the VCE procedure. It is also clear from Fig. 7 that the prominent residuals are located in high-elevation areas for both the terrestrial and airborne data, and a clear correlation with Fig. 1a can be observed. This indicates that a further improvement in our model could be achieved by (1) applying a more accurate terrain model that might be available in the near future, or (2) including a better gravity data distribution on the rugged topography areas.

Fig. 8
figure 8

Results at the GSVS 17 benchmarks

Full size image
Fig. 9
figure 9

a Height anomaly and b its standard deviation

Full size image

5.4.2 Height anomaly and geoid height results at the GSVS17 benchmarks

Our height anomaly as well as the geoid height results are displayed in Fig. 8, in comparison with the mean value of all participants. It is visible that our results agree very well with other contributions, with differences ranging between − 4 and 4 cm. The geoid height (blue) fits worse than the height anomaly (red) with respect to the mean, which is as expected due to the transformation (see Sect. 3.4). According to Wang et al. (2020), the RMS errors of our height anomaly and geoid height compared to the mean value of all groups are 1.0 cm and 1.3 cm, respectively, which are the smallest among all the participants. It is worth mentioning that we have also calculated the geopotential values W, and it has a mean of 0.01 \(\text {m}^2/\text {s}^2\) with a standard deviation of 0.09 \(\text {m}^2/\text {s}^2\) comparing to the mean results of all the contributions, which is also the smallest. A detailed comparison of the geopotential values is presented in Sánchez et al. (2020).

The validation with the GPS/leveling data is done by Wang et al. (2020), and the differences of our height anomaly results compared to the GSVS17 GPS/leveling data range between − 7.6 and 4.5 cm, with a mean value of 0.81 cm and a SD of 2.89 cm. Considering the not homogeneously distributed observations with obvious data gaps, this result is quite satisfying. However, it has to be mentioned that the quality of these GPS/leveling data is not reported by data providers yet, and thus, the validation with the mean values of all participants is of higher importance.

5.4.3 Height anomaly and geoid height results in the whole study area

Figure 9a visualizes the quasi-geoid model for the whole target area \(\partial \varOmega _\mathrm{T}\), with a grid resolution of \(1' \times 1'\). The standard deviation map of the modeled height anomaly is plotted in Fig. 9b, which ranges from only few millimeters to around 2 cm. The values are smaller in regions with denser observations. The RMS error of our height anomaly and geoid height grid model comparing to the mean value of all groups are 1.6 cm (which is the smallest among all the participants) and 2.9 cm, respectively (Wang et al. 2020).

Fig. 10
figure 10

Height anomaly differences between our model and a EGM2008, b EIGEN6c4, c XGM2019, d EIGEN6c4+ERTM2160

Full size image

Comparisons are also made between our height anomaly model and two widely used global gravity models, namely EGM2008 with d/o 2190 (Pavlis et al. 2012, 2013) and EIGEN6c4 with d/o 2190 (Förste et al. 2014). As shown in Fig. 10a, b, the differences are at the decimeter level. Comparing these differences to the terrain map (Fig. 1a), it is clear that the large differences are mainly observed in areas with high topography. These differences could be coming from the effects above degree 2190, i.e., the GGMs are only modeled till degree 2190, while we model the gravity signals till a much higher degree. To verify the reason for these differences, we also compare our height anomaly model to the XGM2019e with d/o 5540 in Fig. 10c, and their difference does not show a correlation with the topography as strong as in Fig. 10a, b. In Fig. 10d, we add the residual terrain model ERTM2160 to the EIGEN6c4 and compare it with our height anomaly model. The difference is heavily reduced in this case, and the plot becomes much smoother. Due to the consideration of the topographic effect as well as the large amount of observations in the mountainous area, our model improves a lot in this study area comparing to the global gravity model. The poor performance of the GGMs implies that they are not reliable for engineering purposes or geophysical investigation (Wu et al. 2017a), especially in mountainous areas. Moreover, the regional gravity field modeling with locally distributed data improves the fine structures primarily, which demonstrate the importance of regional gravity field refinement.

6 Conclusion and outlook

In this study, we calculate the high-resolution quasi-geoid model and geoid model using spherical radial basis functions in Colorado, USA. The results contribute to the ‘1 cm Geoid Experiment,’ which enables a comparison of our SRBF-based results to thirteen independent solutions calculated within other approaches, such as LSC (Moritz 1980; Tscherning 2013) and the least-squares modification of Stokes’ formula (Sjöberg 2003, 2010). Detailed explanations are given regarding the choice of the SRBFs characteristics: the bandwidth, the location, the type of the SRBFs as well as the extensions of the data zone.

We combine two types of basis functions covering the same spectral domain in the analysis step. The non-smoothing Shannon function is applied to the terrestrial data to avoid the loss of spectral information. The CuP function is applied to the airborne data as a low-pass filter, and the smoothing features of this type of SRBFs are used for filtering the high-frequency noise in the airborne data. The RMS error of our height anomaly result along the GSVS17 benchmarks w.r.t the mean results of the other twelve groups drops by 5% when combining the Shannon function for the terrestrial data and the CuP function for the airborne data, compared to those obtained by using the Shannon function for both the two data sets. We present a theorem which shows that the unknown coefficients are independent of the type of SRBFs as soon as they are band-limited to the same degree, and thus, different types of SRBFs can be used for different types of observations. As no publications based on real data are known to the authors which applied the idea of combining different types of SRBFs for different observations, our results also serve as an application of this idea and further indicate its validity and benefits.

We combine the GGM, topographic model, terrestrial gravity data, and airborne gravity data within the RCR procedure and the parameter estimation procedure. Numerical investigations show that including the topographic model is of great importance in mountainous areas, as it helps to obtain a better least-squares fit. However, the topographic model alone does not guarantee an accurate regional gravity field model, despite their high resolution. Comparing to the mean value of other contributions at the GSVS17 benchmarks, combining the GGM and the topographic model gives an RMS error of 4.04 cm, which is reduced to 1.76 cm after adding the terrestrial observations and further reduced to 1.08 cm after including the airborne data. These results indicate the importance of local data sets in regional gravity field refinement.

Comparisons are made with respect to the mean results of all the contributions, and our height anomaly and geoid height solutions at the GSVS17 benchmarks give an RMS error of 1.0 cm and 1.3 cm, respectively. Our quasi-geoid and geoid grid models for the whole study area deliver an RMS value of 1.6 cm and 2.9 cm, respectively. Both our height anomaly and geoid height results at the GSVS17 benchmarks, as well as the height anomaly result in the whole study area, have the smallest RMS value w.r.t the mean values of all participants, which validates our SRBF-based model. However, there is a disagreement between the RMS error w.r.t the mean solutions and w.r.t the GPS/leveling data. Thus, a major concern for the future work is to understand this disagreement after the release of the GPS/leveling data.