The zero length column technique to measure adsorption equilibrium and kinetics: lessons learnt from 30 years of experience

Abstract

The zero length column technique has been developed over the past 30 years as a versatile experimental method to measure adsorption equilibrium and kinetics. In this review we discuss in detail the theory that forms the basis for the technique in order to understand how to design and operate efficiently a system. Experimental checks that should be performed to ensure the correct interpretation of the dynamic response are presented and examples are used to identify how to avoid major errors in determining diffusion time constants. The review concludes with an overview of all experimental studies available in the literature to date and a set of recommendations that should help improve the standard in the reported equilibrium and kinetic properties.

1 Introduction

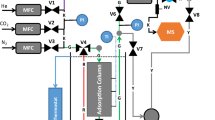
The Zero Length Column (ZLC) technique was first introduced in 1988 by Eic and Ruthven as a novel chromatographic technique to measure intra-crystalline diffusion of organic molecules in zeolites (Eic and Ruthven 1988a). Figure 1 shows a schematic diagram of a ZLC apparatus and the experiment consists in the following steps:

• (1) Equilibration of a small sample exposed to an adsorbate in a carrier gas, typically a dilute mixture;

• (2) Flow is switched to a pure carrier gas;

• (3) Concentration as a function of time is recorded.

Fig. 1

Schematic representation of a ZLC system

The simplicity has made the ZLC an accessible technique because of how the experimental set-up is assembled, how it is operated and how the results are analysed. Over the past 30 years it has been used by more than 25 academic and industrial laboratories to study a wide range of materials and adsorbates. The applications include kinetics of systems dominated by intra-crystalline diffusion, macropore diffusion and surface resistances for both single adsorbates and mixtures. The ZLC is a reliable and flexible technique for the characterization of adsorption equilibrium and kinetics, particularly for strongly adsorbed components.

This contribution is aimed at bringing together the main advances in both experimental and modelling approaches for the measurement of adsorption equilibrium and kinetics using the ZLC technique. To obtain the best results it is necessary to understand the theory as this indicates how to design and run a system optimally. We therefore begin with a discussion of the standard models that are available for the analysis of kinetic experiments. We then use the main results to discuss how to design a system and carry out multiple experiments to arrive at reliable mass transport coefficients. This then leads into a section describing in detail experimental apparatuses. This is then followed by a section outlining what can be measured but also what can go wrong, as this allows to understand more clearly what experimental checks have to be carried out. A summary of published results is included to show the range of applications and few are then discussed in some detail: beads and pellets; distinguishing the diffusion path; combined diffusion and surface barriers; and systems with structural changes due to adsorption. Throughout this contribution several examples will be used based on either published results or data/models from the authors’ laboratory, including previously un-published results.

We conclude with a set of recommendations that should lead to the accurate and reliable use of the ZLC technique.

2 Basic theory of the ZLC

2.1 Column mass balance

What makes the ZLC technique particularly useful is the fact that the mass balance of a normal chromatographic column reduces to that of a perfectly mixed cell in the limit as the length of the column goes to zero, because in this limit the axial dispersion term goes to infinity.

The overall mass balance for a column can be written as

$${V_{S} \frac{{d\bar{q}}}{dt}} + {V_{F} \frac{{d\bar{c}}}{dt}} = {\left({Fc}\right)_{IN}} - {\left( {Fc} \right)_{OUT}}$$

(1)

Here $\bar{c}$ is the average fluid phase concentration; $\bar{q}$ is the average adsorbed phase concentration; $c$ is the fluid phase concentration; $F$ is the volumetric flowrate at the temperature and pressure of the column; ${V}_{S}$ is the volume of the solid in the column; and ${V}_{F}$ is the volume of the fluid in the column.

In reality a ZLC will have a finite length, but “zero” has the meaning of allowing to write the mass balance for a dilute adsorbate in the standard desorption experiment $\left( {c_{IN} = 0\,{\text{and}}\,\bar{c} = c = c_{OUT} } \right)$ as

$$V_{S} \frac{{d\bar{q}}}{dt} + V_{F} \frac{dc}{{dt}} = - Fc$$

(2)

An integral of the mass balance makes it possible to calculate the adsorbed phase concentration at any time

$$V_{S} \left( {\bar{q}_{0} - \bar{q}} \right) + V_{F} \left( {c_{0} - c} \right) = \mathop \smallint \limits_{0}^{t} Fcdt$$

(3)

Note that this is always valid in the desorption experiment, even when the flowrate is not constant. Equation 3 is the basis for measuring equilibrium isotherms using low flowrates (Brandani et al. 2003), which ensure that the fluid concentration is always at equilibrium with the adsorbed phase.

While it would appear that for accurate measurements the volumetric flowrate should be measured, it is possible to show that it can be calculated from the flowrate of the carrier, ${F}_{Carr}$, and the measured concentration (Wang et al. 2011)

$$Fc = \frac{{F_{Carr} - V_{F} \frac{{\frac{c}{{c_{0} }}y_{0} }}{{\mathop \smallint \nolimits_{0}^{\infty } \frac{c}{{c_{0} }}dt}}}}{{1 - \frac{c}{{c_{0} }}y_{0} }}c \approx \frac{{F_{Carr} }}{{1 - \frac{c}{{c_{0} }}y_{0} }}c$$

(4)

where ${y}_{0}$ is the initial fluid phase mole fraction of the adsorbate. The second equality is typically sufficiently accurate in most cases.

The integral of the mass balance can be used to determine the initial concentration at equilibrium

$$V_{S} \bar{q}_{0} + V_{F} c_{0} = \mathop \smallint \limits_{0}^{\infty } Fcdt$$

(5)

Note that as the experiment evolves in time the concentration of the adsorbate will progressively become smaller and eventually the normalised response of the system will reduce to an exponential decay (Brandani and Ruthven 1996a), ${a}_{e}\mathrm{exp}\left(-{b}_{e}t\right)$. Therefore the integral can be calculated numerically up to the point, ${t}_{e}$, where the exponential decay begins and

$$V_{S} \bar{q}_{0} + V_{F} c_{0} = \mathop \smallint \limits_{0}^{{t_{e} }} Fcdt + F_{Carr} c_{0} \mathop \smallint \limits_{{t_{e} }}^{\infty } \frac{c}{{c_{0} }}dt = \mathop \smallint \limits_{0}^{{t_{e} }} Fcdt + F_{Carr} c_{0} \frac{{a_{e} }}{{b_{e} }}\exp \left( { - bt_{e} } \right)$$

(5a)

In an equilibrium measurement the final exponential decay corresponds to the Henry law region of the isotherm (Brandani et al. 2002).

Combining Eqs. 3 and 5 we obtain

$$V_{S} \overline{q} = \int\limits_{0}^{\infty } {Fcdt} - \int\limits_{0}^{t} {Fcdt} - V_{F} c$$

(6)

Finally we note that integration removes random noise in the signal and is easy to implement.

2.2 Diffusion in the solid

To complete the model of the ZLC an adsorption isotherm and a mass transport mechanism have to be considered. When the isotherm is linear the equilibrium adsorbed amount, ${q}^{*}$, is given by

$$q^{*} = Kc$$

(7)

where $K$ is the dimensionless equilibrium constant.

A general solution to the diffusion equation in a sphere of radius ${R}_{P}$ can be obtained for both the fluid phase and the adsorbed phase concentrations (Brandani and Ruthven 1995)

$$\frac{c}{{c_{0} }} = \mathop \sum \limits_{n} \frac{{2L\exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t} \right)}}{{\beta_{n}^{2} + \left( {\gamma \beta_{n}^{2} + 1 - L} \right)^{2} + \gamma \beta_{n}^{2} + L - 1}} = \mathop \sum \limits_{n} a_{n} \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t} \right)$$

(8)

with

$$\beta_{n} \cot \beta_{n} + L - 1 - \gamma \beta_{n}^{2} = 0$$

(8a)

$$\frac{{\overline{q}}}{{q_{0} }} = \mathop \sum \limits_{n} \frac{6}{{\beta_{n}^{2} }}\frac{{L\left( {L - \gamma \beta_{n}^{2} } \right)\exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t} \right)}}{{\beta_{n}^{2} + \left( {\gamma \beta_{n}^{2} + 1 - L} \right)^{2} + \gamma \beta_{n}^{2} + L - 1}} = \mathop \sum \limits_{n} b_{n} \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t} \right)$$

(8b)

where the dimensionless parameters that determine the response are 1/3 the ratio of the accumulation in the fluid phase relative to that of the adsorbed phase and 1/3 the ratio of the diffusion time constant, $\frac{{R}_{P}^{2}}{D}$, and the time constant of the washout of the adsorbed phase, $\frac{K{V}_{S}}{F}$.

$$\gamma = \frac{1}{3}\frac{{V_{F} }}{{KV_{S} }}\quad L = \frac{1}{3}\frac{F}{{KV_{S} }}\frac{{R_{P}^{2} }}{D}$$

(8c)

Equation 8a has one root in each $\pi$ interval. A simple check to determine if enough terms are used and if the roots have been determined correctly is to calculate the sum of the terms for $t=0$, which should be 1.

Given that the ZLC column is not densely packed ${V}_{F}\approx {V}_{S}$. For strongly adsorbed components $\gamma$ is small and the corresponding solution for $\gamma =0$ can be used (Eic and Ruthven 1988a). In this limit the parameter $L$ is also the maximum dimensionless gradient of concentration inside the particle. This shows that it is this parameter that determines in which mode the ZLC is operated. For equilibrium measurements a low value of $L$, $L<1$, ensures that the solid is effectively at equilibrium with the fluid. Therefore a ZLC designed for this purpose should have mass flow controllers that allow to reach small flowrates and the amount of solid in the column should be increased, while maintaining the well mixed behaviour. When the parameter $L\gg 1$ the response is controlled by kinetics inside the particle. In this case the mass flow controllers should be of a range that is sufficiently large to be in this regime and the sample mass should be reduced. Note though that $L$ values that are too high will mean that the measured signal will become too small very rapidly and possibly too close to the baseline of the detector to be able to measure mass transport reliably.

Figure 2 shows the shape of the curves calculated from Eq. 8 for $\gamma =0.05$. It is clear that already for $L=5$ a double exponential curve is obtained. Equation 8 converges rapidly with only a few terms in the series, and for $\frac{D}{{R}_{P}^{2}}t>0.2$ the first exponential is a good approximation. This results in a simple method to estimate the diffusion time constant, $\frac{{R}_{P}^{2}}{D}$, based on the long-time asymptotic exponential decay of the normalised signal. When the accumulation in the fluid is not neglected, the short-time behaviour reduces to

$$\frac{c}{{c_{0} }} = 1 - \exp \left( { - \frac{L}{\gamma }\frac{D}{{R_{P}^{2} }}t} \right) = 1 - \exp \left( { - \frac{F}{{V_{F} }}t} \right)$$

(9)

Fig. 2

Theoretical response curves as a function of the parameter $L$, which is equivalent to curves at different flowrates. $\gamma =0.05$

which combined with Eq. 5 makes it possible to determine $\gamma$. Once this is fixed, the intercept of the long-time asymptote, ${a}_{1},$ provides the information needed to find $L$ and ${\beta }_{1}^{2}$ (since ${\beta }_{1}$ is a function of $\gamma$ and $L$ through Eq. 8a). Finally from the slope of the long-time asymptote $\frac{D}{{R}_{P}^{2}}$ can be obtained.

For strongly adsorbed components ($\gamma <0.01$) the procedure is simpler because $L$ and ${\beta }_{1}^{2}$ are obtained directly from the intercept using the curves shown in Fig. 3. For $L>20$ a rough but simple estimate of the parameters is obtained from $L=\frac{2}{Intercept}$ and ${\beta }_{1}^{2}=9$. Figure 3b shows clearly that for $L>10$ the slope of the long-time asymptote will become less sensitive to a change in flowrate. Therefore measurements around $10<L<50$ will be in the ideal range that gives a good signal (approximately 10% of the initial signal) and sensitivity to the diffusion time constant. From the definition of the parameter $L$, to avoid equilibrium control, smaller sample quantities and higher flowrates are the simplest changes that can be considered. Clearly, larger particles can also be used if available.

Fig. 3

Long-time asymptote curves for $\gamma =0.$

Note that the parameter $L$ has a temperature dependence given by the difference in the energy of adsorption and the activation energy of the diffusivity. It may be therefore possible to find suitable experimental conditions with a given ZLC apparatus by varying the temperature.

Brandani and Ruthven (1996b) discuss in detail also the use of the short-time and intermediate-time analyses to extract a diffusional time constant, $\frac{{R}_{P}^{2}}{D}$, but this part of the response is more sensitive to incomplete equilibration, particle size distributions and nonlinearity of the isotherm and should be used with caution. The short time analysis, including the accumulation in the fluid, allows the estimation of the fluid volume ${V}_{F}$, see Eq. 9. To apply the intermediate time analysis to determine the diffusion coefficient one should always ensure complete equilibration, isotherm linearity and use particles with a narrow size distribution. We refer the interested reader to the analysis in (Brandani and Ruthven 1996b), but our recommendation is to calculate the full solution from Eq. 8 and improve the initial estimate of the parameters obtained from the long-time asymptote.

When experiments at multiple flowrates are performed it is important to produce also the plot of the response curves versus the product of flowrate and time, ie the $Ft$ plot.

Due to the mass balance, Fig. 4 is also a simple graphical check of consistency because the area under the curve is the integral in Eq. 5 and provides two important validations (Brandani 2016). First, this graph confirms if the system is in kinetic control, because under equilibrium conditions curves at different flowrates will coincide. Second, the order of the curves is such that as the flowrate increases the response should be initially steeper but then become less steep. This means that on the $Ft$ plot the curves at different flowrates must cross once and in the short time lower flowrates should be above higher ones.

Fig. 4

Theoretical response curves as a function of the parameter $L$. x-axis is the product of flowrate and time divided by the total accumulation in the system. $\gamma =0.05$

An obvious question to raise at this point is: how many different flowrates are needed? Clearly a minimum of two are required in the kinetic control regime and ideally at least two in the equilibrium control region. These additional equilibrium experiments allow to fix the adsorption isotherm independently from the kinetic model used, but are not strictly needed if linearity of the system is ensured.

Another important question to ask is: how long does it take for the ZLC to reach complete equilibration? The simple answer here is approximately half a diffusion time constant, $\frac{{R}_{P}^{2}}{D}$ (Brandani and Ruthven 1996b), and this is a very important result from the theory, because it suggests a further way in which the experiment can be performed. Instead of allowing complete equilibration, experiments can be run rapidly switching flow between the pure carrier and the adsorbate and then back to the pure carrier. This changes the inlet from a step function to a rectangular pulse. The main benefit of this experiment, the partial loading experiment, is the introduction of a time constant by the user (Brandani and Ruthven 1996b; Brandani et al. 1995a). This means that it is possible to impose a characteristic time constant as well as vary the flowrate. The partial loading experiment does not require any modification to the ZLC system if the pressures in the two lines are balanced. Therefore it should be seen as part of the standard sequence of tests in a ZLC experiment, similar to changing the flowrate. For diffusion into a sphere the solution to the linear model is now

$$\frac{c}{{c_{S} }} = \frac{{\mathop \sum \nolimits_{n} a_{n} \left[ {1 - \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t_{S} } \right)} \right]\exp \left[ { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}\left( {t - t_{S} } \right)} \right]}}{{1 - \mathop \sum \nolimits_{n} a_{n} \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t_{S} } \right)}}\quad {\text{for}}\,t \ge t_{S}$$

(10)

and

$$\frac{{\bar{q}}}{{\bar{q}_{S} }} = \frac{{\mathop \sum \nolimits_{n} b_{n} \left[ {1 - \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t_{S} } \right)} \right]\exp \left[ { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}\left( {t - t_{S} } \right)} \right]}}{{1 - \mathop \sum \nolimits_{n} b_{n} \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t_{S} } \right)}}\quad {\text{for}}\,t \ge t_{S}$$

(10a)

where ${t}_{S}$ is the time between the two concentration changes and ${c}_{S}$ and ${\bar{q}}_{S}$ are the fluid phase concentration and average adsorbed phase concentration when the desorption begins.

By normalizing the curves to be one at $t={t}_{S}$, we obtain a series of curves that will progressively shift down as shown in Fig. 5. This is simply due to the fact that there is less adsorbate in the solid when equilibration is incomplete. The shift of the long-time asymptote is directly related to the ratio of the diffusion time constant and ${t}_{S}$, therefore the partial loading experiment makes it possible to confirm unambiguously the kinetic time constant. In order for the partial loading experiment to be effective, the switch time ${t}_{S}$ should be less than one tenth of the diffusion time constant.

Fig. 5

Theoretical response curves as a function of the switch time, $\frac{{t}_{S}D}{{R}^{2}}=\frac{1}{40},\frac{1}{20},\frac{1}{10} ,>\frac{1}{2}$. $L=20$ and $\gamma =0.05$. a Normalised fluid phase concentration. b Normalised average adsorbed phase concentration

By integrating the fluid phase concentration and plotting the average adsorbed phase concentration for different partial loading experiments, we now achieve an additional very important result. If there is a shift in the adsorbed phase concentration plot, then the kinetic transport includes an internal resistance. From this plot we can therefore distinguish immediately if a system is completely controlled by a surface barrier. To understand this, one needs to consider the difference in the internal concentration profile for a diffusion process and for a surface barrier shown in Fig. 6. The normalized concentration for a surface barrier is exactly the same whether full equilibration is achieved or not. In the case of diffusion more adsorbate will be close to the external surface and therefore desorption will be faster in the partially equilibrated case, ie the response will shift down as seen in Fig. 5b.

Fig. 6

Internal adsorbed phase concentration profiles at different $\frac{{t}_{S}D}{{R}^{2}}$ values. a Diffusion. b Surface barrier. $L=20$ and $\gamma =0.05$

Note that the average concentration in the solid is lower in a partial loading experiment and therefore reducing the switch time brings the system closer to linearity. Therefore, the partial loading experiment can also give an indication of when the system is weakly or strongly nonlinear.

We now consider an example of a system that is sufficiently slow to allow to see the full set of time constants from the diffusion equation (Mangano 2012). Figure 7 shows CO₂ on zeolite Rho for two flowrates, but each snapshot shows only the curves up to a specified time. All the snapshots are matched well by the standard model with different diffusional time constants. In this case, depending on the choice of the range of times one could extract faster diffusitivies than the true value. Note that this is true for both the full model and the long-time asymptote approach. Figure 8 shows the same curves with one partial loading experiment compared with the model prediction using the parameters from Fig. 7a and d. Clearly only one diffusion time constant, $\frac{{R}_{P}^{2}}{D}$, can match also the partial loading curves.

Fig. 7

ZLC desorption curves for 10% CO₂ in He in Na,Cs-Rho at 2.1 and 8.4 ml/min at different observation times, a 200 s, b 1000 s, c 2000s and d 4000 s. In red the prediction of diffusion model, $\gamma =0.045$ for all curves and $L$ values displayed in the plots are proportional to the flowrates

Fig. 8

Full and partial loading ZLC curves of 10% CO₂ in He in Na,Cs-Rho at 2.1 ml/min. Curves are model predictions using the parameters obtained from 200 and 4000 s observation times

The parameters from Fig. 7d provide a very accurate match of the partial loading curve and the model, while on close inspection the fully equilibrated data are higher than the model at intermediate concentrations. This is an indication of a weak nonlinearity of the isotherm and the analysis could be refined to obtain the Henry law constant from the partial loading experiment and an estimate of the Langmuir saturation capacity from the fully equilibrated data.

We can now understand that in an ideal ZLC system the best approach that minimizes the experimental effort and maximizes the reliability of the measured diffusivity is achieved by running experiments at two flowrates in the region where $L>10$ and at least one partial loading experiment at one of the flowrates.

2.3 Experimental apparatus

Having discussed the basic theory of a ZLC system, we now turn to the discussion of the main components. A schematic diagram of a ZLC apparatus is shown in Fig. 9.

Fig. 9

Schematic diagram of a ZLC system

The essential components are: a set of mass flow controllers; either a rotary valve or a set of switching valves; the column; and the detector. Gas chromatographs (GCs) are an example of where all the elements are integrated into a single unit, but modern systems are specialised primarily for analytical measurements and therefore some effort is needed in modifying them to house a ZLC. Figure 10 shows a traditional configuration housed in a GC and a purpose-built system.

Fig. 10

Photos of a conventional b semi-automated ZLC apparatuses

From the discussion of the theory a system that can measure both equilibrium and kinetic properties should have two sets of mass flow controllers: one for low flows, which are typically in the range of 1–3 or 1–5 ml/min; and one for high flows, which depend on the system being studied but are typically in a range at least 10 times larger than the low flow controllers.

For systems housed in a GC, Fig. 10a, the control of the mass flow integrated in the GC may not be in the correct range and it is better to have an independent set of mass flow controllers and use the GC for the valve(s), the housing of the column and the detector. GC valves are typically rotary valves with either a pneumatic or electrical actuator. Fast acting valves are to be preferred, but even in this case there is always a fraction of a second where the flow through the valve stops and then restarts. This will affect only very fast diffusing systems and will create some uncertainty in equilibrium measurements if the signal of the detector oscillates. In most systems the rotary valve is housed either outside the GC oven or in a separate temperature zone, therefore to ensure that the inlet gas reaches the oven temperature a coil of narrow tubing should be inserted between the valve and the column. This is typically achieved using 1/16″ tubing, given that most GC valves are supplied with this tubing size. Having this small diameter pipe will result in a concentration front that is essentially in plug flow, therefore it will not affect the analysis of the response, but this should be checked from blank experiments.

The column is typically a 1/8″ union or tee. Other arrangements are clearly possible and for beads and pellets 1/4″ unions can be used. The sample can be sandwiched between two sinter discs on one side of the union or tee when the sample mass is small, approximately 1 mg. The tee is to be preferred when the detector is a mass spectrometer (MS) given that the capillary to the MS can be inserted immediately after the sample and in line with the middle of the flow. To avoid gas bypass the sample should be in a vertical alignment. For weakly adsorbed components one can also increase the sample mass, and for powders this is done in a straightforward manner by placing the sinter discs on both sides of the 1/8″ union and the sample in the 9 mm length between them. This configuration makes it possible to pack around 10 mg of sample, which will still behave as a ZLC if the adsorbate is not strongly adsorbed. As a practical example 6–10 mg of a hydrophilic MOF and CO₂ at 30 °C will behave as a ZLC, but the same column with water will be a normal chromatographic column and display a delayed breakthrough curve and proportionate pattern in desorption (Ruthven 1984). Figure 11 shows the raw MS signal for the Ni-CPO-27 exposed to a synthetic flue gas. A column with 8.3 mg behaves as a ZLC for CO₂ with a rapid and sharp transition, while the water signal needs almost 2 h before the column reaches equilibration (Mangano et al. 2016). Note that the adsorbing water and SO₂ displace CO₂ that shows an overshoot as the more weakly adsorbed component.

Fig. 11

Experimental outlet raw signal for the exposure of Ni-CPO-27 to humid flue gas. Flue gas concentration: 16% CO₂, 100 ppm SO₂, 10 ppm NO, 1% H₂O in N₂ as balance

Initial experiments with different sample masses should confirm how small the sample should be for the system to behave as a ZLC system for the particular adsorbate (Brandani et al. 1996).

To study diffusion of organic molecules, a flame ionization detector (FID) is one of the best options to use and these are readily available as standard detectors in GCs. This configuration was used by Eic and Ruthven to establish the technique (Eic and Ruthven 1988a). What is important to understand of the FID is the fact that it measures the total quantity, i.e., the product of the concentration and the flowrate. Modern commercial GCs are less flexible than in the past because they are designed almost exclusively to house capillary columns. The FID in use will only allow a limited range of flowrates. This means that for equilibrium measurements a make-up flow is needed, while for high-flow measurements a split-flow is needed. These can be achieved by adding a short capillary before the FID to allow to control the split-flow and a tee union after the ZLC which can be connected to either make-up gas or to split the flow before the FID.

For inorganic molecules a thermal conductivity detector (TCD) is commonly used. TCDs can be either diffusion cells, when the filament is not in the direct path of the flowing gas, or direct flow. Diffusion cells allow a wider range of flowrates, while direct flow arrangements have a rapid response time. In systems housed in a GC similar flowrate restrictions apply to the TCD as for other detectors due to the typical application of commercial systems. The reference side of the TCD can also be either exposed to the carrier gas or blanked-off with a gas added at the factory. Symmetry improves the quality of the signal, therefore the reference with the carrier gas in flow is a better option.

One should always test the blank response of the detector to ensure that the signal is linear with the concentration. This is normally not a problem with dilute mixtures, i.e., the original intended use of the ZLC, but has to be considered when dealing with large concentration steps, particularly when using mass spectrometers. For MSs there are two effects that come into play: the flow of gas primarily in the Knudsen regime in the capillary that feeds the detector; and the turbo-molecular pump that may have difficulties when the molecular weight of the carrier and adsorbate are significantly different. Not all MS models are suitable for a ZLC and issues to consider are the minimum flowrate required by the MS and the way the capillary feeds the detector. Some systems try to avoid Knudsen separation in the capillary by using high flowrates and splitting the gas in a chamber connected to the detector via a small aperture. While a make-up flow can be devised when the flowrate to the MS is too high, the indirect feed to the detector results in an additional time constant that may limit the dynamics of the system to 20–40 s. Note that an MS is not as sensitive as an FID and therefore dilution with a make-up gas results in a poor signal.

When studying multicomponent systems an MS is the normal detector of choice. The possible difficulty that one encounters is linked to the position of the peaks in the MS spectra for two molecules. For example CO₂ has a main peak at amu 44 and a secondary peak at amu 28, therefore care should be taken in decoupling the peak at amu 28 if the pair CO₂/N₂ is being studied, which is not too difficult if a strong signal is available and the ratio of the 28/44 peaks for CO₂ are calibrated on the actual instrument used. There are cases where resolving the dynamic concentrations is not simple, for example for CO/N₂ that have the main peak at amu 28 and when studying isomers. For hydrocarbons, a deuterated isomer makes it possible to shift the main peak for one of the two molecules (Brandani et al. 2000a, b). This is effective but expensive.

When the pair of gases to be studied includes a molecule that does not combust and one that does, then a TCD in line with an FID can also be used, but careful interpretation of the blank responses is needed to determine the additional dispersion introduced by the connections and the TCD.

We cannot describe in greater detail all possible options, but a clear understanding of the detector being used is essential for assembling and operating an effective ZLC system. As a general comment though, it is always better to run small concentration steps. The detectors will be in their linear range and conversion of the signal to a dimensionless concentration ratio is straightforward and does not require calibration.

$$\frac{c}{{c_{0} }} = \frac{{\sigma - \sigma_{\infty } }}{{\sigma_{0} - \sigma_{\infty } }}$$

(11)

where $\sigma$ is the measured signal and ${\sigma }_{0}$ and ${\sigma }_{\infty }$ are the initial and final signals.

For systems not housed in a GC, Fig. 10b, an alternative to rotary valves is the use of 4 on–off valves connected in pairs. This arrangement has the advantage of allowing to balance the pressures on both sides more easily and reduce the fluctuations at the time of the switch in flow. For equilibrium measurements where a constant carrier flow is important, a differential pressure transducer between the inlet lines should be added. Micrometric valves are then added at the outlet to ensure that the two sides are at the same pressure before switching the valve. In large concentration steps the viscosity of the gas will change, so a back-pressure regulator may be used to maintain a constant pressure in the system, but this is needed primarily when the two sides are not symmetric because the pressure of the column is always close to atmospheric.

The 4-valve arrangement can be significantly cheaper than a rotary valve, but the piping not in direct flow will become a dead-end pipe and this section will behave as a ZLC. Care must be taken to reduce the volume between the valves and the tee before the ZLC and the blank response should be characterised carefully in the case of weakly adsorbed components.

With hydrophilic materials it is also important to pre-dry all the gases and to add a short coil of 1/16″ tubing at the outlet when low flowrates are used. This precaution avoids back-diffusion of air and water from the lines after the ZLC.

Preparation of the feed mixture is also a key feature of ZLC systems. Cylinders with set mixtures can be used, but note that drying columns have to be bypassed in this case. With hydrophilic materials it is better to start from pure components. For mixtures of gases, the simplest option is to mix the adsorbate and the carrier in flow. The resulting concentration depends on the relative flowrate of the carrier and adsorbate, but this solution may be not be very accurate and has limitations when very dilute mixtures are required. An alternative option is to use a dosing volume as depicted in Fig. 9 where the mixture can be prepared based on the partial pressure of each component (Hu et al. 2015a). This results in a higher accuracy in the concentration especially for very dilute mixtures.

In the case of mixture preparation involving vapours, the liquid needs to be evaporated and added to the mixture. This can be done by using a capsule connected to the dosing volume (Fig. 9). In this case, temperature and total pressure are set to let the liquid evaporate from the capsule to the dosing volume. An estimate of the amount evaporated is calculated from the weight difference of the capsule, but requires an accurate balance (Mangano et al. 2016; Hu et al. 2018). This represents a good option for mixtures with low concentrations of vapours, generally less than 1%. The mixture flows through to the mass flow controllers, therefore higher concentrations may result in condensation in the capillary of the mass flow controller, especially the low flowrate pair. For this reason, mixtures with higher vapour content should be prepared using a bubbler connected after the mass flow controllers (Eic and Ruthven 1988a; Centineo and Brandani 2020).

2.4 Equilibrium measurements

For accurate equilibrium measurements the ZLC offers some important advantages. Probably the most obvious advantage is that once equilibrium control conditions are established a high resolution isotherm (> 100 points) can be generated easily. This can be particularly useful also for kinetic studies that require the knowledge of the local slope of the isotherm. The small mass used makes it possible to test directly powders without having to worry about pressure drops which would dominate longer columns. Similarly the temperature control of a very small system is highly effective, provided that a thermocouple is attached to the column. For strongly adsorbed components it is very difficult to maintain isothermal conditions in a normal chromatographic system with gram quantities of sample, but in a ZLC this is not a problem, especially with powders (Brandani et al. 1998), considering that all the gas is flowing through the sample and that the sample is in direct contact with a large mass of metal. A recent study using 23 g of 13X and CO₂ in a short chromatographic column shows overshoots in temperature up to 80 K (Wilkins and Rajendran 2019), while an extended ZLC (bulkhead 1/8″ union) packed with 48 mg had a temperature overshoot of only 2 K in adsorption and was essentially isothermal in desorption (Gibson et al. 2016).

What leads to advantages though can also be the reason for potential difficulties, because impurities such as water have a disproportionate effect when the sample mass is very small. With this in mind it is always useful to perform a series of experiments at a set temperature and replicate at the end of the series the first experiment to confirm reproducibility. If the detector is a mass spectrometer it is also possible to monitor the impurities when regenerating the material, by performing a temperature programmed desorption (TPD).

The column should be packed with a larger sample mass, compared to kinetic studies, and the flowrate should be kept as high as possible, while ensuring that the response curves coincide in the $Ft$ plot.

The ZLC provides a very efficient means of measuring the shape of the adsorption isotherm, including Darken thermodynamic correction factors, and to determine the zero loading energy of adsorption. Both do not require the exact knowledge of the sample mass. For accurate adsorbed amounts, an independent measurement should be made on another instrument for one adsorbate, because it is always very difficult to measure exactly the mass that is being packed in a ZLC and when the sinter discs are inserted it is not possible to avoid that at least part of the sample is crushed or lost in transfer. Once the sample mass is cross-checked for one adsorbate the column can then be used for accurate measurements which require very good mass flow controllers and a stable signal in the detector.

Brandani et al. were the first to demonstrate the use of the ZLC to measure adsorption isotherms for pure components (Brandani et al. 2003) and mixtures (Brandani and Ruthven 2003). They were able to investigate the effect of small amounts of water on the adsorption of CO₂ and C₃H₈ in very hydrophilic zeolites (Brandani and Ruthven 2004). Combining the measurement at a fixed temperature and TPD it was possible to identify both physisorbed and chemisorbed CO₂ amounts in the presence of water. Without a TPD only the physisorbed amounts are determined from the ZLC desorption experiment. Measurement of both adsorption and desorption makes it possible to see the difference between the two, but the TPD is needed to trigger the release of the chemisorbed species and identify if more than one are present.

More recently the technique has been extended to measure water adsorption equilibrium on mesoporous materials (Centineo and Brandani 2020). This was the first example of direct measurement of adsorption hysteresis using the ZLC technique. The near vertical condensation step in SBA-15 was particularly challenging, because this leads to very slow kinetics which require flowrates below 1 ml/min to achieve equilibrium control. The method of combining a few points on a commercial gravimetric system with the full isotherm (more than 10,000 points) from the ZLC was shown to provide a very efficient means of obtaining a high resolution isotherm, including the near vertical branches of the hysteresis loop that are otherwise very difficult to measure in a conventional system.

Equilibrium measurements using the ZLC are particularly useful for strongly adsorbed components. At low pressures the ZLC represents one of the most efficient methods to measure isotherms for vapours. On the other hand it is not recommended for weakly adsorbed components, for example N₂ adsorption around 300 K on zeolites. In this case, a careful examination of the blank response will still allow to determine a single point on the isotherm, but the major advantage of a high resolution isotherm is lost.

2.5 Kinetic measurements

If one is interested in kinetic measurements to obtain only approximate estimates of mass transfer time constants, it is not necessary to go through all the additional arrangements needed for accurate equilibrium measurements. If the technique is to be used as a simple screening tool to compare materials, then all that is needed is to ensure that the long-time asymptote can be identified because this will normally allow to estimate the time constant within a factor of 2.

In principle one could also study the adsorption experiment, which mathematically would be the same for a linear system. The reason for carrying out desorption experiments is a reflection of the better signal to noise ratio in the long-time asymptote. From Eq. 11 it is possible to see that in a desorption experiment one is subtracting small numbers (${\sigma }_{\infty }$ is the baseline of the detector), while in an adsorption experiment a large value is subtracted to obtain the normalised signal, which leads to loss of accuracy especially considering that most of the kinetic information is in the final few % of the full scale of the signal. Furthermore, as long as the detector has enough sensitivity, the tail of the desorption experiment will be in a linear region with a constant flowrate.

Care in the design of the apparatus becomes progressively similar to that needed for equilibrium measurements as the system becomes faster. Time constants below 1 min require an accurate pressure balance of the two sides and time constants below 20 s require very careful design of the connection between the column and the detector, particularly for MS systems, and also a systematic reduction of any volume present between the valve and the ZLC. To our knowledge the fastest systems studied using a ZLC to obtain reliable transport parameters are diffusion of C₃H₈ in AlPO₄-5 (Brandani et al. 1997) and diffusion of CO₂ in fragments of a carbon monolith (Brandani et al. 2004). In both cases the kinetic responses were effectively over in less than 10 s. The first study determined directly that the response after the first 2 s was sufficiently far from the blank response, so that reliable long-time asymptotes could be determined. For the second and slightly faster system, a simultaneous regression of curves at five different flowrates was applied to ensure accurate results in estimating the fluid accumulation term and the diffusion time constant, $\frac{{R}_{P}^{2}}{D}$. These represent the likely limit for a well-designed and optimized ZLC system applied to kinetic measurements, with the fastest measurable time constant of approximately 1–2 s.

3 What can be measured and what can go wrong

3.1 Normal ZLC, tracer ZLC and multicomponent ZLC

The traditional ZLC was developed for highly dilute, typically less than 1% v/v, adsorbates in carrier gases, normally He or Ar (Eic and Ruthven 1988a). In this configuration what is measured is the limiting diffusivity at zero adsorbed phase loading. This is an important kinetic parameter in diffusion in nanoporous materials and in this dilute region it should be equal to the self-diffusion coefficient and the Maxwell–Stefan diffusivity of the single adsorbates (Kärger et al. 2012). In many systems, the diffusivity at zero loading combined with the Darken correction factor provides a sound engineering model for mass transport in nanoporous materials. The Darken correction factor is the thermodynamic correction that is obtained when writing the flux in terms of the gradient of the chemical potential in a microporous solid and is given by

$$\Phi \left( {q^{*} } \right) = {{\frac{{d\ln q^{*} }}{{d\ln P^{*} }} = \frac{{dq^{*} }}{{dP^{*} }}\frac{{P^{*} }}{{q^{*} }} = \frac{{dq^{*} }}{{dc^{*} }}} \mathord{\left/ {\vphantom {{\frac{{d\ln q^{*} }}{{d\ln P^{*} }} = \frac{{dq^{*} }}{{dP^{*} }}\frac{{P^{*} }}{{q^{*} }} = \frac{{dq^{*} }}{{dc^{*} }}} {\frac{{q^{*} }}{{c^{*} }}}}} \right. \kern-\nulldelimiterspace} {\frac{{q^{*} }}{{c^{*} }}}}$$

(12)

where ${P}^{*}$ and ${c}^{*}$ are the pressure and concentration that are at equilibrium with the adsorbed phase concentration ${q}^{*}$ at the temperature of the solid.

The last ratio, shows that this correction can be calculated from the slope of the isotherm and the slope of the secant of the isotherm from the origin. Therefore, to be able to measure accurately the diffusivity at zero loading should not be seen as a limitation, if the ZLC can also be used to obtain a high resolution isotherm and calculate the Darken correction factor. Non-dilute desorption steps can also be run, but these will be discussed in the following section dealing with the effects of isotherm non-linearity.

The tracer ZLC technique was developed to be able to compare directly results from experiments using the ZLC and PFG-NMR (Hufton et al. 1994; Brandani et al. 1995b). Here the sample is equilibrated with a mixture of adsorbate and carrier, followed by an exchange with a mixture at the same total concentration of adsorbate and tracer or pure tracer. A deuterated hydrocarbon is a simple tracer that can be detected with a MS. During the exchange, the total concentration remains constant, therefore an added benefit of the tracer ZLC is that the system is always linear with an equilibrium constant

$$K_{t} = \frac{{q_{0} }}{{c_{0} }}$$

(13)

This represents the slope of the secant of the isotherm between the origin and the equilibrium (fixed) point. The measured diffusivity is the tracer diffusivity at the adsorbed phase concentration and its concentration dependence can be measured carrying out experiments at different total concentrations. Transition state theory makes it possible to relate the tracer or self-diffusivity to the transport diffusivity (Kärger et al. 2012; Chmelik and Kärger 2016).

A further advantage of the tracer ZLC experiment lies in the fact that it is an exchange process and therefore for each molecule desorbed there is a corresponding molecule adsorbed, leading to an isothermal process.

The tracer ZLC eliminates two of the most obvious complications in adsorption kinetic experiments, isotherm nonlinearity and nonisothermal conditions, but requires a detector for the tracer molecules (MS) and expensive consumables. An understanding of the theory of both these non-ideal cases has led to a limited need for tracer ZLC experiments, which remain still very valuable for more fundamental mass transport investigations.

When a detector can distinguish different molecules, it is straightforward to extend the technique to measure multicomponent systems. The first ZLC experiments studied benzene and the xylene isomers in silicalite, and combined counter-current exchange with tracer ZLC experiments (Brandani et al. 2000a, b). Benzene/p-xylene conformed closely to a concentration dependent diffusivity that accounted for the gradient of the chemical potential. o-Xylene/p-xylene on the other hand showed some deviation from a standard model indicating a degree of direct interaction.

More recently the ZLC was used to study diffusion of methane with and without CO₂ in DD3R zeolite. This system showed a strong cooperative effect of CO₂ at lower temperatures (Vidoni and Ruthven 2012a). With CO₂ present, methane diffuses up to an order of magnitude faster compared to the case as a single adsorbate.

3.2 Nonlinear isotherm

There are two main reasons that make nonlinear isotherms a very important aspect to consider in ZLC measurements: when dealing with strongly adsorbed components it may be difficult to achieve initial conditions in the Henry law region (Eic and Ruthven 1988a); with a weak signal it is often tempting to increase the fluid phase concentration to obtain what appears to be a better response curve. Both these are not critical issues if one is aware that nonlinear conditions are present. In fact one may wish to carry out experiments with larger concentration steps to test the concentration dependence of the transport diffusivity (Brandani et al. 2000c; Zhu et al. 2004). However, they do become critical when one assumes linearity in the analysis without being aware of that this condition is not met.

As with any nonlinear problem it is conceptually initially difficult to see what the main effects are, but clarity emerges, in particular for type I isotherms such as the Langmuir isotherm, if one considers that the final exponential decay is in the linear region if the detector has enough sensitivity. Additional insight is obtained from the essential features of a Langmuir isotherm: an initial Henry law region; and a finite saturation capacity. If we now consider the simpler linear isotherm up to the saturation capacity followed by a constant adsorbed phase concentration above ${c}_{L}$, it is possible to see that the Darken correction in this case is $\infty$ when the fluid concentration is beyond ${c}_{L}$. Therefore a ZLC experiment that starts above ${c}_{L}$ will be under equilibrium control until the fluid concentration drops to ${c}_{L}$ and from this point onwards the normal ZLC response is recovered (Brandani 1998). The main effects are a shift down of the long-time asymptote and more curvature in the initial region because the real isotherm has a continuous first derivative. This will generate a large uncertainty in the diffusivity only when the parameter $L$ is small and this is why it is essential to carry out ZLC experiments at least for two flowrates (Eic and Ruthven 1988a; Brandani 1998). Figure 12a shows the effect of nonlinearity for a Langmuir isotherm, where the nonlinearity parameter is the ratio of the initial adsorbed phase concentration and the saturation capacity in the isotherm, $\frac{{q}_{0}}{{q}_{S}}.$ Figure 12b shows experimental data for the benzene silicalite system, which conforms closely to the nonlinear model with a Langmuir isotherm. The data were used to confirm the predicted shifts in the intercept of the nonlinear responses and the relationship between the normal nonlinear and tracer ZLC curves.

Fig. 12

a Nonlinear ZLC curves showing shift in long time asymptote for a Langmuir isotherm. Adapted from (Brandani 1998) with permission; Benzene on silicalite ZLC and tracer ZLC curves at 130 °C and 19 ml/min. Adapted from (Brandani et al. 2000c) with permission

If the full linear model is plotted against nonlinear data, the model can have the same long-time asymptote but the initial portion of the experimental data for a type I isotherm will be above the curve. This is due to the concentration dependent diffusivity which gives rise to a faster desorption for short times when the concentration is in the nonlinear region.

The importance of understanding the qualitative behaviour of a ZLC under nonlinear conditions becomes more evident with two examples from experienced adsorption groups. Micke et al. reported ZLC experiments where they measured concentration dependent diffusivities for benzene in H-ZSM5 (Micke et al. 1993, 1994). They used a numerical software tool to fit the entire desorption curve, but what was surprising was the fact that the slopes of the long-time asymptotes were concentration dependent. This is contrary to the basic theory, considering that the system follows a Langmuir isotherm (Micke et al. 1993, 1994). This example makes it possible to discuss the importance of the correct choice of the baseline of the signal. An incorrect baseline is the most likely explanation (Brandani 1998) for the fact that the reported ZLC concentration dependent diffusivities were a match to measurements carried out by the same group using a volumetric apparatus, which measures directly the transport diffusivity as a function of concentration. By adjusting the value of the final signal, ${\sigma }_{\infty }$, there is a direct effect on the slope of the long-time asymptote when the reduced signal is below 0.01. A low baseline will result in lower diffusivities, while a high baseline will lead to a higher diffusivity. Clearly if one expects a value for the diffusivity it is possible to introduce an either conscious or unconscious bias. The important point is that if the theory on the effect of isotherm nonlinearity is understood, then it should be clear that the long-time asymptote should not depend on the initial concentration and this type of incorrect interpretation of the ZLC results would be avoided.

A simple check on the importance of correct baselining of the signal is to plot the reduced curves with the original baseline and $10$ or $1/10$ times the baseline. Figure 13a shows an experimental ZLC curve for heptane in a single pellet of HISIV 3000 at 448 K, where the correct baseline is changed up or down by a factor of 10, to show how the long-time asymptote would be affected for the case where $L\approx 10-20$. In this optimal region, the predicted time constant would vary by no more than $\pm 10\%$ compared to the correct one. This deviation will become larger as the value of the parameter $L$ is increased, as displayed in Fig. 13b, where the same check is applied to a ZLC curve of CO₂ on Na, Cs Rho at 303 K and 31.5 ml/min; here the estimated time constant can vary from 60 to 600% compared to the correct one and care should be taken in establishing the actual value of the baseline.

Fig. 13

Examples with variable baseline at a $L\approx 10{-}20$, b $L>200$

The second more recent example of what can go wrong with a nonlinear system is based on CO₂ adsorption in commercial 13X beads. Here the most important aspect to determine is the controlling mass transport mechanism. If the system is micropore diffusion controlled in a carbon capture process one could use very large beads to reduce losses due to pressure drops. If the system is macropore diffusion controlled, then an optimum size of the beads has to be found to balance the pressure drop losses and the mass transport limitations. Silva et al. reported a series of ZLC curves and showed perfect coincidence of curves for differently sized beads (Silva et al. 2012). They took this as prima facie evidence of micropore diffusion control and proceeded to determine the diffusivity of CO₂ in crystals of 13X without checking for linearity. Brandani (1998) explained clearly that a nonlinear ZLC under equilibrium control is very similar to a normal ZLC response in kinetic control. Experiments using a sufficiently large range of flowrates should have been carried out and clear differentiation on an $Ft$ plot should have been determined before assuming linearity and kinetic control. Mangano et al. replicated the ZLC experiments for this system, reducing the sample mass while maintaining the same range of $L$ values and showed that the system was under equilibrium control (Mangano et al. 2013a). This explains why experiments with different bead sizes gave the same dynamic response and in this case why the reported micropore diffusivities are meaningless, because the long-time asymptote is determined by the Henry law constant, not the mass transfer resistance. Brandani later showed that the original data fail the graphical consistency check, which indicated that curves at different flowrates did not correspond to equal adsorbed amounts (Brandani 2016).

This example shows very well how the incorrect use of the ZLC technique can lead to significant errors, well beyond the factor of 2 that we are often citing. The reported crystal diffusivities (Silva et al. 2012) are 6 orders of magnitude lower that the self-diffusivities measured by PFG-NMR (Kärger et al. 1993). This is not surprising given that Zeolite 13X is a large pore zeolite with windows that are approximately twice the kinetic diameter of CO₂, therefore it is not possible to measure diffusion in small crystals using existing macroscopic techniques. CO₂ in beads of 13X is macropore diffusion limited, something that now seems to be widely understood (Wilkins and Rajendran 2019; Hu et al. 2014; Park et al. 2016; Hossain et al. 2019; Krishnamurthy et al. 2014).

3.3 Bed effects

When larger sample masses are used there are two possible bed effects in a ZLC system. The first leads to a behaviour that becomes progressively similar to a short packed column. The short time transition becomes a smooth curve, rather than a sharp cusp. Duncan and Moller analysed this case and showed that this had a minor effect, which was negligible for $L>15$ for a Peclet number, $Pe$, of 3 (Duncan and Möller 2000a). Note that the ZLC limit corresponds to $Pe=0$. An intuitive way to understand this is the fact that even for a normal packed column the final layer is a ZLC. When the entire column is not a perfectly mixed cell what is affected is the shape of the inlet concentration which becomes s-shaped rather than a perfect step, but the long-time asymptote remains robust for the determination of the diffusion time constant, within 10% of the true value. Duncan and Moller showed that the estimated diffusivity would be slightly larger than the actual value (Duncan and Möller 2000a). This suggests to run experiments with different sample masses or modifying the arrangement of the particles to verify directly when this may be an issue.

The second and potentially more important effect is when particles stick together to form a larger unit. Given the loose packing of the column this is often the case for small crystals, which tend to aggregate more easily. This problem can be reduced by dispersing the powder in glass wool, especially when the ZLC is packed in the space inside a union. While this is an important issue, there is a very simple experimental check that can be carried out which was suggested by Eic and Ruthven in their original paper (Eic and Ruthven 1988a). This is the use of two different carrier gases which is straightforward in the case of strongly adsorbed components. In a ZLC system an aggregate will have an effective macropore diffusivity that depends on the molecular diffusivity, which in turn depends on the square root of the molecular mass of the components of the binary mixture. The use of He and Ar or N₂ is the best way to exclude bed effects experimentally. This will also change the axial dispersion term in a short column, therefore it is always recommended to perform this additional experiment where possible. Brandani et al. report an example where both sample mass and carrier gases were varied as shown in Fig. 14 (Brandani et al. 1996).

Fig. 14

Benzene on 50 µm NaX zeolite crystals. Different sample masses and carrier gases, from (Brandani et al. 1996) with permission

To understand the potential pitfalls associated with particle aggregation we note here that in this case the ZLC will respond as if it had been packed with beads rather than a powder. We will treat the theory of a ZLC with beads/pellets in a dedicated section, but consider the example of toluene in SBA for which tracer ZLC and PFG-NMR data are available for the same sample (Menjoge et al. 2010). The reported diffusivities, which should be the same, differed by 4–5 orders of magnitude. This was explained by considering potential differences in the diffusion paths in the mesopores observed over the different timescales of the experiments, but the difference seems to be too large. An alternative explanation is that in the ZLC, rather than observing individual crystals, aggregates are formed. This is consistent with the SEM images in the paper and with the fact that SBA powders are very sticky. To confirm this hypothesis it would have been necessary to perform experiments with a different carrier gas, but these were not included in the study.

3.4 Heat effects

Of all the macroscopic techniques, the ZLC is the least affected by nonisothermal conditions because of the small sample size, the flow of gas through the sample and the direct contact between the sample and a large mass of metal. This is normally the case for diffusion in powders, but for very strongly adsorbed components in large beads or pellets heat effects may become an issue.

The general problem was analysed by Brandani et al. (1998), who considered a nonlinear numerical solution of the worst case scenario, an equilibrium controlled system with a Nusselt number of 2. The dynamic response of this system is very interesting and at least qualitatively it is simple to understand. At the start of the desorption a large amount of adsorbate leaves the solid, leading to a rapid drop in temperature. An intermediate stable point is reached where the generation term from the desorbing amount is balanced by the heat transfer to the particle. This leads to a near plateau in the adsorbed phase concentration and a plateau in the temperature of the solid. Eventually though the adsorbate is depleted to the point that heat transfer to the particle raises the temperature back to the initial point and the long-time asymptote is recovered. The corresponding concentration curve should therefore show a shallow inflection, as seen in Fig. 15a, which can lead to problems if this part is interpreted as the long-time asymptote, most likely by adjusting the baseline to remove the inflection.

Fig. 15

a Shape of response for nonisothermal equilibrium case. b Limit of region where heat effects become important as a function of the parameter $L$, adapted from (Brandani et al. 1998) with permission

Fortunately it can be shown that for the worst case scenario this complex system is governed by a single dimensionless group and the condition for near isothermal responses is given by (Brandani et al. 1998)

$${\Gamma } = \frac{{\Delta H^{2} }}{{R_{g} T_{0}^{2} }}\frac{{Fc_{0} }}{{3k_{T} V_{S} }}R_{P}^{2} < 1$$

(14)

If mass transfer resistance is included the requirement is less stringent as shown in Fig. 15b.

Using different carrier gases will change the gas phase thermal conductivity ${k}_{T}$. Reducing the sample size and the concentration step will also help. Therefore the same experimental checks used for bed effects and to ensure linearity should be applied in order to exclude heat transfer limitations.

Note that in Eq. 14 the heat of adsorption $-\Delta H$ can be determined from equilibrium measurements, therefore at least a simple order of magnitude calculation of the dimensionless group is possible. For powders the assumption of isothermal conditions is typically valid because the term ${R}_{P}^{2}$ is sufficiently small. For beads or pellets, which include aggregates of sticky particles, strongly adsorbed components ($-\Delta H$ large), and large concentration steps this may not be the case. Curves conforming qualitatively to the nonisothermal model were obtained for beads of NaY zeolite (${R}_{P}=1.4$ mm) using p-xylene (Brandani et al. 1998). Varying the size of the pellets, or even better using fragments of uniform size is normally the simplest method to reduce the system to isothermal conditions.

3.5 Kinetics too fast

We have already discussed the limit in terms of an absolute time constant of 1–2 s that is measurable. But this limit has to be coupled with needing a sufficiently high value of the $L$ parameter. The limit of something too fast to measure can be problematic when one is not aware that the system is in equilibrium control. This is why an important recommendation is to plot the ZLC curves in both the standard plot and the $Ft$ plot. This simple check unfortunately is not included in most studies found in the literature. As an example of when this would have been useful, consider the measurements of diffusion of n-decane in MCM-41 shown in Fig. 16 (Qiao and Bhatia 2005a).

Fig. 16

Experimental ZLC curves n-decane in MCM-41 at 30 °C at different flowrates. Adapted from (Qiao and Bhatia 2005a) with permission. Additional lines are used to read the time at which the curves cross 0.1 to estimate the $Ft$ behaviour

The $Ft$ plot was not included in the original publication, but reading the times at which all the curves cross 0.1 provides a simple estimate to see if a single curve would be obtained. All the flowrates from 60 to 120 ml/min give a value for the eluted volume of 465 ± 5 ml, showing that all these curves are under equilibrium control. Only the 140 ml/min gives a slightly lower value of 445 ml, which is less than 5% lower. There is too much uncertainty because the long-time asymptotes of the low flowrate curves do not go through the origin indicating a small deviation from linearity. This is an example of a system too fast to measure to obtain a reliable estimate of the diffusivity. The values reported (Qiao and Bhatia 2005a) are therefore only lower estimates, i.e., the actual diffusivities will be larger. Note that this information may be all that is needed to establish which transport process may be the controlling mechanism and the curves can be used to obtain reliable equilibrium data.

3.6 Broad particle size distribution

When measuring mass transport it is important to have a narrow particle size distribution to be able to convert the time constant to a diffusivity. If this is not the case then qualitatively the ZLC response will show a distribution of time constants which will be faster than the mean for short times and slower for long-times. In this case the long-time asymptote will bias the result towards a slower apparent diffusion coefficient corresponding to the largest particles present in an appreciable amount. The solution to the diffusion equation will have a smoother curvature which will be similar to the nonlinear isotherm with concentration dependent diffusion coefficients. Therefore it is not possible to distinguish the two cases unless linearity is confirmed.

This problem was put on a more quantitative footing by Duncan and Möller, who showed that from a known size distribution it was possible to match accurately experimental results (Duncan and Möller 2002). Possibly a more important result of this study is the fact that under normal conditions neglecting the effect of the particle size distribution will introduce at most an error of a factor of 2 in the derived diffusivity. They also showed that the approximate approach of taking a weighted sum of the different fractions with the standard model was a slight improvement over taking the characteristic dimension defined by the average surface to volume ratio (Duncan and Möller 2002). Both can be applied if the particle size distribution is known.

3.7 Weakly adsorbed component or kinetics too slow

This case is related to the information that is present in the ZLC desorption curve, which should be always compared to the response of the blank system. For example, if the kinetics of the system are too slow values of the parameter $L>1000$ can be obtained and the signal of the ZLC will drop very rapidly to a region that is too close to the blank response for a reliable measurement.

Similar constraints apply to weakly adsorbed components. An industrially relevant case is adsorption of N₂ on commercial powders of zeolite 4A which can be used in kinetic air separation processes to produce N₂. Because of the small size of commercial crystals this system is fast and the Henry law constant is relatively small (< 50) near ambient temperature.

Figure 17, shows the ZLC desorption curve at 0 °C. Even below room temperature the curve overlaps the blank response of the system before the long-time asymptote becomes evident, preventing the use of the normal methods to extract meaningful kinetic information. Note that there is sufficient information in the data to obtain the amount adsorbed and as a result the Henry law constant.

Fig. 17

Experimental ZLC curves of 5% N₂ in 4A crystals at 0 °C with corresponding blank response curve

From Fig. 17 it is not possible to tell if the system is too fast or too slow, but the same steps that increase sensitivity will reduce the value of the parameter $L$. This can be achieved by adjusting the experimental conditions, acting on: (a) the flowrate, $F$; (b) the Henry’s law constant, $K$; (c) the volume of the sample, ${V}_{s}$.

From the experimental point of view, lowering the flowrate is, in the majority of cases, the easiest option, but checks should be carried out to ensure that the system remains in the kinetic regime. In order to increase $K$, the only option is to decrease the operating temperature. This, in turn, has also the effect of slowing the system, therefore the net effect of the temperature on $L$ is generally compensated by the temperature dependence of the diffusivity. As a final attempt to improve the quality of the signal, one can act on ${V}_{s}$ by maximising the amount of sample in the column, while checking that the system remains a zero-length column.

3.8 Leak in valve(s)

Over time a rotary valve, especially if exposed to many high temperature cycles, will develop a leak. The same applies to standard on–off valves. A model for this case was developed for a liquid ZLC study (Cherntongchai and Brandani 2003). For mild leak rates the blank response in this case has the same qualitative shape as a normal ZLC curve including the dependence on flowrate, as long as the flowrate is not too high relative to the leak. Figure 18 shows the shape of blank curves in the presence of a leak.

Fig. 18

Blank ZLC responses as a function of flowrate with a leak in a channel of length ${l}_{Ch}$ and volume ${V}_{Ch}$, adapted from (Cherntongchai and Brandani 2003) with permission

The presence of an inflection is very similar to the nonisothermal model, but when the flowrate is high a very strange response is observed: the concentration passes through a minimum and a maximum. This can be understood considering that with a leak there is always a small open channel between the two sides of the ZLC lines. There is no net flow if the pressures are balanced and therefore the leak is due to a diffusive flux. At the start of the experiment the leak is from a high concentration to the pure carrier side. When the valve is switched the concentration profile has to invert, because in addition to the desorbing molecules there will be molecules diffusing through the leak. There is an initial period when the gradient inside the small open channel has to change sign, therefore it is possible at high flowrates to reach a minimum followed by a maximum for sufficiently high leak rates. As the deterioration of the valve progresses at a given flowrate there will be a transition from a normal ZLC curve, to one with an inflection to one with a min/max. It is always useful to keep a series of blank responses of the apparatus and periodically check that the system is still operating without a leak.

3.9 Incorrect use of full curve fitting

When used well a numerical regression of the dynamic model to match the data and obtain the physical parameters is recommended. This does not mean a straightforward least-square fit of the parameters using a regression algorithm. It is necessary to understand which parts of the dimensionless curve contain the information on the mass transport process. A normal unweighted least square fit will give more importance to the initial part of the curve (largest values), which is influenced by the accumulation in the fluid phase, the nonlinearity of the isotherm and the effect of a distribution of particle sizes. The part of the curve that contains the information on the diffusion process is the intermediate part and the final exponential decay. When $L>20$ this part of the curve has the lowest weight in a standard unweighted least square fit, and the estimated diffusion coefficient from a full curve fit can be worse than that obtained from the match of the long-time asymptote, see for example Han et al. (1999). The simultaneous fit of multiple runs at different flowrates should be carried out to avoid interpreting an equilibrium controlled system incorrectly (Brandani et al. 2004, 1995b). This is recommended when $L<10$ for all flowrates because in this region the slope of the long-time asymptote is flowrate dependent.

Loos et al. (2000) used a very complex model to fit ZLC experiments for benzene and ethylbenzene in silicalite. The model was a complicated combination of the analytical solution for the isothermal system with an additional empirical double exponential to take into account system effects. Furthermore, 10 different particle sizes were used and the model included a weighted summation of each particle size. Considering that the blank experiment for ethylbenzene was at 0.001 after 60 s for the lowest flowrate, and that the corresponding desorption experiment reached the same value after 3000 s, it should be clear that for this system the blank correction should be negligible. Before adopting a very complex model, a comparison of the curves with the standard model should have been included, because in a ZLC many effects are averaged and therefore the simple model will often match 90 +% of the characteristic response. An important and more general point though is the fact that at lower temperatures the system was nonlinear and experiments at different concentrations and with different carrier gases were not performed. If a complex model is to be used this should be accompanied with additional experiments to produce enough information to be able to quantify all the parameters. Particularly useful for this are partial loading experiments and low flowrate experiments used to determine the adsorption isotherm independently.

The simple long-time asymptote analysis provides an estimate of the diffusivity that is normally within ± 20% of the expected value, and the uncertainty can be reduced if a partial loading experiment is included. For a more accurate match of the model to the data full curve fits can be used, but if linearity of the system is not confirmed it does not make much sense to do this using the analytical solution to the model equations. Friedrich et al. (2015) have demonstrated the use of a numerical approach for CO₂ adsorption on 13X beads. The ZLC apparatus is modelled as a short 1-D column, including the response of the detector and the mass balance of the carrier. The response of the detector is determined from blank experiments. Treating the system as a binary mixture makes it possible to obtain a very accurate match of the equilibrium and kinetic properties even when the carrier is also adsorbed. This study matched simultaneously curves under nonlinear conditions for different flowrates and He and N₂ as the carrier gas. Figure 19 shows the accuracy obtained with a dual-site Langmuir isotherm and macropore diffusion control. Note that the blank response is also included and shows that for CO₂ on 13X beads, system effects are minor.

Fig. 19

Simultaneous full curve fits for 2 flowrates and 2 temperatures. From (Friedrich et al. 2015) with permission

The full fits (Friedrich et al. 2015) were consistent with kinetic parameters determined from the analysis of the long-time asymptotes (Hu et al. 2014). Note that the main advantage of this approach is the automation of the analysis of the ZLC curves. To start an automated regression one needs an initial estimate of the parameters, which can be obtained from the moments of the ZLC curves calculated with increased accuracy using the analytical expression for the long-time asymptote (Brandani and Ruthven 1996a).

3.10 Range of applications

To provide an overview of the wide range of applications and adaptations of the ZLC technique over the years we have summarised in Tables 1, 2, 3, 4 all the relevant experimental ZLC studies to date. In each table the list provided is ordered chronologically and includes the details of the systems studied (adsorbent/adsorbate) as well as the technique and the kinetic or equilibrium model used. As a general point, it was surprising to see how few papers implemented basic experimental checks and almost none included $Ft$ plots or partial loading experiments.

Table 1 Experimental ZLC studies on crystalline and/or powder materials

Table 2 Experimental ZLC studies on pellet and/or structured materials

Table 3 Experimental ZLC equilibrium studies

Table 4 Experimental liquid ZLC studies

The vast majority of studies over the past 30 years looked at gas transport kinetics on a variety of systems. Table 1 summarises the studies of mass transport in powders and crystals, showing the wide range of conditions where the original ZLC technique can be used. The majority of studies are on single component measurements.

Table 2 includes all the studies on gas systems for pelletized or more generally structured materials. This second category shows that the ZLC is well established as a technique for mass transport kinetics, particularly for strongly adsorbed components.

Table 3 lists the experimental studies on equilibrium measurements. These include the application of the ZLC as a tool for rapid screening and direct comparison of materials. In this case a quick comparison among novel materials can be made based on the uptake at conditions relevant to the real process. This requires calculating the amount adsorbed applying the mass balance in Eq. 5, regardless of the kinetic/equilibrium regime. When an isotherm is used to fit the equilibrium data, the isotherm model is detailed in the “Technique/model” column.

Experimental studies on liquid systems are listed in Table 4. We have not included papers that refer to the experimental setups as liquid ZLC systems, see for example (Babić et al. 2008; Wegmann et al. 2011), when these are in fact batch adsorption experiments where a short bed is placed in a liquid circulation loop. The relatively small number of systems included points to the difficulty in achieving good results in liquid systems. This is in part due to the lower sensitivity of liquid phase detectors and in part to the smaller equilibrium constants in liquid phase, which place an increased emphasis on understanding well the blank response before attempting to interpret kinetic measurements.

Variants of the ZLC which do not fall in the categories above have been collected in Table 5. There are unconventional systems that measure the adsorbed phase concentration (Banas et al. 2005) and concentration-swing frequency response experiments where the sample masses are around 10 mg or below (Wang and LeVan 2008; Glover et al. 2008). These are particularly interesting because they demonstrate the potential to measure also transport diffusivities at different concentration levels using a carrier flowrate that oscillates in time.

Table 5 Additional experimental ZLC applications and/or variants

In Table 5 we have also included the use of the ZLC in testing the stability of novel materials (Mangano et al. 2016; Hu et al. 2018). In this case, ZLC experiments are carried out before and after exposing the sample to impurities and regenerating the material. Repeating the process in a sequence, the effect on equilibrium and kinetics can be observed. What makes this approach particularly useful is the reduced sample mass required, which means that even with a relatively small flowrate, the sample can be exposed in just a few hours to the volume of gas per mass equivalent to weeks or months of large scale test facilities. The overall result is an acceleration of the degradation process that provides information in a few days.

A more extended version of the information included in Tables 1, 2, 3, 4 and 5 is provided in the supplementary information.

In the remaining sections we discuss briefly the models used for pellets and beads in greater detail; the use of the ZLC to determine the diffusion path; the case of combined surface barrier and diffusion; and show an example of ZLC curves when the adsorbent undergoes structural changes.

3.11 Beads and pellets

Xu and Ruthven carried out the first ZLC study on mass transport of N₂ and O₂ in commercial pellets of zeolite 5A (Ruthven and Xu 1993). They used a GC that could spray liquid nitrogen to control the oven temperature down to 174 K to slow down the system and increase the adsorbed amount. They also measured the diffusivities in large crystals of 5A and showed that the system was macropore diffusion controlled.

To understand how this regime is obtained we need to consider the mass balance in a biporous material

$$\varepsilon_{P} \frac{{\partial c_{P} }}{\partial t} + \left( {1 - \varepsilon_{P} } \right)\frac{{\partial \bar{q}}}{\partial t} = \frac{{\varepsilon_{P} }}{\tau }\frac{{D_{P} }}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{{\partial c_{P} }}{\partial r}} \right)$$

(15)

where ${c}_{P}$ is the concentration in the macropores and $\bar{q}$ is the concentration in the adsorbed phase. ${\varepsilon }_{P}$ is the porosity and $\tau$ the tortuosity. When diffusion inside the crystals is fast compared to the diffusion in the bed of particles

$$\frac{{\partial \bar{q}}}{\partial t} = \frac{{dq^{*} }}{{dc_{P} }}\frac{{\partial c_{P} }}{\partial t}$$

(16)

where ${q}^{*}$ is the adsorbed phase concentration at equilibrium with ${c}_{P}$ and Eq. 15 reduces to the diffusion equation with an effective pore diffusivity

$$\frac{{\partial c_{P} }}{\partial t} = \frac{{\varepsilon_{P} }}{\tau }\frac{{D_{P} }}{{\varepsilon_{P} + \left( {1 - \varepsilon_{P} } \right)\frac{{dq^{*} }}{{dc_{P} }}}}\frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{{\partial c_{P} }}{\partial r}} \right)\quad {\text{with }}\,D_{P}^{E} = \frac{{\varepsilon_{P} }}{\tau }\frac{{D_{P} }}{{\varepsilon_{P} + \left( {1 - \varepsilon_{P} } \right)\frac{{dq^{*} }}{{dc_{P} }}}}$$

(17)

For a dilute system $\frac{d{q}^{*}}{d{c}_{P}}={K}_{c}$ and the solution of the model for the ZLC remains the same but the macropore diffusion control parameters become

$$\gamma_{M} = \frac{1}{3}\frac{{V_{F} }}{{\left[ {\varepsilon_{P} + \left( {1 - \varepsilon_{P} } \right)K_{c} } \right]V_{S} }}\quad L_{M} = \frac{1}{3}\frac{F}{{V_{S} }}\frac{{R_{P}^{2} }}{{\frac{{\varepsilon_{P} }}{\tau }D_{P} }}$$

(18)

One interesting difference is that unless the pore diffusivity includes surface diffusion, the parameter ${L}_{M}$ is now only very mildly dependent on temperature and experiments at different temperatures will have similar long-time asymptote intercepts, with the corresponding slopes increasing in magnitude as the temperature increases.

To identify which mass transport mechanism is controlling the desorption rate, it is necessary to compare the diffusion time constant of the crystals $\frac{{R}_{c}^{2}}{{D}_{c}}$ and the effective pellet time constant $\frac{\tau }{{\varepsilon }_{P}}\frac{{R}_{P}^{2}}{{D}_{P}}\left[{\varepsilon }_{P}+\left(1-{\varepsilon }_{P}\right){K}_{c}\right]$. As a simple order of magnitude guide for a typical 1 mm equivalent radius of the pellet $\frac{\tau }{{\varepsilon }_{P}}\approx 10$, $\frac{{R}_{P}^{2}}{{D}_{P}}\approx 10$ s, ${\varepsilon }_{P}\approx 0.25$ and ${K}_{c}$ can vary from 10² to 10⁶. This means that a pellet with crystals that have ${R}_{c}=1$ µm will be micropore diffusion limited only when $D_{c} < 10^{{ - 16}}$ to 10⁻²⁰ m² s^–1.

Experiments with different pellet sizes and with different carriers should be performed to confirm macro- or micro-pore diffusion control.

This order of magnitude analysis shows clearly that particle aggregation can lead to very low apparent diffusivities and given that the pellet size in this case cannot be changed, it is essential to perform experiments with different carrier gases, especially for strongly adsorbed components.

Normally only one resistance dominates, but when the two diffusion time constants are similar both resistances have to be considered. In this case the analytical solution for the ZLC with a biporous material is available (Brandani 1996), but has double infinite summations and it can be computationally easier and faster to invert numerically the solution in the Laplace domain using the approach of Duncan and Möller for the model with a distribution of particle sizes (Duncan and Möller 2002), or similar numerically efficient schemes (Cohen 2007; Brandani et al. 2020).

3.12 Distinguishing the diffusion path

To estimate the diffusion time constant it is normal to use the solution to the diffusion equation for a sphere and define the characteristic dimension that gives the same surface to volume ratio of the particle. There are however some distinct differences between the solution for a sphere and a slab geometry. These have been used to determine the diffusion path in nanoporous materials (Vidoni and Ruthven 2012a; Cavalcante et al. 1997; Lima et al. 2008; Huang et al. 2010).

The solution for a slab with negligible accumulation in the fluid phase, $\gamma =0$, is given by

$$\frac{c}{{c_{0} }} = \mathop \sum \limits_{n} \frac{{2L_{s} \exp \left( { - \beta_{n}^{2} \frac{D}{{\lambda_{P}^{2} }}t} \right)}}{{\beta_{n}^{2} + \left( {L_{s} - 1} \right)L_{s} }}$$

(19)

with

$$\beta_{n} \tan \beta_{n} - L_{s} = 0\quad {\text{with}}\,L_{s} = \frac{F}{{KV_{S} }}\frac{{\lambda_{P}^{2} }}{{D_{P} }}$$

(19a)

where ${\lambda }_{P}$ is the half-thickness of the slab.

Qualitatively this is similar to Eq. 8, but on closer inspection the intermediate-time behaviour is different (Brandani and Ruthven 1996b; Hufton and Ruthven 1993). To use this property the system has to be relatively slow, linearity should be confirmed, the parameter $L$ should be greater than 10 but not too high, and a narrow particle size distribution is needed. When these conditions are met the two geometries will give the following approximate responses valid for $\frac{c}{{c}_{0}}<0.2$

$$\frac{c}{{c_{0} }} = \frac{1}{{L_{s} }}\sqrt {\frac{{\lambda_{P}^{2} }}{{\pi D_{P} t}}} \quad {\text{slab}}$$

(20a)

$$\frac{c}{{c_{0} }} = \frac{1}{L}\left( {\sqrt {\frac{{R_{P}^{2} }}{{\pi D_{P} t}}} - 1} \right)\quad {\text{sphere}}$$

(20b)

Cavalcante (Cavalcante et al. 1997) was the first to observe that when plotting $\frac{c}{{c}_{0}}$ vs $\sqrt {\frac{1}{t}}$ for a pure offretite sample resulted in an intercept through the origin, indicating a 1-D diffusion path consistent with the structure of this zeolite, while erionite-rich samples showed a negative intercept consistent with a 3-D diffusion path and the structure of offretite-erionite intergrowths. From Eq. 20b it is clear that $L$ should not be too large to be able to differentiate the two geometries.

Note that while the conditions needed to apply this test may appear somewhat restrictive, the property should not depend on the molecule used, therefore it is possible to test different probes and find one for which the system meets the criteria.

3.13 Combined diffusion and surface barriers

Figure 20 shows an example of the ZLC response curve for $\gamma =0.05$ with pure diffusion and pure surface barrier when the long-time asymptote is the same. The two models are qualitatively similar but the diffusion model has more time constants and therefore has a smoother transition from the initial exponential to the final long-time asymptote. The intermediate region is therefore the part that is more sensitive to the difference and is reflected also in a difference in the higher moments of the response curve (Brandani and Ruthven 1996a).

Fig. 20

Pure diffusion vs pure surface barrier with the same long-time asymptote. $L=20.$

The general solution to the ZLC model with both surface barriers and internal diffusion has the same structure as Eq. 8, ie

$$\frac{c}{{c_{0} }} = \mathop \sum \limits_{n} ak_{n} \exp \left( { - \beta_{n}^{2} \frac{D}{{R_{P}^{2} }}t} \right)$$

(21)

$$ak_{n} = \frac{{2L\delta_{k}^{2} }}{{2\gamma \delta_{k}^{2} \beta_{n}^{2} + \left[ {\delta_{k} - \left( {\delta_{k} - 1} \right)\left( {L - \gamma \beta_{n}^{2} } \right)} \right]^{2} + \left( {L + \delta_{k} - \gamma \beta_{n}^{2} } \right)^{2} \beta_{n}^{2} - \left( {L + \delta_{k} - \gamma \beta_{n}^{2} } \right)\left[ {\delta_{k} - \left( {\delta_{k} - 1} \right)\left( {L - \gamma \beta_{n}^{2} } \right)} \right]}}$$

(21a)

where

$$\delta_{k} = \frac{{kR_{P} }}{{D_{P} }}\quad {\text{with}}\,\beta_{n} cot\beta_{n} + \frac{{\left( {\delta_{k} - 1} \right)\left( {L - \gamma \beta_{n}^{2} } \right) - \delta_{k} }}{{L + \delta_{k} - \gamma \beta_{n}^{2} }} = 0$$

(21b)

and the surface barrier coefficient $k$ is defined from the mass balance of the solid

$$\frac{{d\bar{q}}}{dt} = ka\left( {Kc - q_{{r = R_{P} }} } \right)$$

(22)

where $a$ is the surface to volume ratio.

Note that there is an extra root in the interval where $L+{\delta }_{k}-\gamma {\beta }_{n}^{2}=0$.

In the limit of pure diffusion, as ${\delta }_{k}\to \infty$, Eq. 8 is recovered.

In the limit of pure surface barrier the model of Ruthven and Stapleton, which corresponds to only two roots, is recovered (Ruthven and Stapleton 1993)

$$\beta_{1,2}^{2} = \frac{{\left( {L_{k} + 1 + 3\gamma } \right) \pm \sqrt {\left( {L_{k} + 1 + 3\gamma } \right)^{2} - 12\gamma L_{k} } }}{6\gamma }\delta_{k} \quad {\text{with}}\quad L_{k} = \frac{1}{3}\frac{F}{{KV_{S} }}\frac{{R_{P} }}{k}$$

(23)

and

$$ak_{1,2} = \frac{{L_{k} \left( {\delta_{k} - \beta_{1,2}^{2} } \right)}}{{L_{k} + 1 + 3\gamma - 6\frac{\gamma }{{\delta_{k} }}\beta_{1,2}^{2} }}\frac{1}{{\beta_{1,2}^{2} }}$$

(23a)

When the accumulation in the fluid phase is negligible, $\gamma =0$, Eq. 21 reduces to the solution obtained by Duncan and Möller (Duncan and Möller 2005). This solution has a similar structure to the pure diffusion case, Eq. 8, with the parameter $L$ replaced by ${L}_{kD}$ defined as

$$\frac{1}{{L_{kD} }} = \frac{1}{L} + \frac{1}{{\delta_{k} }}$$

(24)

The fluid phase concentration has a discontinuity at time zero, therefore Eq. 8 needs to be pre-multiplied by $\frac{{L}_{kD}}{L}<1$. Only with the accumulation in the fluid phase, Eq. 21, $\frac{c}{{c}_{0}}$ starts from 1. What is continuous is the adsorbed phase concentration, which is given by Eq. 8b with $L$ replaced by ${L}_{kD}$. This is the main reason for which Eq. 21 should be used as it corresponds to the actual response of the system, which is always continuous.

Note that the use of the standard solution with $L$ replaced by ${L}_{kD}$ in the case of $\gamma >0$ (Teixeira et al. 2013) is not correct.

Duncan and Möller (2005) commented on the fact that as the flowrate increases ${L}_{kD}\to {\delta }_{k}$ and the intercept of the long-time asymptote becomes

$$\frac{{2L_{kD} }}{{\beta_{1}^{2} + L_{kD} \left( {L_{kD} - 1} \right)}}\frac{{L_{kD} }}{L} \approx \frac{{\delta_{k}^{2} }}{{\beta_{1}^{2} + \delta_{k} \left( {\delta_{k} - 1} \right)}}\frac{2}{L}$$

(25)

At high flowrates, or more correctly at high values of the $L$ parameter, this deviates from $\frac{2}{L}$ by a constant factor, dependent on ${\delta }_{k}$. Duncan and Möller (2005) concluded that it would be unlikely that favourable conditions could be found where the flowrate dependence of the intercept could be used to decouple ${\delta }_{k}$ and $L$.

Ruthven and Vidoni (Vidoni and Ruthven 2012b; Ruthven and Vidoni 2012) used an approximate solution to the problem, without the pre-multiplier $\frac{{L}_{kD}}{L}$, but they obtained ${L}_{kD}$ from the long-time asymptote and the intermediate-time approximation using Eq. 20b with $L$ replaced by ${L}_{kD}$. They showed that it was possible to use the flowrate dependence of Eq. 24 to obtain reliable values of the ratio of the mass transport time constants, ${\delta }_{k}$. The conditions of the experiments (Vidoni and Ruthven 2012b; Ruthven and Vidoni 2012) with small hydrocarbons in DD3R zeolite where such that ${\delta }_{k}>150$, therefore $L\sim {L}_{kD}$ or $\frac{{L}_{kD}}{L}\approx 1$; values of $L$ where in the correct range for accurate asymptotes to be determined; large crystals with a narrow size distribution were used and the isotherm was linear, therefore the intermediate time analysis would provide accurate results. Under more general conditions, if the pre-multiplier is correctly included, what is actually obtained from the long-time asymptote is a complex function, Eq. 25, not ${L}_{kD}$. The intermediate-time analysis would appear to yield $L$ from the intercept, but given the approximate nature of this analysis it is possible that the method yields values that are closer to ${L}_{kD}$. This probably points to the fact that the methodology of Ruthven and Vidoni (2012) is applicable only to mild surface resistances and that Duncan and Möller (2005) may have not considered this particular set of very favourable conditions.

More recent studies, have applied the methodology of Ruthven and Vidoni (2012) without realising its approximate nature, requiring $\frac{{L}_{kD}}{L}\approx 1$, using it in systems where the $\frac{{L}_{kD}}{L}$ was as low as 0.32 (Gelles et al. 2020). For this reason, when investigating combined surface barrier and diffusion, we recommend the use of the partial loading experiment, because this requires only $L>10$. By comparing the adsorbed phase responses it provides an immediate indication of pure surface barrier control and if the solution to the pure diffusion model is plotted it is possible to see directly whether a combined model is needed. Figure 21 shows an example of a zeolite that has been etched for a short time (Qin et al. 2017), which has a response for both the fully equilibrated and the partial loading curve that is always between the pure surface barrier and the pure diffusion cases. Here a combined model can be applied to obtain meaningful parameters.

Fig. 21

Full and partial loading adsorbed phase curves for mesitylene on etched NaY crystals at 280 °C. Lines are predictions from the pure diffusion and surface barrier models

There is an increased tendency to assume that the combined model should be used even when only one resistance dominates, see for example some recent measurements on zeolite 5A and carbon molecular sieves which were essentially pure diffusion and pure surface barrier cases, respectively (Shirani et al. 2020). We recommend that one always starts with the single resistance models (Eqs. 8 and 23) and progresses to the combined model only when needed, otherwise parameters can be generated that are meaningless for the resistance that is not controlling. The system shown in Fig. 21 is an example where the data have sufficient deviation from the simple models and can be used to determine also the additional parameter represented by the ratio of the time constant for the diffusion and surface barrier processes.

3.14 Systems with structural changes due to adsorption

The advances in the ZLC technique have often been pushed by the development of novel and more complex materials, which have in turn required the use of wider operating conditions, more sophisticated models, and upgraded instrumentation. In recent years, a class of adsorbents which undergo structural changes during the adsorption process has attracted the attention of both academia and industry for their potential as next generation adsorbents. While this behaviour is typically associated with MOF adsorbents (Remy et al. 2011; Zhao et al. 2016; Serre et al. 2002), which are characterised by intrinsically flexible structures, a growing number of zeolite species have shown evidence of structural transition(Palomino et al. 2012; Lozinska et al. 2014; Greenaway et al. 2015; Li te al. 2017). In most cases structural modifications are triggered by a specific adsorbate concentration, but cases of temperature and pressure induced transitions have also been reported (Li et al. 2017). Structural changes can manifest in number of ways including change of the cage volume, breathing (Barthelet et al. 2002) and gate opening (Lozinska et al. 2012; Georgieva et al. 2019). The possibility of triggering a controlled change in the kinetic and/or equilibrium selectivity opens a range of unexplored opportunities both from the materials and processes point of view. Research in this field is still in its earliest stages and in many cases the mechanisms of modifications are yet to be fully understood. This sets a number of new, nontrivial, challenges in terms of experimental characterisation, transport and equilibrium modelling as well as process simulation. Cation-exchanged Rho are the most commonly reported example of zeolites with a flexible structure which undergo structural change during adsorption. Figure 22 shows an example of experimental ZLC desorption curves of CO₂ in Na-Rho crystals, complete with the standard model prediction.

Fig. 22

ZLC full and partial loading curves for Na-Rho at a 10% CO₂ and b 1% CO₂. Lines are model predictions. From (Lozinska et al. 2012) with permission

At a first glance, it is clear that the model provides an excellent match of the partial loading experiment and the long-time asymptote of the full loading, but fails to predict the shape of the full loading curve in the short time. The prediction of the partial loading confirms that the time constant of the process is correct, but the shape of the curve indicates the presence of an additional mechanism. The mismatch between the diffusion model and the fully equilibrated curve shows that the model underestimates significantly the CO₂ transport in the high concentration region. In addition, a careful observation of the experimental desorption curves shows a clear difference in shape between the full and partial loading responses which cannot be simply ascribed to a nonlinearity effect. The presence of structural change was confirmed by in-situ XRD measurements of CO₂ adsorption showing the transition to a structure with larger window opening at partial pressures of CO₂ higher than 0.1 bar (Lozinska et al. 2012). As a result, CO₂ desorbs faster in the high concentration region and gradually slows down as the configuration changes to smaller windows. Figure 22b shows the ZLC desorption curve for CO₂ at 1%, where the model now matches the data in the full range of concentrations because the entire curve is at concentrations lower than those needed to trigger the structural transition. This is also consistent with the very good match of the partial loading curve, which is also below the transition region given that the average adsorbed phase concentration, ${\bar{q}}_{s},$ in the partial loading experiment is approximately one 10th of the fully equilibrated experiment.

The example shows that kinetic studies, coupled with advanced characterisation techniques, can provide essential pieces of information to gain a better understanding of the underlying mechanism of structural transition of these materials. A deeper insight would require, for example, more sophisticated models which include the kinetics of the configurational change and that could be linked to real physical parameters. This definitely represents one of the areas that will require further investigation to tackle the challenges set by the growing number of materials with unusual behaviours.

4 Recommendations

We conclude our discussion with a series of recommendations based on our cumulative experience of thousands of ZLC experiments. The aim is to allow more groups to use the ZLC technique accurately and efficiently and avoid incorrect interpretations of the dynamic responses.

4.1 Equilibrium measurements

When measuring full equilibrium isotherms it is important to produce curves at different flowrates and show that these coincide in the $Ft$ plot.

The curves on the $Ft$ plot should be compared with the blank response to show whether a more detailed analysis (Friedrich et al. 2015) is needed.

Experiments with at least two different sample sizes should be used to confirm zero-length behaviour.

With hydrophilic adsorbents it is important to check for reproducibility by replicating the first experiment of the day at the end of the sequence of experiments. When it is possible to monitor the water composition, a check should be made during regeneration or a TPD added at the end of the sequence of experiments.

4.2 Kinetic measurements

Always run experiments with different carrier gases. This is the one experimental check that can avoid major errors in the interpretation of the kinetic experiments.

Only for weakly adsorbed components it may not be possible to find a second inert carrier in addition to helium, when hydrogen is not available.

Experimental conditions should be adjusted to achieve where possible values of the $L$ parameter between 10 and 50. This should include varying the sample mass to confirm also zero-length behaviour.

Curves at different flowrates (at least 2) and partial loading experiments should be used to identify unambiguously the kinetic time constant.

An $Ft$ plot should be included to show that the responses are in the kinetic regime and are consistent. The blank responses should be shown on this plot to confirm that there is sufficient information to analyse the curves, particularly for weakly adsorbed components.

Check for linearity by performing experiments at different initial concentrations.

When more complex models are adopted, the experimental campaign should be designed to maximise the information required to determine additional parameters. As examples:

• If a nonlinear isotherm is used, experiments at low flowrates should be used to determine independently the isotherm parameters.

• If a combined surface resistance and diffusion model is adopted, the partial loading experiments should be used and a plot of the reduced adsorbed phase concentration should be compared to the pure diffusion and pure surface barrier model to confirm that an additional kinetic parameter can be determined, see Fig. 21.

• When studying multicomponent systems, pure component experiments should be used in conjunction with a consistent model that reduces to the pure component values. Ideally one should start with predictions of the multicomponent response to determine if additional mixture parameters are needed.

• When including the effect of particle size distributions, experiments with different adsorbates should be carried out to confirm that results are invariant with respect to the probe molecule and linearity must be checked.