1 Introduction

After the discovery of superconductivity, considerable attempts have been done to understand the different aspects of this phenomenon [1]. The most successful way to describe the superconductivity within a microscopic theory was proposed by Bardeen, Cooper and Schrieffer (BCS), who could address the superconductivity as a microscopic effect that originates from the condensation of Cooper pairs into a boson-like state [2]. However, it was not suitable to declare this effect completely. More specifically, it is only practical for s-wave superconductors, while there are other types of superconductors such as p-waves and d-waves [3, 4]. Besides, the BCS theory cannot explain the mechanism of high temperature superconductors, because the Cooper pairs are decoupled and no longer exist when the temperature of the system becomes high [4]. By applying the AdS/CFT correspondence, which relates the strong coupling conformal field theory on the boundary in d-dimensions to a weak coupling gravity in \((d+1)\)-dimensional bulk, the novel idea of holographic superconductors was proposed by Hartnoll et al. [5, 6]. The holographic superconductors opened up a new window for studying all kinds of superconductors. Based on this idea, the system undergoes spontaneous U(1) symmetry breaking during a phase transition from a black hole with no hair (normal phase) to a hairy one (superconducting phase) below the critical temperature [7]. The holographic superconductors have many properties similar to real world superconductors such as a second order phase transition at the critical temperature. One of the most important successes of holographic superconductors is that all these models show exact mean-field behaviors at the critical temperature, just like the Landau–Gindzburg (LG) theory for continuous phase transitions. All the critical exponents for the order parameter at \(T_\mathrm{{c}} \) are equal to 1/2 [6]. Nevertheless, the idea of a holographic superconductor is a theoretical attempt for addressing the puzzle of high temperature superconductivity and the experimental features of this idea are still an open problem. In the past decade, holographic superconductors gained a lot of attention (see e.g. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]). While the p-wave and d-wave superconductors are are known as strong coupling superconductors, the investigations on them based on the holographic setup has attracted a lot of attention during the past years (see e.g. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]). There are different ways to investigate the properties of holographic p-wave superconductors, including condensation of a real or complex massive charged vector field on the gravity side which is dual to the vector order parameter in the boundary as well as introducing a 2-form field or a SU(2) Yang–Mills gauge field in the bulk as the origin of a spin-1 order parameter [38,39,40,41,42]. The impact of the Gauss–Bonnet term on the holographic p-wave superconductor is characterized in different references [53,54,55]. Moreover, in the framework of condensed matter physics, dynamical scaling appears near the critical point. In the vicinity of the critical point, the scale transformation turns out to be [56]

$$\begin{aligned} t \rightarrow \lambda ^{z} t, \ \ x_{i} \rightarrow \lambda x_{i}, \ \ z\ne 0; \end{aligned}$$
(1)

when \(z=1\), the usual AdS spacetime is obtained. Otherwise, the temporal and the spatial coordinates scale anisotropically. Many investigations have been done regarding anisotropic superconductors [57]. Nowadays, the application of superconductors is not limited to physics. However, the actual use of superconducting devices is limited due to the fact that they must be cooled to low temperatures to become superconductors and hence cannot be used for ordinary (lab) temperatures. So in recent times, p-wave and d-wave superconductors as candidates for high temperature superconductors gained a lot of attention. In some cases p- wave superconductors show anisotropic behavior [3]. In addition, heavy fermion compounds and other materials including high \(T_\mathrm{{c}} \) superconductors have a metallic phase (such a metal is dubbed a strange metal), whose properties cannot be explained within ordinary Landau–Fermi liquid theory. In this phase some quantities exhibit universal behavior such as a resistivity which is linear in the temperature, \(\sigma \sim T\). Such universal properties are believed to be the consequence of quantum criticality. At the quantum critical point there is a Lifshitz scaling – the same as in Eq. (1) [58]. Much research was carried out in Lifshitz scaling by using the holographic approach (see e.g. [59,60,61,62]). However, all the previous work about the effects of Lifshitz scaling on holographic p-wave superconductor was done by considering a SU(2) Yang–Mills gauge field in the bulk in the presence of Maxwell electrodynamics [56, 59]. In this work, we have explored the effects of Lifshitz scaling on holographic p-wave superconductor by introducing a charged vector field in the bulk. As a consequence of this method all following calculations to analyze the behavior of condensation and conductivity became different from the previous work. However, there is good agreement between our results with the case of \(m^{2}=0\) in [59]. This approach allows us to consider the effects of the mass term and the spacetime dimension and Lifshitz scaling z, while in the previous method the mass term plays no role and is set to zero. Besides, we can study the effect of conductivity more easily by turning on only the component \(\delta A_{y}=A_{y} e^{-i \omega t}\) as a perturbation on the black hole background, to be compared to the treatment in [59]. Moreover, it is worthful to investigate this model in the presence of nonlinear electrodynamics [56, 59]. There exist several types of nonlinear electrodynamics in the literature, including Born–Infeld (BI) [63], exponential [64], logarithmic [65] and Power–Maxwell methods [13]. Among them, BI nonlinear electrodynamics is perhaps the one best known; it was proposed to address the problem of the divergence of the electrical field at the position of a point particle. It was later pointed out that the BI Lagrangian could be reproduced through string theory, and its action naturally possesses electric–magnetic duality invariance, which makes it suitable for describing gauge fields arising from open strings on D-branes [37, 50, 63, 64]. Disclosing the effects of the nonlinear electrodynamics on the behavior of superconductors is of interest both for practical applications and for the study of the fundamental properties of the materials. In any practical electronic application, the designer must know how much power the conductors can handle and at which power level nonlinear effects, such as harmonic generation and intermodulation (IM) distortion, become appreciable. Therefore, the magnitude and the detailed nature of the nonlinear effects must be measured and understood in order to facilitate widespread application of superconductors in microwave frequency electronics. The effects of nonlinear electrodynamics were widely studied in the literature (see e.g. [66,67,68,69,70,71]). Although these investigations extend over many years, new interest in these nonlinear effects has been kindled since the discovery of the high-T oxide materials [71]. Therefore, it is worthwhile to provide a theoretical approach for the prediction of the behavior of real high temperature superconductors in the presence of nonlinear electrodynamics based on the holographic approach. For example we find that by increasing the effect of nonlinearity, the critical temperature decreases. The effects of nonlinear electrodynamics on holographic superconductors have been explored widely in the literature (see e.g. [13, 30,31,32,33,34,35,36,37, 50]).

Our aim in this work is to investigate the effects of Lifshitz scaling on the holographic p-wave superconductor in arbitrary dimensions. We shall study the phase transition between conductor and superconductor, which depends crucially on the parameters m, b and z. In spite of the fact that there is a dynamical exponent, we find that the condensation shows a mean-field behavior near the critical temperature, which is the same as AdS spacetime. Additionally, electrical conductivity in the gauge/gravity correspondence is achieved by imposing an appropriate perturbation on the gauge field. Besides the conductivity formula, we calculate the behavior of the real and imaginary parts of conductivity as a function of the frequency. Although there are obvious differences in graphs based on our choice of m, b and z, they follow the same trends in some cases. A good illustration of this is obeying the Kramers–Kronig relation by having a delta function and a pole in the real and imaginary parts of conductivity. However, the gap frequency which occurred below the critical temperature, becomes less obvious by enlarging the anisotropy between space and time. The effects of nonlinearity parameter on the conductivity will be clearly indicated via graphs. Our choice of the mass in each dimension has a direct outcome on the effect of BI nonlinear electrodynamics on the conductivity but generally the gap energy and minimum of conductivity shift toward larger values of the frequency by enlarging the nonlinearity effects.

This article is organized as follows. In Sect. 2, we analyze the holographic setup via condensation of the vector field in the context of Lifshitz spacetime and in the presence of nonlinear BI electrodynamics. We explore the electrical conductivity of this model in Sect. 3. Finally, our results are summarized in Sect. 4.

2 Holographic p-wave superconductors with Lifshitz scaling

We consider a \((d+1)\)-dimensional holographic p-wave superconductor living on the boundary of a \((d+2)\)-dimensional Lifshitz black hole in the presence of BI nonlinear electrodynamics, which is described by the following action [39]:

$$\begin{aligned} S= & {} \int d^{d+2}x\sqrt{-g} \left( R-2 \Lambda +\mathcal {L}_{m}\right) , \nonumber \\ \mathcal {L}_{m}= & {} \mathcal {L}(\mathcal {F})-\frac{1}{2}\rho _{\mu \nu }^{\dagger } \rho ^{\mu \nu }-m^{2} \rho _{\mu }^{\dagger } \rho ^{\mu } + i q \gamma \rho _{\mu } \rho _{\nu }^{\dagger } F^{\mu \nu } , \end{aligned}$$
(2)

where m and q are the mass and charge of vector field \(\rho _{\mu }\). The metric determinant, the Ricci scalar and the negative cosmological constant are symbolized by g, R and \(\Lambda \), respectively. In terms of the radius of Lifshitz spacetime, l, we can formulate the cosmological constant as [59]

$$\begin{aligned} \Lambda =-\frac{(d+z-1)(d+z)}{2 l^2}, \end{aligned}$$
(3)

where z, the Lifshitz scaling, is a dynamical critical exponent standing for the anisotropy between space and time. Hereafter, for simplicity we set \(l=1\). The Lagrangian density of the BI nonlinear electrodynamics \(\mathcal {L}(\mathcal {F})\) is given by [63]

$$\begin{aligned} \mathcal {L}(\mathcal {F})=\frac{1}{b}\left( 1-\sqrt{1+\frac{b\mathcal {F}}{2}} \right) , \end{aligned}$$
(4)

where \(\mathcal {F}=F_{\mu \nu } F^{\mu \nu }\) is the Maxwell invariant and b, with dimension of \([\mathrm{{length}}]^2\), represents the strength of nonlinearity. When \(b\rightarrow 0\), \(\mathcal {L}(\mathcal {F})\) restores the standard Maxwell Lagrangian \(\mathcal {L}_\mathrm{{max}}(\mathcal {F})=-\mathcal {F}/4\). The strength of the electromagnetic field is represented by \(F_{\mu \nu }=\nabla _{\mu } A_{\nu }-\nabla _{\nu } A_{\mu }\) where \(A_{\mu }\) is the vector potential. In the Lagrangian of the matter field, \(\mathcal {L}_{m}\), by using the covariant derivative \(D_{\mu }=\nabla _{\mu }- i q A_{\mu }\), we can set \(\rho _{\mu \nu }=D_{\mu } \rho _{\nu }-D_{\nu } \rho _{\mu }\). The last term in the matter Lagrangian shows the strength of interaction between \(\rho _{\mu }\) and \(A_{\mu }\) with \(\gamma \) as the magnetic moment in the case with an applied magnetic field, which will be ignored in this work. The equations of motion, for the matter fields, can be obtained by varying the action (2) with respect to the gauge field \(A_{\mu }\) and the vector field \(\rho _{\mu }\),

$$\begin{aligned}&\nabla ^{\nu }\left[ -4 \mathcal {L}_{\mathcal {F}} F_{\nu \mu }\right] \nonumber \\&\quad =i q \left( \rho ^{\nu } \rho ^{\dagger }{}_{\nu \mu }- \rho ^{\nu \dagger } \rho _{\nu \mu }\right) + i q \gamma \nabla ^{\nu } \left( \rho _{\nu } \rho ^{\dagger }{}_{\mu }-\rho ^{\dagger }{}_{\nu } \rho _{\mu } \right) , \end{aligned}$$
(5)
$$\begin{aligned}&D ^{\nu } \rho _{\nu \mu }-m^{2} \rho _{\mu }+ i q \gamma \rho ^{\nu } F_{\nu \mu } =0, \end{aligned}$$
(6)

where \(\mathcal {L}_{\mathcal {F}}=\partial \mathcal {L(\mathcal {F})}/\partial {\mathcal {F}}\). Since we work in the probe limit, the background spacetime is not affected by the vector and gauge fields. Thus, we can write down the metric of \((d+2)\)-dimensional Lifshitz spacetime as [59]

$$\begin{aligned}&{ds}^{2}=-r^{2 z} f(r) {dt}^{2}+\frac{{dr}^{2}}{r^{2} f(r)}+r^{2} \sum _{i=1}^{d}{dx_{i}}^{2} , \end{aligned}$$
(7)
$$\begin{aligned}&f(r)=1-\frac{r_{+}^{d+z}}{r^{d+z}}, \end{aligned}$$
(8)

where \(r_{+}\) denotes the black hole horizon obeying \(f(r_{+})=0\). We also assume that the vector and gauge field has the following form:

$$\begin{aligned}&\rho _{\nu } dx^{\nu }=\rho _x(r) dx, \ \ \ \ A_{\nu } dx^{\nu }=\phi (r) dt. \end{aligned}$$
(9)

The regularity condition for the gauge field, on the horizon, implies that \(\phi (r_{+})=0\) [56]. The Hawking temperature of the black hole, associated with the horizon, is defined by [59]

$$\begin{aligned} T=\frac{f^{^{\prime }}(r_{+})}{4\pi }=\frac{(d+z) r_{+}^{z}}{4\pi }. \end{aligned}$$
(10)

Inserting Eqs. (7) and (9) in the field equations (5) and (6), we arrive at

$$\begin{aligned}&\phi ''(r)+ \left[ \frac{d-z+1}{r}-\frac{b d }{ r^{2 z-1}} \phi '^2(r)\right] \phi '(r)\nonumber \\&\quad -\frac{ 2 q^2 \rho _{x}^2(r) }{f(r) r^{4}}\left[ 1-\frac{b}{r^{2 z -2}} \phi '^2(r)\right] ^{3/2}\phi (r)=0, \end{aligned}$$
(11)
$$\begin{aligned}&\rho _x''(r)+\left[ \frac{d+z-1}{r}+\frac{f'(r)}{f(r)}\right] \rho _x'(r) \nonumber \\&\quad +\frac{\rho _x(r) }{r^2 f(r)}\left[ \frac{q^2 \phi ^2 (r)}{f(r) r^{2 z}}-m^2\right] =0, \end{aligned}$$
(12)

where the prime denotes the derivative with respect to r. The linear electrodynamic form of the above equations of motion are recovered in the limiting case where \(b\rightarrow 0\) [59]. In the remaining part of this paper, without loss of generality, we will set \(r_{+}=1\) and \(q=1\). At the boundary where \(r\rightarrow \infty \), the above equations have the asymptotic solutions

$$\begin{aligned}&\phi (r)= \left\{ \begin{array}{lr} \mu - \rho r^{z-d}+\cdots , &{} z<d\\ \mu -\rho \log (r)+\cdots , &{} z=d\\ \end{array} \right. \end{aligned}$$
(13)
$$\begin{aligned}&\rho _x(r)= \frac{\rho _{x_+}}{r^{\Delta _+}}+\frac{\rho _{x_-}}{r^{\Delta _-}}+\cdots , \ \ \ \ \Delta _\pm \nonumber \\&\quad =\frac{1}{2} \left[ (d+z-2)\pm \sqrt{(d+z-2)^2+4 m^2}\right] . \end{aligned}$$
(14)

According to the gauge/gravity duality \(\mu \), \(\rho \), \(\rho _{x_+}\) and \(\rho _{x_-}\) play, respectively, the role of the chemical potential, charge density, x-component of the vacuum expectation value of the order parameter \(\langle J_{x} \rangle \) and the source. Since we expect spontaneous U(1) symmetry breaking, we impose the source free condition i.e. \(\rho _{x_-}=0\). In addition, we follow the Breitenlohner–Freedman (BF) bound for our choice of the mass,

$$\begin{aligned} m^{2}\geqslant -\frac{(d+z-2)^2}{4}. \end{aligned}$$
(15)
Table 1 Numerical results for critical temperature \(T_\mathrm{{c}}\) for different values of z, m and b in \(D=d+2=4\) and 5 spacetime dimension
Full size table

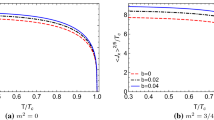
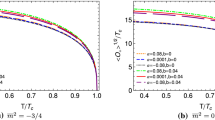
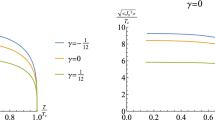
Considering the canonical ensemble with fixed \(\rho \), and employing the shooting method, we perform the numerical calculations to derive the relation between critical temperature, \(T_\mathrm{{c}}\), and charge density, \(\rho ^{z/d}\), for \(z=1, 2\) in \(D=d+2=4\) and 5 spacetime dimensions. Our results are summarized in Table 1. We find that increasing the values of z, m and nonlinearity b, in each dimension, hinders the superconductivity phase by diminishing the critical temperature. Moreover, the trends of condensation \(\langle J_{x} \rangle ^{1/(1+\Delta _{+})}\) as a function of the temperature impressed by different values of z, m and b are shown in Figs. 1 and 2. Based on these graphs, condensation decreases by increasing z.

Fig. 1
figure 1

The behavior of the condensation parameter as a function of temperature for different values of the model parameters in \(D=d+2=4\) dimension

Full size image
Fig. 2
figure 2

The behavior of the condensation parameter as a function of the temperature for different values of the mass, the dynamical critical exponent and nonlinearity parameters in \(D=d+2=5\) dimension

Full size image

3 Electric conductivity

In this section, we are going to investigate the effects of Lifshitz scaling and nonlinear parameter on the electric conductivity of the holographic p-wave superconductor. For this purpose, we apply an appropriate electromagnetic perturbation by turning on \(\delta A_{y}=A_{y} e^{-i \omega t}\) on the black hole background which acts as a boundary electrical current in holographic setup [59]. So, we have

$$\begin{aligned}&A_y''(r)+ \left[ \frac{d+z-1}{r}+\frac{f'(r)}{f(r)}+\frac{b r (z-1) \phi '^2(r)}{b r^2 \phi '^2(r)-r^{2 z}}\right. \nonumber \\&\quad \left. +\frac{b r^2 \phi '(r) \phi ''(r)}{r^{2 z}-b r^2 \phi '^2(r)}\right] A_y'(r)\nonumber \\&\quad + \left[ \frac{\omega ^2}{r^{2 z+2} f^2(r) }-\frac{2 q^2 \rho _{x}^2(r) }{r^4 f(r)}\sqrt{1-\frac{b \phi '^2(r)}{r^{2 z-2}}}\right] A_y(r)=0. \end{aligned}$$
(16)

In the Maxwell limit Eq. (16), except for a factor 2 in the last term, which originates with different approaches to calculating conductivity, turns to the corresponding equation in Ref. [59]. The above equation has the asymptotic behavior

$$\begin{aligned} A_y''(r)+\frac{(d-1+z) }{r}A_y'(r)+\frac{\omega ^2}{r^{2 z+2}} A_y(r)=0, \end{aligned}$$
(17)

which admits the following solution for \(A_{y}\):

$$\begin{aligned} A_{y} = \left\{ \begin{array}{lr} A^{(0)}+\frac{A^{(1)}}{r}+\cdots , &{} d=2, z=1,\\ A^{(0)}+\frac{A^{(1)}}{r^{2}}+\cdots , &{} d=2, z=2,\\ A^{(0)}+\frac{A^{(1)}}{r^2}+\frac{A^{(0)} \omega ^2 \log (\Omega r)}{2 r^2}+\cdots , &{} d=3,z=1,\\ A^{(0)}+\frac{A^{(1)}}{r^{3}}+\cdots , &{} d=3, z=2,\\ \end{array} \right. \end{aligned}$$
(18)

where \(A^{(0)}\), \(A^{(1)}\) and \(\Omega \) are constant parameters. Furthermore, by considering \(z=1\), Eqs. (17) and (18) have the same form as in AdS case [55]. Based on gauge/gravity duality, the electrical current is given by

$$\begin{aligned} J=\frac{{\delta S}_{\text {bulk}}}{{\delta A}^{(0)}}=\frac{{\delta S}_{o.s}}{{\delta A}^{(0)}}=\frac{\partial (\sqrt{-g}\mathcal {L}_{m})}{\partial A_y'}\vert r\rightarrow \infty , \end{aligned}$$
(19)

in which the on-shell bulk action \(S_{o.s}\) by using Eq. (19) is defined by

$$\begin{aligned} S_{o.s.}= & {} \int _{r_+}^{\infty }\, \mathrm{{d}}r \int \, {d}^{d-1}x \sqrt{-g}\mathcal {L}_{m}\nonumber \\= & {} - \frac{1}{2} \int \, {d}^{d-1}x \left[ \frac{ f(r) A_{y}(r) A_{y}'(r)}{1-b r^{2-2 z} \phi '^2(r)}\right] \nonumber \\&\qquad r^{d+z-1} \sqrt{1-b r^{2-2 z} \phi '^2(r)}. \end{aligned}$$
(20)

The electrical conductivity in a corresponding framework is [6]

$$\begin{aligned} \sigma _{yy}=\frac{J_{y}}{E_{y}}, \ \ \ E_{y}=-\partial _{t} \delta A_{y}. \end{aligned}$$
(21)

Employing Eqs. (19), (20) and (21) and using appropriate counterterms, based on the renormalization method to remove the divergency, the electrical conductivity is obtained [72]:

$$\begin{aligned} \sigma _{yy} = \left\{ \begin{array}{lr} \frac{A^{(1)}}{i \omega A^{(0)} }, &{} d=2, z=1,\\ \frac{2 A^{(1)}}{i \omega A^{(0)} }, &{} d=2, z=2,\\ \frac{2 A^{(1)}}{i \omega A^{(0)} }+\frac{i}{2}\omega , &{} d=3,z=1,\\ \frac{3 A^{(1)}}{i \omega A^{(0)} }, &{} d=3, z=2.\\ \end{array} \right. \end{aligned}$$
(22)

For \(z=1\), we obtain the same equations as in the AdS background [55]. In order to proceed with our research, we address an ingoing wave boundary condition near the horizon as follows:

$$\begin{aligned} A_{y}(r)=f(r)^{-i \omega / (4 \pi T)} \left[ 1+a(1-r)+b(1-r)+\cdots \right] , \end{aligned}$$
(23)

where by Taylor expansion of Eq. (17) around the horizon, the coefficients a and b are obtained. The behaviors of the real and imaginary parts of the conductivity as a function of \(\omega / T\) are shown in Figs. 3, 4, 5 and 6. The conductivity along the y direction in Lifshitz holographic p-wave superconductors is the same as \(\sigma _{xx}\) in s-types [59]. Although the figures follow different trends, in all cases the behavior of the real part of the conductivity in the large frequency regime can be predicted by a power law function, \(\mathrm{{Re}}[\sigma ]=\omega ^{D-4}\), similar to [55]. The real and imaginary parts of the conductivity follow the Kramers–Kronig relation. Thus, we observe the appearance of a delta function and pole, respectively. By increasing the Lifshitz scaling z, the gap energy becomes unclear like the minimum of the imaginary part. However, in some cases, we observe that by decreasing the temperature [56] for strong BI nonlinear electrodynamics, the gap and minimum in the real and imaginary parts of conductivity appear, which is obvious in \(D=5\) with \(m^{2}=0\) and \(b=0.04\). When \(z=1\), below the critical temperature, the superconducting gap appears and becomes deeper and sharper by diminishing the temperature, which yields larger values of \(\omega _\mathrm{{g}}\), which makes the conductor/superconductor phase transition harder to form because it can be interpreted in terms of the energy needed to break the fermion pairs. With the use of Figs. 7 and 8, which are graphed in \(T=0.3 T_\mathrm{{c}}\), the value \(\omega _\mathrm{{g}}=8 T_\mathrm{{c}}\) is generally obtained for \(z=1\), which differs from the predicted value 3.5 of BCS theory. This difference originates with the fact that holographic superconductors are strongly coupled systems and, because of this character, they are expected to be suitable for a description of the high temperature superconductors [53]. In addition, larger values of the nonlinearity parameter shift the maximum and minimum parts of the conductivity toward larger values but the effects of nonlinearity on the value of energy gap depends on our choice of the mass, which implies the fact that the value of \(\omega _\mathrm{{g}}/T_\mathrm{{c}}\) is characterized by our selection of mass m, nonlinearity b and dynamical critical exponent z in each dimension.

Fig. 3
figure 3

The behavior of the real part of the conductivity in \(D=4\)

Full size image
Fig. 4
figure 4

The behavior of the imaginary part of the conductivity in \(D=4\)

Full size image
Fig. 5
figure 5

The behavior of the real part of the conductivity in \(D=5\)

Full size image
Fig. 6
figure 6

The behavior of the imaginary part of the conductivity in \(D=5\)

Full size image
Fig. 7
figure 7

The behavior of the real and imaginary parts of the conductivity in \(D=4\) for \(T/T_\mathrm{{c}}=0.3\)

Full size image
Fig. 8
figure 8

The behavior of real and imaginary parts of the conductivity in \(D=5\) for \(T/T_\mathrm{{c}}=0.3\)

Full size image

4 Summary and conclusion

In this work by employing gauge/gravity duality, we have studied the holographic p-wave superconductors with Lifshitz scaling in the presence of BI nonlinear electrodynamics. We applied the shooting method to calculating the equations of motion and analyzing the behavior of the condensation as a function of the temperature numerically. We found the relation between critical temperature \(T_\mathrm{{c}}\) and \(\rho ^{z/d}\) for different values of mass m, nonlinearity effect b and Lifshitz scaling z in 4D and 5D spacetime. Based on our results, we observe that the temperature decreases with increasing each of three parameters m, z and b, which means that superconductivity phase faces with more difficulties. The condensation behavior in Lifshitz scaling is similar to the AdS spacetime by obeying the mean-field trend in the vicinity of the critical point. Increasing the anisotropy between space and time diminishes the condensation value. After that, by applying a suitable perturbation on the black hole background as \(\delta A_{y}=A_{y} e^{-i \omega t}\), we investigated the effects of Lifshitz scaling on the electrical conductivity of the holographic p-wave superconductors and plotted the behavior of the real and imaginary parts of conductivity as a function of the frequency. The plotted figures are different from each other but they follow some universal behaviors. For instance, for large frequencies, we can predict the behavior of the real part of the conductivity to be \(Re[\sigma ]=\omega ^{D-4}\). In addition, the real and imaginary parts of the conductivity are related to each other via the Kramers–Kronig relation. Actually, the real part shows a delta function behavior and the imaginary part has a pole at zero frequency. At low frequencies with \(z=1\), the real and imaginary parts of conductivity show a gap energy and minimum which shift toward larger frequencies by diminishing temperature. In this regime, increasing the Lifshitz critical exponent z makes the gap energy and minimum unclear. However, in some cases they occurred under decreasing temperatures and increasing the nonlinearity effect. Our choice of mass in each dimension has a direct impact on the effect of the BI nonlinear electrodynamics on the conductivity but generally the gap energy and minimum of conductivity shift toward larger values of the frequency by enlarging the nonlinearity effect. In the limit case where \(z=1\), the ratio \(\omega _\mathrm{{g}}/T_\mathrm{{c}}\simeq 8\) is obtained generally, which is larger than the BCS value because of the strong coupling between the pairs.