1 Introduction

Fluidization involves modifying the characteristics of particle-phase to behave as a fluid, thereby enhancing mixing and heat transfer properties. It is common in several industrial applications including combustion, gasification, catalytic cracking and food processing [29]. Of particular interest is dense-bubbling fluidization, which is the most common mode of operation in large-scale systems. However, it is difficult to control the homogeneity of properties like temperature and species composition. This is largely due to voids or bubbles which provide paths of least resistance to the gas phase leading to minimal contact with the solid particles. Besides, there is cascade of energy in the particle-phase through inelastic collisions between neighbouring particles as well as particle and wall. Thus, complex inter-phase and particle interactions result in a highly non-linear system [14].

Previous studies [10, 13, 27, 36, 40, 46] have shown that bubbling could be controlled using a periodic pulsation of gas flow at the inlet, and subsequently the setup is termed pulsed-fluidized bed. Research on these systems is primarily restricted to analyzing the effect of particle characteristics [18, 30] or inlet gas properties [6, 8, 13, 36] on the flow structures. Recently, pulsed-fluidized beds have been used to demonstrate enhanced fluidization, mixing and heat transfer characteristics [1–3, 25, 31, 32]. Despite its growing popularity, a thorough description of granular rheology associated with periodic pulsing is lacking. From a modelling perspective, it is essential to understand the physics surrounding structured bubbling patterns. The state-of-the-art continuum formulation of particle-phase is inadequate to model the recurring pattern in a pulsed-fluidizd bed [48]. This is most likely due to uncertainties in constitutive relations in the frictional or close-packed limit. Elucidating the underlying mechanism would enable improving such models and the overall predictive capability.

In the current study, we use proper orthogonal decomposition (POD) technique to understand granular dynamics in a laboratory-scale pulsed-fluidized bed. The method has been adopted in several areas of application and consequently referred to as Karhunen–Loève Decomposition, Singular Value Decomposition (SVD) or Principal Components Analysis (PCA) [26, 28, 33, 38, 41]. POD is an eigen-based approach to describe features in a system using spatial coherence which translates to characterizing coherent structures in a flow-field from a fluid dynamics point of view. There have been numerous efforts to successfully implement POD in this area of research and application [5, 19, 22, 24, 43, 44]. In essence, POD extracts the following: a set of spatial modes ranked by their variance (here we analyze velocity, and variance corresponds to fluctuating kinetic energy); a set of singular values which describe contribution of each spatial mode; and, a set of temporal coefficients which describe the time evolution of spatial modes as show by Higham et al. [23]. Periodicity in these spatial modes can be obtained using decomposition techniques such as Fourier transform, wavelet transform or Wigner distribution. Williams and Rege [47] apply POD to identify spatially coherent regions in granular flows, however the granular dynamics are not described which is well within the reach of POD methodology. Williams and Rege [47] also conclude that POD is far under-utilized in this field. In the present work, we demonstrate the applicability of POD to understand granular dynamics in a pulsed-fluidized bed system. This could have significant impact in industrial processes where such systems could be scaled to achieve efficient mixing and heat transfer properties.

The paper is structured as follows: first, we outline the experimental setup and the POD approach; second, we derive time-averaged statistics from raw particle-velocity data obtained using particle tracking; third, we apply POD on instantaneous flow-field and explain the features observed in leading POD modes followed by a low-order reconstruction using these modes; Finally, we summarize our findings in the conclusions section.

2 Procedure

2.1 Experiment setup

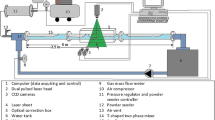
The experiments were performed at the US Department of Energy’s National Energy Technology Laboratory. The setup consists of a 300 mm tall rectangular domain made of acrylic, having a cross-section of 50 mm by 5 mm (Fig. 1). The chosen dimensions result in a quasi-two-dimensional flow, where the resulting meso-scale structures (bubbles) are larger than the shortest dimension of the domain. 18g of glass beads having a Sauter mean diameter of \(394\,\upmu \hbox {m}\) was added resulting in a 50 mm tall bed. The particle size distribution is narrow having the \(5^{th}\) and \(95^{th}\) percentile values as \(362\,\upmu \hbox {m}\) and \(470\,\upmu \hbox {m}\). Uniform flow of air was created using a fractal distributor at the inlet shown in Fig.  2, which was printed using a high precision ultraviolet curing 3D printer. The distributor splits the flow from an inlet of cross section \(19\,\hbox {mm}^2\) into 128 holes at the outlet each having an area of 1 mm\(^2\). Flow rate is pulsed in the form of sine wave given by,

$$\begin{aligned} {\text{Q(t)}} = {\text{A}} + {\text{B}} \mathrm{sin} (2{\text{f}} \pi {\text{t}}) \end{aligned}$$
(1)

where \({\text{A}}=2.6\) l/min and \({\text{B}}=2.1\) l/min represent the baseline and amplitude of the wave form. The sinusoidal waveform has a mean value of A, and consists of two phases, first when \({\text{Q}} > {\text{A}}\) and the second when \({\text{Q}} < {\text{A}}\). While the bubbling pattern is also dependent on particle properties, bed dimensions, mean velocity, and amplitude of pulsing, only the pulsing frequency was changed. Three different values of f, viz. 4 Hz, 5 Hz and 6 Hz were used in this study. The images were captured using a 120 mm Nikon lens and Fastec IL5L sensor at 300 Hz. The bed was lit from the back using an LED light source such that the high-intensity bubble patterns could be recorded using a threshold procedure. Also, the front of the test section was lit to track glass particles using an in-house code PTVResearch [15] and all optical distorisons removed using a calibration grid and polynomial de-warping [20]. The individual motions were determined by Optical Flow Equations using the Lucas-Kanade method [16, 34, 35]. The particle tracks were binned using a cubic interpolator to obtain the solids velocity field for POD analysis. The outliers were detected using the PODDEM algorithm [21]. Given the scale of geometry used in this study and the need for a clear field of view for tracking particles, it was not possible to have pressure ports in the test section. This would have been useful to measure differential pressure across regions and confirm uniform flow conditions at the inlet. However, the fractal nature of the distributor should effectively decouple the plenum and bed dynamics which is essential to sustain bubbling patterns. Previous research including the work of Coppens [12], He et al. [17] and Andrzej Stankiewicz [4] have demonstrated the performance of such fractal distributors in generating uniform flow at the inlet by minimizing channeling and dead spaces. Instantaneous snapshots from experiments show repeatable bubbling patterns. Fluidization occurs during the first phase of a pulsing cycle, where bubbles provide paths of least resistance and attract gas from immediate vicinity. Particles are locally defluidized in these regions and are supported by layers beneath them. Force chains are formed with an increase in compressive stress which deters passage of gas. The stress in the particle-phase increases further when conditions at the inlet reach sub-fluidization during the second phase of the pulsing cycle. The following bubble originates at a different location to provide an alternative path for movement of gas. Force chains are altered periodically in this process, which get disrupted by pulsing at a specified frequency. The rate at which this occurs dictates the wavelength of bubbling pattern, λ, i.e., the size and spacing of bubbles. Bubbles shift by λ/2 between successive pulsing cycles.

At 6 Hz and 5 Hz, a recurring structure having two bubbles along the sides followed by a single bubble along the centre is produced (see Fig. 3a, b). We refer to this as one–two (1:2) pattern. When the frequency of the wave form is reduced to 4 Hz, the location of bubbles alternates from one side to another over two complete pulsing cycles and we refer to this as one–one (1:1) pattern (Fig. 3c). The results indicate an inverse relation between λ and f as previously reported by Wu et al. [49]. Similar observations have been recorded for other periodically forced non-linear systems including Faraday waves [7] and vibrating granular bed [9].

Fig. 1
figure 1

Illustration of the experimental setup (not to scale)

Full size image
Fig. 2
figure 2

Photograph showing the front view of fractal distributor used in the experiments (inset shows a schematic)

Full size image
Fig. 3
figure 3

Snapshots of bubbles patterns with velocity vectors overlaid for f = 6 Hz (a), 5 Hz (b) and 4 Hz (c)

Full size image

2.2 Proper orthogonal decomposition

In the present study, we follow the method of Sirovich [44] to perform POD on the flow-field data. The approach is described as follows: A set of \(t = 1, 2, \ldots ,{\text{T}}\) temporally ordered snapshots, \(\mathbf {V}({\text{x,y;t}})\), is obtained from the experiments, where time-step size is, \(\varDelta {\text{t}}\) = 0.003 s (300 Hz) and spatial resolution is, \(\varDelta {\text{x}}\) = \(\varDelta {\text{y}}\) = 0.71 mm. An \({\text{N}} \times {\text{T}}\) matrix \(\mathbf {Z}\) is constructed from T columns of length \({\text{N}} = {\text{XY}}\), each corresponding to a column-vector version of transformed snapshot \(\mathbf {{\text{V}}}({\text{x,y;t}})\). X and Y represent the number of spatial bins in the x and y directions. Very high-resolution events including particle rain inside a bubble are not considered in this work besides being limited by instrumentation. The tracking procedure neglects particles inside a bubble and their velocities are set to zero. However, this should not affect the values in the surrounding granular medium which is of primary interest. Using matrix notation, POD is formulated as:

$$\begin{aligned} \mathbf {Z} \equiv {\varvec{\Phi }} \, \mathbf {S} \, \mathbf {C}^{*} \end{aligned}$$
(2)

where \({\varvec{\Phi }}\) of dimension \({{\text{N}} \times \boldsymbol {\Theta} }\) contains the spatial structure, and \(\mathbf {C}\) of dimension \({{\text{T}} \times \boldsymbol {\Theta} }\) pertains to the temporal evolution in each mode. \((\cdot )^*\) represents conjugate transpose operation. \(\varTheta\) is the number of modes in the truncated decomposition. \(\mathbf {S}\) of dimension \({\boldsymbol {\Theta} \times \boldsymbol {\Theta} }\) contains the singular values of matrix \(\mathbf {Z}\), which is made of particle-phase fluctuating velocities from 15,000 instantaneous snapshots. A vector \({\lambda } = \text {diag}(\mathbf {S})^{2} / {({\text{N}}-1)}\) can then be constructed from \(\mathbf {S}\) proportional to fluctuating kinetic energy in each mode, where the elements are arranged in descending order, i.e. (\(\lambda _{1} \ge \lambda _{2} \ge \cdots \lambda _{\varTheta } \ge 0\)). The relative contribution of \(\lambda _{i}\) is evaluated as:

$$\begin{aligned} E_{i}(\%) = \frac{\lambda _i}{\sum ^N_{i=1} \lambda _i} \cdot 100 \end{aligned}$$
(3)

3 Results

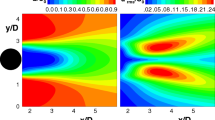
Data at intervals of two pulsing cycles along eight linearly spaced temporal locations were used for periodic time-averaging, and the statistics were generated from 100 samples. First, the average location of bubbles was determined. Bubbles were identified by thresholding using the technique of Bradley and Roth [11] and binarized, where the voids are defined by ones and the particle-phase by zeros. By periodically time-averaging the identified binary bubbles, two-dimensional bubble location histograms (\(\mathbf {B}\)) were created, which are then normalized by the maximum value, \(\mathbf {B}_0\). Second, the averaged sum of the square of fluctuating velocity components, \(\mathbf {v}^2\) was determined. These values are normalized by the square of maximum inlet velocity (\(\mathbf {v}_0^2\)). The results are shown in Figs. 4, 5 and 6, where the dimensions are normalized by the domain width, W = 50 mm. Particle-phase velocity fluctuations are intense around bubbles. As the pulsing frequency is decreased, bubbles become larger and their locations become less predictable. Time-averaged statistics provide valuable information relating to average bubble size and location. They also show that increasing the periodic forcing frequency modifies the bubble size and formation, as well as the way in which the bubbles interact with the surrounding grains. However, they do not provide any information regarding the dynamics, nor do they elucidate the multiple mechanisms and non-linear interactions which manifest in these changes; this is where a POD can provide better insight. It must be stressed that bubble location histograms are superimposed with velocity vectors in Figs. 4, 5 and 6, and the two are calculated independently. Periodic time-averaging is performed using binned velocities. Once the tracking algorithm loses a particle’s trajectory, the value assigned to the corresponding grid would be 0. This holds true inside a bubble since the majority of tracks if not all disappear.

Fig. 4
figure 4

Periodic time-averaged bubble patterns and velocity fields at different phase angles for f = 6 Hz. The bubble location histograms are shown in grey scale, and normalized \(\mathbf {v}^2\) in color, overlaid with quiver plots of velocity components

Full size image
Fig. 5
figure 5

Periodic time-averaged bubble patterns and velocity fields at different phase angles for f = 5 Hz. The bubble location histograms are shown in grey scale, and normalized \(\mathbf {v}^2\) in color, overlaid with quiver plots of velocity components

Full size image
Fig. 6
figure 6

Periodic time-averaged bubble patterns and velocity fields at different phase angles for f = 4 Hz. The bubble location histograms are shown in grey scale, and normalized \(\mathbf {v}^2\) in color, overlaid with quiver plots of velocity components

Full size image
Fig. 7
figure 7

POD for f = 6 Hz: the top row shows the leading spatial modes \({\varvec{\Phi }}\), here the components are plotted as the sum of the square of velocity fluctuations divided by the maximum inlet gas velocity (\(\mathbf {v}/{\text{v}}_0\)) with overlaid quiver plots. The middle row shows their temporal coefficients \(\mathbf {C}_i\), and the bottom row shows the Fourier transform of temporal coefficients

Full size image
Fig. 8
figure 8

POD for f = 5 Hz: the top row shows the leading spatial modes \({\varvec{\Phi }}\), here the components are plotted as the sum of the square of velocity fluctuations divided by the maximum inlet gas velocity (\(\mathbf {v}/{\text{v}}_0\)) with overlaid quiver plots. The middle row shows their temporal coefficients \(\mathbf {C}_i\), and the bottom row shows the Fourier transform of temporal coefficients

Full size image
Fig. 9
figure 9

POD for f = 4 Hz: the top row shows the leading spatial modes \({\varvec{\Phi }}\), here the components are plotted as the sum of the square of velocity fluctuations divided by the maximum inlet gas velocity (\(\mathbf {v}/v_0\)) with overlaid quiver plots. The middle row shows their temporal coefficients \(\mathbf {C}_i\), and the bottom row shows the Fourier transform of temporal coefficients

Full size image
Fig. 10
figure 10

Relative energy contribution (E%) of each POD mode

Full size image
Table 1 Table summarizing key features for each case and each POD mode \({\varvec{\Phi }}\), where \(\hbox {f/f}_0\) is the frequency determined from a Fourier spectra of the temporal coefficients \(\mathbf {C}_i\) normalized by the input frequency, and E is the modal energy content (relative)
Full size table

The four leading POD spatial modes which adequately capture the dynamical scales are presented in Figs. 7, 8 and 9. As previously discussed, by taking a Fourier Power Spectra of the temporal coefficients (those relating the spatial modes) we can determine the dominant frequency. We find the higher-energy modes are either harmonic (the pulsing frequency) or sub-harmonic (half of the pulsing frequency) for all values of f. Spatially, the harmonic component is associated with stream-wise transport of particles and the sub-harmonic component is related to their transverse motion. \({\varvec{\Phi }}_{1}\), the most energetic mode is harmonic and \({\varvec{\Phi }}_{2}\) is sub-harmonic for all values of f. The change in pulsing frequency clearly has an effect on modal energy content (Fig.  10). As f is reduced from 6 to 4 Hz, the energy in \({\varvec{\Phi }}_{1}\) changes from 26% to 36% while the energy in \({\varvec{\Phi }}_{2}\) drops to 16% from 20%. \({\varvec{\Phi }}_{3}\) is sub-harmonic, and \({\varvec{\Phi }}_{4}\) is harmonic for f = 6 Hz and 5 Hz. There is a noticeable secondary peak associated with \({\varvec{\Phi }}_{4}\) whose amplitude increases from 6 to 5 Hz. At f = 4 Hz, \({\varvec{\Phi }}_{3}\) is harmonic and along with \({\varvec{\Phi }}_{1}\) forms a conjugate pair, although only accounting for 10% of the total energy. \({\varvec{\Phi }}_{4}\) has a dominant sub-harmonic component, while the spectrum contains non-trivial contributions from a broad range of frequencies. This indicates suppression of chaos at higher f consistent with the findings of Pence and Beasley [40]. The key features of leading POD modes are summarized in Table 1.

POD analysis also reveals redistribution of energy between the harmonic and sub-harmonic components. At higher frequencies, the harmonic (\({\varvec{\Phi }}_{1 \& 4}\)) and sub-harmonic (\({\varvec{\Phi }}_{2 \& 3}\)) modes account for 36% and 33% of total energy. In comparison at f = 4 Hz, the contributions from the harmonic (\({\varvec{\Phi }}_{1 \& 3}\)) and sub-harmonic (\({\varvec{\Phi }}_{2 \& 4}\)) modes are 46% and 29%. Energy in the harmonic modes associated with stream-wise transport is transferred to sub-harmonic modes as f is increased. It is possible to describe regions of spatial coherence in the granular medium through the POD modes as shown by Williams and Rege [47]. However, it is further possible to describe the modal dynamics and energy budget, perhaps two significant features which characterize non-linear interactions between the different spatio-temporal scales. It is intuitive that the coherent regions identified by POD along with velocity distribution functions [37, 39, 42, 45] could provide valuable information on energy cascading mechanism in particle-laden flows. This is analogous to describing turbulent flows using Fourier modes which represent cascade from large eddies to Kolmogorov scales. However, such a rigorous description might require a much finer resolution in the flow-field data.

It is possible to create a low-order reconstruction using any specified number of modes as suggested by Eq. 2. By creating these models for each case, and time averaging, we determine the origin of non-linear mechanisms identified previously. First we use the modes relating to harmonic frequencies (Figs.  11, 12 and 13). The vector streamlines confirm that the harmonic modes are associated with streamwise transport of particles. The flow field reconstructed using sub-harmonic modes (Figs. 14, 15 and 16) suggest these modes relate to the mixing process and are characterized by vortex-like structures. The size of these structures increases as f is reduced.

Finally, a low-order representation is created using the four leading POD modes (Figs. 17, 18 and 19). The reconstructed flow fields are markedly similar to the time-averaged data especially at higher pulsing frequencies. Subsequent POD modes are required to further resolve events containing shorter spatial scales. The quality of reconstruction also depends on gradients in the velocity field. Bubbles are in essence concentration wave instabilities and the particle-phase motion in their vicinity contains a broad range of spatio-temporal scales. A higher dimensional reconstruction is hence required for a more accurate representation of granular dynamics. The disparity between the time-averaged raw data and reconstructed field is more noticeable at f = 4 Hz where the bubbles are larger. To conclude, factors including the inherent spatio-temporal scales, resolution of raw data and frequency of sampling determine the overall quality of reconstructed flow-field. Although the work presented does not attempt to quantify these effects, a systematic study is required to enhance our understanding.

Fig. 11
figure 11

Flow field reconstruction using \({\varvec{\Phi }}_{1 \& 4}\) representing the harmonic frequency for f = 6 Hz

Full size image
Fig. 12
figure 12

Flow field reconstruction using \({\varvec{\Phi }}_{1 \& 4}\) representing the harmonic frequency for f = 5 Hz

Full size image
Fig. 13
figure 13

Flow field reconstruction using \({\varvec{\Phi }}_{1 \& 3}\) representing the harmonic frequency for f = 4 Hz

Full size image
Fig. 14
figure 14

Flow field reconstruction using \({\varvec{\Phi }}_{2 \& 3}\) representing the sub-harmonic frequency for f = 6 Hz

Full size image
Fig. 15
figure 15

Flow field reconstruction using \({\varvec{\Phi }}_{2 \& 3}\) representing the sub-harmonic frequency for f = 5 Hz

Full size image
Fig. 16
figure 16

Flow field reconstruction using \({\varvec{\Phi }}_{2 \& 4}\) representing the sub-harmonic frequency for f = 4 Hz

Full size image
Fig. 17
figure 17

Flow field reconstruction using \({\varvec{\Phi }}_{1-4}\) for f = 6 Hz

Full size image
Fig. 18
figure 18

Flow field reconstruction using \({\varvec{\Phi }}_{1-4}\) for \(\hbox {f}=5\,\hbox {Hz}\)

Full size image
Fig. 19
figure 19

Flow field reconstruction using \({\varvec{\Phi }}_{1-4}\) for \(\hbox {f}=4\,\hbox {Hz}\)

Full size image

4 Conclusions

POD of particle-velocity field is used to characterize granular dynamics in a pulsed-fluidized bed. The results indicate inverse relation between pulsing frequency, f and wavelength of the bubbling pattern. The bubble size increases and the histogram becomes more diffuse when f is reduced. There is a marked transition in bubbling pattern between f = 6 Hz, 5 Hz and f = 4 Hz. POD analysis reveals a redistribution of energy between the harmonic and sub-harmonic modes associated with this change. Furthermore, the modal dynamics and energy budget are described using POD which are pivotal in characterizing non-linear interactions between the dominant modes. We also notice that the flow-field reconstruction using the leading POD modes is reasonably accurate especially at higher f. Even though low-order reconstruction may be valid for flows having significant self-similar features, its resolution is compromised by the presence of sharp gradients. In this case, such gradients exist in the vicinity of bubbles, and hence their size effects the quality of reconstruction. Thus, we have demonstrated the applicability of POD to analyze granular rheology which would not have been possible using conventional statistics-based approaches. Such techniques based on modal decomposition are capable of providing even higher resolution to granular dynamics with more rigorously designed experiments and data acquisition, which will be the focus of our future work.