1 Introduction

Understanding the origin and development of the solar system starts with better knowledge of the geologic histories of all solid bodies. For several decades it has been possible to obtain both images and digital elevation models (DEMs) of solid planetary bodies surfaces. These datasets serve as support for mapping the different geological units and later for dating the respective geological processes. Hartmann (1970, 1972) and Neukum et al. (1975a, b) proposed and thoroughly examined an approach to determin the age of different surfaces using the size and frequency of impact craters. Assuming that the impactor flux on a given surface is known, measuring the density of impact craters observed on visible images or DEMs then allows surface age to be determined. The detection of impact craters is thus a key challenge in planetary science, because it requires a large effort of annotation each time a new set of images is acquired. However, the manual detection by experts has been—and still is—the commonly used method. The increasing amount of image data makes it highly time consuming to manually identify all observed craters, especially the smaller ones. In the case of Mars, only kilometer-sized craters can be measured on a global or even large regional scale (e.g., Barlow 1988; Robbins and Hynek 2012) due to the amount of manual effort required, even though global and regional high resolution imaging is available [e.g., Context and HiRISE cameras on board the Mars Reconnaissance Orbiter; Malin et al. (2007)]. This, together with new developments in computer vision, has lead to new efforts to develop an automatic Crater Detection Algorithm (CDA) with the highest possible detection rate and the lowest possible false detection rate. A reliable CDA would definitely speed up the crater detection process, further it would allow in-depth statistical analysis of the crater morphology (e.g., depth-to-diameter ratio) thanks to the identification of a huge number of new craters. This would in turn will give access to possible variations of the impact rate on the studied surface in addition to determining its age.

The development of an efficient CDA requiring minimum human intervention is a challenging task for computer vision, discrete geometry and planetary sciences. Many approaches (Michael 2003; Urbach and Stepinski 2009; Ding et al. 2013; Salamunićcar et al. 2014; Wang et al. 2015) have been already proposed and they mainly rely on the use of images or DEMs, which are 2.5D data (projection, which reproduces the appearance of being three-dimensional). In this paper, an automatic innovative method is proposed for efficiently detecting craters from 3D meshes, but also for characterizing their morphology. This method can be applied on classical 2.5D DEMs. The performance of the proposed method will be tested on topographic models built from the laser altimeter (MOLA) instrument onboard NASA’s Mars Global Surveyor spacecraft (Zuber et al. 1992).

The article is organized as follows: in Sect. 2, some popular existing approaches related to crater detection are reviewed. In Sect. 3, the pre-processing steps over the input data are presented, then the core of this approach is described in Sect. 4. Section 5 is dedicated to the results and validation of the method. Conclusions and direction of future research are given in Sect. 6.

2 Related Works

The manual identification of craters, applied to 2D images, is a well-established and standardized procedure among geologists (e.g., Chapman 2002). This method uses a Geographic Information System (GIS) software to geo-reference the craters and to measure their diameter (among other properties). The method is very safe (relatively little false positives are negatives), but highly time-consuming for large areas that contain tens or hundreds of thousands of craters. Particularly as new global to near global imaging data sets at high resolutions are obtained, as for example the imaging campaigns of Mars Express HRSC instrument (Gwinner et al. 2016) and by the Mars Reconnaissance Orbiter Context camera (Malin et al. 2007), which acquired images at 10–20 m/pixel and 6 m/pixel respectively.

Automatic CDAs diminish the need for an operator to manually delimit all craters within a region. There are many methods that have been proposed. They can be grouped by type of input data, but also by the type of output data (just crater or not a crater, or with a fitting of circles, ellipse, etc.). Several CDAs, using image data as input (Leroy et al. 2001; Urbach and Stepinski 2009; Ding et al. 2013) or 2.5D data (Salamunićcar et al. 2012, 2014; Stepinski et al. 2012; Wang et al. 2015), have been developed in the last few decades (Urbach and Stepinski 2009). Others using DEMs data, are based either on the stereo analysis of image data (e.g.,  Gwinner et al. 2016) or, directly on laser altimetry measurements such as those built from the MOLA instrument (Zuber et al. 1992 and Smith et al. 1998). More recently 3D reconstructions are starting to be used (Capanna et al. 2012) as input data for CDAs.

The current state of development of computer vision and machine learning gives the possibility of expansion of approaches based on 3D mesh processing, but unfortunately the prevalence of such methods is scarce (Schmidt et al. 2015). Also, we can distinguish the approaches according to whether they use the texture (Bandeira et al. 2012), the value of elevation (Bue and Stepinski 2007) and/or the curvature (Schmidt et al. 2015). Other authors like (Kim et al. 2005) combine image data and the DEM data in detecting craters. We propose a method, which is based on the use of 3D and curvatures.

It is not enough to only detect craters, Barata et al. (2004), and Zhang and Jin (2015) focus on the morphology of the crater: fresh or old. There are authors who have tried to extract the diameters of the crater, based on the assumption of it having a round shape. Such CDAs, commonly use Hough transform (Leroy et al. 2001), are based on the detection of round shapes. Sawabe et al. (2006) and Luo et al. (2011) have developped circle fitting approaches.  Salamunićcar et al. (2012), employ DEM data and consider the crater as having circular or ellipsoidal shape.

Pattern recognition allows to easily combine human expertise with automation. The combination of the two techniques (manual and automated) is a good solution for the problem because, as already shown, fully automatic methods (Palafox et al. 2017) are not sufficient for crater detection at this time and manual correction by an expert is needed. CDAs diminish the need for an operator to manually delimit all craters within a region, which is useful for generating impact crater inventories over large areas. Manual inspection is still required to validate the results. A good approach would be based on a rapid pre-detection of craters which would serve as a base for the human validation. Our approach accounts for this limitation and does not aim at entirely replacing human experts. It proposes an algorithm for crater detection using manually selected information for validation to make the results more reliable.

Recently, Bandeira et al. (2012), Stepinski et al. (2012), Cohen and Ding (2014), and Jin and Zhang (2014) propose an image-based crater detection technique. Their works apply an “AdaBoost” or “Boosting algorithms” machine learning approach. Stepinski et al. (2012) employ an algorithm for detection of craters from topographic data. Salamunićcar and Lončarić (2010) propose a “support vector machines” approach, applied to DEM data. The method of  Di et al. (2014) uses image processing techniques on Mars DEM data obtained by the MOLA instrument. It uses a boosting algorithm to detect square features in the two-dimensional DEM. Three classes of features are used to train the detection algorithm: Haar-like, local binary pattern (LBP) and scaled Haar-like features. Then the round limit of the crater in the square region is identified using a local terrain analysis and the Circular Hough Transform (CHT). For testing, they apply their algorithm to three local DEMs of Mars, extracted from the global MOLA data. The authors achieved a reasonable detection rate of \(76\%\) and a false positive rate of \(13.23\%\). However, it is not full 3D and densely distributed, overlapped and heavily degraded craters could not be detected.

Based on the recent developments in computer vision and machine learning we propose a method based on machine learning like Di et al. (2014), combining human expertise and automation. Like Schmidt et al. (2015), this approach works as well in 3D and in addition it gives information on craters, as in Chapman (2002). Moreover, it does not rely on the information about the topography alone, but on its curvature, i.e. its strong/weak concavity or convexity as in Schmidt et al. (2015). Curvatures are known in computer science to give important information on geometry (Kudelski et al. 2011).

The presented approach therefore uses an manual/expert method, can be applied either in 2.5D or 3D input data, uses all the possible information about the topography and detects not only frequencies but also circles and morphological characteristics of the craters. We will compare the performances of our approach with the the approach described in Di et al. (2014), because it is the one that comes closest to the work proposed in this article.

3 Preprocessing Steps

The proposed method relies on the notion of discrete curvature computed on a 3D mesh. This notion is then succinctly explained in the next two subsections before describing the preprocessing step providing the descriptors used in the proposed machine learning algorithm.

3.1 Triangle Mesh

A triangle mesh is a discrete geometric structure representing 3D objects. It is composed of a set of triangles that are connected by their edges or corners. The point where two or more edges meet is a vertex and every edge is shared by two triangular faces. Each triangular face has an associated normal vector. 3D triangulated meshes are not so commonly available compared to DEMs 2D structured grids. However, any polyhedron can be transformed into a triangle mesh without any loss of information simply by adding edges on the non-triangular faces. This asserts that the proposed approach can be applied on any topographic data types. Besides, the meshes used in this research work have an identical homogeneous distribution of vertices on their surface. The input data consists of MOLA data (Zuber et al. 1992) at a scale of 128 pixels per degree.

3.2 Discrete Curvatures on a Mesh

The curvature is a differential descriptor of the local appearance of a curve or a surface. This indicator is used extensively in mesh processing since it offers information on the concavity or convexity of a surface along its principal directions.

Fig. 1
figure 1

A representation of \(k_1\), the maximal curvature and \(k_2\), the minimal curvature lying on a surface (courtesy of  Polette et al. 2017)

Full size image

Let us respectively denote \(k_1\) and \(k_2\) (see Fig. 1) the maximal and minimal curvatures at a vertex of the triangulated surface. The algebraic point set surfaces variant based on local fitting of algebraic spheres is used in this paper to estimate the two principal curvature values at each point of the surface (Guennebaud and Gross 2007). These quantities are related to the Mean and Gaussian curvatures, respectively H and K, through the following equations:

$$\begin{aligned}&H = \frac{(k_{1} + k_{2})}{2} \end{aligned}$$
(1)
$$\begin{aligned}&K = k_{1} \cdot k_{2} \end{aligned}$$
(2)
Fig. 2
figure 2

The 8 fundamental possible shapes at a point considering the signs of mean curvature H and Gaussian curvature K: Saddle Ridge \((K<0, \, H<0)\), Ridge \((K=0, \, H<0)\), Peak \((K>0, \, H<0)\), Minimal \((K<0, \, H=0)\), Flat \((K=0, \, H=0)\), Saddle Valley \((K<0, \, H>0)\), Valley \((K=0, \, H>0)\) and Pit \((K>0, \, H>0)\)

Full size image

An impact crater is characterized by a circular depression surrounded by a circular ridge. This is due to the isotropic dissipation of the kinetic energy of the impactor on the surface during the impact. Using the Mean and Gaussian curvatures, the depression area can be delimited by vertices with \(H>0\) and \(K>0\) while the ridge area is represented by vertices with \(H<0\) and \(K\approx 0\) (see Fig. 2). However, this criterion does not take into account the possible overlapping of multiple craters.

Fig. 3
figure 3

Rendered topography of b the maximal and c the minimal curvatures \((k_1\) and \(k_2\) respectively), d the mean curvature H and e the Gaussian curvature K on a a surface mesh at a scale of 128 pixels per degree. Values ranges of curvatures: \(k_1 \in [-0.3705, 0.5683]\), \(k_2 \in [-0.6154, 0.3881]\), \(H \in [-0.4256, 0.4703]\) and \(K \in [-0.0994, 0.2116]\)

Full size image

Figure 3 shows an area of a Mars’ surface sample. Convex areas are colored blue (\(H < 0\) and \(K<0\), \(K>0\) or \(K\approx 0\)), relatively flat areas are colored green (\(H\approx 0\), \(K\approx 0\)) and concave areas are colored yellow (\(H > 0\) and all three possible values for K). The sign of H characterizes the local convexity or concavity of the surface. Based on the visual information, it become clear, that detection of craters can be based on geometry.

3.3 Noise Filtering, Data Normalization and Feature Extraction

Regarding the geometrical form of the impact craters, characterized by a circular depression surrounded by a circular ridge, the minimal curvature is chosen as a good descriptor of the local concavity of the surface. The argumentation for this choice is visible in Fig. 3. The Mean curvature and the Gaussian curvatures obviously do not allow to obtain a continuous contour. Tests described in Christoff et al. (2017) demonstrate the usefulness of Minimal curvature compared to Maximum curvature.

Fig. 4
figure 4

Latitude longitude map of Mars, obtained using the Planetary Cesium Viewer (GEOPS). The areas A, B and C are the training sites. The areas 1, 2 and 3 are the validation samples. Detailed descriptions are given in Table 1

Full size image
Table 1 Information about the training and testing sites
Full size table
Fig. 5
figure 5

(A) Minimal curvature, with values in the range \([-1.1848, 0.7607]\). (B) With applied adaptive 2D linear filter, with values in the range \([-0.6033, 0.3284]\)

Full size image

Five areas were chosen on Mars (Fig. 4, Table 1): the training areas A, B and C and the validation areas 1, 2 and 3. Regions C and 1 are one and the same, used for both learning and validation, this area is used for comparison with other approaches described in the Sect. 5. The minimal curvature \(k_2\) was computed at each point of these five areas.

Fig. 6
figure 6

(A) Histogram of minimal curvature with values \(\in [-1.1848,\, 0.7607]\) , computed for Area 3. (B) Histogram after filtering (values \(\in [-0.6033,\, 0.3284]\)), applied on the same region

Full size image

For MOLA data, Jarmołowski and Łukasiak (2015) report the presence of “Along-Track” and “Cross-Track” noise. The direction along the trajectory of the remote sensing instrument forms the longitudinal direction “Along-Track”. The direction orthogonal to the trajectory of the satellite corresponds to the transverse direction “Cross-Track” (Zyl 2006). These two types of noise can be observed on Fig. 5A. On Fig. 5A’ some of the Along-Tracks schematically are visualized as black lines and Cross-Tracks are with red lines.

In  Gauthier et al. (2017) an efficient method for noise characterization in 3D processes based on curvature histogram analysis of noisy spheres is presented. The authors illustrate an example showing that adding Gaussian noise to an ideal sphere geometry leads to Gaussian histograms of the curvature values. The histogram of the minimal curvature values computed from the Mars dataset (Fig. 5A) is illustrated in Fig. 6A. It can be observed that the form of the histogram is very similar to a Gaussian one. We assume that the noise of the Mars topography acquisition could be considered as a Gaussian one. Based on this assumption, to eliminate the noise due to the scanning process, first we calculate the quantile of the distribution for values lying outside the interval in only \(5\%\) of cases (see Rees 1987):

$$\begin{aligned}&X_{1,2} = \mu \pm 1.96*\sigma \end{aligned}$$
(3)

\(X_{1}\) and \(X_{2}\) are the standard normal random variables, \(\mu\) is the mean value and \(\sigma\) is the standard deviation. For outlier values in the intervals \(]-\infty ,X_{1}]\) and \([X_{2},+\infty [\), to preserve the spatial neighborhood relationships of pixel values, we apply an adaptive 2D linear filter with values:

$$\begin{aligned} \frac{1}{8} \begin{bmatrix} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \end{bmatrix} \end{aligned}$$

The result of the filtering is presented in Fig. 5B. The histogram of the distribution of these values is shown in Fig. 6B. It can be observed that the “Along-Tracks” and “Cross-Tracks” noise is suppressed without damaging the topography of the surface.

Fig. 7
figure 7

The minimal curvature in grayscale

Full size image

An 8-bit image, equivalent to a grayscale image, is often used as an input for many common feature extraction methods. It is also a common practice for color feature extraction methods, instead of using the original color spaces (Kanan and Cottrell 2012). For this reason, the values of minimal curvatures \(k_2\) of areas A, B and C are converted into a quantified grayscale data with values between 0 and 255. It is important to note, that these gray levels are actually RGB colors mapped to a lower range of values. To do this, for each area, the minimum and maximum values \(k_{2,min}\) and \(k_{2,max}\) are calculated. After that, the values of \(k_2\) are represented as an image of \(3200 \times 1665\) pixels containing the grayscale curvature \(k_{2,G}\). The three output images (for samples A, B and C) of this preprocessing step, hereafter called “\(k_{2,G}\)-images”, are used as input for our algorithm. In Fig. 7 is presented an example of this quantification. The input minimal curvature is the same as that shown in Fig. 5B.

The next step is the extraction of the areas around the craters, present in a catalog of Martian craters, and the preparation of the data set. In this study the Barlow Northern Hemisphere Database version 2 (Barlow 1987, 2006) is used. Pixel coordinates of the center of the craters in the \(k_{2,G}\)-images are calculated from their geographic coordinates (longitude and latitude) and stored in a data file. Their diameter is converted from kilometer to pixel unit using the local pixel scale for each of the three \(k_{2,G}\) images.

Sub-windows in the \(k_{2,G}\) image around all the craters in the Barlow catalog for each of the training areas need to be delimited. The craters rim are represented as circles with radius equal to the radius of each crater in the Barlow Barlow (1987) dataset. They are positioned at the coordinates, existing in the catalogue.

Since the minimum pixel scale at the Equator is 463 m, a sub-window about 1.5 times the diameter of the crater (see  Di et al. 2014) plus 5 pixels is automatically delimited around its central position. We’ve observed a shift between the catalog and MOLA topography in x and y coordinates, which differs in direction and size. The constant of 5 pixels is chosen to manage the errors of the position of the centers (it had been chosen according to the calculated average difference). This allows a region of interest, representing the sub-window, containing the crater, including the possible ejecta around it to be calculated.

In addition to these sub-windows each containing a crater in the middle (positive samples), we automatically select an equivalent number of “background” images (negative samples) at random locations with sizes between 2 and 100 pixels, in order to build a training and validation set for our neural network that contains 1505 positive samples and 1505 negative samples.

The neural network requires all the samples to have the same dimensions, which can be achieved by interpolation. All the sub-windows are bi-linearly resampled to create a normalized window of \(20 \times 20\) pixels (like  Di et al. 2014), hereafter called Area.

Fig. 8
figure 8

Overview of the proposed approach

Full size image

4 Algorithm for Crater Rim Extraction

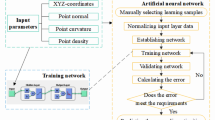
A diagram of the proposed algorithm is shown in Fig. 8. After the data preparation, the algorithm continues with the proposed method for feature extraction on the minimal curvature \(k_2\). This information is fed into the neural network to perform an automatic detection of the shapes (regions) of interest. From all positive outputs, the crater rims are then extracted via CHT.

4.1 Computing Features

The proposed approach is based on the idea that the crater rim is higher than the bottom of the crater. The ratio between the height of the rim and the depth is larger for a fresh crater than for a degraded one. The method should meet the following requirements:

  • Applicable for different sizes (different radii);

  • Independent of rotation and angle of observation;

  • Suitable for different craters’ morphologies;

  • Adapted according to the regional topography (including the case of overlap);

  • Able to predict the state of degradation.

 Ponti et al. (2016) hypothesized that using a reduced number of colors with a proper quantization method will significantly reduce the dimensionality, while improving or maintaining the accuracy of a classification system.

The basic idea behind the algorithm is the separation of each Area defined in Sect. 3 into six zones, as a dimensionality reduction step, but still keeping the existing crater information.

Each of these areas (in the general case) will contain the following information:

  • Interval 1: the average ridge of the crater rim

  • Interval 2: the average height of the crater and the appearance of the terraces

  • Interval 3: the average height of the ejecta, if present

  • Interval 4: the average surface before the impact

  • Interval 5: the average surface towards the bottom

  • Interval 6: the average bottom of the crater

Fig. 9
figure 9

Theoretical representation of a simple crater, b complex crater, c degraded crater (modified from Christoff et al. 2017)

Full size image

Figure 9 schematically shows a simple crater (A), a complex crater (B) and a crater in a state of degradation (C), considered to be valid for both cases A and B. The positions of the minimum, maximum and mean values are represented by dots. The colored rectangular intersection areas show the positions of the computed constraint domains.

For a given Area, we compute the minimal (Min), the maximal (Max) and the mean pixel value (Mean). The proposed method is a fast quantization method that consists in labeling pixels depending on the calculated Mean, Max and Min values for a given Area as described in Table 2. Each label stands for interval number, with the associated information beginning from the top to the bottom of the crater (with 1, the average ridge of the crater rim is labeled, label 2 represents the average height of the crater rim and the appearance of the crater etc.).

Table 2 Categorization limits and label values
Full size table

A parameter P is introduced to delimit six domains. After testing with several different values, we propose P to be between 2% and 3% and no larger than 4%. Setting the value of P in these intervals means that the significant crater descriptor information (such as the average bottom of the crater, average rim, etc.) will be included. We explore what different values of P imply for our results below.

Fig. 10
figure 10

Representation of the quantization method for feature extraction based on six labels. The change of the delimitation of the six domains, using different values of P over the reshaped minimal curvature \(k_2\) (a, c, e) (in scale \([-0.05 0.05]\)) and the gray minimal curvature \(k_{2G}\) (b, d, f) of different size craters (A, B, C) is visualized in scale [0, 255]. Crater A is old, overlapped, huge crater with radius of 55 px. Crater B is old, overlapped by crater C, medium crater with radius of 16 px. Crater C is fresh, overlapped, medium crater 8 px in radius

Full size image

In Fig. 10 an example of the proposed method for computing the features is presented, using the quantization rules in Table 2. Figure 10A–C describe the neighborhood of craters present in the Barlow catalog. The crater in Fig. 10B can be seen on lower right side of 10A and the one in Fig. 10C on the upper right side of Fig. 10B. Figure 10a, c and e represent the resized \(20 \times 20\) window around each crater and the Fig. 10 b, d and f are their respective grayscale representations. All six images are quantized according to the proposed approach using different values for the parameter P. The goal is to show that regardless of the size of the window, the proposed algorithm deals very well with the visualization of the crater’s features. It is noticeable that \(P= 0.02\) is suitable for craters with a diameter bigger than 6 km. According to the goal of this article and after experimental testing with different values, for detecting smaller craters with diameters less than 6 km, a \(P = 0.03\) is chosen because of best results.

The information extracted from the Area, which can contain (or not) craters, hereafter called newArea, is a set of categorization attributes, obtained with the quantization procedure explained in Table 2. The values reveal certain characteristics of particular area of the image, such as edges or changes in texture.

For fresh craters, the average rim receives values 1 (blue) and 2 (green). The values of 3 (yellow) represent the transitions from the average rim to the average bottom of the crater. The transition from the average rim to the average surface of Mars is labeled with 4 (orange). The values of 5 (red) is the transition of the average surface of Mars and the average bottom of the crater has a value of 6 (violet). Regarding the ratio radius/depth of the crater and the level of the degradation, it is possible that some values are not present. For large and heavily degraded craters, the average rim indices can obtain the values 1, 2 and 3. The average bottom of those craters is filled and is on the same level as the surface. They both are labeled with 6.

4.2 Classification with Multilayer Perceptron (MLP)

For the classification task we use the classical feedforward multilayer perceptron with supervised learning, described in details in Kasabov (1996). This is an arrangements of units into layers. The single unit (hereafter called neuron) is a component in a network, connected to other units through weights. The information moves in only one direction, forward, begins from the input, make connections (nodes), similar to the human brain and goes to the output, where the probability being in a given group (class) is computed. The procedure is divided into three phases: learning, validation and test.

The features, calculated in Sect. 4.1, presented as vectors, and the class label are injected into the neural network as inputs. The basic idea of the proposed model of the neural network is to be independent of the number of inputs (the feature vectors). The number of hidden neurons, defining the depth of the network, needs to be defined. Finding the optimal number of these nodes is a difficult task (Kasabov 1996). One of the solution that the author proposes is the Growing neural network. It is a neural network, that start the training procedure with a small number of hidden nodes. The number may increase, subject to the error calculated. After several tests, the best results were obtained with 50 hidden neurons.

The conjugate back propagation gradient is used for the training of the network, which offers the best compromise between quality classification and performance according to  Møller (1993).

We estimate how well the model is able to be trained with some data and then if it will make a reliable classification using some new provided data (i.e. data it has not been trained with). To ensure that the validation results will be not overfitted, due to the optimization of the data (Hawkins 2004), k-fold cross validation is used to tune the model hyper parameters. This is a procedure for estimation of the abilities of the given neural network to work with new data. An independent test set corresponds to dividing the database into three sets: training, validation and test (Ripley 1996).

Values of k equal to 5 or 10 are typically chosen (Kasabov 1996; and James 2013). Our data set, obtained in Sect. 3.3 to train and test the neural network, contains 1505 positive samples (containing crater) and same number negative samples (does not contain crater). We wanted to provide an output of k fitted models that are less correlated with each other. Having this presumption, we chose \(k = 5\), since the overlap between the training sets in each model is smaller. The distribution of the three sets is set to \(80\%\), \(10\%\) and \(10\%\). Four folds or 80% are used for the training. As far as we know, there is not any research finding which suggests that the percentages for the validation (V) and percentages for the test (T) need to be the same or different. We used nested cross-validation [estimates the generalization error of the underlying model and its (hyper)parameter search], where the 20% are equally divided into \(V=T=10\). A detailed explanation of the results is given in Sect. 5.

Once the learning step is completed, the classes assigned to each sample are obtained as an output that represents the detection (or not) of craters on the specific newArea.

To test the network’s performance, the previously trained network is reused for crater detection on the testing areas 1, 2 and 3 (see Fig. 4), with previously applied preprocessing step.

For the detection of craters of different sizes, the curvatures \(k_{2,G}\) are resized and a pyramid is constructed. The size of each layer is reduced with \(1.2^{-1}\) times the size of the previous layer. The first layer of the pyramid represents the original dimensions of the \(k_{2,G}\) and the last is the smallest crater region with a width and height of at least 20 pixels. On each layer, a window of \(20 \times 20\) pixels is slided each time by 3 pixels to scan the minimal curvature \(k_{2,G}\). For each window, the characteristics are extracted using the algorithm described in Sect.  4.1. The local values Max, Mean and Min are used to mark the domains defined in Table 2. Each window indicates a new entry for the neural network. It aims to estimate the probability for each entry to belong to one of two classes “crater” or “non-crater”. The decision for the region is made on the basis of the class with the highest probability. These are the regions of interest for which we will seek to extract the edges of the craters.

4.3 Extraction of Crater Contours

The rim extraction is the last step of the proposed algorithm. The coordinates of the area newArea in which a crater is detected are saved. Then, a CHT technique is applied over the corresponding \(k_{2,G}\) images of those saved coordinates. This is a specific feature extraction technique, whose purpose is to draw potential circles from imperfect image inputs. The circle candidates are produced by voting in the Hough parameter space and then selecting local maxima in a so-called accumulator matrix.

Over the detected crater regions,  Di et al. (2014) proposed to position a mask over each pixel of the original DEM. For each mask, the authors calculate the local mean, the largest deviations from this mean to the minimum or to the maximum of the values. These ranges of values, assigned to each region, are used to calculate the binarization threshold of the image, therefore a topology change on the region. In  Di et al. (2014) a morphological closing is then performed, followed by a thinning in order to reduce the lines of the image to the width of a pixel. The transformed image is ready to undergo the CHT.

Fig. 11
figure 11

Result after CHT on the image \(k_{2,G}\): a delimitation of the edge of the crater, b fine delimitation of the edge of the crater

Full size image

Delimitation of the edge of the crater In this work, to save time and memory, the parameters, such as the threshold for determining edge pixels in the image, sensitivity for the circular Hough transform accumulator matrix, the radius and the polarity of the object, are directly indicated. The object polarity adapts the circle (the dark area of the image). The radius is chosen with values raging from \(\in\) [5, 10], assuming detected circle crater in the sub-window \(20 \times 20\). Circles, bigger then the size of the window, are excluded (the center coordinates are in the \(20 \times 20\) window, but the edge is outside). The local darkest points of the three dimensional accumulator provide the position and radius of the crater. The completeness of the circle is given by the accumulator. Reducing the threshold condition generates more false positive circles, so the minimal threshold value is set to 0.1. Data from the circle, thus obtained (estimated center coordinates and diameter), are finally readjusted and resized according to the coordinates of the map. In Fig. 11a), the obtained results of applied Circular Hough Transform on the \(k_{2,G}\) image, containing a crater are shown. The blue circle is the estimated crater rim and the red line is the circle radius r, estimated at 14.8 km.

Fine delimitation of the edge of the crater In nature, crater diameters are not power of 2 and resizing will not give correct coordinates for centers and exact limits. From the list of radii and centers of resampled craters, the CHT is again applied. We try to obtain a radius in the constraints \([r*0.5, r*1.5]\) and we change the minimal threshold to 0.001. The results of this delimitation are presented in Fig. 11b). We estimate the edge of the same crater at 13.06 km, visualized by the green circle. This hardly changes the center of the crater.

We apply the similarity criteria: once after each layer, which is used for the construction of the list; the second is for each element of this list. The new values are obtained, based on the following equations:

$$\begin{aligned}&x_{cr}=\frac{\sum _{1}^{m}x_{m}}{m} ;&y_{cr}=\frac{\sum _{1}^{m}y_{m}}{m} ; &r_{cr}=\frac{\sum _{1}^{m}r_{m}}{m} \end{aligned}$$
(4)

In case of coincidence, the coordinates (\(x_{cr}, y_{cr}\)) and the radius \(r_{cr}\) for a crater are computed from the division of the sum special coordinates and radius by the number of similar entries m.

5 Results and Discussion

The fine delimitation has already been shown to correctly detect the edges of craters, but the number of detections is decreasing. We will explore the quality of the results, before and after delimitation, to prove that delimitation also increases the ability of detection.

The accurate identification of the diameter of the impact crater is an important criterion to validate the efficiency of the impact crater detection approach. The diameter of impact craters, detected automatically in Christoffet al. (2018) and the results presented in this article are compared in Table 3.

Table 3 Crater counting over the testing sites 1, 2 and 3, before and after the fine delimitation of the crater rim
Full size table

The results of the detection before the precise delimitation are presented in our previous work (Christoffet al. 2018). They are validated by the Barlow catalog. The reader should keep in mind that all crater centers presented in the Barlow catalog are counted, as well as those that are not entirely within the boundaries of each zone. We decided to do the validation with the Robbins and Hynek (2012), so that the comparison with the method of Di et al. be fairer. In the statistics given, we exclude these craters, that are not entirely included in the selected areas.

Fig. 12
figure 12

Finally readjusted and resized craters rim (green circles) and their radius, resulted after CHT on the \(k_{2,G}\) image and craters rims, according to Robbins and Hynek (2012) (purple circles on the left) and according to Barlow catalogue (yellow circles on the right). The shift between the catalogue and our positions of craters centers are represented with blue arrows

Full size image

Figure 12 shows a small area with resized, readjusted craters rim, obtained using our approach. The edges of the craters are colored in green, because they appear in at least one catalogue and in red, because they are not considered as a crater by the expert. On the left, the entries in the Robbins and Hynek (2012) are displayed in purple. It can be seen that there is no big difference with respect to the position of the circles. On the right, craters noted in Barlow’s catalog are shown by yellow circles. We can observe that they are not centered. We align the coordinates of the centers with a distance and a direction as they are represented in Fig. 12 (on the right) (with blue arrows). The size of our diameters varies between 1 and 1.3 times the diameter of the crater rim, defined by Barlow.

Fig. 13
figure 13

Three patches on Mars, a site 1, b site 2 and c site 3, used for the validation of the proposed approach. They are presented as images of computed gray-scale minimal curvature \(k_{2,G}\). Green circles represent correctly detected crater rims (correspond to at least one of the four catalogs). Green rectangles correspond to craters in Robbins and Hynek (2012). Blue circles indicate all craters manually labeled as craters. Red rectangles are FN, they are those that have been omitted by our method. The red circles represent the wrongly detected craters

Full size image

The quality factors of detection percentage (see Eq. 5), quality percentage (see Eq. 6) and branching factor (see Eq. 7) developed by Shufelt (1999) are used in many other CDAs to evaluate the performance of the method ( Bandeira et al. 2012; and Di et al. 2014). The craters classification can be true positive (TP), which stands for the number of real detected craters, false positives (FP) stands for the number detected craters that are not actually craters and FN stands for the number of false negative detections (undetected real craters).

To calculate the quality factors and evaluate the performance of our method, we categorize each crater as TP or FP, according to the principle of Shufelt (1999). It is applied to match a crater to the Barlow catalog crater and the Robbins and Hynek (2012). To validate all the craters and save time, we matched our craters with two other catalogs: Rodionova et al. (2000) and Salamunićcar et al. (2012). The number of TPs is completed by the number of craters that are manually checked and signed as craters. Entries that did not appear in any catalog and are not counted as craters are the number of FP. During the similarity process, for the Robbins catalogs, we count the number of these craters that do not match any of our craters. This sum indicates the value of false negatives (FN).

$$\begin{aligned}&Detection~Percentage = 100 \times \left( \frac{TP}{TP + FN}\right) \end{aligned}$$
(5)
$$\begin{aligned}&Quality~Percentage = 100 \times \left( \frac{TP}{TP + FP+ FN}\right) \end{aligned}$$
(6)
$$\begin{aligned}&Branching~factor = \left( \frac{FP}{TP}\right) \end{aligned}$$
(7)
Table 4 Standard quantitative quality assessment of impact craters detected by the proposed algorithm
Full size table

Table 4 lists the impact crater counts and accuracy of the CDA in the validation sites. The crater-detection results are shown in Fig. 13. The correctly classified by the neural network craters and confirmed by the Robin’s catalogue are delimited with green box on the computed gray-scale minimal curvature \(k_{2,G}\). The green circles are the craters, provided by CHT, that exist in at least in one of the four catalogs. Craters that are TP but have not been identified in any of the catalogs are manually labeled as craters and are visualized by blue circles. Red circles represent FP. The red boxes surround the craters in the Robbins catalogue that are omitted by our method.

Table 5 Comparison with Di’s CDA
Full size table

In Table 5 are compared the quality factors for our approach and the one described by Di et al. (2014). For Site 2 and 3 we obtain higher detection rate than Di et al. (2014), but the branching factor is on the downside (smaller is better) because of the larger number of FP. On Site 1, we obtain better branching factor, due to the small quantity of FP detections. As it can be observed, the quality factor from our approach is similar to the one of Di et al. (2014). It is worth noting that: (1) the results in Di et al. (2014) are also obtained using Robbins catalogue (Robbins and Hynek 2012) as ground truth; (2) to detect the crater regions, they use a sliding window on DEM data layers, beginning with the original DEM size. Each new layer is resized \(1.2^{-1}\) times.

For Di et al. (2014), the TP and FP values change when the threshold T of the classifiers is adjusted. Di et al. (2014) restrained the evaluation factor B at around 0.15 and they cannot detect some of the craters. Most of these non detected craters are deeply degraded and modified so they are rejected by the classifiers. Notably, the smallest crater detected with a \(20 \times 20\) pixels window is about \(4 \times 4\) pixels. Very small craters cannot be detected by their approach because the features for the classifier are absent.

6 Conclusion and Future Work

With the proliferation of computer vision algorithms, the availability of more detailed and with higher resolution planetary image datasets, there is a need for effective CDAs. These algorithms can save time and effort to the planetary experts and facilitate their work in determining the age of a particular solid surface planetary body.

In this article we have described a new approach for crater detection. This method is an original combination between differential estimators on a surface mesh and a neural network algorithm in order to consolidate the results. This combination produces much better detection results than other methods, and this can undoubtedly be used to detect more generic round shapes on meshes, in other contexts.

The detection rates of the method on a validation Sites 1, 2 and 3 are respectively \(76.3\%\), \(81.5\%\) and \(96.1\%\).

As future work, we plan to test the algorithm on bigger areas with a higher number of vertices. This would allow for an enhancement of the detection rate while also producing more robust results and a better visualization.