Seismic vulnerability of above-ground storage tanks with unanchored support conditions for Na-tech risks based on Gaussian process regression

Abstract

This paper aims to investigate the seismic vulnerability of an existing unanchored steel storage tank ideally installed in a refinery in Sicily (Italy), along the lines of performance-based earthquake engineering. Tank performance is estimated by means of component-level fragility curves for specific limit states. The assessment is based on a framework that relies on a three-dimensional finite element (3D FE) model and a low-fidelity demand model based on Gaussian process regression, which allows for cheaper simulations. Moreover, to approximate the system response corresponding to the random variation of both peak ground acceleration and liquid filling level, a second-order design of experiments method is adopted. Hence, a parametric investigation is conducted on a specific existing unanchored steel storage tank. The relevant 3D FE model is validated with an experimental campaign carried out on a shaking table test. Special attention is paid to the base uplift due to significant inelastic deformations that occur at the baseplate close to the welded baseplate-to-wall connection, offering extensive information on both capacity and demand. As a result, the tank performance is estimated by means of component-level fragility curves for the aforementioned limit state which are derived through Monte Carlo simulations. The flexibility of the proposed framework allows fragility curves to be derived considering both deterministic and random filling levels. The comparison of the seismic vulnerability of the tank obtained with probabilistic and deterministic mechanical models demonstrates the conservatism of the latter. The same trend is also exhibited in terms of risk assessment.

1 Introduction

1.1 Background and motivation

The integrity of the oil and gas industry, and in particular of large-capacity atmospheric tanks for hazardous material storage, is important not only for maintaining the flow of energy products but also for preventing significant potential catastrophic events. Therefore, the assurance of adequate levels of safety of liquid storage tanks and the use of advanced seismic performance assessment techniques that account for all possible sources of uncertainty is of paramount importance within the performance-based earthquake engineering (PBEE) (Cornell and Krawinkler 2000; Hermkes et al. 2014; Saha et al. 2016). Along the same vein, Kameshwar and Padgett (2018), Bernier and Padgett (2019) and Bernier et al. (2019) proposed specific approaches to quantify both vulnerability and risk of anchored storage tanks subjected to hurricane effects.

Two crucial steps of the PBEE are represented by the damage analysis that incorporates any engineering demand parameter (EDP) distribution into fragility functions; and the loss analysis that is typically expressed in the form of mean annual frequency (MAF) of exceeding a threshold of interest for industrial owners and stakeholders.

Concerning fragility functions of steel storage tanks, very few public databases are available, e.g. ALA (2001a, b) and HAZUS (2001). They are empirically built for general types of components with substantial amounts of assumptions and uncertainties involved in material and geometry properties and limit states. Other research efforts for establishing fragility functions used: (1) historical or empirical observations employed in probit functions, e.g. Salzano et al. (2003) or (2) analytical approaches covering single failure modes that use simplified or refined models for fluid–structure interaction modelling, e.g. Iervolino et al. (2004), Buratti and Tavano (2014), Phan et al. (2016), (2017), Cortes and Prinz (2017) and Phan et al. (2019). Regarding analytical approaches, fragility functions are derived using the results of nonlinear dynamic analyses of structural models; therefore, the accuracy of fragility functions strongly depends on the reliability of relevant models. As a result, given the complexity of various nonlinear mechanisms involved in unanchored storage tanks such as liquid-tank and tank-foundation interactions, three-dimensional finite element (3D FE) models are more suitable for predicting nonlinear responses of the whole system. In this respect, 3D FE models outperform because: (1) they account for full interaction between limit states; (2) they distinctly indicate the interaction between tank and liquid as well as tank and foundation; (3) they minutely allow for the estimation of system fragility curves. Unfortunately, the computational time involved in these high-fidelity (HF) models is rather high. Hence, a fragility analysis that can rely on such complex models and accounts for all possible sources of uncertainty seems not to be viable.

A valid alternative to improve computational efficiency, also in this context, is the use of surrogate models [low-fidelity (LF) models] that can be defined as a synthetic model family representing the statistical relation between seismic inputs and structural outputs. They can be built from a few numbers of response samples generated through accurate numerical models or experimental data (Bhosekar and Ierapetritou 2018). Several LF approaches are available in the literature, which are based either on regression or interpolation models; in particular, high-dimensional model representations, polynomial regressions, artificial neural networks, Bayesian networks, multivariate adaptive regression splines, radial basis function networks, support vector regressions, and Kriging were proposed (Van Beers and Kleijnen 2003; Kleijnen 2017; Forrester et al. 2008).

Among various types of LF models, Kriging or Gaussian process regression is adopted in this study. The basic idea of Kriging is to predict the value of a function at a given point by computing a weighted average of known values of the function in proximity of the point. This approach treats the function of interest as a realization of a Gaussian random process whose parameters are estimated from available inputs and model responses (Rasmussen and Williams 2006; Lu et al. 2018). This specific metamodel was selected because: (1) it represents the best linear unbiased predictor (Sacks et al. 1989); (2) it is only based on matrix manipulations; (3) it can provide an exact interpolation, i.e. it performs as the high-fidelity model when the input is the same as that of the training data; (4) it provides both the prediction but also the local variance of the prediction error. Inevitable drawbacks are related to: (1) the inversion of the covariance matrix, whose size could entail serious computational problems; (2) the estimation of the hyperparameters that involves a constrained iterative search. This why kriging was successfully used both in seismic risk assessment and seismic fragility analysis (Gidaris et al. 2015; Ghosh et al. 2019), and in real-time storm/hurricane risk assessment (Jia and Taflanidis 2013). As a result, Gidaris et al. (2015) adopted a Kriging model to approximate mean and standard deviation values of structural demands, allowing to analytically evaluate seismic fragility functions of a four-story concrete office building. Zhang and Wu (2017) further applied a Kriging model for the seismic fragility analysis of an elastoplastic single-degree-of-freedom (SDOF) system and a reinforced concrete bridge. More recently, Ghosh et al. (2019) also employed a Kriging metamodel-based Monte Carlo simulation to improve the seismic fragility analysis of structures. More precisely, they implicitly considered record-to-record variability of earthquakes utilizing the adaptive nature of Kriging.

1.2 Scope

From a PBEE viewpoint, the seismic fragility of a liquid storage tank has not been adequately investigated with the implementation of an accurate 3D structural model which accounts for the randomness both in the input motion and structure level, for instance, peak ground acceleration ($\text {PGA}$) and liquid filling level; these are the issues that the paper explores further. Thus, in order to set seismic fragility functions, both HF and LF models of a steel storage tank with unanchored support conditions based on a Kriging model and a design of experiments (DOE) method are proposed herein. Though both Eurocode 8, part 4 (2006) and API 650 (2007) restrict uplift of unanchored above-ground storage tanks, their seismic response is highly nonlinear, dependent on several parameters and much more complex than that predicted by design standards based on a mechanical spring-mass analogy. Therefore, several unanchored above-ground storage tanks stand in areas with a high risk of earthquakes either because they are not properly designed or because they were not seismically designed at all. Moreover, both Ormeño et al. (2012) and Pineda et al. (2012) indicated that very strong earthquakes caused uplifting and sliding and, therefore, damage even in the presence of self-anchored tanks resulted to be often inefficient.

Accordingly, Sect. 2 describes the main features of Kriging to be used for unanchored storage tanks. In turn, 3D FE models for an unanchored tank characterized by different liquid filling levels are developed using the ABAQUS software in Sect. 3, where the fluid–structure interaction between liquid and tank is taken into account by a coupled acoustic-structure analysis. A calibration/validation of a HF model is also carried out in this section using the results of a wide experimental investigation. In Sect. 4, in order to sample random variable realizations within a set of eight ground motion records and filling levels, the central composite design (CCD) for the DOE is introduced, that enables least square estimation of all effects in a second-order polynomial. Then, in Sect. 5, the fragility analysis is performed based on a large number of samples generated with the Monte Carlo technique by using the proposed meta-model. Finally, conclusions and future developments are provided in Sect. 6.

2 Kriging-based low-fidelity model for unanchored storage tanks

2.1 Basic equations of Kriging model

In this section, the basic equations of the Kriging model are briefly overviewed. As well-known from the literature, Gaussian process regression also known as Kriging, is a method of approximation used in statistics, by which unknown interpolated values are modelled by a Gaussian process (Van Beers and Kleijnen 2003). The Kriging model is useful for predicting spatially correlated data and its flexibility is a result of a wide range of correlation functions to build the model. The formulation of the Kriging model is composed of two terms, as shown in Eq. (1) (Santner et al. 2003), where the computer model output $y\left( {\mathbf{x}} \right)$ is a realization of a Gaussian process,

$$Y\left( {\mathbf{x}} \right) = {\varvec{\upbeta}}^{T} {\mathbf{f}}\left( {\mathbf{x}} \right) + Z\left( {\mathbf{x}} \right).$$

(1)

The first term is the mean value of the Gaussian process represented by a vector of known regression functions ${\mathbf{f}}\left( {\mathbf{x}} \right)$ and a vector of unknown regression coefficient vector $\upbeta$, and the second term $Z\left( {\text{x}} \right)$ is a zero-mean stationary Gaussian process with a covariance function,

$$cov\left( {Z\left( {\varvec{x}_{i} } \right),Z\left( {\varvec{x}_{j} } \right)} \right) = \sigma^{2} R\left( {\varvec{x}_{i} - \varvec{x}_{j} |\varvec{\theta}} \right),$$

(2)

where $\sigma^{2}$ is the process variance. The spatial correlation function $R\left( {{\mathbf{x}}_{\text{i}} - {\mathbf{x}}_{\text{j}} |{\varvec{\uptheta}}} \right)$ with known or unknown correlation parameters ${\varvec{\uptheta}}$ controls the smoothness of the resulting Kriging model and the influence of nearby points.

Given the input points ${\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{n}$ and the corresponding computer output values ${\mathbf{Y}}^{n} = (Y\left( {{\mathbf{x}}_{1} } \right),Y\left( {{\mathbf{x}}_{2} } \right), \ldots ,Y\left( {{\mathbf{x}}_{\text{n}} } \right))^{T}$, the output $Y\left( {{\mathbf{x}}_{0} } \right)$ at a new input point ${\mathbf{x}}_{0}$ can be predicted using the above Kriging model. Assuming the hyperparameters ${\varvec{\uptheta}}$ is known,

$$\left( {\begin{array}{*{20}c} {Y\left( {\varvec{x}_{0} } \right)} \\ {\varvec{Y}^{n} } \\ \end{array} } \right)\;\sim\;N_{n + 1} \left( {\left( {\begin{array}{*{20}c} {f_{0}^{T} } \\ \varvec{F} \\ \end{array} } \right)\varvec{\beta},\sigma^{2} \left( {\begin{array}{*{20}c} 1 & {r_{0}^{T} } \\ {r_{0} } & \varvec{R} \\ \end{array} } \right)} \right),$$

(3)

where ${\mathbf{f}}_{0} = f\left( {{\mathbf{x}}_{0} } \right)$ is the $p \times 1$ vector of regression functions of $Y\left( {{\mathbf{x}}_{0} } \right),\;{\mathbf{F}} = f_{j} \left( {{\mathbf{x}}_{i} } \right)$ is the $n \times p$ matrix of regression functions for the training data, $r_{0}$ is the $n \times 1$ vector of correlation of ${\mathbf{Y}}^{n}$ with $Y\left( {{\mathbf{x}}_{0} } \right),\;{\mathbf{R}}$ is the $n \times n$ matrix of correlation among ${\mathbf{Y}}^{n}$.

Then, the best linear unbiased predictor of $Y\left( {{\mathbf{x}}_{0} } \right)$ is extracted from Eq. (3), i.e.

$$\hat{Y}\left( {\varvec{x}_{0} } \right) = \left( {\varvec{f}_{0}^{T} (\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{F})^{ - 1} \varvec{F}^{T} \varvec{R}^{ - 1} + \varvec{r}_{0}^{T} \varvec{R}^{ - 1} (\varvec{I}_{n} - \varvec{F}\left( {\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{F})^{ - 1} \varvec{F}^{T} \varvec{R}^{ - 1} } \right)} \right)\varvec{Y}^{n} ,$$

(4)

and the mean standardized error of the estimate $\hat{Y}\left( {{\mathbf{x}}_{0} } \right)$ is formulated as

$$MSE\left( {\hat{Y}\left( {\varvec{x}_{0} } \right)} \right) = \sigma^{2} \left( {1 - \varvec{r}_{0}^{T} \varvec{R}^{ - 1} \varvec{r}_{0} + \left( {\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{r}_{0} - \varvec{f}_{0} } \right)^{T} \left( {\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{F}} \right)^{ - 1} \left( {\varvec{F}^{T} \varvec{R}^{ - 1} \varvec{r}_{0} - \varvec{f}_{0} } \right)} \right).$$

(5)

In order to obtain a Kriging LF model, usually, the hyperparameter vector ${\varvec{\uptheta}}$ is unknown and needs to be estimated. In this respect, the maximum likelihood estimation is commonly used to identify the vectors ${\varvec{\upbeta}}$, $\sigma^{2}$, ${\varvec{\uptheta}}$ such that the likelihood of observations ${\mathbf{Y}}^{n}$ is maximum.

2.2 Kriging-based LF model with random effects

In view of the fragility evaluation of unanchored storage tanks based on Kriging, the entire procedure for defining fragility functions is reframed herein. Initially, input random variables ${\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{n}$ need to be distinctly defined. Generally, uncertain modelling parameters of storage tanks include both geometry and material properties. In this respect, in order to find which modelling parameters entail a significant effect on the seismic response of unanchored tanks, Phan et al. (2019) carried out a screening study; the authors found that the liquid filling level, among other geometry and material random variables such as shell plate thickness, baseplate thickness, steel yielding strength and liquid density, is the most significant one for the purpose of determining fragility functions. They have also found that fragility curves developed considering only the most significant modelling parameter are almost the same as those considering all random variables. As a result, the liquid filling level and $\text {PGA}$ are considered as random variables in this study, representing the randomness of both structural modelling and seismic ground motions.

The next step of the proposed framework foresees the generation of samples of input random variables using a proper DOE methodology. Among different sampling methods available in the literature, Latin hypercube sampling (LHS) is often suggested for the Kriging metamodeling (Jack and Kleijnen 2017). Nonetheless, the CCD also represents a viable alternative (Jack and Kleijnen 2017; Paolacci and Giannini 2009). More precisely, this sampling method is widely adopted in physical experiments where replication errors exist due to unknown randomness. By minutely selecting corner, axial, and centre points, it approximates in a second-order response surface model, where all higher-order effects are zero. However, given the fact that seismic records with the same $\text {PGA}$ are characterized by different frequency content, and only two random variables are considered, a relatively low number of sample points, i.e. simulations, is involved in the CCD. An in-depth discussion is presented in Subsection 4.2.

In a subsequent step, a 3D FE model of the unanchored tank is developed for each sample with a distinct filling level and $\text {PGA}$, and nonlinear time history dynamic analyses are performed. Peak responses are measured for each simulation and both mean and standard deviation of the response quantities are computed assuming a lognormal distribution. This is a common assumption in earthquake engineering; see, among others, Gidaris et al. (2015) and Jalayer and Cornell (2009). As a result, two distinct experiment designs are obtained, one for the mean value of measured responses and the other one for relevant standard deviations.

The following step consists in the development of the Kriging LF model for both mean and standard deviation of the response that is defined as

$$\hat{\varvec{Y}} = e^{{\hat{\varvec{Y}}_{\mu } + LogN\left( {0,\hat{\varvec{Y}}_{\sigma } } \right)}}$$

(6)

where $\hat{\varvec{Y}}_{\mu }$ and $\hat{\varvec{Y}}_{\sigma }$ are the Kriging model of the mean and standard deviation of the response quantity vector ${\mathbf{Y}}^{n}$. Equation (6) assumes a lognormal distribution of the response vector. Finally, in the last step Monte Carlo simulations are conducted based on the built proposed Kriging LF model. As a result, fragility curves that provide a probability of exceeding a given EDP associated with a critical limit state are derived.

2.3 Validation of Kriging model

The performance of the metamodel can be validated by calculating the error between observed and estimated values. The most common approach is the leave-one-out (LOO) cross validation. In order to perform the LOO, one point $\varvec{x}_{i}$ of the design of experiments is subsequently removed and the metamodel $\hat{\varvec{Y}}_{{\left( { - i} \right)}} \left( {\varvec{x}_{i} } \right)$ is computed from the remaining points of the design. The relative LOO error between the predicted and real responses for all $\varvec{x}_{i}$ is then investigated by means of

$$\varepsilon_{LOO} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left[ {\varvec{Y}\left( {\varvec{x}_{i} } \right) - \hat{\varvec{Y}}_{{\left( { - i} \right)}} \left( {\varvec{x}_{i} } \right)} \right]^{2} .$$

(7)

For an easier interpretation of this LOO error, a determination coefficient $Q^{2} = 1 - \varepsilon_{LOO} /{\text{Var}}\left( {\hat{\varvec{Y}}} \right)$ can be extracted, where ${\text{Var}}\left( {\hat{\varvec{Y}}} \right)$ defines the estimated variance of the output variable. Therefore, a $Q^{2}$ value close to 1 indicates a better prediction capability of a metamodel.

3 3D FE model of an unanchored storage tank

3.1 Case study

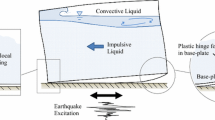
In order to facilitate a comparison with previous works, the case study of an existing unanchored storage tank presented in Phan et al. (2016) and Phan et al. (2019) is selected for this study. The tank falls under the category of broad configuration due to the slenderness ratio $H/R =$ 0.51 and is unanchored with respect to the foundation. The tank diameter is 54.8 with a total height of 15.6 m, which is divided into nine shell courses. The tank is equipped with a floating roof, whose effect is overlooked in this study. The thickness of the shell courses is designed to vary from 33 mm at the bottom to 8 mm at the top. Dimensions of the actual tank and tested mock-up are shown in Fig. 1. As the tank was designed in the 1970s, due to the lack of European seismic design standards, no annular plate was present at the base. The baseplate is endowed with a uniform thickness of 8 mm. The tank, here selected as the prototype for an experimental campaign (Bursi et al. 2018), is assumed to contain water at a maximum filling level of 14 m, i.e. about 90% of the tank height. Both wall and baseplate are made of S235 carbon structural steel.

Fig. 1

Broad tank subjected to shake table tests: a dimensions of the prototype tank; b dimensions of the $1/\uplambda = 1/18$ tested mock-up

3.2 A 3D FE model based on the acoustic-structural coupling technique

The numerical modelling of unanchored storage tanks considering fluid–structure interaction, as well as foundation-structure interaction, has been widely studied in recent years. As a recent work, Phan et al. (2019) presented a 3D model of the whole system, seismically analysed by using a coupled acoustic-structural analysis available in the software ABAQUS (SIMULIA 2014). From a numerical viewpoint, the acoustic approach is relatively simple and effective because there is no material flow and thus no mesh distortion; and therefore, this modelling approach is selected in this study. In detail, the liquid domain is modelled using eight-node brick acoustic elements (AC3D8) while four-node doubly curved quadrilateral shell elements (S4R) are used to model the steel tank. The tank-liquid interaction is simulated employing a surface-based tie constraint between the inner tank and liquid surface; this constraint is formulated based on a master–slave contact method, where normal forces throughout the simulation are transmitted using tied normal contact between surfaces. The sloshing waves of the free surface are also considered in the liquid model by means of a small-amplitude gravity waves assumption (Akyildiz and Unal 2006). Nonlinear phenomena are indeed mainly due to impulsive waves that act in the region of the baseplate-to-wall connection. The tank baseplate is assumed to rest on a rigid slab that is modelled using solid elements. Both the uplift and sliding phenomena between the tank base and the rigid slab are taken into account by a general contact modelling algorithm. The relevant boundary conditions of the 3D model are shown in Fig. 2 and the FE mesh for each part is illustrated in Fig. 3. Following Phan et al. (2019), a FE mesh size of 0.4 × 0.8 m for the longitudinal and circumferential direction is used, respectively. The aforementioned size is the outcome of a mesh convergence analysis, Phan et al. (2019), carried out utilizing nonlinear static analyses on the prototype tank, i.e. the one with H = 14 m, with a coarse mesh − 0.8 × 1.6 m-, a normal mesh − .6 × 1.2 m-, a fine mesh − 0.4 × 0.8 m- and a refined mesh − 0.2 × 0.4 m-. In order to achieve a good compromise between accuracy and computational time insofar as possible, a more refined mesh for the region near the connection is finally coupled to a size of 0.1 m for the longitudinal direction.

Fig. 2

Boundary conditions of the coupled acoustic-structure approach

Fig. 3

Numerical model of each part of the interaction system

Geometric and material nonlinearities are considered in the analysis. In particular, the plasticity of the steel is simulated using the true stress-true strain relationship of the material obtained from mechanical tests (Bursi et al. 2018). The liquid has a water density of 998.2 ${\text{kg}}/{\text{m}}^{3}$ and a bulk modulus is equal to 2150 MPa. Concerning the damping model, a mass proportional damping model is employed with a damping ratio of 2.0% at the first impulsive vibration mode of 77.15 Hz. Since the nonlinear behaviour of the liquid free surface due to the convective motion is neglected and the small-amplitude gravity assumption is used, both the first convective and impulsive modes have been considered as the most significant modes contributing to the total response of the system (Malhotra 1995). As a result, to reduce the computation time, symmetric boundary conditions are adopted both for the acoustic and other domains.

3.3 An experimental campaign for the validation of the 3D FE model

The ability of the aforementioned FE model to simulate typical phenomena present in unanchored tanks is carried out through the results of a shaking table test campaign performed on a broad tank (Bursi et al. 2018). The latter represents a reduced scale model of the tank introduced in Subsection 3.1. Since a perfect downscaling of the prototype was not possible, due to the very limited thin thickness, the test program was conducted with the minimum 1.5 sheet thickness available on the market. Accordingly, a 3 m diameter and 0.868 m height cylindrical tank, which is approximatively a “1/λ = 1/18” reduced scale model of the broad tank presented in Subsection 3.1, was used in the test program. The shell wall of the tested mock-up is made of a cylindrical stainless-steel sheet with a thickness of 1.5 mm and is welded to the baseplate, which has the same material and thickness. A circular stiffener is present at the top of the shell. The specimen is simply rested on the shake table using an intermediate ethylene-propylene-diene monomer (EPDM) rubber sheet. This allowed both to obtain a friction coefficient between the tank base and the shaking table equal to $\upmu = 0.15$ and to protect the mechanical bearings and electrical circuits in case of water overtopping. The estimated mass of the empty tank is 123 kg; conversely, the tank filled with water at 90% of its height, i.e. 0.781 m, leads to a total mass of 5600 kg.

The horizontal components of the Chi–Chi Taiwan and Northridge USA earthquakes were used for testing (Bursi et al. 2018). The main characteristics of the seismic records are listed in Table 1. They were chosen to maximize distinct mechanical effects on the tank; in particular, the Chi–Chi record emphasized the sloshing behaviour for the potential damage of the floating roof while the Northridge excited more the uplift behaviour.

Table 1 Selected natural records and relevant mechanical effects

As a matter of fact, whilst the Chi–Chi signal conveys more energy in the high periods, with a significant influence on the top fluid dynamics, Northridge carries more energy in the low period range. However, in order to guarantee the activation of the desired mechanical behaviour in the scaled specimen, both natural records were properly scaled in time and amplitude.

With regard to the sloshing effect, the scaling factor was derived imposing the equivalence between actual $F$ and prototype $F_{0}$ Froude numbers, respectively. According to the more general Buckingham’s theorem,

$${{F}}_{ 0} { = }\frac{{{{V}}_{ 0}^{ 2} }}{{{{g L}}_{ 0} }}{ = }\frac{{{{V}}^{ 2} }}{{g L}}{{ = F,}}$$

(8)

where $L$ represents the geometrical dimension and $V$ the velocity of the examined phenomenon. Moreover, given $g = const$ and ${{L}} =\uplambda{t{L}}_{0}$, $V_{0} = \frac{V}{{\sqrt\uplambda }}$. As a result, in order to scale $V$ without modifying the record intensity, the same factor $\sqrt \lambda$ is applied to time t, i.e.

$${{t}}_{ 0} { = }\frac{{t}}{{\sqrt\uplambda }}.$$

(9)

On the other hand, the uplift of an unanchored tank is influenced by the ratio $\upsigma_{{p}} /\upsigma_{{y}}$ between plastic stresses reached at the tank baseplate and its yielding threshold. More precisely, plastic stresses generated by a seismic action depend on the intensity $\gamma$ of this action, the inertia of the tank defined by its fluid density $\rho_{f}$, and the tank geometry, assimilated to its radius, $R$. In order to properly investigate the uplift at the prototype scale, according to Buckingham’s theorem, the equivalence is established as

$$\frac{{\upgamma_{0} \uprho_{{f }} {{R}}_{0} }}{{\upsigma_{{y}} }}{ = }\frac{{\upgamma \uprho_{{f}} {{R}}}}{{\upsigma_{{y}} }}.$$

(10)

Given that ${{R = }}\uplambda{{R}}_{ 0}$, in order to impose the equivalence in Eq. (10), the intensity of the seismic input is scaled as well,$\upgamma { = }\frac{{\upgamma_{ 0} }}{\uplambda}$. Moreover, in order to preserve equivalence in terms of stresses, a velocity similarity needs to be imposed; provided that the accelerations are scaled by a factor $\lambda$, the velocity similarity is granted by scaling the time t as

$${{t = }}\uplambda{{t}}_{ 0} .$$

(11)

The resulting signals are depicted in Fig. 4 in terms of the acceleration time history and corresponding elastic response spectrum.

Fig. 4

Input signals used for shaking table tests: a Chi–Chi signal and b Northridge signal

The numerical hydrodynamic pressure on the shell wall is first obtained with the Chi–Chi signal. Figure 5 shows the numerical/experimental comparison of the hydrodynamic pressure distribution on the tank wall, whereas the time history data observed at the left end of the baseplate are also shown in Fig. 6. Both figures show a good matching.

Fig. 5

A comparison of peak hydrodynamic pressure distribution on the shell wall at $t$ = 4.04 s

Fig. 6

A comparison of hydrodynamic pressure time history at the left end of the baseplate

Time history data of sloshing wave height at the left end of the free surface are depicted in Fig. 7 based on the Chi–Chi record. The matching between the numerical and experimental results in terms of both frequency and amplitude is evident. Moreover, Fig. 8 highlights the time history data of the base uplift measured at the right end of the baseplate based on the Northridge input signal. A careful reader may notice that experimental uplift displacements include negative values because the tank is settled on an EPDM rubber sheet. Nonetheless, the numerical and experimental results match. In sum, from the comparisons above, one can argue that the proposed 3D FE model of the fluid–structure system represents a HF model of the filled broad tank.

Fig. 7

A comparison of maximum sloshing wave height time history at the left end of the liquid free surface

Fig. 8

A comparison of uplift time history at the right end of the baseplate

4 Hazard analysis and design of experiments method

4.1 Seismic hazard and record selection

Owing to the use of the DOE technique discussed in Subsection 4.2, only eight seismic records are selected for time history dynamic analyses with the HF 3D FE model described in Subsection 3.2. The tank is supposed to be ideally placed in one of the most seismically active zones in Sicily (Italy), the Priolo Gargallo village, characterized by soil type B, whose seismic hazard curve is depicted in Fig. 9a.

Fig. 9

a Seismic hazard curve of Priolo Gargallo (Italy) and b response spectra based on the UHS-based record selection

On the basis of a safe shutdown earthquake design condition (Bursi et al. 2018), the eight natural records, as collected in Table 2, have been identified for a return period of 2475 years. The relevant selection has been performed matching the mean ($\epsilon= 0$) and the mean + standard deviation ($\epsilon = 1$) uniform hazard spectrum (UHS), respectively; they are depicted with the solid red and black line for the mean and the dashed red and black line for the relevant mean + standard deviation in Fig. 9b. As a result, the hazard analysis takes into account only the uncertainties in magnitude, location and fault mechanism, while the uncertainties of record-to-record variability, expressed by the dispersion of the spectral ordinates, are directly transferred to the fragility functions when the multiple stripe analysis is carried out. This procedure reduces the record-to-record variability and at the same time preserves full hazard consistency.

Table 2 Main characteristics of the selected records

The record sample size ${{n}} = 8$ adopted is derived by the rule suggested by Baltzopoulos et al. (2018). More precisely, they suggested to relate n to the coefficient of variation of the failure rate estimator $COV$ as $\sqrt {{n}} { = }\Delta / {{COV}}$, where $\Delta$ is a parameter that depends on both the dispersion of structural responses and the shape of the hazard curve at the site. Based on the localized nonlinearities involved herein, a non-particularly efficient intensity measure (IM), e.g. $\text {PGA}$, and a high seismicity zone (Phan and Paolacci 2016), corresponding to a slope of the hazard curve of about 3, $\Delta$ can read 0.5–0.6 (Jalayer and Cornell 2003). As a result, for a coefficient of variation ${{COV}} = 0.2$, considered acceptable to maintain a certain accuracy, the number of records $n$ ranges between 6.2 and 9. Given the small value of the ratio $\Delta /{{COV}}$, and therefore of n, the number of selected ground motions of Table 2 is chosen to be 8; in practice, this figure is limited given the 72 HF FE simulations carried out in Subsection 4.2. Moreover, the value of $COV$ selected is considered to be acceptable because it refers to risk error and not to record-to-record variability (Baltzopoulos et al. 2018).

4.2 Central composite design

As mentioned in Subsection 2.2, both tank filling level and seismic records, with different scaled $\text {PGA}$ values, are identified as random variables that can significantly capture the seismic vulnerability of unanchored tanks (Phan et al. 2019). In particular, we assume a variation of the filling level between 50 and 100% of the maximum level, i.e. 7−14 m, to follow a uniform distribution; conversely, $PGA$ is assumed to obey to a lognormal distribution with a mean of 0.6 g and a variation in a logarithmic scale of 0.2. Hence, the lower and upper bounds of $PGA$ read, 0.45 g and 0.8 g respectively. The aforementioned values are gathered in Table 3.

Table 3 Random variables considered in the model

As anticipated in Subsection 1.2, in order to generate a sample of random variables, we use herein the CCD method. It simulates an experimental design, based on the response surface methodology, where a second-order (quadratic) model for the response variable is built without needing to use a complete three-level factorial experiment (Gilmour and Trinca 2012). In particular, $k$ central points and $2^{k}$ points (i.e. full factorial two-level design) are generated to correctly derive the second-order terms of the surface, whereas additional $2k$ points obtained by changing one design variable at a time by an amount $\alpha = k/4$ to accurately estimate the linear terms. The value of $\alpha$ depends on the number of experimental runs in the factorial portion of the CCD. From Table 4, being $k = 2$ and assuming only one central point, nine samples are obtained. Figure 10 shows the CCD for $k = 2$, where $\alpha = 2^{2/4} = 1.41.$

Table 4 Central composite design samples

Fig. 10

Representation of a CCD with $k = 2$, one central point, four factorial design points and four axial points

The application of the CCD appropriate to the case to hand is summarized in Table 4, where the values of $H$ and $PGA$ for each sample are provided. As a result of the CCD, nine model samples with different combinations of $H$ and $PGA$ and eight selected records entail 72 simulations on the HF 3D FE model.

4.3 Static pushover analysis

In order to primarily evaluate the static behaviour of the generated samples in terms of both global and local response, nonlinear pushover analyses are performed on five samples filled with different liquid levels. In this respect, the procedure proposed by Vathi and Karamanos (2018) is used, which has shown a reliable capability to assess the nonlinear static behaviour of unanchored tanks. In order to develop the pushover model, acoustic elements are ignored and a distributed load on the tank wall that replicates liquid pressure is used instead. Three loading steps are applied as shown in Fig. 11 (gravity + hydrostatic + hydrodynamic) and the hydrodynamic loading is calculated using the Eurocode 8 formula (EN1998-4 2006). This pressure action on both tank wall and baseplate is increased until a maximum acceleration value, for which numerical instability occurs due to high level of the plastic strains at the shell of the baseplate-to-wall connection.

Fig. 11

Loading steps of pushover analyses

The global responses in terms of uplift displacement of the baseplate are shown in Fig. 12. While Samples 1, 2 and 5 exhibit no uplift even a high level of the acceleration reached ($> 1\;{\text{g}}$). The remaining cases show a clear uplift response with the increase of the base acceleration, especially Sample 6, which is filled with the highest liquid level.

Fig. 12

Static uplift responses

In addition, local responses in terms of axial compressive stresses of the base shell courses, von Mises stresses and equivalent plastic strains of both shell wall and baseplate are also investigate. The representative results of the most severe case, i.e. Sample 6, are collected in Table 5. Typical distribution of equivalent plastic strain and von Mises stress contours are also shown in Fig. 13 respectively.

Table 5 Static responses of Sample 6 at acceleration level of 0.63 g

One can notice from Fig. 13 that stresses at baseplate-to-wall connection reach high values while the wall is still in the elastic range. This result demonstrates the vulnerability of shell wall-to-baseplate welded connection in unanchored storage tanks. Moreover, stress levels in the baseplate significantly increase due to the uplift. Although a high level of uplift has been observed, buckling of the shell wall is not activated. In this respect, a small value of axial compressive stress in the bottom shell course is observed in Table 5. As a result, from the pushover analysis, one can deduce that: (1) the occurrence of the buckling phenomenon in the wall is rather limited; (2) the most critical failure mode of the analysed tank is represented by the failure of the wall-to-baseplate connection. Consequently, in the following, only this failure mode of the tank will be considered.

Fig. 13

Contours at the last time step of the analysis of a von Mises stresses and b equivalent plastic strain

4.4 Nonlinear time history analysis and observed training data for Kringing model

Nonlinear time history analyses on the 3D FE model are carried out using the set of eight ground motion records of Table 2. According to the CCD, a total of 72 simulations are obtained, where nines samples are respectively paired with eight records which are scaled to a given PGA level illustrated in Table 4. As an example, time history data of both uplift and equivalent plastic strain at two ends of the baseplate, which are obtained from the simulation of Sample 6 subjected to the Kalamata earthquake, are highlighted in Fig. 14. A maximum uplift displacement of 0.5 m is achieved whilst the maximum equivalent plastic strain reads about 12%. Typical von Mises stress and equivalent plastic strain contours for this case are also depicted in Fig. 15, where response quantities are measured a $t = 4.06 \;{\text{s}}$. In particular, one can observe from the figures that the region near to the shells of the baseplate-to-wall connection experiences yielding whilst the remaining ones remain in the elastic region; this behaviour agrees well with the results provided by nonlinear static analysis.

Fig. 14

Time history data measured for Sample 6 in terms of a uplift displacement and b equivalent plastic strain at the left and right ends of the baseplate due to the Kalamata earthquake

Fig. 15

HF model results measured for Sample 6 in terms of a von Mises stress contours and b equivalent plastic strain contours due to the Kalamata earthquake at t = 4.06 s

Similarly, peak responses in terms of uplift displacement and equivalent plastic strain are estimated for all samples of Table 4; the relevant results are plotted in Fig. 16. A careful reader can notice that Sample 4 and 6 exhibit high seismic demands due to the high values of H, whereas responses induced from Sample 1 and 5 are rather small.

Fig. 16

HF model outputs in terms of a uplift displacement and b equivalent plastic strain of the baseplate

With regard to Kriging, each analysis takes into account the uncertainty of ground motions in terms of $PGA$. Nonetheless, for each $PGA$ value, mechanical responses vary also due to the relevant frequency content. Therefore, time history analysis results cannot be directly used as input of the LF Kriging model. Hence, both mean and standard deviation of logarithmic values of the dataset composed by the 72 responses -the combination of Tables 3 and 4- are used instead. This is different from the objective of Giovanis et al. (2016), where means and variances of medians were used for estimation of epistemic uncertainties. Those values are obtained using the UQLAB software (Lataniotis et al. 2018), in which a linear function is used as the baseline of the LF model.

4.5 Selection of basis and correlation functions for Kriging model

Based on observed training responses including mean and standard deviation, Kriging metamodels are developed herein by means of the UQLAB software (Lataniotis et al. 2018). Therefore, the optimal type of basis and correlation functions is selected based on the Leave-one-out (LOO) error and the coefficient of determination of the LOO cross validation. Thus, the most commonly used basis functions of UQLAB are tested. For this purpose, the default correlation, i.e. Matern-5_2, is set and the maximum likelihood estimation method is used for the optimization problem. More precisely for the kriging model of the mean logarithmic response, the measures of fit for four different basis functions are shown in Table 6. A careful reader can observe that the optimal type of basis functions is the linear function, with a coefficient of determination value to 97%. The three others that include quadratic, 2nd and 3rd degree polynomial functions exhibit worst correlations ($Q^{2} < 70\%$).

Table 6 LOO cross validation results for different basis functions

The selection of the optimal correlation function is subsequently carried out considering four different correlation functions as shown in Table 6. It is evident that all the correlation functions paired with the linear basic function exhibit a favourable level of performance ($Q^{2} > 96\%$); for the case of linear correlation function, $Q^{2}$ approaches $98\%$.

As a result of the selection process, the linear type of basis and correlation functions are selected for the development of Kriging models for both mean and standard deviation of response values. Finally, the composite Kriging model whose output assumes a lognormal distribution is defined by means of Eq. (6).

5 Fragility analysis with Kriging metamodel

The conditional probability $P\left[ {D \ge C|IM} \right]$ that the demand $D$ exceeds the limit state capacity $C$ is known as fragility function. Given the closed form of the Kriging model in Eq. (6), fragility function can be determined by means of Monte Carlo simulations, which is defined as the fraction of the number of points such that $D \ge C$ and the total number of points,

$$P\left[ {D \ge C|IM} \right] = \frac{1}{{N_{si} }}\mathop \sum \limits_{1}^{{N_{si} }} I\left( {D_{si} \ge C} \right),$$

(12)

where $N_{si}$ indicates the total number of simulations performed and $I\left( {D_{si} \ge C} \right)$ defines the indicator function. As anticipated in Subsection 2.2, Phan et al. (2019) deeply investigated the uplift response of unanchored storage tanks. They concluded that important inelastic deformations occur at the baseplate of the welded baseplate-to-wall connection, leading to either failure due to excessive tensile strain or low-cycle fatigue damage.

In that model, the plastic rotation demand has been used with a rotation limit of 0.2 rad (EN1998-4 2006); this threshold corresponds to a tensile strain value of the baseplate of about 5%. Even though, values between 2 and 5% have been suggested for the ultimate tensile resistance of baseplates (Vathi and Karamanos 2017), only the aforementioned first type of failure is considered. As a result, the maximum local tensile strain limit at the baseplate is adopted as the EDP with a threshold of 5% as the corresponding limit state. The corresponding fragility curves have been found on the basis of Monte Carlo simulations carried out on the composite Kriging model, i.e. Eq. (6). In particular, simulations are repeated for each specific $\text {PGA}$ value with a step size of 0.005 g, in the range 0.005–1.6 g of $PGA$. The data post-processing on the 100000 observations leads to fragility functions depicted in Figs. 17 and 18. Functions are smooth because of the large sample set adopted. The fragility curves presented in Fig. 17 indicate the probability of exceeding the tensile strain limit of 5% at the baseplate. Owing to the high flexibility of the Kriging model, we have investigated both deterministic and probabilistic conditions in terms of the filling level $H$. More precisely, $H = H_{max}$ corresponds to the most conservative condition, with a median value of $PGA$ closed to 0.6 g. Conversely, $H = 0.5H_{max}$ corresponds to a median $PGA$ = 1.6 g. In addition, Fig. 18 depicts the fragility curves relevant to $H$ assumed as a random variable. Two ranges of filling level are considered: 75–100% and 50–100%, respectively. As a result, the median value of $PGA$ changes from 0.65 g ($H = 100\% H_{max}$) to 0.9 g ($H = 75 - 100\% H_{max}$). These figures highlight that a deterministic assumption for the filling level could lead to an erroneous fragility evaluation which is found to be highly variable with reference to this parameter.

Fig. 17

Fragility curves of the baseplate-to-wall connection failure with fixed liquid levels

Fig. 18

Fragility curve of the baseplate-to-wall connection failure with variable liquid levels

With regard to the outcome of mechanical models, Vathi and Karamanos (2018) proposed, among others, a mechanical lumped model, where the uplift phenomenon is represented by a rotational spring derived using a pushover analysis on a 3D FE model. Therefore, we can compare herein both the fragility curves derived by means of Kriging and mechanical models.

The features of this model derived for the present case study can be found in Phan et al. (2019), where component fragility curves are built with ${{H}} = 100\% {{H}}_{{max} }$ and the use of cloud analysis (Mackie and Stojadinovic 2005). In this case, the plastic rotation demand has been used instead, with a corresponding rotation limit of 0.2 rad (EN1998-4 2006). It is important to stress that the HF model suggested herein can directly capture the local behaviour of the tank, in terms of stresses and strains, whereas the mechanical model needs to resort to approximate definitions of strains. As expected, Fig. 19a highlights that the LF model is less conservative than the mechanical model. The reason is mainly due to the limited prediction capability of the mechanical model. In order to estimate the accuracy of the Kriging model, i.e. Eq. (6), Monte Carlo simulations are performed on Kriging models generated using bounded values of $\hat{\varvec{Y}}_{\mu }$ and $\hat{\varvec{Y}}_{\sigma }$ which are assumed to Gaussian distributed. Figure 19b indicates relevant mean value and 95% confidence interval of failure probability estimates. The error propagation associated with the Kriging model is limited.

Fig. 19

Fragility curves relevant to baseplate failure: a provided by Kriging and mechanical models for $H = H_{max}$, b provided by Kriging with mean value and 95% confidence interval

The effect of using different fragility models for the evaluation of seismic risk of the unanchored tank to hand is analysed. Given the Kriging model, the MAF of failure λ_c can be computed from the numerical integration of the risk equation, i.e.

$$\lambda_{c} = \mathop \sum \limits_{i = 1}^{N} \left[ {\left[ {P\left[ {D > C|PGA_{i} } \right] + P\left[ {D > C|PGA_{i - 1} } \right]} \right]\left[ {P\left( {PGA_{i} } \right) - P\left( {PGA_{i - 1} } \right)} \right]/2} \right],$$

(13)

where $\lambda$ is the hazard function in terms of $\text {PGA}$. Along this line, Table 7 collects the MAF values both for Kriging and mechanical models.

Table 7 Failure mean annual frequency

Also, in this case, the mechanical model is overly conservative with respect to the proposed Kriging model of about four times. Finally, the results of Table 7 highlight that in the case of $H$ = (75–100%) $H_{max}$ the MAF value remarkably decreases -about three times- as compared with that of the deterministic case, i.e. $H$ = 100%$H_{max}$.

6 Conclusions

A reliable seismic vulnerability assessment of steel storage tanks with unanchored support conditions based on PBEE has been developed. It relies on a HF model for broad tanks that consists of a 3D FE model set in the ABAQUS software and adopts a Kriging-based LF demand model that allows for cheaper simulations of the whole model. In addition, a second-order DOE method is adopted to approximate the system response considering both peak ground acceleration and liquid filling level as random variables. A parametric investigation that involves the aforementioned analysis techniques is conducted on an existing unanchored steel storage tank. Special consideration is paid to base uplift due to significant inelastic deformations that can occur at the baseplate close to the welded baseplate-to-wall connection. As a result, to estimate the tank performance, component-level fragility curves of the aforementioned limit state are derived by means of Monte Carlo simulations. Therefore, fragility curves are derived considering the filling level both deterministic and probabilistic. Results highlighted that a deterministic assumption for the filling level could lead to a biased vulnerability assessment. Moreover, the comparison of the seismic vulnerability of the tank achieved with both a probabilistic and a deterministic simplified mechanical model demonstrates their conservatism. The same trend also applies in terms of risk assessment. Finally, with a focus on one storage unit, the exam of simultaneous states of damage triggered by an increased seismic intensity and their correlations that can be better tracked by means of a HF model deserves further studies; and the analysis of a portfolio of tanks in a tank farm is the natural outcome of future analyses based on Kriging.