Numerical investigation of detonation initiation by a focusing shock wave

Abstract

This work presents a numerical study of detonation initiation by means of a focusing shock wave. The investigated geometry is a part of a pulsed detonation combustion chamber, consisting of a circular pipe in which the flow is obstructed by a single convergent–divergent axisymmetric nozzle. This obstacle acts as a focusing device for an incoming shock wave, serving as a low-energy detonation initiator. The chamber is filled with stoichiometric premixed hydrogen-enriched air. The simulation uses a one-step chemical model with variable parameters optimized by the adjoint approach in terms of the induction time $\tau _{\text {c}}$. The model reproduces $\tau _{\text {c}}$ of a complex kinetics model in the range of pressures and temperatures appearing at the focusing point. The results give a comprehensive description of the shock-induced detonation initiation, which is the mechanism for the deflagration-to-detonation transition in this type of configurations. Potential geometry design improvements for technical applications are discussed. The first attempt to parameterize the transition process is also undertaken.

1 Introduction

The evolution of gas turbines’ efficiency in the last thirty years has not shown significant improvements [1]. The predictions project a convergence to a maximum of 45 % efficiency, and a revolutionary technology change is not foreseen [1]. This indicates that gas turbines based on constant-pressure combustion are a mature technology and any substantial enhancement of its efficiency demands a paradigm change.

Fig. 1

Geometry of the shock-focusing nozzle (left), initial conditions (center), and formation of the imploding shock wave after reflection (right)

The rapid mixture combustion and high chemical energy release rate in detonations lead to more efficient systems [2]. The detonation thermodynamic cycle is close to the constant-volume cycle (Humphrey cycle) and is more efficient than the constant-pressure cycle (Brayton cycle), which is characteristic of conventional engines [3]. Therefore, it is advantageous to utilize detonative combustion in gas turbines due to its inherent efficiency gain over deflagrative combustion.

The direct initiation of detonations requires an impractically large amount of energy and deposition rate. The alternative is to use a low-energy ignition of a deflagration, and let the front evolve to a detonation wave via deflagration-to-detonation transition (DDT) [2]. For practical implementation of pulse detonation engines (PDEs), a robust and reliable low-energy initiation of detonations is needed. Accordingly, it is a must to control and to accurately understand the transition in the combustion chamber.

DDT is subjected to an active research effort, not only in PDEs but also in its various branch applications, since the transition details are not completely understood. The universality of the mechanism is an open question, as several theories describe different transition mechanisms [4,5,6,7]. A typical setup is a flame accelerating in a semi-infinite pipe or channel. Obstacles are commonly used to support turbulence formation and reduce the run-up distance to DDT [8]. Also, the focusing of shock waves as a detonation initiator for PDEs was investigated by Jackson et al. in [9, 10]. Frolov et al. considered the experimental examination of detonation transition using a shock wave-focusing nozzle for application in pulsed detonative burners [11]. In the experimental and numerical works of Gray et al. [12] and Bengoechea et al. [13], a cylindrical PDE’s combustion chamber is obstructed by a single convergent–divergent axisymmetric nozzle. This single obstacle configuration does not reduce the impulse significantly, unlike standard turbulence-producing devices with significant thrust losses [2]. In [13], the two key elements for a successful transition to detonation are identified as: (1) a high burning rate to create a strong leading shock wave and (2) the focusing of this leading shock wave due to the obstacle geometry. The latter is further analyzed in this paper to confirm the initiation mechanism and to reveal the details of this process.

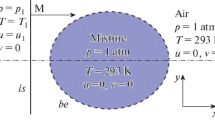
The present study is devoted to the numerical investigation of the self-ignition process of detonations caused by a focusing shock wave at the nozzle-shaped obstacle from [13]. The shock wave is induced by a turbulent flame, so that this specific initiation mechanism is more precisely described as flame-to-shock-to-detonation transition. The obstacle geometry is sketched in Fig. 1 with a blockage ratio (BR) of 75 %, a converging angle of $45^\circ$, and a diverging angle of $131^\circ$. The results presented here allow a reliable description of the onset of detonation, and thus, decisive aspects of the shock-induced detonation initiation can be extracted. The first attempt to parameterize the transition process is also undertaken with the aim to estimate a priori the outcoming reaction front propagation. Understanding of the investigated PDE configuration is enhanced, pointing towards its use in gas turbines.

The rest of this paper is organized as follows. Section 2 describes the numerical model. In Sect. 3, the results are included and discussed. Section 4 outlines the conclusions. Finally, the appendices summarize the validation and derivation of the model.

2 Numerical methods

The following compressible reactive Navier–Stokes equations are solved numerically:

$$\begin{aligned}&\sqrt{\rho } \frac{\partial \sqrt{\rho }}{\partial t} + \frac{1}{2} \frac{\partial \rho u_{i}}{\partial x_{i}} = 0 \end{aligned}$$

(1a)

$$\begin{aligned}&\sqrt{\rho } \frac{\partial \sqrt{\rho } u_{i}}{\partial t} + \frac{1}{2} \left( \frac{\partial \rho u_{j} u_{i}}{\partial x_{j}} + \rho u_{j} \frac{\partial u_{i}}{\partial x_{j}} \right) + \frac{\partial p}{\partial x_{i}} = \frac{\partial \tau _{ij}}{\partial x_{j}} \end{aligned}$$

(1b)

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \frac{p}{\gamma -1} \right) + \frac{\partial }{\partial x_{i}} \left( \frac{\gamma }{\gamma -1} u_{i} p \right) - u_{i} \frac{\partial p}{\partial x_{i}} \nonumber \\&\quad = \frac{\partial u_{i}\tau _{ij}}{\partial x_{j}} - u_{j}\frac{\partial \tau _{ji}}{\partial x_{i}} + \frac{\partial }{\partial x_{i}} \left( \lambda \frac{\partial T}{\partial x_{i}} \right) + {\dot{\omega }}_{\text {T}} \end{aligned}$$

(1c)

$$\begin{aligned}&\frac{\partial \rho Y}{\partial t} + \frac{\partial \rho u_{i} Y}{\partial x_{i}} = \frac{\partial }{\partial x_{i}} \left( \rho D\frac{\partial Y}{\partial x_{i}} \right) + {\dot{\omega }} \end{aligned}$$

(1d)

$$\begin{aligned}&\tau _{ij} = \mu \left( \left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \right) - \delta _{ij} \frac{2}{3} \frac{\partial u_k}{\partial x_{k}}\right) . \end{aligned}$$

(1e)

Therein, $x_{i}$ (or $x_{j}$, $x_{k}$) denotes the i-th (or j-th, k-th) spatial dimension, t the temporal variable, $\rho$ the density, $u_{i}$ (or $u_{j}$, $u_{k}$) the i-th (or j-th, k-th) velocity component, p the pressure, $\tau _{ij}$ the viscous stress tensor, T the temperature, and $\delta _{ij}$ the Kronecker symbol. The summation convention applies with i, j, $k = 1,2,3$. The equations (1a–1c) are written in skew-symmetric form [14], and hence, the computational variables are set to $[\sqrt{\rho }$, $\sqrt{\rho }u_{i}$, p, $\rho Y]^{\text {T}}$. This approach guarantees the conservation properties for finite difference schemes [13, 14].

Fig. 2

Sensible energy $e_{\text {s}}$ and T relation for different $\gamma$ definitions (upper left). The $\gamma (T)$ polynomial used in this study (upper right). Relative and absolute errors in T of the seventh-order polynomial with respect to the CHEMKIN database [20] (lower left). The quantity $\gamma (T_{\text {max}}^{t^{n+1}}) - \gamma (T_{\text {max}}^{t^n})$ with a maximum error of $1\cdot 10^{-3}$ (lower right)

The dependence on temperature of the dynamic viscosity $\mu$ is calculated with Sutherland’s law [15]. The mass diffusion coefficient is described by Fick’s law with $D= \frac{\mu }{\rho \, \text {Pr}\,\text {Le}}$, a constant Prandtl number $\text {Pr} = \frac{\mu c_{p}}{\lambda }= 0.71$, and the Lewis number $\text {Le}= 1$. This simplified transport assumption (Fick’s law and Le set to unity) is used in many theoretical approaches [16]. The specific heat capacity at constant pressure $c_{p} = \frac{\gamma (T) R_{\text {s}}}{\gamma (T) - 1}$ is also dependent on temperature. The thermal conduction coefficient $\lambda$ is determined by $c_{p}$, $\text {Le}$, $\text {Pr}$, and $\mu$. The specific gas constant is defined as $R_{\text {s}} = \frac{R}{W}$, with R the universal gas constant and W the mean molecular weight of the mixture. The model parameters are stated in Tables 2 and 3, see Appendix 1.

The mixture used in the numerical experiments is stoichiometric hydrogen–air enriched to 40% oxygen, as in the previous study [13]. The global reaction is modeled by a one-step, irreversible reaction, with one effective species Y, varying from one (unburned) to zero (burned). The source terms responsible for the changes during the reaction are the mass reaction rate ${\dot{\omega }}$ and the heat release due to combustion ${\dot{\omega }}_{\text {T}}$. These are defined as:

$$\begin{aligned} {\dot{\omega }} = - K_{\text {f}} \rho Y \, \text { and } \, {\dot{\omega }}_{\text {T}} = - Q {\dot{\omega }} \, , \end{aligned}$$

(2)

with the reaction rate constant $K_{\text {f}}$ described by the Arrhenius law $K_{\text {f}} = A \hbox {e}^{-\frac{T_{\text {a}}}{T}}$ and the heat release per unit mass of fuel Q [16]. The parameters of the model are pressure and temperature dependent, see Sect. 2.1.

The adiabatic exponent $\gamma$ defines the conversion of sensible (non-chemical) energy $e_{\text {s}}$ into the thermodynamic quantities p and T. This is a crucial part of the chemical model, since T is the link between the fluid dynamics and the heat released by the reaction [17]. The sensible energy $e_{\text {s}}$ is here described as $e_{\text {s}} = \frac{p}{\rho (\gamma (T) - 1)} + \text {const}$ [18, 19], with $\gamma (T)$ temperature dependent. This automatically assumes an ideal gas mixture with $e_{\text {s}}$ only a function of T. Figure 2 depicts the function $\gamma (T)$ used in this work. It is built with a seventh-order polynomial that closely reproduces $e_{\text {s}}$ specified in the CHEMKIN database [20]. The maximum absolute and relative errors in the polynomial interpolation are 9.6 K and 0.67 %, respectively, see Fig. 2. The same figure shows the large discrepancy made by a constant $\gamma$ approach, which only applies for a small change of T.

The term $\frac{\partial }{\partial t} \left( \frac{p}{\gamma (T)-1} \right)$ of (1c) calculates the temporal change of the sensible energy density. This means that the thermodynamic quantities of the flow (p and T) must be extracted implicitly for each time integration sub-step. By assuming that $\gamma (T)^{t^{n+1}} \approx \gamma (T)^{t^n}$ in the integration time step $\varDelta t$, this temporal term in (1c) can be rewritten via p as $\frac{\partial }{\partial t} \left( \frac{p}{\gamma (T)-1} \right) \approx \frac{1}{\gamma (T)-1} \frac{\partial p}{\partial t}$. The numerical effort simplifies then considerably, since an explicit relation between $e_{\text {s}}$ and T is given above by the definition of $e_{\text {s}}$. The validity of this assumption is verified on-the-fly; Fig. 2 contains the results.

2.1 Adjustment of the chemical model

The pre-exponential factor A and the activation temperature $T_{\text {a}}$ are the available degrees of freedom to fit the chemical model. In the current study, these model parameters are chosen to match the induction time $\tau _{\text {c}}$ of the detailed San Diego kinetics mechanism with 21 reactions [21] at the conditions relevant to this investigation, namely the temperature and pressure intervals appearing at the focusing of the shock wave (in the following referred to as $\tau _{\mathrm {c_{ref}}}$). Since two parameters (A and $T_{\text {a}}$) do not suffice to reproduce the behavior of $\tau _{\mathrm {c_{ref}}}$ accurately, A and $T_{\text {a}}$ of the one-step model are allowed to be pressure and temperature dependent with a piecewise-constant function. In order to select their optimal values, the adjoint method is applied [19, 22]. To this end, the zero-dimensional equations for isochoric reactions are considered in the form:

$$\begin{aligned} \frac{\partial q}{\partial t} = f(q,\alpha ) \,, \end{aligned}$$

(3)

Fig. 3

Induction time $\tau _{\text {c}}$ (isochoric) for stoichiometric hydrogen–air enriched to 40% oxygen ($4\text {H}_{2} + 2\text {O}_{2} + 3\text {N}_{2}$). Solid line: San Diego mechanism, 21 reactions ($\tau _{\mathrm {c_{ref}}}$). Dotted line: one-step model. Left: pre-adjoint optimization, right: post-adjoint optimization. The maximum relative error in $\tau _{\text {c}}$ for the one-step model is 0.033 %

with the vector space $q = [Y,T]^{\text {T}}$ as the solution to the system, the right-hand side $f = \left[ \left( \frac{1}{\rho }\right) {\dot{\omega }} , {\dot{\omega }}_{\text {T}}\right] ^{\text {T}}$, and the vector $\alpha = [A,T_{\text {a}}]^{\text {T}}$ as the chemical parameters space. Equation (3) is linearized with respect to a base state ($q_o,f_o$) with $q = q_o + \delta q$ and $f = f_o + \delta f$, resulting in $\frac{\partial \delta q}{\partial t} = \delta f$ with $\delta f = \frac{\partial f_o}{\partial q_o} \delta q + \frac{\partial f_o}{\partial \alpha _{o,l}} \delta \alpha _l$ and summation convention $l = 1,2$.

The induction time $\tau _{\text {c}}$ is defined by the timescale of the maximum reaction rate [5], i.e.,  $\tau _{\text {c}}=\frac{\partial T}{\partial t} \bigr |_{\text {max}}$. To obtain the intended $\tau _{\text {c}}$ optimization, the objective function J is determined as the integral difference between the system state for the one-step model q and for the detailed San Diego kinetics $q_{\text {ref}}$:

$$\begin{aligned} J(q) = \frac{1}{2} ( q - q_{\text {ref}} )^{\text {T}}( q - q_{\text {ref}} ) \, . \end{aligned}$$

(4)

The integral difference is indicated in (4) by the scalar product. The linearization of J results in $\delta J = g^\text {T} \delta q$ with $g=q - q_{\text {ref}}$.

The adjoint equation is derived by including the additional constraint of equation $\frac{\partial \delta q}{\partial t} = \delta f$ with the Lagrange multiplier $q^*$ in the objective function and integrating by parts:

$$\begin{aligned} \delta J =&g^{\text {T}}\delta q - {q^*}^{\text {T}}\underbrace{\Bigg (\overbrace{\frac{\partial \delta q}{\partial t} - \frac{\partial f_o}{\partial q_o} \delta q }^{B \delta q} - \frac{\partial f_o}{\partial \alpha _{o,l}} \delta \alpha _l \Bigg )}_{=0} \nonumber \\&={q^*}^{\text {T}} \frac{\partial f_o}{\partial \alpha _{o,l}} \delta \alpha _l + \delta q^{\text {T}} \underbrace{\left( g - B^{\text {T}}q^*\right) }_{\text {Adjoint equation} \overset{!}{=}0} \, \text {.} \end{aligned}$$

(5)

By equalizing the adjoint equation to zero, the dependency of $\delta J$ on the system solution $\delta q$ is eliminated. The variation in J is directly related to the model parameters variation $\delta \alpha _l$ via $q^*$, namely $\frac{\partial J}{\partial \alpha _l} \approx \frac{\delta J}{\delta \alpha _l} = {q^{*}} \frac{\partial f_o}{\partial \alpha _{o,l}}$. By adjusting the model parameters $\alpha$, the minimum of J is sought. With the change of f to $\alpha$ and the adjoint solution $q^*$, the sensitivity of J to $\alpha$ is given. The calculated gradient $\nabla _{\alpha _l} J$ is then used iteratively in the steepest descent algorithm [19]. In this study, only the coefficient A is adjusted. The optimized values of A are reported in Table 4, Appendix 1. The results before and after the adjoint fitting are depicted in the left-hand and right-hand plots of Fig. 3, respectively. The good performance of the optimized one-step model in $\tau _{\text {c}}$ terms is evident. For the sake of completeness, the equations and the intermediate steps of the adjoint derivation are summarized in Appendix 2.

The endothermic–exothermic character of the reaction is not well described by the one-step model, which acts as exothermic for all temperatures [5]. Having said that, in the present case the large pressure and temperature values prior to detonation (above 250 bar and 1400 K) put the ignition below the crossover temperature (2150 K for 250 bar) [23]. This reduces considerably the chain branching endothermic stage [5], making this case less sensitive to the radical building phase. Therefore, the endothermic induction phase can be neglected [24]. With a precise calibration, the one-step model is able to accurately reproduce the detonation ignition process when the exothermic termination–recombination dominates the reaction [24]. Based on this principle, the use of the optimized one-step kinetics is justified.

2.2 Simulation and implementation details

The equation set (1) is solved with an in-house code, fully MPI-parallelized by a layer decomposition approach for the space derivatives [25]. The cylindrical-like geometry of the left sketch in Fig. 1 is mapped onto an uniform computational domain. The discretization in radial, azimuthal, and longitudinal directions fulfills $s := \{ \theta ,r,z \, :\, 0< \theta \le 2\pi , \, 0 < r \le \text {radius}, \, 0 \le z \le \text {length}\}$. The pole is not included in the set of nodes, in order to avoid the geometrical singularity $\lim \limits _{r \rightarrow 0} 1/r$ in the radial direction [26, 27]. Taking into account the antisymmetric property with respect to $\pi$ in the polar space, the scalar and vector quantities must be transformed from s to ${\tilde{s}} := \{ \theta ,r,z \, :\, 0 < \theta \le \pi , \,- \text {radius} \le r \le \text {radius}, \, 0 \le z \le \text {length}\}$ coordinates [26], prior to the calculation of the radial derivative. This method delivers the “internal boundary” around the pole. Note that the transformation s to ${\tilde{s}}$ is only required for radial derivatives, whereas azimuthal and longitudinal ones do not need special treatment.

Space and time are both evaluated with fourth-order schemes: in space by finite-difference central stencils to avoid artificial dissipation and in time by the explicit Runge–Kutta integration. The number of grid points corresponds to $n_{\theta }, n_{r}, n_{z} = 128, 1024, 1024 \approx 134$ millions, computed on 1024 CPUs. The inflow and outflow boundaries are set as non-reflecting ones by the method of characteristics, while the enveloping surface is set to non-slip adiabatic wall. To handle discontinuities, an adaptive high-order shock-capturing filter is applied [28].

The reflections at the nozzle of incoming shock waves with different strengths are analyzed. Three cases are contemplated with Mach numbers $M = 1.8, 1.9, \text { and }2.3$ and pressure ratios $p/p_{0} = 3.5, 4.0, \text { and } 6.0$. The overall picture of the configuration under study is shown in Fig. 1. Table 1 contains further details of the initial conditions for the three performed simulations. The quiescent pre-shock conditions are kept constant for the three cases with $p_{0} = 1.01330$ bar and $T_{0} = 298.15$ K.

Table 1 Post-shock and Mach number initial conditions

Fig. 4

Pressure (left column) and temperature (right column) evolution of the direct initiation process in a two-dimensional slice for $p/p_{0} = 6.0$. Center of the domain shown as dashed green line

A first group of computations was conducted with the purpose of validating the solution of the equation model. Within this context, the convergence and correctness of the imploding (converging) shock wave is investigated and compared with the self-similar Guderley solution [29]. Also, a resolution study proves the mesh independence of the results on the reference cases of a laminar premixed flame and a detonation front. All these results and analyses are collected in Appendix 3.

3 Results

In the conducted numerical experiments, after the reflection of the incoming shock wave at the convergent part of the nozzle, an imploding (or converging) shock wave is formed, see right plot in Fig. 1. Similar to imploding cylindrical waves, the reflected wave travels inwards increasing its amplitude proportional to $1/\sqrt{r}$ [29]. The self-similar solution for this type of waves predicts an infinite value at the focusing point, certainly limited in practice by diffusion. In the following, the effect on the detonation initiation of changes in the incoming shock wave amplitude ($p/p_{0} = 3.5, 4.0, 6.0$) is analyzed.

Fig. 5

Focusing of the imploding shock, formation and traveling of the collapsing (focusing) points for $p/p_{0} = 4.0$. Center of the domain shown as dashed green line

Fig. 6

Pressure (p), temperature (T), and mass fraction (Y) values superimposed in time at the center line along the longitudinal direction ($x_3$) for $p/p_{0} = 4.0$. Legend indicates the time interval. Equal time step of $\varDelta t = 2.5\cdot 10^{-10}$  s. Initial stage (left column) and feedback stage (right column)

Fig. 7

Pressure (p), temperature (T), and mass fraction (Y) values superimposed in time at the center line for $p/p_{0} = 4.0$. Legend indicates the time interval. Equal time step of $\varDelta t = 2.5\cdot 10^{-10}$ s. Final feedback stage (left column) and the onset of detonation (right column)

Fig. 8

Pressure (left column) and temperature (right column) evolution of the detonation initiation process in a two-dimensional slice for $p/p_{0} = 4.0$. Inset (upper right): induction time $\tau _{\text {c}}$ for the travel-collapsing points. Center of the domain shown as dashed green line

3.1 Direct (strong) initiation $p/p_{0} = 6.0$

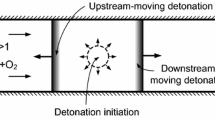
The results in Fig. 4 show the onset of detonation in a two-dimensional slice for an incoming shock wave of $p/p_{0} = 6.0$. In the upper row of this figure ($t = 24.37$ $\mu$s), the imploding shock wave is about to collapse at the center. The initial focusing results in values of 500 bar and 1700 K for pressure and temperature, respectively (see Fig. 4 for $t = 24.77$ $\mu$s). Shortly after the initial focusing, the detonation origin can be identified in the temperature field for $t = 24.77$ $\mu$s. At this spot, the mixture is compressed and heated by the focusing event, resulting in the spontaneous detonation ignition. The rate and amount of energy released by the focusing of the imploding shock wave is the cause for this direct (or strong) initiation mechanism. This mechanism is analogous to the supercritical initiation in the blast wave theory [30].

3.2 Mild initiation $p/p_{0} = 4.0$

Due to the spatial curvature, the converging (reflected) shock wave focuses at different points for different times, developing in a consecutive sequence of focusing events along the longitudinal direction ($x_3$). As a result, two collapsing points are identified traveling backwards and forwards, as shown in Fig. 5 by the two pressure peaks. At these collapsing points, large values of pressure and temperature are detected (above 200 bar and 1200 K). From the temporal evolution, the displacement of the collapsing points can be interpreted as traveling points, i.e.,  travel-collapsing points.

In Figs. 6 and  7, the values of pressure, temperature, and mass fraction are extracted from the center line along the longitudinal direction ($x_3$) and superimposed in time. The initial stage of the focusing results in values of pressure and temperature of approximately 280 bar and 1300 K, respectively. The time span of these high levels is of the same order of magnitude as the induction time of the mixture $\tau _{\text {c}}$. Hence, the reaction starts at this point. This can be observed in the temporal consumption of Y around 19 mm in the left column in Fig. 6. However, the pressure and temperature amplitudes at this focusing point do not suffice to trigger the detonation directly. Unlike in the previous case ($p/p_{0} = 6.0$), the focusing alone does not explain how the detonation occurs.

To clarify the detonation initiation process, the next analysis is centered on the travel-collapsing points. Following the initial wave focusing, the travel-collapsing points experience a velocity and amplitude reduction due to the convex curvature of the imploding shock wave. Furthermore, the non-symmetrical nozzle in the longitudinal axis ($x_3$) leads to different rates of change of these velocities and amplitudes for the two travel-collapsing points.

The pressure decay for the backward travel-collapsing point is visualized in the results in Fig. 6 (marked with A). A temperature deficit is not obtained for this travel-collapsing point, since the heat released by the reaction creates a compensation effect. The mixture has been ignited at the initial focusing stage, and the heat release due to combustion supports a steady increase in the temperature at the backward travel-collapsing point, marked with B in Fig. 6. The rise in temperature further enhances the reaction progress, releasing higher amounts of heat and in addition amplifying the temperature amplitude. A positive feedback mechanism is established. This is caused by the deceleration of the backward travel-collapsing point, enabling the reaction developing behind it to catch up. Consequently, the mutual reinforcement of the progressing reaction and the temperature of the backward travel-collapsing point is started. At this stage, the interaction of the reaction front with the travel-collapsing point intensifies the temperature and the burning rate of Y, while the pressure decreases. Once the reaction has developed enough, it starts to support the pressure, marked with C in Fig. 7. This accelerates the resonance amplification and culminates in the autoignition of the detonation. The backward travel-collapsing point is restructured extremely fast into a coupled combustion-pressure wave, as shown in Fig. 7 (marked with D). From this point on, the detonation is self-sustained and the isochoric combustion takes over in the chamber. The results in Fig. 8 describe this evolution towards the abrupt formation of the detonation in a two-dimensional slice.

The forward travel-collapsing point suffers a lower deceleration than the backward point. This causes the non-coherence in time between the forward travel-collapsing point and the reaction front trailing behind. The higher velocity of the forward point and the slightly lower temperature and pressure values prevent the coupling with the reaction. The heat released does not significantly influence the temperature amplitude as in the backward point, marked with E in Fig. 6. In the results in Figs. 6 and  7, the forward point presents a constant decrease in amplitude and no detonation initiation is observed.

Fig. 9

Normalized velocities of the travel-collapsing points $\frac{V_{\text {tc}}}{D_{\text {CJ}}}$ (solid line) and the reaction fronts $\frac{V_{\text {rf}}}{D_{\text {CJ}}}$ (dashed line) for $p/p_{0} = 4.0$. A priori estimation of $V_{\text {tc}}$ based on $|\partial \eta / \partial x_3|^{-1}$ (dotted line). Inset: parameterization of the imploding shock wave

Fig. 10

Temperature (left column) evolution of the implosion process in a two-dimensional slice for $p/p_{0} = 3.5$. Center of the domain shown as dashed green line. Pressure (p), temperature (T), and mass fraction (Y) values superimposed in time at the center line for $p/p_{0} = 3.5$ (right column). Legend indicates the time interval. Equal time step of $\varDelta t = 5.0\cdot 10^{-10}$ s. Starting of the feedback stage and front decoupling

To complete the examination of the onset of detonation, the normalized velocities of the travel-collapsing points $V_{\text {tc}}$ and the reaction fronts $V_{\text {rf}}$ during the process are plotted in Fig. 9. The reaction front is detected at 0.05 % of fuel consumption. The velocity of the travel-collapsing points $V_{\text {tc}}$ initially reaches infinite values as a result of the approximately flat wave focusing. Subsequently, a strong decline is identified as long as the wave curvature increases (solid blue lines in Fig. 9). This strong deceleration leads to the feedback stage, thereby also accelerating the reaction front $V_{\text {rf}}$ (dashed red lines in Fig. 9). In the backward point, the velocity match of the two fronts extends until the detonation materializes. Note that at the stage prior to the transition the velocity drops below the final CJ detonation velocity ($D_{\text {CJ}}$). This velocity decay has been reported [30] as a prelude to the onset of detonation. Here, the initiation process is equivalent to the critical initiation in the blast initiation theory [6], with a quasi-steady (feedback) stage, followed by an abrupt transition. Analogous to the SWACER mechanism [30], the coherence of the chemical energy released by the reaction ignited at the initial focusing with the series of focusing events along the axis $x_3$ is the cause of the rapid amplification in the feedback stage, leading to the detonation initiation.

The scenario is completely different in the forward point, where the two fronts coincide for a temporal interval with a velocity higher than $D_{\text {CJ}}$ and then decouple (right-hand side of Fig. 9). The rate at which the forward collapsing events occur is too high for the chemical reaction to develop sufficiently.

3.3 Geometrical dependence of the detonation initiation for $p/p_{0} = 4.0$

The results for $p/p_{0} = 4.0$ establish two decisive elements to explain the successful initiation of detonations via the implosion of curved shock waves which have initially not sufficient energy for a direct initiation: (1) the high pressure and temperature levels at the initial focusing of the imploding shock wave and (2) the velocity of the travel-collapsing point $V_{\text {tc}}$.

The first one determines the ignition of the mixture at the initial focusing stage of the process. The pressure and temperature values at this stage depend on the blockage ratio (BR) of the nozzle (and obviously the strength of the incoming shock wave). By narrowing the aperture, i.e.,  raising the top peak of the obstacle (see Fig. 1), the amplitude increases at the focusing point and a weaker incoming shock could ensure a solid initial ignition.

With regard to the second element, the results show that the travel-collapsing points develop into detonation when it decelerates beyond $D_{\text {CJ}}$. The velocity $D_{\text {CJ}}$ could be seen as the upper threshold of this initiation process. For an a priori prediction of the outcoming reaction front propagation, the relation of the velocity $V_{\text {tc}}$ with the imploding wave curvature can be extrapolated. The form of the imploding shock wave is parameterized with the function $\eta (x_2,x_3)$ just before collapsing (inset of Fig. 9). The velocity $V_{\text {tc}}$ is then estimated from this parameterization curve $\eta$ as $V_{\text {tc}} \approx K | \partial \eta / \partial x_3 |^{-1}$ with the proportionality constant K. The free parameter K sets the offset of the curve on the y-axis. Its value was selected in order to match $V_{\text {tc}}$ at the last stage of the coupling under $D_{\text {CJ}}$. The good performance of this approximation is depicted in Fig. 9.

To reinforce the transition, the deceleration of the travel-collapsing point could be augmented by means of increasing the gradient of $\eta$ in $x_3$. This can be achieved by reducing the diverging top angle of the obstacle, see Fig. 1 (right). At the same time, a larger gradient has a negative side effect on the amplitude (Amp) decay of the travel-collapsing point, since $\partial (\text {Amp})/\partial t \sim |\partial \eta / \partial x_3|$. At the collapsing point, part of the momentum is lost in the non-normal direction, see inset of Fig. 9. A large gradient results in a slow travel-collapsing point with fast amplitude decay, while a small gradient implies a fast point with slow amplitude decay. From these two competing effects, the temporal rate of change in velocity ($V_{\text {tc}}$) dominates over the amplitude decay, since the slight difference in amplitude between the forward and backward points after the initial focusing does not prevent any positive feedback interaction, leading to detonation initiation of the forward point, see Fig. 6. The velocity ($V_{\text {tc}}$) and the amplitude rates (p and T) of the travel-collapsing point are thereby the quantities which can be used to optimize the process by, for example, geometry variations.

3.4 No initiation $p/p_{0} = 3.5$

For the sake of completeness, a case with a non-successful initiation ($p/p_{0} = 3.5$) is also presented. The results are shown in Fig. 10. In this figure, the backward and forward travel-collapsing points formed by the spatial curvature of the imploding shock wave are found again, see Fig. 5. The trigger of the feedback stage with an increase in the temperature’s amplitude and the consumption of mass fraction (Y) in the backward point resembles the previous case ($p/p_{0} = 4.0$), see Sect. 3.2. However, this positive feedback process is not established completely and the decoupling of the reaction and the focusing events takes place. Finally, no ignition is observed in the results in Fig. 10. The energy released at the focusing in the current case ($p/p_{0} = 3.5$) is lower than the detonation initiation threshold.

4 Conclusions

The results of the numerical experiments provide an accurate description of the initiation process at the focusing of the imploding shock wave. Different mechanisms are observed as the strength of the incoming shock wave ($p/p_{0}$) is varied. The energy release rate at the focusing classifies the outcome in mild, direct or no initiation.

For $p/p_{0} = 3.5$, the release of energy at the focusing is not sufficient for the initiation.

In the results for $p/p_{0} = 4.0$, the feedback between wave focusing events and progressing reaction is found to be the underlying cause of the onset of detonation. In particular, the velocity of the sequence of focusing events is controlled by the curvature of the converging shock wave, which likewise is defined by the shape of the obstacle. By parameterizing the imploding shock wave, this velocity can be estimated, which paves the way for a priori predictions of the outcoming reaction front propagation. This mild detonation initiation represents the transition from no initiation to direct initiation in the lower threshold.

The direct (or strong) initiation modus is found for the results of $p/p_{0} = 6.0$. The high energy released at the focal area dominates this initiation process.

In the combustion chamber under investigation, the strength of the incoming shock wave ($p/p_{0}$) is generated by the burning rate of fuel in a pre-chamber. Therefore, it is of great interest to extend the study to evaluate the potential for optimizing the nozzle geometry with the aim of reducing oxygen enrichment by a better obstacle form. This would offer the possibility of reducing the incoming shock wave amplitude and still guarantee a robust detonation initiation for lower burning rates of less reactive mixtures. In that sense, a direct relation between the geometry and the resulting combustion regime eases the design improvements for technical applications in detonation-based engines.

Appendices

Appendix 1: Physical–chemical model

See Tables 2, 3, and 4.

Table 2 Physical–chemical model parameters and CJ detonation values for stoichiometric $4\text {H}_{2} + 2\text {O}_{2} + 3\text {N}_{2}$

Table 3 The adiabatic exponent $\gamma (T)=\sum _{n=0}^7 b_n T^n$ and the specific heat capacity $c_{v}(T) = \sum _{n=0}^7 r_n T^n$ polynomial coefficients (T is in K; $c_v$ in J/(kg$\cdot$ K))

Table 4 Optimized values of the pre-exponential factor A in $10^{10}/s$

Appendix 2: Adjoint equations

Zero-dimensional system of equations for isochoric reactions [16] (the specific heat capacity $c_v(T)$ is implemented with a seventh-order polynomial, see Table 3):

Fig. 11

$x_2$–t diagram of the converging shock (left), converging shock solution (center), and maximum amplitude convergence test at the pole (right)

$$\begin{aligned} \frac{\partial q}{\partial t}= & {} \frac{\partial }{\partial t} \begin{pmatrix} Y \\ T \end{pmatrix} = \begin{pmatrix} {\frac{1}{\rho }\dot{\omega }}(q,\alpha ) \\ {\dot{\omega }}_{\text {T}}(q,\alpha ) \end{pmatrix} = \begin{pmatrix} {\frac{1}{\rho }\dot{\omega }}(q,\alpha ) \\ \frac{-Q}{\rho c_v(T)}{\dot{\omega }}(q,\alpha ) \end{pmatrix} =\nonumber \\= & {} \begin{pmatrix} - Y A \hbox {e}^{\frac{-T_{\text {a}}}{T}} \\ \frac{Q}{c_v(T)} Y A \hbox {e}^{\frac{-T_{\text {a}}}{T}} \end{pmatrix} = f(q,\alpha ) \end{aligned}$$

(6)

$$\begin{aligned} {\dot{\omega }}(q,\alpha )= & {} - K_{\text {f}} \rho Y \; , \; {\dot{\omega }}_{\text {T}}(q,\alpha ) = \frac{-Q}{\rho c_v(T)} {\dot{\omega }}(q,\alpha ) \end{aligned}$$

(7)

$$\begin{aligned} K_{\text {f}}(T,\alpha )= & {} A \hbox {e}^{\frac{-T_{\text {a}}}{T}} \; , \; \begin{array}{c} q = [Y,T]^{\text {T}} \\ \alpha = [A,T_{\text {a}}]^{\text {T}} \end{array} \end{aligned}$$

(8)

Fig. 12

Refinement test for T of a laminar premixed flame (left). Computed with 8, 10, 11, 22, and 45 computational points per flame thickness $\delta _o$. Inset left: convergence and accuracy test. Refinement test for p of a detonation front (right). Computed with 4, 5, 6, 11, and 19 computational points per half reaction length $L_{1/2}$. Inset right: convergence of the detonation velocity

Linearized system of equations $\frac{\partial q_o}{\partial t} + \frac{\partial \delta q}{\partial t} = f_o + \delta f$:

$$\begin{aligned}&\frac{\partial }{\partial t} \begin{pmatrix} \delta Y \\ \delta T \end{pmatrix} = \begin{pmatrix} \frac{\partial {\dot{\omega }}_o}{\partial Y_o} \delta Y + \frac{\partial {\dot{\omega }}_o }{\partial A_o}\delta A + \frac{\partial {\dot{\omega }}_o }{\partial T_{\text {a}_o}}\delta T_\text {a} \\ \frac{\partial {\dot{\omega }}_{T_o}}{\partial T_o} \delta T + \frac{\partial {\dot{\omega }}_{T_o}}{\partial A_o}\delta A + \frac{\partial {\dot{\omega }}_{T_o}}{\partial T_{\text {a}_o}}\delta T_\text {a} \end{pmatrix} = \delta f \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial {\dot{\omega }}_o}{\partial Y_o} = - {A}_o \mathrm{e}^{\frac{-T_{\text {a}_o}}{T}} \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\partial {\dot{\omega }}_{T_o}}{\partial T_o} = \frac{-Q c_v(T)'}{c_v(T)^2} + \frac{Q}{c_v(T)} Y_o A_o \frac{T_{\text {a}_o}}{{T_o}^2} \hbox {e}^{\frac{-T_{\text {a}_o}}{T_o}} \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial {\dot{\omega }}_o }{\partial A_o} = - Y_o \mathrm{e}^{\frac{-T_{\text {a}_o}}{T}} \; , \; \frac{\partial {\dot{\omega }}_o }{\partial T_{\text {a}_o}} = \frac{Y_o A_o}{T} \mathrm{e}^{\frac{-T_{\text {a}_o}}{T}} \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\partial {\dot{\omega }}_{\text {T}_o}}{\partial A_o} = \frac{-Q}{c_v \rho } \frac{\partial {\dot{\omega }}_o }{\partial A_o} \; , \; \frac{\partial {\dot{\omega }}_{\text {T}_o}}{\partial T_{\text {a}_o}} = \frac{-Q}{c_v \rho } \frac{\partial {\dot{\omega }}_o }{\partial T_{\text {a}_o}} \end{aligned}$$

(13)

Scalar-valued objective function:

$$\begin{aligned} J(Y,T) = \frac{1}{2}\int _{t} \left( Y - Y_{\text {ref}} \right) ^2 \hbox {d}t + \frac{1}{2}\int _{t} \left( T - T_{\text {ref}} \right) ^2 \hbox {d}t \end{aligned}$$

(14)

Linearized objective function $J(q_o+\delta q) = J(q_o) + \delta J$:

$$\begin{aligned} \begin{aligned} \delta J&= \int _{t} \overbrace{ \left( Y - Y_{\text {ref}} \right) }^{g_1} \delta Y \hbox {d}t + \int _{t} \overbrace{ \left( T - T_{\text {ref}} \right) }^{g_2} \delta T \hbox {d}t = g^\text {T} \delta q \;, \\ g&= [g_1,g_2]^\text {T} \end{aligned} \end{aligned}$$

(15)

System of adjoint equations (with $B^{\text {T}} = -B$):

$$\begin{aligned} \begin{aligned}&- \frac{\partial q^*}{\partial t} + \frac{\partial f_o}{\partial q_o} q^* = - \frac{\partial }{\partial t} \begin{pmatrix} Y^* \\ T^* \end{pmatrix} + \begin{pmatrix} \frac{\partial {\dot{\omega }}_o }{\partial Y_o} Y^* \\ \frac{\partial {\dot{\omega }}_{\text {T}_o}}{\partial T_o} T^* \end{pmatrix} = \\&\quad = \begin{pmatrix} Y - Y_{\text {ref}} \\ T - T_{\text {ref}} \end{pmatrix} = \begin{pmatrix} g_1 \\ g_2 \end{pmatrix} \end{aligned} \end{aligned}$$

(16)

Adjoint solution, sensitivity of J with respect to $\alpha$:

$$\begin{aligned} \frac{\partial J}{\partial \alpha _l} \approx \frac{\delta J}{\delta \alpha _l} = {q^*}^{\text {T}}\frac{\partial f_o}{\partial \alpha _{o,l}} \end{aligned}$$

(17)

Appendix 3: Code validation

The calculated imploding shock is compared against the Guderley solution for cylindrical imploding shock waves [29]. The simulated pressure values are extracted from the slice $x_1$–$x_2$ at the maximum focusing amplitude. In the cut $x_1$–$x_2$, the flow gradients in $x_3$ direction are less dominant than the inward components of the imploding shock wave. Therefore, the flow can be approximated to a cylindrical imploding wave. The left plot in Fig. 11 shows the $x_{_{\raisebox {2pt}{2}}}$–t diagram for both cases. Not only the wave velocity is accurately captured also its form, see center plot in Fig. 11. Due to the difference in diffusion and right-hand side boundary conditions with respect to the reference case, a minor discrepancy is shown in this plot. The convergence of the pressure amplitude at the imploding point is also tested by doubling the number of points in the radial direction. In Fig. 11 (right), the convergence of the solution is proved with approximately the order of fifty. In general, the validation results are in very good agreement for this reference case.

The mesh independence of the results is studied by the discretization of a laminar premixed flame and a detonation front in a one-dimensional domain. The same five successively finer grids are applied to both cases: flame and detonation. The results are presented in Fig. 12 relative to flame thickness $\delta _o$ and to half reaction length $L_{1/2}$ for the flame and the detonation, respectively. The left plot of this figure shows that the resolution of the flame temperature is quite satisfactory already with 8 points per $\delta _o$. The inset of this plot depicts the convergence of the solution with 11 points. The right plot in Fig. 12 contains the resolution of the pressure in a detonation front. As in the previous case, the front is fairly captured even with the lowest refinement of 4 points per $L_{1/2}$. In the inset, the variation in the detonation wave velocity with time is shown. The computed detonation velocities converge to the theoretical CJ value for this gas mixture, independently of the mesh.

The discretization at the focusing area in the numerical experiments of this work ranges between 11 and 22 points per $\delta _o$ or, equivalently, between 6 and 11 points per $L_{1/2}$. These results indicate that the reactive fronts are well resolved with the used refinement.