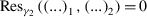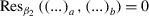Abstract
Ericksen’s problem consists of determining all equilibrium deformations that can be sustained solely by the application of boundary tractions for an arbitrary incompressible isotropic hyperelastic material whose stress-free configuration is geometrically flat. We generalize this by first, using a geometric formulation of this problem to show that all the known universal solutions are symmetric with respect to Lie subgroups of the special Euclidean group. Second, we extend this problem to its anelastic version, where the stress-free configuration of the body is a Riemannian manifold. Physically, this situation corresponds to the case where nontrivial finite eigenstrains are present. We characterize explicitly the universal eigenstrains that share the symmetries present in the classical problem, and show that in the presence of eigenstrains, the six known classical families of universal solutions merge into three distinct anelastic families, distinguished by their particular symmetry group. Some generic solutions of these families correspond to well-known cases of anelastic eigenstrains. Additionally, we show that some of these families possess a branch of anomalous solutions, and demonstrate the unique features of these solutions and the equilibrium stress they generate.
Similar content being viewed by others
1 Introduction
Universal deformations in nonlinear elasticity are deformations that exist for all members of a particular class of materials in the absence of body forces. Given any member of a particular class of materials, any universal deformation for that class can be maintained by the application of surface tractions alone. For instance in unconstrained isotropic elastic materials, only homogeneous deformations are universal. However, adding material constraints, i.e., restricting the class under consideration, expands the set of universal solutions. In particular, under the imposition of incompressibility, there are five known families of universal deformations in addition to the universal homogeneous deformations, now restricted to isochoric homogeneous deformations in keeping with the material constraint.
The process of obtaining and classifying all universal solutions is a highly nontrivial task. This line of research originates in the seminal work of Jerald Ericksen. In 1954, he made the first systematic attempt to classify all universal deformations in isotropic incompressible elasticity [7]. His work revealed four families of universal solutions in addition to homogeneous solutions. In 1955, he completely solved the analogous problem for unconstrained elastic bodies, proving that the only compressible universal solutions are homogeneous deformations [8]. In the case of incompressible elasticity, another family of universal solutions was then discovered by Singh and Pipkin [33], with a special case of this family discovered by Klingbeil and Shield [16]. Additionally, Fosdick [9] noted that a different special case of this deformation represented a universal solution with constant invariants, a special case not addressed by Ericksen’s initial work. Further contributions and specializations of this problem were made by a number of authors [10, 15, 17, 19, 21] and the current conjecture is that no other solution to Ericksen’s problem exist but a proof of it remains an outstanding open problem of rational mechanics [1].
Here, we are interested in generalizing Ericksen’s problem to nonlinear anelasticity. In anelasticity, we consider geometric deformations combining both elastic deformations and an additional anelastic component to the deformation, i.e., one that does not contribute to the strain energy. Such theories are known to be relevant in many situations that generalize classical nonlinear elasticity [5] such as thermal effects [27, 34], plastic flows [18], dislocations and defects [3, 25, 37], growth and remodeling [14, 23, 30, 35, 36], and swelling [28, 29]. Such processes are characterized by the presence of eigenstrains [22] that do not produce corresponding stresses or, equivalently, by changing the intrinsic geometry of the reference configuration from Euclidean to Riemannian. These eigenstrains are generally incompatible, and therefore further elastic strains are typically required to embed bodies with nontrivial eigenstrains into Euclidean space, with the resulting self-equilibrating elastic stresses generated by this strain referred to as residual stresses.
The first step in this research program was to generalize Ericksen’s theorem for compressible isotropic materials to anelastic deformations. By using a geometric formulation, it was proved that only covariantly homogeneous deformations are universal [40]. The second step, considered here, is to extend the current classification of isotropic incompressible nonlinear elasticity to isotropic incompressible nonlinear anelasticity. This general problem is more involved than the classical Ericksen problem as we have to determine simultaneously both the anelastic and elastic components that render the solutions universal.
While anelastic deformations can be modeled through a multiplicative decomposition [31], it is equivalent but more appropriate in our context to model them as a stress-free evolution of a general Riemannian manifold, the material manifold, via some anelastic process [6, 14, 24, 37]. This non-Euclidean material configuration contains all the information of the anelastic processes. It can then be mapped by an elastic deformation into the current Euclidean configuration. Only the strain induced by the elastic component appears in the strain-energy formulation, which models the notion that the anelastic deformation changes the relaxed geometry of the material, and that only the further elastic deformation stores energy by straining the material. In looking for universal solutions, both the Riemannian metric of the material manifold and the elastic deformation are unknowns to be determined.
In this paper, we extend the currently known families of incompressible universal solutions to the anelastic setting in an appropriately symmetric way, which will be precisely defined shortly. In the process of doing this, we discover that under these symmetry conditions, all families exhibit a branch of generic universal solutions that contain arbitrary functions as parameters, but some families also contain anomalous universal solution branches outside of these, whose form is fixed up to a finite number of constants. Additionally, we find that the six classical families of universal solutions merge into three distinct anelastic families, characterized by their respective symmetry groups. The Cauchy deformation tensors of the generic branches of these families can all be expressed in the forms presented here in Table 1, with the standard forms of the anomalous branches presented in Sect. 8, as they are more involved. In Sect. 2, we provide an overview of the geometric features of anelasticity and provide the relevant governing equations of elasticity in this context. The known universal solution families are summarized in Sect. 3. Then, in Sect. 4 we compute the appropriate symmetry group for each family and impose this symmetry on the metric tensor field a priori. We then formulate the problem of extending the universal families to the anelastic setting and outline the techniques used in our analysis in Sect. 5. In Sect. 6 we derive the form of the generic solutions for each family and obtain the constant invariant conditions that are necessary for anomalous solutions to exist. In Sect. 7 we present the general form of the anomalous solutions, relegating the explicit calculations to Appendix B. In Sect. 8, we examine the overlap of these families of solutions. Finally, we present some visualizations of the Riemannian geometry of strains and stresses induced by these anomalous solutions in Sect. 9, and summarize our results in Sect. 10. We have provided two other appendices, Appendix A containing summaries of the algebraic and group theoretic tools we employ in our analysis, and Appendix C, detailing particular features of the Lie algebra \(\mathfrak{se}(3)\), which plays a key role in our analysis.
2 Nonlinear Elasticity and Anelasticity
In the geometric formulation of nonlinear elasticity, we define the ambient space to be a Riemannian manifold \((\mathcal{S},\mathbf{m})\), where \(\mathbf{m}\) is a fixed background metric. Since we are interested in universal deformations that take place in Euclidean space we assume that the ambient space is Euclidean. Then, a body is defined as a Riemannian manifold \((\mathcal{B},\mathbf{M})\). We define a motion as an isotopy \(\varphi \)
parameterized by time \(t\) that gives a homeomorphism at each time \(t\) between the reference configuration ℬ and the physical configuration at time \(t\) defined by \(\varphi (\mathcal{B},t)\) (see Fig. 1): We use coordinate charts \(\{X^{A}\}\) and \(\{x^{a}\}\) for ℬ and \(\mathcal{C}\), respectively. We utilize uppercase Latin letters to denote most quantities and indices in the reference configuration, and lowercase Latin letters to denote most quantities and indices in the physical configuration.
The homeomorphism at time \(t\), \(\varphi (-,t)\), can be interpreted physically as determining the position of a small piece of material at time \(t\), given its position in ℬ, which is interpreted as an initial position, though the important feature of the reference configuration is that it specifies the relaxed geometry of the body; it is not necessarily the initial configuration of the body. While in elasticity, \((\mathcal{B},\mathbf{M})\) is Euclidean, for an anelastic system, \((\mathcal{B},\mathbf{M})\) may not be Euclidean and, in such case, \(\varphi _{0}\equiv \varphi (-,0)\) is not the identity map. Since \(\varphi _{0}(\mathcal{B})\) and \(\varphi (\mathcal{B},t)\) correspond to physical configurations, we model them as subsets of Euclidean space, and hence, we identify positions with vectors.
Since we are interested in equilibrium states, we restrict our attention to a finite time \(t^{*}>0\) and suppress the explicit time-dependence so that we define, with a slight abuse of notation, \(\varphi (\mathcal{B})=\varphi (\mathcal{B},t^{*})\).
2.1 Kinematics
The local properties of deformations are encapsulated in the derivative of the map \(\varphi \) that we explore next. The tangent space of ℬ at \(X\in \mathcal{B}\) is denoted by \(T_{X}\mathcal{B}\). The tangent space of the corresponding point \(x=\varphi (X)\) in the ambient space is denoted by \(T_{\varphi (X)}\mathcal{C}\). The deformation gradient \(\mathbf{F}\) is the derivative map of \(\varphi \):
With respect to the coordinate charts \(\{X^{A}\}\) and \(\{x^{a}\}\), \(\mathbf{F}\) it is defined as follows
The adjoint of \(\mathbf{F}\) is
In components, \((F^{\mathsf{T}})^{A}{}_{a}=M^{AB}m_{ab}F^{b}{}_{B}\). Note that the adjoint explicitly depends on the metrics \(\mathbf{M}\) and \(\mathbf{m}\). The right Cauchy-Green deformation tensor is defined as
It is straightforward to see that \(\mathbf{C}^{\flat }=\varphi ^{*}\mathbf{m}\), which has components \(C_{AB}=F^{a}{}_{A}F^{b}{}_{B}m_{ab}\) [20]. The Jacobian relates the material and spatial Riemannian volume elements as \(dv(x,\mathbf{m})=JdV(X,\mathbf{M})\), where \(J\) is given by
2.2 Equilibrium Equations
The balance of linear momentum in the absence of body and inertial forces in terms of the Cauchy stress tensor reads
where \(\mathrm{div}\) is the spatial divergence operator, defined in components as
and \(\gamma ^{a}{}_{bc}\) is the Christoffel symbol of the Levi-Civita connection \(\nabla ^{\mathbf{m}}\) of the metric \(\mathbf{m}\) in the coordinate chart \(\{x^{a}\}\), defined as \({\nabla ^{\mathbf{m}}}_{\partial _{b}}\partial _{c}=\gamma ^{a}{}_{bc} \partial _{a}\). The local form of the balance of angular momentum reads \(\sigma ^{ab}=\sigma ^{ba}\), i.e., the Cauchy stress is symmetric.
The first Piola-Kirchhoff stress is defined as \(\mathbf{P}=J\boldsymbol{\sigma }\mathbf{F}^{-\star }\), and in components, \(P^{aA}=J\sigma ^{ab}(F^{-1})^{A}{}_{b}\). \(\mathbf{F}^{\star }\) is the deal of \(\mathbf{F}\), and is defined as \(\mathbf{F}^{\star }=\frac{\partial \varphi ^{a}}{\partial X^{A}}dX^{A} \otimes \frac{\partial }{\partial x^{a}}\). The balance of linear momentum in terms of \(\mathbf{P}\) reads \(\operatorname{Div}\mathbf{P}=\mathbf{0}\). In components
where \(\Gamma ^{A}{}_{BC}\) is the Christoffel symbol of the Levi-Civita connection \(\nabla ^{\mathbf{M}}\) of the metric \(\mathbf{M}\) in the coordinate chart \(\{X^{A}\}\), defined as \({\nabla ^{\mathbf{M}}}_{\partial _{B}}\partial _{C}=\Gamma ^{A}{}_{BC} \partial _{A}\). The balance of angular momentum in terms of \(\mathbf{P}\) reads \(\mathbf{P}\mathbf{F}^{\mathsf{T}}=\mathbf{F}\mathbf{P}^{\mathsf{T}}\).
2.3 Constitutive Equations
In this paper we restrict ourselves to bodies that are isotropic in the absence of eigenstrains. We also assume that the elastic deformations are incompressible. The left Cauchy-Green stretch tensor is defined as \(\mathbf{B}^{\sharp }=\left (\varphi ^{-1}\right )_{*}(\mathbf{m}^{-1})\) and has components \(B^{AB}=(F^{-1})^{A}{}_{a}(F^{-1})^{B}{}_{b}~m^{ab}\), where \(m^{ab}\) are components of \(\mathbf{m}^{-1}\). The spatial analogues of \(\mathbf{C}^{\flat }\) and \(\mathbf{B}^{\sharp }\) are defined as
where \(\mathbf{b}^{\sharp }\) is called the Finger deformation tensor. The two tensors \(\mathbf{C}\) and \(\mathbf{b}\) have the same principal invariants, which are denoted by \(I_{1}\), \(I_{2}\), and \(I_{3}\) [26]. In the case of an isotropic solid the energy function \(W\) depends only on \(I_{1}\), \(I_{2}\), and \(I_{3}\). If the material is incompressible (\(I_{3}=1\)), \(W=W(I_{1},I_{2})\), and the Cauchy stress has the following representation [32]Footnote 1
where \(p\) is a Lagrange multiplier that is associated with the incompressibility constraint \(J=1\).
2.4 Ericksen’s Problem
The classical elastic Ericksen problem is stated as follows: Determine all equilibrium deformations \(\varphi :\mathcal{B}\rightarrow \mathcal{C}\) with \(\mathcal{B},\mathcal{C}\subset \mathbb{E}^{3}\) that can be sustained by an arbitrary incompressible isotropic hyperelastic solid with suitable boundary tractions.
The emphasis of the classical problem is that both configurations are Euclidean. Here, we consider a generalized version of this problem applicable to anelastic systems. The anelastic Ericksen problem relaxes the requirement that \(\mathcal{B}\subset \mathbb{E}^{3}\) and is stated as follows: Determine all Riemannian manifolds \(\left (\mathcal{B},\mathbf{M}\right )\), and all maps \(\varphi :\mathcal{B}\rightarrow \mathcal{C}\) with \(\mathcal{C}\subset \mathbb{E}^{3}\) that can be sustained by an arbitrary incompressible isotropic hyperelastic solid with suitable boundary tractions.
These problems are treated locally in the sense that the equilibrium equations are locally satisfied by these deformations for arbitrary incompressible isotropic hyperelastic materials. We do not address non-local problems such as self-intersection or self-contact beyond requiring that our solutions be locally homeomorphisms, which is guaranteed by the condition \(\operatorname{det}\mathbf{F}>0\). This condition ensures that over some domain our solution is an embedding, rather than an immersion.
3 The Known Universal Deformations
We begin with the known families of incompressible universal solutions in the absence of eigenstrains. We merely present them and direct the reader to the original papers for their derivation [7, 8, 16, 33]. The corresponding deformation gradients are derived explicitly in [14]. The emphasis and novelty here is in the particular type of symmetry associated to each family as they will play a key role in the generalization of the problem to anelastic systems. Expressed in terms of the standard Cartesian coordinates \(\{x,y,z\}\), cylindrical polar coordinates \(\{r,\theta ,z\}\), or spherical polar coordinates \(\{r,\theta ,\phi \}\) (letting capital letters denote reference configuration coordinates, and lower case letters denote current configuration coordinates), we have the following six universal families.
Family 0: Homogeneous Deformations
Using the Cartesian coordinates \(\{x^{a}\}=\{x,y,z\}\) and \(\{X^{A}\}=\{X,Y,Z\}\), this family is most compactly expressed as
where \(F^{a}{}_{A}\) is a constant tensor with \(\operatorname{det}F^{a}{}_{A}=1\), and \(c^{a}\) is a constant vector. A deformation of this type is depicted in Fig. 2. The form of equation (13) immediately reveals that the deformation gradient is \(F^{a}{}_{A}\), as evidenced by the induced tangent map \(dx^{a}=F^{a}{}_{A}dX^{A}\). Since the deformation gradient \(\mathbf{F}\) is constant, \(F^{a}{}_{A}(X^{A})=F^{a}{}_{A}\), the transformation
leaves the deformation gradient unchanged, and hence, \(C_{AB}\) remains unchanged. In terms of symmetry group, we notice that the action \(X^{A}\rightarrow X^{A}+C^{A}\) is precisely the action of \(\text{T}(3)\subset \text{SE}(3)\) on \(\mathbb{E}^{3}\).
Family 1: Bending, Stretching, and Shearing of a Rectangular Block
When expressed using cylindrical polar coordinates \(\{r,\theta ,z\}\) and Cartesian coordinates \(\{X,Y,Z\}\) in the current and reference configurations, respectively, universal deformations in this family take the form
though the parameters \(E\) and \(F\) correspond to rigid motions, and hence, can be safely disregarded. These parameters generate rotation around and translation along the \(r=0\) axis, as seen in Fig. 3. We can compute the deformation gradient, which when expressed on mixed orthonormal frames, takes the form
or in terms of a mixed coordinate bases, we have the components
Working in terms of the mixed bases will often be advantageous when computing symmetries and the components of arbitrary metric tensors, as these bases are automatically induced by the coordinate map. Additionally, we demand \(AB\neq 0\) to ensure the deformation is invertible; the incompressibility condition is automatically satisfied. We compute \(C_{AB}\) as
and note that this remains unchanged under the transformation
This is precisely the action of \(\text{T}(2)\subset \text{SE}(3)\) on \(\mathbb{E}^{3}\).
Family 2: Straightening, Stretching, and Shearing of an Annular Wedge
Deformations in this family are most naturally expressed using Cartesian and cylindrical polar coordinates \(\{x,y,z\}\) and \(\{R,\Theta ,Z\}\) in the current and reference configurations respectively, and take the form
An example of one of these deformations is depicted in Fig. 4. The corresponding deformation gradient is
or, in terms of the induced coordinate bases
We demand \(AB\neq 0\) to ensure the deformation is invertible, and as in the previous case, the incompressibility condition is automatically satisfied. Thus
The transformation
leaves these components unchanged. This is the action of \(\text{SO}(2)\times \text{T}(1)\subset \text{SE}(3)\) on \(\mathbb{E}^{3}\).
Family 3: Torsion, Extension, and Shearing of an Annular Wedge
When expressed in cylindrical polar coordinates, deformations in this family take the form
and an example of a deformation from this family is depicted in Fig. 5. The deformation gradient can be naturally expressed on orthonormal cylindrical polar bases as
or equivalently on the coordinate bases, it has components
We have the incompressibility condition \(A\left (CF-DE\right )=1\), which also ensures invertibility. Thus, \(C_{AB}\) is written as
and notice that \(C_{AB}\) does not depend on \(\Theta \) or \(Z\).
Family 4: Inflation/Eversion of a Sphere
In spherical polar coordinates \(\{r,\theta ,\phi \}\) and \(\{R,\Theta ,\Phi \}\), deformations in this family take the form
An example of one of these deformations is depicted in Fig. 6. The deformation gradient on orthonormal bases reads
or, in terms of the coordinate bases, we have the components
Incompressibility and invertibility are trivially satisfied. Thus
We can then represent this tensor on an orthonormal spherical basis (using the standard Euclidean metric) as
where \(\mathbf{I}\) is the identity tensor, and \(\mathbf{E}_{R}=\frac{\mathbf{X}}{|\mathbf{X}|}\). This obeys the symmetry transformation
which is symmetry under the prolonged action of \(\text{SO}(3)\subset \text{SE}(3)\) on \(\text{T}\mathbb{E}^{3}\otimes \text{T}^{*}\mathbb{E}^{3}\).
Family 5: Inflation, Bending, Extension, and Azimuthal Shearing of an Annular Wedge
When expressed in cylindrical polar coordinates \(\{r,\theta ,z\}\) and \(\{R,\Theta ,Z\}\), deformations in this family take the form
An example of one of these deformations is presented in Fig. 7. The deformation gradient expressed on orthonormal bases is written as
or, on the coordinate bases
In order to satisfy incompressibility, we have \(A^{2}CE=1\). This family is peculiar, as the stretch generated by the other inhomogeneous families has an eigenvector along the direction of inhomogeneity, but this one does not. Additionally, the invariants of \(\mathbf{b}\) for this family are spatially constant.
When we generalize these deformations to include an anelastic component, we have to change the incompressibility condition from \(\operatorname{det}\mathbf{F}=1\) to
to reflect the fact that we are only constraining the elastic component of the deformation to be isochoric. It is easier however, to consider square of this equation in the form
which in components reads
This is because when we move to the anelastic setting, the stretch \(\mathbf{b}\) is a more natural object to work with, since it captures geometric data about the material manifold, but itself lives in Euclidean space. The right Cauchy-Green strain reads
which is invariant under changes in \(Z\) or \(\Theta \).
3.1 Summary of the Symmetry Groups
The symmetries we have calculated are all generated by the usual action of Lie subgroups of the special Euclidean group on the reference configuration. For each family, there is some continuous family of rotations and/or translations, which once prolonged, leaves the right Cauchy-Green stretch tensor field unchanged. In a similar manner, we can compute symmetries of the left Cauchy-Green stretch tensor field, which also happen to be Lie subgroups of the special Euclidean group but, acting now on the current configuration. These groups are summarized in Table 2, expressed in terms of the group of \(n\)-dimensional rotations \(\text{SO}(n)\) and the group of \(n\)-dimensional translations \(\text{T}(n)\).
Interestingly enough, for each family, the symmetry group of \(\mathbf{C}\) does not necessarily match the symmetry group of \(\mathbf{b}\), but the dimensions of these two groups do match, as their actions are related through the maps relating the coordinates in the two configurations. Additionally, when we impose the symmetries of \(\mathbf{C}\) on the material manifold, families with 3-dimensional Lie symmetries automatically satisfy the equilibrium conditions, but those only containing a 2-dimensional Lie symmetry require additional constraints to satisfy equilibrium. This seems to suggest that the dimension of the symmetry group plays a role in constraining the material response, and sufficiently high dimensional symmetries are sufficient for guaranteeing equilibrium.
These symmetries can be summarized as a single key property, namely that for a given universal deformation and its associated deformation gradient \(\mathbf{F}\) and right Cauchy-Green tensor, \(\mathbf{C}=\mathbf{F}^{\mathsf{T}}\mathbf{F}=\mathbf{M}^{-1}\varphi ^{*} \mathbf{m}\), we have that \(\mathbf{C}^{\flat }=\varphi ^{*}\mathbf{m}\) is invariant under the prolonged action of a Lie subgroup of the special Euclidean group acting on the reference configuration. We will use this key property when studying the anelastic Ericksen problem, and accordingly refer to the symmetries of \(\mathbf{C}^{\flat }\) as ‘universal symmetries’.
4 General Construction
The previous section demonstrated a remarkable symmetry property of the known universal solutions in the absence of eigenstrain. We can use these symmetries to generalize Ericksen’s problem to anelastic systems. The problem is then to find a suitable metric on the material manifold that preserves both the symmetry and the general functional form of the universal deformations. The eigenstrains and metric associated with this new metric are referred to as ‘universal’. This can be achieved by the following construction:
-
First, in the absence of eigenstrains, the body is embedded in the ambient space with an induced metric \(\bar{\mathbf{M}}\). The material manifold is the flat Riemannian manifold \((\mathcal{B},\bar{\mathbf{M}})\) and the deformation is a map from this manifold to the ambient space.
-
Second, in the presence of eigenstrains the natural configuration of the body is a Riemannian manifold \((\mathcal{B},\mathbf{M})\), where \(\mathbf{M}\) has non-vanishing curvature [12, 38, 39]. In this case, the deformation is a map from \((\mathcal{B},\mathbf{M})\) to the ambient space \((\mathcal{S},\mathbf{m})\).
-
Third, we choose curvilinear coordinates \(\{X^{A}\}\) on ℬ and curvilinear coordinates \(\{x^{a}\}\) on \(\mathcal{C}\subset \mathcal{S}\). These coordinates are not necessarily associated with the metrics \(\bar{\mathbf{M}}\) and \(\mathbf{M}\). We know of the previously presented classes of universal deformations \(x^{a}=\varphi (X^{A})\) for \((\mathcal{B},\bar{\mathbf{M}})\). We fix these functional dependences \(\varphi \) on the coordinates and determine the metrics \(\mathbf{M}\) compatible with these solutions.
-
Fourth, we pull back \(\mathbf{m}\) under the deformation \(\varphi \), and consider the three manifolds: \((\mathcal{B},\bar{\mathbf{M}})\), \((\mathcal{B},\mathbf{M})\), and \((\mathcal{B},\varphi ^{*}\mathbf{m})\). We have two candidates for determining the symmetry to apply to \(\mathbf{M}\): \(\bar{\mathbf{M}}\) and \(\varphi ^{*}\mathbf{m}\). We use \(\varphi ^{*}\mathbf{m}\) since it captures information about the deformation. We compute its symmetries, and demand \(\mathbf{M}\) to have these same symmetries. Explicitly, since both \(\bar{\mathbf{M}}\) and \(\mathbf{m}\) are Euclidean metrics, both are invariant under the full action of \(\text{SE}(3)\) acting on their respective base spaces. By considering Euclidean symmetries of \(\varphi ^{*}\mathbf{m}\), we are identifying Euclidean symmetries in the current configuration that are mapped to Euclidean symmetries in the reference configuration when pulled back under the classical universal deformation in question.
-
Fifth, we compute the deformation mapping \((\mathcal{B},\mathbf{M})\) to \((\mathcal{C},\mathbf{m})\), where now \(\mathbf{M}\) is restricted by the derived symmetries, and compute the specific metrics \(\mathbf{M}\) that generate universal eigenstrains.
4.1 Universal Equilibrium Equations
We fix the coordinate labels for the anelastic component of the local deformation; if \(X^{A}\) are coordinates for the material manifold, we write the anelastic deformation in terms of coordinates as
where \(\delta ^{A}_{\bar{A}}\) is the Kronecker delta, and use the metric tensor field to reflect the change in geometry (see Fig. 8). In other words, we convect the referential coordinates along with the anelastic motion onto the intermediate configuration. This allows us to trivially pull the material metric tensor back to the reference configuration using
and treat \(M_{\bar{A}\bar{B}}\) as our unknown quantity. Since \(M_{\bar{A}\bar{B}}\) and \(C_{\bar{A}\bar{B}}\) live in the same space, we can immediately impose the symmetry of \(C_{\bar{A}\bar{B}}\) on \(M_{\bar{A}\bar{B}}\), which naturally imposes a symmetry on \(M_{AB}\) via (43).
After determining the most general form of a metric tensor field obeying these symmetries, we can compute the general form of the elastic left Cauchy-Green tensor
and its inverse in terms of the undetermined components of the metric tensor field. Both of these appear in the Cauchy stress of an incompressible isotropic elastic solid, which has the following representation
in terms of \(W_{i}={\partial W}/{\partial I_{i}}\), where \(I_{1}\) and \(I_{2}\) are the two non-trivial invariants of \(\mathbf{b}\), and \(p\) is the Lagrange multiplier corresponding to the incompressibility constraint. We seek equilibrium solutions, hence we must satisfy
We wish to eliminate the pressure field from the analysis, so we take a second covariant derivative, lower the upper free index, and compute the antisymmetric part. This operation eliminates the pressure identically and yields the condition
which must be satisfied for arbitrary choices of the strain energy function \(W\). Because \(W\) is arbitrary, we can freely vary its partial derivatives independently, so in order to satisfy (47) for any \(W\), we require each of the terms multiplying a partial derivative of \(W\) to vanish independently. This yields nine independent conditions that must be satisfied, corresponding to the nine independent mixed partial derivatives of \(W\) that appear: \(W_{1}\), \(W_{2}\), \(W_{11}\), \(W_{12}\), \(W_{22}\), \(W_{111}\), \(W_{112}\), \(W_{122}\), and \(W_{222}\). These universal equilibrium equations are
Each of these nine equations is antisymmetric in the two free indices. Therefore, each equation has three independent components providing an overdetermined system of 27 scalar conditions that must be satisfied. Imposing the universal symmetries lead to two different situations depending on the symmetry:
Case I: For two universal families (the homogeneous and spherical deformations) these equations are trivially satisfied and do not lead to any new conditions.
Case II: For the other families, these equations will either require particular off-diagonal components of the metric tensor to vanishFootnote 2 (Case IIa) or the invariants to be constant (Case IIb). For Case IIa the equilibrium equations are trivially satisfied. This is the so-called generic case for all the remaining families analysed in Chap. 7. Case IIb corresponds to the anomalous solutions. In this case the symmetry condition generates a set of ordinary differential equations constraining these components in terms of a single independent variable. In addition to satisfying these, we also must satisfy three algebraic constraints, namely that the invariants of \(\mathbf{b}\) are spatially constant. This leaves us with an overdetermined system of four linear differential equations, one linear algebraic equation and two nonlinear algebraic equations for the six unknown components of the metric tensor field. We can integrate the differential equations, and use the linear algebraic equation to express the other two algebraic equations in terms of the following \(15\leq n\leq 18\) variables: a single unknown component of the metric tensor, the remaining independent variable in space (e.g., radius), the integration constants introduced by our integration of the ordinary differential equations, the deformation parameters, and the two constant invariants. Therefore, the remaining algebraic conditions are polynomial equations in these \(n\) variables that are quadratic in the unknown component of the material metric tensor field. We compute the resultant (see Appendix A.1) of these polynomials in this component, and demand it vanish for the two equations to have a common solution, since our metric tensor must simultaneously satisfy both. This resultant is itself a polynomial in the dependent variable that must vanish. Because we seek solutions that are universal over an open set, we can send each of the coefficients of the resultant to zero identically. This leaves us with a set of algebraic equations relating the integration constants, the deformation parameters, and the invariants that must be necessarily satisfied in order for these anomalous solutions to exist. These algebraic equations are solved in Chap. 8.
5 Symmetries of the Material Metric
Family 0: Homogeneous Deformations
Recall that the action \(X^{A}\rightarrow X^{A}+C^{A}\) is the action of \(\text{T}(3)\subset \text{SE}(3)\) on \(\mathbb{E}^{3}\). We seek to impose this symmetry on the material metric tensor field, and hence demand
Taking the derivative of this with respect to \(C^{D}\) gives
and hence, we consider constant metric tensor fields. It is however, more useful to express this condition in terms of the current configuration variables, which we can do via the chain rule
Since \(\mathbf{F}\) is invertible, this implies that \(M_{AB}\) is constant when expressed in terms of the current configuration coordinates as well. Additionally, it is more useful to consider the inverse metric tensor field \(M^{AB}\), which also must be constant in order for the identity
to hold.
Family 1: Bending, Stretching, and Shearing of a Rectangular Block
Recall, that the symmetry associated with this deformation is the action of \(\text{T}(2)\subset \text{SE}(3)\) on \(\mathbb{E}^{3}\). We therefore require the same invariance for \(M_{AB}\):
Taking the derivative with respect to \(C_{1}\) and \(C_{2}\) independently gives the conditions
Therefore, we assume that the metric tensor is of the form \(M_{AB}(X)\), which because of the form of the deformation, can be recast into the form \(M_{AB}(r)\), and equivalently \(M^{AB}(r)\).
Family 2: Straightening, Stretching, and Shearing of a Sector of a Cylinder
Here, we require that the metric is invariant under the action of \(\text{SO}(2)\times \text{T}(1)\subset \text{SE}(3)\) on \(\mathbb{E}^{3}\):
and hence, by the same reasoning as before one finds
Note that this does not imply \(\frac{\partial \mathbf{M}}{\partial \Theta }=\mathbf{0}\), since the basis vectors of \(\mathbf{C}\) do change with \(\Theta \). Rather, the components \(M_{AB}\) do not change with \(\Theta \) when \(\mathbf{M}\) is represented with respect to a cylindrical polar basis. We can use the equation \(M_{AB}M^{BC}=\delta _{A}^{C}\) to show that \(\frac{\partial M^{AB}}{\partial \Theta }= \frac{\partial M^{AB}}{\partial Z}=0\). Hence, we write \(M^{AB}(R)\) or equivalently \(M^{AB}(x)\). This symmetry of \(M^{AB}\) is precisely the action \(\text{SO}(2)\times \text{T}(1)\subset \text{SE}(3)\) prolonged to \(\text{T}\mathbb{E}^{3}\otimes \text{T}\mathbb{E}^{3}\), with ⊗ denoting the tensor product bundle, the bundle formed by taking fiberwise tensor products.
Family 3: Inflation, Bending, Torsion, Extension, and Shearing of an Annular Wedge
As with Family 2, we demand that \(M_{AB}\) be invariant under the transformation
which renders the conditions
So we consider metric tensor fields of the form \(M_{AB}(R)\), or equivalently, \(M^{AB}(r)\).
Family 4: Inflation/Eversion of a Sphere
Here, we demand the invariance of \(\mathbf{M}(\mathbf{X})\) under the prolonged action of \(\text{SO}(3)\subset \text{SE}(3)\) on \(\text{T}^{*}\mathbb{E}^{3}\otimes \text{T}^{*}\mathbb{E}^{3}\). We then seek the most general positive-definite symmetric tensor field that satisfies
Because \(\mathbf{M}(\mathbf{X})\) is positive-definite and symmetric, we can represent it in spectral form on an orthonormal basis \(\{\mathbf{u}_{a}\}\) as
We then consider the subgroup of rotations leaving \(\mathbf{X}\) fixed. Under this one-parameter family, we have the symmetry condition
This implies that (suppressing the \(\mathbf{X}\) dependence)
i.e., the rotated vector \(\mathbf{Q}^{\mathsf{T}}\mathbf{u}_{i}\) lies in the same eigenspace as the eigenvector \(\mathbf{u}_{i}\). For this to hold for all \(\mathbf{Q}\) in this one-parameter family, the eigenspaces of \(\mathbf{M}\) at the point \(\mathbf{X}\) must be unchanged by these rotations, i.e., the swept vector \(\mathbf{Q}^{\mathsf{T}}\mathbf{u}_{i}\) remains in the eigenspace. Generally, a rotating vector sweeps out a cone, which not being an affine space, cannot be the eigenspace of a linear operator, as depicted in Fig. 9.
However, there are two degenerate cases where cones become affine spaces, where the rotation axis and swept vector are coincident, and where they are perpendicular, which means that the eigenspaces of \(\mathbf{M}\) at \(\mathbf{X}\) must contain the axis of the rotation, and the plane orthogonal to it, as depicted in Fig. 10, forcing \(\mathbf{M}(\mathbf{X})\) to be of the form
because for each \(\mathbf{X}\), the axis of rotation is \(\mathbf{E}_{R}(\mathbf{X})\). Imposing the more general symmetry condition (68), on this spectral form, we get the condition
which implies that
This ultimately requires that \(m_{1}\) and \(m_{2}\) depend on \(\mathbf{X}\) solely through its norm, \(R=|\mathbf{X}|\), since for any two points, \(\mathbf{X}_{1}=R\mathbf{n}_{1}\), and \(\mathbf{X}_{2}=R\mathbf{n}_{2}\), where \(\mathbf{n}_{1}\) and \(\mathbf{n}_{2}\) are unit vectors, we can construct orthogonal transformations such that \(\mathbf{n}_{2}=\mathbf{Q}\mathbf{n}_{1}\). Hence, because the functions \(m_{1}\) and \(m_{2}\) take on the same values whenever their arguments have the same norm, these functions must only depend on their argument through its norm, as shown in Fig. 11. We then have
which is the general form of the pullback of our material metric tensor.Footnote 3 Computing the components of \(M_{AB}\) then gives
Since \(m_{1}\) and \(m_{2}\) are arbitrary, and \(R\) is only a function of \(r\), this can be rewritten as
and equivalently
These metrics are precisely the form considered by Ben Amar and Goriely [2], and Yavari and Goriely [38], though the first represents this tensor on an orthonormal spherical basis, and the second works with the components of the metric tensor rather than its inverse, as we have done.
Family 5: Inflation, Bending, Extension, and Azimuthal Shearing of an Annular Wedge
As in other cases, we have the following symmetry relations for \(\mathbf{M}\):
so we ultimately consider inverse metric tensor fields of the form \(M^{AB}(r)\).
In conclusion, we note that the application of the symmetry condition leads to a reduction of the independent variables to a single one (either the radial variable \(r\) in cylindrical or spherical coordinates, or \(x\) for the deformation of rectangular blocks).
6 Generic Universal Solutions
Having established the symmetry conditions on the material metric, we can express the universal equilibrium equations under these restrictions. For all families (Case I and IIa), these equations will have generic solutions, and in some cases, these solutions are the only ones satisfying the symmetry conditions. Other families also have anomalous solutions (Case IIb) outside of these generic branches that occur only when the invariants of the tensor \(\mathbf{b}\), or equivalently \(\mathbf{C}\), are constant; these will be addressed in the next section. The nature of the anomalous solutions differs markedly from the generic solutions found here: generic solutions contain arbitrary functions as free parameters, while the form of the anomalous solutions is determined up to a finite number of undetermined constants. Additionally, for generic solutions, the eigenvectors of \(\mathbf{b}\) are contained within or perpendicular to the span of the infinitesimal generators of the symmetry group, while for anomalous solutions, this alignment does not occur. While the invariants, and hence, their gradients could be calculated explicitly in terms of the unknown inverse metric components, it is easier to keep these functions unevaluated at the moment, because we will ultimately show that they must be constant for the anomalous solution to exist.
We then fix an orthonormal frame on these constructed intermediate configurations, and express the anelastic deformation required to generate these intermediate configurations in terms of these frames. We note that since we are in reality only determining the elastic component of these motions, the factor \(\mathbf{A}\) corresponds to the universal motion, while the factor \(\mathbf{G}\) corresponds to the stretch required to obtain the universal intermediate configurations from the classical reference configurations, which play no dynamic role. Hence after computing \(\mathbf{A}=\mathbf{F}\mathbf{G}^{-1}\), so long as the geometry of the intermediate configuration is retained, the factor \(\mathbf{G}\) can be discarded, which corresponds to the fact that we can prepend an arbitrary compatible anelastic deformation onto our universal deformations. As this is supplementary to our main results, we will simply give \(\mathbf{G}\) on some orthonormal anholonomic frame, leaving further computations to interested readers.
Family 0: Homogeneous Deformations
The deformation mapping written in Cartesian coordinates is given by (13), and the deformation gradient \(F^{a}{}_{A}\) is constant. We compute the left Cauchy-Green tensor as
which is also constant, and hence its invariants are constant. The Cauchy stress takes the form
and the equilibrium equations read
Because \(m^{ab}\) is invertible, this implies that \(p\) is constant, and the equilibrium equations are satisfied simply because of the assumed form of \(M^{AB}\). The only remaining condition is the incompressibility condition which, in the chosen coordinate systems, reads
We can express this constraint as a condition on \(M^{AB}\), or as a condition on \(F^{a}{}_{A}\). In reality, these conditions are equivalent, since we have
and one can be freely transformed into the other by changing coordinates. However, for the other families, it will be easier to express this condition as a restriction on the inverse metric tensor, so for consistency we choose the invertible tensor \(F^{a}{}_{A}\) and then enforce
which ensures that the volume form in the material manifold agrees with that in the current configuration.
Because the material metric is constant, its Levi-Civita connection produces no curvature, and thus the material manifold is Euclidean. This is useful when using a multiplicative decomposition of the deformation gradient into elastic and anelastic factors \(\mathbf{F}=\mathbf{AG}\), as we can choose a Cartesian frame \(\{\mathbf{e}_{\alpha }\}\) in the material manifold and its corresponding coframe \(\{\vartheta ^{\alpha }\}\), in which case the anelastic factor must satisfy \(G^{\alpha }{}_{A}G^{\beta }{}_{B} \delta _{\alpha \beta }=M_{AB}\). Since the matrix of components \(M_{AB}\) is positive definite and symmetric, we can take the matrix of components \(G^{\alpha }{}_{A}\) to be its unique positive-definite symmetric square root, in which case we satisfy \(G^{\alpha }{}_{A}G^{\beta }{}_{B} \delta _{\alpha \beta }=M_{AB}\). Alternatively, we may prescribe the anelastic factor in such a way that the induced material metric is valid. In this case, since \(M_{AB}\) is constant, any constant invertible anelastic factor will furnish a valid material metric. The incompressibility constraint becomes \(\operatorname{\det }(A^{a}{}_{\alpha }A^{b}{}_{\beta } \delta ^{\alpha \beta }m_{bc})=1\), which furnishes a differential equation constraining the volume in the current configuration to agree with that in the material manifold.
Family 1: Bending, Stretching, and Shearing of a Rectangular Block
The deformation for this family is given in (15) with the deformation gradient (16). We compute the quantity \(m_{a[l}\nabla _{k]}\nabla _{b} \sigma ^{ab}=0\), which for this family, only has two independent nonzero components, and we take the coefficients of the partial derivatives of \(W\) to vanish independently. The \(W_{111}\) coefficient of this equation gives the conditions
The first equation implies that either \(M^{12}(r)=0\), or \(I_{1}\) is constant, because \(AB\neq 0\) to ensure the invertibility of the deformation. If \(I_{1}\) is not constant, we have \(M^{12}(r)=0\). The second component then becomes \(M^{13}(r)=0\). Therefore, if \(I_{1}\) is not constant, we have that \(M^{12}(r)=M^{13}(r)=0\).
If \(I_{1}\) is constant, we can examine the \(W_{122}\) component, which implies the conditions
Therefore, \(I_{2}\) is constant, or \(M^{12}(r)=M^{13}(r)=0\) and we have established that either \(M^{12}(r)=M^{13}(r)=0\), or all the invariants of \(\mathbf{b}\) are constant, which is the condition for the anomalous solution. Hence, in this section, we take \(M^{12}(r)=M^{13}(r)=0\) and we consider the constant invariant case in the next section. With \(M^{12}(r)=M^{13}(r)=0\), we have the equilibrium equation satisfied, i.e., all of its terms identically vanish. We only have to satisfy incompressibility. Demanding \(\operatorname{det}b^{ab}=\operatorname{det} m^{ab}\), we have the condition
Since \(M^{11}(r)\neq 0\), and \(M^{22}(r)\neq 0\), the relation
ensures that the incompressibility is satisfied. Hence, we have the generic solution
which, by writing \(M^{AB}(X)=M^{AB}\left (r(X)\right )\), can finally be written in terms of the referential variables as
The current form of \(M_{AB}\) automatically captures incompressibility because we imposed a particular form of \(r(X)\). If we leave this unspecified, we can simply say that \(M_{AB}\) is of the form
and use the incompressibility constraint to determine \(r(X)\). This is equivalent to introducing a change in coordinates rescaling \(X\).
When using a multiplicative decomposition, \(\mathbf{F}=\mathbf{AG}\), we can choose an orthonormal frame \(\{\mathbf{e}_{\alpha }\}\) and its coframe \(\{\vartheta ^{\alpha }\}\) in the material manifold, and require \(G^{\alpha }{}_{A}G^{\beta }{}_{B} \delta _{\alpha \beta }=M_{AB}\). Since \(M_{AB}\) is block diagonal, positive definite, and symmetric, we can take \(G^{\alpha }{}_{A}\) to be its unique positive definite symmetric square root. Because the components \(M_{AB}\) are arbitrary functions of \(X\), we can take \(G^{\alpha }{}_{A}\) to be of the form
which will yield a suitable \(M_{AB}\). Additionally, we can multiply \(\mathbf{G}\) by an arbitrary local rotation \(\mathbf{Q}\) yielding \(\mathbf{QG}\), which may be more useful depending on the particular problem.Footnote 4 This is equivalent to choosing a different orthonormal frame in the material manifold, which being non-Euclidean in general, does not possess a preferred orthonormal frame to begin with.
Family 2: Straightening, Stretching, and Shearing of a Sector of a Cylinder
Recall that any deformation in this family is given by (20) with deformation gradient (21). We compute the equilibrium condition \(m_{a[l}\nabla _{k]}\nabla _{b} \sigma ^{ab}=0\), and to aid computations, we use the incompressibility constraint \(\operatorname{det}b^{ab}=\operatorname{det} m^{ab}\) by evaluating \(c^{ab}\) as \(c^{ab}\operatorname{det}\left (b^{n}{}_{m}\right )= c^{ab}\operatorname{det}\left (b^{np} m_{pm}\right )\).
The \(W_{111}\) coefficient of the equilibrium equation has two independent components giving the conditions
If \(I_{1}\) is constant, we satisfy these equations, but if \(I_{1}\) is not constant, we have \(M^{12}(x)=M^{13}(x)=0\), since \(A\left (x-D\right )\neq 0\).
If \(I_{1}\) is constant, we then consider the \(W_{122}\) component of the equilibrium condition to obtain
which again implies that either \(M^{12}(x)=M^{13}(x)=0\), or \(I_{2}\) is constant. Therefore, unless the invariants of \(\mathbf{b}\) are constant, we have \(M^{12}(x)=M^{13}(x)=0\). Setting these components to 0 satisfies equilibrium, and so we compute the incompressibility condition \(\operatorname{det}b^{ab}=\operatorname{det} m^{ab}\). This becomes
which implies that
Bringing all of these together we have
or in terms of referential coordinates, writing \(M^{AB}(R)=M^{AB}\left (x(R)\right )\),
This is the generic solution, and we have set up the conditions for the anomalous solution, namely that the invariants of \(\mathbf{b}\) must be constant.
As before, we can introduce a coordinate rescaling, treating \(x\) as an unknown function of \(R\), which allows the tensor \(M^{AB}\) to take the form
and turns the incompressibility constraint into a differential equation that can be integrated to determine \(x(R)\). If a multiplicative decomposition of \(\mathbf{F}=\mathbf{AG}\) is used, we can express \(\mathbf{G}\) on an orthonormal frame in the form
which guarantees that \(M_{AB}=G^{\alpha }{}_{A}G^{\beta }{}_{B} \delta _{\alpha \beta }\) is of the proper form. As before, an arbitrary local rotation \(\mathbf{Q}\) can be imposed yielding the factor \(\mathbf{QG}\), where \(\mathbf{G}\) is as above, and this new factorization will yield a material metric of the proper form.
Family 3: Inflation, Bending, Torsion, Extension, and Shearing of an Annular Wedge
This family of deformations can be written using cylindrical polar coordinates in both configurations as given in (25) with deformation gradient (26).
As before, we compute the \(W_{111}\) coefficient of the equilibrium equation and obtain
The matrix on the left-hand side is invertible, since its determinant, \(CF-DE\), being a factor of the determinant of \(\mathbf{F}\), is nonzero to ensure invertibility. Therefore, we have either \(I_{1}\) being constant, or both \(M^{12}(r)\) and \(M^{13}(r)\) must be zero.
If \(I_{1}\) is constant, we examine the \(W_{122}\) coefficient of the equilibrium equation and obtain
which as before implies that \(M^{12}(r)=M^{13}(r)=0\), or \(I_{2}\) is constant. Therefore, to satisfy equilibrium, we must have all of the invariants of \(\mathbf{b}\) being constant, or \(M^{12}(r)=M^{13}(r)=0\). The latter of these conditions is also sufficient to guarantee equilibrium. We only have to satisfy incompressibility, which amounts to the equation
which we can do by setting
This gives the generic solution
or in referential variables, writing \(M^{AB}(R)=M^{AB}(r(R))\),
As in the other families, we can introduce a coordinate rescaling to express the material metric in the form
which means that on some orthonormal frame, the anelastic factor of a multiplicative decomposition \(\mathbf{F}=\mathbf{AG}\) takes the form
Doing this turns the incompressibility condition into a differential equation for the unknown function \(r(R)\), and as before, any other compatible anelastic factor can be expressed as \(\mathbf{QG}\), where \(\mathbf{Q}\) is an arbitrary local rotation and \(\mathbf{G}\) is as above.
Family 4: Inflation/Eversion of a Sphere
For this family, the symmetry enforced on the metric tensor automatically satisfies the universal equilibrium equations without additional restrictions. Demonstrating this, under this symmetry, the left Cauchy-Green tensor reads
and its inverse is
We can compute the invariants of \(\mathbf{b}\) as
Notice in particular, that these invariants only depend on \(r\). The Cauchy stress is diagonal with components
Taking the divergence of this tensor and setting it equal to zero gives
Therefore, the undetermined pressure must only depend on \(r\), and the components of \(\nabla _{b}\sigma ^{ab}\) only depend on \(r\). Using \(\frac{\partial p}{\partial \theta }=0\) and \(\frac{\partial p}{\partial \phi }=0\), and defining \(v^{a}=\nabla _{b}\sigma ^{ab}\), we can compute \(V^{a}{}_{c}=\nabla _{c}v^{a}\). For simplicity, we will only compute the off-diagonal components of this tensor. Note that
and \(V^{a}{}_{c}=\partial _{c}v^{a}+v^{d} \gamma _{cd}{}^{a}\). Computing the off-diagonal components, we get
Therefore, \(V^{a}{}_{c}\) is diagonal. Because \(m_{ab}\) is also diagonal, we conclude that \(V_{bc}\) is diagonal, and hence, is identically symmetric. Recognizing \(V_{bc}\) as \(m_{ba}V^{a}{}_{c}=m_{ba}\left ( \nabla _{c}\nabla _{d}\sigma ^{ad}\right )\), this means that the equilibrium equations are automatically satisfied for an appropriate pressure field, because the antisymmetric part of \(m_{ba}\left (\nabla _{c}\nabla _{d} \sigma ^{ad}\right )\) vanishes simply due to the symmetry of the tensor field \(M^{AB}\).
We now only need to satisfy the incompressibility condition \(\operatorname{det}\mathbf{b}=1\). Computing this yields
or in referential variables, writing \(m_{1}(R)=m_{1}(r(R))\), \(R^{4}m_{1}^{2}(R)m_{2}^{4}(R)=1\). Therefore, the final form of the inverse material metric tensor for this family is
Alternatively, introducing a coordinate rescaling as before, the material metric tensor takes the form
and we obtain a differential equation that can be integrated to determine \(r(R)\). Then, taking a multiplicative decomposition of \(\mathbf{F}=\mathbf{AG}\), we can express \(\mathbf{G}\) using an orthonormal frame in the material manifold yielding
which again can be left multiplied by an arbitrary local rotation \(\mathbf{Q}\) if desired.
Family 5: Inflation, Bending, Extension, and Azimuthal Shearing of an Annular Wedge
For this family, we have the deformation as given in (35) with deformation gradient (36). Again, we compute the equilibrium condition \(m_{a[l}\nabla _{k]}\nabla _{b} \sigma ^{ab}=0\), and look at the \(W_{111}\) coefficient. This contains two independent equations:
If \(I_{1}\) is constant, this equation is satisfied, and if \(I_{1}\) is not constant, we require \(M^{13}(r)=0\), and \(M^{12}(r)=-\frac{ABM^{11}(r)}{Cr}\). If \(I_{1}\) is constant, we examine the \(W_{122}\) coefficient in the equilibrium equation and obtain
which implies either \(I_{2}\) is constant, or \(M^{13}(r)=0\) and \(M^{12}(r)=-\frac{ABM^{11}(r)}{Cr}\). Hence, we either have all of the invariants of \(\mathbf{b}\) constant, or we have \(M^{13}(r)=0\) and \(M^{12}(r)=-\frac{ABM^{11}(r)}{Cr}\), which characterizes the generic solution.
The conditions on the components of the metric are sufficient to satisfy equilibrium, so we only have to satisfy incompressibility. The incompressibility condition in this case reads
We solve this for \(M^{22}(r)\) to obtain
which gives the generic solution
or in referential variables, writing \(M^{AB}(R)=M^{AB}(r(R))\),
Unlike the other families, the standard Euclidean inverse metric \(M^{AB}(R)= \text{diag}\{1,R^{-2},1\}\) is not a member of the generic solution branch for this family. This is because this Euclidean metric yields a special case of the anomalous solution, having constant invariants.
In principle, we can rescale our coordinates and compute the form of the anelastic factor in a multiplicative decomposition for a member of this family as we have done for the previous families. However we will not concern ourselves with the multiplicative decomposition for this family, because its generic solution branch does not contain the solution without eigenstrain. As such, any continuous process based on this family beginning with zero eigenstrain will not lie in this solution branch, but rather on the anomalous branch, and so the multiplicative decomposition associated with this generic branch is of limited use.
7 The Anomalous Universal Solutions
As we have covered cases I and IIa in the previous section, we turn our attention to case IIb. The groundwork for this case, namely the spatial constancy of the strain invariants has already been laid in our analysis of case IIa in Sect. 6. The analysis for each family follows the same general pattern, so we will merely outline these steps here in an example appearing in Family 5, then present the results. Details are given in Appendix B.
Step 1: For the anomalous solution, we start with the equations derived from the equilibrium conditions: four second-order linear differential equations for each family, involving the six undetermined components of the inverse metric tensor. By integrating the equilibrium conditions, up to two of these components can be expressed in terms of the other variables.
We take, as an example the deformation
for which we compute the components of \(b^{ab}\) as
The first universal equilibrium equation is \(m_{a[l}\nabla _{k]}\nabla _{b} b^{ab}=0\), which in these coordinates amounts to the two equations
The general solution of these equations is
For the purposes of our example, we will take \(\gamma _{2}=0\), \(\gamma _{1}=0\), and \(M^{13}(r)=r\). With this, \(b^{ab}\) becomes
Next, we compute the equilibrium condition \(m_{a[l}\nabla _{k]}\nabla _{b} c^{ab}=0\), which is simplified by multiplying \(c^{ab}\) by the condition \(\operatorname{det}\mathbf{b}=1\). This condition puts the remaining two ODEs in the form
Integrating these equations gives the solutions
which gives \(b^{ab}\) as
Step 2: After integrating these equations, we have the three constant invariant conditions for each family to solve. The constant trace condition is linear in the unknown components of the inverse metric, so we can use it to solve for one undetermined inverse metric component in exchange for introducing the trace of \(\mathbf{b}\) as a parameter.
We have the constant trace condition
hence,
The incompressibility condition \(\operatorname{det}\mathbf{b}=1\) then can be written as
and the constant second invariant condition can be written as
Step 3: We are left with two nonlinear algebraic equations. The first is the incompressibility condition \(\operatorname{det}\mathbf{b}=1\), and the second is the constancy of the second invariant of \(\mathbf{b}\). Both are quadratic equations in the remaining component of the inverse metric tensor, which creates an overdetermined system. We compute the resultant of these two equations in this component, and demand this resultant vanish to ensure that these two equations have a common root. The resultant of these equations is itself a polynomial in the other undetermined integration constants: the invariants of \(\mathbf{b}\), and the remaining independent spatial coordinate.
Even in our simplified example, the resultant of these equations in \(M^{11}(r)\) yields a relatively lengthy polynomial equation \(p(r)=0\). It can be immediately simplified by noticing that one of the coefficients is simply \(\mu _{2}^{6}\), so \(\mu _{2}=0\) is a necessary condition for there to be a common solution to these two equations. It can be further simplified by noting that after using \(\mu _{2}=0\), one of the coefficients becomes \(\beta _{2}^{6}\), so we demand \(\beta _{2}=0\). With this, a different coefficient becomes \(\mu _{1}^{6}\), and hence \(\mu _{1}=0\) as well.
Step 4: Therefore, the resultant is a polynomial equation of the form \(p\left (q\right )=0\), which must hold for all values of the independent variable \(q\) (which is either \(r\) or \(x\) depending on the family). Accordingly, we set each coefficient to zero independently, and obtain an overdetermined system of nonlinear polynomial equations for the undetermined constants. We wish to find all the solutions to these equations, and so we compute a primary decomposition of the radical ideal generated by these equations. These equations are simple enough that this can be done with the assistance of a symbolic algebra package, though even then the computations are rather cumbersome (see Appendix B). After we have done this, we are left with a set of conditions on the undetermined constants that are necessary and sufficient for the existence of a common root of the original quadratic equations in the undetermined inverse metric component over an open set. We substitute these constants into these equations and use them to solve for the final component of the inverse metric tensor, which gives us the general form of the anomalous solution. In all of these cases, despite encountering branching conditions in the course of analyzing the conditions on the constants, the separate branches ultimately are redundant, and we are left with a single anomalous solution branch for each family.
For our example, using the conditions \(\mu _{2}=0\), \(\beta _{2}=0\), and \(\mu _{1}=0\), the polynomial simply becomes \(\left (\beta _{1}^{3}-I_{1}\beta _{1}^{2}+I_{2}\beta _{1}-1\right )^{2}r^{18}=0\), which demands \(\beta _{1}^{3}-I_{1}\beta _{1}^{2}+I_{2}\beta _{1}-1=0\), because \(r>0\). We recognize that this is the eigenvalue equation for the tensor \(\mathbf{b}\), so we require \(\beta _{1}\) to be an eigenvalue of \(\mathbf{b}\). We can satisfy this by writing \(I_{1}=\beta _{1}+e_{1}\) and \(I_{2}=\beta _{1}e_{1}+\frac{1}{\beta _{1}}\), where \(e_{1}=\lambda _{1}+\lambda _{2}\) is the sum of the other two eigenvalues of \(\mathbf{b}\) and we have used incompressibility in the form \(\lambda _{1}\lambda _{2}\beta _{1}=1\). When we substitute these conditions back into the original equations for \(M^{11}\), they both become (up to some nonzero constant)
This equation can be solved for \(M^{11}\) and we obtain
which gives one example of \(M^{AB}\) as
This lets us compute the corresponding elastic left Cauchy-Green stretch tensor as
We can verify that \(b^{ab}\) satisfies the equilibrium conditions and the constant invariant conditions.
Completely determining the universal anelastic extensions of these families amounts to doing a similar analysis for each of the remaining families, but in full generality, i.e., not assuming particular values for the parameters appearing in the deformation, nor selecting values for the integration constants a priori. These computations are included in Appendix B, only the results are presented next. As we are considering the case where the strain invariants are constant, the set of universal equilibrium equations reduces to (48) and (49). Ordinarily these equations have three independent components, but in our case, one of these components vanishes identically for each equation, hence we have four ordinary differential equations to solve for each anomalous branch, together with the three algebraic equations constraining the strain invariants to be constant.
Family 1: Bending, Stretching, and Shearing of a Rectangular Block
Integrating the equilibrium equations (48) and (49) and solving the constant invariant conditions gives the following anomalous solution branch for this family:
Here the constants \(e_{1}\) and \(e_{2}\) are the elementary symmetric polynomials in two of the three free eigenvalues of \(\mathbf{b}\)
with the incompressibility condition determining the third eigenvalue as \(\lambda _{3}=\frac{1}{\lambda _{1} \lambda _{2}}\). The parameters \(e_{1}\) and \(e_{2}\) must be positive with \(e_{1}^{2}>4e_{2}\), since \(\mathbf{b}\) is positive definite. The remaining constants, \(\alpha _{1}\), \(\alpha _{2}\), \(\gamma _{1}\), and \(\gamma _{2}\) are arbitrary, subject to the condition that the choice of \(e_{1}\), \(e_{2}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\gamma _{1}\), and \(\gamma _{2}\) must yield a positive-definite metric tensor. One can explicitly verify that the invariants of \(\mathbf{b}\) generated by this metric are
Additionally, we can express this in terms of the referential variables by expressing \(r\) in terms of \(X\) by the relation \(r=\sqrt{A\left (2X+D\right )}\).
Family 2: Straightening, Stretching, and Shearing of a Sector of a Cylinder
With this family, it is prudent to make the substitution \(\xi =x-D\), which allows us to express the anomalous solution branch as
Alternatively, we can express this in terms of referential variables using the equation \(\xi =\frac{1}{2}AB^{2}R^{2}\). As in the previous case, \(e_{1}\) and \(e_{2}\) are the elementary symmetric polynomials in the free eigenvalues of \(\mathbf{b}\), \(\lambda _{1}\) and \(\lambda _{2}\).
With this, the third eigenvalue is determined via the incompressibility condition \(\lambda _{3}=\frac{1}{\lambda _{1}\lambda _{2}}\). This ensures that the invariants of \(\mathbf{b}\) are
The constants \(e_{1}\), \(e_{2}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\gamma _{1}\), \(\gamma _{2}\) are largely arbitrary, apart from the condition that \(e_{1}>0\), and \(e_{1}^{2}>4e_{2}>0\), and that the constants are chosen such that the metric tensor is positive definite.
Alternatively, we have the case where the anelastic strain is compatible, and we have
where \(\{M_{11},M_{12},M_{13}, M_{22},M_{23},M_{33}\}\) are constants and \(\operatorname{det}M_{AB}(R)=R^{2}\). At first glance this case appears slightly more general than the previous one under the special case \(\alpha _{1}=\gamma _{1}=0\), because for a fixed overall deformation, there are five independent parameters determining this solution, while setting \(\alpha _{1}=\gamma _{1}=0\) in the other family yields a special case of (165) depending on the free parameters \(\alpha _{2}\), \(\gamma _{2}\), \(e_{1}\), and \(e_{2}\). However, this case causes the stretch tensor \(b^{ab}\) to be constant, which requires that the material manifold be Euclidean, and a constant isochoric stretch only depends on two independent stretches, with the remaining degrees of freedom representing a global rotation, which we can freely add or remove. This case appears to not be a special case of the previous branch, because once we eliminate the dependence on \(\xi \), we no longer have a preferred direction, and hence we spontaneously gain additional rotational degrees of freedom that can be removed by the choice of the orientation of our current configuration Cartesian coordinates.
Physically, this amounts to the reference configuration deforming anelastically into a parallelepiped, which can be elastically deformed into the desired block, as that elastic deformation is homogeneous. Indeed, the stress required to accomplish this is always constant, and hence equilibrium conditions are trivially satisfied. One can easily verify that the only nonzero Christoffel symbol generated by this metric is \(\Gamma ^{1}{}_{11}=\frac{1}{R}\), which generates a vanishing curvature tensor \(\mathcal{R}=\mathbf{0}\). In fact, the anelastic strain can be integrated up to an arbitrary rigid rotation and translation to obtain the position vector
where \(\boldsymbol{\varepsilon }_{a}\) is an arbitrary right-handed set of linearly independent vectors spanning a parallelepiped with unit volume. With this, the constants \(M_{ab}=\boldsymbol{\varepsilon }_{a}\cdot \boldsymbol{\varepsilon }_{b}\), i.e., the arbitrary constants appearing in the metric tensor are given by the Euclidean inner products of the constant basis vectors.
Family 3: Inflation, Bending, Torsion, Extension, and Shearing of an Annular Wedge
For this solution, it is prudent to define the functions
With these definitions, we have the following anomalous solution branch
As with the other families, we can use the deformation equation \(r=\sqrt{AR^{2}+B}\), to recast this into the referential variables. Additionally, the parameters \(e_{1}\) and \(e_{2}\) are the same as the previous families, and other than demanding that the eigenvalues they determine be positive, we also demand that the choice of variables \(\alpha _{1}\), \(\alpha _{2}\), \(\gamma _{1}\), \(\gamma _{2}\), \(e_{1}\), and \(e_{2}\) leaves the metric tensor positive definite.
Family 5: Inflation, Bending, Extension, and Azimuthal Shearing of an Annular Wedge
To facilitate the analysis of this family, it is useful to define the function \(f(r)=\gamma _{1}+\frac{\gamma _{2}}{r^{2}}\). With this, we have
Again, the constraints on the constants appearing are as before, and are only necessary to ensure the positive definiteness of \(\mathbf{b}\) and the metric tensor. We can recast this into referential variables using \(r=AR\), if desired.
8 Merging of Universal Solution Families
After obtaining the previous results, it is natural to ask if solutions in one family correspond to solutions in another, and if so, to what extent? It is possible that the material manifolds, and the corresponding elastic deformations from two different families differ only by a change of coordinates, or equivalently, by a compatible anelastic deformation connecting the reference configurations of the two total deformations.
8.1 Equivalent Universal Solutions
Two universal deformations, \(\varphi _{1}:\left (\mathcal{M}^{1}_{R},\mathbf{M}^{1}\right ) \rightarrow \left (\mathcal{M}^{1}_{c},\mathbf{m}^{1}\right )\), and \(\varphi _{2}:\left (\mathcal{M}^{2}_{R},\mathbf{M}^{2}\right ) {\rightarrow} \left (\mathcal{M}^{2}_{c},\mathbf{m}^{2}\right )\) are said to be equivalent if there exist two isometries \(\Psi :\left (\mathcal{M}^{1}_{R},\mathbf{M}^{1}\right )\rightarrow \left (\mathcal{M}^{2}_{R},\mathbf{M}^{2}\right )\), and \(\psi :\left (\mathcal{M}^{1}_{c},\mathbf{m}^{1}\right )\rightarrow \left (\mathcal{M}^{2}_{c},\mathbf{m}^{2}\right )\) such that
or, equivalently, the following diagram commutes:

For general manifolds, this is a difficult task, as we not only have to determine whether or not two isometries exist, i.e., solve the Riemannian manifold equivalence problem twice, but also whether or not they satisfy equation (180). However, in our case, the current configurations of the universal deformations are both Euclidean, and hence \(\psi \) must be an element of \(\text{SE}(3)\). Additionally, \(\varphi _{1}\) and \(\varphi _{2}\) are invertible and in principle known, so if we can find \(\psi \), we can solve for \(\Psi =\varphi _{2}^{-1}\circ \psi \circ \varphi _{1}\). It is then a simple matter of checking whether or not \(\Psi \) is an isometry.
We choose coordinates for all of these manifolds, writing current configuration coordinates as \(\{x^{a}\}\), and material manifold coordinates as \(\{X^{A}\}\), with each set numbered by the universal deformation pertaining to it. In terms of these coordinates, these maps are
where we have used different indices on the different sides of the equations to emphasize that in principle each new coordinate depends on all of the old coordinates. These maps prolong to tangent maps \(\left (F_{1}\right )^{a}{}_{A}\), \(\left (F_{2}\right )^{a}{}_{A}\), \(\mathsf{h}^{a}{}_{b}\), \(\mathsf{H}^{A}{}_{B}\), satisfying
In terms of these tangent maps, we then have the isometry conditions
and the prolongation of equation (180) as
Because both current configurations are Euclidean, we can trivially satisfy equation (185) by choosing \(\psi \) to be an element of \(\text{SE}(3)\), and we can then use equation (186) to express equation (184) in terms of \(\mathsf{h}^{a}{}_{b}\) as
We can write this expression in terms of the inverse of \(b^{ab}=F^{a}{}_{A}F^{b}{}_{B}M^{AB}\) for each deformation and obtain
and hence
8.2 Relationships Between the Six Universal Families
We would like to identify which families are likely to contain overlap, and take note of Table 2. Specifically, the left Cauchy-Green tensor of each family is symmetric with respect to the prolonged action of a subgroup of \(\text{SE}(3)\). Therefore, if two universal deformations are equivalent, their corresponding strain tensors should have isomorphic symmetry groups. Denoting the symmetry group of \(\mathbf{b}_{1}\) as \(K_{1}\subset \text{SE}(3)\), and the symmetry group of \(\mathbf{b}_{2}\) as \(K_{2}\subset \text{SE}(3)\), we seek \(\psi \in \text{SE}(3)\) such that
This immediately identifies a possible correspondence between Families 1, 3, and 5, because their symmetry groups are isomorphic. Additionally, we expect that there might be some universal solutions in Family 2 that are also in Family 0, since the symmetry group of Family 2 is a subgroup of that of Family 0, though we can immediately recognize that there are solutions in Family 2 that are not equivalent to any in Family 0, because not all solutions in Family 2 are invariant under the action of the full symmetry group of Family 0.
This observation immediately reveals that, up to an element of these symmetry groups, \(\psi \) must be the obvious one implied by our choice of coordinates in each family, because it must send invariant sets of \(K_{1}\) to invariant sets of \(K_{2}\). We recall that if a (sub)group \(K\) acts on a manifold ℳ, an invariant set of \(K\) is a set \(\mathcal{S}_{K}\subset \mathcal{M}\) such that \(\forall x\in \mathcal{S}_{K}\), and \(\forall k\in K\), \(k\bullet x\in \mathcal{S}_{K}\). Here we consider the smallest nonempty invariant sets: the orbits of a single point under the action of the subgroup \(K_{i}\). The invariant sets of the symmetry groups of Families 1, 3, and 5 are concentric cylinders, hence any potential \(\psi \) connecting these two families must map a family of concentric cylinders to another. The coordinates for each family were chosen such that this family of cylinders is centered on the \(z\) axis, hence we require \(\psi \) to be a Euclidean isometry mapping the \(z\) axis to itself. Apart from rotations and translation that leave the left Cauchy-Green tensor fields unchanged, this restricts \(\psi \) to either be the identity, or a rotation reversing the orientation of the \(z\) axis. We will see that we can freely take \(\psi \) to be the identity.
We first show that Family 0 is contained within Family 2. To do this, we must find an equivalent deformation in Family 2 for any choice of deformation in Family 0. Identifying our coordinate systems (i.e., taking \(\psi \) to be the identity), we can express the left Cauchy-Green tensor field for any deformation in Family 0 as
We choose a universal solution in Family 2 with material inverse metric of the form
with \(\tilde{M}^{AB}\) being appropriate constants, which is one of the cases where the material manifold is Euclidean. Pushing this forward to the current configuration, we obtain the equations
Therefore, for any given element of Family 0, the choices
yield an equivalent member of Family 2. Also we note that these compatible material manifolds are contained as special cases of the non-homogeneous branch of Family 2 via the same argument presented in Sect. 7. Denoting \(\mathcal{U}_{A}\) to be the set of universal deformations corresponding to family \(A\), we conclude that
We then seek to establish similar correspondences between the sets \(\mathcal{U}_{1}\), \(\mathcal{U}_{3}\), and \(\mathcal{U}_{5}\). First, we consider an element of \(\mathcal{U}_{5}\) lying in its generic branch. The left Cauchy-Green tensor field of this element is fully determined by specifying three functions of \(R\), hence implicitly of \(r\) through \(R=\frac{A}{r}\), namely \(M^{11}(r)\), \(M^{23}(r)\), and \(M^{33}(r)\), along with values for the constants \(A\), \(C\), and \(E\). Labeling these choices \(\tilde{M}^{11}(r)\), \(\tilde{M}^{23}(r)\), \(\tilde{M}^{33}(r)\), \(\tilde{A}\), \(\tilde{C}\), and \(\tilde{E}\), we seek elements in Families 1 and 3 that generate the same stretch tensor field.
The left Cauchy-Green tensor field for the generic branch of Family 1 depends on three arbitrary functions of \(X(r)=\frac{r^{2}}{2A}-\frac{D}{2}\), \(M^{11}(X(r))\), \(M^{22}(X(r))\), and \(M^{23}(X(r))\) as well as the constants \(A\), \(B\), \(C\). If we select the functions and constants such that
it is straightforward to verify that the stretch tensor fields generated coincide. Therefore, the generic solution branch of Family 5 is contained in the generic solution branch of Family 1, since we can find universal solutions in Family 1 that are equivalent to any universal solution in Family 5.
Similarly, the generic branch of Family 3 depends on three functions of \(r\) through \(R(r)=\frac{r^{2}-B}{A}\): \(M^{11}(R(r))\), \(M^{22}(R(r))\), and \(M^{23}(R(r))\) as well as the constants \(A\), \(B\), \(C\), \(D\), \(E\), and \(F\). The choice
also generates an identical stretch field, hence the generic branch of Family 5 is also contained in the generic branch of Family 3.
We have shown that the generic branch of Family 5 is contained in those of both Family 1 and Family 3. To examine the opposite direction, suppose we take an arbitrary member of the generic branch of Family 1, defined by parameters \(\tilde{M}^{11}(X(r))\), \(\tilde{M}^{22}(X(r))\), \(\tilde{M}^{23}(X(r))\), \(\tilde{A}\), \(\tilde{B}\), and \(\tilde{C}\), and seek to find a solution in Family 5 that generates the same stretch tensor field. Elements in Family 5 depend on the parameters \(M^{11}(R(r))\), \(M^{23}(R(r))\), \(M^{33}(R(r))\), \(A\), \(C\), and \(E\), and the choice
generates the same stretch tensor fields as the member of Family 1. Hence, the generic solution branch of Family 1 is contained in the generic branch of Family 5. Coupled with the previous result, we conclude that the generic solution branches for Families 1 and 5 are equivalent, in that every universal solution in one of these branches has at least one equivalent universal solution in the other.
Next, choosing an arbitrary universal solution in the generic branch of Family 3, we seek a universal solution in Family 5 that is equivalent. Choosing parameters \(\tilde{M}^{11}(r)\), \(\tilde{M}^{22}(r)\), \(\tilde{M}^{23}(r)\), \(\tilde{A}\), \(\tilde{B}\), \(\tilde{C}\), \(\tilde{D}\), \(\tilde{E}\), and \(\tilde{F}\) determining an arbitrary solution in Family 3, we can choose an element of Family 5 by specifying the parameters \(A\), \(C\), \(E\), \(M^{11}(R(r))\), \(M^{23}(R(r))\), and \(M^{33}(R(r))\), where \(R(r)=\frac{r}{A}\). If we choose these such that
we obtain a universal solution that is equivalent to the specified solution in Family 3. Hence, the generic solution branch of Family 3 is contained within that of Family 5. Coupled with our previous results, this result implies that the generic solution branches of Families 1, 3, and 5 are all equivalent to each other.
Next we consider the anomalous solution branches for these families. First, we select an arbitrary member of Family 3 anomalous solution branch by specifying the parameters \(\tilde{A}\), \(\tilde{B}\), \(\tilde{\eta }=\tilde{D}\tilde{E}-\tilde{C}\tilde{F}\),Footnote 5\(\tilde{e_{1}}\), \(\tilde{e_{2}}\), \(\tilde{\alpha _{1}}\), \(\tilde{\alpha _{2}}\), \(\tilde{\gamma _{1}}\), and \(\tilde{\gamma _{2}}\). We seek to find solutions in Family 1 anomalous solution branch, and Family 5 solution branches that generate equivalent solutions.
First examining Family 1, we can select values for constants \(\alpha _{1}\), \(\alpha _{2}\), \(\gamma _{1}\), \(\gamma _{2}\), \(e_{1}\), \(e_{2}\), \(A\), \(B\), and \(C\). It is straightforward to verify that the choice
generates an equivalent solution. Likewise for Family 5, we can choose values for the parameters \(\alpha _{1}\), \(\alpha _{2}\), \(\gamma _{1}\), \(\gamma _{2}\), \(e_{1}\), \(e_{2}\), \(A\), and \(E\), where the specific choices
generate a solution that is equivalent to the arbitrary solution from Family 3. Hence the anomalous branch from Family 3 is contained in both that of Family 1 and Family 5.
Conversely, we select an arbitrary member of the anomalous branch of Family 5 by specifying the parameters \(\tilde{\alpha _{1}}\), \(\tilde{\alpha _{2}}\), \(\tilde{\gamma _{1}}\), \(\tilde{\gamma _{2}}\), \(\tilde{e_{1}}\), \(\tilde{e_{2}}\), \(\tilde{A}\), and \(\tilde{E}\). We can verify that the choice of parameters
yields a solution from Family 3 that is equivalent to the arbitrary one from Family 5.
Finally, we select an arbitrary member of the anomalous branch of Family 1 by specifying the parameters \(\tilde{\alpha _{1}}\), \(\tilde{\alpha _{2}}\), \(\tilde{\gamma _{1}}\), \(\tilde{\gamma _{2}}\), \(\tilde{e_{1}}\), \(\tilde{e_{2}}\), \(\tilde{A}\), \(\tilde{B}\), and \(\tilde{C}\), and seek an equivalent solution in Family 3. The parameter choices
generate such a solution. Hence, we deduce that the anomalous branches of Families 1 and 5 are contained in that of Family 3, which combined with our previous results implies that the anomalous branches of all the three families are the same.
Therefore, having examined both the generic and anomalous branches of these families, we conclude that \(\mathcal{U}_{1}=\mathcal{U}_{3}=\mathcal{U}_{5}\). Hence, in the anelastic setting, our initial six families of universal solutions have collapsed into three families \(\mathcal{U}_{2}\), \(\mathcal{U}_{3}\), and \(\mathcal{U}_{4}\), one corresponding to each of the three surfaces with constant principal curvatures in 3D Euclidean space: planes, cylinders, and spheres, respectively. These surfaces are the invariant sets of the symmetry groups of the left Cauchy-Green tensor fields, and they played a central role in [7], being the level sets of the strain invariants. Here, we see that not only are the invariants of \(\mathbf{b}\) constant on these surfaces, but \(\mathbf{b}\) itself is symmetric with respect to these surfaces in the manner induced by the action of the special Euclidean group. This symmetry is present even in the degenerate case when the invariants of \(\mathbf{b}\) are constant, which is why we can identify the symmetry groups even in the anomalous solution branches. In the classical problem, similar surfaces can be identified in the material manifold, since in the absence of eigenstrains, the material manifold and the reference configuration coincide. These surfaces are invariant sets of the symmetry groups of the right Cauchy-Green tensor fields, and prevent the identification of the classical families with each other, since the only two classical families with matching invariant sets in both configurations are Families 3 and 5. These however cannot be identified with each other because solutions in Family 5 have constant invariants, while those in Family 3 do not. Hence, it is only after the addition of eigenstrains that many of the classical families become redundant.
8.3 Standard Forms of the Three Distinct Universal Families
We note that there is some redundancy in the parameterizations we currently have, which is exhibited by observing that the parameter selections we have used to identify the families with each other are not mutual inverses. We can reparametrize to eliminate this redundancy and have a single representation for strain field of each family. Concretely, we can express the left Cauchy-Green stretch field for the anomalous branches of \(\mathcal{U}_{3}\) in the following standard form:
where \(p\) is the product of the two free eigenvalues of \(\mathbf{b}\), and \(m\) is the mean of the two free eigenvalues. The inverse of this, \(c_{ab}\), is the push forward of the material metric, and has components
The generic branch of this family likewise has a standard expression:
with the incompressibility condition \(\operatorname{det}\mathbf{b}=1\) taking the form \(r^{2}b^{11}(r) [b^{22}(r)b^{33}(r)- (b^{23}(r) )^{2} ]=1\). The inverse of this form then takes the form
with the incompressibility condition being \(c_{11}(r)\left [c_{22}(r)c_{33}(r)- \left (c_{23}(r)\right )^{2}\right ]=r^{2}\). The positive definiteness condition is equivalent to \(c_{11}\left (r\right )>0\), \(c_{22}(r)>0\), and \(c_{33}(r)>0\) in addition to the incompressibility condition (221), or in the anomalous solution, requiring \(m>0\), and \(0< p< m^{2}\). An example of one of these generic solutions was investigated by Yavari and Goriely [39], with the parameter choices \(c_{11}\left (r\right )=\lambda ^{2}\), \(c_{22}\left (r\right )=\lambda ^{2}r^{2}\), \(c_{23}\left (r\right )=r^{2}\left (\psi \left (\lambda r \right )-\tau \right )\), and \(c_{33}\left (r\right )= \frac{1+\lambda ^{2}r^{2}\left (\psi \left (\lambda r\right )-\tau \right )^{2}}{\lambda ^{4}}\).
Similarly, the left Cauchy-Green tensor field for the anomalous branch of the family \(\mathcal{U}_{2}\) takes the standard form
with \(p\) and \(m\) defined as previously. Inverting this to obtain \(c_{ab}\), one obtains
The left Cauchy-Green tensor for the generic branch of this family also has a standard form
with the incompressibility condition becoming \(b^{11}(x)\left [b^{22}(x)b^{33}(x)- \left (b^{23}(x)\right )^{2}\right ]=1\). The inverse of this then takes the standard form
with the incompressibility condition
The positive-definiteness condition is equivalent to requiring \(c_{11}(x)>0\), \(c_{22}(x)>0\), and \(c_{33}(x)>0\), in addition to the incompressibility condition (226), or in the anomalous case, requiring \(m>0\), and \(0< p< m^{2}\).
Finally, the spherically-symmetric family \(\mathcal{U}_{4}\) can be expressed in the standard form through its left Cauchy-Green tensor
which has the inverse
The incompressibility condition and positive definiteness is automatically satisfied for arbitrary functions \(g(r)\) satisfying \(g(r)>0\). In terms of parameters defined by Goriely [14] in Chapter \(15.1.1\), this function is \(g(r)=\alpha _{r}=\alpha ^{-2}\): it is the radial stretch.
These standard forms make it clear that universal solutions in anelasticity can be categorized by computing the tensor \(\mathbf{c}^{\flat }\), and comparing the result with the standard forms here. As a consequence of this, the symmetry of the elastic strain in the current configuration determines which family any particular universal solution belongs to, as it is this symmetry that is reflected in \(\mathbf{c}^{\flat }\).
We have examined particular symmetry groups, namely T\((2)\), T\((1)\times \)SO\((2)\), and SO\((3)\). All of these are Lie subgroups of SE\((3)\), and specifically they are generated by two independent generators; choosing two translational generators yields T\((2)\), choosing a rotation and a translation about the axis of that rotation yields T\((1)\times \)SO\((2)\), and choosing two rotations fixing a common point yields SO\((3)\). We show in Appendix C that any Lie subgroup of SE\((3)\) generated by two arbitrary independent generators contains at least one of these groups by necessity, hence we have the following theorem:
Theorem 8.1
(Classification of symmetric universal solutions)
Any universal solution that is equivariant under the action of two independent 1-dimensional Lie subgroups of SE\((3)\) is contained in one of the three universal families \(\mathcal{U}_{2}\), \(\mathcal{U}_{3}\), or \(\mathcal{U}_{4}\).
This allows us to precisely state our conjecture regarding the completeness of our classification in terms of symmetry:
Conjecture 8.1
(Symmetry necessity)
A deformation must be equivariant with respect to the action of two independent one-dimensional Lie subgroups of SE\((3)\) in order to be universal, hence our classification is complete.
9 Graphic Representation
Because the material manifolds are generally non-Euclidean, visualizing them is difficult. A way to overcome this difficulty is to approximate their geometry as “piecewise Euclidean” and examine the deformation of each piece. This approach is similar to the three-dimensional version of approximating a curved surface with a polyhedron, and then representing that polyhedron in the plane by its net. The original surface can then be build up by connecting appropriate edges, but because of the curved nature of the surface, these edges cannot all be connected without distorting the pieces, or lifting them out of the plane. To demonstrate this technique, we will first start with a two-dimensional example, and then move on to a Euclidean three-dimensional example, and then finally apply the techniques to examples of material manifolds obtained from our analysis.
9.1 A Two-Dimensional Example
We know that representing spherical geometry in the plane isometrically is an egregiously impossible task [11]. To get around this, we only do this approximately, and allow for incompatibility by partitioning and separating our domain in multiple pieces. We can then stretch each piece in such a way that the deformed pieces can be approximately recombined in three-dimensional space to form an upper hemisphere. The deformed pieces are individually flat, so they can all be placed in the plane, but not in a way such that they can be pieced together without gaps (see Fig. 12).
We start with a disk, partition it, and separate the resulting pieces to allow for room for each piece to strain without overlapping its neighbors. We then strain each piece, and recombine the deformed cells to create an approximation of an upper hemisphere. Here each cell \([R_{i-1},R_{i}]\times [\Theta _{j-1},\Theta _{j}]\) is positioned so both the position of the point \((r,\theta )=((R_{i-1}+R_{i})/{2}, (\Theta _{j-1}+\Theta _{j})/{2})\), and the orientation of its tangent plane match that of the exact map from the disk to the hemisphere
Explicitly, we want to take the region \(r\in \left [0,1\right ]\), \(\theta \in \left [0,2\pi \right )\), where \(r\) and \(\theta \) are polar coordinates in the plane, and map it to the surface \(z=\sqrt{1-r^{2}}\) in three-dimensional space. The stretch induced by this map is described by the metric tensor with cylindrical components
which we can approximate as constant on each piece, while keeping each piece in the plane, by evaluating the metric at \(r^{*}=(r_{max}-r_{min})/2\). The deformed pieces can then be rigidly translated and rotated in three-dimensional space to approximate the desired spherical surface, with the approximation becoming better as the partition becomes finer (see Fig. 13).
This two-dimensional example allows one to see the correspondence between the deformed partitioned approximation and the recombined non-Euclidean configuration, which is important because once we move up to three-dimensional examples, we are no longer able to recombine the strained pieces; we must deduce properties of its geometry from the deformed partitioned approximation alone. Additionally, while we assembled the resulting deformed pieces into a hemisphere by lifting them into a higher dimensional Euclidean space, we could have assembled them into any number of other surfaces that are isometric to the hemisphere. Because we only determine the intrinsic geometry of the material manifold, there is no preferred isometric embedding in some higher dimensional Euclidean space, unless as above, we explicitly specify the embedding.
9.2 A Three-Dimensional Euclidean Example
Just as in the two-dimensional example, we can partition a flat three-dimensional body, explode it, and approximate strains on each piece to represent the non-Euclidean geometry of our deformations. The only difference is that, in general, we cannot recombine the distorted pieces into a cohesive whole, because the resulting shape is not globally flat. However, if the strain that we impose is actually induced by a map between Euclidean spaces, we can apply this procedure to the partitioned pieces, and observe the local strain, while separately observing the global deformation. We can then compare the two results to see which features are preserved by this local partitioning approach to better interpret the results of applying this procedure to our derived material metrics.
Consider the following map given in cylindrical polar coordinates
This map produces azimuthal shear and angular stretching. Choosing \(\mu =2\) and \(\nu =\frac{1}{2}\), and mapping the domain \(R\in \left [2,3\right ]\), \(\Theta \in \left [0,\frac{2\pi }{3}\right ]\), \(Z\in \left [0,1\right ]\), we obtain a transformation shown in Fig. 14. If we instead compute the strain tensor, and use it as a material metric for the current configuration, we obtain
Applying this stretch to our partitioned domain, we obtain the depiction shown in Fig. 15. This side-by-side comparison shows what is happening when we do this piecewise transformation, namely we capture the strain of each piece, but we do not capture any local rotation that is present in the global deformation. This is because local rotations produce no strain, so they do not contribute to the strain tensor, and hence, we cannot expect to be able to capture them through this reconstruction.
9.3 Anomalous Anelastic Strains
For the anomalous families, we will use the partitioning technique to attempt to visualize the deformations. We note that not all choices of parameters are valid over arbitrary domains. In particular, the parameters must be chosen such that the metric is positive definite over the chosen domain, in addition to making sure that the strain tensor \(\mathbf{b}\) is positive definite, a much simpler task as this requires \(e_{1}\) and \(e_{2}\) to be positive with \(e_{1}^{2}>4e_{2}\). We also depict the total overall deformation, coloring the current configuration by the trace of the Cauchy stress required to maintain it for a Mooney-Rivlin solid with strain energy of the form
both in the presence and absence of anelastic strain. Because the invariants of the left Cauchy-Green tensor are constant for the anomalous universal eigenstrains, any choice of strain energy is indistinguishable from a Mooney-Rivlin energy, and the only invariant of the Cauchy stress that can potentially vary spatially is the pressure generated due to the constraint stress. Here we choose the two material parameters in the Mooney-Rivlin energy to each be equal to 1, though different choices of parameters would yield qualitatively similar results.
Family 1
For this family we choose the reference domain \(X \in \left [0,1\right ]\), \(Y \in \left [0,6\right ]\), and \(Z \in \left [0,4\right ]\), and take the deformation parameters \(A=\frac{3}{2}\), \(B=1\), \(C=\frac{1}{4}\), \(D=2\), \(E=0\), \(F=0\). To examine the effects of anomalous universal eigenstrain on the equilibrium stress distribution, we consider the same overall deformation, and contrast the stress generated in the presence of eigenstrain with that generated in the absence of eigenstrain. For the anelastic strain parameters, we use
One can verify that this ensures that \(\mathbf{M}\) is positive definite over the chosen domain. To visualize the anelastic strain, we subdivide the domain, separate the pieces, and approximate the anelastic strain on each (see Fig. 16). This anelastic strain is generally not compatible, i.e., the deformed pieces cannot be reassembled in Euclidean space without further deformation. We map the body into the current configuration, and color it to denote the spherical part of the Cauchy stress generated by a Mooney-Rivlin solid. This requires us to integrate the indeterminate constraint pressure field, both with and without eigenstrain. Without eigenstrain, we have the following differential equations for the constraint pressure
which can be easily integrated to obtain
Notice in particular that \(p\) does not vary with \(z\) or \(\theta \). Additionally, only the gradient of \(p\) affects the motion, which allowed us to ignore the integration constant when integrating the above equations.
When there is eigenstrain, we obtain a different set of differential equations determining \(p(\mathbf{X})\):
where \(k(R)\) is an algebraic function of \(r\) alone. We can in principle integrate these to obtain
In contrast with the ordinary case, when we have eigenstrain, we can generate pressure gradients that vary with \(\theta \) and \(z\). Interestingly enough, even the generic universal eigenstrain cannot generate pressure gradients in these directions; the anomalous universal eigenstrain is the only universal eigenstrain that can create pressure gradients in these directions. This suggests that the measurement of these pressure gradients can be used to partially measure the eigenstrain, and conversely these anomalous solutions can be used to generate pressure gradients in these directions to, for example, counteract the pressure generated by body forces. We then compute the first stress invariant, the trace of the Cauchy stress, or equivalently its spherical part, for the material both in the absence and presence of eigenstrain, and plot the resulting stress invariant in Fig. 17.
Family 2
For this family, we choose the reference domain \(R \in \left [2,3\right ]\), \(\Theta \in \left [0,5\right ]\), and \(Z \in \left [0,4\right ]\), and take the deformation parameters \(A=1\), \(B=\frac{3}{4}\), \(C=\frac{1}{4}\), \(D=0\), \(E=0\), \(F=0\). These parameters define the total deformation, allowing us to examine the effects of eigenstrain on the Cauchy stress. In particular, we take the parameters appearing in the anelastic strain to be
This ensures that the metric is positive definite over the chosen domain. We subdivide and explode the domain, and apply our anelastic strain to each piece, as shown in Fig. 18. We are then left with a set of differential equations determining the constraint stress. In the absence of eigenstrain, we have
Upon integration, we obtain
In contrast, when we consider eigenstrain, we have the equations
where as before \(k(x)\) is an algebraic function of \(x\). We can integrate these equations to obtain
As before, the presence of this anomalous universal eigenstrain generates pressure gradients in directions that are not possible in their absence, in this case, the \(y\) and \(z\) directions. Again, even the generic branch of universal eigenstrains cannot generate pressure gradients in these directions, further highlighting the unique nature of the anomalous solutions. We then compute the trace of the Cauchy stress, and plot the resultant distributions both in the absence and presence of eigenstrain (see Fig. 19).
Family 3
For this family, we choose the domain \(R \in \left [2,3\right ]\), \(\Theta \in \left [0,5\right ]\), and \(Z \in \left [0,4\right ]\), and the deformation parameters \(A=1\), \(B=0\), \(C=\frac{5}{4}\), \(D=\frac{1}{6}\), \(E=\frac{1}{4}\), \(F=\frac{5}{4}\), \(G=\frac{-\pi }{4}\), \(H=0\). This completely defines the total deformation, allowing us to examine the stress generated with eigenstrain in contrast with that generated without eigenstrain. We take
as our anelastic parameters. Over the defined domain, these choices ensure that the anelastic metric tensor is positive definite. We then partition and explode the domain, approximating the eigenstrain on each piece, depicting the result in Fig. 20. As before, we obtain differential equations for \(p\), yielding in the elastic case
which can be integrated to obtain
In contrast, in the presence of eigenstrain, we have the differential equations
with \(k(R)\) an algebraic expression in \(r\) as in other families. This pressure can be integrated to obtain
We compute the first invariant of the Cauchy stress and color the deformation according to it in Fig. 21. As in other families, the presence of this anomalous branch of universal eigenstrain can generate pressure gradients in directions that do not occur otherwise, specifically pressure that varies with \(\theta \) and \(z\). This property would allow one to indirectly measure the eigenstrain by measuring the pressure variation required to sustain this deformation. Likewise, if we can specify the eigenstrain, we can create specific pressure gradients that would otherwise be impossible for the generic branch.
Family 5
For this final family, we choose the same domain as in Family 3, i.e., \(R \in \left [2,3\right ]\), \(\Theta \in \left [0,5\right ]\), and \(Z \in \left [0,4\right ]\), and we take the deformation parameters to be \(A=\sqrt{\frac{4}{5}}\), \(B=1\), \(C=1\), \(D=-\frac{\pi }{4}\), \(E=\frac{5}{4}\), \(F=0\). Choosing the anomalous eigenstrain parameters as
we subdivide and explode our domain, then approximate the eigenstrain on each piece. The result of this is depicted in Fig. 22. As with the other families, we are left with a set of differential equations determining the constraint stress. When eigenstrain is absent, we have the equations
which can be integrated to obtain
When we consider the anomalous solution, we have the equations
in terms of an algebraic function \(k(R)\) which can be integrated to obtain
When we compute the pressure gradient in the case of the generic universal solution, we obtain a pressure that only varies with \(r\). We see that the anomalous branch generates pressure gradients that vary with \(\theta \) and \(z\), unlike the generic solutions. We can compute the trace of the Cauchy stress, both with eigenstrain and without eigenstrain, and use this to color the deformed configurations in Fig. 23. Notice that unlike other families, the constraint pressure in the absence of eigenstrains can vary in a direction different than in the generic anelastic situation, specifically, for an eigenstrain in the generic solution branch, we have \({\partial p}/{\partial \theta }=0\), but in the absence of eigenstrain, we have \({\partial p}/{\partial \theta }={2B\left (A^{4}+\frac{1}{C^{2}} \right )}/{A^{2}}\). This is due to the fact that the standard Euclidean metric in terms of cylindrical polar coordinates lies on the anomalous solution branch, and not within the generic branch. In the elastic case, when the azimuthal shearing term does not vanish, corresponding to \(B\neq 0\), we have a pressure variation in \(\theta \) that is necessarily nonzero. In the anomalous case, we can determine the pressure variation in both \(\theta \) and \(z\) by adjusting our choices for \(\gamma _{1}\) and \(\alpha _{1}\), allowing us to determine the pressure variation in these directions independently of the overall total deformation by choosing the anelastic strain appropriately. Specifically, we can have arbitrarily large azimuthal shearing, while also causing the azimuthal pressure variation to vanish. While the other families also allow us to select the ordinarily absent components of the pressure gradient in a similarly arbitrary way, this family is unique in having one of these pressure gradients present without eigenstrain, so the anomalous universal eigenstrain allows us to both create pressure variations in these directions, but also remove pressure variations that are ordinarily necessary to maintain the overall deformation.
Additionally, with the anomalous anelastic solution branch, the azimuthal pressure variation \({\partial p}/{\partial \theta }={2A\left (1+e_{2}\right )}\gamma _{1}/e_{2}\) does not depend on the degree of azimuthal shearing, i.e., it is independent of \(B\). While the anomalous eigenstrain itself does depend explicitly on \(B\), if the eigenstrain and the total deformation are simultaneously varied by changing \(B\), the azimuthal pressure gradient should not change. Doing this in practice would be difficult, because fundamentally the parameter \(B\) partially determines the overall deformation, hence both the overall deformation and the eigenstrain would have to be simultaneously controlled in precise ways to realize this thought-experiment. Thankfully, this does not have to be done dynamically; a new value of \(B\) could be selected, the overall deformation could be controlled, and once it is established, it is fixed. Then the eigenstrain could be controlled until the universal eigenstrain corresponding to the chosen value of \(B\) is obtained. After this is done, the pressure variation could be measured, and this process can be repeated to establish the independence of the azimuthal pressure gradient.
10 Conclusions
We have generalized the universal solutions of Ericksen’s problem to the case of anelasticity. The main idea was to first identify the symmetry group associated with each solution of the classical Euclidean problem and use this symmetry group in a non-Euclidean setting by finding the possible metrics that guarantee each symmetry group. We used both the structure of existing universal solutions for a given \(\bar{\mathbf{M}}\) and their symmetries to find possible material metrics \(\mathbf{M}\). This was done by interpreting the classical universal deformations passively as coordinate changes. Then all local changes in geometry can be captured by changing the metrics. In this way, once we moved away from \(\bar{\mathbf{M}}\) to the general \(\mathbf{M}\), we recognized that any homeomorphism can be expressed by the particular coordinate maps for each family, since the coordinates themselves no longer hold any specific interpretation. By identifying an appropriate symmetry to impose on \(\mathbf{M}\) for each family a priori, we accomplished the following:
-
First, we constrained this problem to a point where it is still nontrivial, but solvable in a systematic algorithmic way.
-
Second, because this symmetry depends on the classical family of universal solutions, our construction provided a direct extension and classification of the new anelastic solutions consistent with the elastic ones.
-
Third, it is likely that these symmetries play a fundamental role in constraining the classical problem; the known classes of universal deformations all have particular symmetries. Identifying the relevant symmetries to impose on \(\mathbf{M}\) highlights this explicitly and we conjecture that all possible cases of anelastic universal solutions possess such symmetry. Specifically, all known universal solutions are preserved under the induced action of subgroups of the special Euclidean group. These subgroups are precisely those having two-dimensional invariant sets, which are either parallel planes, concentric cylinders, or concentric spheres.
It should also be noted that the generic solution branches and the anomalous solution branches differ largely in character. The generic solution branches contain arbitrary functions, and as such are infinite dimensional, while the anomalous solution branches are entirely determined up to a handful \(\left (\sim 10\right )\) of arbitrary constants, 6 of which are not redundant, and have a highly nontrivial structure. In all cases, the different branches of the analysis ultimately yield the same family of anomalous solutions. These anomalous branches also allow for the pressure required to sustain these deformations to vary in directions that would otherwise not be supported, even on the generic anelastic branch. This suggests possible applications of these anomalous branches in manipulating the surface tractions required to sustain these deformations, as well as a way to indirectly measure some of the eigenstrain parameters.
Additionally, symmetry appears to play an important role in these universal solutions. The right Cauchy-Green stretch tensor field for every family is invariant under some subgroup of \(\text{SE}(3)\), the group of orientation preserving isometries of 3D Euclidean space. The dimension of the Lie symmetry seems to play an important role as well; equilibrium conditions for families with three-dimensional Lie symmetries (Families 0 and 4) are trivially satisfied by imposing that symmetry on the material manifold, while families containing two-dimensional Lie symmetries require further restrictions.
While we have framed this problem in the context of an anelastic deformation from Euclidean space with the usual metric in the chosen coordinates to some Riemannian manifold, and a further elastic deformation back to Euclidean space, we do not make use of the initial Euclidean space in our analysis, nor do we detail any specific mechanism driving the anelastic deformation. The Euclidean reference configuration appears in the initial presentation of these universal solutions in nonlinear elasticity, therefore we use it as a comparison when displaying the elastic stress generated by these deformations, but there is no need for it to be the initial state of our undefined anelastic process. Provided our anelastic evolution arrives at the material manifolds derived here, the remainder of the deformation can be accomplished elastically. Therefore, the anelastic deformation can in principle map from any configuration; there is no need for a Euclidean reference. Even if the reference is Euclidean (as we tend to model physical space as Euclidean), there is no need for the coordinates used to be the typical Cartesian, cylindrical polar, or spherical polar coordinates used in the elastic case; they can be curvilinear coordinates, dramatically broadening the range of anelastic deformations to which our results are applicable.
Finally, we remark that neither the classical Ericksen’s problem, nor the anelastic Ericksen’s problem presented here has been proved to be fully solved and there may still be universal solutions unaccounted for. However, our conjecture, based on the correspondence between solution families and their symmetry groups, is that both classifications are actually complete. An additional work demonstrating that the strain fields of these universal solutions must by necessity be symmetric with respect to two one-dimensional Lie subgroups of SE\((3)\) would prove that this classification is complete.
Notes
As \(p\) is a scalar field to be determined the stress representation can equivalently be written as
$$ \boldsymbol{\sigma }=-p\mathbf{m}^{-1} +2 \frac{\partial W}{\partial I_{1}}\mathbf{b}^{\sharp }-2 \frac{\partial W}{\partial I_{2}}\mathbf{c}^{\sharp }. $$(11)More precisely, in Family 5 one off diagonal component vanishes, and another becomes fully determined by the other metric components; it does not vanish, but its indeterminacy is eliminated nonetheless.
The methodological difference in the symmetry calculation for this family is due to the topology of \(\text{SO}(3)\). This group is not the product of Lie groups, and hence, we cannot express its action by independently varying coordinates as we do in the other families; while \(\Theta \rightarrow \Theta +\Psi _{1}\) is a rotation, \(\Phi \rightarrow \Phi +\Psi _{2}\) is not.
For example, if the eigenstrain corresponds to anelastic simple shear, it may be more natural to express \(\mathbf{G}\) in an upper triangular form, rather than a symmetric form.
While the anomalous branch for Family 3 depends on the parameters \(C\), \(D\), \(E\), and \(F\), they only appear in the combination \(DE-CF\), hence it is sufficient to only specify this value.
Symbolic computations were done with Mathematica Version 12.0.0.0, Wolfram Research, Champaign, IL.
References
Antman, S.S.: Nonlinear Problems of Elasticity. Springer, New York (1995)
Ben Amar, M., Goriely, A.: Growth and instability in elastic tissues. J. Mech. Phys. Solids 53, 2284–2319 (2005)
Bilby, B.A., Bullough, R., Smith, E.: Continuous distributions of dislocations: a new application of the methods of non-Riemannian geometry. Proc. R. Soc. Lond. A 231(1185), 263–273 (1955)
Cox, D., Little, J., O’Shea, D.: Ideals, Varieties, and Algorithms. Springer, Berlin (1992)
Epstein, M., Maugin, G.A.: Geometric material structure of finite-strain elasticity and anelasticity. Z. Angew. Math. Mech. 76, 125–128 (1996)
Epstein, M., Maugin, G.A.: On the geometrical material structure of anelasticity. Acta Mech. 115(1), 119–131 (1996)
Ericksen, J.L.: Deformations possible in every isotropic, incompressible, perfectly elastic body. Z. Angew. Math. Phys. 5(6), 466–489 (1954)
Ericksen, J.L.: Deformations possible in every compressible, isotropic, perfectly elastic material. Stud. Appl. Math. 34(1–4), 126–128 (1955)
Fosdick, R.L.: Remarks on compatibility. In: Modern Developments in the Mechanics of Continua, pp. 109–127 (1966)
Fosdick, R.L., Schuler, K.W.: On Ericksen’s problem for plane deformations with uniform transverse stretch. Int. J. Eng. Sci. 7(2), 217–233 (1969)
Gauss, C.F.: Disquisitiones generales circa superficies curvas (1828)
Golgoon, A., Yavari, A.: Nonlinear elastic inclusions in anisotropic solids. J. Elast. 130(2), 239–269 (2018)
Gorbatsevich, V., Onishchik, A., Kozlowski, T., Vinberg, E.: Lie Groups and Lie Algebras I: Foundations of Lie Theory Lie Transformation Groups. Encyclopaedia of Mathematical Sciences. Springer, Berlin (2013). ISBN 9783642579998. https://books.google.co.uk/books?id=4mBsCQAAQBAJ
Goriely, A.: The Mathematics and Mechanics of Biological Growth, vol. 45. Springer, Berlin (2017)
Kafadar, C.B.: On Ericksen’s problem. Arch. Ration. Mech. Anal. 47(1), 15–27 (1972)
Klingbeil, W.W., Shield, R.T.: On a class of solutions in plane finite elasticity. Z. Angew. Math. Phys. 17(4), 489–511 (1966)
Knowles, J.K.: Universal states of finite anti-plane shear: Ericksen’s problem in miniature. Am. Math. Mon. 86(2), 109–113 (1979)
Kondo, K.: A proposal of a new theory concerning the yielding of materials based on Riemannian geometry, I. J. Soc. Appl. Mech. Jpn. 2(11), 123–128 (1949)
Marris, A.: Two new theorems on Ericksen’s problem. Arch. Ration. Mech. Anal. 79(2), 131–173 (1982)
Marsden, J., Hughes, T.: Mathematical Foundations of Elasticity. Dover Civil and Mechanical Engineering Series. Dover, New York (1983). ISBN 9780486678658
Martin, S.E., Carlson, D.E.: A note on Ericksen’s problem. J. Elast. 6(1), 105–108 (1976)
Mura, T.: Micromechanics of Defects in Solids. Springer, Berlin (2013)
Naumov, V.E.: Mechanics of growing deformable solids: a review. J. Eng. Mech. 120(2), 207–220 (1994)
Noll, W.: Materially uniform simple bodies with inhomogeneities. Arch. Ration. Mech. Anal. 27(1), 1–32 (1967)
Nye, J.F.: Some geometrical relations in dislocated crystals. Acta Metall. 1(2), 153–162 (1953)
Ogden, R.W.: Non-Linear Elastic Deformations. Dover, New York (1984)
Ozakin, A., Yavari, A.: A geometric theory of thermal stresses. J. Math. Phys. 51(3), 032902 (2010)
Pence, T.J., Tsai, H.: Swelling-induced microchannel formation in nonlinear elasticity. IMA J. Appl. Math. 70(1), 173–189 (2005)
Pence, T.J., Tsai, H.: Swelling-induced cavitation of elastic spheres. Math. Mech. Solids 11(5), 527–551 (2006)
Rodriguez, E.K., Hoger, A., McCulloch, A.D.: Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27, 455–467 (1994)
Sadik, S., Yavari, A.: On the origins of the idea of the multiplicative decomposition of the deformation gradient. Math. Mech. Solids 22, 771–772 (2017)
Simo, J.C., Marsden, J.E.: Stress tensors, Riemannian metrics and the alternative descriptions in elasticity. In: Trends and Applications of Pure Mathematics to Mechanics, pp. 369–383. Springer, Berlin (1984)
Singh, M., Pipkin, A.C.: Note on Ericksen’s problem. Z. Angew. Math. Phys. 16(5), 706–709 (1965)
Stojanović, R., Djurić, S., Vujošević, L.: On finite thermal deformations. Arch. Mech. Stosow. 16, 103–108 (1964)
Takamizawa, K.: Stress-free configuration of a thick-walled cylindrical model of the artery – an application of Riemann geometry to the biomechanics of soft tissues. J. Appl. Mech. 58, 840–842 (1991)
Yavari, A.: A geometric theory of growth mechanics. J. Nonlinear Sci. 20(6), 781–830 (2010)
Yavari, A., Goriely, A.: Riemann–Cartan geometry of nonlinear dislocation mechanics. Arch. Ration. Mech. Anal. 205(1), 59–118 (2012)
Yavari, A., Goriely, A.: Nonlinear elastic inclusions in isotropic solids. Proc. R. Soc. A 469(2160), 20130415 (2013)
Yavari, A., Goriely, A.: The twist-fit problem: finite torsional and shear eigenstrains in nonlinear elastic solids. Proc. R. Soc. A 471, 20150596 (2015)
Yavari, A., Goriely, A.: The anelastic Ericksen problem: universal eigenstrains and deformations in compressible isotropic elastic solids. Proc. R. Soc. A 472(2196), 20160690 (2016)
Acknowledgements
This research was supported by NSF – Grant No. CMMI 1561578, and ARO W911NF-18-1-0003 to Arash Yavari, and by the Engineering and Physical Sciences Research Council grant EP/R020205/1 to Alain Goriely.
Author information
Authors and Affiliations
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Methods and Tools
In the course of our analysis, we shall use a few tools that are infrequently used in nonlinear elasticity. Here we present a brief summary of these tools, and provide references to further sources for interested readers.
1.1 A.1 Algebraic Tools
Some techniques from elimination theory [4] will be used in our analysis of universal solutions. Chiefly among these is the method of resultants. We will not use resultants in their full generality, but rather will only need to compute the resultant of two quadratic polynomials, and as such will only provide the details necessary to substantiate our usage. Consider two polynomials
The resultant of \(p_{1}\) and \(p_{2}\) is a multivariate polynomial in \(\{a_{0},\ldots,a_{k},b_{0},\ldots,b_{r}\}\) that vanishes if and only if there exists a common solution to the equations \(p_{1}(x)=0\), and \(p_{2}(x)=0\). This will be useful to us because we will consider multivariate polynomials recursively as single variable polynomials, with coefficients in some extended field, and the method of resultants gives us a way of reducing the number of necessary equations that must be satisfied, while reducing the number of variables we must consider.
As an example, consider two quadratic polynomials \(p_{1}(x)=a_{1} x^{2}+b_{1} x+c_{1}\), and \(p_{2}(x)=a_{2}x^{2}+b_{2} x+c_{2}\). We seek a condition on \(\{a_{1},b_{1},c_{1},a_{2},b_{2},c_{2}\}\) such that there exists \(\hat{x}\) satisfying \(p_{1}\left (\hat{x}\right )=p_{2}\left (\hat{x}\right )=0\). Taking the linear combination \(a_{2}p_{1}\left (\hat{x}\right )-a_{1}p_{2}\left (\hat{x}\right )=0\) gives us a linear condition on \(\hat{x}\), namely
Then taking the combination \(b_{1} p_{2}\left (\hat{x}\right )-b_{2}p_{1}\left (\hat{x}\right )=0\) gives the condition \(\left (a_{2} b_{1}-a_{1} b_{2}\right )\hat{x}^{2}+b_{1}c_{2}-b_{2}c_{1}=0\), which under the above linear restriction becomes
Cross multiplying and subtracting the two linear equations (254) and (255) gives a necessary condition on the coefficients of \(p_{1}\) and \(p_{2}\) for there to be a common solution, namely
The left hand side is precisely the resultant of two quadratic polynomials, and so we denote
The vanishing of the resultant is a necessary condition for the existence of a common root of the two quadratic equations in \(x\).
Additionally, we will repeatedly use the fact that if a polynomial \(p(x)\) vanishes on an open set \(U\), i.e., \(p(x)=0\), \(\forall x\in U\), then, by the fundamental theorem of algebra, all its coefficients vanish identically, i.e., \(p(x)\) is the zero polynomial.
1.2 A.2 Group Action on Manifolds
Symmetry will play an important role in our construction. As group theory lies at the heart of any discussion of symmetry, we present some definitions from the theory of Lie groups, and reference the reader to Gorbatsevich et al. [13] for a full treatment. We recall that a semi-direct product is a generalization of a direct product, where only one factor must be a normal subgroup of the result. For instance, \(\text{T}(n)\), the group of translations of Euclidean space, is a normal subgroup of the special Euclidean group \(\text{SE}(n)\), while the group of rotations, \(\text{SO}(n)\) is not, hence \(\text{SE}(n)\neq \text{SO}(n)\times \text{T}(n)\), but rather \(\text{SE}(n)=\text{SO}(n)\ltimes \text{T}(n)\). The special Euclidean group, denoted \(\text{SE}(n)\), consists of all orientation preserving global isometries of Euclidean space, and is a semi-direct product of \(\text{SO}(n)\), and \(\text{T}(n)\). Therefore, an element of \(\text{SE}(n)\) can be identified with a tuple \(\left (\mathbf{Q}|\mathbf{c}\right )\) consisting of an element \(\mathbf{Q}\) of \(\text{SO}(n)\), and an element \(\mathbf{c}\) of \(\text{T}(n)\). The defining feature of \(\text{SE}(n)\) being how it acts on \(\mathbb{E}^{n}\), we must now express this action, and hence the natural group operation of \(\text{SE}(n)\) on \(\mathbb{E}^{n}\) in terms of \(\left (\mathbf{Q}|\mathbf{c}\right )\).
The action of a group \(\left (G,\star \right )\) on a manifold ℳ, informally, is a map \(\rho :G\times \mathcal{M}\rightarrow \mathcal{M}\) that preserves the group structure of \(G\). Denoting this action for \(g\in G\) and \(\mathbf{x}\in \mathcal{M}\) as \(\rho \left (g,\mathbf{x}\right )=g\bullet \mathbf{x}\), this demands \(\left (m_{2}\star m_{1}\right )\bullet \mathbf{x}=m_{2}\bullet \left (m_{1}\bullet \mathbf{x}\right )\) for all \(m_{1}\), \(m_{2}\in G\), and all \(\mathbf{x}\in \mathcal{M}\). Additionally, denoting the identity of \(G\) as \(e\), we demand \(\rho \left (e,\mathbf{x}\right )=e\bullet \mathbf{x}=\mathbf{x}, \, \forall \mathbf{x}\in \mathcal{M}\). Concisely, a group \(G\) acts on an object ℳ via a homomorphism \(\rho :G\rightarrow \operatorname{Aut}\left (\mathcal{M}\right )\).
Example A.1
Treating \(\mathbb{E}^{n}\) as a vector space, i.e., fixing an origin, the action of \(\text{SE}(n)\) on \(\mathbb{E}^{n}\) in terms of the tuple \(\left (\mathbf{Q}|\mathbf{c}\right )\) sends the point \(\mathbf{x}\in \mathbb{E}^{n}\) to the point \(\mathbf{Q}\mathbf{x}+\mathbf{c}\). One can easily verify that this is an isometry. The action of the element \(\left (\mathbf{Q}_{1}|\mathbf{c}_{1}\right )\) followed by the action of the element \(\left (\mathbf{Q}_{2}|\mathbf{c}_{2}\right )\) is then \(\mathbf{x}\mapsto \mathbf{Q}_{2}\mathbf{Q}_{1}\mathbf{x}+\mathbf{Q}_{2} \mathbf{c}_{1}+\mathbf{c}_{2}\), hence, in this representation, the product of the special Euclidean group, ⋆, takes the form \(\left (\mathbf{Q}_{2}|\mathbf{c}_{2}\right )\star \left (\mathbf{Q}_{1}| \mathbf{c}_{1}\right )=\left (\mathbf{Q}_{2}\mathbf{Q}_{1}|\mathbf{Q}_{2} \mathbf{c}_{1}+\mathbf{c}_{2}\right )\). We will eventually see that the right Cauchy-Green stretch tensor for each of the known families of universal solutions is preserved under the prolonged action of some Lie subgroup of \(\text{SE}(3)\).
The action of a group on a manifold can then be prolonged to its tangent bundle. This prolonged action can be determined by fixing an arbitrary group element \(\tilde{g}\), and considering the action of this element as a map \(\rho (\tilde{g}):\mathcal{M}\rightarrow \mathcal{M}\). The existence of inverse elements in \(G\) guarantees that this map is invertible, since \(\rho (\tilde{g})^{-1}=\rho (\tilde{g}^{-1})\). Provided ℳ has a smooth structure, and \(\rho (\tilde{g})\) is a smooth function of \(\mathbf{x}\), this map can then be differentiated to obtain the corresponding induced tangent map, i.e., the push forward map, which then determines the action of \(\tilde{g}\) on the tangent bundle of ℳ. The invertibility of \(\rho (\tilde{g})\) then provides a group action on the cotangent bundle via the pull-back induced by the inverse map. Notice that, generally, we consider the prolonged action of a group on bundles over ℳ, not merely on individual tangent spaces, because underlying points in the base space are not generally fixed, i.e., the base space and the total space are transformed together. Additionally, even if certain points in the base space are fixed points under the action of a group element, this does not guarantee that the tangent spaces at these points are similarly preserved. For example, in \(\mathbb{E}^{3}\), a rigid rotation preserves the position of the points on its axis, but rotates the tangent spaces at those points.
Appendix B: Explicit Calculations of the Anomalous Solutions
For families containing anomalous solution branches, we have the necessary (but not sufficient) condition that the invariants of \(\mathbf{b}\) are constant, with \(\operatorname{det}\mathbf{b}=1\) for incompressibility. For each of these families, we have four linear differential equations, one linear algebraic equation, and two nonlinear algebraic equations for the six unknown functions comprising the components of \(M^{AB}\). We will use the linear equations to solve for five of these unknown functions in terms of the sixth, and then characterize the common solutions to the remaining two equations to determine the final component.
Family 1
For this family, we consider the case where the invariants of \(\mathbf{b}\) are constant. This gives the equation
which, when applying the constant invariant condition and forcing this to hold for all energy functions requires
The first of these has two nonzero components after substituting the form of \(M^{AB}\). One of these components yields the differential equation \(3M^{12}(r)'+rM^{12}(r)''=0\). This equation is readily integrated to obtain
Applying this to the second nonzero component of the condition on the divergence of \(\mathbf{b}\) yields the differential equation \(r^{4}M^{13}(r)''-r^{3}M^{13}(r)'-8AB^{2}C\alpha _{1}=0\), which again can be integrated to obtain
After this, we must compute the condition on \(\mathbf{c}\), which we can simplify first by noting that \(\operatorname{det}\mathbf{b}=1\), so we can utilize \(\mathbf{c}=\left (\operatorname{det}\mathbf{b}\right )\mathbf{c}\), which gives
i.e., the cofactor tensor of \(\mathbf{b}\) equals the inverse of \(\mathbf{b}\). When we use this, we obtain two differential equations, which can be expressed as
and
These equations can be integrated to obtain the conditions
We also have the constant trace condition on \(\mathbf{b}\), which becomes
We can express this system of equations, linear in \(M^{22}(r)\), \(M^{23}(r)\), and \(M^{33}(r)\), as the matrix equation
which is invertible, because the determinant of the matrix on the left hand side is
since \(M^{12}(r)\) and \(M^{13}(r)\) cannot simultaneously vanish. We invert these equations to obtain expressions for these components of the inverse metric in terms of \(M^{11}(r)\), \(r\), and various constants.
We then have the other two restrictions, the constancy of the second invariant of \(\mathbf{b}\) and the incompressibility constraint. After substituting the above expressions into these conditions, they become
and
We then computeFootnote 6 the resultant of these two equations in \(M^{11}(r)\), yielding a polynomial in \(r\) that must identically be equal to zero. In order for this to be satisfied, each of its coefficients must vanish independently. This can be shown by repeatedly taking derivatives of the equation in \(r\), which will ultimately require each of the coefficients to vanish independently. Computing this resultant we obtain
The factors explicitly shown are identically nonzero, since \(A\) and \(B\) are nonzero for the deformation to be invertible, \(r>0\), and the other factor only vanishes if both \(M^{12}(r)\) and \(M^{13}(r)\) vanish, in which case we are no longer on the anomalous solution branch. Therefore, we take \(\left (...\right )=0\). This factor is massive, being approximately 8000 terms, so it is far too large to list here, but enough information has been provided to compute it explicitly if the reader desires. We next take its coefficients to vanish independently, and factor each coefficient. The shortest of these factors is
which can be satisfied in one of two ways. Either both \(\mu _{2}\) and \(\gamma _{1}\) are zero, or \(\nu =\frac{B^{2}\mu _{2}}{\gamma _{1}}\) is an eigenvalue of \(\mathbf{b}\). In the first case, after simplification of the other coefficients, we obtain another equation
which implies either \(\alpha _{2}=\beta _{2}=0\), or \(\nu =\frac{\beta _{2}}{A^{2}B^{2}\alpha _{2}}\) is an eigenvalue of \(\mathbf{b}\).
Taking \(\alpha _{2}=\beta _{2}=0\), we obtain another similar eigenvalue equation that implies \(\gamma _{2}=\mu _{1}=0\) or \(\nu =\frac{B^{2} \mu _{1}}{\gamma _{2}}\) is an eigenvalue of \(\mathbf{b}\).
Taking \(\gamma _{2}=\mu _{1}=0\), we obtain another eigenvalue equation, but this equation demands \(\nu =\frac{\beta _{1}}{A^{2}B^{2}\alpha _{1}}\), because we already have \(\alpha _{2}=\gamma _{1}=\gamma _{2}=0\); \(\alpha _{1}=0\) would result in both \(M^{12}(r)=0\) and \(M^{13}(r)=0\), a contradiction. This condition is sufficient for solving all of the necessary conditions.
Backing up a branch, we can take \(\nu =\frac{B^{2}\mu _{1}}{\gamma _{2}}\) as an eigenvalue of \(\mathbf{b}\). We then perform the substitutions \(I_{1}=e_{1}+\frac{1}{e_{2}}\) and \(I_{2}=\frac{e_{1}}{e_{2}}+e_{2}\) with \(\nu =\frac{1}{e_{2}}\), which expresses the invariants of \(\mathbf{b}\) in terms of the elementary symmetric polynomials in the other two eigenvalues. This reveals an equation with \(\beta _{1}-\frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}\) as a factor. If this factor is zero, we satisfy all of the necessary equations. If this factor is not zero, we have either \(e_{2}^{3}-e_{2} e_{1}+1=0\), or \(\alpha _{1}\left (e_{2}\beta _{1}+AC\gamma _{2}\right )=0\). In the later case, plugging in \(\alpha _{1}=0\) we obtain \(\beta _{1}=\frac{-AC\gamma _{2}}{e_{2}}\), which corresponds to the vanishing of the other factor. Likewise, if we take \(e_{2}\beta _{1}+AC\gamma _{2}=0\), we obtain \(\alpha _{1}=0\) as a condition. Both of these together however imply that \(\beta _{1}-\frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}=0\), which is a contradiction.
If \(e_{2}^{3}-e_{1}e_{2}+1=0\), this implies that \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\) or \(\lambda _{2}=\frac{1}{\lambda _{1}^{2}}\). In either case we can express the remaining equation in terms of only one remaining eigenvalue. This equation has one factor that we know is nonzero because it corresponds to \(\beta _{1}=\frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}\), which would yield a contradiction. So we take the remaining factor to vanish. This factor is quadratic in \(\alpha _{1}\). Taking the discriminant of this equation in \(\alpha _{1}\), we obtain
where \(\lambda _{a}\) is the repeated eigenvalue. This discriminant must be non-negative in order for the factor to vanish with real values of \(\alpha _{1}\). However, this discriminant is identically non-positive, which means it must be zero. However, the only way for this to happen would be for \(\gamma _{2}=0\), which is a contradiction.
Having exhausted the options corresponding to \(\alpha _{2}=\beta _{2}=0\), we consider \(\nu =\frac{\beta _{2}}{A^{2}B^{2}\alpha _{2}}\) as an eigenvalue of \(\mathbf{b}\), and perform the substitutions on the invariants to express the invariants in terms of elementary symmetric polynomials in \(\lambda _{1}\) and \(\lambda _{2}\). Doing this gives five remaining polynomial equations, which are still rather long and complicated. Ordering these equations by their length, and taking the second shortest one, we note that this equation is quadratic in \(e_{1}\). Taking the discriminant of this equation in \(e_{1}\), and demanding it be non-negative, we obtain
This quantity is identically non-positive, and so the only way we can have solutions with real values for \(e_{1}\) is if this quantity is zero. There are four factors that can possibly be zero: \(\alpha _{1}\), \(\beta _{1}+AB^{2}C\mu _{1}\), \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}\), and \(AB^{2}C\alpha _{2}\beta _{1}-\beta _{1}\gamma _{2}+A^{2}B^{4}\alpha _{1} \mu _{1}+A^{2}B^{4}C^{2}\alpha _{2}\mu _{1}-AB^{2}C\gamma _{2}\mu _{1}\).
First consider \(\alpha _{1}=0\). Inserting this, many of the remaining equations have a factor \(\beta _{1}+AB^{2}C\mu _{1}\). If this factor vanishes, the remaining equations both contain the factor \(AB^{2}C\alpha _{2}-\gamma _{2}+B^{2}e_{2}\mu _{1}\). The vanishing of this factor satisfies all of the equations. If this factor does not vanish, we can take the resultant of the remaining factors in \(e_{1}\), and obtain
Only two factors here can vanish, namely \(\mu _{1}\) and \(AB^{2}C\alpha _{2}-\gamma _{2}\). If we take \(\mu _{1}=0\) and insert it into the remaining two equations, one simplifies to imply \(AB^{2}C\alpha _{2}-\gamma _{2}=0\). Likewise, if we instead take \(AB^{2}C\alpha _{2}-\gamma _{2}\) to vanish, we obtain \(\mu _{1}=0\), hence both must vanish. However, if both of these vanish, the original term \(AB^{2}C\alpha _{2}-\gamma _{2}+B^{2}e_{2}\mu _{1}\) vanishes, a contradiction.
We can then consider the case when \(\beta _{1}\neq -AB^{2}C\mu _{1}\). Taking the remaining factor of the shortest equation, we have
This requires \(AB^{2}C\alpha _{2}-\gamma _{2}=0\) and \(\beta _{1}+AB^{2}C\mu _{1}=0\), but the second of these is a contradiction. This exhausts the case where \(\alpha _{1}=0\), so we take \(\alpha _{1}\neq 0\), and consider the next factor \(\beta _{1}+AB^{2}C\mu _{1}=0\). Inserting this into the equations, we obtain
This cannot vanish for \(\alpha _{1}\neq 0\), so we come to a contradiction.
Next, we consider \(\alpha _{1}\neq 0\) and \(\beta _{1}+AB^{2}C\mu _{1}\neq 0\), and take \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}=0\). Solving this for \(\beta _{1}\), and inserting this into the equations, we obtain the condition
which can be solved for \(\mu _{1}\) and is sufficient to satisfy the remaining equations. Finally, we consider the remaining option with \(\alpha _{1}\neq 0\), \(\beta _{1}+AB^{2}C\mu _{1}\neq 0\), and \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}\neq 0\) with \(AB^{2}C\alpha _{2}\beta _{1}-\beta _{1}\gamma _{2}+A^{2}B^{4}\alpha _{1} \mu _{1}+A^{2}B^{4}C^{2}\alpha _{2}\mu _{1}-AB^{2}C\gamma _{2}\mu _{1}=0\). This equation can be solved for either \(\beta _{1}\) or \(\mu _{1}\). If \(\gamma _{2}\neq AB^{2}C\alpha _{2}\), we can solve this for \(\beta _{1}\) and obtain
If we insert this, we obtain
as a necessary and sufficient condition for the remaining equations to be satisfied. This yields
However, with these, the equation \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}= 0\) is satisfied, a contradiction. Hence, we consider \(\gamma _{2}= AB^{2}C\alpha _{2}\), which requires \(\mu _{1}=0\). With this, we have the conditions \(\beta _{1}\neq 0\), \(\alpha _{1}\neq 0\), and \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}\neq 0\). With these, the remaining equations demand
which in turn demands either \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\) or \(\lambda _{2}=\frac{1}{\lambda _{1}^{2}}\). Denoting the repeated eigenvalue as \(\lambda _{a}\), we obtain the necessary condition \(\lambda _{a}=1\). However, with this we have \(\beta _{1}=A^{2}B^{2}\alpha _{1}\), which contradicts the above inequality conditions, i.e., this case is already accounted for in the previous cases.
This exhausts the options with \(\mu _{2}=\gamma _{1}=0\), so we consider \(\nu =\frac{B^{2}\mu _{2}}{\gamma _{1}}\) as an eigenvalue of \(\mathbf{b}\). Inserting this into our equations yields
This requires \(e_{2}^{3}-e_{1}e_{2}+1=0\), or if not, \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\).
In the later case, we have \(\alpha _{2}=0\) or \(\beta _{1}= \frac{A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2}\right )-AC\gamma _{2}}{e_{2}}\). This second option satisfies the remaining equation, so we then consider \(\alpha _{2}=0\). With this, we obtain \(\beta _{1}=\frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}\), which is a special case of the previous option.
We then consider \(e_{2}^{3}-e_{1}e_{2}+1=0\), which demands a repeated eigenvalue. This then demands that this repeated eigenvalue \(\lambda _{a}=1\), which means that all eigenvalues are the same. This allows us to solve for \(\beta _{1}\) and \(\mu _{1}\) as
This satisfies the remaining conditions, and so our analysis is complete, having exhausted all possible branches of solutions.
In order to depict this branching set of conditions, we can express the steps of the analysis in a tree. Each node on these trees represents a system of equations, and each edge represents one partial solution to these equations. Terminal nodes are color coded corresponding to whether they are consistent (green) or not (red). Nodes and edges are then labelled below the tree with the relevant equation/solutions utilized at each step of the analysis. The following is the tree for this family:

Nodes
-
0: \(B^{6}\mu _{2}^{3}-I_{1}B^{4}\mu _{2}^{2}\gamma _{1}+I_{2}B^{2}\mu _{2} \gamma _{1}^{2}-\gamma _{1}^{3}=0\)
-
−: \(\beta _{2}^{3}-I_{1}A^{2}B^{2}\beta _{2}^{2}\alpha _{2}+I_{2}A^{4}B^{4} \beta _{2}\alpha _{2}^{2}-A^{6}B^{6}\alpha _{2}^{3}=0\)
-
+: \(\beta _{2}=\frac{A^{2}B^{2}\alpha _{2}-AC\gamma _{1}}{e_{2}}\), and \((B^{2}\mu _{1}e_{2}-\gamma _{2}+AB^{2}C\alpha _{2})(e_{2}^{3}-e_{2}e_{1}+1)=0\)
-
−−: \(B^{6}\mu _{1}^{3}-I_{1}B^{4}\mu _{1}^{2}\gamma _{2}+I_{2}B^{2}\mu _{1} \gamma _{2}^{2}-\gamma _{2}^{3}=0\)
-
−+: \(\alpha _{1}\left (\beta _{1}+AB^{2}C\mu _{1}\right )\left (A^{2}B^{2} \alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}\right )\)
\(\left (AB^{2}C\alpha _{2}\beta _{1}-\beta _{1}\gamma _{2}+A^{2}B^{4} \alpha _{1}\mu _{1}+A^{2}B^{4}C^{2}\gamma _{2}\mu _{1}\right )=0\)
-
+−: \(\alpha _{2}\left (A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2} \right )-AC\gamma _{2}-\beta _{1}e_{2}\right )=0\)
-
++: \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}}\), and \(\beta _{1}=A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2}\right )-AC \gamma _{2}\)
-
−−−: \(\beta _{1}^{3}-I_{1}A^{2}B^{2}\beta _{1}^{2}\alpha _{1}+I_{2}A^{4}B^{4} \beta _{1}\alpha _{1}^{2}-A^{6}B^{6}\alpha _{1}^{3}=0\)
-
−−+: \(\frac{B^{2}\mu _{1}}{\gamma _{2}}\) is an eigenvalue of \(\mathbf{b}\)
-
−+−: \(\left (\beta _{1}+AB^{2}C\mu _{1}\right )\left (...\right )=0\)
-
−++: \(\left (\beta _{1}+AB^{2}C\mu _{1}\right )\left (A^{2}B^{2}\alpha _{1}-e_{2} \beta _{1}-AB^{2}Ce_{2}\mu _{1}\right )\)
\(\left (AB^{2}C\alpha _{2}\beta _{1}-\beta _{1}\gamma _{2}+A^{2}B^{4} \alpha _{1}\mu _{1}+A^{2}B^{4}C^{2}\gamma _{2}\mu _{1}\right )=0\)
-
+−−: \(\beta _{1}=\frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}\), and \(\beta _{1}\neq \frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}\)
-
+−+: \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\), and \(\beta _{1}= \frac{A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2}\right )-AC\gamma _{2}}{e_{2}}\)
-
−−+−: \(\beta _{1}=\frac{A^{2}B^{2}\alpha _{1}-AC\gamma _{2}}{e_{2}}\)
-
−−++: \(\alpha _{1}\left (e_{2}^{3}-e_{2}e_{1}+1\right )\left (e_{2}\beta _{1}+AC \gamma _{2}\right )=0\)
-
−+−−: \(\left (\gamma _{2}-AB^{2}C\alpha _{2}-B^{2}e_{2}\mu _{1}\right ) \left (...\right )=0\)
-
−+−+: \(\gamma _{2}=AB^{2}C\alpha _{2}\Rightarrow \beta _{1}=-AB^{2}C\mu _{1}\), and \(\beta _{1}\neq -AB^{2}C\mu _{1}\)
-
−++−: \(\alpha _{1}=0\), and \(\alpha _{1}\neq 0\)
-
−+++: \(\left (A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1} \right )\)
\(\left (AB^{2}C\alpha _{2}\beta _{1}-\beta _{1}\gamma _{2}+A^{2}B^{4} \alpha _{1}\mu _{1}+A^{2}B^{4}C^{2}\gamma _{2}\mu _{1}\right )=0\)
-
−−++−: \(\gamma _{2}=0\), and \(\gamma _{2}\neq 0\)
-
−−+++: \(\beta _{1}e_{2}-A^{2}B^{2}\alpha _{1}-AC\gamma _{2}=0\), and \(\beta _{1}e_{2}-A^{2}B^{2}\alpha _{1}-AC\gamma _{2}\neq 0\)
-
−+−−−: \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\)
-
−+−−+: \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\), and \(\mu _{1}\neq \frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\)
-
−+++−: \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\)
-
−++++: \(\mu _{1}=\frac{\gamma _{2}-AB^{2}C\alpha _{2}}{B^{2}e_{2}}\), and \(\beta _{1}= \frac{A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2}\right )-AC\gamma _{2}}{e_{2}} \Rightarrow A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}=0\), and \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}\neq 0\)
Edges (labelled by child node):
-
−: \(\gamma _{1}=0\), and \(\mu _{2}=0\)
-
+: \(\frac{B^{2}\mu _{2}}{\gamma _{1}}\) is an eigenvalue of \(\mathbf{b}\)
-
−−: \(\beta _{2}=0\), and \(\alpha _{2}=0\)
-
−+: \(\frac{\beta _{2}}{A^{2}B^{2}\alpha _{2}}\) is an eigenvalue of \(\mathbf{b}\)
-
+−: \(e_{2}^{3}-e_{1}e_{2}+1\neq 0\)
-
++: \(e_{2}^{3}-e_{1}e_{2}+1=0\Rightarrow \lambda _{a}=1\)
-
−−−: \(\gamma _{2}=0\), and \(\mu _{1}=0\)
-
−−+: \(\frac{B^{2}\mu _{1}}{\gamma _{2}}\) is an eigenvalue of \(\mathbf{b}\)
-
−+−: \(\alpha _{1}=0\)
-
−++: \(\alpha _{1}\neq 0\)
-
+−−: \(\beta _{1}\neq \frac{A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2}\right )-AC\gamma _{2}}{e_{2}}\), and \(\alpha _{2}=0\)
-
+−+: \(\beta _{1}= \frac{A^{2}B^{2}\left (\alpha _{1}+C^{2}\alpha _{2}\right )-AC\gamma _{2}}{e_{2}}\)
-
−−+−: \(\beta _{1}e_{2}-A^{2}B^{2}\alpha _{1}-AC\gamma _{2}=0\)
-
−−++: \(\beta _{1}e_{2}-A^{2}B^{2}\alpha _{1}-AC\gamma _{2}\neq 0\)
-
−+−−: \(\beta _{1}=-AB^{2}C\mu _{1}\)
-
−+−+: \(\beta _{1}\neq -AB^{2}C\mu _{1}\)
-
−++−: \(\beta _{1}+AB^{2}C\mu _{1}=0\)
-
−+++: \(\beta _{1}+AB^{2}C\mu _{1}\neq 0\)
-
−−++−: \(e_{2}^{3}-e_{2}e_{1}+1=0\)
-
−−+++: \(\alpha _{1}=0\Leftrightarrow e_{2}\beta _{1}+AC\gamma _{2}=0\)
-
−+−−−: \(\gamma _{2}=AB^{2}C\alpha _{2}+B^{2}e_{2}\mu _{1}\)
-
−+−−+: \(\gamma _{2}\neq AB^{2}C\alpha _{2}+B^{2}e_{2}\mu _{1}\Rightarrow \mu _{1}=0\), and \(\gamma _{1}=AB^{2}C\alpha _{2}\)
-
−+++−: \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}=0\)
-
−++++: \(A^{2}B^{2}\alpha _{1}-e_{2}\beta _{1}-AB^{2}Ce_{2}\mu _{1}\neq 0\)
The reader should note that this tree is not unique; there are potentially numerous ways we could have performed these algebraic eliminations, but ultimately, we have derived these conditions as necessary, and we have shown they are sufficient as well, and so any other sequence of algebraic reductions would yield equivalent results. The branches of this tree are all special cases of the conditions
Note that these values are always well defined, since \(B\neq 0\), and \(e_{2}=\lambda _{1}\lambda _{2}>0\), even though in their derivation we considered branching cases that are mutually exclusive. After these substitutions, both of the constant invariant conditions become
which let us solve for \(M^{11}(r)\) as
and hence, completely determine the anomalous inverse metric tensor field for this family.
One can check that in all cases, the equilibrium conditions are satisfied, and that the invariants of \(\mathbf{b}\) are
as expected.
Family 2
As above, we compute the equations
The first of these contains a component
where here we have made the substitution \(x=\xi +D\). The denominator is nonzero, so we can simply take the numerator to be zero, and integrate it. This yields
Substituting this into the other component of this equation, we obtain a differential equation for \(M^{13}(\xi )\):
which has the same general solution as the equation for \(M^{12}(\xi )\), and hence
The first of the remaining differential equations is
which equivalently reads \(\left [\left (\alpha _{1}\xi +\alpha _{2}\right )M^{23}( \xi )-\left (\gamma _{1}\xi +\gamma _{2}\right )M^{22}(\xi ) \right ]''=0\), and integrates to
The second equation is
or equivalently
We can add \(C\) times the previous differential equation, and divide by \(A\) to obtain
which integrates to
Finally, we have the constant trace condition on \(\mathbf{b}\), which reads
These equations can be solved for \(M^{22}(\xi )\), \(M^{23}(\xi )\), and \(M^{33}(\xi )\), as the determinant of these equations is
which only vanishes if both \(M^{12}(\xi )\) and \(M^{13}(\xi )\) vanish.
We then have the solution in terms of the yet-to-be determined component \(M^{11}(\xi )\), and numerous undetermined constants. Denoting \(\alpha =\alpha _{1}\xi +\alpha _{2}\), \(\gamma =\gamma _{1}\xi +\gamma _{2}\), \(\mu =\mu _{1} \xi +\mu _{2}\), \(\beta =\beta _{1}\xi +\beta _{2}\), and \(h=A^{2}B^{2}I_{1}-2A^{3}B^{4}\xi M^{11}(\xi )\), we have
Under these substitutions, the constant second invariant condition is written as
and the incompressibility condition reads
Clearing denominators and computing the resultant of these equations in \(M^{11}(\xi )\), we obtain
This must vanish for solutions to exist, so we take \(\left (...\right )=0\), since the remaining factors are nonzero.
We then take the coefficients of this polynomial in \(\xi \) to vanish independently, factor these coefficients, and order them by length. The first of these demands
If this equation can be solved for \(\beta _{1}\), we can perform this substitution and obtain the condition
which requires that \(\nu =- \frac{\mu _{1}}{AB^{2}\left (C\alpha _{1}+A\gamma _{1}\right )}\) be an eigenvalue of \(\mathbf{b}\). We perform the usual substitutions with the invariants to express equations in terms of \(e_{1}\) and \(e_{2}\), then take discriminants of the resulting equations in \(e_{1}\), and demand non-negativity. This yields the condition
or
In the first case, substitution yields either
or not, in which case \(e_{2}^{3}-e_{1}e_{2}+1=0\). In the first case, we satisfy the equations and obtain
Otherwise, we take \(e_{2}^{3}-e_{2}e_{1}+1=0\).
Substituting this yields \(\lambda _{1}=\lambda _{2}=1\), which reduces the equations to only one. After removing nonzero factors of this equation, we obtain something quadratic in \(\mu _{2}\), which after taking the discriminant and demanding non-negativity yields \(\alpha _{2} \gamma _{1}=\alpha _{1} \gamma _{2}\). With this, if \(\alpha _{1}\neq 0\), we obtain the final necessary result \(\mu _{2}=-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )\), which is a contradiction, since it is the case considered earlier with \(\lambda _{1}=\lambda _{2}=1\). If \(\alpha _{1}=0\), we require \(\alpha _{2}=0\), since \(C\alpha _{1}+A\gamma _{1}\neq 0\). With this, we require \(\mu _{2}=-A^{2}B^{2}\gamma _{2}\), again, a contradiction.
Next, we consider the case where
If \(\alpha _{1}\neq 0\), we solve this expression for \(\beta _{2}\) and obtain the necessary and sufficient condition
with
If \(\alpha _{1}=0\), we can solve for \(\mu _{2}\) to obtain
This requires
Alternatively, if \(C\alpha _{1}+A\gamma _{1}=0\), we obtain \(\gamma _{1}=\frac{-C\alpha _{1}}{A}\), which implies \(\alpha _{1}\mu _{1}=0\). If we assume \(\alpha _{1}=0\), and insert this relation into the equations, we obtain \(\mu _{1}^{2}+\left (A\beta _{1}-C\mu _{1}\right )^{2}=0\), so we can freely take \(\mu _{1}=0\). With this, we obtain an eigenvalue equation that demands that either \(\nu =-\frac{\beta _{1}}{B^{2}\alpha _{1}}\) is an eigenvalue of \(\mathbf{b}\), or that \(\beta _{1}=\alpha _{1}=0\). In the first case, we perform the usual substitutions and take discriminants in \(e_{1}\) and demand non-negativity, which yields
or not, in which case
In the first case, we have the sufficient condition
or not, in which case \(e_{2}^{3}-e_{1}e_{2}+1=0\). With this, we then obtain the condition \(\lambda _{1}=\lambda _{2}=1\), and then requiring discriminants in \(\beta _{2}\) to be non-negative, \(C\alpha _{2}+A\gamma _{2}=0\). With this, we take \(\gamma _{2}=-\frac{C}{A}\alpha _{2}\), which requires \(\beta _{2}=-B^{2}\alpha _{2}\), which is a special case of the previous solution.
Next, we consider \(\beta _{2}=\frac{Ce_{2}\mu _{2}-AB^{2}\alpha _{2}}{Ae_{2}}\). This requires the necessary and sufficient condition
which is the same as before.
The previously examined cases are all particular instances of the following anomalous solution:
Finally, when \(\beta _{1}=\alpha _{1}=0\), we are left with only one equation. In principle it can be solved for \(I_{2}\), but because \(I_{2}\) does not appear in any of the other equations, we can simply use the remaining constants as a transcendence basis in lieu of actually solving it. When we do this, we recognize that with \(\gamma _{1}=\alpha _{1}=\beta _{1}=\mu _{1}=0\), we obtain \(b^{ab}\) being constant. Hence, we can take any constant positive-definite tensor with \(\operatorname{det}\mathbf{b}=1\), and obtain \(M^{AB}\) via \(M^{AB}=(F^{-1})^{A}{}_{a}b^{ab} (F^{-1})^{B}{}_{b}\), which one can easily see generates a positive-definite symmetric metric tensor, since \(\mathbf{b}\) is positive-definite and symmetric. This, however, implies that the material manifold is Euclidean, since \(\mathbf{c}\) is the push forward of the material metric tensor, and it is constant in Cartesian coordinates. Therefore, the curvature tensor based on \(\mathbf{c}\) vanishes, and the anelastic deformation is stress free, i.e., Euclidean.
In general, a metric \(M_{AB}(R)\) arising from this case has the form
where the constants \(\{M_{11},M_{12},M_{13}, M_{22},M_{23},M_{33}\}\) satisfy \(M_{11}M_{22}M_{33}+2M_{12} M_{13}M_{23}-M_{13}^{2}M_{22}- M_{23}^{2}M_{11}-M_{12}^{2} M_{33}=1\). Any choice of these constants that yields a positive-definite metric generates an admissible constant tensor \(\mathbf{b}\). Though not immediately obvious, all of the above solutions are part of the same branch, apart from a global rigid rotation, which can be freely removed. The analysis tree for this family is:

Nodes:
-
0: \(A\left (C\alpha _{1}+A\gamma _{1}\right )\beta _{1}=\left (AC\gamma _{1}+ \left (1+C^{2}\right )\alpha _{1}\right )\mu _{1}\)
-
−: \(\beta _{1}^{3}+I_{1}B^{2}\alpha _{1}\beta _{1}^{2}+I_{2}B^{4}\alpha _{1}^{2} \beta _{1}+B^{6}\alpha _{1}^{3}\)
-
+: \(\left (A\beta _{2}e_{2}\left (C\alpha _{1}+A\gamma _{1}\right )-A^{2}B^{2} \left (\gamma _{2}\alpha _{1}-\alpha _{2}\gamma _{1}\right )-\left (1+C^{2} \right )e_{2}\alpha _{1}\mu _{2}-ACe_{2}\gamma _{1}\mu _{2}\right )\)
\(\left (e_{2}\alpha _{1}\beta _{2}+B^{2}\left (A\gamma _{1}\left (C \alpha _{2}+A\gamma _{2}\right )+\alpha _{1}\left (\alpha _{2}+C^{2} \alpha _{2}+AC\gamma _{2}\right )\right )+e_{2}\gamma _{1}\mu _{2} \right )=0\)
-
−−: \(b^{ab}\) is constant
-
−+: \(\left (\mu _{2}e_{2}+AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right ) \right )\left (A\beta _{2}e_{2}+AB^{2}\alpha _{2}-Ce_{2}\mu _{2} \right )=0\)
-
+−: \(\left (\mu _{2}e_{2}+AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right ) \right )\left (e_{2}^{3}-e_{1}e_{2}+1\right )=0\)
-
++: \(e_{2}\alpha _{1}\beta _{2}+B^{2}\left (A\gamma _{1} \left (C\alpha _{2}+A\gamma _{2}\right )+\alpha _{1}\left (\alpha _{2}+C^{2} \alpha _{2}+AC\gamma _{2}\right )\right )+e_{2}\gamma _{1}\mu _{2}=0\)
-
−+−: \(\left (\beta _{2}e_{2}+B^{2}\left (\left (1+C^{2}\right )\alpha _{2}+AC \gamma _{2}\right )\right )\left (e_{2}^{3}-e_{1}e_{2}+1\right )=0\)
-
−++: \(\mu _{2}= \frac{-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )}{e_{2}}\)
-
+−−: \(\mu _{2}= \frac{-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )}{e_{2}}\)
-
+−+: \(\alpha _{1}\gamma _{2}=\alpha _{2}\gamma _{1}\)
-
++−: \(\mu _{2}= \frac{-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )}{e_{2}}\)
-
+++: \(\beta _{2}= \frac{-B^{2}\left (\left (1+C^{2}\right )\alpha _{2}+AC\gamma _{2}\right )}{e_{2}}\)
-
−+−−: \(\mu _{2}= \frac{-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )}{e_{2}}\) and \(\beta _{2}=- \frac{B^{2}\left (\left (1+C^{2}\right )\alpha _{2}+AC\gamma _{2}\right )}{e_{2}}\)
-
−+−+: \(\lambda _{a}=1\Rightarrow C\alpha _{2}+A\gamma _{2}=0\Rightarrow \beta _{2}=-B^{2}\alpha _{2} \& \beta _{2}\neq -B^{2}\alpha _{2}\)
-
+−+−: \(\mu _{2}=-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )\neq -AB^{2} \left (C\alpha _{2}+A\gamma _{2}\right )\)
-
+−++: \(\mu _{2}=-A^{2}B^{2}\gamma _{2}\neq -A^{2}B^{2}\gamma _{2}\)
Edges (labelled by child node):
-
−: \(\gamma _{1}=-\frac{C}{A}\alpha _{1} \Rightarrow \mu _{1}=0\)
-
+: \(\gamma _{1}\neq \frac{C}{A}\alpha _{1}\Rightarrow \nu =- \frac{\mu _{1}}{AB^{2}\left (C\alpha _{1}+A\gamma _{1}\right )}\)
-
−−: \(\beta _{1}=\alpha _{1}=0\)
-
−+: \(\nu =-\frac{\beta _{1}}{B^{2}\alpha _{1}}\)
-
+−: \(\beta _{2}= \frac{A^{2}B^{2}\left (\alpha _{1}\gamma _{2}-\alpha _{2}\gamma _{1}\right )+\left (1+C^{2}\right )e_{2}\alpha _{1}\mu _{2}+ACe_{2}\gamma _{1}\mu _{2}}{Ae_{2}\left (C\alpha _{1}+A\gamma _{1}\right )}\)
-
++: \(e_{2}\alpha _{1}\beta _{2}=-\left (B^{2}\left (A\gamma _{1}\left (C \alpha _{2}+A\gamma _{2}\right )+\alpha _{1}\left (\alpha _{2}+C^{2} \alpha _{2}+AC\gamma _{2}\right )\right )+e_{2}\gamma _{1}\mu _{2} \right )\)
-
−+−: \(\mu _{2}= \frac{-AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )}{e_{2}}\)
-
−++: \(\beta _{2}=\frac{Ce_{2}\mu _{2}-AB^{2}\alpha _{2}}{Ae_{2}}\)
-
+−−: \(\mu _{2}e_{2}+AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )=0\)
-
+−+: \(\mu _{2}e_{2}+AB^{2}\left (C\alpha _{2}+A\gamma _{2}\right )\neq 0\) and \(e_{2}^{3}-e_{1}e_{2}+1=0\)
-
++−: \(\beta _{2}= \frac{-\left (B^{2}\left (A\gamma _{1}\left (C\alpha _{2}+A\gamma _{2}\right )+\alpha _{1}\left (\alpha _{2}+C^{2}\alpha _{2}+AC\gamma _{2}\right )\right )+e_{2}\gamma _{1}\mu _{2}\right )}{e_{2}\alpha _{1}}\)
-
+++: \(\alpha _{1}=0\) and \(\mu _{2}= \frac{-AB^{2}\left (\left (1+C^{2}\right )\alpha _{2}+AC\gamma _{2}\right )}{e_{2}}\)
-
−+−−: \(\beta _{2}=- \frac{B^{2}\left (\left (1+C^{2}\right )\alpha _{2}+AC\gamma _{2}\right )}{e_{2}}\)
-
−+−+: \(\beta _{2}\neq - \frac{B^{2}\left (\left (1+C^{2}\right )\alpha _{2}+AC\gamma _{2}\right )}{e_{2}} \& e_{2}^{3}-e_{1}e_{2}+1=0\)
-
+−+−: \(\gamma _{2}=\frac{\alpha _{2}\gamma _{1}}{\alpha _{1}}\)
-
+−++: \(\alpha _{1}=\alpha _{2}=0\)
Family 3
For this family, we can write the remaining equations corresponding to the coefficients of terms involving \(W_{1}\) and \(W_{2}\), and solve them before recasting the results in terms of the components of \(\mathbf{M}\). First, we take the equation \(m_{a[l}\nabla _{k]}\nabla _{b} b^{ab}=0\), which has two nonzero components yielding
Solving these yields
Reparameterizing these equations to simplify constants yields the equation
which gives
With this, we have the \(W_{2}\) equations involving \(\mathbf{c}\), which are
and
which have the common solution
We also have the constant trace condition that amounts to \(b^{11}(r)+r^{2}b^{22}(r)+b^{33}(r)=I_{1}\), which lets us solve for \(b^{22}(r)\), \(b^{23}(r)\), and \(b^{33}(r)\), as these equations are linear in these components, and the determinant of the linear system is \(- [ (r (r^{2}\gamma _{1}+\gamma _{2} ) )^{2}+ (r^{2} (r^{2}\alpha _{1}+\alpha _{2} ) )^{2} ]\), which is nonzero. Additionally, we have the following relations between the components of \(\mathbf{b}\) and the components of \(\mathbf{M}\)
which can be inverted, as the determinant of this system is \(\left (CF-DE\right )^{3}\neq 0\). Doing this, we define
and obtain
We are then left with the constant invariant condition for \(I_{2}\) and the incompressibility condition. We simplify notation by writing \(\mu =\mu _{1}+r^{2}\mu _{2}\) and \(\beta =\beta _{1}+r^{2}\beta _{2}\). These equations are
We take the discriminant of these equations in \(M^{11}(r)\), and demand this vanish. We remove nonzero factors, and then demand each coefficient in \(r\) vanish independently. The first condition we obtain is \(\alpha _{1}^{3}+I_{2}\alpha _{1}^{2}\beta _{2}+I_{1}\alpha _{1} \beta _{2}^{2}+\beta _{2}^{3}=0\), which implies that either \(\nu =-\frac{\beta _{2}}{\alpha _{1}}\) is an eigenvalue of \(\mathbf{b}\), or \(\alpha _{1}=\beta _{2}=0\). In the first case, we obtain \(\mu _{2}=\frac{\gamma _{1}}{e_{2}}\). This yields two subcases:
or alternatively
In this first subcase, we obtain the sufficient condition \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\), or \(e_{2}^{3}-e_{1}e_{2}+1=0\). However, when we take \(e_{2}^{3}-e_{1}e_{2}+1=0\), we obtain the same value for \(\mu _{1}\), and hence, this second condition is redundant. If we take the subcase, \(e_{2}^{3}-e_{1}e_{2}+1=0\) and \(\beta _{1}\neq -\frac{\alpha _{2}}{e_{2}}\), we obtain \(\lambda _{1}=\lambda _{2}=1\).
We then obtain the sufficient condition
which further yields \(\beta _{1}=-\alpha _{2}\), which is again a special case of the already discovered solutions. Next, we consider \(\alpha _{1}=\beta _{2}=0\). Inserting this, we obtain the equation \(\mu _{2}^{3}-I_{1}\mu _{2}^{2}\gamma _{1}+I_{2}\mu _{2}\gamma _{1}^{2}- \gamma _{1}^{3}=0\), which implies \(\nu =\frac{\mu _{2}}{\gamma _{1}}\) is an eigenvalue of \(\mathbf{b}\), or \(\mu _{2}=\gamma _{1}=0\). In the first case, we take discriminants in \(e_{1}\) and demand non-negativity, which yields the condition
Beginning with \(\gamma _{2}=0\), we obtain
which requires that \(\mu _{1}=0\). With this, we then obtain equations with the common factor \(\alpha _{2}+e_{2}\beta _{1}\). Hence, it is sufficient if this factor vanishes. If it does not, we can take the resultant of the remaining two equations in \(\beta _{1}\) to obtain \((e_{2}^{3}-e_{1}e_{2}+1)\alpha _{2}=0\). If \(\alpha _{2}=0\), we obtain that \(\beta _{1}=0\) as well, which is a case of the previously solved condition. If we instead take \(e_{2}^{3}-e_{1}e_{2}+1=0\), we obtain the condition \(\beta _{1}=-\alpha _{2}\lambda _{2}\), which is a special case of the previously solved condition, so we can always take \(\beta _{1}=-\frac{\alpha _{2}}{e_{2}}\).
Next, we assume \(\gamma _{2}\neq 0\) and take \(\mu _{1}=0\). Doing this yields
which demands \(\gamma _{2}=0\), a contradiction. We then assume \(\gamma _{2}\neq 0\), \(\mu _{1}\neq 0\), and take \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\). This requires \(\beta _{1}=-\frac{\alpha _{2}}{e_{2}}\), which is also sufficient. Finally, we assume \(\mu _{1}e_{2}-\gamma _{2}\neq 0\) in addition to \(\gamma _{2}\neq 0\) and \(\mu _{1}\neq 0\), and take \(\beta _{1}=-\frac{\alpha _{2}\mu _{1}}{\gamma _{2}}\). This demands
Making the first factor vanish reveals \(\lambda _{1}=\lambda _{2}\) or \(\lambda _{2}=\frac{1}{\lambda _{1}^{2}}\). The first case ultimately requires \(\lambda _{2}=1\), but this also means \(e_{2}=1\), and hence \(\mu _{1}e_{2}-\gamma _{2}=0\), a contradiction. In the case where \(\lambda _{2}=\frac{1}{\lambda _{1}^{2}}\), this contradiction is immediate. The steps are identical for the case where \(\mu _{1}=\lambda _{2}\gamma _{2}\), and so we have exhausted this branch of solutions.
Next, we take \(\mu _{2}=\gamma _{1}=0\). This returns
which requires \(\nu =-\frac{\beta _{1}}{\alpha _{2}}\) be an eigenvalue of \(\mathbf{b}\), or \(\alpha _{2}=\beta _{1}=0\). In the first case, we obtain a sufficient condition \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\). If this condition is not met, we can take the resultant of the remaining two equations in \(\gamma _{2}\) and obtain the necessary condition
Taking \(\mu _{1}=0\) yields \(\gamma _{2}=0\). Taking \(e_{2}^{3}-e_{1}e_{2}+1=0\), i.e., \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\) yields \(\mu _{1}=\gamma _{2}\lambda _{2}=\frac{\gamma _{2}}{e_{2}}\), again obtaining the previous sufficient condition. Finally, if \(\alpha _{2}=\beta _{1}=0\), we obtain
which demands that \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\), since \(\gamma _{2}\) cannot vanish without leaving the anomalous solution branch. This exhausts all solution branches of this family and reveals all solutions to be cases of the anomalous solution
This lets us solve for \(M^{11}(r)\), and finally obtain the anomalous solution
The analysis tree for this family is

Nodes:
-
0: \(\alpha _{1}^{3}+I_{2}\alpha _{1}^{2}\beta _{2}+I_{1}\alpha _{1} \beta _{2}^{2}+\beta _{2}^{3}=0\)
-
−: \(\left (\beta _{1}e_{2}+\alpha _{2}\right )\left (e_{2}^{3}-e_{1}e_{2}+1 \right )=0\)
-
+: \(\gamma _{1}^{3}-I_{2}\gamma _{1}^{2}\mu _{2}+I_{1}\mu _{2}^{2} \gamma _{1}-\mu _{2}^{3}=0\)
-
−−: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\)
-
−+: \(\beta _{1}=-\alpha _{2}\neq -\alpha _{2}\)
-
+−: \(\gamma _{2}\mu _{1}\left (e_{2}\mu _{1}-\gamma _{2}\right )\left ( \beta _{1}\gamma _{2}+\alpha _{2}\mu _{1}\right )=0\)
-
++: \(\beta _{1}^{3}+I_{1}\beta _{1}^{2}\alpha _{2}+I_{2}\beta _{1}\alpha _{2}^{2}+ \alpha _{2}^{3}=0\)
-
+−−: \(\mu _{1}=0\) and \(\beta _{1}=-\frac{\alpha _{2}}{e_{2}}\)
-
+−+: \(\mu _{1}\left (e_{2}\mu _{1}-\gamma _{2}\right )\left (\beta _{1} \gamma _{2}+\alpha _{2}\mu _{1}\right )=0\)
-
++−: \(\left (\mu _{1}e_{2}-\gamma _{2}\right )\left (...\right )_{1}=0\) and \(\left (\mu _{1}e_{2}-\gamma _{2}\right )\left (...\right )_{2}=0\)
-
+++: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\)
-
+−+−: \(\gamma _{2}=0\neq 0\)
-
+−++: \(\left (e_{2}\mu _{1}-\gamma _{2}\right )\left (\beta _{1}\gamma _{2}+ \alpha _{2}\mu _{1}\right )=0\)
-
++−−: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\)
-
++−+: \(\left (e_{2}^{3}-e_{1}e_{2}+1\right )\mu _{1}=0\)
-
+−++−: \(\beta _{1}=-\frac{\alpha _{2}}{e_{2}}\)
-
+−+++: \(\left (\mu _{1}-\lambda _{1}\gamma _{2}\right )\left (\mu _{1}- \lambda _{2}\gamma _{2}\right )=0\)
-
++−+−: \(\mu _{1}=\gamma _{2}=0\)
-
++−++: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\)
-
+−+++−: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\neq \frac{\gamma _{2}}{e_{2}}\)
-
+−++++: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\neq \frac{\gamma _{2}}{e_{2}}\)
Edges (labelled by child node):
-
−: \(\nu =-\frac{\beta _{2}}{\alpha _{1}}\Rightarrow \mu _{2}= \frac{\gamma _{1}}{e_{2}}\)
-
+: \(\alpha _{1}=\beta _{2}=0\)
-
−−: \(\beta _{1}=-\frac{\alpha _{2}}{e_{2}}\)
-
−+: \(\beta _{1}\neq -\frac{\alpha _{2}}{e_{2}}\) and \(e_{2}^{3}-e_{1}e_{2}+1=0\Rightarrow \lambda _{a}=1\)
-
+−: \(\nu =\frac{\mu _{2}}{\gamma _{1}}\)
-
++: \(\mu _{2}=\gamma _{1}=0\)
-
+−−: \(\gamma _{2}=0\)
-
+−+: \(\gamma _{2}\neq 0\)
-
++−: \(\nu =\frac{-\beta _{1}}{\alpha _{2}}\)
-
+++: \(\beta _{1}=\alpha _{2}=0\Rightarrow \mu _{1}^{3}-I_{1}\gamma _{2} \mu _{1}^{2}+I_{2}\gamma _{2}^{2}\mu _{1}-\gamma _{2}^{3}=0\)
-
+−+−: \(\mu _{1}=0\)
-
+−++: \(\mu _{1}\neq 0\)
-
++−−: \(\mu _{1}e_{2}-\gamma _{2}=0\)
-
++−+:
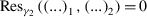
-
+−++−: \(\mu _{1}=\frac{\gamma _{2}}{e_{2}}\)
-
+−+++: \(\mu _{1}\neq \frac{\gamma _{2}}{e_{2}}\), \(\mu _{1}\neq 0\), and \(\gamma _{2}\neq 0\)
-
++−+−: \(\mu _{1}=0\)
-
++−++: \(\mu _{1}\neq 0\)
-
+−+++−: \(\mu _{1}=\lambda _{1} \gamma _{2}\)
-
+−++++: \(\mu _{1}=\lambda _{2} \gamma _{2}\)
Family 5
First addressing the equilibrium equations involving \(\mathbf{b}\), we obtain the equations
which simplify upon defining the auxiliary function \(f=CrM^{12}(r)+ABM^{11}(r)\), which makes the second equilibrium equation \(rf''(r)+3f'(r)=0\). These equations can be integrated to obtain
Next, we have the equilibrium equations derived from \(\mathbf{c}\), which are
These equations can be integrated to obtain
which coupled with the constant trace condition
lets us solve for \(M^{22}(r)\), \(M^{23}(r)\), and \(M^{33}(r)\) in terms of undetermined constants, and \(M^{11}(r)\). The determinant of this system is \(-C^{3}r^{6}\left [E^{2}r^{2}\left (r^{2}\alpha _{1}+\alpha _{2} \right )^{2}+\left (r^{2}\gamma _{1}+\gamma _{2}\right )^{2}\right ] \neq 0\), so we can always invert these equations. Denoting \(\gamma =\gamma _{1}r^{2}+\gamma _{2}\), \(\alpha =\alpha _{1}r^{2}+\alpha _{2}\), \(\mu =\mu _{1}r^{2}+\mu _{2}\), and \(\beta =\beta _{1}r^{2}+\beta _{2}\), we obtain
This leaves us with the incompressibility condition, and the constant second invariant of \(\mathbf{b}\) to satisfy. As in the other cases, these equations are quadratic in \(M^{11}(r)\), and we compute their resultant in \(M^{11}(r)\), factor each coefficient in \(r\) and demand they all vanish independently.
The first of these is the equation
which implies that either \(\nu =\frac{\beta _{1}+AB\alpha _{1}\gamma _{1}}{\alpha _{1}}\) is an eigenvalue of \(\mathbf{b}\), or \(\alpha _{1}=0\) and \(\beta _{1}=0\). In the first case, we immediately obtain \(\mu _{1}=2AB\alpha _{1}\alpha _{2}+\frac{\gamma _{1}}{E^{2}e_{2}}\), which upon substitution yields
which requires \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\left (\alpha _{2}\gamma _{1}+ \alpha _{1}\gamma _{2}\right )\), or if not, \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\). Tackling this latter case first, after substitution we demand \(\lambda _{2}=1\) to avoid a contradiction and obtain
This, however, reduces the remaining equations to requiring \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\left (\alpha _{2}\gamma _{1}+ \alpha _{1}\gamma _{2}\right )\), so we can immediately consider this case. One of the remaining equations then implies
Taking \(\mu _{2}=\frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\) is sufficient, so then we consider the case where \(\mu _{2}\neq \frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\). With this, we first take \(\gamma _{1}=0\), but this leads immediately to a contradiction, so we then consider \(e_{2}^{3}-e_{1}e_{2}+1=0\). However, this case also immediately leads to a contradiction, so we next consider \(\beta _{1}=\alpha _{1}=0\). This yields the equation
which implies that \(\nu =\frac{E^{2}\mu _{1}}{\gamma _{1}}\) is an eigenvalue of \(\mathbf{b}\), or \(\gamma _{1}=\mu _{1}=0\). In the first case, we take discriminants in \(e_{1}\) and demand non-negativity to obtain
Examining these factors one at a time, we first consider \(\gamma _{2}=0\). With this, we get the equation
hence, we take \(\mu _{2}=AB\alpha _{2}^{2}\). Inserting this yields either the sufficient condition
or \(\beta _{2}\neq \frac{\alpha _{2}}{e_{2}}-AB\alpha _{2}\gamma _{1}\), in which case we can take the resultant of the remaining nonzero factors in \(\beta _{2}\) to require
If we take \(\alpha _{2}=0\) we obtain \(\beta _{2}=0\), which is a special case of the sufficient condition above. If we take \(e_{2}^{3}-e_{1}e_{2}+1=0\), we ultimately see that the sufficient condition is also necessary. Considering \(\gamma _{2}\neq 0\), we then take \(\mu _{2}=AB \alpha _{2}^{2}\). However, substituting this yields an expression that is positive-definite in \(\gamma _{2}\) being equal to 0, so we have a contradiction.
Next, considering \(\gamma _{2}\neq 0\) and \(\mu _{2} \neq AB \alpha _{2}^{2}\), we take \(ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2}=0\). Doing this reveals the necessary and sufficient condition \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\alpha _{2}\gamma _{1}\). In the last case, we have
which implies the sufficient condition
or if not we can take resultants in \(\mu _{2}\) with the remaining nonzero factors to obtain the necessary condition
which requires either \(\lambda _{1}=\lambda _{2}\) or \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\), i.e., \(\mathbf{b}\) has a repeated eigenvalue. If we take \(\lambda _{1}=\lambda _{2}\), and look for different values of \(\mu _{2}\), we obtain
Substituting this into the remaining equations, we see that either \(\lambda _{2}=1\) or \(\alpha _{2}=0\), both of which reduce this value of \(\mu _{2}\) to the previous sufficient condition. Taking \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\) and looking for different solutions immediately requires \(\alpha _{2}=0\), which then further implies \(\mu _{2}=\frac{\gamma _{2}}{E^{2}\lambda _{2}^{2}}\). This, however, demands \(\lambda _{2}=1\), and we realize that the previous sufficient condition was also necessary.
Next, considering \(\mu _{1}=\gamma _{1}=0\), we obtain the eigenvalue equation \(\beta _{2}^{3}-I_{1}\alpha _{2}\beta _{2}^{2} +I_{2}\alpha _{2}^{2} \beta _{2}-\alpha _{2}^{3}=0\), which demands \(\mathbf{b}\) have the eigenvalue \(\nu =\frac{\beta _{2}}{\alpha _{2}}\), or \(\beta _{2}=\alpha _{2}=0\). In the first case, we obtain the sufficient condition
Taking the resultant of the remaining factors yields \(\gamma _{2}(e_{2}^{3}-e_{1}e_{2}+1 )=0\), which has solutions \(\gamma _{2}=0\) or \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\). Taking \(\gamma _{2}=0\) shows that in this case the sufficient condition is also necessary, and taking \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\) reveals that the sufficient condition is necessary in all cases.
Finally, we take \(\alpha _{2}=\beta _{2}=0\). This reveals only one remaining equation \(E^{6}\mu _{2}^{3}-I_{1}\gamma _{2}E^{4}\mu _{2}^{2}+I_{2}\gamma _{2}^{2}E^{2} \mu _{2}-\gamma _{2}^{3}=0\), which, since \(\gamma _{2}\neq 0\), requires the eigenvalue \(\nu =\frac{E^{2}\mu _{2}}{\gamma _{2}}\), and hence \(\mu _{2}=\frac{\gamma _{2}}{E^{2}e_{2}}\). The analysis tree is then

Nodes:
-
0: \(\left (\beta _{1}+AB\alpha _{1}\gamma _{1}\right )^{3}-I_{1}\left ( \beta _{1}+AB\alpha _{1}\gamma _{1}\right )^{2}\alpha _{1}+I_{2} \left (\beta _{1}+AB\alpha _{1}\gamma _{1}\right )\alpha _{1}^{2}- \alpha _{1}^{3}=0\)
-
−: \(\left (e_{2}^{3}-e_{1}e_{2}+1\right )\left (e_{2}\beta _{2}-\alpha _{2}+ABe_{2} \left (\alpha _{2}\gamma _{1}+\alpha _{1}\gamma _{2}\right )\right )=0\)
-
+: \(\left (E^{2}\mu _{1}\right )^{3}-I_{1}\left (E^{2}\mu _{1}\right )^{2} \gamma _{1}+I_{2}\left (E^{2}\mu _{1}\right )\gamma _{1}^{2}-\gamma _{1}^{3}=0\)
-
−−: \(\left (E^{2}e_{2}\mu _{2}-ABE^{2}e_{2}\alpha _{2}^{2}-\gamma _{2} \right )\left (e_{2}^{3}-e_{1}e_{2}+1\right )=0\)
-
−+: \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\left (\alpha _{2}\gamma _{1}+ \alpha _{1}\gamma _{2}\right )\neq \frac{\alpha _{2}}{e_{2}}-AB\left ( \alpha _{2}\gamma _{1}+\alpha _{1}\gamma _{2}\right )\)
-
+−: \(\gamma _{2}\left (AB\alpha _{2}^{2}-\mu _{2}\right )\left (ABE^{2}e_{2} \alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2}\right )\)
\(\left (ABE^{2}e_{2} \alpha _{2}^{3}+\beta _{2}\gamma _{2}+AB\alpha _{2}\gamma _{1}\gamma _{2}-E^{2} \alpha _{2}\mu _{2}\right )=0\)
-
++: \(\beta _{2}^{3}-I_{1}\alpha _{2}\beta _{2}^{2}+I_{2}\alpha _{2}\beta _{2}- \alpha _{2}^{3}=0\)
-
−−−: \(\mu _{2}=\frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\)
-
−−+: \(\mu _{2}=\frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}} \neq \frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\)
-
+−−: \(AB\alpha _{2}^{2}-\mu _{2}=0\) and \(\left (\beta _{2}e_{2}-\alpha _{2}+ABe_{2}\alpha _{2}\gamma _{1} \right )\left (...\right )_{a}=0\)
-
+−+: \(\gamma _{2}=0\neq 0\)
-
++−: \(\mu _{2}=\frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\)
-
+++: \(\mu _{2}=\frac{\gamma _{2}}{E^{2}e_{2}}\)
-
+−−−: \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\alpha _{2}\gamma _{1}\)
-
+−−+: \(\alpha _{2}\left (e_{2}^{3}-e_{1}e_{2}+1\right )=0\)
-
+−+−: \(\gamma _{2}=0\neq 0\)
-
+−++: \(\left (ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2} \right )\left (ABE^{2}e_{2}\alpha _{2}^{3}+\beta _{2}\gamma _{2}+AB \alpha _{2}\gamma _{1}\gamma _{2}-E^{2}\alpha _{2}\mu _{2}\right )=0\)
-
+−++−: \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\alpha _{2}\gamma _{1}\)
-
+−+++: \(\left (e_{1}^{2}-4e_{2}\right )\left (e_{2}^{3}-e_{1}e_{2}+1\right )=0\)
-
+−+++−: \(ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2}=0\neq 0\)
-
+−++++: \(ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2}=0\neq 0\)
Edges (labelled by child node):
-
−: \(\nu =\frac{\beta _{1}+AB\alpha _{1}\gamma _{1}}{\alpha _{1}}\)
-
+: \(\alpha _{1}=\beta _{1}=0\)
-
−−: \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\left (\alpha _{2}\gamma _{1}+ \alpha _{1}\gamma _{2}\right )\)
-
−+: \(\lambda _{1}=\frac{1}{\lambda _{2}^{2}}\)
-
+−: \(\nu =\frac{E^{2}\mu _{1}}{\gamma _{1}}\)
-
++: \(\gamma _{1}=\mu _{1}=0\)
-
−−−: \(\mu _{2}=\frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\)
-
−−+: \(\mu _{2}\neq \frac{ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}}{E^{2}e_{2}}\) and \(e_{2}^{3}-e_{1}e_{2}+1=0\)
-
+−−: \(\gamma _{2}=0\)
-
+−+: \(\gamma _{2}\neq 0\)
-
++−: \(\nu =\frac{\beta _{2}}{\alpha _{2}}\)
-
+++: \(\beta _{2}=\alpha _{2}=0\)
-
+−−−: \(\mu _{2}=AB\alpha _{2}^{2}\) and \(\beta _{2}=\frac{\alpha _{2}}{e_{2}}-AB\alpha _{2}\gamma _{1}\)
-
+−−+:
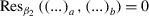
-
+−+−: \(\mu _{2}=AB\alpha _{2}^{2}\)
-
+−++: \(\mu _{2}\neq AB\alpha _{2}^{2}\)
-
+−++−: \(ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2}=0\)
-
+−+++: \(ABE^{2}e_{2}\alpha _{2}^{2}+\gamma _{2}-E^{2}e_{2}\mu _{2}\neq 0\)
-
+−+++−: \(e_{1}^{2}=4e_{2}\)
-
+−++++: \(e_{2}^{3}-e_{1}e_{2}+1=0\)
These are all special cases of the solution
which lets us solve for \(M^{11}(r)\) and obtain the anomalous solution
Appendix C: The Role of Symmetry
We note that the left Cauchy-Green stretch tensor fields present in all the known universal solutions, both classical and anelastic, are equivariant under the defining action of a Lie subgroup of the special Euclidean group. In particular, these subgroups all have at least two independent generators, with the three anelastic families separated by the nature of these generators; taking two purely translational generators yields \(\mathcal{U}_{2}\), taking one translational and one rotational yields \(\mathcal{U}_{3}\), and taking two rotational yields \(\mathcal{U}_{4}\). Of course, these families are not simply symmetric with respect to an arbitrary choice of generators of these natures; the translational generator in \(\mathcal{U}_{3}\) is orthogonal to the plane of rotation determined by the rotational generator of \(\mathcal{U}_{3}\), and both of the rotational generators for \(\mathcal{U}_{4}\) fix a common point. It is then natural to ask if there are other universal solutions that are likewise equivariant with respect to a similar subgroup, but without these specific generator choices.
3.1 C.3 The Lie Algebra \(\mathfrak{se}(n)\)
To examine the subgroup structure in terms of generators, we turn our attention to \(\mathfrak{se}(3)\), the Lie algebra associated to the Lie group SE\((3)\). We can represent the group SE\((n)\) as a subgroup of GL\(\left (n+1 \right )\) in the following way: The element \(\left (\mathbf{Q}|c\right )\in \text{SE}(n)\) is identified with the \(\left (n+1\right )\times \left (n+1\right )\) matrix
where \(\mathbf{0}\) is a \(1\times n\) block of 0’s. It is clear that the standard matrix multiplication in GL\(\left (n+1\right )\) agrees with the group action determined by the defining action of SE\((n)\) on \(\mathbb{E}^{n}\). As a reminder of Example A.1, the defining action of the special Euclidean group induces the group action
Translating this into the representation (417), we have
which clearly captures the induced group structure in terms of standard matrix multiplication. Taking the derivative of this representation around the identity yields a representation of the Lie algebra \(\mathfrak{se}(n)\):
where \(\boldsymbol{\Omega }\) is a skew symmetric matrix, \(u\) is an \(n\times 1\) column vector, and \(\mathbf{0}\) is a \(1\times n\) block of 0’s. We seek to examine the subalgebra structure of \(\mathfrak{se}(n)\), and in particular, \(\mathfrak{se}(3)\), since subalgebras with two generators will directly correspond to Lie subgroups with two generators by way of the exponential map.
The defining feature of SE\((n)\) being its action on \(\mathbb{E}^{n}\), we expect there to be an analogous representation for \(\mathbb{E}^{n}\) such that this action is reflected by the standard action of GL\(\left (n+1 \right )\) on \(\mathbb{R}^{n+1}\). Indeed the analogous representation takes the point with position vector \(X\in \mathbb{R}^{n}\) to the vector \(\begin{bmatrix} X \\ 1 \end{bmatrix} \in \mathbb{R}^{n+1}\). Under this representation, the special Euclidean group acts via matrix multiplication as follows:
which clearly agrees with the action as defined previously.
3.2 C.4 Subalgebras of \(\mathfrak{se}(3)\)
Under the above representation, an arbitrary element of \(\mathfrak{se}(3)\) takes the form
and the Lie bracket becomes the matrix commutator. Clearly elements of this form span a 6-dimensional subspace of \(\mathbb{R}^{4\times 4}\). We are interested in Lie subalgebras generated by the two generators, hence we consider two arbitrary elements of \(\mathfrak{se}(3)\), examine their product, and check for linear dependence. Doing this successively will identify proper subalgebras generated by two elements.
We first want to choose our coordinates in such a way to simplify our calculations. We seek to align our coordinate frame with the axial vector of the skew symmetric submatrix \(\boldsymbol{\Omega }\). The axial vector of \(\boldsymbol{\Omega }\) lies in the null space of \(\boldsymbol{\Omega }\), which is spanned by the vector \(\begin{bmatrix} \delta ,\epsilon ,\zeta \end{bmatrix} ^{\mathsf{T}}\), unless \(\boldsymbol{\Omega }=\mathbf{0}\), in which case we do not have to do anything at this step. These two options are exhaustive, since the eigenvalues of \(\boldsymbol{\Omega }\) are \(\{0,\pm \sqrt{-\delta ^{2}-\epsilon ^{2}-\zeta ^{2}}\}\).
Provided \(\boldsymbol{\Omega }\neq \mathbf{0}\), we can choose a Cartesian coordinate system such that \(\mathbf{e}_{3}\) is the normalized axial vector:
We do this by considering any rotation mapping the normalized axial vector to \(\mathbf{e}_{3}\). Denoting such a rotation \(\mathbf{R}\), we change coordinates by computing
When we apply this coordinate transformation, our chosen element of the Lie algebra takes the form
where \(\omega =\sqrt{\delta ^{2}+\epsilon ^{2}+\zeta ^{2}}\), and the \(\alpha \), \(\beta \), and \(\gamma \) here have been relabeled, being independent linear combinations depending on \(\mathbf{R}\) of the old \(\alpha \), \(\beta \), and \(\gamma \), which were arbitrary to begin with.
Next, we seek to apply a coordinate translation to simplify the translation portion of our chosen element. To do this, we seek to identify the fixed points of this action. The velocity of points under the action of the one-parameter subalgebra generated by this element is given by
Hence, if \(\omega \neq 0\), we can choose a coordinate translation that sets the point \([-\beta /\omega\ \ \alpha /\omega\ \ 0 ] ^{\mathsf{T}}\) to be the origin. Under this transformation, our chosen element takes the form
Here, \(u=\gamma \), but we shall explicitly use \(u\) and \(\omega \) to emphasize that we have expressed this element of \(\mathfrak{se}(3)\) in a coaxial coordinate system. In the case where \(\boldsymbol{\Omega }=\mathbf{0}\), we simply choose our coordinate rotation so that our translation vector is aligned with \(\mathbf{e}_{3}\), which sets our chosen Lie algebra element to the form above with \(\omega =0\).
3.2.1 C.4.1 2-Dimensional Subalgebras
Obviously, provided that the generators we select are linearly independent, they span a two-dimensional vector space, hence all subalgebras containing them are at least two-dimensional. In order for us to identify two-dimensional subalgebras, we simply need to establish necessary and sufficient conditions for the two generators and their bracket to be linearly dependent. We select a coordinate system that is coaxial with one of our generators, and hence have
and select another arbitrary generator,
Taking the Lie bracket of these two elements, we obtain
We then require the Lie bracket of our generators to be within their span, i.e., we seek all solutions to the equations
which explicitly become
Taking the combination \(\delta \left (a_{2}\epsilon +\delta \omega =0\right )-\epsilon \left (a_{2}\delta -\epsilon \omega =0\right )\) yields the equation
which implies that either \(\omega =0\), or both \(\delta =0\) and \(\epsilon =0\). If \(\omega =0\), we consider the combinations
Since \(v_{1}\neq \mathbf{0}\), \(u\neq 0\), hence we require \(\delta =\epsilon =0\). With these substitutions, \(\left [v_{1},v_{2}\right ]\) vanishes, and we have
and
If \(\zeta \neq 0\), we can always reselect our origin to eliminate \(\alpha \) and \(\beta \), while leaving \(v_{1}\) unchanged. Hence we obtain the symmetry of family \(\mathcal{U}_{3}\). If \(\zeta =0\), we have two independent translational symmetries, which yields the symmetry found in family \(\mathcal{U}_{2}\).
Now we turn our attention to the case where \(\omega \neq 0\), and consider the combination
Since \(\omega \neq 0\), we require \(\alpha =\beta =0\). This leaves us with \(v_{1}\) as initially specified and
which means that \(v_{1}\) and \(v_{2}\) generate independent screw motions about the same axis, corresponding to the symmetry of family \(\mathcal{U}_{3}\).
3.2.2 C.4.2 3-Dimensional Subalgebras
Defining \(v_{3}=\left [v_{1},v_{2}\right ]\), and provided \(v_{3}\neq 0\), \(v_{1}\), \(v_{2}\), and \(v_{3}\) span a three-dimensional vector space. The span of these three vectors must be closed under the Lie bracket, hence we require
and
We know that if \(v_{3}=0\) then \(v_{1}\) and \(v_{2}\) generate a two-dimensional subalgebra, hence we can freely assume \(v_{3}\neq 0\).
First, we recognize that if \(\omega =0\), both \(v_{1}\) and \(v_{3}\) are pure translations. They are linearly independent provided \(\delta \neq 0\) and \(\epsilon \neq 0\), in which case \(v_{3}=0\). Hence, the bracket of a pure translation with a non-coaxial rotation yields another translation that is linearly independent of the original translation. Hence, \(\mathfrak{t}(2)\) is contained in such a Lie subalgebra, and hence all universal solutions that are symmetric with respect to the subgroups corresponding to these subalgebras are contained in \(\mathcal{U}_{2}\). If the rotation is coaxial with the translation, then the bracket vanishes and we are reduced to the already solved two-dimensional case; hence from now on, we can safely assume \(\omega \neq 0\).
The equations we must tackle are explicitly
Taking the linear combination
coupled with the condition \(\omega \neq 0\) yields either \(a_{3}=0\) or both \(\delta =0\) and \(\epsilon =0\). If \(\delta =\epsilon =0\), \(v_{3}\) is a pure translation that is orthogonal to the axis of \(v_{1}\), hence, taking \(\left [v_{1},v_{3}\right ]\) generates another pure translation orthogonal to the axis of \(v_{1}\) and that of \(v_{3}\), hence we capture the symmetry \(\mathfrak{t}(2)\) as a subgroup of our symmetry group, and hence this case is captured in family \(\mathcal{U}_{2}\).
If either \(\epsilon \neq 0\) or \(\delta \neq 0\), we have \(a_{3}=0\), which upon substitution yields \(\delta (a_{2}-\omega ^{2} )=0\) and \(\epsilon \left (a_{2}-\omega ^{2}\right )=0\). These equations together imply \(a_{2}=\omega ^{2}\). Substituting this new relation into our equations, two of our equations reduce to
which together imply that \(u=0\), since \(\delta \) and \(\epsilon \) cannot simultaneously vanish and \(\omega \neq 0\); hence \(v_{1}\) must be a pure rotation, not simply a screw motion. With this, our first equation becomes \(\gamma \omega ^{2}=0\), hence \(\gamma =0\) as well. When we insert this relation into our equations, we obtain
which implies that the inner product of the axial vector of \(v_{2}\) with its translation vector is zero. This implies that \(v_{2}\) is also a pure rotation, since this inner product is unchanged under coordinate transformations. This can be seen by noting that the velocity field \(\mathbf{u}\) induced by the action of an element of \(\mathfrak{se}(3)\) is given by
Taking the inner product of this with the embedding of the axial vector \(\begin{bmatrix} \delta &\epsilon &\zeta &1 \end{bmatrix} ^{\mathsf{T}}\) yields
which, not depending on position, is an invariant of the velocity field. Since the velocity field is coordinate independent, we know that this invariant will be preserved under coordinate changes. When we express our generator in a coordinate system aligned with its axis, this invariant becomes \(\omega u\), which vanishes if either our generator is a pure translation or a pure rotation. In our analysis, we have for \(v_{2}\), \(\alpha \delta +\beta \epsilon =0\) together with \(\gamma =0\), hence we know \(v_{2}\) is either a pure translation or a pure rotation. We know that \(v_{2}\) is not a pure translation since either \(\delta \) or \(\epsilon \) is nonzero. Additionally, we know that the axial vectors of \(v_{1}\) and \(v_{2}\) are linearly independent, since either \(\delta \) or \(\epsilon \) is nonzero.
Summing up our progress thus far, we have shown that both \(v_{1}\) and \(v_{2}\) must be pure rotations. In fact, their axes of rotation intersect, hence they generate \(\mathfrak{so}(3)\), the symmetry present in \(\mathcal{U}_{4}\), indicating that our classification captures all three-dimensional cases. To see this, note that we have aligned our coordinates so that the axis of rotation for \(v_{1}\) is the \(z\) axis. We seek to show that the axis of rotation for \(v_{2}\) intersects the \(z\) axis.
First notice that for rotations about the origin, the velocity field generated is of the form
where \(\boldsymbol{\omega }\) is the axial vector of \(\boldsymbol{\Omega }\), and ∧ is the standard cross product. This implies that the velocity vector at a point is orthogonal to the plane spanned by the axial vector of the rotation, and the position vector \(X\). Since (446) assumes we have chosen our origin such that the axis of rotation passes through the origin, this plane is equivalently the plane containing the axis of rotation and the point \(X\). Therefore, for the generator \(v_{2}\), we can examine the velocity generated at the origin, and recognize that it lies entirely in the \(x,y\) plane. If this velocity is nonzero, we know that the plane passing through the origin that is orthogonal to this translation contains the axis of rotation of \(v_{2}\). This plane also contains the \(z\) axis, since all planes passing through the origin that are orthogonal to a nonzero vector in the \(x,y\) plane contain the \(z\) axis. Therefore the axes of rotation for \(v_{1}\) and \(v_{2}\) are coplanar. We have already established that they are not parallel, since the axial vectors for \(v_{1}\) and \(v_{2}\) are linearly independent, hence they must intersect at some point. If the velocity generated by \(v_{2}\) at the origin is zero, then the axis of rotation of \(v_{2}\) passes through the origin, and hence not only intersects the \(z\) axis, but intersects it at the origin.
We have therefore shown that all three-dimensional Lie subalgebras of \(\mathfrak{se}(3)\) that are generated by two linearly independent generators either contain \(\mathfrak{t}(2)\) as a subalgebra, or are \(\mathfrak{so}(3)\), the algebra associated with the set of rotations about a fixed point, and hence universal solutions that are equivariant with respect to the associated Lie groups are contained in one of our discovered families.
3.2.3 C.4.3 4+ Dimensional Subalgebras
Without loss of generality, we assume \(v_{1}\), \(v_{2}\), \(v_{3}\), and \(v_{4}=\left [v_{1},v_{3}\right ]\) are linearly independent, since the other choice would be \(v_{4}=\left [v_{2},v_{3}\right ]\), which would be equivalent. Specifically, we denote \(V_{2}=\operatorname{Span}\left (v_{1},v_{2}\right )\), and \(V_{3}=\operatorname{Span}\left (v_{1},v_{2},\left [v_{1},v_{2} \right ]\right )\). Provided that \(v_{1}\), \(v_{2}\), and \(\left [v_{1},v_{2}\right ]\) are linearly independent, we can write \(V_{3}=V_{2}\oplus \operatorname{Span}\left (\left [v_{1},v_{2} \right ]\right )\). It suffices to take the fourth linearly independent element to be of the form
since for all \(u,w\in V_{2}\), \(\left [u,w\right ]\in V_{3}\), and for all \(u,w\in \operatorname{Span}\left (\left [v_{1},v_{2}\right ]\right )\), \(\left [u,w\right ]=0\). Since \(v_{1}\) and \(v_{2}\) are arbitrary, we can choose this fourth linearly independent element to be \(\left [v_{1},v_{3}\right ]\). Doing this, we have
Notice that the axial vectors of \(v_{1}\), \(v_{3}\), and \(v_{4}\) are \([0,0,\omega ]^{\mathsf{T}}\), \([-\epsilon \omega ,\delta \omega ,0 ]^{\mathsf{T}}\), and \([-\delta \omega ^{2},-\epsilon \omega ^{2},0 ]^{\mathsf{T}}\) respectively. These vectors are mutually orthogonal, hence provided \(\omega \neq 0\) and that \(\epsilon \neq 0\) or \(\delta \neq 0\), these span \(\mathbb{R}^{3}\), and hence the rotational components of these three generators can be used to reduce any fourth linearly independent generator to a pure translation. As shown earlier, taking the bracket of a pure translation with any other linearly independent element of \(\mathfrak{se}(3)\) generates a two-dimensional subalgebra: either \(\mathfrak{t}(2)\) or \(\mathfrak{so}(2)\times \mathfrak{t}(1)\). Therefore, all subalgebras of dimension four or higher contain one of these two-dimensional subalgebras, hence universal solutions that are symmetric with respect to such a four-dimensional subalgebra will be contained in either \(\mathcal{U}_{2}\) or \(\mathcal{U}_{3}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goodbrake, C., Yavari, A. & Goriely, A. The Anelastic Ericksen Problem: Universal Deformations and Universal Eigenstrains in Incompressible Nonlinear Anelasticity. J Elast 142, 291–381 (2020). https://doi.org/10.1007/s10659-020-09797-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-020-09797-2
Keywords
- Universal deformation
- Nonlinear elasticity
- Eigenstrain
- Residual stress
- Lie group symmetry
- Riemannian geometry
- Material manifold
- Commutative algebra