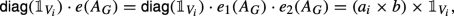Abstract
There is a long tradition in understanding graphs by investigating their adjacency matrices by means of linear algebra. Similarly, logic-based graph query languages are commonly used to explore graph properties. In this paper, we bridge these two approaches by regarding linear algebra as a graph query language. More specifically, we consider MATLANG, a matrix query language recently introduced, in which some basic linear algebra functionality is supported. We investigate the problem of characterising the equivalence of graphs, represented by their adjacency matrices, for various fragments of MATLANG. That is, we are interested in understanding when two graphs cannot be distinguished by posing queries in MATLANG on their adjacency matrices. Surprisingly, a complete picture can be painted of the impact of each of the linear algebra operations supported in MATLANG on their ability to distinguish graphs. Interestingly, these characterisations can often be phrased in terms of spectral and combinatorial properties of graphs. Furthermore, we also establish links to logical equivalence of graphs. In particular, we show that MATLANG-equivalence of graphs corresponds to equivalence by means of sentences in the three-variable fragment of first-order logic with counting. Equivalence with regards to a smaller MATLANG fragment is shown to correspond to equivalence by means of sentences in the two-variable fragment of this logic.
Similar content being viewed by others
Change history
11 January 2021
A Correction to this paper has been published: <ExternalRef><RefSource>https://doi.org/10.1007/s00224-020-10020-x</RefSource><RefTarget Address="10.1007/s00224-020-10020-x" TargetType="DOI"/></ExternalRef>
Notes
We use
 to denote the all-ones vector (of appropriate dimension) and use
to denote the all-ones vector (of appropriate dimension) and use  (with brackets) for the corresponding one-vector operation.
(with brackets) for the corresponding one-vector operation.Underlying this observation is that AG is a symmetric matrix and hence diagonalisable.
The diag(⋅) operation is also defined for 1 × 1-matrices (scalars) in which case it just returns that scalar.
We remark that we cannot rely yet on the conjugation-preservation Lemma 5.3 to show that \(G\equiv _{\textsf {ML}({\mathscr{L}}^{+})} H\) if and only if \(G\equiv _{\textsf {ML}({\mathscr{L}})} H\). Indeed, at this point we do not know yet for what kind of matrices T, T-conjugation is preserved by the diag(⋅)-operation. This will only be settled in Lemma 7.1 later in this section.
It was incorrectly stated in the conference version [33] that diag(⋅) and ⊙v are interchangeable.
I am indebted to David E. Roberson for providing these two graphs [63].
We here use that we work in the algebraically closed field \(\mathbb {C}\) for which being diagonalisable coincides with the minimal polynomial being a product of monic linear factors of the form (x − λ). So, since the characteristic polynomial of C divides that of AG, also the minimal polynomial of C divides that of AG. Since AG is diagonalisable, its minimal polynomial is a product of monic linear factors. Hence, also the minimal polynomial of C has this form and C is diagonalisable as well.
The use of Apply[f> 0](⋅) is just for convenience. Its application inside sentences can be simulated with operations in
 when evaluated on given adjacency matrices.
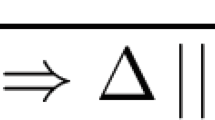
when evaluated on given adjacency matrices.With a triangle one simply means a triple (v1, v2), (v1, v3) and (v2, v3) of vertex pairs, none of which has to be an edge in G.
References
Alon, N., Yuster, R., Zwick, U.: Finding and counting given length cycles. Algorithmica 17(3), 209–223 (1997). https://doi.org/10.1007/BF02523189
Angles, R., Arenas, M., Barceló, P., Hogan, A., Reutter, J., Vrgoč, D.: Foundations of modern query languages for graph databases. ACM Comput. Surv. 50(5), 68:1–68:40 (2017). https://doi.org/10.1145/3104031
Arvind, V., Fuhlbrück, F., Köbler, J., Verbitsky, O.: On weisfeiler-leman invariance: Subgraph counts and related graph properties. CoRR, arXiv:1811.04801 (2018)
Atserias, A., Maneva, E.N.: Sherali-Adams relaxations and indistinguishability in counting logics. SIAM J. Comput. 42(1), 112–137 (2013). https://doi.org/10.1137/120867834
Axler, S.: Linear Algebra Done Right, 3rd edn. Springer, Berlin, (2015). https://doi.org/10.1007/978-3-319-11080-6
Barceló, P.: Querying graph databases. In: Proceedings of the 32nd ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, PODS, pp. 175–188. https://doi.org/10.1145/2463664.2465216 (2013)
Barceló, P., Higuera, N., Pėrez, J., Subercaseaux, B.: On the expressiveness of LARA: A unified language for linear and relational algebra. In: proceedings of the 23rd International Conference on Database Theory, ICDT, pp. 6:1–6:20. https://doi.org/10.4230/LIPIcs.ICDT.2020.6 (2020)
Bastert, O.: Stabilization procedures and applications. PhD thesis, Technical University Munich, Germany, http://nbn-resolving.de/urn:nbn:de:bvb:91-diss2002070500045 (2001)
Boehm, M., Dusenberry, M.W., Eriksson, D., Evfimievski, A.V., Manshadi, F.M., Pansare, N., Reinwald, B., Reiss, F.R., Sen, P., Surve, A.C., Shirsih, T.: SystemML: Declarative machine learning on Spark. Proc. VLDB Endowment 9(13), 1425–1436 (2016). https://doi.org/10.14778/3007263.3007279
Boehm, M., Reinwald, B., Hutchison, D., Sen, P., Evfimievski, A.V., Pansare, N.: On optimizing operator fusion plans for large-scale machine learning in SystemML. Proc. VLDB Endowment 11(12), 1755–1768 (2018). https://doi.org/10.14778/3229863.3229865
Brijder, R., Geerts, F., den Bussche, J.V., Weerwag, T.: On the expressive power of query languages for matrices. In: 21st International Conference on Database Theory, ICDT, 10:1–10:17. https://doi.org/10.4230/LIPIcs.ICDT.2018.10 (2018)
Brijder, R., Geerts, F., den Bussche, J.V., Weerwag, T.: On the expressive power of query languages for matrices. ACM Trans on Database Systems. To appear (2019)
Brijder, R., Gyssens, M., den Bussche, J.V.: On matrices and K-relations. In: Proceedings of the 11th International Symposium on Foundations of Information and Knowledge Systems, FoIKS, volume 12012 of Lecture Notes in Computer Science, pp. 42–57. Springer. https://doi.org/10.1007/978-3-030-39951-1_3 (2020)
Brouwer, A.E., Haemers, W.H.: Spectra of graphs universitext. Springer. https://doi.org/10.1007/978-1-4614-1939-6 (2012)
Cai, J.-Y., Fürer, M., Immerman, N.: An optimal lower bound on the number of variables for graph identification. Combinatorica 12(4), 389–410 (1992). https://doi.org/10.1007/BF01305232
Chan, A., Godsil, C.D.: Symmetry and eigenvectors. In: Graph symmetry (Montreal, PQ, 1996), volume 497 of NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., pp. 75–106. Kluwer Acad. Publ., Dordrecht. https://doi.org/10.1007/978-94-015-8937-6_3(1997)
Chen, L., Kumar, A., Naughton, J., Patel, J.M.: Towards linear algebra over normalized data. Proc. VLDB Endowment 10(11), 1214–1225 (2017). https://doi.org/10.14778/3137628.3137633
Cvetković, D.M.: Graphs and their spectra. Publikacije Elektrotehničkog fakulteta. Serija Matematika i fizika, 354/356, 1–50. http://www.jstor.org/stable/43667526 (1971)
Cvetković, D.M.: The main part of the spectrum, divisors and switching of graphs. Publ. Inst. Math. (Beograd) (N.S.), 23(37), 31–38. http://elib.mi.sanu.ac.rs/files/journals/publ/43/6.pdf (1978)
Cvetković, D.M., Rowlinson, P., Simić, S.: Eigenspaces of Graphs: Encyclopedia of Mathematics and its Applications. Cambridge University Press. https://doi.org/10.1017/CBO9781139086547 (1997)
Cvetković, D.M., Rowlinson, P., Simić, S.: An Introduction to the Theory of Graph Spectra. London Mathematical Society Student Texts. Cambridge University Press. https://doi.org/10.1017/CBO9780511801518 (2009)
Dawar, A.: On the descriptive complexity of linear algebra. In: Proceedings of the 15th International Workshop on Logic, Language, Information and Computation, WoLLIC, pp. 17–25. https://doi.org/10.1007/978-3-540-69937-8_2 (2008)
Dawar, A., Grohe, M., Holm, B., Laubner, B.: Logics with rank operators. In: Proceedings of the 24th Annual IEEE Symposium on Logic In Computer Science, LICS, pp. 113–122. (2009)
Dawar, A., Holm, B.: Pebble games with algebraic rules. Fund. Inform. 150(3-4), 281–316 (2017). https://doi.org/10.3233/FI-2017-1471
Dawar, A., Severini, S., Zapata, O.: Descriptive complexity of graph spectra. In: Proceedings of the 23rd International Workshop on Logic, Language, Information and Computation, WoLLIC, pp. 183–199. https://doi.org/10.1007/978-3-662-52921-8_12(2016)
Dawar, A., Severini, S., Zapata, O.: Descriptive complexity of graph spectra. Ann. Pure Appl. Log. 170(9), 993–1007 (2019). https://doi.org/10.1016/j.apal.2019.04.005
Dell, H., Grohe, M., Rattan, G.: Lovȧsz meets Weisfeiler and Lehman. In: 45th International Colloquium on Automata, Languages, and Programming, ICALP, pp. 40:1–40:14. https://doi.org/10.4230/LIPIcs.ICALP.2018.40 (2018)
Elgohary, A., Boehm, M., Haas, P.J.: Frederick R. Reiss, and Berthold Reinwald. Compressed linear algebra for large-scale machine learning. The VLDB Journal, 1–26. https://doi.org/10.1007/s00778-017-0478-1 (2017)
Farahat, H. K.: The semigroup of doubly-stochastic matrices. Proc. Glasgow Math. Assoc. 7 (4), 178–183 (1966). https://doi.org/10.1017/S2040618500035401
Friedland, S.: Coherent algebras and the graph isomorphism problem. Discret. Appl. Math. 25(1), 73–98 (1989). https://doi.org/10.1016/0166-218X(89)90047-4
Fürer, M.: On the power of combinatorial and spectral invariants. Linear Algebra Appl. 432(9), 2373–2380 (2010). https://doi.org/10.1016/j.laa.2009.07.019
Fürer, M., Paschos, V.Th.: On the combinatorial power of the Weisfeiler-Lehman algorithm. In: Pagourtzis, A. (ed.) Algorithms and Complexity. https://doi.org/10.1007/978-3-319-57586-5_22, pp 260–271. Springer (2017)
Geerts, F.: On the expressive power of linear algebra on graphs. In: Proceedings of the 22nd International Conference on Database Theory, ICDT, pp. 7:1–7:19. https://doi.org/10.4230/LIPIcs.ICDT.2019.7 (2019)
Geerts, F.: When can matrix query languages discern matrices? In: Proceedings of the 23nd International Conference on Database Theory ICDT. https://doi.org/10.4230/LIPIcs.ICDT.2020.12 (2020)
Godsil, C., Royle, G.F.: Algebraic Graph Theory volume 207 of Graduate Texts in Mathematics. Springer. https://doi.org/10.1007/978-1-4613-0163-9 (2001)
Gorodentsev, A.L.: Algebra I: Textbook for Students of Mathematics. Springer. https://doi.org/10.1007/978-3-319-45285-2 (2016)
Grȧdel, E, Pakusa, W.: Rank logic is dead, long live rank logic! In: 24th EACSL Annual Conference on Computer Science Logic, CSL, pp. 390–404. https://doi.org/10.4230/LIPIcs.CSL.2015.390 (2015)
Grohe, M., Kersting, K., Mladenov, M., Selman, E.: Dimension reduction via colour refinement. In: 22th Annual European Symposium on Algorithms, ESA, pp. 505–516. https://doi.org/10.1007/978-3-662-44777-2_42 (2014)
Grohe, M., Otto, M.: Pebble games and linear equations. J. Symbol. Log. 80(3), 797–844 (2015). https://doi.org/10.1017/jsl.2015.28
Grohe, M., Pakusa, W.: Descriptive complexity of linear equation systems and applications to propositional proof complexity. In: 32nd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS, 1–12. https://doi.org/10.1109/LICS.2017.8005081(2017)
Haemers, W.H., Spence, E.: Enumeration of cospectral graphs. Eur. J. Combin. 25(2), 199–211 (2004). https://doi.org/10.1016/S0195-6698(03)00100-8
Harary, F., Schwenk, A.J.: The spectral approach to determining the number of walks in a graph. Pacif. J. Math. 80(2), 443–449. https://projecteuclid.org:443/euclid.pjm/1102785717 (1979)
Hella, L.: Logical hierarchies in PTIME. Inf. Comput. 129(1), 1–19 (1996). https://doi.org/10.1006/inco.1996.0070
Hella, L.auri, Libkin, L., Nurmonen, J., Wong, L.: Logics with aggregate operators. J. ACM 48(4), 880–907 (2001). https://doi.org/10.1145/502090.502100
Holm, B.: Descriptive Complexity of Linear Algebra. PhD thesis, University of Cambridge (2010)
Hutchison, D., Howe, B., Suciu, D.: LaraDB: A minimalist kernel for linear and relational algebra computation. In: Proceedings of the 4th ACM SIGMOD Workshop on Algorithms and Systems for MapReduce and Beyond, BeyondMR, pp. 2:1–2:10. https://doi.org/10.1145/3070607.3070608 (2017)
Immerman, N., Lander, E.: Describing graphs: A first-order approach to graph canonization. In: Selman, A.L. (ed.) Complexity Theory Retrospective: In Honor of Juris Hartmanis on the Occasion of His Sixtieth Birthday. https://doi.org/10.1007/978-1-4612-4478-3_5, pp 59–81. Springer (1990)
Jing, N.: Unitary and orthogonal equivalence of sets of matrices. Linear Algebra Appl. 481, 235–242 (2015). https://doi.org/10.1016/j.laa.2015.04.036
Johnson, C.R., Newman, M.: A note on cospectral graphs. J. Comb. Theory Ser. B 28(1), 96–103 (1980). https://doi.org/10.1016/0095-8956(80)90058-1
Kaplansky, I.: Linear Algebra and Geometry. A Second Course. Chelsea Publishing Company (1974)
Kersting, K., Mladenov, M., Garnett, R., Grohe, M.: Power iterated color refinement. In: Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, AAAI’14, pp. 1904–1910. AAAI Press. https://www.aaai.org/ocs/index.php/AAAI/AAAI14/paper/view/8377 (2014)
Kunft, A., Alexandrov, A., Katsifodimos, A., Markl, V.: Bridging the gap Towards optimization across linear and relational algebra. In: Proceedings of the 3rd ACM SIGMOD Workshop on Algorithms and Systems for MapReduce and Beyond, BeyondMR, pp. 1:1–1:4. https://doi.org/10.1145/2926534.2926540 (2016)
Kunft, A., Katsifodimos, A., Schelter, S., Rabl, T., Markl, V.: Blockjoin: Efficient matrix partitioning through joins. Proc. VLDB Endowment 10 (13), 2061–2072 (2017). https://doi.org/10.14778/3151106.3151110
Libkin, L.: Expressive power of SQL. Theor. Comput. Sci. 296, 379–404 (2003). https://doi.org/10.1016/S0304-3975(02)00736-3
Libkin, L.: Elements of Finite Model Theory. Texts in Theoretical Computer Science: An EATCS series. Springer. https://doi.org/10.1007/978-3-662-07003-1 (2004)
Luo, S., Gao, Z.J., Gubanov, M., Perez, L.L., Jermaine, C.: Scalable linear algebra on a relational database system. SIGMOD Rec. 47(1), 24–31 (2018). https://doi.org/10.1145/3277006.3277013
Malkin, P.N.: Sherali–Adams relaxations of graph isomorphism polytopes. Discret. Optim. 12, 73–97 (2014). https://doi.org/10.1016/j.disopt.2014.01.004
Ngo, H.Q., Nguyen, X., Olteanu, D., Schleich, M.: In-database factorized learning. In: Proceedings of the 11th Alberto Mendelzon International Workshop on Foundations of Data Management and the Web, AMW. http://ceur-ws.org/Vol-1912/paper21.pdf (2017)
Otto, M.: Bounded Variable Logics and Counting: A Study in Finite Models, volume 9 of Lecture Notes in Logic. Springer. https://doi.org/10.1017/9781316716878(1997)
Pech, C.: Coherent algebras. https://doi.org/10.13140/2.1.2856.2248 (2002)
Perlis, S: Theory of matrices. Addison-Wesley Press, Inc, Cambridge Mass (1952)
Ramana, M.V., Scheinerman, E.R., Ullman, D.: Fractional isomorphism of graphs. Discret. Math. 132(1-3), 247–265 (1994). https://doi.org/10.1016/0012-365X(94)90241-0
Roberson, D.: Co-spectral fractional isomorphic graphs with different laplacian spectrum. MathOverflow. https://mathoverflow.net/q/334539
Rowlinson, P.: The main eigenvalues of a graph: A survey. Appl. Anal. Discret. Math. 1(2), 455–471. http://www.jstor.org/stable/43666075 (2007)
Scheinerman, E.R., Ullman, D.H.: Fractional Graph Theory: a Rational Approach to the Theory of Graphs. Wiley. https://www.ams.jhu.edu/ers/wp-content/uploads/sites/2/2015/12/fgt.pdf (1997)
Schleich, M., Olteanu, D., Ciucanu, R: Learning linear regression models over factorized joins. In: Proceedings of the 2016 International Conference on Management of Data, SIGMOD, pp. 3–18. https://doi.org/10.1145/2882903.2882939 (2016)
Thüne, M.: Eigenvalues of Matrices and Graphs. PhD thesis, University of Leipzig (2012)
Tinhofer, G.: Graph isomorphism and theorems of Birkhoff type. Computing 36 (4), 285–300 (1986). https://doi.org/10.1007/BF02240204
Tinhofer, G.: A note on compact graphs. Discret. Appl. Math. 30(2), 253–264 (1991). https://doi.org/10.1016/0166-218X(91)90049-3
van Dam, E.R., Haemers, W.H.: Which graphs are determined by their spectrum? Linear Algebra Appl. 373, 241–272 (2003). https://doi.org/10.1016/S0024-3795(03)00483-X
Van Dam, E.R., Haemers, W.H., Koolen, J.H.: Cospectral graphs and the generalized adjacency matrix. Linear Algebra Appl. 423(1), 33–41 (2007). https://doi.org/10.1016/j.laa.2006.07.017
Weisfeiler, B.J., Lehman, A.A.: A reduction of a graph to a canonical form and an algebra arising during this reduction. Nauchno-Tech.Inform. 2(9), 12–16. https://www.iti.zcu.cz/wl2018/pdf/wl_paper_translation.pdf (1968)
Acknowledgments
The author is grateful to Joeri Rammelaere (and his Python skills) for computing the numerical quantities of the example graphs used in this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: Special Issue on Database Theory (ICDT 2019)
Guest Editor: Pablo Baceló
The original version of this article was revised due to the incorrect typesetting of mathematical formulas.
Appendices
Appendix
Proof of Lemma 5.1
Lemma 5.1
Let \(\mathsf {ML}({\mathscr{L}})\) be any matrix query language fragment and let G and H be graphs of the same order. Consider expressions e1(X) and e2(X) in \(\mathsf {ML}({\mathscr{L}})\). If ei(AG) and ei(AH) are T-similar, for i = 1, 2, for an arbitrary matrix T, then e1(AG) ⋅ e2(AG) is also T-similar to e1(AH) ⋅ e2(AH).
Proof
To show this lemma, we distinguish between the following cases, depending on the dimensions of e1(AG) and e2(AG) (or equivalently, the dimensions of e1(AH) and e2(AH)). Let e(X) := e1(X) ⋅ e2(X). Let n be the order of G (and H).
-
(n ×n,n ×n): e1(AG) and e2(AG) are of dimension n × n. By assumption, e1(AG) ⋅ T = T ⋅ e1(AH) and e2(AG) ⋅ T = T ⋅ e2(AH). Hence,
$$ \begin{array}{@{}rcl@{}} e(A_{G})\cdot T&=&e_{1}(A_{G})\cdot e_{2}(A_{G})\cdot T=e_{1}(A_{G})\cdot T\cdot e_{2}(A_{H})\\ &=&T\cdot e_{1}(A_{H})\cdot e_{2}(A_{H}) =T\cdot e(A_{H}). \end{array} $$ -
(n ×n,n ×1): e1(AG) is of dimension n × n and e2(AG) is of dimension n × 1. By assumption, e1(AG) ⋅ T = T ⋅ e1(AH) and e2(AG) = T ⋅ e2(AH). Hence,
$$ e(A_{G}) = e_{1}(A_{G})\cdot e_{2}(A_{G}) = e_{1}(A_{G})\cdot T\cdot e_{2}(A_{H}) = T\cdot e_{1}(A_{H})\cdot e_{2}(A_{H})=T\cdot e(A_{H}).$$ -
(n ×1,1 ×n): e1(AG) is of dimension n × 1 and e2(AG) is of dimension 1 × n. By assumption, e1(AG) = T ⋅ e1(AH) and e2(AG) ⋅ T = e2(AH). Hence,
$$ \begin{array}{@{}rcl@{}} e(A_{G})\cdot T&=&e_{1}(A_{G})\cdot e_{2}(A_{G})\cdot T =e_{1}(A_{G})\cdot e_{2}(A_{H})\\ &=& T\cdot e_{1}(A_{H})\cdot e_{2}(A_{H})=T\cdot e(A_{H}). \end{array} $$ -
(n ×1,1 ×1): e1(AG) is of dimension n × 1 and e2(AG) is of dimension 1 × 1. By assumption, e1(AG) = T ⋅ e1(AH) and e2(AG) = e2(AH). Hence,
$$ e(A_{G})=e_{1}(A_{G})\cdot e_{2}(A_{G})=e_{1}(A_{G})\cdot e_{2}(A_{H})=T\cdot e_{1}(A_{H})\cdot e_{2}(A_{H}) =T\cdot e(A_{H}).$$ -
(1 ×n,n ×n): e1(AG) is of dimension 1 × n and e2(AG) is of dimension n × n. By assumption, e1(AG) ⋅ T = e1(AH) and e2(AG) ⋅ T = T ⋅ e2(AH). Hence,
$$ e(A_{G})\cdot T = e_{1}(A_{G})\cdot e_{2}(A_{G})\cdot T = e_{1}(A_{H})\cdot T \cdot e_{2}(A_{H}) = e_{1}(A_{H})\cdot e_{2}(A_{H})=e(A_{H}).$$ -
(1 ×n,n ×1): e1(AG) is of dimension 1 × n and e2(AG) is of dimension n × 1. By assumption, e1(AG) ⋅ T = e1(AH) and e2(AG) = T ⋅ e2(AH). Hence,
$$ e(A_{G})=e_{1}(A_{G})\cdot e_{2}(A_{G})=e_{1}(A_{G})\cdot T\cdot e_{2}(A_{H})= e_{1}(A_{H})\cdot e_{2}(A_{H})=e(A_{H}).$$ -
(1 ×1,1 ×n): e1(AG) is of dimension 1 × 1 and e2(AG) is of dimension 1 × n. By assumption, e1(AG) = e1(AH) and e2(AG) ⋅ T = e2(AH). Hence,
$$ e(A_{G})\cdot T=e_{1}(A_{G})\cdot e_{2}(A_{G})\cdot T=e_{1}(A_{G})\cdot e_{2}(A_{H})=e_{1}(A_{G})\cdot e_{2}(A_{H})=e(A_{H}).$$ -
(1 ×1,1 ×1): e1(A) and e2(A) are of dimension 1 × 1. By assumption, e1(AG) = e1(AH) and e2(AG) = e2(AH). Hence, e(AG) = e1(AG) ⋅ e2(AG) = e1(AH) ⋅ e2(AH) = e(AH).
This concludes the proof. □
Continuation of the proofs of Proposition 7.2 and Theorems 8.1 and 9.1
In all three proofs we relied on the presence of addition and scalar multiplication to compute either equitable partitions or stable edge partitions. Since addition and scalar multiplication are used in the proofs before the proper conjugacy notion was identified, we cannot simply rely on Lemma 5.3. We therefore show that when \({\mathscr{L}}\) is either  (for Proposition 7.2),
(for Proposition 7.2),  (Theorem 8.1) or
(Theorem 8.1) or  (Theorem 9.1), that \(G\equiv _{\mathsf {ML}({\mathscr{L}})} H\) implies \(G\equiv _{\mathsf {ML}({\mathscr{L}}^{+})} H\), where \({\mathscr{L}}^{+}={\mathscr{L}}\cup \{+,\times \}\).
(Theorem 9.1), that \(G\equiv _{\mathsf {ML}({\mathscr{L}})} H\) implies \(G\equiv _{\mathsf {ML}({\mathscr{L}}^{+})} H\), where \({\mathscr{L}}^{+}={\mathscr{L}}\cup \{+,\times \}\).
We show this by verifying that any expression e(X) in \(\mathsf {ML}({\mathscr{L}}^{+})\) can be equivalently written as a linear combination of expressions in \(\mathsf {ML}({\mathscr{L}})\). We denote equivalence by ≡ and \(e(X)\equiv e^{\prime }(X)\) means that \(e(A)=e^{\prime }(A)\) for all matrices A. We verify our claim by induction on the structure of expressions.
(base case)
Let e(X) := X. This already has the desired form.
(matrix multiplication)
Let e(X) := e1(X) ⋅ e2(X). By induction we have that \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\) and \(e_{2}(X)\equiv {\sum }_{i=1}^{q} b_{i}\times {e_{i}^{2}}(X)\). Hence, \(e(X)\equiv {\sum }_{i=1}^{p}{\sum }_{j=1}^{q} (a_{i}\times b_{i}) \times ({e_{i}^{1}}(X)\cdot {e_{j}^{2}}(X)\)).
(complex conjugate transposition)
Let e(X) := (e1(X))∗. By induction, \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\). Then, \(e(X)\equiv {\sum }_{i=1}^{p} \bar {a}_{i}\times (e_{i}(X))^{*}\).
(trace)
Let e(X) := tr(e1(X)). By induction, \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\). Then, \(e(X)\equiv {\sum }_{i=1}^{p} a_{i}\times \mathsf {tr}(e_{i}(X))\).
(ones-vector)
Let  . By induction, \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\). Then,
. By induction, \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\). Then,  .
.
(diag)
Let e(X) := diag(e1(X)). By induction, \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\). Then, \(e(X)\equiv {\sum }_{i=1}^{p} a_{i}\times \textup {diag}({e_{i}^{1}}(X))\).
(pointwise vector product)
Let e(X) := e1(X) ⊙ve2(X). By induction we have that \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\) and \(e_{2}(X)\equiv {\sum }_{i=1}^{q} b_{i}\times {e_{i}^{2}}(X)\). Hence, \(e(X)\equiv {\sum }_{i=1}^{p}{\sum }_{j=1}^{q} (a_{i}\times b_{i}) \times ({e_{i}^{1}}(X)\odot _{v} {e_{j}^{2}}(X)\)).
(Schur-Hadamard) (pointwise vector product)
Let e(X) := e1(X) ⊙ e2(X). By induction we have that \(e_{1}(X)\equiv {\sum }_{i=1}^{p} a_{i}\times {e_{i}^{1}}(X)\) and \(e_{2}(X)\equiv {\sum }_{i=1}^{q} b_{i}\times {e_{i}^{2}}(X)\). Hence, \(e(X)\equiv {\sum }_{i=1}^{p}{\sum }_{j=1}^{q} (a_{i}\times b_{i}) \times ({e_{i}^{1}}(X)\odot {e_{j}^{2}}(X)\)).
This concludes the proof. \(\square \)
Proof of Proposition 7.4
Proposition 7.4
 , ×,Applys[f], f ∈Ω)-vectors are constant on equitable partitions.
, ×,Applys[f], f ∈Ω)-vectors are constant on equitable partitions.
Proof
Let \({\mathscr{L}}^{\#}\) denote  , ×,Applys[f], f ∈Ω}. Consider a graph G of order n with equitable partition \(\mathcal {V}=\{V_{1},\ldots ,V_{\ell }\}\). As before, let
, ×,Applys[f], f ∈Ω}. Consider a graph G of order n with equitable partition \(\mathcal {V}=\{V_{1},\ldots ,V_{\ell }\}\). As before, let  be the corresponding indicator vectors. We will show that for any expression \(e(X)\in \textsf {ML}({\mathscr{L}}^{\#})\) such that e(AG) is an n × 1-vector, e(AG) can be uniquely written in the form
be the corresponding indicator vectors. We will show that for any expression \(e(X)\in \textsf {ML}({\mathscr{L}}^{\#})\) such that e(AG) is an n × 1-vector, e(AG) can be uniquely written in the form  for scalars \(a_{i}\in \mathbb {C}\).
for scalars \(a_{i}\in \mathbb {C}\).
We show, by induction on the structure of expressions in \(\mathsf {ML}({\mathscr{L}}^{\#})\), that the following properties hold:
-
(a)
if e(AG) returns an n × n-matrix, then for any pair i, j = 1,…, ℓ there exists a scalars \(a_{ij}, b_{ij}\in \mathbb {C}\) such that
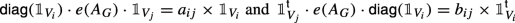
-
(b)
if e(AG) returns an n × 1-vector, then for any i = 1,…, ℓ, there exists a scalar ai ∈ C such that
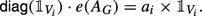
Clearly, if (b) holds for every i = 1,…, ℓ, then,  because
because  . We remark these properties can be seen as a generalisation of the known fact that the vector space spanned by indicator vectors of an equitable partition of G is invariant under multiplication by AG (See e.g., Lemma 5.2 in [16]). That is, for any linear combination
. We remark these properties can be seen as a generalisation of the known fact that the vector space spanned by indicator vectors of an equitable partition of G is invariant under multiplication by AG (See e.g., Lemma 5.2 in [16]). That is, for any linear combination  we have that
we have that  . In our setting, (a) and (b) imply that e(AG) ⋅ v is again a linear combination of indicator vectors, when e(AG) returns an n × n-matrix. We next verify properties (a) and (b). We often use that
. In our setting, (a) and (b) imply that e(AG) ⋅ v is again a linear combination of indicator vectors, when e(AG) returns an n × n-matrix. We next verify properties (a) and (b). We often use that  and
and  . □
. □
(base case)
Let e(X) := X. The required property is simply a restatement of the being equitable. That is,

for an arbitrary vertex v ∈ Vi. So, we can take aij = deg(v, Vj). Similarly, because AG is a symmetric matrix,

for an arbitrary vertex v ∈ Vi. So, we can take aij = deg(v, Vj).
Below, for condition (a) we only verify that  holds. The verification of
holds. The verification of  is entirely similar.
is entirely similar.
(multiplication)
Let e(X) := e1(X) ⋅ e2(X). We distinguish between a number of cases, depending on the dimensions of e1(AG) and e2(AG). We first check the cases when e(AG) returns an n × n-matrix and need to show that property (a) holds.
-
(n ×n,n ×n): e1(AG) and e2(AG) are of dimension n × n. By induction,
 and
and 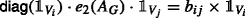 . Then,
. Then, 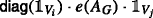 is equal to
is equal to
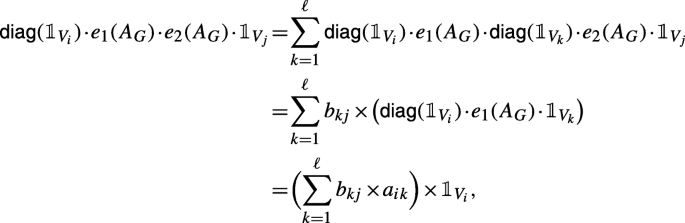
as desired.
-
(n ×1,1 ×n): e1(AG) is of dimension n × 1 and e2(AG) is of dimension 1 × n. By induction we have that
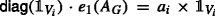 and
and 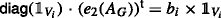 . Hence,
. Hence,  is equal to
is equal to
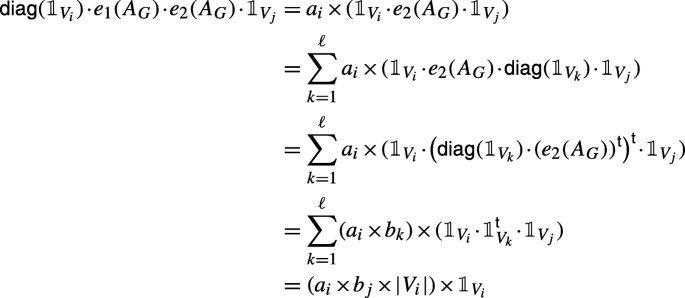
as desired. Here we used that
 is either 0, in case that k≠j, or |Vj| in case that j = k.
is either 0, in case that k≠j, or |Vj| in case that j = k.
We next check that condition (b) holds when e(AG) returns an n × 1-vector.
-
(n ×n,n ×1): e1(AG) is of dimension n × n and e2(AG) is of dimension n × 1. By induction, we have that
 and
and 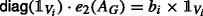 . Hence,
. Hence,  is equal to
is equal to
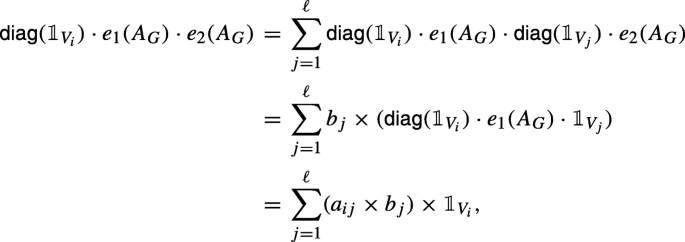
as desired.
-
(n ×1,1 ×1): e1(AG) is of dimension n × 1 and e2(AG) is of dimension 1 × 1. By induction we have that
 and \(e_{2}(A_{G})=b\in \mathbb {C}\). Hence,
and \(e_{2}(A_{G})=b\in \mathbb {C}\). Hence,
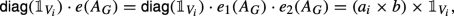
as desired.
(ones vector)
 . We only need to consider the case when e1(AG) is an n × n-matrix or n × 1-vector. In both cases, it suffices to observe that
. We only need to consider the case when e1(AG) is an n × n-matrix or n × 1-vector. In both cases, it suffices to observe that  . Indeed,
. Indeed,

(conjugate transpose)
e(X) := (e1(X))∗. If e1(AG) returns a 1 × n-vector, then  . Hence,
. Hence,  returns an n × n-matrix, then by induction,
returns an n × n-matrix, then by induction,  . Hence,
. Hence,

as desired.
(diag operation)
e(X) := diag(e1(X)) where e1(AG) is an n × 1-vector. By induction,  . Hence, in view of the linearity of the diagonal operation,
. Hence, in view of the linearity of the diagonal operation,

since  is
is  when k = j and the zero vector otherwise.
when k = j and the zero vector otherwise.
(addition)
e(X) := e1(X) + e2(X). Clearly, when condition (a) or (b) hold for e1(AG) and e2(AG), they remain to hold for e(AG).
(scalar multiplication)
e(X) := a × e1(X). Clearly, when condition (a) or (b) hold for e1(AG), they remain to hold for e(AG).
(trace)
e(X) := tr(e1(X)). Such sub-expressions do not return matrices or vectors.
(pointwise function applications)
\(e(X):=\textsf {Apply}_{\mathsf {s}}[f](e_{1}(X),\dots ,e_{p}(X))\) where each ei(X) is a sentence. Again, such sub-expressions do not return matrices or vectors.
Proof of Proposition 8.2
Proposition 8.2
 ,×,Applys[f], f ∈Ω)-vectors are constant on equitable partitions
,×,Applys[f], f ∈Ω)-vectors are constant on equitable partitions
Proof
Given that we verified this property for all operations except for ⊙v in the proof of Proposition 7.4, we only need to verify that ⊙v can be added to the list of supported operations. We use the same induction hypotheses as in the proof of Proposition 7.4 and verify that these hypotheses remain to hold for ⊙v: □
(pointwise vector multiplication)
e(X) := e1(X) ⊙ve2(X) where e1(X) and e2(X) return vectors. By induction we have that  and
and  . As a consequence,
. As a consequence,

because  is either
is either  when i = j, or the zero vector when i≠j.
when i = j, or the zero vector when i≠j.
Continuation of the proof of Theorem 8.1
In the proof in the main body of the paper we left open the verification that  , for i = 1,…, ℓ, implies that O preserves equitable partitions of G and H. In particular, we need to verify that
, for i = 1,…, ℓ, implies that O preserves equitable partitions of G and H. In particular, we need to verify that  , for i = 1,…, ℓ. This can be easily shown, just as in the proof of Theorem 7.2 (based on Lemma 4 in Thüne [67]), in which we verified that J ⋅ O = O ⋅ J implies that
, for i = 1,…, ℓ. This can be easily shown, just as in the proof of Theorem 7.2 (based on Lemma 4 in Thüne [67]), in which we verified that J ⋅ O = O ⋅ J implies that  .
.
First, we observe that  with
with  and
and  . In other words,
. In other words,  where
where  . Furthermore, because
. Furthermore, because  is a scalar,
is a scalar,  . We next show that α = ±ni. Indeed, since O is an orthogonal matrix
. We next show that α = ±ni. Indeed, since O is an orthogonal matrix

and thus \({\alpha _{i}^{2}}={n_{i}^{2}}\) or αi = ±ni. Hence,  . We note that
. We note that  . We now argue that either
. We now argue that either  for all i = 1,…, ℓ, or
for all i = 1,…, ℓ, or  for all i = 1,…, ℓ. Indeed, suppose that we have
for all i = 1,…, ℓ. Indeed, suppose that we have  for i ∈ K ⊂{1,…, ℓ} and
for i ∈ K ⊂{1,…, ℓ} and  for \(i\in \bar K=\{1,\ldots ,\ell \}\setminus K\), for some non-empty subset K of {1,…, ℓ}. Then
for \(i\in \bar K=\{1,\ldots ,\ell \}\setminus K\), for some non-empty subset K of {1,…, ℓ}. Then  and hence since
and hence since  and
and  ,
,

This contradicts that  . Hence, when
. Hence, when  for all i = 1,…, ℓ, O satisfies the desired property already. Otherwise, when
for all i = 1,…, ℓ, O satisfies the desired property already. Otherwise, when  for all i = 1,…, ℓ, we simply replace O by (− 1) × O to obtain that
for all i = 1,…, ℓ, we simply replace O by (− 1) × O to obtain that  . This rescaling does not impact that AG ⋅ O = O ⋅ AH and we can thus indeed conclude that O preserves equitable partitions of G and H.
. This rescaling does not impact that AG ⋅ O = O ⋅ AH and we can thus indeed conclude that O preserves equitable partitions of G and H.
Rights and permissions
About this article
Cite this article
Geerts, F. On the Expressive Power of Linear Algebra on Graphs. Theory Comput Syst 65, 179–239 (2021). https://doi.org/10.1007/s00224-020-09990-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-020-09990-9



 to denote the all-ones vector (of appropriate dimension) and use
to denote the all-ones vector (of appropriate dimension) and use  (with brackets) for the corresponding one-vector operation.
(with brackets) for the corresponding one-vector operation. when evaluated on given adjacency matrices.
when evaluated on given adjacency matrices.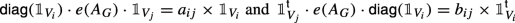
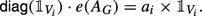
 and
and 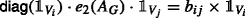 . Then,
. Then, 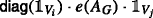 is equal to
is equal to
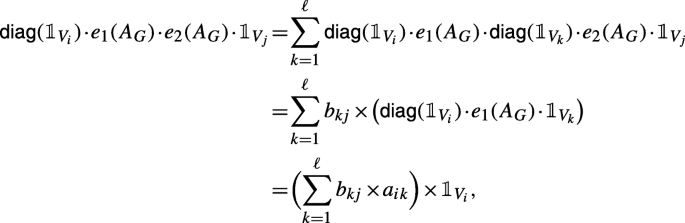
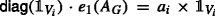 and
and 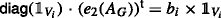 . Hence,
. Hence,  is equal to
is equal to
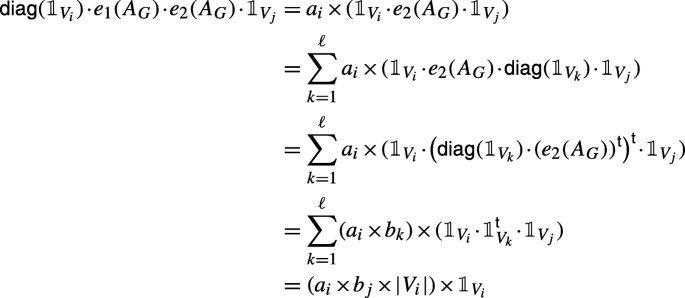
 is either 0, in case that k≠j, or |Vj| in case that j = k.
is either 0, in case that k≠j, or |Vj| in case that j = k. and
and 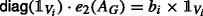 . Hence,
. Hence,  is equal to
is equal to
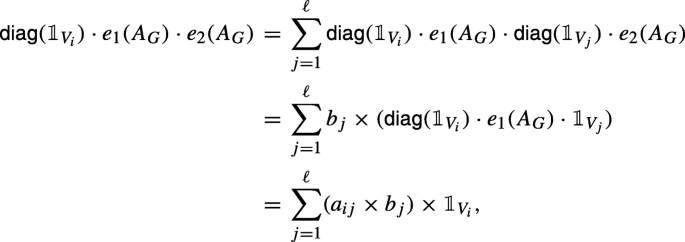
 and
and