Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T17:23:45.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit symmetric DGLA models of 3-cells

Part of: Applied homological algebra and category theory Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  01 July 2020

Itay Griniasty  and
Ruth Lawrence Open the ORCID record for Ruth Lawrence [Opens in a new window]
Itay Griniasty
Affiliation:
Laboratory of Atomic and Solid State Physics, Cornell University, Ithaca, NY14853 e-mail: ig324@cornell.edu
Ruth Lawrence*
Affiliation:
Einstein Institute of Mathematics, Hebrew University of Jerusalem, Jerusalem91904
*
e-mail: ruthel.naimark@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We give explicit formulae for differential graded Lie algebra (DGLA) models of 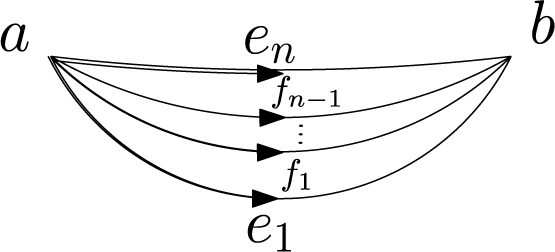$3$ -cells. In particular, for a cube and an 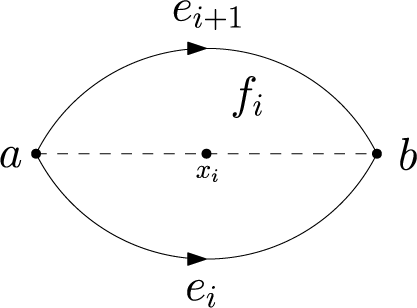$n$ -faceted banana-shaped 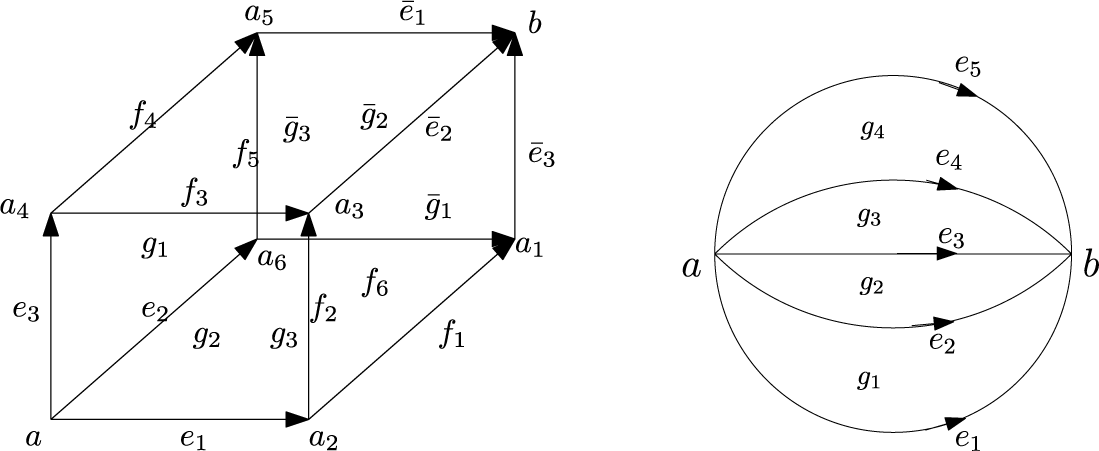$3$ -cell with two vertices, 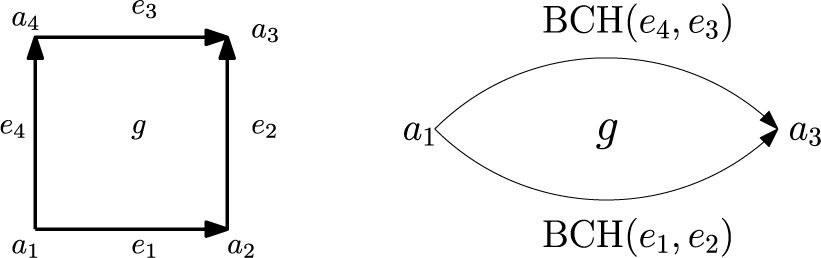$n$ edges each joining those two vertices, and 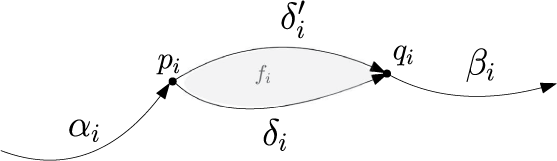$n$ bi-gon $2$ -cells, we construct a model symmetric under the geometric symmetries of the cell fixing two antipodal vertices. The cube model is to be used in forthcoming work for discrete analogues of differential geometry on cubulated manifolds.

Keywords

DGLAMaurer–CartanBaker–Campbell–Hausdorff formula

MSC classification

Primary: 17B55: Homological methods in Lie (super)algebras
Secondary: 17B01: Identities, free Lie (super)algebras 55U15: Chain complexes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 2 , June 2021 , pp. 368 - 382
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported in part by Grant No. 2016219. from the United States-Israel Binational Science Foundation (BSF). Griniasty is grateful to the Azrieli Foundation for the award of an Azrieli Fellowship.

References

Buijs, U., Félix, Y., Murillo, A., and Tanré, D., Lie models of simplicial sets and representability of the Quillen functor . Preprint, 2015. arxiv:1508.01442 Google Scholar
Buijs, U., Félix, Y., Murillo, A., and Tanré, D., Maurer-Cartan elements in the Lie models of finite simplicial complexes. Canad. Math. Bull. 60(2017), 470–477. http://dx.doi.org/10.4153/cmb-2017-003-7 CrossRefGoogle Scholar
Dynkin, E., Calculation of the coefficients in the Campbell-Hausdorff formula . Dokl. Akad. Nauk USSR (Russian) 57(1947), 323–326.Google Scholar
Eichler, M., A new proof of the Baker-Campbell-Hausdorff formula . J. Math. Soc. Jpn. 20(1968), 23–25. http://dx.doi.org/10.2969/jmsj/02010023 CrossRefGoogle Scholar
Gadish, N., A free differential Lie algebra model of the 2-cell. Bachelor's thesis, Hebrew University, Jerusalem, 2011.Google Scholar
Gadish, N., Griniasty, I., and Lawrence, R., An explicit symmetric DGLA model of a bi-gon . J. Knot Th. Ramif. 28(2019), 1940008. http://dx.doi.org/10.1142/s021821651940008x Google Scholar
Griniasty, I. and Lawrence, R., An explicit symmetric DGLA model of a triangle . High. Struct. 3(2019), 1–16. arxiv.org/abs/1802.02795 Google Scholar
Lawrence, R., Ranade, N., and Sullivan, D., Discrete analogues of differential geometry on cubulated manifolds. In preparation. Google Scholar
Lawrence, R. and Siboni, M., Universal averages in gauge actions. J. Lie Theory 31(2021), 351–366.Google Scholar
Lawrence, R. and Sullivan, D., A formula for topology/deformations and its significance . Fund. Math. 225(2014), 229–242. http://dx.doi.org/10.4064/fm225-1-10 CrossRefGoogle Scholar
Tradler, T. and Zeinalian, M., Infinity structure of Poincaré duality spaces . Algebr. Geom. Topol. 7(2007), 233–260. http://dx.doi.org/10.2140/agt.2007.7.233 CrossRefGoogle Scholar