Phenomenology of scotogenic scalar dark matter

Abstract

We reexamine the minimal Singlet $+$ Triplet Scotogenic Model, where dark matter is the mediator of neutrino mass generation. We assume it to be a scalar WIMP, whose stability follows from the same ${\mathbb {Z}}_{2}$ symmetry that leads to the radiative origin of neutrino masses. The scheme is the minimal one that allows for solar and atmospheric mass scales to be generated. We perform a full numerical analysis of the signatures expected at dark matter as well as collider experiments. We identify parameter regions where dark matter predictions agree with theoretical and experimental constraints, such as neutrino oscillations, Higgs data, dark matter relic abundance and direct detection searches. We also present forecasts for near future direct and indirect detection experiments. These will further probe the parameter space. Finally, we explore collider signatures associated with the mono-jet channel at the LHC, highlighting the existence of a viable light dark matter mass range.

1 Introduction

After the discovery of the Higgs boson, the particle physics community is eager to discover new phenomena, that would imply physics beyond the Standard Model (SM). Together with the evidence for dark matter, neutrino physics remains as the most solid indication of new physics. Neutrino experiments point towards two different neutrino mass squared differences, associated to solar and atmospheric oscillations. Hence, at least two of the three active neutrino species must be massive. Here we adopt the minimal picture in which one of the neutrinos is (nearly) massless. This is achieved in “missing partner” seesaw mechanisms [1] where one of the “left-handed” neutrinos fails to pair-off.¹ The presence of a massless neutrino has a very simple and clear implication concerning neutrinoless double beta ($0\nu 2 \beta$) decay.

Indeed, if the lightest neutrino is massless, there is only one physical Majorana phase, and the effective mass parameter characterizing the amplitude for $0\nu 2 \beta$ decay has a lower limit, even for a normal neutrino mass ordering, as currently preferred by oscillation data [3, 4]. This is in sharp contrast to the standard three-massive-neutrino-scenario in which there can be in general a destructive interference amongst the three light neutrinos (such cancellation in $0\nu 2 \beta$ decay may also be avoided in the three-massive-neutrino case in the presence of specific family symmetries [5,6,7]).

Our minimal scenario is a generalization of the scotogenic model initially proposed in [8]. The basic idea of this approach is that dark matter is the mediator of neutrino mass generation, and that the same ${\mathbb {Z}}_{2}$ symmetry that makes the neutrino mass to have radiative origin also serves to stabilize dark matter. We reexamine the Singlet + Triplet Scotogenic Model extension proposed in [9], which generalizes the original idea introduced in [8], making its phenomenology viable and substantially richer. The presence of Singlet and Triplet fermions in such a scotogenic model extension automatically leads to two oscillation lengths associated to solar and atmospheric oscillations, that can be traced to each of the dark fermion types, leaving a massless neutrino. Compared to the simple scotogenic model, the unwanted spontaneous breaking of the ${\mathbb {Z}}_{2}$ parity symmetry [10] can be naturally avoided due to the effect of the new couplings, as discussed in [11]. Two dark matter candidates can be envisaged within the scotogenic framework, either the lightest dark fermion or the isodoublet dark scalar boson. Either possibility corresponds to that of a weakly interacting massive particle (WIMP), produced thermally in the early Universe, similarly to the SM particles. Either will constitute what is called cold dark matter.

Following [12] here we focus on the case of scalar WIMP dark matter. The fermionic dark matter case mimics neutralino dark matter in supersymmetry [9] and has been recently re-visited in Refs. [13,14,15]. As we will see, scalar WIMP dark matter phenomenology in the Singlet + Triplet Scotogenic Model provides a rich scenario, sharing common features with other dark matter models such as the Inert Higgs Doublet Model [16,17,18,19,20] and with discrete dark matter models [21, 22]. In this paper we build upon previous analyses, expanding them by including a more detailed phenomenological study of the scalar dark matter candidate. From the dark matter point of view our work contains many new improvements. The updated experimental constraints, in particular from dark matter direct detection experiments like XENON-1T, cut out a relevant region of the parameter space especially in the mass range around and above 100 GeV. Then we present a novel analysis of indirect probes via $\gamma$ rays. Here we compare both current as well as future $\gamma$-ray telescopes. Finally, we perform a new collider study focusing on the ${\not \!\!E}_{T}+$ jet (mono-jet) signal, with relevant implications for future Large Hadron Collider (LHC) searches with higher luminosity. Moreover, we stress an interesting feature of this scenario for neutrinoless double beta decay facilities, namely the existence of a lower bound that holds even for normal neutrino mass ordering. This is very promising for the upcoming experiments. While this feature is generic to any theory in which one of the light neutrinos is massless, we stress that it comes automatically in this model, allowing for a testable connection between neutrino physics and dark matter.

The paper is organised as follows. In Sect. 2 we introduce the model, detailing the new fields and new interactions present. We describe in detail the scalar and fermionic sector, as well as the radiative neutrino mass generation, emphasizing that the lightest neutrino is massless and discussing the resulting lower bound for neutrinoless double beta decay.

Section 3 describes the numerical analysis used to study the dark matter sector of the model, listing the main constraints included. Here we have assumed that the dark matter is a scalar particle. In Sect. 4 we present the main results concerning the relic scalar dark matter density, direct and indirect detection. In Sect. 5 we deal with the implications for the LHC searches, taking into account the main results of the previous section. We focus on the ${\not \!\!E}_{T}+$ jet (mono-jet) signal. Finally, we give our conclusions in Sect. 6.

2 The Singlet + Triplet scotogenic model

In this section we will review the Singlet $+$ Triplet Scotogenic Model. This generalization of the scotogenic model [8] was proposed in [9] and further studied in several papers [11,12,13,14]. In addition to the SM gauge symmetry there is a discrete ${\mathbb {Z}}_{2}$ symmetry, whose role is to make the lightest ${\mathbb {Z}}_{2}$-odd or “dark” particle stable and to ensure the radiative generation of neutrino masses. The SM particle content is augmented by the inclusion of a Majorana fermion triplet $\Sigma$ and a Majorana fermion singlet F, both odd under the ${\mathbb {Z}}_{2}$ symmetry. Moreover, the model includes a new scalar doublet $\eta$ – odd under the ${\mathbb {Z}}_{2}$ symmetry, which does not acquire a vacuum expectation value (VEV) – and a triplet scalar $\Omega$, which allows for the mixing of the neutral parts of the new fermions. This triplet scalar field has a zero hypercharge and it is even under the ${\mathbb {Z}}_{2}$ symmetry, thus, its neutral component can acquire a nonzero VEV. The full particle content of the model is given in Table 1, with the corresponding charge assignment under the different symmetry groups.

Table 1 Particle content and quantum numbers of the Singlet + Triplet Scotogenic Model. The charge assignments of the fields under the global Lepton Number symmetry ($\mathrm L$) are also shown

Taking into account the new fields and symmetries of the model, the relevant terms of the Lagrangian read

$$\begin{aligned}&{\mathcal {L}} \subset -Y^{\alpha \beta } L_\alpha e_\beta \phi -Y_{F}^{\alpha }(\bar{L}_{\alpha }\tilde{\eta })F- Y^{\alpha }_{\Sigma }\bar{L}_{\alpha }^{c}\Sigma ^{\dag }\tilde{\eta }\nonumber \\&\qquad -Y_{\Omega } \mathrm{Tr} [\bar{\Sigma }\Omega ]F \nonumber \\&\qquad - \frac{1}{2} M_{\Sigma } \mathrm{Tr} (\overline{\Sigma }^{c} \Sigma ) - \frac{M_F}{2} \overline{F^{c}} F + h.c. \end{aligned}$$

(1)

where $\tilde{\eta }=i\sigma _2 \eta ^{*}$. The first Yukawa term $Y^{\alpha \beta }$ is the Standard Model interaction for leptons, which we can assume to be diagonal in flavor (Greek indices stand for family indices).

2.1 Scalar sector

The scalar potential ${\mathcal {V}}$ invariant under the SU(2)$\times$U(1)$\times {\mathbb {Z}}_{2}$ symmetry is

$$\begin{aligned} {\mathcal {V}}= & {} -m_{\phi }^2\phi ^{\dag }\phi +m_{\eta }^{2}\eta ^{\dag }\eta -\frac{m_{\Omega }^{2}}{2}\mathrm{Tr} (\Omega ^{\dag }\Omega ) \nonumber \\&+ \frac{\lambda _1}{2}(\phi ^{\dag }\phi )^{2}+\frac{\lambda _2}{2} (\eta ^{\dag }\eta )^{2}+\frac{\lambda _3}{2}(\phi ^{\dag }\phi ) (\eta ^{\dag }\eta ) \nonumber \\&+\lambda _{4}(\phi ^{\dag }\eta ) (\eta ^{\dag }\phi )+\frac{\lambda _5}{2}[(\phi ^{\dag }\eta )^2 +(\eta ^{\dag }\phi )^2 ]\nonumber \\&+ \mu _{1}\phi ^{\dag }\Omega \phi + \mu _{2}\eta ^{\dag }\Omega \eta \nonumber \\&+\frac{\lambda _{1}^{\Omega }}{2}(\phi ^{\dag }\phi ) \mathrm{Tr} (\Omega ^{\dag }\Omega ) +\frac{\lambda _{2}^{\Omega }}{4} [ \mathrm{Tr}(\Omega ^{\dag }\Omega ) ]^2\nonumber \\&+\frac{\lambda _{\eta }^{\Omega }}{2}(\eta ^{\dag }\eta ) \mathrm{Tr} (\Omega ^{\dag }\Omega ), \end{aligned}$$

(2)

where we make the conservative assumption that $m_{\phi }^2, m_{\eta }^2$ and $m_{\Omega }^2$ are all positive, so that the spontaneous electroweak symmetry breaking will be driven by $\phi$ and (sub-dominantly) by the neutral component of $\Omega$, while $\eta$ cannot acquire a VEV. Notice that we are using the standard $2 \times 2$ matrix notation for the $\mathrm SU(2)_L$ triplets:

$$\begin{aligned} \Sigma = \left( \begin{array}{cc} \frac{\Sigma ^0}{\sqrt{2}} &{}\quad \Sigma ^+ \\ \Sigma ^- &{}\quad -\frac{\Sigma ^0}{\sqrt{2}} \end{array} \right) \, , \quad \Omega =\left( \begin{array}{cc} \frac{\Omega ^0}{\sqrt{2}} &{}\quad \Omega ^+ \\ \Omega ^- &{}\quad -\frac{\Omega ^0}{\sqrt{2}} \end{array} \right) . \end{aligned}$$

(3)

The other couplings appearing in Eq. (2) are constrained by a number of theoretical considerations. First, they must comply with the condition that the potential is bounded from below in order to have a stable minimum. This requirement leads to the following conditions [11, 12]

$$\begin{aligned}&\lambda _{1}\ge 0,\quad \lambda _{2}\ge 0,\quad \lambda _{2}^{\Omega }\ge 0, \end{aligned}$$

(4)

$$\begin{aligned}&\lambda _{3}+\sqrt{\lambda _{1}\lambda _{2}}\ge 0, \quad \lambda _{3}+\lambda _{4}-|\lambda _{5}|+\sqrt{\lambda _{1}\lambda _{2}}\ge 0, \end{aligned}$$

(5)

$$\begin{aligned}&\lambda _{1}^{\Omega }+\sqrt{2\lambda _{1}\lambda _{2}^{\Omega }}\ge 0, \quad \lambda _{\eta }^{\Omega }+\sqrt{2\lambda _{2}\lambda _{2}^{\Omega }}\ge 0, \end{aligned}$$

(6)

$$\begin{aligned}&\sqrt{2\lambda _{1}\lambda _{2}\lambda _{2}^{\Omega }}+\lambda _{3} \sqrt{2\lambda _{2}^{\Omega }}+\lambda _{1}^{\Omega }\sqrt{\lambda _{2}} +\lambda _{\eta }^{\Omega }\sqrt{\lambda _{1}}\nonumber \\&\, +\sqrt{\left( \lambda _{3} \!+\!\sqrt{\lambda _{1}\lambda _{2}}\right) \left( \lambda _{1}^{\Omega } \!+\!2\sqrt{\lambda _{1}\lambda _{2}^{\Omega }}\right) \left( \lambda _{\eta }^{\Omega }\!+\!\sqrt{\lambda _{2}\lambda _{2}^{\Omega }}\right) }\!\ge \! 0.\nonumber \\ \end{aligned}$$

(7)

It is worth noticing that while these conditions ensure that ${\mathcal {V}}$ is consistently bounded from below at the electroweak scale, the running of the RGEs may lead to breaking of the ${\mathbb {Z}}_{2}$ symmetry at some higher energy scale. Another theory restriction comes from the requirement that the expansion of the potential ${\mathcal {V}}$ around its minimum must be perturbatively valid. In order to ensure this we require that the scalar quartic couplings in Eq. (2) are $\lesssim 1$.

As mentioned before, $\eta$ does not acquire a VEV and therefore the symmetry breaking is driven only by $\phi$ and $\Omega$, which have non-zero VEVs:

$$\begin{aligned} \langle \phi ^0 \rangle = v_\phi ,~~~~\langle \Omega ^0 \rangle = v_\Omega \end{aligned}$$

(8)

The fields $\eta$, $\phi$ and $\Omega$ are written as follows

$$\begin{aligned}&\eta =\left( \begin{array}{c} \eta ^{+} \\ (\eta _{R}+i\eta _{I})/\sqrt{2} \end{array}\right) , ~~ \phi =\left( \begin{array}{c} \varphi ^{+} \\ (h_{0}+v_{\phi }+i\psi )/\sqrt{2} \end{array}\right) ,\nonumber \\&\Omega =\left( \begin{array}{cc} (\Omega _{0}+v_{\Omega })/\sqrt{2} &{}\quad \Omega ^{+} \\ \Omega ^{-} &{}\quad -(\Omega _{0}+v_{\Omega })/\sqrt{2} \end{array}\right) , \end{aligned}$$

(9)

where $\Omega _{0}$ is real and does not contribute to the CP-odd scalar sector. After symmetry breaking there are three charged scalar fields (only two of which are physical, since one is absorbed by the W boson), plus three CP-even neutral fields, and one physical CP-odd neutral field (since the other is absorbed by the Z boson). The VEVs in Eq. (8) are restricted by the following tadpole equations or minimization conditions

$$\begin{aligned} \frac{\partial {\mathcal {V}}}{\partial \phi }= & {} v_{\phi } \left( -m_{\phi }^{2}+\frac{1}{2}\lambda _{1}v_{\phi }^{2} -\frac{\mu _1}{2} v_{\Omega } + \frac{\lambda _1^\Omega }{4} v_\Omega ^2 \right) = 0,\nonumber \\ \frac{\partial {\mathcal {V}}}{\partial \Omega }= & {} - 2m_{\Omega }^{2}v_{\Omega } +\lambda _{2}^{\Omega }v_{\Omega }^3 + v_{\phi }^{2} \left( \lambda _{1}^{\Omega } v_{\Omega } -\mu _1\right) = 0, \end{aligned}$$

(10)

which we solve for $m_{\phi }^{2}$ and $m_{\Omega }^{2}$.

As for the neutral sector, the mass matrix of the CP-even (and ${\mathbb {Z}}_{2}$-even) neutral scalars in the basis $(\phi _{0}, \Omega _{0})$ reads

$$\begin{aligned} {\mathcal {M}}^2_{h} = \left( \begin{array}{cc} \Big (- m_\phi ^2 + \frac{3}{2} \lambda _1 v_\phi ^{2} + v_\Omega \Big (- \mu _1 + \frac{\lambda ^\Omega _1}{4} v_\Omega \Big )\Big ) &{}\quad \frac{1}{2} v \Big (\lambda ^\Omega _1 v_\Omega - 2\mu _1 \Big )\\ \frac{1}{2} v_\phi \Big (\lambda ^\Omega _1 v_\Omega - 2\mu _1 \Big ) &{}\quad \Big (-\frac{1}{2} m_\Omega ^2 + \frac{3}{4} \lambda ^\Omega _2 v_{\Omega }^{2} + \frac{1}{4} \lambda ^\Omega _1 v_\phi ^{2} \Big ) \end{array}\right) . \end{aligned}$$

(11)

The lightest of the neutral scalar mass eigenstates is identified with the SM Higgs boson, $h^0$ with mass $\sim 125\ \hbox {GeV}$, while the second state, H is a heavier neutral scalar.

On the other hand, the mass matrix for the charged scalars is given as

$$\begin{aligned} {\mathcal {M}}^2_{H^\pm } =\left( \begin{array}{cc} \frac{1}{4} \Big (2 \lambda _1 v_\phi ^{2} -4 m_\phi ^2 + v_\Omega \Big (2 \mu _1 + \lambda ^\Omega _1 v_\Omega \Big )\Big ) &{}\quad \frac{\mu _1 v_\phi }{\sqrt{2}} \\ \frac{\mu _1 v_\phi }{\sqrt{2}} &{}\quad \frac{1}{2} \Big (-2 m_\Omega ^2 + \lambda ^\Omega _1 v_\phi ^{2} + \lambda ^\Omega _2 v_\Omega ^{2} \Big ) \end{array}\right) . \end{aligned}$$

(12)

Note that, while the Z boson gets its longitudinal component only from the Higgs doublet $\phi$ and not from the triplet (because $\Omega ^{0}$ is real), the charged Goldstone boson is instead a linear combination of $\phi ^{+}$ and $\Omega ^{+}$. The VEV of $\Omega$ will then contribute to the W boson mass, thus leading to an upper limit $v_\Omega \lesssim 5\ \hbox {GeV}$ [23, 24]:

$$\begin{aligned} m_Z^2= & {} \frac{1}{4} (g^2 + g'^2 ) v_\phi ^2 \, , \nonumber \\ m_W^2= & {} \frac{1}{4} \, g^2 ( v_\phi ^2 + 4 \, v_\Omega ^2 ). \end{aligned}$$

(13)

The mass of the new charged scalar bosons will be

$$\begin{aligned} m_{H^\pm }^{2}= & {} \mu _{1}\frac{(v^{2}_{\phi }+2v^{2}_{\Omega })}{2v_{\Omega }}, \end{aligned}$$

(14)

$$\begin{aligned} m_{\eta ^{\pm }}^{2}= & {} m_{\eta }^{2}+\frac{1}{2}\lambda _{3}v_{\phi }^{2} +\frac{1}{\sqrt{2}}\mu _{2}v_{\Omega }+ \frac{1}{2} \lambda _{\eta }^{\Omega } v_{\Omega }^{2}. \end{aligned}$$

(15)

Because of the conservation of the ${\mathbb {Z}}_{2}$ symmetry, the ${\mathbb {Z}}_{2}$-odd scalar field $\eta$ does not mix with any other scalar. It proves convenient to write it in terms of its CP-even and CP-odd components:

$$\begin{aligned} \eta ^0 = \frac{(\eta _{R}+i\eta _{I})}{\sqrt{2}}. \end{aligned}$$

The physical masses of the neutral $\eta$ field are easily determined as

$$\begin{aligned} m_{\eta _{R}}^{2}= & {} m_{\eta }^{2}+\frac{1}{2}(\lambda _{3}+\lambda _{4} +\lambda _{5})v_{\phi }^{2}+\frac{1}{2}\lambda _{\eta }^{\Omega } v_{\Omega }^{2} -\frac{1}{\sqrt{2}}\mu _{2}v_{\Omega }, \nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned} m_{\eta _{I}}^{2}= & {} m_{\eta }^{2}+\frac{1}{2}(\lambda _{3}+\lambda _{4} -\lambda _{5})v_{\phi }^{2}+\frac{1}{2}\lambda _{\eta }^{\Omega } v_{\Omega }^{2} -\frac{1}{\sqrt{2}}\mu _{2}v_{\Omega }.\nonumber \\ \end{aligned}$$

(17)

The difference $m_{\eta _{R}}^{2} -m_{\eta _{I}}^{2}$ depends only on the parameter $\lambda _{5}$ which, as we shall see in the next paragraph, is also responsible for the smallness of neutrino masses. In the limit $\lambda _{5} \rightarrow 0$ lepton number conservation is restored. Hence, by construction, neutrino masses are “natural”, in ’t Hooft’s sense [25], i.e. they are “symmetry-protected”. Moreover, the ${\mathbb {Z}}_{2}$ symmetry conservation also makes the lightest of the two eigenstates $\eta _{R,I}$ a viable dark matter candidate, as we will discuss in detail in Sect. 4.

2.2 Fermionic sector

Concerning the fermionic sector, the new triplet scalar $\Omega$ allows for a mixing between the singlet and triplet fermion fields – F and $\Sigma$ – through the Yukawa coupling $Y_\Omega$, as shown in Eq. (1): The mass matrix for the new fermions, in the basis $(\Sigma _{0},F)$ is given as

$$\begin{aligned} {\mathcal {M}}_{\chi }=\left( \begin{array}{cc} M_\Sigma &{}\quad \frac{1}{\sqrt{2}}Y_{\Omega }v_{\Omega }\\ \frac{1}{\sqrt{2}}Y_{\Omega }v_{\Omega } &{}\quad M_{F} \end{array}\right) . \end{aligned}$$

(18)

When the neutral part of $\Omega$ acquires a VEV $v_{\Omega } \ne 0$, the diagonalization of the mass matrix Eq. (18) leads to eigenstates with the following masses (at tree level):

$$\begin{aligned} m_{\chi }^{\pm }= & {} M_{\Sigma }, \end{aligned}$$

(19)

$$\begin{aligned} m_{\chi _{1}^{0}}= & {} \frac{1}{2}\left( M_{\Sigma }+M_{F} -\sqrt{\left( M_{\Sigma }-M_{F}\right) ^{2}+4(2Y_{\Omega }v_{\Omega })^2}\right) , \nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} m_{\chi _{2}^{0}}= & {} \frac{1}{2}\left( M_{\Sigma }+M_{F}+\sqrt{\left( M_{\Sigma } -M_{F}\right) ^{2}+4(2Y_{\Omega }v_{\Omega })^2}\right) ,\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} \tan (2\theta )= & {} \frac{4Y_{\Omega }v_{\Omega }}{M_{\Sigma }-M_{F}}, \end{aligned}$$

(22)

where $\theta$ is the mixing angle between the neutral fermion triplet $\Sigma _{0}$ and F, $M_{\Sigma }$ and $M_F$ are the Majorana mass terms for the triplet and the singlet, respectively. Although we will not consider this case here, it is interesting to notice that the lightest neutral eigenstate, $\chi _{1}^{0}$ or $\chi _{2}^{0}$ may also play the role of the dark matter [9], for more recent analyses see [13, 14].

2.3 Neutrino masses

The previous subsection has been dedicated to the spectrum of the new fermions. Let us now comment on neutrino masses. By construction, in the scotogenic approach, the dark matter candidate acts as a messenger for neutrino mass generation. Since the ${\mathbb {Z}}_{2}$ symmetry is exact, all vertices including new particles must contain an even number of ${\mathbb {Z}}_{2}$-odd fields. For this reason neutrinos cannot acquire a tree-level mass term, their masses arising only at the loop level as portrayed in Fig. 1.

Fig. 1

“Scotogenic” neutrino masses. After electroweak symmetry breaking the SM-like Higgs acquires a VEV $\left\langle {\phi _0}\right\rangle$

The relevant interactions for the generation of neutrino masses arise from Eqs. (1) and (2). The expression for the neutrino mass matrix is [9, 11, 12]

$$\begin{aligned} {\mathcal {M}}_{\alpha \beta }^{\nu }= & {} \sum \limits _{\sigma =1,2} \frac{Y^\nu _{\alpha \sigma }Y^\nu _{\beta \sigma }}{32\pi ^2} {\mathcal {I}}_\sigma \left( m_{\chi _\sigma }^2,m_{\eta _R}^2,m_{\eta _I}^2\right) \nonumber \\= & {} \sum \limits _{\sigma =1,2}\frac{Y^\nu _{\alpha \sigma }Y^\nu _{\beta \sigma }}{32\pi ^2} m_{\chi _\sigma }\nonumber \\&\left( \frac{m_{\eta _R}^2}{m_{\eta _R}^2-m_{\chi _\sigma }^2} \ln \left( \frac{m_{\eta _R}^2}{m_{\chi _\sigma }^2}\right) -\frac{m_{\eta _I}^2}{m_{\eta _I}^2-m_{\chi _\sigma }^2}\ln \left( \frac{m_{\eta _I}^2}{m_{\chi _\sigma }^2}\right) \right) ,\nonumber \\ \end{aligned}$$

(23)

where $\alpha$ and $\beta$ are generation indices ($\alpha ,\beta =1,2,3$), $m_{\chi _\sigma }$ are the masses of the $\chi ^{0}_{1,2}$ fermion fields and $Y^\nu _{\alpha \beta }$ are the new neutrino Yukawa couplings introduced as a $3\times 2$ matrix,²

$$\begin{aligned} Y^\nu= & {} \begin{pmatrix} Y_{\Sigma }^1 &{}\quad Y_{F}^1\\ Y_{\Sigma }^2 &{}\quad Y_{F}^2\\ Y_{\Sigma }^3 &{}\quad Y_{F}^3 \end{pmatrix} \cdot V(\theta ). \end{aligned}$$

(24)

The matrix $V(\theta )$ is a $2 \times 2$ orthogonal matrix that diagonalizes the fermionic mass matrix ${\mathcal {M}}_\chi$ given in Eq. (18). As already noticed before, in the limit $\lambda _5 \rightarrow 0$ the two eigenstates $m_{\eta _R}$ and $m_{\eta _I}$ are degenerate, hence neutrino masses are zero and the lepton number symmetry is restored. This limit would correspond to an exact cancellation between the $\eta _R$ and $\eta _I$ loops. The expression ${\mathcal {I}}_\sigma (m_{\chi _\sigma }^2,m_{\eta _R}^2, m_{\eta _I}^2)$ in Eq. (23) involves differences of Passarino–Veltman functions $B_0$ [26], evaluated in the limit of vanishing external momentum.

We can then rewrite Eq. (23) more compactly as:

$$\begin{aligned} {\mathcal {M}}_{\alpha \beta }^{\nu } = Y^\nu _{\alpha \beta } v_{\phi } \cdot \frac{{\mathcal {F}}}{v_{\phi }^{2}}\cdot Y^{\nu , T}_{\alpha \beta } v_{\phi }\sim m_{D}\frac{1}{M_{R}}m_{D}^{T}, \end{aligned}$$

(25)

where

$$\begin{aligned} {\mathcal {F}} = \left( \begin{array}{cc} \frac{{\mathcal {I}}_1}{32 \pi ^2 } &{}\quad 0 \\ 0 &{}\quad \frac{{\mathcal {I}}_2}{32 \pi ^2 } \end{array} \right) \, . \end{aligned}$$

(26)

This recalls the structure of the standard type-I seesaw neutrino mass relation, with the Dirac mass term given by $Y^\nu _{\alpha \beta } v_{\phi }$ and $M_{R}^{-1} =\frac{{\mathcal {F}}}{v_{\phi }^{2}}$ where ${\mathcal {F}}$ includes the loop functions. In order to compare with the current determination of neutrino oscillation parameters [3], we will apply a Casas–Ibarra parametrization [27]:

$$\begin{aligned} Y^\nu _{\alpha \beta } =U_{\nu }\sqrt{m_{\nu }}\rho \sqrt{{\mathcal {F}}}^{-1}, \end{aligned}$$

(27)

where $U_{\nu }$ is the lepton mixing matrix, $m_{\nu }$ are the neutrino masses (whose squared differences are constrained as in [3]) and the matrix $\rho$ is an arbitrary $2\times 3$ rotation matrix that can be parametrized as [9]

$$\begin{aligned} \rho= & {} \begin{pmatrix} 0 &{}\quad \mathrm{cos}(\beta ) &{}\quad \pm \mathrm{sin}(\beta )\\ 0 &{} \quad -\mathrm{sin}(\beta ) &{} \quad \pm \mathrm{cos}(\beta ) \end{pmatrix}. \end{aligned}$$

(28)

An interesting prediction of this model is that the lightest neutrino is massless. This feature is reminiscent of the “missing partner” nature of this “radiative” seesaw mechanism, in which one of the “right-handed” fermions is missing (there is only one $\Sigma$ and one F). As a consequence one of the “left” neutrinos can not pair-off and hence remains massless [1].

2.4 Neutrinoless double beta decay

Within the symmetrical parametrisation of the lepton mixing matrix [1] the $0\nu 2 \beta$ effective mass parameter can be neatly expressed as [28]

$$\begin{aligned} \left\langle {m_{ee}}\right\rangle&=\left| \sum _jU_{\nu , ej}^2m_j\right| \nonumber \\&=\left| \mathrm{cos}\theta _{12}^2 \mathrm{cos}\theta _{13}^2 m_1+ \mathrm{sin}\theta _{12}^2 \mathrm{cos}\theta _{13}^2 m_2e^{2i\phi _{12}}\right. \nonumber \\&\quad \left. + \mathrm{sin}\theta _{13}^2 m_3e^{2i\phi _{13}}\right| , \end{aligned}$$

(29)

where $m_i$ are the three neutrino masses and $\theta _{1x}$ are the neutrino mixing angles measured in oscillation experiments. Note that in our case the lightest neutrino is massless ($m_1 = 0$), so that there is only one physical Majorana phase ($\phi \equiv \phi _{12} - \phi _{13}$). Since there is currently no restriction on its value, this phase is a free parameter. Except for this, all other parameters are well measured in oscillation experiments.

We show in Fig. 2 the dependence of $\left\langle {m_{ee}}\right\rangle$ on this phase. One sees that, in contrast to the general case where the three active Majorana neutrinos are massive, here the effective mass parameter describing the $0\nu 2 \beta$ decay amplitude has a lower limit [29, 30].

The pink (light green) band refers to the $3\sigma$ C.L. region allowed by current oscillation experiments [3] for normal (inverted) mass ordering. The black lines correspond to the best fit values for both cases. We also show for comparison the 90% C.L. upper limits (shaded regions) from different experiments: CUORE ($\langle {m_{\beta \beta }}\rangle <110{-}520$ meV) [31], EXO-200 Phase II (147–398 meV) [32], GERDA Phase II (120–260 meV) [33] and KamLAND-Zen (61–165 meV) [34] experiments. The width of these bands is mainly a reflection of the uncertainty in the relevant nuclear matrix elements. The black dashed lines represent the most optimistic future sensitivities for SNO+ Phase II (19–46 meV) [35], LEGEND (15–50 meV) [36] and nEXO after 10 years of data taking (5.7–17.7 meV) [37].

Fig. 2

Effective $0\nu 2 \beta$ Majorana mass parameter versus the Majorana phase. The pink (light green) band represents the prediction for the $3\sigma$ C.L. region allowed by current oscillation experiments for normal (inverted) mass ordering

3 Numerical analysis

We now confront the model with current (and future) observations associated both with the primordial cosmological abundance of dark matter, as well as various phenomenological constraints, including the experimental prospects for direct and indirect dark matter detection.

3.1 Parameter scan

We have developed a numerical code using Python, to perform a scan varying randomly the main free parameters which characterize the model. This code is connected to some public computer tools used in particle physics in order to examine the constraints on the model parameters and also quantify the expected sensitivities of future experiments. In particular, our Singlet + Triplet Scotogenic Model is first implemented in SARAH 4.9.1 [38, 39], which calculates all vertices, mass matrices, tadpole equations, one-loop corrections for tadpoles and self-energies. The physical particle spectrum and low-energy observables are computed with SPheno 4.0.3 [40, 41] and FlavorKit [42]. In order to perform the dark matter analysis, we use Micromegas 5.0.2 [43] to compute the thermal component to the dark matter relic abundance as well as the dark matter-nucleon scattering cross sections. For the calculation of the cross sections relevant for the collider analysis, we have used MadGraph5 [44], importing the UFO files generated with SARAH 4.9.1. Our numerical scan was performed with 60,000 points, varying the input parameters as given in Table 2, assuming logarithmic steps. In particular, in the ranges of variation for the values of $m_{\eta }^{2}$ and $|\lambda _5|$, the lower limits considered were 100 $\mathrm GeV^2$ and $10^{-5}$ respectively, to ensure good behaviour for the ${\mathbb {Z}}_{2}$ symmetry [11].

Table 2 Ranges of variation of the input parameters used in the numerical scan

This model has in principle three potentially viable dark matter candidates: $\eta _R$, $\eta _I$ or $\chi _0$. In the following we will fix $\lambda _5 < 0$ so as to ensure $\eta _{R}$ to be the dark matter candidate. This choice is made for definiteness, having in mind that the opposite case with $\lambda _5 > 0$ and $\eta _{I}$ as the lightest neutral scalar would also be potentially viable. Notice that the parameters that are not shown in the table are calculated from the ones displayed. For example, $m_{\phi }^{2}$ and $m_{\Omega }^{2}$ are obtained from the tadpole equations (10) and $Y^\nu _{\alpha \beta }$ is calculated via Eq. (27). Note that the smallness of neutrino masses does not preclude these Yukawas from being sizeable, since the neutrino masses are controlled by $\lambda _5$ and they are further suppressed by their radiative origin.

3.2 Constraints

The presence of new particles, absent in the Standard Model, will induce departures from the SM predictions for a number of observables. Throughout our analysis, we take into account the following constraints.

a. Theoretical constraints As already discussed in Sect. 2, the coupling and mass parameters appearing in the Lagrangian Eq. (1) are subject to several theoretical constraints. First of all, we must ensure that the scalar potential is bounded from below, which we do by applying the conditions summarised in Eqs. (4567). Moreover we must ensure the perturbativity of the couplings, i.e. the scalar quartic couplings are assumed to be $\lesssim {\mathcal {O}} (1)$. Another theoretical consideration concerns the validity of the ${\mathbb {Z}}_{2}$ parity symmetry which is an essential ingredient of this model. Its role is indeed twofold: it stabilises the dark matter candidate $\eta _R$ and it justifies the one-loop radiative seesaw mechanism which gives mass to neutrinos. Compared to the simple scotogenic model initially proposed in [8], the spontaneous breaking of the ${\mathbb {Z}}_{2}$ parity symmetry can be naturally avoided in this extension thanks to the effect on the running of the couplings in the scalar sector induced by the inclusion of ${\mathbb {Z}}_{2}$-even scalar triplets. Nevertheless, even if the scalar potential is ${\mathbb {Z}}_{2}$-preserving at the electroweak scale, the RGEs running could lead to situations where the ${\mathbb {Z}}_{2}$ is broken at some higher energy scale [11].³ While a dedicated analysis of the RGE running is beyond the scope of the present work, we have not ignored this restriction. Following the prescriptions in [11] we have avoided this problem by fixing the ranges of variation of the relevant parameters ($m_\eta ^2$, $\mu _2$ and $v_\Omega$) so that the ${\mathbb {Z}}_{2}$ parity symmetry holds up to higher energies.⁴ Moreover, we have checked numerically that, for benchmarks we chose for the collider study in Sect. 5$m_{\eta }^2$ remains positive at all energy scales. Finally, although experimental constraints place no upper limit on the mass of the heavy neutral scalar H, we require that its decay width should comply with the perturbative unitarity condition, i.e. $\frac{\Gamma _{H}}{m_{H}}\, < \, \frac{1}{2}$.

b. Neutrino oscillation parameters One of the main motivation of our scotogenic model is to provide an explanation to the generation of neutrino masses. To ensure this, throughout our analysis we require compatibility with the best-fit ranges of the neutrino oscillation parameters. This is enforced via Eq. (27), where the mixing angles and squared mass differences are fixed according to Ref. [3]. For simplicity, the yet unknown Dirac and Majorana phases in $U_\nu$ are set to zero. We further assume the currently preferred normal ordering of the light neutrino masses. Interestingly, as already mentioned, this model predicts the lightest active neutrino to be massless.

c. Lepton flavour violation This model could be in principle probed through the observation of charged lepton flavour violation, for example, at high intensity muon facilities [47]. However, the negative results of charged lepton flavor violation searches can be used to set constraints on the parameters of the model, in particular on $\lambda _5$ which controls the magnitude of the Yukawa couplings. We apply the most stringent limits to date on the branching fraction of some of such rare processes, namely BR$(\mu \rightarrow e \gamma ) < 4.2 \times 10^{-13}$ [48], BR$(\mu \rightarrow e e e) < 1. \times 10^{-12}$ [49], CR$(\mu ^-, \mathrm{Au} \rightarrow e^-, \mathrm Au) < 7 \times 10^{-13}$ [50].

d. Electroweak precision tests The presence of new physics will affect the gauge boson self-energies, parameterised by the oblique parameters [51]. The most important constraint is expected from the T parameter, which is sensitive to the mass splitting between the neutral and charged components of the scalar fields. From the one-loop contribution to the T parameter it follows that $m_{\eta ^\pm } - m_{\eta _R} \lesssim 140\ \hbox {GeV}$ [52]. Given the perturbativity constraint on the relevant $\lambda _i$ parameters, this condition is automatically fulfilled in all phenomenologically viable solutions of our numerical scan. We require consistency with electroweak precision data by requiring $v_\Omega \lesssim 5\ \hbox {GeV}$, in order to get an adequately small deviation of the $\rho$ parameter from one [11] (and consequently a negligible tree level contribution from the triplet to the T parameter), namely we impose $-\,0.00018 \lesssim \delta \rho \lesssim 0.00096$ ($3\sigma$). Moreover, we fix the Higgs VEV $v_\phi$ in order to get the correct mass of the W boson, inside its experimental range.

e. Invisible decay widths of the Higgs boson If the new neutral scalar masses $m_{\eta _{R, I}}$ are small enough, there can appear new invisible decay channels – at tree level – of the Higgs boson into the lighter stable particles. In the region of parameters where these new invisible decays are possible we enforce that BR$(h^0 \rightarrow \mathrm inv) \lesssim 24\%$ [53]. At the loop level, the decay of the Higgs boson into two photons may also be modified by its coupling to the charged scalars. We require consistency at the $3\sigma$ level, that is $0.62\lesssim$ BR$(h^0 \rightarrow \gamma \gamma )/$BR$(h^0 \rightarrow \gamma \gamma )_\mathrm{SM} \lesssim 1.7$.

f. Dipole moments of leptons At the one-loop level the charged scalars present in our model may also induce sizeable contributions to the magnetic dipole moments of leptons. We have required that the contributions to the anomalous muon magnetic dipole moment induced by the new physics do not exceed the allowed discrepancy between the measured value and the one predicted within the SM [53], $\Delta (a_{\mu }) =a^\text {exp}_{\mu }-a^\text {SM}_{\mu }= 268(63)(43)\times 10^{-11}\,$. Contributions to the electric dipole moments arise instead only at the two-loop level, so they are suppressed [52].

g. Dark matter and cosmological observations In the following, we assume a standard cosmological scenario, where the dark matter candidate, the scalar $\eta _R$, was in thermal equilibrium with the SM particles in the early Universe. If $\eta _R$ is the only candidate contributing to the cosmological dark matter, its relic density must comply with the cosmological limits for cold dark matter derived by the Planck satellite data [54, 55]: $0.1126 \le \Omega _{\eta _R} h^2 \le 0.1246$ (3$\sigma$ range). Values of $\Omega _{\eta _R} h^2 \le 0.1126$ are also allowed, if $\eta _R$ is a subdominant component of the cosmological dark matter and allowing for the existence of another candidate. Moreover, our scenario can be tested at direct detection (DD) experiments, which are meant to probe the nuclear recoil in the scattering of galactic $\eta _R$ off-nuclei inside the detector. We apply the current most stringent limit on WIMP-nucleon spin-independent (SI) elastic scattering cross section, which has been set by the XENON1T experiment at LNGS [56].

h. Colliders Existing searches for new charged particles at colliders such as LEP and LHC, already set lower limits on their masses in the region below $100\ \hbox {GeV}$ or so [53]. In our analysis we apply the following limits: $m_{H^\pm } \ge 80 \,\mathrm{GeV}$ and $122~\mathrm{GeV} \le m_{h^0} \le 128\ \hbox {GeV}$, the latter to take into account numerical uncertainties.

4 Phenomenology of scalar scotogenic dark matter

In this section we collect the results of our analysis of dark matter in the Triplet + Singlet Scotogenic Model. As already commented before, this model can harbor either fermionic or bosonic WIMP dark matter. Detailed studies of the phenomenology of the fermionic dark matter candidate $\chi ^0$ [9] have been presented in Refs. [13, 14]. Here we will assume the ${\mathbb {Z}}_{2}$-odd scalar $\eta _R$ to be the dark matter candidate and investigate its phenomenology. The latter has common features with those of the simplest scotogenic constructions [8] as well as the Inert Higgs Doublet Model [18, 19, 57].

4.1 Relic density

Fig. 3

Relic abundance $\Omega _{\eta _R} h^2$ as a function of the $\eta _R$ mass. Blue points denote solutions with viable relic density, although leading to underabundant dark matter. Cyan points fall within the $3\sigma$ C.L. cold dark matter measurement by the Planck collaboration [54, 55]. Grey dots are excluded by at least one of the bounds in Sect. 3.2. Dark grey points are in conflict with the current limit on WIMP-nucleon SI elastic scattering cross section set by XENON1T [56]

We show in Fig. 3 the expected dark matter relic abundance as a function of the mass of the scalar dark matter candidate $\eta _R$. The narrow black band depicts the 3$\sigma$ range for cold dark matter derived by the Planck satellite data [54, 55]. Only for solutions falling exactly in this band (cyan points) the totality of dark matter can be explained by $\eta _R$. Blue points refer to solutions where $\eta _R$ would be subdominant, and another dark matter candidate would be required. Grey points are instead excluded by any of the constraints discussed in Sect. 3.2, mainly by the Planck constraint itself. Dark grey points are solutions in conflict with the current limit on WIMP-nucleon SI elastic scattering cross section set by XENON1T [56]. The features appearing in the plot can be explained by looking in detail into the $\eta _R$ annihilation channels. The first dip on the left depicts the Z-pole, that is where $m_{\eta _R} \sim M_Z/2$ and the coannihilation via s-channel Z exchange becomes relevant. Similarly, the second depletion of the relic density around $m_{\eta _R} \sim 60\ \hbox {GeV}$ corresponds to efficient annihilations via s-channel Higgs exchange. Notice that it is likely for solutions in this dip to be in conflict with current collider limits on BR$(h^0 \rightarrow \mathrm inv)$. The latter depletion is more efficient than the Z-mediated one, which is momentum suppressed. For heavier $\eta _R$ masses, quartic interactions with gauge bosons become effective and, when kinematically allowed, also two-top final states. Annihilations of $\eta _R$ into $W^+ W^-$ via quartic couplings are particular important at $m_{\eta _R} > rsim 80\ \hbox {GeV}$ thus explaining the third drop in the relic abundance. Finally, in the range $m_{\eta _R} > rsim 120\ \hbox {GeV}\ \eta _R$ can annihilate also into two Higgs bosons. At even heavier $m_{\eta _R}$ the annihilation cross section drops as $\sim \frac{1}{m_{\eta _R}^2}$ and the relic density increases proportionally. Eventually, heavy $\eta _R$ mainly annihilate into $W^+ W^-$, $h^0 h^0$, HH. We collect all the Feynman diagrams contributing to $\eta _R$ annihilations and co-annihilations in Appendix A. We may also notice that the relic abundance constraint does not put any bound on the absolute value of the $|\lambda _5|$ parameter. On the other hand, coannihilations with $\eta _I$ and $\eta ^\pm$ may occur in all regions of the parameter space with the effect of lowering the relic abundance.

We show in Fig. 4 the most relevant branching ratios (at tree level) for the annihilation cross section of $\eta _R$ into SM final states versus the mass of $\eta _R$, from our numerical scan. Different kinematical regimes are visible from this figure: below $M_W$, $\eta _R$ annihilates predominantly into $b \bar{b}$, gluons or $\tau ^+ \tau ^-$; when the quartic coupling with W becomes kinematically accessible, $\eta _R$ annihilates mainly into $W^+ W^-$. Similarly, annihilations into $h^0 h^0$, HH and $Z^0 Z^0$ become relevant as soon as kinematically open.

Fig. 4

Main branching fractions of the annihilation cross section of $\eta _R$ into SM final states versus the mass of $\eta _R$. Orange points refer to annihilation into $b \bar{b}$, dark cyan to $\tau ^+ \tau ^-$, blue to gluons, dark red to $W^+ W^-$, green to $Z^0 Z^0$ and magenta to $h^0 h^0$

4.2 Direct detection

Let us discuss now the $\eta _R$ direct detection prospects. The tree-level spin-independent $\eta _R$-nucleon interaction cross section is mediated through the Higgs and the Z portals. The relevant Feynman diagrams for this process are summarised in Appendix A. Since the $\eta$ doublet has nonzero hypercharge, the $\eta _R$ – nucleon interaction through the Z boson would in general exceed the current constraints from direct detection experiments. Nevertheless, in most of the solutions, $\lambda _5$ induces a mass splitting between the CP-odd partner $\eta _I$ and $\eta _R$ such that the interaction through the Z boson is kinematically forbidden, or leads to inelastic scattering. The $\eta _R$-nucleon interaction via the Higgs is therefore dominant in most of the parameter space. As a consequence, the coupling between $\eta _R$ and the Higgs boson (which depends on the sum $\lambda _3 +\lambda _4 + \lambda _5$ and on $v_\Omega$, $\mu _2$ and $\lambda _{\eta }^{\Omega }$) turns out to be the relevant quantity controlling both this cross section and the signals at LHC that we will discuss in Sect. 5. We show in Fig. 5 the spin-independent $\eta _R$-nucleon elastic scattering cross section weighted by $\xi =\frac{\Omega _{\eta _R}}{\Omega _\mathrm{Planck}}$ versus the $\eta _R$ mass. The color code of displayed points is the same as in Fig. 3. The dark green plain line denotes the most recent upper bound from XENON1T [56]. Although we only show the most stringent up-to-date limit from XENON1T, we note that other leading liquid xenon experiments such as LUX [58] and PandaX-II [59] can also probe the spin-independent dark matter-nucleon elastic scattering cross section for dark matter heavier than $\sim 50\ \hbox {GeV}$. On the other hand, DarkSide-50 [60] and DEAP-3600 [61] are less competitive for medium and high-mass WIMPs, because of their higher thresholds and lower exposures.

Finally, we also depict as for comparison the lower limit (dashed orange line) corresponding to the “neutrino floor” from coherent elastic neutrino-nucleus scattering (CE$\nu$NS) [62] and the projected sensitivity for LUX-ZEPLIN (LZ, green dot-dashed) [63]. The extended particle content characteristic of the Singlet + Triplet Scotogenic Model in principle allows for a viable scalar dark matter candidate in a wider region of masses, compared to the simplest scotogenic or Inert Higgs Doublet models. Nevertheless, because of current experimental constraints, most of the new allowed solutions with a relic abundance within the $3\sigma$ C.L. cold dark matter measurement by the Planck collaboration [54, 55] lie in a tight vertical region around $m_{\eta _R} \sim 500{-}600\ \hbox {GeV}$. Lighter $\eta _R$ lead to viable dark matter, although under-abundant, hence it would then require the existence of an additional dark matter candidate.

Fig. 5

Spin-independent $\eta _R$-nucleon elastic scattering cross section versus the $\eta _R$ mass. Colour code as in Fig 3. The dark green line denotes the most recent upper bound from XENON1T [56]. The dashed orange line depicts the lower limit corresponding to the “neutrino floor” from coherent elastic neutrino-nucleus scattering (CE$\nu$NS) [62], while the green dot-dashed one stands for the projected sensitivity for LZ [63]

Finally, it is worth commenting on how the phenomenology of $\eta _R$ dark matter compares to that of the scalar dark matter in the simple Scotogenic Model [8]. While the two candidates have similar properties, the presence of a scalar triplet in the Singlet + Triplet Scotogenic Model slightly changes the interaction of $\eta _R$ with the Higgs boson. As a consequence, both its Higgs-mediated annihilation cross section as well as the $\eta _R$-nucleon interaction cross section contain a term dependent on $\mu _2$ and on $v_\Omega$ (see the relevant vertex in Appendix B). This is nonetheless weighted by the (small) mixing between $h^0$ and H. As a result the $\eta _R$ dark matter phenomenology turns out to be very similar in both models. The real advantage of the Singlet + Triplet Scotogenic Model comes from the enlarged viable parameter space, especially at low $\eta _R$ masses, as it avoids the unwanted spontaneous breaking of the ${\mathbb {Z}}_{2}$ parity symmetry [11].

4.3 Indirect detection

If $\eta _R$ annihilates into SM products with a cross section near the thermal relic benchmark value, it may be detected indirectly. Among its annihilation products, $\gamma$ rays are probably the best messengers since they proceed almost unaffected during their propagation, thus carrying both spectral and spatial information. First we consider prospects of detecting $\gamma$ rays from $\eta _R$ annihilations by considering the continuum spectrum up to the $\eta _R$ mass which originates from decays of the annihilation products. We consider annihilations into $b \bar{b}$, $\tau ^+ \tau ^-$ and $W^+ W^-$ to compare with current limits set by the Fermi Large Area Telescope (LAT) satellite [64] and HESS telescope [65]. We show in Fig. 6 the results of our numerical scan of the annihilation cross section (weighted by $\xi ^2$ and by the correspondent branching ratio) versus the $\eta _R$ mass, for $\eta _R$ annihilating into $b \bar{b}$ (orange points), $\tau ^+ \tau ^-$ (dark cyan) and $W^+ W^-$ (dark red). Grey points are excluded by any of the constraints listed in Sect. 3.2. Points in light red are solutions with relic abundance falling exactly within the $3\sigma$ band measured by Planck. In the same figure we also show the 95% C.L. upper limits currently set by the Fermi-LAT with $\gamma$-ray observations of Milky Way dwarf spheroidal satellite galaxies (dSphs) based on 6 years of data processed with the Pass 8 event-level analysis [64] (plain lines assuming annihilation into $b \bar{b}$ (orange), $\tau ^+ \tau ^-$ (dark cyan) and $W^+ W^-$ (dark red)). Moreover we show as a red dot-dashed curve the current upper limit obtained by H.E.S.S. using Galactic Center (GC) $\gamma$-ray data accumulated over 10 years [65], assuming a $W^+ W^-$ channel and an Einasto dark matter density profile. Finally, we also depict sensitivity projections for Fermi-LAT from a stacked analysis of 60 dSphs and 15 years of data, in the $b \bar{b}$ channel [66] (dashed orange) and for CTA, for the Milky way galactic halo target, $W^+ W^-$ channel and an Einasto dark matter density profile [67]. Although current limits lie a couple of orders of magnitude above the predicted signals in this model, future data from Fermi-LAT and CTA offer promising prospects, eventually allowing one to test part of the parameter space both in the low ($\sim 70\ \hbox {GeV}$) as well as in the high ($> rsim 500\ \hbox {GeV}$) mass regions.⁵

Fig. 6

Predicted $\eta _R$ annihilation cross section into $\gamma$ rays – weighted by the relative abundance – for annihilations to $b \bar{b}$ (orange), $\tau ^+ \tau ^-$ (dark cyan) and $W^+ W^-$ (dark and light red) final states. The orange, dark cyan and dark red plain lines refer to the corresponding 95% C.L. upper limits currently set by the Fermi-LAT with $\gamma$-ray observations of dSphs [64]. The dark red dot-dashed curve is the current upper limit obtained by H.E.S.S. using GC data [65]. We also compare with sensitivity projections for Fermi-LAT ($b \bar{b}$, 60 dSphs and 15 years of data) [66] and for CTA (GC, $W^+ W^-$) [67]. See text for more details

Besides $\gamma$ rays, charged cosmic rays can be used to probe $\eta _R$ as a dark matter candidate. The positron fraction measured by PAMELA [73, 74] and more recently by AMS-02 [75, 76], allows us to place constraints on annihilating WIMPs, which are particularly stringent in the case of annihilations to the first two generations of charged leptons. In our scenario, light $\eta _R$ annihilate mainly to $\tau ^+ \tau ^-$, as can be seen from Fig. 4. As a result bounds from cosmic positrons are less relevant than those from $\gamma$ rays. In addition to cosmic-ray positrons, AMS-02 has also provided a high-precision measurement of the cosmic-ray antiproton spectrum [77]. These can be translated into upper limits on hadronic dark matter annihilation, which can be a factor of few stronger than those from $\gamma$-ray observations of dSphs [78, 79]. Since these results rely on a careful treatment of systematic uncertainties, namely the antiproton production cross-section, and the modelling of the effect of solar modulation we decided not to include them here and leave it for a dedicated work. Similarly, searches for anti-deuterium or anti-helium events could potentially provide a powerful probe of $\eta _R$ annihilations [80,81,82,83], although also affected by substantial uncertainties.

5 Scalar dark matter signatures at the LHC

In this section we confront our scalar dark matter candidate with the latest data from particle colliders, in particular from the LHC run at $\sqrt{s}=13\ \hbox {TeV}$. As in any model with a dark matter candidate, the generic signature to be searched for is missing energy (${\not \!\!E}_{T}$), measured from the total transverse momentum recoil of the visible particles in the event (see for instance [84, 85]).

Fig. 7

Relevant Feynman diagrams for mono-jet production through $\eta _{R} \eta _{R}+j$ at the LHC; here $h_k\equiv h^{0}$ or H

In the Triplet + Singlet Scotogenic Model typical signatures are ${\not \!\!E}_{T}+ X$, where X can be one or two jets [86, 87], two leptons [88] or one photon [89]. Although all of them are in principle interesting, we have checked numerically that in our scenario the most promising one is ${\not \!\!E}_{T}+$ jet (mono-jet). In the following we will focus on mono-jet final states, arising from $p p \rightarrow \eta _{R} \eta _{R}+g$ and $p p \rightarrow \eta _{R} \eta _{R}+q$ processes. Here ones looks for events with one high-$p_T$ jet (higher than $100-200\ \hbox {GeV}$ in the central region of the detector, with pseudorapidity $|\eta |<2.4$) and ${\not \!\!E}_{T}$ above roughly $200\ \hbox {GeV}$ in the $13\ \hbox {TeV}$ analyses for the ATLAS and CMS detectors [86, 90]. The dominant irreducible SM background for this channel comes from $Z + j$, with the Z boson subsequently decaying invisibly $Z \rightarrow \nu \bar{\nu }$. There is also a subdominant irreducible background from $W + j$, with $W \rightarrow \tau \nu$, where the $\tau$ decays hadronically. In addition, there are backgrounds from $W + j$ with $W \rightarrow \mu \nu$ or $e \nu$, where the lepton is either missed or misidentified as a jet. However, $Z + j$ constitutes approximately 60% of events.

At leading order, the relevant Higgs-mediated Feynman diagrams for mono-jet events are shown in Fig. 7. In all cases, the dark matter is produced via the decay of a neutral scalar ($h^0$ or H), produced from its interaction with quarks, or through its effective coupling to gluons. The latter involves a top quark loop and enters in gluon-gluon fusion (ggF) processes. An important point is that in ggF processes only the SM-like Higgs doublet couples with fermions. Indeed, since H is mainly a triplet, its coupling with quarks is suppressed. The interaction vertex between $\eta _{R}$ and $h_{k}$ is given in Appendix B. Note that if the mass difference between $\eta _I$ and $\eta _R$ is small, $\eta _I$ should also contribute to the invisible final states. In this case, $\eta _{I}$ would subsequently decay to $\eta _{R}$ plus soft fermions or jets which are not energetic enough to be detected. Besides Higgs mediation, the mono-jet signal can proceed also via Z-mediation. Therefore we also include the contributions shown in Fig. 8, which are described as $p p \rightarrow \eta _{R} \eta _{I}+g$ and $p p \rightarrow \eta _{R} \eta _{I}+q$ processes. Finally, we must mention that in this same scenario of small mass differences, a pair of $\eta _I$ can also be produced.

Fig. 8

Feynman diagrams illustrating Z-mediated production of $\eta _{R} \eta _{I}+j$ at the LHC

5.1 Benchmark points

The constraints previously described in Sect. 3.2 restrict the parameter space allowed by a vast array of experimental probes, among which are the relic density, direct detection and indirect detection analyses. Motivated by these preliminary studies, we now investigate using the CheckMATE 2 collaboration tools [91,92,93,94,95] whether the solutions that satisfy all experimental limits in Sect. 3.2 could lead to detectable dark matter mono-jet signals at LHC $13\ \hbox {TeV}$. This code allows us to determine whether or not a given parameter configuration of our model is excluded at 95% C.L, recasting the results of the simulated model in terms of the existing analyses of the LHC, which automatically include the simulation and elimination of the background. Indeed, for each signal region, CheckMATE 2 computes the expected number of signal events S after cuts, and directly compare it to the 95% C.L. upper limit $S^{95}_{exp}$, given a signal error $\Delta S$. The most relevant analysis for our study is Ref. [86].

In this way, we identify two interesting benchmark points which survive the entire set of constraints described in Sect. 3.2 (including the theoretical ones, such as the conservation of the ${\mathbb {Z}}_{2}$ parity symmetry up to higher energy scales) and shown in Table 3. Values of the relevant parameters and the corresponding scalar spectrum are summarised. We also show in this table the value of observables obtained in Sect. 3.2 for each benchmark.

The main difference between the two benchmark points is the value of H mass, which is governed by $\mu _{2}$ and $v_{\Omega }$.

However, because this heavy scalar is mainly triplet, its coupling with quarks in the ggF processes is suppressed, so that a significant change in its mass is not expected to lead to a large variation in the magnitude of the cross sections.

Table 3 Benchmark points which survive the entire set of constraints described in Sect. 3.2 and corresponding parameters relevant to the calculation of diagrams in ${\not \!\!E}_{T}+$jet final states

5.2 Mono-jet signatures at the LHC $\sqrt{s}={13}\ \hbox {TeV}$

We display in Table 4 the CheckMATE 2 results for the evaluation in the ${\not \!\!E}_{T}+$jet channel (corresponding to an integrated luminosity of $36.1 \mathrm{fb}^{-1}$ in the $\sqrt{s}=13\ \hbox {TeV}$ analysis) for the two benchmark points of Table 3. For this study, the cross sections shown in Table 4 correspond to both contributions to the final state studied: Z boson (Fig. 8) and Higgs-mediated processes (Fig. 7), respectively.

Table 4 Results obtained with CheckMATE 2 based on the atlas_conf_2017_060 [86] analysis by the ATLAS collaboration, for LHC data at $\sqrt{s}=13\ \hbox {TeV}$

The main result of Table 4 is the value of the parameter r

$$\begin{aligned} r \equiv \frac{S-1.96\Delta S}{S^{95}_{exp}} \end{aligned}$$

(30)

calculated by CheckMATE 2,⁶ which translates into a significant number of signal events after the cuts, S. These specific cuts are implemented by the ATLAS analysis in order to map out the associated regions of consistent parameter choices, and will be described later.

Our dark matter candidate $\eta _R$ with mass around $\sim 50{-}60\ \hbox {GeV}$ and chosen to satisfy all theoretical and experimental constraints of Sect. 3.2 would lead to a signature in the ${\not \!\!E}_{T}+$jet channel in the ATLAS experiment.

For that we require, for both benchmark points, that the leading jet has $p_{T}> 250\ \hbox {GeV}$ and $|\eta |<2.4$, separation in the azimuthal plane of $\Delta \phi (\text {jet}, p_{T}^{miss})>0.4$ between the missing transverse momentum direction and each selected jet.

Fig. 9

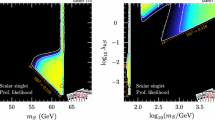
Cross sections of mono-jet signals at LHC $\sqrt{s}={13~(14)}\ \hbox {TeV}$. The left panel shows the Higgs boson mediated events from $p p \rightarrow \eta _{R} \eta _{R}+$ jet. The maximum value of the cross section is $\sim 1400(1800)$ fb for $\sqrt{s}=13~(14)\ \hbox {TeV}$ respectively. The right panel is the Z-mediated process, $p p \rightarrow \eta _{R} \eta _{I}+$ jet, with peak contribution $\sim 190~(220)$ fb

The difference between our benchmarks are the ${\not \!\!E}_{T}$ thresholds. While for Benchmark 2 a ${\not \!\!E}_{T}$ minimum of $500\ \hbox {GeV}$ is required, in the other case we take ${\not \!\!E}_{T}>600\ \hbox {GeV}$.

For larger $\eta _{R}$ masses we investigate the behaviour of the cross sections at $\sqrt{s}=13\ \hbox {TeV}$ and the projected signal events at $\sqrt{s} = 14\ \hbox {TeV}$. We assume the coupling $|\lambda _{345}|$ to lie in the range [0.02, 0.9] and we fix the other parameters according to Benchmark 1 in Table 3. We analyse $\eta _R \eta _R +j$ and $\eta _R \eta _I +j$ separately because the rate of these processes depends on different parameters and we want to analyze their contributions to the total cross section separately.

In Fig. 9 we present the production cross section for ${\not \!\!E}_{T}+$ jet process at LHC $\sqrt{s}=13~(14)\ \hbox {TeV}$. Using Madgraph5 [44] we simulate events with an initial cut of $p_{T}^{jet}>100\ \hbox {GeV}$, according to the latest analyses in mono-jet searches [97, 98]. Since the relevant processes leading to these events are mediated by mainly the SM Higgs (left panel) and Z boson (right panel), one has the characteristic peaks at $m_ {\eta _{R}}\sim m_{h^0}/2$ and at $m_ {\eta _{R}}\sim m_{Z}/2$ respectively, providing larger cross sections in these mass ranges. Therefore, the Higgs boson mediated processes are dominant up to $m_{\eta _R}\sim 60\ \hbox {GeV}$ and also contribute in the range $\sim [700{-}1400]$ fb ($13\ \hbox {TeV}$).

In addition, Z-mediated processes complements the search for $p p \rightarrow \eta _{R} \eta _{R} +$ jet process at the LHC. For this mass range, the cross sections are $\sim [190{-}80]$ fb while, for dark matter masses between $[65{-}200]\ \hbox {GeV}$, we have $\sim [70{-}5]$ fb, providing a sizeable contribution to the total mono-jet cross section, which could be within LHC sensitivity. At $\sqrt{s} = 14\ \hbox {TeV}$ the cross section increases by a few fb. These results agree with expectations of other models, such as the Inert Higgs Doublet Model, whose contributions to this signal are very similar [97]. In summary, one sees that there are good prospects for probing the mono-jet signal at the LHC for dark matter masses up to $\sim 60\ \hbox {GeV}$.

There are regions of parameters in which $\eta _I$ and $\eta _R$ are relatively close in mass, as shown in Fig. 10. This as required for model consistency, as the mass difference between these particles is intimately connected with the smallness of neutrino mass as generated in the scotogenic picture. This requires the violation of lepton number through the value of $\lambda _5$, as seen by Eqs. (16) and (17). Indeed, if $m_{\eta _R}-m_{\eta _I}$ is small we can obtain neutrino mass square differences, as needed to account for neutrino oscillation data [4]. Moreover, the particles produced from the decay $\eta _I \rightarrow \eta _R$+X are not energetic enough to have the trajectories reconstructed by the detector (soft particles), leading to our ${\not \!\!E}_{T}+$ jet final state signal.

Fig. 10

Mass difference $m_{\eta _{I}} - m_{\eta _{R}}$ as a function of $m_{\eta _{R}}$ in mono-jet events mediated by the Z boson, $p p \rightarrow \eta _{R} \eta _{I}+$ jet. The color shades represent values of the cross section in fb

As already commented in previous sections, as a result of its small coupling with quarks, the heavy neutral scalar H does not influence significantly our signal. As shown in Ref. [12], the production cross section of H at the LHC is 3 to 5 orders of magnitude smaller than the production of the SM Higgs boson, independent of the center-of-mass energy. Hence our results for the scalar dark matter jet + missing energy final states within the Singlet + Triplet Scotogenic Model should also hold within the simplest Scotogenic scenario of [8].

6 Summary and conclusions

In this work we have reexamined the generalized version of the minimal Singlet + Triplet Scotogenic Model, in which dark matter emerges naturally as the mediator of neutrino mass generation and its stability follows from the same ${\mathbb {Z}}_{2}$ symmetry also responsible for the radiative origin of neutrino masses. Notice that, while the simplest model of Ma [8] fails to be consistent over a wide range of parameters [10], our generalized scotogenic model is the minimal one allowing for a conserved ${\mathbb {Z}}_{2}$ symmetry all the way up to high mass scales [11]. We have assumed dark matter to be a scalar WIMP and we have presented a full numerical analysis of the signatures expected at dark matter detectors as well as collider experiments. We have shown that direct detection data from XENON-1T already disfavour part of the parameter space, in particular solutions with mass in the $\sim 100\ \hbox {GeV}$ range. We have highlighted the importance of complementary searches, for instance via indirect detection with $\gamma$ rays. Although current limits from Fermi-LAT and HESS lie a couple of orders of magnitude above the predicted signals in this model, future sensitivities also for CTA offer promising prospects, eventually allowing to probe both the low and the high WIMP mass regions. We have identified the regions of parameters where dark matter predictions are in agreement with theoretical and experimental constraints, such as those coming from neutrino oscillation data, Higgs data, dark matter relic abundance and direct detection searches. We have also presented expectations for near future direct and indirect detection experiments. These will further probe the parameter space of our scenario. Finally, we have examined the collider signatures associated to the mono-jet channel at the LHC. In particular, we have found a viable light dark matter mass range in the region $50{-}60\ \hbox {GeV}$. This should encourage future studies at the upcoming high-luminosity run of the LHC.

Appendices

Appendix A: Feynman diagrams for relic abundance and direct detection searches

Here we present some of the main Feynman diagrams relevant to determine the cosmological relic density, assuming that $\eta _R$ is the dark matter. Fig. 11 shows the main dark matter annihilation and coannihilation channels. Besides the standard s-wave annihilation into quarks and gauge bosons, mediated by the SM-like Higgs boson, coannihilations with both $\eta _R$ and $\eta ^\pm$ are possible. These can be mediated either by the $Z^0$ boson, or also by the new fermions $\chi _\sigma$. These channels can lead to both charged or neutral leptons in the final state, and involve the contribution of the new Yukawas described in Sect. 2. Notice that these processes are not present in the simplest scotogenic constructions [8] nor in the case of the Inert Higgs Doublet Model [12]. Diagrams with quartic interactions will appear when kinematically allowed, starting at $m_{\eta _R} > rsim 80\ \hbox {GeV}$.

Fig. 11

Relevant annihilation and coannihilation diagrams contributing to the relic abundance of $\eta _R$

The diagrams in Fig. 12 contribute to the spin-independent $\eta _R$-nucleon elastic scattering cross section at tree level, discussed in Sect. 4.2. The contribution of the diagram on the right is important only when the splitting between the masses of $\eta _R$ and $\eta _I$ is small (small $\lambda _5$ values) and leads to inelastic signals.

Fig. 12

Tree-level diagrams contributing to the elastic scattering of $\eta _R$ off nuclei via the Higgs exchange (left) and $Z^0$-boson exchange (right)

Fig. 13

Relevant $\eta _R$ interaction vertices. All particle momenta are considered as incoming. In the interaction with neutral scalars, $Z_{k1}^H$ and $Z_{k2}^H$ are entries of the mixing matrix that diagonalizes the mass matrix in Eq. (11) ($k=1$ refers to the SM Higgs $h^0$ and $k=2$ to the heavy scalar H). In the interaction with the $Z^0$ boson, $g_1$ and $g_2$ are the electroweak coupling constants associated to the SM groups $U(1)_Y$ and $SU(2)_L$, respectively

Appendix B: Relevant Feynman rules for the Singlet + Triplet Scotogenic Model

Figure 13 shows the most important Feynman rules for the relevant scalar dark-matter-physics interactions in the Singlet + Triplet Scotogenic Model. These are important for all the signatures studied in this paper, like the $\eta _R$-nucleon spin-independent elastic scattering and for the searches in the ${\not \!\!E}_{T}+$jet channel at the LHC.

In contrast to the simplest Scotogenic Model, the interaction vertex with the Higgs is not fully determined by $\lambda _{345}$, as it contains an extra contribution dependent on $\lambda _{\eta }^{\Omega }$ and $\mu _2$, involving the heavy neutral scalar H, although weighted by its mixing with $h^0$. Instead, the interaction vertex with the $Z^0$ boson depends on the quadrimomenta $p_\mu ^{\eta _R}$, $p_\mu ^{\eta _I}$ and on the electroweak couplings $g_1$ and $g_2$.