Abstract
The arithmetic version of Anderson localization (AL), i.e., AL with explicit arithmetic description on both the localization frequency and the localization phase, was first given by Jitomirskaya (Ann Math 150:1159–1175, 1999) for the almost Mathieu operators (AMO). Later, the result was generalized by Bourgain and Jitomirskaya (Invent Math 148:453–463, 2002) to a class of one dimensional quasi-periodic long-range operators. In this paper, we propose a novel approach based on an arithmetic version of Aubry duality and quantitative reducibility. Our method enables us to prove the same result for the class of quasi-periodic long-range operators in all dimensions, which includes Jitomirskaya (Ann Math 150:1159–1175, 1999) and Bourgain and Jitomirskaya (Invent Math 148:453–463, 2002) as special cases.
Similar content being viewed by others
Notes
\(\alpha \in {{\mathbb {T}}}^d\) is called Diophantine, denoted by \(\alpha \in \mathrm{DC}_d(\kappa ,\tau )\), if there exist \(\kappa >0\) and \(\tau >d-1\) such that
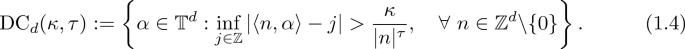
Let \(\mathrm{DC}_d:=\bigcup _{\kappa >0} \mathrm{DC}_d(\kappa ,\tau )\).
\(\theta \in {{\mathbb {T}}}\) is called Diophantine, denoted by \(\alpha \in \mathrm{DC}_\alpha (\kappa ,\tau )\), if there exist \(\kappa >0\) and \(\tau >d-1\) such that
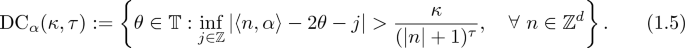
Let \(\Theta :=\bigcup _{\kappa >0} \mathrm{DC}_\alpha (\kappa ,\tau )\).
See Sect. 2.3 for more details.
The Anderson localization phase given in [BJ02] is a little larger than \(\Theta \), we mention that we can prove Anderson localization for the same phase set with minor modifications of the proof.
See Sect. 2.2 for definition.
We always have \(\ell _E\in {{\mathbb {Z}}}^d\) since \(\bar{B}_E\in C^0({{\mathbb {T}}}^d,SL(2,{{\mathbb {R}}}))\).
If \(\ell _E\ne {\tilde{\ell }}_E\), let \(D_E(x)=B_E(x)MR_{\langle {\tilde{\ell }}_E-\ell _E,x\rangle }M^{-1}=\begin{pmatrix}d_E^{11}(x)&{}d_E^{12}(x)\\ d_E^{21}(x)&{}d_E^{22}(x)\end{pmatrix}\). It is obvious that \(B_E\) and \(D_E\) define the same \(u_E\). So, one only need to prove the lemma for \(D_E\) and \({\tilde{B}}_E\). Thus, without loss of generality, we can assume that \(\deg {B_E}=\deg {\tilde{B}_E}\).
\(T_{-m}\) is a translation defined by \(T_{-m}u(n):=u(n+m)\).
Note that \(k_0\) maybe not unique.
We say u(n) is normalized if \(\sum _n|u(n)|^2=1\).
References
S. Aubry and G. André. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Israeli Phys. Soc. 3 (1980), 133–164.
A. Avila. Global theory of one-frequency Schrödinger operators. Acta Math. 215 (2015), 1–54.
A. Avila. Almost reducibility and absolute continuity. preprint. http://w3.impa.br/~avila/ (2704,2711).
A. Avila. KAM, Lyapunov exponent and the spectral dichotomy for one-frequency Schrödinger operators. Preprint.
A. Avila and S. Jitomirskaya. The Ten Martini Problem. Ann. of Math. 170 (2009), 303–342.
A. Avila and S. Jitomirskaya. Almost localization and almost reducibility. J. Eur. Math. Soc. 12 (2010), 93–131.
A. Avila, J. You and Q. Zhou. Sharp phase transitions for the almost Mathieu operator. Duke Math. J. 166 (2017), 2697–2718.
A. Avila, J. You, Q. Zhou. Dry Ten martini problem in the noncritical case. Preprint.
J. Bourgain. Green’s function estimates for lattice Schrödinger operators and applications. Annals of Mathematics Studies, Vol. 158. Princeton University Press, Princeton, NJ (2005).
J. Bourgain. Anderson localization for quasi-periodic lattice Schrödinger operators on \({\mathbb{Z}}^d\), \(d\) arbitrary. Geom. Funct. Anal. 17 (2007), 682–706.
J. Bourgain and M. Goldstein. On nonperturbative localization with quasi-periodic potential. Ann. of Math. 152 (2000), 835–879.
J. Bourgain, M. Goldstein and W. Schlag. Anderson localization for Schrödinger operators on \({\mathbb{Z}}^2\) with quasi-periodic potential. Acta Math. 188 (2002), 41–86.
J. Bourgain and S. Jitomirskaya. Anderson localization for the band model. Geometric aspects of functional analysis. Lecture Notes in Math. 1745 (2000), 67–79.
J. Bourgain and S. Jitomirskaya. Absolutely continuous spectrum for 1D quasi-periodic operators. Invent. Math. 148 (2002), 453–463.
A. Cai and L. Ge. Reducibility of finitely differentiable quasi-periodic cocycles and its spectral applications. 1712.09041.
A. Cai, C. Chavaudret, J. You and Q. Zhou. Sharp Hölder continuity of the Lyapunov ecponent of finitely differentiable quasi-periodic cocycles. Math. Z. 291 (2019), 931–958.
V. Chulaevsky and E. Dinaburg. Methods of KAM-Theory for Long-Range Quasi-Periodic Operators on \({\mathbb{Z}}^\mu \). Pure Point Spectrum. Commun. Math. Phys. 153 (1993), 559–577.
E. Dinaburg and Ya. Sinai. The one dimensional Schrödinger equation with a quasi-periodic potential. Funct. Anal. Appl. 9 (1975), 279–289.
L. Eliasson. Floquet solutions for the 1-dimensional quasi-periodic Schrödinger equation. Commun. Math. Phys. 146 (1992), 447–482.
L. Eliasson. Discrete one-dimensional quasi-periodic Schrödinger operators with pure point spectrum. Acta Math. 179 (1997), 153–196.
J. Fröhlich, T. Spencer and P. Wittwer. Localization for a class of one dimensional quasi-periodic Schrödinger operators. Commun. Math. Phys. 132 (1990), 5–25.
L. Ge, J. You and Q. Zhou. Exponential dynamical localization: Criterion and applications. arXiv:1901.04258.
A. Gordon, S. Jitomirskaya, Y. Last and B. Simon. Duality and singular continuous spectrum in the almost Mathieu equation. Acta Mathematica. 178 (1997), 169–183.
M. Herman. Une méthode pour minorer les exposants de Lyapounov et quelques exemples montrant le caractère local d’un théorème d’Arnol’d et de Moser sur le tore de dimension 2. Comment. Math. Helv. (3)58 (1983), 453–502.
X. Hou and J. You. Almost reducibility and non-perturbative reducibility of quasiperiodic linear systems. Invent. Math. 190 (2012), 209–260.
S. Jitomirskaya. Almost everything about the almost Mathieu operator, II. In: Proc. of XI Int. Congress of Math. Physics. Int. Press, Somerville, Mass. (1995), pp. 373–382.
S. Jitomirskaya. Metal-Insulator Transition for the almost Mathieu operator. Ann. of Math. 150 (1999), 1159–1175.
S. Jitomirskaya and I. Kachkovskiy. \(L^2\)-reducibility and localization for quasi-periodic operators. Math. Res. Lett. 23 (2016), 431–444.
S. Jitormiskya and W. Liu. Universal hierarchical structure of quasi-periodic eigenfuctions. Ann. of Math. (3)187, 721–776 (2018).
S. Jitormiskya and W. Liu. Universal reflective-hierarchical structure of quasiperiodic eigenfunctions and sharp spectral transition in phase. arXiv:1802.00781.
S. Jitormiskya, W. Liu and Y. Shi. Anderson localization for multi-frequency quasiperiodic operators on \({{\mathbb{Z}}}^d\). arXiv:1908.03805.
R. Johnson and J. Moser. The rotation number for almost periodic potentials. Commun. Math. Phys. 84 (1982), 403–438.
S. Klein. Anderson localization for the discrete one-dimensional quasi-periodic Schrödinger operator with potential defined by a Gevery-class function. J. Funct. Anal. 218 (2005), 255–292.
Y. Last. A relation between a.c. spectrum of ergodic Jacobi matrices and the spectra of periodic approximants. Comm. Math. Phys. 151 (1993), 183–192.
M. Leguil, J. You, Z. Zhao and Q. Zhou. Asymptotics of spectral gaps of quasi-periodic Schrödinger operators. arXiv:1712.04700.
J. Puig. A non-perturbative Eliasson’s reducibility theorem. Nonlinearity (2)19 (2006), 355–376.
Y. Sinai. Anderson localization for one-dimensional difference Schrödinger operator with quasi-periodic potential. J. Stat. Phys. 46 (1987), 861–909.
Acknowledgements
L. Ge was partially supported by NSF DMS-190146. J. You was partially supported by NNSF of China (11871286) and Nankai Zhide Foundation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
We list some reducibility results for quasi-periodic \(SL(2,{{\mathbb {R}}})\)-cocyle, one can consult [DS75, Eli92, GYZ] for details.
Theorem 5.1
([DS75, GYZ, Eli92, HY12]) Let \(\alpha \in DC_d(\kappa ,\tau )\), \(h>\tilde{h}>0\), \(\tau '>d-1\), \(\tau >d-1\), \(\kappa >0\), \(\gamma >0\), \(R\in SL(2,{{\mathbb {R}}})\). Let \(A\in C_{h}^\omega ({{\mathbb {T}}}^d,SL(2,{{\mathbb {R}}}))\) with \(\rho (\alpha ,A)\in DC_\alpha (\kappa ,\tau )\). Then there exist numerical constant \(C_0\), constant \(D_0=D_0(\kappa ,\tau ,d)\), \(\epsilon =\epsilon (\tau ',\tau ,\kappa ,\gamma ,h,\tilde{h},d,R)\), such that if
then there exist \(B\in C_{\tilde{h}}^\omega ({{\mathbb {T}}}^d,SL(2,{{\mathbb {R}}}))\) and \(\tilde{A}\in SL(2,{{\mathbb {R}}})\) such that
with estimates \(\Vert B-id\Vert _{\tilde{h}}\le \Vert A(x)-R\Vert _{h}^{\frac{1}{2}}\) and \(\Vert \tilde{A}-R\Vert \le \Vert A(x)-R\Vert _{h}\).
Proposition 5.1
([GYZ]) For any \(0<\tilde{h}<h\), \(\kappa>0,\gamma >0\), \(\tau >d-1\), \(\tau '>d-1\). Suppose that \(\alpha \in DC_d(\kappa ,\tau )\), \(\rho (\alpha ,A_0e^{f_0})\in DC_\alpha (\gamma ,\tau ')\). Then there exist \(B\in C_{\tilde{h}}^\omega ({{\mathbb {T}}}^d, PSL(2,{{\mathbb {R}}}))\) and \(A\in SL(2,{{\mathbb {R}}})\) satisfying
provided that \(\Vert f_0\Vert _h<\epsilon _*\) for some \(\epsilon _*>0\) depending on \(A_0,\kappa ,\tau ,\tau ',h,\tilde{h},d\). In particular, \(\Vert B\Vert _{\tilde{h}}\le C(\alpha ,V,d,\gamma ,\tau ',h,\tilde{h})\).
Remark 5.1
If \(A_0\) varies in \(\mathrm{SO}(2,{{\mathbb {R}}})\), then \(\epsilon _*\) can be taken uniform with respect to \(A_0\).
Rights and permissions
About this article
Cite this article
Ge, L., You, J. Arithmetic version of Anderson localization via reducibility. Geom. Funct. Anal. 30, 1370–1401 (2020). https://doi.org/10.1007/s00039-020-00549-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-020-00549-x