Drag Distribution in Idealized Heterogeneous Urban Environments

Abstract

Large-eddy simulations of nine idealized heterogeneous urban morphologies with identical building density and frontal area index are used to explore the impact of heterogeneity on urban airflow. The fractal-like urban morphologies were generated with a new open-source Urban Landscape Generator tool (doi:10.5281/zenodo.3747475). The vertical structure of mean flow and the dispersive vertical momentum transport within the roughness sublayer are shown to be strongly influenced by the building morphologies. The friction velocity and displacement height show high correlations with the maximum building height rather than the average height. Well-known roughness parametrizations of the logarithmic layer cannot adequately capture the large spread observed in the large-eddy simulation data. A generalized frontal area index ${\Lambda }_f$ is introduced that characterizes the vertical distribution of the frontal area in the urban canopy. The vertically distributed stress profiles, which differ significantly per simulation, are shown to roughly collapse upon plotting them against ${\Lambda }_f$. The stress distribution representing urban drag can be fitted with a third degree polynomial. The results can be used for more detailed and robust representations of building effects in the development of urban canopy models.

1 Introduction

Buildings modify the airflow and momentum exchange within cities, and therefore strongly affect local wind, temperature, humidity, and pollution. Because buildings cannot be explicitly resolved in numerical weather prediction (NWP), the impacts on airflow need to be parametrized. Developing parametrizations of urban terrain is a formidable challenge: the parameter space is very large and neither the atmosphere nor the urban surface are typically in a statistically steady state (Martilli 2007; Barlow 2014). Regional weather models typically represent buildings by ground-based surface-cover parameters such as building density $\lambda _p$ (building plan area per unit plan area) and frontal area index $\lambda _f$ (frontal area per unit plan area), and the vertical extent of buildings is often simply represented by an average building height $z_H$, which may refer to the mean building height, or a (frontal-area-) weighted average height (Grimmond and Oke 1999).

These geometric parameters are used in NWP to describe the aerodynamic effect of buildings, commonly in terms of a logarithmic wind profile with a displacement height $z_d$ and roughness length $z_0$ (e.g., Porson et al. 2010). However, there are large uncertainties associated with estimating the functional relation between the surface geometry and the aerodynamic roughness parameters (Grimmond and Oke 1999; Hagishima et al. 2009; Kanda et al. 2013; Kent et al. 2017). Moreover, real urban canopies have a vertical structure, where building density and frontal area vary with height. Several studies have highlighted that an average building height is an insufficient representation of the real urban environment and that the maximum building height, even in case of an isolated tall building, has a disproportionately large impact on the velocity and building drag of urban areas (Xie et al. 2008; Millward-Hopkins et al. 2011; Kanda et al. 2013; Hertwig et al. 2019). Alternative parametrizations for the logarithmic wind profile incorporate extended morphology statistics such as the maximum height $z_{\max }$ and the height standard deviation $\sigma _H$ (Millward-Hopkins et al. 2012; Kanda et al. 2013), but developing robust parametrizations of the aerodynamic roughness parameters remains challenging (Kent et al. 2017).

To provide insight into the aerodynamic effects of buildings, two approaches are typically adopted: (1) a bottom-up approach, which starts at idealized urban morphologies and then gradually adds complexity; (2) a top-down approach, in which real or realistic urban morphologies are considered. Studies pursuing the bottom-up approach have a particular strength in forming an understanding of the fundamental processes governing these flows, and have brought insight on the effects of building cover, building alignment, and wind angle (Coceal et al. 2006; Kanda 2006; Neophytou et al. 2014; Cheng and Porté-Agel 2015; Castro et al. 2017). Case studies pursuing the top-down approach create specific insights for that particular morphology. They show the complexity and rich variety of flow features at a specific location, and highlight the spatial variability of the flow field over urban sites (Carpentieri et al. 2009; Giometto et al. 2016; Hertwig et al. 2019). However, the two are not necessarily compatible, as concepts based on idealized geometries may not match realistic morphologies well (cf. Barlow 2014). And although much progress has been made on the representation of impacts of idealized buildings, the effects of heterogeneity of urban morphologies — differently sized and shaped buildings — are not well understood.

There is a need to improve our fundamental understanding of the effect of heterogeneity on flow in urban morphologies of intermediate complexity. That is, realistic urban heterogeneity needs to be introduced without adding too many new degrees of freedom to the parameter space, such that fundamental studies remain tractable. Our first aim is to introduce a tool, the Urban Landscape Generator, that can generate idealized heterogeneous urban environments with identical $\lambda _p$ and $\lambda _f$. The second aim is to investigate how the drag of these idealized heterogeneous surfaces is distributed in the vertical direction.

In the present study, we investigate the impact of heterogeneous morphologies on urban airflow. Building-resolving large-eddy simulations (LES) are performed for different heterogeneous urban morphologies. The simulations have a similar building density and frontal area index, but vary in complexity with different building heights, plan areas, and street geometries. We explore effects on mean flow structure and turbulence statistics and analyze how they can be quantified with an extended range of building statistics. Aerodynamic roughness parameters for the logarithmic wind profile are estimated, compared with values from the standard parametrizations of Macdonald et al. (1998) and Kanda et al. (2013), and correlated to building statistics. The variation in vertical momentum transport across the simulations is explored, including the separate contributions of turbulent and dispersive momentum fluxes. A generalized frontal area function is proposed that characterizes the vertical structure of urban morphologies. Using this representation of building morphology and the LES data, we derive a parametrization model that describes the vertical distribution of drag inside the urban canopy. The urban drag represents the momentum loss due to buildings and can be incorporated as an additional stress term in the momentum equations.

The paper is organized as follows: Sect. 2 reviews the governing equations and how building effects can be quantified using the spatially-averaged momentum-budget equation. Section 3 presents the numerical set-up and generation of heterogeneous morphologies using the Urban Landscape Generator. Section 4 analyzes the simulation data. First, instantaneous and mean-flow structures are evaluated and logarithmic wind profiles are analyzed; thereafter, vertical momentum transport is explored. Section 5 derives a parametrization for vertical drag distribution based on building morphology. The main conclusions are presented in Sect. 6.

2 Quantification of Momentum Loss in Urban Environments

Urban settlements modify the flow by forcing it around and over buildings, thus generating complicated flow structures in the wake of the buildings and producing turbulent motion around them (Belcher 2005; Oke et al. 2017). Below we review how buildings affect the mixing and vertical transport processes throughout and above the urban canopy. A momentum-budget equation may be derived by integrating the governing flow equations over the horizontal (x and y) directions, which describes the balance of horizontally-averaged forces acting on the fluid, such as a large-scale pressure gradient accelerating the flow, and a drag force by the building obstacles opposing it.

The horizontal spatial average of a flow quantity $\phi (t, x, y, z)$ over the fluid area in the x–y plane, denoted by $\Omega$, is defined by

$$\begin{aligned} \langle \phi \rangle (t, z) = \frac{1}{A_a(z)} \int _{\Omega } \phi (t, x, y, z) \,\text {d}{A}, \end{aligned}$$

(1)

where $A_a(z) = \int _{\Omega } \,\text {d}{A}$ is the fluid area at height z. For a statistically steady-state process, the Reynolds average can be obtained by taking a time average of $\phi (t, x, y, z)$ over a time span T longer than the typical flow-fluctuation time scale; the average is defined as

$$\begin{aligned} \overline{\phi }(x, y, z) = \frac{1}{T} \int _0^T \phi (t, x, y, z) \,\text {d}{t}. \end{aligned}$$

(2)

A framework for studying flow over spatially heterogeneous surfaces has been established for vegetated canopies (e.g., Raupach and Shaw 1982; Finnigan 2000; Nepf 2012), where flow variables are decomposed to isolate the effects of spatial inhomogeneity by means of a triple decomposition

$$\begin{aligned} \phi (t, x, y, z) = \langle \overline{\phi } \rangle (z) + \overline{\phi }^{\prime \prime }(x, y, z) + \phi ^{\prime } (t, x, y, z), \end{aligned}$$

(3)

where $\langle \overline{\cdot } \rangle$ is a space-time mean, $\overline{\cdot }^{\prime \prime }$ represents spatial variations of the time mean, and $\cdot ^{\prime }$ represents the turbulent fluctuations. This decomposition is a further refinement of classical Reynolds averaging, since $\overline{\phi } = \langle \overline{\phi } \rangle + \overline{\phi }^{\prime \prime }$, where $\overline{\phi }$ is the Reynolds average.

2.1 Momentum-Budget Equation over Spatially Heterogeneous Surfaces

Ignoring buoyancy effects by assuming constant density, the airflow in and above cities is described by the incompressible Navier–Stokes equations

$$\begin{aligned} \frac{\partial u_i}{\partial t} + u_j\frac{\partial u_i}{\partial x_j}&= - \frac{\partial p}{\partial x_i} + \nu \frac{\partial ^2u_i}{\partial x^2_j} + F_i, \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial u_i}{\partial x_i}&= 0, \end{aligned}$$

(5)

where the Einstein summation notation has been used. In the equation above, $u_i$ represents the velocity in the i-direction; $p = \tilde{p}/\rho _0 + F_x x + F_y y + g z$ is the kinematic pressure deviation, where $\tilde{p}$ is pressure; $\rho _0$ is a constant density; $F_{i}$ denotes large-scale kinematic pressure forcings in the x and y directions; and g is the standard acceleration due to gravity. We will assume a constant pressure-gradient forcing $F_i = - \rho _0^{-1} \partial P/\partial x_i = \mathrm{constant}($ $> 0$).

Time-averaging, spatial integration over the x–y planes $\Omega$, and division of (4) by the total area of the x–y plane, $A_T$, yield

$$\begin{aligned} \frac{\,\text {d}{}}{\,\text {d}{z}} \frac{1}{A_T} \int _{\Omega } \left( \, \overline{ w u_i - \nu \frac{\,\text {d}{} u_i}{\,\text {d}{z}} } \, \right) \,\text {d}{A} = \frac{A_a}{A_T} F_{i} -f_{D,i}, \end{aligned}$$

(6)

where

$$\begin{aligned} f_{D,i}&= - \frac{1}{A_T} \oint _{\partial \Omega } \left( \, \overline{ p n_i - \nu \frac{\partial u_i }{\partial x_j} n_j } \, \right) \,\text {d}{l}. \end{aligned}$$

(7)

For simplicity, we have assumed that the flow is in a statistically steady state, which implies that the z-direction variable is the only independent one. The line integral is defined along the building contours $\partial \Omega$ at height z with the normal vector $n_i$ pointing into the fluid region. The volumetric aerodynamic drag $f_{D,i}(z)$ describes the air resistance of the obstacles. The pressure contributions are referred to as form drag [first integral term in (7)], the frictional force related to molecular diffusion when air is moving parallel to the surface of the obstacles is the skin (or viscous) drag [second term in (7)].

Triple decomposition of the velocity variables using (3) and introducing the spatial-average notation (1), gives

$$\begin{aligned} - \frac{\,\text {d}{\tau _i}}{\,\text {d}{z}} = \frac{A_a}{A_T} F_i - f_{D,i}, \end{aligned}$$

(8)

where

$$\begin{aligned} \tau _i&= -\frac{A_a}{A_T} \left( \langle \overline{w}^{\prime \prime } \overline{u}^{\prime \prime }_i \rangle + \langle \overline{ w^{\prime } u^{\prime }_i } \rangle - \nu \frac{\,\text {d}{\langle \overline{u}_i \rangle }}{\,\text {d}{z}} \right) . \end{aligned}$$

(9)

Since the spatial average is defined as an intrinsic quantity of the flow variable, a correction term of the area ratio of fluid to total plane area $A_a(z)/A_T$ arises in Eq. 9. Changes in fluid area with height are substantial in urban areas, and therefore this term cannot be neglected. In the following we denote $\frac{A_a(z)}{A_T} \langle \cdot \rangle (z) = \langle \cdot \rangle _c (z)$, which is also known as superficial (Nikora et al. 2007) or comprehensive (Xie and Fuka 2018) spatial average. This simplifies the notation to

$$\begin{aligned} - \frac{\,\text {d}{\tau _i}}{\,\text {d}{z}} = \langle F_i \rangle _c - f_{D,i}, \quad \tau _i&= - \langle \overline{w}^{\prime \prime } \overline{u}^{\prime \prime }_i \rangle _c - \langle \overline{ w^{\prime } u^{\prime }_i } \rangle _c + \nu \frac{\,\text {d}{\langle \overline{u}_i \rangle _c}}{\,\text {d}{z}}. \end{aligned}$$

(10)

The term $\tau _i(z)$ represents the averaged total kinematic shear stress (turbulent and viscous), which describes the vertical momentum transfer. It consists of the dispersive flux $\langle \overline{w}^{\prime \prime } \overline{u}^{\prime \prime }_i \rangle _c(z)$, which represents the vertical transport due to the spatial inhomogeneity in the mean flow, the turbulent momentum flux $\langle \overline{ w^{\prime } u^{\prime }_i} \rangle _c(z)$, and the viscous momentum flux $- \nu \frac{\partial \langle \overline{u}_i \rangle _c}{\partial z}(z)$.

2.2 Force Balance for Streamwise Velocity and Constant Pressure Gradient

For an illustration of the force balance, the airflow is assumed only in the x direction with the streamwise velocity component $u_i = u$. We denote $\langle {F_x} \rangle _c = F(z)$, $\tau _x (z) = \tau (z)$ and $f_{D, x}(z) = f_D(z)$. Equation 10 then simply reads

$$\begin{aligned} F(z) + \frac{\,\text {d}{\tau }}{\,\text {d}{z}} (z) - f_D(z) = 0. \end{aligned}$$

(11)

A pressure gradient results in acceleration of airflow from higher pressure towards lower pressure. The averaged forcing F(z) is therefore an acceleration term and a source of momentum. Aerodynamic drag describes air resistance due to the obstacles, which is a force acting opposite to the fluid motion, decreasing the velocity, and therefore $f_D(z)$ is a deceleration term and a momentum sink. The change of momentum flux $\frac{\,\text {d}{\tau }}{\,\text {d}{z}}(z)$ describes the transport of momentum from higher altitudes, where the wind speed is greater, driven by large-scale flows and undisturbed from the influence of surface elements, down towards the surface, where surface friction and building drag generate resistance and lower velocities. This is a shear force acting throughout the atmosphere with equal acceleration and deceleration, and therefore a momentum-transport term. The implications of an assumption of steady flow are that the time-averaged forces balance and are unchanging over time. The force balance also provides a quantitative description of the different sublayers in the urban boundary layer (cf. Belcher 2005)

$$\begin{aligned}&\text {ISL:}&\frac{\,\text {d}{}}{\,\text {d}{z}} \langle \overline{ w^{\prime } u^{\prime } } \rangle&= F,&\end{aligned}$$

(12)

$$\begin{aligned}&\text {RSL:}&\frac{\,\text {d}{}}{\,\text {d}{z}} \left( \langle \overline{ w^{\prime } u^{\prime } } \rangle + \langle \overline{w}^{\prime \prime } \overline{u}^{\prime \prime } \rangle \right)&= F,&\end{aligned}$$

(13)

$$\begin{aligned}&\text {UCL:}&\frac{\,\text {d}{}}{\,\text {d}{z}} \left( \langle \overline{ w^{\prime } u^{\prime } } \rangle _c + \langle \overline{w}^{\prime \prime } \overline{u}^{\prime \prime } \rangle _c \right)&= F - f_D.&\end{aligned}$$

(14)

Note that above the buildings $\langle \cdot \rangle (z) = \langle \cdot \rangle _c(z)$, and that we have ignored viscous terms by assuming high Reynolds number flow. Far above the surface in the inertial sublayer (ISL), the only force acting on the fluid is the constant pressure-gradient force, which is balanced by the constant rate of downward momentum transport, initiated by the surface. Coming closer towards the buildings in the roughness sublayer (RSL), the mean flow becomes inhomogeneous due to the presence of obstacles below, and spatial patterns emerge in mean-flow quantities. Vertical transport initiated by the obstacles on the surface corresponds to a dispersive flux in the force balance that changes with height. Within the bottom urban canopy layer (UCL), all downwards-transported momentum from the upper layers is absorbed by the building drag. An illustration of the balancing forces in the urban sublayers is shown in Fig. 1a.

Fig. 1

Momentum budget in the urban boundary layer. a Force balance of pressure F (momentum source) and drag $f_D$ (momentum sink). Momentum transport $\,\text {d}{\tau }/\,\text {d}{z}$ consists of change of turbulent $- \,\text {d}{ \langle \overline{ w^{\prime } u^{\prime }} \rangle _c } /\,\text {d}{z}$ (dotted line) and dispersive $- \,\text {d}{ \left\langle \overline{w}^{\prime \prime } \overline{u}^{\prime \prime } \right\rangle _c} /\,\text {d}{z}$ (dashed line) momentum fluxes. b Kinematic stresses $\tau _F$, $\tau _D$, and $\tau$ show the areas under F, $f_D$, and $-\,\text {d}{\tau }/\,\text {d}{z}$, integrated downwards. Data from simulation S1

2.3 Cumulative Stresses and Volume Forces

Integrating the streamwise momentum budget (11) from some height z within the urban boundary layer to its top at height h we obtain

$$\begin{aligned} \tau (z) + \tau _D(z) = \tau _F(z), \end{aligned}$$

(15)

where the non-negative cumulative stress functions for drag and pressure are given by

$$\begin{aligned} \tau _D(z) = \int _z^{h} f_D(z') \,\text {d}{z'}, \quad \tau _F(z) = \int _z^{h} F(z') \,\text {d}{z'}. \end{aligned}$$

(16)

Figure 1b illustrates the kinematic stresses in Eq. 15. The profile of the constant pressure force $\tau _F(z)$ does not extend as a straight line due to the volume occupied by buildings within the UCL. The function $\tau _D(z)$ accumulates the drag force exerted by the buildings from the highest building point throughout the urban canopy layer, reaching the total canopy drag at the ground surface. There, total net momentum sinks and sources are equal, which means that $\tau _D(0) = \tau _F(0) \equiv \tau _0$, where the kinematic surface stress $\tau _0$ represents the effective drag of the urban canopy.

The total drag force $F_D$ due to the urban canopy is thus given by

$$\begin{aligned} F_D = \rho _0 A_T \int _0^h f_D(z') \,\text {d}{z'} = \rho _0 F_x \int _0^{h} A_a (z') \,\text {d}{z'} = \rho _0 F_x V_{\mathrm{air}}, \end{aligned}$$

(17)

where $F(z) = F_x A_a (z) / A_T$ and $V_{\mathrm{air}}$ is the volume of air inside the domain.

3 Simulation Set-up

3.1 Numerical Model and Set-up

Large-eddy simulations were performed using the Dutch Atmospheric LES model (DALES; Heus et al. 2010), which has recently been extended for the urban environment (uDALES, Tomas et al. 2016; Suter 2018; Grylls et al. 2019, 2020), providing the capability to model buildings using an immersed boundary method. The eddy-viscosity subgrid scheme follows Vreman (2004) and subgrid-scale (SGS) dynamics close to the building walls and street surface are modelled by logarithmic wall functions (Uno et al. 1995; Suter 2018). The numerical schemes are second-order central differences on a staggered Arakawa C-grid for spatial discretization and an explicit third-order Runge–Kutta time-integration scheme.

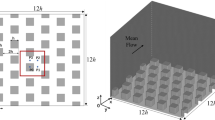
Nine different urban morphologies S1–S9 are considered, all with a building density of $\lambda _p =$ 0.45–0.46 and frontal area index of $\lambda _f = 0.22$, but with different numbers, shapes and heights of buildings. The method by which these are generated is discussed in Sect. 3.2. Layouts S1–S3 have uniform building heights. Note that S1 and S2 have approximately the same structure but at different scales. However, the external length scales bounding the flow (in this case the model domain, or the inversion height in the environment) produce different flows, as will be evident later. Layouts S4–S9 have heterogeneous building heights and differ in the street networks. The layouts are illustrated in Fig. 2 and geometry statistics are presented in Table 1. We distinguish three different definitions of mean height: a (plain) average building height $z_H$, an average height where each building height is weighted by its frontal area $z_{H,f}$, and an average height where buildings are weighted by their plan area $z_{H,p}$. Weighted standard deviations $\sigma _{H,f}$ and $\sigma _{H,p}$ are defined with the respective weighted means. Immediately, these morphologies illustrate the wide variation in urban layout which may be encompassed within near-identical values of $\lambda _p$ and $\lambda _f$.

Fig. 2

Urban morphologies for simulations S1–S9, generated with the Urban Landscape Generator

Table 1 Building statistics for morphologies S1–S9: number of buildings $n_b$, average building height $z_H$, maximum building height $z_{\max }$, average building height weighted by the frontal area $z_{H,f}$, average building height weighted by the plan area $z_{H,p}$, building height standard deviation $\sigma _H$, building height standard deviation weighted by frontal area $\sigma _{H,f}$ and by plan area $\sigma _{H,p}$

The simulation domain size is 480 m $\times$ 240 m $\times$ 234 m with a horizontal resolution of 2 m. The vertical resolution is constant at 1 m for the lower half of the grid cells and stretched thereafter with a stretching ratio of 1.01. Each layout describes a 120 m $\times$ 120 m region and is repeated eight times within the domain (see Fig. 3). This ensures a domain, in which the integral length scales of the turbulence can develop without interference, and has the added benefit of improving convergence of the averages within the RSL. Periodic boundary conditions are applied in the lateral directions, which implies that the simulations capture the atmospheric flow in a larger urban area. The domain-top boundary condition for momentum is free-slip.

The numerical simulations are performed under neutral atmospheric stability, and for each of the simulations the domain-average wind speed is kept constant at $U = 2\,\hbox {m s}^{-1}$. Since the drag will be different for each of the urban morphologies, this implies that the associated pressure-gradient forcing will be different for each simulation.

Fig. 3

Building plan area of simulations S1–S9. Layouts are repeated eight times within the simulation domain

The simulations are spun up for 10,000 s. An averaging time of 20,000 s is sufficient to produce converged statistics for the momentum budget. For the correct attribution of dispersive stresses, a much longer averaging time is required (Coceal et al. 2006). We found that an averaging time of 80,000 s is sufficiently long to average out slowly evolving mean streamwise circulations. Simulation S3 experiences more persistent slow-transient flow structures, and we therefore increased the averaging time to 100,000 s for this simulation to obtain converged statistics. Later, in Sect. 4.5 some examples of dispersive flux profiles are plotted in context. On the scale of those plots, the averages at 20,000 s would be indistinguishable from those at 80,000 s. Convergence times vary, and other simulations were similar at 60,000 s.

3.2 Urban Landscape Generator

To generate a range of idealized heterogeneous urban morphologies we developed the Urban Landscape Generator (ULG) tool, which is a procedural algorithm generating randomized urban landscapes with the morphological parameters $\lambda _p$ and $\lambda _f$ as input. The tool is available as open-source code (Sützl and van Reeuwijk 2020). The ULG tool was designed to gradually introduce more realistic features to idealized urban environments, such as variable building heights and shapes, and more complex street networks. The ULG creates fractal-like street networks by dividing building blocks into smaller blocks until the target building density is reached. Building heights are then chosen to reach the target frontal area density. The resulting buildings are cuboid-shaped and their faces are aligned in the streamwise and cross-stream directions. The ULG has parameters to control the level of randomness in the urban morphology. Layouts with little randomness are similar to the set-ups of generic block simulations (i.e., similar shaped and aligned blocks) as previously used in studies of idealized urban geometries (e.g., Coceal et al. 2006). A more organic city layout can be obtained by increasing the randomization. The resulting layouts are of self-similar structure, this means that they have similar statistical properties at many scales and therefore they are also useful to describe urban landscapes on different scales, for instance they can describe both the layout of individual buildings and the layout of entire similar structured neighbourhoods. More details on the ULG are provided in the Appendix.

4 Results

4.1 Instantaneous Flow Fields

Instantaneous flow fields reveal significant features of the fully-developed turbulent flow around buildings. Figure 4a shows a vertical section of the instantaneous horizontal wind speed $\sqrt{u(t,x,y,z)^2 + v(t,x,y,z)^2}$ for the heterogeneous simulation S4. The influence of the buildings extends well above the maximum height, and particularly the wakes of tall buildings show wind sheltering effects (Xie et al. 2008). The flow displays great spatial variability despite the repeated layouts. Figure 4b shows a horizontal section of the same wind field with velocity components u(x, y), v(x, y). Within the urban canyon, street corridors are important for redistributing the displaced air, with much higher wind speeds than more sheltered areas of the domain. The complex layout of buildings leads to spatially diverse patterns of wind speed and direction.

Fig. 4

Instantaneous wind-speed field of simulation S4 in a vertical a and horizontal b section

4.2 Mean Flow

Figure 5 shows profiles of the average wind speed $\langle \overline{u} \rangle (z)$, with height and velocity normalized by the weighted mean height $z_{H,f}$ and mean wind velocity at this height, respectively. The mean wind profiles of simulations with uniform building heights (S1–S3) are evidently distinct from simulations with non-uniform building heights (S4–S9). Wind profiles of the simulations with uniform building heights show a clear separation in within-canopy flow and above-canopy flow with an inflection point around the average building height. Within the canopy, airflow is obstructed by buildings and the velocity profile has a concave shape. Above the canopy, a typical boundary-layer profile develops quickly and the velocity profile changes to a convex shape. Simulations S4–S9 with heterogeneous building heights lack a clear separation in above- and within-canopy flow, instead the velocity profiles show a gradual change from approximately linear (within) to strictly convex (above the canopy); see in particular the difference between the wind profiles of uniform S2 (b) and non-uniform S4 (c) in Fig. 5.

Fig. 5

Normalized wind profiles of simulations S1–S9 in and above the urban canopy (a). Wind profiles of simulation S2 with uniform building heights (b) and simulation S4 with non-uniform building heights (c). A range for estimated logarithmic wind profiles is shown by the shaded grey area (b and c)

4.3 Estimation of Aerodynamic Roughness Parameters

It is commonly assumed that the wind profile in the inertial sublayer can be approximated by a logarithmic profile (Tennekes 1973)

$$\begin{aligned} \langle \overline{u} \rangle (z) = \frac{u_{*}}{\kappa } \ln \left( \frac{z - z_d}{z_0} \right) , \end{aligned}$$

(18)

where $u_{*}$ is the friction velocity, $\kappa =0.4$ is the von Kármán constant, $z_d$ is the displacement height, and $z_0$ is the aerodynamic roughness length. The parameters $z_d$ and $z_0$ are of interest for weather or climate models, as they are often used to determine wind profile or exchange fluxes for near-surface flows over urban areas.

An advantage of LES is the availability of complete vertical profiles of mean wind speed $\langle \overline{u} \rangle (z)$, and friction velocity by $u_{*} = \sqrt{\tau _0}$ (recall $\tau _0$ is a kinematic stress), which is directly available from (17) via $\tau _0=F_D/(\rho _0 A_T) = F_x(V_{\mathrm{air}}/A_T)$. The friction-velocity values for simulations S1–S9 are shown in Table 2.

Since $u_{*}$ is known a priori, $z_0$ and $z_d$ can be obtained by rewriting (18) as

$$\begin{aligned} z = z_0 \exp \left( {\frac{\kappa }{u_{*}} \langle \overline{u} \rangle (z)} \right) + z_d. \end{aligned}$$

(19)

Indeed, given z and $\langle \overline{u} \rangle (z)$, linear regression can be used to estimate parameters $z_d$ and $z_0$ as the slope and intercept of a least-squares fit. The log law is assumed to be valid in the ISL, therefore only wind speeds from within the ISL are appropriate for the linear regression.

We tested several fitting regions that are likely to be within the ISL: $[ 2z_{\max }, 2z_{\max } + 2z_H ]$, $[ 3z_{\max }, 3z_{\max } + 2z_H ]$, and $[ 4z_{\max }, 4z_{\max } + 2z_H ]$ for each simulation. However, these ranges may exceed an upper limit to the log law with respect to the boundary layer height, as argued in Jimenez (2004) for example. The resulting logarithmic wind profiles generally match well the wind profile data above the height of $2 z_{\max }$. For simulation layouts with uniform building heights, there is little difference between the different fitting ranges, and the logarithmic wind profiles yield a good approximation to the LES wind profiles even within the RSL. For layouts with non-uniform building heights there can be significant differences in the logarithmic wind profiles, depending on the fitting range. The estimated logarithmic wind profiles vary strongly below the height of $2 z_{\max }$, particularly for simulations with higher friction velocity and larger building-height variation (larger $\sigma _H$), showing that the log-law relation breaks down near the surface for strongly heterogeneous building heights. These strong variations in the lower parts of the logarithmic profiles suggest that the region where a log profile may be suitable is at least a length scale of height variation above the buildings. The difference between uniform and non-uniform layouts is illustrated in Fig. 5b and c, where the ranges of logarithmic wind profiles are indicated as grey-shaded areas.

A higher fitting range generally results in greater displacement heights and smaller roughness lengths, and a better agreement between the estimated logarithmic and LES wind profiles higher up. Conversely, a lower range results in lesser displacement heights and higher roughness lengths, with better agreement of the wind profiles closer to the canopy top. A similar trend is reported by Kanda et al. (2013) for their tests of various fitting regions. Ranges of the estimated roughness parameters are presented in Table 2.

Table 2 Estimated values for logarithmic law parameters. First column shows the friction velocity $u_{*}$ estimated from LES data. Ranges for displacement height $z_d$ and roughness length $z_0$ in the second and third columns are estimated with a least-square fit from the logarithmic law. Values estimated using the Jackson (1981) hypothesis are labelled with (J), including the then variable von Kármán parameter $\kappa$

An alternative calculation for the displacement height (e.g., used in Kanda et al. 2013; Castro et al. 2017; Giometto et al. 2017) follows a hypothesis by Jackson (1981), that the displacement height corresponds to the centre of moment of the forces acting on the buildings. In other words the displacement height is assumed to be the level of the mean momentum sink. The centre of mass of the volumetric drag function is

$$\begin{aligned} \frac{\int _0^{h} z f_D(z) \,\text {d}{z}}{\int _0^{h} f_D(z) \,\text {d}{z}} = \frac{\int _0^{h} \tau _D(z) \,\text {d}{z}}{\tau _0}. \end{aligned}$$

(20)

Rewriting the log law to

$$\begin{aligned} \ln (z - z_d) = \frac{\kappa }{u_{*}} \langle \overline{u} \rangle (z) + \ln (z_0) \end{aligned}$$

(21)

yields an alternative form for linear regression, where the parameters $\kappa /u_{*}$ and $\ln (z_0)$ are slope and intercept respectively of a least squares fit. Using (20) as an estimate for $z_d$ and consequently also $u_{*} = \sqrt{\tau _0}$, we must assume that $\kappa$ is the variable parameter. Linear regression with fitting region $[3 z_{\max }, 3 z_{\max } + 2z_H]$ yields new values of the von Kármán constant ranging from 0.29–0.37 and consistently lower displacement heights compared to the previous method. A reason for this may be that using the centroid of drag does not consider any displacement effects from dispersive fluxes in the RSL, opposed to the purely statistical fit of $z_d$. The smaller displacement heights are partly compensated for by higher estimates for roughness length, compared to the previous log-law fits. However, a well-defined displacement height as the centre of drag comes at the cost of losing a fixed value for the von Kármán constant, as the variability in $\kappa$ shows. Values for estimated $z_d$, $z_0$, and $\kappa$ using (21) are listed in Table 2.

4.4 Comparison and Scaling of Roughness Parameters

Figure 6 shows the displacement heights $z_d$ and roughness lengths $z_0$ normalized by the average height $z_H$ for simulations S1–S9 estimated with (19) in the fitting region $[ 3z_{\max }, 3z_{\max } + 2z_H ]$, compared to values obtained from two standard parametrizations: Macdonald et al. (1998) and Kanda et al. (2013). The Macdonald et al. parametrizations depend only on the building density $\lambda _p$, frontal area index $\lambda _f$, and average building height $z_H$. The normalized quantities $z_d/z_H$ and $z_0/z_H$ therefore map to a single value for all simulations. Kanda et al. additionally consider, as parameters, maximum building height $z_{\max }$ and standard height deviation $\sigma _H$, which yields different values of $z_d/z_H$ and $z_0/z_H$ for each simulation. However, the range of values using their parametrization still does not encompass all values estimated from the data fit. Particularly the displacement heights from simulations with larger friction velocities are underestimated by these parametrizations. The smaller displacement height of Macdonald et al. is related to the fact that no building effects above the average building height are considered. The lower displacement heights of Kanda et al. may be partly explained by their usage of a lower fitting range ($[ z_{\max } + 0.2 z_H, z_{\max } + z_H ]$) for estimating the log-law parameters, which generally results in lower displacement heights.

Fig. 6

Comparison of estimated roughness parameters. Normalized displacement height (a) and roughness length (b) for simulations S1–S9 with fitting range $[ 3z_{\max }, 3z_{\max } + 2z_H ]$ (markers), and estimated using Macdonald et al. (1998) parametrization (grey dot). Parameter curves for Macdonald et al. (1998) (dashed line) and Kanda et al. (2013) (grey shaded)

The average building height $z_H$ is usually taken as the scaling length for the roughness parameters (Macdonald et al. 1998 and other parametrizations, see citations in Kent et al. 2017); however, also $z_{\max }$ and $\sigma _H$ are suggested to be important indicators for roughness parameters in the logarithmic law (Millward-Hopkins et al. 2012; Kanda et al. 2013; Kent et al. 2017). In the following, we investigate potential scaling parameters and, more generally, the effects of building morphology on aerodynamic roughness. This is achieved by correlating the urban morphology statistics from Table 1 to $z_d$, $z_0$ and the friction factor $c_f = 2 \tau _0/ U^2$ as a non-dimensional and velocity-independent representation of friction. The values of $z_d$ and $z_0$ are taken from the mid-range fitting region $[3 z_{\max }, 3 z_{\max } + 2z_H]$. It should be noted that our aim is to elicit which parameters correlate strongly with $c_f$, $z_d$, and $z_0$; not to provide improved parametrizations of these quantities since these would require a much larger dataset.

Figure 7 shows the correlations of a linear regression between the roughness parameters $c_f$, $z_d$, and $z_0$, and average height $z_H$, maximum height $z_{\max }$, and $z_H, z_{\max }$ combined with the standard deviation of heights $\sigma _H$. Perhaps the most striking aspect of this figure is that average building height $z_H$ correlates very weakly with $c_f, z_d$, and $z_0$ (Fig. 7a–c). The weighted average heights $z_{H,f}$ and $z_{H,p}$ also show no significant correlation, with the exception of $z_{H,f}$ correlating to $z_d$ (not shown). This finding is consistent with Hagishima et al. (2009), Millward-Hopkins et al. (2011), Zaki et al. (2011), and Kanda et al. (2013). Furthermore, the maximum height $z_{\max }$ correlates strongly with both the friction factor and the displacement height, as the only parameter from Table 1. Higher correlations are obtained for combining parameters to a multiple linear regression. Both average height $z_H$ combined with the building height standard deviation $\sigma _H$ (g–i), and the maximum height $z_{\max }$ combined with height deviation $\sigma _H$ (j–l) show strong correlations for $c_f, z_d$, and $z_0$.

In agreement with Kanda et al. (2013), we conclude that $z_{\max }$ is more likely to be the relevant scaling length for $z_d$. The maximum height shows a better correlation than the average height parameters $z_H$ and $z_{H,p}$ (only the frontal-area weighted average height $z_{H,f}$ has a comparable correlation to the displacement height), and also correlates for $c_f$ and $z_0$, which is not the case for the average heights. The height structure of buildings clearly affects roughness parameters, which suggests that $z_{\max }$ and $\sigma _H$ are important indicators for the length scale of surface variation. The large spread in roughness parameters for similar $\lambda _p$ and $\lambda _f$ (cf. Fig. 6) and the uncertainties of characterizing friction with morphology statistics, demonstrate the challenges of using the logarithmic wind profile to represent momentum transport over heterogeneous urban surfaces. We suggest that it might be more productive to consider the momentum balance directly, from which a velocity profile could be inferred.

Fig. 7

Correlations between urban morphology and log-law parameters. The vertical axes show the log-law parameters of friction factor $c_f$ (a, d, g, j), displacement height $z_d$ (b, e, h, k) and roughness length $z_0$ (c, f, i, l). On the horizontal axes are the urban morphology parameters with the respective best fit coefficients $c_i$. Note that the coefficients differ for each of the subplots. Uniform height simulations S1–S3 are shown with circles, non-uniform S4–S9 with triangles

4.5 Vertical Transport

Figure 8a shows the vertical momentum fluxes $\tau (z)$, which have all different slopes due to the difference in the pressure-gradient forcings (recall that the volume flux was prescribed). The integral effect of drag is given by the different kinematic surface stresses $\tau _0$, which vary greatly between the simulations. From simulation S3 with the lowest canopy drag to simulation S4 with the highest canopy drag, the surface stress roughly doubles. This once more highlights that the interaction of urban morphology and the atmospheric boundary layer is not determined solely by the building density and frontal area index.

Fig. 8

Vertical fluxes of horizontal momentum. a shows vertical momentum fluxes $\tau$ (solid lines), stress profiles $\tau _F$ (dotted lines), and kinematic surface stresses $\tau _0$ (markers). Normalized stress profiles of simulation S2 with uniform building heights (b) and simulation S4 with non-uniform building heights (c). The stress profiles are: total momentum (solid lines), turbulent (dotted), dispersive (dashed), and subgrid-scale (dashed dotted)

Several physical processes in urban environments initiate vertical momentum transport. Mixing from turbulent eddies is the main contribution to the vertical momentum transport, although dispersive momentum fluxes, which represent the effects of spatial inhomogeneity of the mean flow, also play a role in the roughness sublayer and canopy layer. In simulations S1–S9, both turbulent and total momentum fluxes reach their maximum at the top of the urban canopies. The overall contribution of dispersive momentum fluxes is about 5% of the total momentum fluxes. Subgrid momentum fluxes, which represent unresolved momentum fluxes in regions of high shear, contribute a maximum of 1% of the total momentum fluxes and are only present at heights with large horizontal surfaces (i.e., the ground and building tops). Figure 8b and c show a detailed view of the momentum fluxes of two simulations with uniform (S2) and non-uniform (S4) building heights in the lower levels of the urban boundary layer.

Locally, dispersive fluxes are significant and can make up to 50% of the total fluxes at some heights within the canopy. Except for S1, all dispersive fluxes peak within the canopy layer. Above the canopy, the dispersive fluxes quickly reduce and turbulent fluxes become dominant. Non-zero dispersive fluxes range up to 2–6 times the maximum building height, suggesting a roughness sublayer up to these heights. For uniform building heights (S1–S3) the RSL does not extend further than three building heights. The shape of the dispersive flux varies with the building layout. In simulations with uniform building heights (S1–S3), the dispersive downward momentum transport increases continuously with height up until the canopy top. Heterogeneous building heights (S4–S9) show more variation in the dispersive transport, due to several height levels where the flow is displaced above the building tops and decelerates. Dispersive fluxes within the urban canopies are larger for heterogeneous simulations with larger total canopy drag (S4, S7, S8). The downward dispersive momentum transport peaks typically below the canopy top, and often around the frontal-area weighted average height. Some simulations have re-circulation zones with strong flows in the opposite direction to the driving flow near the bottom surface, so that the dispersive fluxes change sign.

5 Drag Parametrization

The cumulative drag function $\tau _D(z)$ describes the accumulation of building drag in the urban canopy layer towards the ground. Figure 9a shows the cumulative drag profiles of all simulations S1–S9. The profiles vary strongly for each of the simulations with no apparent trend. The drag increases quickly at the top of the buildings, which is evident from the profiles of simulations S1–S3. We may further assume that the buildings’ surface area higher up contributes more drag, due to the generally higher wind speeds at higher altitudes. In order to measure the effects of the wind-facing building surfaces relative to a reference level, a descriptor of the vertical structure of the building layouts is needed, which will be a generalized version of the frontal area index $\lambda _f$.

Let $L(z,\theta )$ be the total projected building width at height z for wind direction $\theta$. With this definition, the frontal area index is

$$\begin{aligned} \lambda _f(\theta ) = \frac{1}{A_T}\int _0^h L(z', \theta ) \,\text {d}{z'}. \end{aligned}$$

(22)

A generalized frontal area index ${\Lambda }_f$ can be defined as

$$\begin{aligned} {\Lambda }_f(z, \theta ) = \frac{1}{A_T} \int _z^{h} L(z', \theta ) \,\text {d}{z'}, \end{aligned}$$

(23)

which is essentially the normalized projected frontal area above height z. Clearly, ${\Lambda }_f(0, \theta ) = \lambda _f$ and ${\Lambda }_f(z > z_{\max }, \theta ) = 0$. In the simulations S1–S9, the wind orientation and the buildings are aligned with the x axis. This means that $\theta = 0$ and the total building width is $L(z) = \sum _i B_{w,i}(z)$, where $B_{w,i}(z)$ denotes the width of building $B_i$ at height z. Note that for the current set-up $B_{w,i}$ is constant with height. The scaled frontal area

$$\begin{aligned} \zeta (z) = \frac{{\Lambda }_f(z)}{\lambda _f} = \frac{1}{A_F} \int _z^{h} L(z') \,\text {d}{z'} \end{aligned}$$

(24)

shown in Fig. 9b can be used to serve as an alternative height representation of the buildings where $\zeta = 0$ represents the top of the buildings and $\zeta = 1$ represents ground level. Because the height coordinate is scaled as $z/z_{\max }$, the $\zeta$ profiles of layouts S1–S3 with uniform buildings heights overlap to a linear function with constant slope. Layouts with non-uniform building heights have piecewise linear functions $\zeta (z)$.

The LES data reveal a strong relationship between the cumulative drag and the vertical building structure. Figure 9c shows that plotting $\tau _D(z)/\tau _0$ as a function of $1 - \zeta (z)$ results in a practically full collapse of all the data. The collapsed data can be fitted reasonably well using a single third-order polynomial of the form

$$\begin{aligned} s(\zeta ) = A \zeta ^3 + B \zeta ^2 + (1 - A - B) \zeta , \end{aligned}$$

(25)

with $A = 1.88$ and $B = - 3.89$. Testing the polynomial regression with different orders shows that the third-order polynomial captures sufficiently well the vertical shape of $\tau _D(z)$; increasing the polynomial order does not result in significantly more accurate approximations.

Note that (25) enables direct evaluation of the cumulative canopy-drag profile

$$\begin{aligned} \tau _D(z) = \tau _0 \, s (\zeta (z)), \end{aligned}$$

(26)

provided that the net total canopy drag $\tau _0$ is known. Figure 9 shows the estimated profiles in (d), which closely resemble the data in (a). It shows that a distribution of the urban canopy drag can be reconstructed using only the building layout and an estimation for the total canopy drag.

Fig. 9

Cumulative drag functions and their parametrization. Cumulative drag $\tau _D$ (a), scaled frontal area $\zeta$ (b), correlation between these (c), and estimated cumulative drag $\tau _0 \, s(\zeta )$ (d)

By differentiating (26), the volumetric drag term can be determined as

$$\begin{aligned} f_D(z) = - \frac{\,\text {d}{\tau _D}}{\,\text {d}{z}} (z) = - \tau _0 \frac{\,\text {d}{s}}{\,\text {d}{\zeta }} \frac{\,\text {d}{\zeta }}{\,\text {d}{z}} (z) = \tau _0 \, s^{\prime } (\zeta (z)) \frac{L(z)}{A_F}. \end{aligned}$$

(27)

The term $L(z)/A_F$ expresses the ratio of the frontal area above height z to the total frontal area, and it shows that the wind-facing area of the buildings play a key role in the production of drag. That the production of drag is not necessarily constant across the urban canopy is represented by $s^{\prime } (\zeta (z))$, a nonlinear function of the building layout $\zeta (z)$.

Equation 27 is a generalization of the canopy-drag model for uniform buildings of Coceal and Belcher (2004) and Belcher (2005). In Coceal and Belcher ’s model with N uniform buildings, $L(z) = N B_w$, from which it follows that $\zeta (z) = 1 - z/z_H$ for $z \le z_H$. Belcher (2005) assumes constant canopy drag, in which case $s(\zeta ) = \zeta$ and therefore $s^{\prime }(\zeta ) = 1$. The volumetric drag is then given by $f_D(z) = \tau _0/z_H$ with an appropriate estimation for the net total canopy drag.

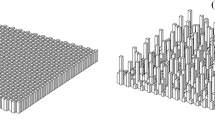
Figure 10 shows two generic examples, one of a single uniform building and one of several heterogeneous buildings, which illustrate the drag distribution throughout the canopy given by Eq. 27. Because the cumulative drag has been fitted with a cubic polynomial function, the volumetric drag profile is quadratic in shape. For a single building, the volumetric drag initially decreases above the ground, then increases nonlinearly towards the top of the building, where most drag is produced. The volumetric drag for multiple buildings with heterogeneous shapes and heights combines the drag of individual buildings in a nonlinear way, with spikes in volumetric drag clearly indicating each building top.

Fig. 10

Illustration of the derived relation between building geometry and volumetric drag. Geometries of a single building (a, solid line) and several heterogeneous buildings (b, dashed grey line) with corresponding projected building width L (c) and volumetric drag $f_D$ (d)

6 Conclusions

Urban areas are intrinsically heterogeneous. Parametrizations of urban areas often rely on simple characterizations based on building density and frontal area index, implicitly assuming homogeneous surface conditions. In this study, the differences in mean-flow structure and turbulence statistics resulting from idealized heterogeneous morphologies were explored. The urban morphologies were generated using a new tool, the Urban Landscape Generator, which is capable of generating idealized heterogeneous urban morphologies with identical $\lambda _p$ and $\lambda _f$.

The heterogeneity of an urban site was shown to strongly influence the vertical structure of mean flow and dispersive vertical momentum transport. At equal average wind velocity U, the total surface drag varies as much as almost a factor two between a uniform and strongly heterogeneous morphology. Regression analysis showed that the variations are correlated to the height structure of buildings, particularly to the maximum building height $z_{\max }$ and height variation $\sigma _H$, rather than average height $z_H$.

Developing parametrizations for heterogeneous building morphologies based on the logarithmic wind profile is challenging. First, even with a detailed velocity height-profile and known friction velocity, the estimated displacement height $z_d$ and roughness length $z_0$ for heterogeneous morphologies cannot be uniquely identified, because they depend on the selected fitting range of the data. Whilst this may partially be attributed to the limited domain height used in the simulations, it demonstrates intrinsic uncertainty in estimates for $z_0$ and $z_d$. Second, our results indicate that current well-known parametrizations of the log law such as Macdonald et al. (1998) and Kanda et al. (2013) cannot sufficiently capture the large spread of roughness-parameter values, even with additional building statistics such as the maximum height $z_{\max }$ and height variation $\sigma _H$.

An exploration of the vertical structure of the surface drag revealed that, at first sight, there is very little that the different simulations have in common. However, the generalized frontal area index ${\Lambda }_f(z)$ (23), which encapsulates the height distribution of the surface area, was shown to be able to collapse all distributed stress profiles on a single curve. This paved the way to a parametrization of the drag distribution via a third-order polynomial (25). Importantly, this relationship is not linear and the top of the urban canopy, i.e. the highest building in the morphology, produces significantly more drag than the buildings below.

The new drag-distribution model can be used to guide the development of urban canopy models. Numerical weather prediction models may benefit from a distributed-drag approach, because it allows for a more robust and detailed representation of building effects. This is especially important for urban areas with high-rise buildings, i.e. with a large subgrid heterogeneity. However, the distributed-drag model developed here still relies on the friction velocity as an input parameter. The current study investigated the correlations between friction velocity and urban morphology which showed particularly high correlations with the maximum height $z_{\max }$. Extensive simulation/experimental campaigns are necessary to provide improved parametrizations of the friction velocity that are statistically significant.

Appendix: Urban Landscape Generator

This appendix describes the technical details of the Urban Landscape Generator (ULG) tool, which is open-source and can be downloaded from https://github.com/bss116/citygenerator (Sützl and van Reeuwijk 2020). The Urban Landscape Generator is a procedural algorithm that builds fractal-like street networks based on urban morphology parameters. The algorithm divides building blocks into smaller blocks until a target plan-area density is reached. Building blocks are then given heights to match the target frontal-area density. A chosen level of randomness influences the street widths, intersection points and building heights. The ULG can generate arbitrarily many urban landscapes with a fixed set-up of $\lambda _f$ and $\lambda _p$, and gradually increases the complexity of the layouts based on the degree of randomness in the procedural generation.

At the start the Urban Landscape Generator initializes the full domain as first block. The algorithm then chooses a street intersection within the block to subdivide the block into four new blocks. For as long as the sum of the newly created block areas is larger than the target plan-area, the algorithm continues subdividing blocks. On the street level, heterogeneity is introduced by specifying a fractal type, which determines how a block is chosen for subdivision. The ‘hierarchical’ type chooses the blocks in a set order, such that all blocks on the same level of hierarchy are divided first, before going into a lower hierarchy level. This type produces fairly idealized structures, the simplest of which is a regular grid. The ‘random’ type selects a random block out of all available blocks. If the selected block is too small for further subdivision, the algorithm selects the next suitable block. This type is designed to better resemble the organic growth of cities.

Two distinct randomness parameters control the street widths and intersections (layout randomness $r_l$), and the height of blocks (height randomness $r_h$). The randomness parameter $r_i, \, i \in \{ l, h \},$ defines a probability distribution across a given interval or set of points, from which the ULG draws sample values. No randomness $r_i = 0$ returns a pre-set value from the interval, e.g. the mid-points of the block sides for a new intersection. With randomness $r_i = 1$ the algorithms chooses freely from the given interval. For $0< r_i < 1$, the algorithm chooses points such that the probability of obtaining the pre-set value is $r_i$, the remaining probability is uniform across the rest of the interval. For new intersections, the probability of obtaining the mid-points of the block sides is therefore $r_l$, the remaining probability is uniform across the rest of the block sides, obeying certain margins at the edges. A similar distribution is defined over the range of potential street widths. Note that the probability density function is written as a separate module to the code and can therefore easily be modified or replaced e.g. with a p.d.f. based on morphology data.

Fig. 11

Fractal types and randomness of the Urban Landscape Generator. a Hierarchical layout, no randomness ($r_l = 0$). b Hierarchical layout with randomness ($r_l = 0.6$). c Random layout with randomness ($r_l = 0.7$)

Realistic values for street widths of various types (e.g. high street, residential street; following, Department for Transport 2007) are defined and chosen according to the level of hierarchy, i.e. how often the algorithm has already subdivided the domain. After the final layout is set, the algorithm adds heights to each of the blocks, until the prescribed frontal area is reached. The height randomness parameter $r_h$ defines how a height is selected from a range of possible heights, where a uniform height is added to each of the blocks if $r_h = 0$. Figure 11 illustrates three typical layouts with different configurations. Algorithms 1–3 describe the layout-generation code.