Abstract
We consider the Fermi–Pasta–Ulam–Tsingou (FPUT) chain composed by \(N \gg 1\) particles and periodic boundary conditions, and endow the phase space with the Gibbs measure at small temperature \(\beta ^{-1}\). Given a fixed \({1\le m \ll N}\), we prove that the first m integrals of motion of the periodic Toda chain are adiabatic invariants of FPUT (namely they are approximately constant along the Hamiltonian flow of the FPUT) for times of order \(\beta \), for initial data in a set of large measure. We also prove that special linear combinations of the harmonic energies are adiabatic invariants of the FPUT on the same time scale, whereas they become adiabatic invariants for all times for the Toda dynamics.
Similar content being viewed by others
1 Introduction and Main Results
The FPUT chain with N particles is the system with Hamiltonian
which we consider with periodic boundary conditions \(q_N=q_0\,\), \(p_N=p_0\) and \({\mathtt b}> 0\). We observe that any generic nearest neighborhood quartic potential can be set in the form of \(V_F(x)\) through a canonical change of coordinates. Over the last 60 years the FPUT system has been the object of intense numerical and analytical research. Nowadays it is well understood that the system displays, on a relatively short time scale, an integrable-like behavior, first uncovered by Fermi, Pasta, Ulam and Tsingou [13, 14] and later interpreted in terms of closeness to a nonlinear integrable system by some authors, e.g. the Korteweg-de Vries (KdV) equation by Zabusky and Kruskal [41], the Boussinesq equation by Zakharov [42], and the Toda chain by Manakov first [31], and then by Ferguson, Flaschka and McLauglin [12]. On larger time scales the system displays instead an ergodic behavior and approaches its micro-canonical equilibrium state (i.e. measure), unless the energy is so low to enter a KAM-like regime [25, 26, 36].
In the present work we show that a family of first integrals of the Toda system are adiabatic invariants (namely almost constant quantities) for the FPUT system. We bound their variation for times of order \(\beta \), where \(\beta \) is the inverse of the temperature of the chain. Such estimates hold for a large set of initial data with respect to the Gibbs measure of the chain and they are uniform in the number of particles, thus they persist in the thermodynamic limit.
In the last few years, there has been a lot of activity in the problem of constructing adiabatic invariants of nonlinear chain systems in the thermodynamic limit, see [8, 9, 18, 19, 29, 30]. In particular adiabatic invariants in measure for the FPUT chain have been recently introduced by Maiocchi, Bambusi, Carati [29] by considering the FPUT chain a perturbation of the linear harmonic chain. Our approach is based on the remark [12, 31] that the FPUT chain (1.1) can be regarded as a perturbation of the (nonlinear) Toda chain [39]
which we consider again with periodic boundary conditions \(q_N=q_0\,\), \(p_N=p_0\). The equations of motion of (1.1) and (1.2) take the form
where H stands for \(H_F\) or \(H_T\) and V for \(V_F\) and \(V_T\) respectively.
According to the values of \({\mathtt b}\) in (1.1), the Toda chain is either an approximation of the FPUT chain of third order (for \({\mathtt b}\ne 1\)), or fourth order (for \({\mathtt b}= 1\)). We remark that the Toda chain is the only nonlinear integrable FPUT-like chain [11, 37].
The Toda chain admits several families of N integrals of motion in involution (e.g. [16, 24, 40]). Among the various families of integrals of motion, the ones constructed by Henon [22] and Flaschka [15] are explicit and easy to compute, being the trace of the powers of the Lax matrix associated to the Toda chain. In the following we refer to them simply as Toda integrals and denote them by \(J^{(k)}\), \(1 \le k \le N\) (see (2.12)).
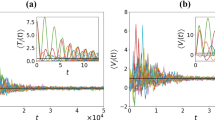
As the \(J^{(k)}\)’s are conserved along the Toda flow, and the FPUT chain is a perturbation of the Toda one, the Toda integrals are good candidates to be adiabatic invariants when computed along the FPUT flow. This intuition is supported by several numerical simulations, the first by Ferguson–Flaschka–McLaughlin [12] and more recently by other authors [4, 6, 10, 20, 35]. Such simulations show that the variation of the Toda integrals along the FPUT flow is very small on long times for initial data of small specific energy. In particular, the numerical results in [4, 6, 20] suggest that such phenomenon should persists in the thermodynamic limit and for “generic” initial conditions.
Our first result is a quantitative, analytical proof of this phenomenon. More precisely, we fix an arbitrary \(m \in {\mathbb N}\) and provided N and \(\beta \) sufficiently large, we bound the variations of the first m Toda integrals computed along the flow of FPUT, for times of order
where \(C_1\) is a positive constant, independent of \(\beta , N\). Such a bound holds for initial data in a large set with respect to the Gibbs measure. Note that the bound (1.4) improves to \(\beta ^{\frac{3}{2}}\) when \({\mathtt b}= 1\), namely when the Toda chain becomes a fourth order approximation of the FPUT chain. Such analytical time-scales are compatible with (namely smaller than) the numerical ones determined in [4,5,6].
An interesting question is whether the Toda integrals \(J^{(k)}\)’s control the normal modes of FPUT, namely the action of the linearized chain. It turns out that this is indeed the case: we prove that the quadratic parts \(J^{(2k)}_2\) (namely the Taylor polynomials of order 2) of the integral of motions \(J^{(2k)}\), are linear combinations of the normal modes. Namely one has
where \(E_j\) is the jth normal mode (see (2.21) for its formula), \(({\widehat{\mathbf{p}}}, {\widehat{\mathbf{q}}})\) are the discrete Hartley transform of \((\mathbf{p},\mathbf{q})\) (see definition below in (2.18)) and \({\widehat{\mathbf{c}}}^{(k)}\) are real coefficients.
So we consider linear combinations of the normal modes of the form
where \(({\widehat{g}}_j)_j\) is the discrete Hartley transform of a vector \(\mathbf{g}\in {\mathbb R}^N\) which has only \(2\lfloor \frac{m}{2}\rfloor +2\) nonzero entries with m independent from N, here \(\lfloor \frac{m}{2}\rfloor \) is the integer part of \(\frac{m}{2}\). Our second result shows that linear combinations of the form (1.6), when computed along the FPUT flow, are adiabatic invariants for the same time scale as in (1.4).
Further we also show that linear combinations of the harmonic modes as in (1.6), are approximate invariant for the Toda dynamics (with large probability).
Examples of linear combinations (1.6) that we control are
These linear combinations weight in different ways low and high energy modes.
Finally we note that, in the study of the FPUT problem, one usually measures the time the system takes to approach the equilibrium when initial conditions very far from equilibrium are considered. On the other hand, our result indicates that, despite initial states are sampled from a thermal distribution, nonetheless complete thermalization is expected to be attained, in principle, over a time scale that increases with decreasing temperature.
Our results are mainly based on two ingredients. The first one is a detailed study of the algebraic properties of the Toda integrals. The second ingredient comes from adapting to our case, methods of statistical mechanics developed by Carati [8] and Carati–Maiocchi [9], and also in [18, 19, 29, 30].
2 Statement of Results
2.1 Toda integrals as adiabatic invariants for FPUT
We come to a precise statements of the main results of the present paper. We consider the FPUT chain (1.1) and the Toda chain (1.2) in the subspace
which is invariant for the dynamics. Here \({\mathcal L}\) is a positive constant.
Since both \(H_F\) and \(H_T\) depend just on the relative distance between \(q_{j+1}\) and \(q_j\), it is natural to introduce on \({\mathcal M}\) the variables \(r_j\)’s as
which are naturally constrained to
due to the periodic boundary condition \(q_N = q_0\). We observe that the change of coordinates (2.2) together with the condition (2.3) is well defined on the phase space \({\mathcal M}\), but not on the whole phase space \({\mathbb R}^N\times {\mathbb R}^N\). In these variables the phase space \({\mathcal M}\) reads
We endow \({\mathcal M}\) by the Gibbs measure of \(H_F\) at temperature \(\beta ^{-1}\), namely we put
where as usual \(Z_F(\beta )\) is the partition function which normalize the measure, namely
We remark that we can consider the measure \(\mathrm{d}\mu _F\) as the weak limit, as \(\epsilon \rightarrow 0\), of the measure
Given a function \(f:{\mathcal M}\rightarrow {\mathbb C}\), we will use the probability (2.5) to compute its average \(\left\langle f \right\rangle \), its \(L^2\) norm \(\Vert f \Vert \), its variance \(\sigma _f^2\) defined as
In order to state our first theorem we must introduce the Toda integrals of motion. It is well known that the Toda chain is an integrable system [22, 39]. The standard way to prove its integrability is to put it in a Lax-pair form. The Lax form was introduced by Flaschka in [15] and Manakov [31] and it is obtained through the change of coordinates
By the geometric constraint (2.3) and the momentum conservation \(\sum _{j=0}^{N-1} p_j = 0\) (see (2.1)), such variables are constrained by the conditions
The Lax operator for the Toda chain is the periodic Jacobi matrix [40]
We introduce the matrix \(A=L_+-L_-\) where for a square matrix X we call \(X_+\) the upper triangular part of X
and in a similar way by \(X_-\) the lower triangular part of X
A straightforward calculation shows that the Toda equations of motions (1.3) are equivalent to
It then follows that the eigenvalues of L are integrals of motion in involutions.
In particular, the trace of powers of L,
are N independent, commuting, integrals of motions in involution. Such integrals were first introduced by Henon [22] (with a different method), and we refer to them as Toda integrals. We give the first few of them explicitly, written in the variables \((\mathbf{p}, \mathbf{r})\):
Note that \(J^{(2)}\) coincides with the Toda Hamiltonian \(H_T\).
Our first result shows that the Toda integral \(J^{(m)}\), computed along the Hamiltonian flow \(\phi ^t_{H_F}\) of the FPUT chain, is an adiabatic invariant for long times and for a set of initial data in a set of large Gibbs measure. Here the precise statement:
Theorem 2.1
Fix \(m \in {\mathbb N}\). There exist constants \(N_0, \beta _0, C_0, C_1>0\) (depending on m), such that for any \(N > N_0\), \(\beta > \beta _0\), and any \(\delta _1,\delta _2>0\) one has
for every time t fulfilling
In (2.14) \(\mathbf{P}\) stands for the probability with respect to the Gibbs measure (2.5).
We observe that the time scale (2.15) increases to \(\beta ^{\frac{3}{2}}\) for \({\mathtt b}= 1\), namely if the Toda chain is a fifth order approximation of the FPUT chain.
Remark 2.2
By choosing \(0< \varepsilon < \frac{1}{4}\), \(\delta _1=\beta ^{-\epsilon }\) and \(\delta _2=\beta ^{-2\epsilon }\) the statement of the above theorem becomes:
for every time t fulfilling
Remark 2.3
We observe that our estimates in (2.14) and (2.15) are independent from the number of particles N. Therefore we can claim that the result of theorem 2.1 holds true in the thermodynamic limit, i.e. when \(\lim _{N\rightarrow \infty } \frac{\langle H_F\rangle }{N} = e > 0\) where \(\langle H_F\rangle \) is the average over the Gibbs measure (2.5) of the FPUT Hamiltonian \(H_F\). The same observation applies to Theorems 2.5 and 2.6 below.
Our Theorem 2.1 gives a quantitative, analytical proof of the adiabatic invariance of the Toda integrals, at least for a set of initial data of large measure. It is an interesting question whether other integrals of motion of the Toda chain are adiabatic invariants for the FPUT chain. Natural candidates are the actions and spectral gaps.
Action-angle coordinates and the related Birkhoff coordinates (a cartesian version of action-angle variables) were constructed analytically by Henrici and Kappeler [23, 24] for any finite N, and by Bambusi and one of the author [1] uniformly in N, but in a regime of specific energy going to 0 when N goes to infinity (thus not the thermodynamic limit).
The difficulty in dealing with these other sets of integrals is that they are not explicit in the physical variables \((\mathbf{p}, \mathbf{r})\). As a consequence, it appears very difficult to compute their averages with respect to the Gibbs measure of the system.
Despite these analytical challenges, recent numerical simulations by Goldfriend and Kurchan [20] suggest that the spectral gaps of the Toda chain are adiabatic invariants for the FPUT chain for long times also in the thermodynamic limit.
2.2 Packets of normal modes
Our second result concerns adiabatic invariance of some special linear combination of normal modes. To state the result, we first introduce the normal modes through the discrete Hartley transform. Such transformation, which we denote by \({\mathcal H}\), is defined as
and one easily verifies that it fulfills

The Hartley transform is closely related to the classical Fourier transform \({\mathcal F}\), whose matrix elements are \({\mathcal F}_{j,k}:= \frac{1}{\sqrt{N}} e^{- \mathrm{i}2\pi j k/N }\), as one has \({\mathcal H}= \mathfrak {R}{\mathcal F}- \mathfrak {I}{\mathcal F}\). The advantage of the Hartley transform is that it maps real variables into real variables, a fact which will be useful when calculating averages of quadratic Hamiltonians (see Sect. 5.2).
A consequence of (2.18) is that the change of coordinates
is a canonical one. Due to \(\sum _j p_j =0, \, \sum _j q_j = {\mathcal L}\), one has also \({\widehat{p}}_0 =0, \, {\widehat{q}}_0 = {\mathcal L}/\sqrt{N}\). In these variables the quadratic part \(H_2\) of the Toda Hamiltonian (1.2), i.e. its Taylor expansion of order two nearby the origin, takes the form
We observe that (2.20) is exactly the Hamiltonian of the Harmonic Oscillator chain. We define
the jth normal mode.
To state our second result we need the following definition:
Definition 2.4
(m-admissible vector). Fix \(m \in {\mathbb N}\) and \( {\widetilde{m}} : = \left\lfloor \frac{m}{2}\right\rfloor \). For any \(N > m\), a vector \(\mathbf{x}\in {\mathbb R}^N\) is said to be m-admissible if there exits a non zero vector \(\mathbf{y}=(y_0, y_1, \ldots , y_{{\widetilde{m}}}) \in {\mathbb R}^{{\widetilde{m}} +1}\) with \(K^{-1} \le \sum _j |y_j| \le K\), K independent from N, such that
We are ready to state our second result, which shows that special linear combinations of normal modes are adiabatic invariants for the FPUT dynamics for long times. Here the precise statement:
Theorem 2.5
Fix \(m\in \mathbb {N}\) and let \(\varvec{g}=(g_0,\dots ,g_{N-1})\in {\mathbb R}^N\) be a m-admissible vector (according to Definition 2.4). Define
where \( {\widehat{\mathbf{g}}}\) is the discrete Hartley transform (2.18) of \(\mathbf{g}\), and \(E_j\) is the harmonic energy (2.21). Then there exist \(N_0, \beta _0, C_0, C_1>0\) (depending on m), such that for any \(N > N_0\), \(\beta > \beta _0\), \(0< \varepsilon < \frac{1}{4}\), one has
for every time t fulfilling
Again when \({\mathtt b}= 1\) the time scale improves by a factor \(\beta ^{\frac{1}{2}}\).
Finally we consider the Toda dynamics generated by the Hamiltonian \(H_T\) in (1.2). In this case we endow \({\mathcal M}\) in (2.4) by the Gibbs measure of \(H_T\) at temperature \(\beta ^{-1}\), namely we put
where as usual \(Z_T(\beta )\) is the partition function which normalize the measure, namely
We prove that the quantity (2.22), computed along the Hamiltonian flow \(\phi ^t_{H_T}\) of the Toda chain, is an adiabatic invariant for all times and for a large set of initial data:
Theorem 2.6
Fix \(m\in \mathbb {N}\); let \(\mathbf{g}\in {\mathbb R}^N\) be an m-admissible vector and define \(\Phi \) as in (2.22). Then there exist \(N_0, \beta _0, C>0\) such that for any \(N > N_0\), \(\beta > \beta _0\), any \(\delta _1 >0\) one has
for all times.
Remark 2.7
It is easy to verify that the functions \(\Phi \) in (2.22) are linear combinations of
(choose \(g_\ell = g_{N-\ell }=1\), \(g_j = 0\) otherwise). Then, using the multi-angle trigonometric formula
where the \(T_n\)’s are the Chebyshev polynomial of the first kind, it follows that we can control (1.7). Actually these functions fall under the class considered in [29].
Let us comment about the significance of Theorems 2.5 and 2.6. The study of the dynamics of the normal modes of FPUT goes back to the pioneering numerical simulations of Fermi, Pasta, Ulam and Tsingou [13]. They observed that, corresponding to initial data with only the first normal mode excited, namely initial data with \(E_1\ne 0\) and \(E_j =0\) \(\, \forall j \ne 1\), the dynamics of the normal modes develops a recurrent behavior, whereas their time averages \(\frac{1}{t}\int _0^t E_j\circ \phi ^\tau _{H_F} \mathrm{d}\tau \) quickly relaxed to a sequence exponentially localized in j. This is what is known under the name of FPUT packet of modes.
Subsequent numerical simulations have investigated the persistence of the phenomenon for large N and in different regimes of specific energies [4, 6, 7, 17, 27, 32] (see also [2] for a survey of results about the FPUT dynamics).
Analytical results controlling packets of normal modes along the FPUT system are proven in [1, 3]. All these results deal with specific energies going to zero as the number of particles go to infinity, thus they do not hold in the thermodynamic limit. Our result controls linear combination of normal modes and holds in the thermodynamic limit.
2.3 Ideas of the proof
The starting point of our analysis is to estimate the probability that the time evolution of an observable \(\Phi (t)\), computed along the Hamiltonian flow of H, slightly deviates from its initial value. In our application \(\Phi \) is either the Toda integral of motion or a special linear combination of the harmonic energies and H is either the FPUT or Toda Hamiltonian. Quantitatively, Chebyshev inequality gives
So our first task is to give an upper bound on the variance \(\sigma _{\Phi (t) - \Phi (0)}\) and a lower bound on the variance \(\sigma _{\Phi (0)}\). Regarding the former bound we exploit the Carati-Maiocchi inequality [9]
where \(\{\Phi , H\}\), denotes the canonical Poisson bracket
Next we fix \(m \in {\mathbb N}\), consider the m-th Toda integral \(J^{(m)}\), and prove that the quotient
scales appropriately in \(\beta \) (as \(\beta \rightarrow \infty \)) and it is bounded uniformly in N (provided N is large enough). It is quite delicate to prove that the quotient in (2.32) is bounded uniformly in N and for the purpose we exploit the rich structure of the Toda integral of motions.
This manuscript is organized as follows. In Sect. 3 we study the structure of the Toda integrals. In particular we prove that for any \(m \in {\mathbb N}\) fixed, and N sufficiently large, the m-th Toda integral \(J^{(m)}\) can be written as a sum \(\frac{1}{m}\sum _{j=1}^N h_j^{(m)}\) where each term depends only on at most m consecutive variables, moreover \(h_j^{(m)}\) and \(h_k^{(m)}\) have disjoint supports if the distance between j and k is larger than m. Then we make the crucial observation that the quadratic part of the Toda integrals \(J^{(m)}\) are quadratic forms in \(\mathbf{p}\) and \(\mathbf{q}\) generated by symmetric circulant matrices. In Sect. 3 we approximate the Gibbs measure with the measure were all the variable are independent random variables. and we calculate the error of our approximation. In Sect. 4 we obtain a bound on the variance of \(J^{(m)}(t)-J^{(m)}(0)\) with respect to the FPUT flow and a bound of linear combination of harmonic energies with respect to the FPUT flow and the Toda flow. Finally in Sect. 5 we prove our main results, namely Theorems 2.1, 2.5 and 2.6. We describe in the “Appendices” the more technical results.
3 Structure of the Toda Integrals of Motion
In this section we study the algebraic and the analytic properties of the Toda integrals defined in (2.12). First we write them explicitly:
Theorem 3.1
For any \(1 \le m \le N-1\), one has
where \( h_{j}^{(m)}:= [L^m]_{jj}\) is given explicitly by
where it is understood \(r_j \equiv r_{j {\,\mathrm{mod}\,}N}, \, p_j \equiv p_{j {\,\mathrm{mod}\,}N}\) and \({\mathcal A}^{(m)}\) is the set
The quantity \({\widetilde{m}} := \lfloor m/2\rfloor \), \({\mathbb N}_0={\mathbb N}\cup \{0\}\) and \(\rho ^{(m)}(\mathbf{n}, \mathbf{m}) \in {\mathbb N}\) is given by
We give the proof of this theorem in “Appendix D”.
Remark 3.2
The structure of \(J^{(N)}\) is slightly different, but we will not use it here.
We now describe some properties of the Toda integrals which we will use several times. The Hamiltonian density \( h_{j}^{(m)} (\mathbf{p},\mathbf{r})\) depends on the set \({\mathcal A}^{(m)}\) and the coefficient \(\rho ^{(m)}(\mathbf{n}, \mathbf{k})\) which are independent from the index j. This implies that \(h_j^{(m)}\) is obtained by \(h_1^{(m)}\) just by shifting \(1\rightarrow j\); in [18, 19] this property was formalized with the notion of cyclic functions, we will lately recall it for completeness.
A second immediate property, as one sees inspecting the formulas (3.3) and (3.4), is that there exists \(C^{(m)} >0\) (depending only on m) such that
namely the cardinality of the set \({\mathcal A}^{(m)}\) and the values of the coefficients \(\rho ^{(m)}(\mathbf{n}, \mathbf{k})\) are independent of N.
The last elementary property, which follows from the condition \(2|\mathbf{n}| + |\mathbf{k}| = m\) in (3.3), is that
Now we describe three other important properties of the Toda integrals, which are less trivial and require some preparation. Such properties are
-
(i)
cyclicity;
-
(ii)
uniformly bounded support;
-
(iii)
the quadratic parts of the Toda integrals are represented by circulant matrices.
We first define each of these properties rigorously, and then we show that the Toda integrals enjoy them.
Cyclicity Cyclic functions are characterized by being invariant under left and right cyclic shift. For any \(\ell \in {\mathbb Z}\), and \(\mathbf{x}=(x_1, x_2, \ldots , x_N)\in \mathbb {R}^N\) we define the cyclic shift of order \(\ell \) as the map
For example \(S_1\) and \(S_{-1}\) are the left respectively right shifts:
It is immediate to check that for any \(\ell , \ell ' \in {\mathbb Z}\), cyclic shifts fulfills:

Consider now a a function \(H:{\mathbb R}^N \times {\mathbb R}^N \rightarrow {\mathbb C}\); we shall denote by \(S_\ell H:{\mathbb R}^N \times {\mathbb R}^N \rightarrow {\mathbb C}\) the operator
Clearly \(S_\ell \) is a linear operator. We can now define cyclic functions:
Definition 3.3
(Cyclic functions). A function \(H:{\mathbb R}^N \times {\mathbb R}^N \rightarrow {\mathbb C}\) is called cyclic if \(S_1 H = H\).
It is clear from the definition that a cyclic function fulfills \(S_\ell H = H\) \(\, \forall \ell \in {\mathbb Z}\).
It is easy to construct cyclic functions as follows: given a function \(h :{\mathbb R}^N \times {\mathbb R}^N \rightarrow {\mathbb C}\) we define the new function H by
H is clearly cyclic and we say that H is generated by h.
Support Given a differentiable function \(F :{\mathbb R}^N \times {\mathbb R}^N \rightarrow {\mathbb C}\), we define its support as the set

and its diameter as
where \({\mathtt d}\) is the periodic distance
Note that \(0\le {\mathtt d}(i,j) \le \lfloor N/2\rfloor \).
We often use the following property: if f is a function with diameter \(K \in {\mathbb N}\), and \(K \ll N\), then
where \(S_j\) is the shift operator (3.7). With the above notation and definition we arrive to the following elementary result.
Lemma 3.4
Consider the Toda integral \(J^{(m)}= \frac{1}{m} \sum _{j=1}^N h_{j}^{(m)} \,\), \(1 \le m \le N\) in (3.1). Then \(J^{(m)}\) is a cyclic function generated by \(\frac{1}{m} h^{(m)}_1\), namely
Further, each term \(h_j^{(m)}\) has diameter at most m. In particular \(h_j^{(m)}\) and \(h_k^{(m)}\) have disjoint supports provided \({\mathtt d}(j,k) > m\).
Circulant symmetric matrices We begin recalling the definition of circulant matrices (see e.g. [21, Chap. 3]).
Definition 3.5
(Circulant matrix). An \(N \times N\) matrix A is said to be circulant if there exists a vector \(\mathbf{a}=(a_j)_{j=0}^{N-1} \in {\mathbb R}^N\) such that
We will say that A is represented by the vector \( \mathbf{a}\).
In particular circulant matrices have all the form
where each row is the right shift of the row above.
Moreover, A is circulant symmetric if and only if its representing vector \(\mathbf{a}\) is even, i.e. one has
One of the most remarkable property of circulant matrices is that they are all diagonalized by the discrete Fourier transform (see e.g. [21, Chap. 3]). We show now that circulant symmetric matrices are diagonalized by the Hartley transform:
Lemma 3.6
Let A be a circulant symmetric matrix represented by the vector \(\mathbf{a}\in {\mathbb R}^N\). Then
where \(\widehat{\mathbf{a}}= {\mathcal H}\mathbf{a}\).
Proof
First remark that a circulant matrix acts on a vector \(\mathbf{x}\in {\mathbb R}^N\) as a periodic discrete convolution,
where it is understood \(a_\ell \equiv a_{\ell {\,\mathrm{mod}\,}N}\). As the Hartley transform of a discrete convolution is given by
we obtain (3.17), using that the Hartley transform maps even vectors (see (3.16)) in even vectors. \(\square \)
Our interest in circulant matrices comes from the following fact: quadratic cyclic functions are represented by circulant matrices. More precisely consider a quadratic function of the form
where A, B, C are \(N \times N\) matrices. Then one has
This result, which is well known (see e.g. [21]), follows from the fact that Q cyclic is equivalent to A, B, C commuting with the left cyclic shift \(S_1\), and that the set of matrices which commute with \(S_1\) coincides with the set of circulant matrices.
We conclude this section collecting some properties of Toda integrals. Denote by \(J_2^{(m)}\) the Taylor polynomial of order 2 of \(J^{(m)}\) at zero; being a quadratic, symmetric, cyclic function, it is represented by circulant symmetric matrices. We have the following lemma.
Lemma 3.7
Let us consider the Toda integral
Then \(h_1^{(m)}(\mathbf{p},\mathbf{q})\) has the following Taylor expansion at \(\mathbf{p}= \mathbf{r}= 0\):
where each \({\varphi }_k^{(m)}(\mathbf{p},\mathbf{r})\) is a homogeneous polynomial of degree \(k=0,1,2\) in \(\mathbf{p}\) and \(\mathbf{r}\) of diameter m and coefficients independent from N. The reminder \( {\varphi }_{\ge 3}^{(m)}(\mathbf{p},\mathbf{r})\) takes the form
with \( {\mathcal A}^{(m)}\) and \( \rho ^{(m)}\) defined in (3.3) and (3.4) respectively. Moreover the Taylor expansion of \(J^{(m)}(\mathbf{p},\mathbf{r})\) at \(\mathbf{p}= \mathbf{r}= 0\) takes the form
where
-
\( J^{(m)}_0={\left\{ \begin{array}{ll} c \in {\mathbb R}, &{} m \text{ even } \\ 0\,, &{} m \text{ odd } \text{. } \end{array}\right. }\)
-
\(J^{(m)}_2(\mathbf{p},\mathbf{r})\) is a cyclic function of the form
$$\begin{aligned} J^{(m)}_2(\mathbf{p},\mathbf{r}) = {\left\{ \begin{array}{ll} \mathbf{p}^\intercal A^{(m)} \mathbf{p}+ \mathbf{r}^\intercal A^{(m)} \mathbf{r}, &{} m \text{ even } \\ \mathbf{p}^\intercal B^{(m)} \mathbf{r}, &{} m \text{ odd } \end{array}\right. } \end{aligned}$$(3.24)with \(A^{(m)}, B^{(m)}\) circulant, symmetric \(N \times N\) matrices; their representing vectors \( \mathbf{a}^{(m)}\), \(\mathbf{b}^{(m)}\) are m-admissible (according to Definition 2.4) and
$$\begin{aligned} a_k^{(m)} = a_{N-k}^{(m)}> 0 , \qquad b_k^{(m)} = b_{N-k}^{(m)} > 0 , \qquad \forall 0 \le k \le {\widetilde{m}} : =\Big \lfloor \frac{m}{2}\Big \rfloor . \end{aligned}$$(3.25) -
The reminder \(J^{(m)}_{\ge 3}\) is a cyclic function generated by \(\frac{\varphi _{\ge 3}^{(m)}}{m}\).
The proof is postponed to “Appendix A”. We conclude this section giving the definition of m-admissible functions and we prove a lemma that characterizes them in terms of \(\{J_2^{(l)}\}_{l=1}^{N}\).
Definition 3.8
\(G_1,G_2:{\mathbb R}^N\times {\mathbb R}^N\rightarrow {\mathbb R}^N\) are called m-admissible functions of the first and second kind respectively if there exists a m-admissible vector \(\varvec{g}\in {\mathbb R}^N\) such that
Remark 3.9
From Definition 3.8 and (3.20) one can deduce that both \(G_1\) and \(G_2\) can be represented with circulant and symmetric matrices. Indeed we have that \(G_1=\mathbf{p}^\intercal {\mathcal G}_1\mathbf{r}\) where \({(\mathcal G}_1)_{jk}=g_{(j-k) {\,\mathrm{mod}\,}N} \) and similarly for \(G_2\).
An immediate, but very useful, corollary of Lemma 3.7, is the fact that the quadratic parts of Toda integrals are a basis of the vector space of m-admissible functions.
Lemma 3.10
Fix \(m\in {\mathbb N}\) and let \(G_1\) and \( G_2\) be m-admissible functions of the first and second kind defined by a m-admissible vector \(\varvec{g}\in {\mathbb R}^N\). Then there are two unique sequences \(\{c_j\}_{j=0}^{{\widetilde{m}}}, \, \{d_j\}_{j=0}^{{\widetilde{m}}}\), with \(\max _j |c_j|, \, \max _j |d_j| \) independent from N, such that:
where \(J_2^{(m)}\) is the quadratic part (3.24) of the Toda integrals \(J^{(m)}\) in (3.1).
Proof
We will prove the statement just for functions of the first kind. The proof for functions of the second kind can be obtained in a similar way. Let \(J^{(2l+1)}_2 = \mathbf{p}^\intercal B^{(2l+1)} \mathbf{r}\) where the circulant matrix \(B^{(2l+1)} \) is represented by the vector \(\mathbf{b}^{(2l+1)}\) and let \(G_1=\mathbf{p}^\intercal {\mathcal G}_1\mathbf{r}\) where \({(\mathcal G}_1)_{jk}=g_{(j-k) {\,\mathrm{mod}\,}N} \). Then
From Lemma 3.7 the matrix \(\mathfrak {B}=[b^{(2l+1)}_k]_{k,l=0}^{{\widetilde{m}}}\) is upper triangular and the diagonal elements are always different from 0 (see in particular formula (3.25)). This implies that the above linear system is uniquely solvable for \((c_0,\dots , c_{{\widetilde{m}}})\). \(\square \)
4 Averaging and Covariance
In this section we collect some properties of the Gibbs measure \(\mathrm{d}\mu _F\) in (2.5). The first property is the invariance with respect to the shift operator. Namely for a function \(f:{\mathbb R}^N \times {\mathbb R}^N \rightarrow {\mathbb R}\); we have that
which follows from the fact that \((S_j)_*\mathrm{d}\mu _F = \mathrm{d}\mu _F\).
It is in general not possible to compute exactly the average of a function with respect to the Gibbs measure \(\mathrm{d}\mu _F\) in (2.5). This is mostly due to the fact that the variables \(p_0, \ldots , p_{N-1}\) and \(r_0, \ldots , r_{N-1}\) are not independent with respect to the measure \(\mathrm{d}\mu _F\), being constrained by the conditions \(\sum _i r_i = \sum _i p_i = 0\).
We will therefore proceed as in [29], by considering a new measure \(\mathrm{d}\mu _{F,\theta }\) on the extended phase space according to which all variables are independent. We will be able to compute averages and correlations with respect to this measure, and estimate the error derived by this approximation.
For any \(\theta \in {\mathbb R}\), we define the measure \(\mathrm{d}\mu _{F,\theta }\) on the extended space \({\mathbb R}^N\times {\mathbb R}^N\) by
where we define \(Z_{F,\theta }(\beta )\) as the normalizing constant of \(\mathrm{d}\mu _{F,\theta }\). We denote the expectation of a function f with respect to \(\mathrm{d}\mu _{F,\theta }\) by \( \left\langle f \right\rangle _\theta \). We also denote by
If \(\Vert f \Vert _\theta < \infty \) we say that \(f \in L^2(\mathrm{d}\mu _{F,\theta })\).
The measure \(\mathrm{d}\mu _{F,\theta }\) depends on the parameter \(\theta \in {\mathbb R}\) and we fix it in such a way that
Following [29], it is not difficult to prove that there exists \(\beta _0 >0\) and a compact set \({\mathcal I}\subset {\mathbb R}\) such that for any \(\beta > \beta _0\), there exists \(\theta = \theta (\beta ) \in {\mathcal I}\) for which (4.3) holds true. We remark that (4.3) is equivalent to require that \(\left\langle r_j \right\rangle _\theta = 0\) for \(\, j=0,\dots , N-1\) and as a consequence \( \left\langle \sum _{j=0}^{N-1} r_j \right\rangle _\theta = 0 .\) We observe that \(\left\langle \sum _{j=0}^{N-1} r_j \right\rangle = 0\) with respect to the measure \(\mathrm{d}\mu _F\).
The main reason for introducing the measure \(\mathrm{d}\mu _{F, \theta }\) is that it approximates averages with respect to \(\mathrm{d}\mu _F\) as the following result shows.
Lemma 4.1
Fix \({\widetilde{\beta }}>0\) and let \(f :{\mathbb R}^N\times {\mathbb R}^N \rightarrow {\mathbb R}\) have support of size K (according to Definition 3.11) and finite second order moment with respect to \(\mathrm{d}\mu _{F,\theta }\), uniformly for all \(\beta > {\widetilde{\beta }}\). Then there exist positive constants \(C, N_0\) and \(\beta _0 \) such that for all \(N > N_0\), \(\beta > max\{\beta _0,\tilde{\beta }\}\) one has
The above lemma is an extension to the periodic case of a result from [29], and we shall prove it in “Appendix C”. As an example of applications of Lemma 4.1, we give a bound to correlations functions.
Lemma 4.2
Fix \(K \in {\mathbb N}\). Let \(f, g :{\mathbb R}^{N}\times {\mathbb R}^N \rightarrow {\mathbb C}\) such that :
-
1.
f, g and \( fg \in L^2(\mathrm{d}\mu _{F,\theta })\),
-
2.
the supports of f and g have size at most \(K \in {\mathbb N}\).
Then there exist \(C, N_0, \beta _0 >0\) such that for all \(N > N_0\), \(\beta > \beta _0\)
Moreover, if f and g have disjoint supports, then
Proof
We substitute the measure \(\mathrm{d}\mu _F\) with \(\mathrm{d}\mu _{F,\theta }\) and then we control the error by using Lemma 4.1. With this idea, we write
and estimate the different terms. We will often use the inequality
valid for any function \(f \in L^2(\mathrm{d}\mu _{F,\theta })\).
Estimate of (4.7): By Lemma 4.1, and the assumption that fg depends on at most 2K variables,
Estimate of (4.8): By Cauchy-Schwartz and (4.10) we have
Estimate of (4.9): We decompose further
again by Lemma 4.1 and (4.10) we obtain
Combining the three bounds above and redefining \(C=\text{ max }\{C,C'\}\) one obtains (4.5). To prove (4.6) it is sufficient to observe that if f and g have disjoint supports, then \(\left\langle fg\right\rangle _\theta = \left\langle f\right\rangle _\theta \left\langle g \right\rangle _\theta \) and consequently (4.8) is equal to zero.\(\square \)
In order to make Lemma 4.2 effective we need to show how to compute averages according to the measure (4.2).
Lemma 4.3
There exists \(\beta _0 >0\) such that for any \(\beta > \beta _0\), the following holds true. For any fixed multi-index \(\mathbf{k},\mathbf{l},\mathbf{n},\mathbf{s}\in {\mathbb N}_0^{N}\) and \(d,d' \in \{ 0,1,2\}\), there are two constants \(C_{\mathbf{k},\mathbf{l}}^{(1)} \in {\mathbb R}\) and \(C_{\mathbf{k},\mathbf{l}}^{(2)}>0\) such that
where \(\mathbf{p}^\mathbf{k}=\prod _{j=1}^Np_j^{k_j}\) and \( \mathbf{r}^\mathbf{l}=\prod _{j=1}^N r_j^{l_j} \). Moreover:
-
(i)
if \(k_i\) is odd for some i then \(C^{(1)}_{\mathbf{k},\mathbf{l}} = C^{(2)}_{\mathbf{k},\mathbf{l}} = 0\);
-
(ii)
if \(k_i, l_i\) are even for all i then \(C^{(1)}_{\mathbf{k},\mathbf{l}} >0\).
The lemma is proved in “Appendix B”.
Remark 4.4
Actually all the results of this section hold true (with different constants) also when we endow \({\mathcal M}\) with the Gibbs measure of the Toda chain in (2.25) and we use as approximating measure
here \(\theta \) is selected in such a way that
We show in “Appendix B” that it is always possible to choose \(\theta \) to fulfill (4.13) (see Lemma B.1) and we also prove Lemma 4.3 for Toda. In “Appendix C” we prove Lemma 4.1 for the Toda chain.
5 Bounds on the Variance
In this section we prove upper and lower bounds on the variance of the quantities relevant to prove our main theorems.
5.1 Upper bounds on the variance of \(J^{(m)}\) along the flow of FPUT
In this subsection we only consider the case \({\mathcal M}\) endowed by the FPUT Gibbs measure. We denote by \(J^{(m)}(t) := J^{(m)}\circ \phi ^t_{H_F}\) the Toda integral computed along the Hamiltonian flow \(\phi ^t_{H_F}\) of the FPUT Hamiltonian. The aim is to prove the following result:
Proposition 5.1
Fix \(m \in {\mathbb N}\). There exist \(N_0, \beta _0, C_0, C_1>0\) such that for any \(N > N_0\), \(\beta > \beta _0\), one has
Proof
As explained in the introduction, applying formula (2.30) we get
Therefore we need to bound \(\left\langle \{J^{(m)}, H_F\}^2 \right\rangle \). For the purpose we rewrite this term in a more convenient form. Since \(\left\langle \cdot \right\rangle \) is an invariant measure with respect to the Hamiltonian flow of \(H_F\), one has
Furthermore, since \(J^{(m)}\) is an integral of motion of the Toda Hamiltonian \(H_T\), we have
We apply identities (5.3) and (5.4) to write
The above expression enables us to exploit the fact that the FPUT system is a fourth order perturbation of the Toda chain. To proceed with the proof we need the following technical result.\(\square \)
Lemma 5.2
One has
where the functions \(H_j^{(m)}\) fulfill
-
(i)
\(H_j^{(m)} = S_{j-1} H_1^{(m)}\) \(\ \forall j \), moreover the diameter of the support of \(H^{(m)}_j\) is at most m;
-
(ii)
there exist \(N_0, \beta _0, C, C'>0\) such that for any \(N > N_0\), \(\beta > \beta _0\), any \(i, j = 1, \ldots , N\), the following estimates hold true:
$$\begin{aligned} \Vert H_j^{(m)} \Vert _\theta \le C\left( \frac{({\mathtt b}-1)^2}{\beta ^4} + \frac{C'}{\beta ^5} \right) ^{1/2}, \qquad \Vert H_i^{(m)} H_j^{(m)} \Vert _\theta \le C\left( \frac{\left( {\mathtt b}-1\right) ^4}{\beta ^8} + \frac{C'}{\beta ^{10}}\right) ^{1/2} . \end{aligned}$$(5.7)
The proof of the lemma is postponed at the end of the subsection.
We are now ready to finish the proof of Proposition 5.1. Substituting (5.6) in (5.5) we obtain
Therefore estimating \(\left\langle \left\{ J^{(m)}, H_F\right\} ^2\right\rangle \) is equivalent to estimate the correlations between \(H_i^{(m)}\) and \(H_j^{(m)}\). Exploiting Lemma 4.2 and observing that if \({\mathtt d}(i,j) > m\) then \(H_i^{(m)}\) and \(H_j^{(m)}\) have disjoint supports (see Lemma 5.2 (i) and (3.14)), we get that there are positive constants that for convenience we still call C and \(C'\), such that \(\forall N, \beta \) large enough
From (5.8) we split the sum in two terms:
We now apply estimates (5.9), (5.10) to get
for some positive constants \(C_1\) and \(C_2\). \(\square \)
5.1.1 Proof of Lemma 5.2
We start by writing the Poisson bracket \(\{J^{(m)}, H_F- H_T\}\) in an explicit form. First we observe that for any \(1 \le m < N\) one has from (2.12)
for all \(j=1, \ldots , N\). In the above relation \( h_{j}^{(m-1)}\) is the generating function of the \(m-1\) Toda integral defined in (3.2).
Next we observe that
This implies also that
where, to obtain the second identity, we are using that \(h_{j}^{(m-1)}(\mathbf {0},\mathbf {0})\) is by (3.15) and (3.21) a constant independent from j and the second term in the last relation is a telescopic sum. Define
then item (i) of Lemma 5.2 follows because clearly \(H_j^{(m)}=S_{j-1}H_1^{(m)}\). Furthermore, since \(h_j^{(m-1)}\) has diameter bounded by \(m-1\), the same property applies to \(H_j^{(m)}\).
To prove item (ii) we start by expanding \(R'(r_{j-1}) - R'(r_j)\) in Taylor series with integral remainder. Since
we get that
where explicitly
Combining (3.21) with (5.16) we rewrite \(H_j^{(m)}\) in (5.15) in the form
where \({\varphi }^{(m)}_{j}\), \( j=0,1,2\), are defined in (3.21). Thus the squared \(L^2\) norm of \(H_j\) is given by (we suppress the superscript to simplify the notation)
Consider now the terms in (5.19); by (3.24), (3.22) and (5.17), we know that each element is a linear combinations of functions of the form
with \(|\mathbf{k}| + |\mathbf{l}| \ge 6 + \ell + \ell ' \ge 8\), \(d,d'\in \{0,1,2\}\). The number of these functions and their coefficients are independent from N (see Lemma 3.7). By Lemma 4.3 it follows that there exists a constant \(C>0\), depending only on m, such that
Analogously, line (5.20) is a linear combination of functions of the form (5.22) with \(|\mathbf{k}| + |\mathbf{l}| \ge 9\), \(d,d'\in \{0,1,2\}\). Applying Lemma 4.3 we get the estimate
for some constant \(C'>0\). In a similar way the expression (5.21) is a linear combination of functions of the form (5.22) with \(|\mathbf{k}| + |\mathbf{l}| \ge 10\), \(d,d'\in \{0,1,2\}\). Applying Lemma 4.3 we get the estimate
for some constant \(C''>0\). Combining (5.23), (5.24) and (5.25) we obtain estimate (5.7) for \(\Vert H_j \Vert _\theta \). The estimate for \(\Vert H_i^{(m)} H_j^{(m)} \Vert _\theta \) can be proved in an analogous way. \(\square \)
5.2 Lower bounds on the variance of m-admissible functions
From now on we consider \({\mathcal M}\) endowed with either the FPUT or the Toda Gibbs measure; the following result holds in both cases.
Proposition 5.3
Fix \(m \in {\mathbb N}\), let G be an m-admissible function of the first or second kind (see Definition 3.8). There exist \(N_0, \beta _0, C >0\) such that for any \(N > N_0\), \(\beta > \beta _0\), one has
Proof
We first prove (5.26) when \(G = G_1= \mathbf{p}^\intercal {\mathcal G}_1 \mathbf{r}\) where \({\mathcal G}_1\) is a circulant, symmetric matrix represented by the m-admissible vector \(\mathbf{a}\in {\mathbb R}^N\). We now make the change of coordinates \((\mathbf{p}, \mathbf{r}) = ({\mathcal H}{\widehat{\mathbf{p}}}, {\mathcal H}{\widehat{\mathbf{r}}})\) which diagonalizes the matrix \({\mathcal G}_1\) (see (3.17)), getting
So we have just to compute
where we used that \({\widehat{p}}_k, {\widehat{r}}_j\) are random variables independent from each other.
We notice that \({\widehat{p}}_1, {\widehat{p}}_2,\ldots , {\widehat{p}}_{N-1}\) are i.i.d. Gaussian random variable with variance \(\beta ^{-1}\), \({\widehat{p}}_0 = 0\) (see (2.1)), so that we have \(\left\langle {\widehat{p}}_j \right\rangle = 0\) and \(\left\langle {\widehat{p}}_j{\widehat{p}}_i\right\rangle = \frac{\delta _{i,j}}{\beta } \, \, i,j = 1,\ldots , N-1\) (remark that this holds true both for the FPUT and Toda’s potentials as the \(\mathbf{p} \)-variables have the same distributions).
As a consequence, (5.27) becomes:
Since \({\mathcal G}_1\) is circulant symmetric matrix so is \({\mathcal G}_1^2\) and its representing vector is \(\mathbf{d}:= \mathbf{g}\star \mathbf{g}\).
Next we remark that the identity \(\left\langle \left( \sum _{j=0}^{N-1} r_j\right) ^2\right\rangle = 0\) implies
Applying this property to (5.28) we get
By Lemmas 4.1 and 4.3 we have that, for N sufficiently large, \(\left\langle r_0^2 \right\rangle \ge c \beta ^{-1}\). Finally, since the vectors \({\mathbf{g}},{\mathbf{d}}\) are m-admissible and 2m-admissible respectively we have that
for some constants \(c_m>0\) and \(C_m>0\). Plugging (5.30) into (5.29) we obtain (5.26) for the case of m-admissible functions of the first kind.
For the case of admissible functions of the second kind, one has \(G_2 = {\mathbf{p}}^\intercal {\mathcal G}_2 {\mathbf{p}} + {\mathbf{r}}^\intercal {\mathcal G}_2 {\mathbf{r}}\) with \({\mathcal G}_2\) circulant, symmetric and represented by an m-admissible vector. Since \(\mathbf{p}\) and \( \mathbf{r}\) are independent random variables one gets
Then arguing as in the previous case one gets (5.26).\(\square \)
By applying Proposition 5.3 to the quantity \(J^{(m)}_2\) that is an m-admissible function of the first or second kind depending on the parity of m, we obtain the following result.
Corollary 5.4
The quadratic part \(J_2^{(m)}\) of the Taylor expansion of the Toda integral \(J^{(m)}\) near \((\mathbf{p}, \mathbf{r}) = (0, 0) \) satisfies
for some constant \(C>0\).
In a similar way we obtain a lower bound on the reminder \(J^{(m)}_{\ge 3}\) of the Taylor expansion of the Toda integral \(J^{(m)}\) near \(\mathbf{p}=0\) and \(\mathbf{r}=0\).
Lemma 5.5
Fix \(m \in {\mathbb N}\). There exist \(N_0, \beta _0, C >0\) such that for any \(N > N_0\), \(\beta > \beta _0\), one has
Proof
Recall from Lemma 3.7 that \(J^{(m)}_{\ge 3}\) is a cyclic function generated by \({\widetilde{h}}_1^{(m)}:=\frac{1}{m} {\varphi }^{(m)}_{\ge 3}\). Thus, denoting \(h^{(m)}_j := S_{j-1} {\widetilde{h}}^{(m)}_1\), we have \( J^{(m)}_{\ge 3} = \sum _{j = 1}^N {\widetilde{h}}^{(m)}_j \) and its variance is given by
We can bound the correlations in (5.33) exploiting Lemma 4.2, provide we estimate first the \(L^2(\mathrm{d}\mu _{F,\theta })\) and \(L^2(\mathrm{d}\mu _{T,\theta })\) norms of \({\widetilde{h}}^{(m)}_i \) and \({\widetilde{h}}^{(m)}_i {\widetilde{h}}^{(m)}_j\). Proceeding with the same arguments as in Lemma 5.2, one proves that there exists \(\tilde{C}>0\) such that for any \(N > N_0\), \(\beta > \beta _0\),
By Lemma 3.7, the function \({\widetilde{h}}_1^{(m)}\) has diameter at most m, so in particular if \({\mathtt d}(i,j) > m\), the functions \({\widetilde{h}}_i^{(m)}\) and \({\widetilde{h}}_j^{(m)}\) have disjoint supports (recall (3.14)).
We are now in position to apply Lemma 4.2 and obtain
for some constant \(C'>0\). Thus we split the variance in (5.33) in two parts
and apply estimates (5.35), (5.36) to get (5.32).\(\square \)
Combining Corollary 5.4 and Lemma 5.5 we arrive to the following crucial proposition.
Proposition 5.6
Fix \(m\in {\mathbb N}\). There exist \(N_0, \beta _0, C >0\) such that for any \(N > N_0\), \(\beta > \beta _0\), one has
Proof
By Lemma 3.7, we write \(J^{(m)} = J^{(m)}_0 + J^{(m)}_2+ J^{(m)}_{\ge 3}\) with \(J^{(m)}_0\) constant. By Corollary 5.4 and Lemma 5.5 we deduce that for N and \(\beta \) large enough,
which leads immediately to the claimed estimate (5.37).\(\square \)
6 Proof of the Main Results
In this section we give the proofs of the main theorems of our paper.
6.1 Proof of Theorem 2.1
The proof is a straightforward application of Proposition 5.1 and 5.6. Having fixed \(m \in {\mathbb N}\), we apply (2.29) with \(\Phi = J^{(m)}\) and \(\lambda = \delta _1\) to get
from which one deduces the the statement of Theorem 2.1.
6.2 Proof of Theorem 2.5 and Theorem 2.6
The proofs of Theorems 2.5 and 2.6 are quite similar and we develop them at the same time. As in the proof of Theorem 2.1, the first step is to use Chebyshev inequality to bound
where the time evolution is intended with respect to the FPUT flow \(\phi ^t_{F}\) or the Toda flow \(\phi ^t_{T}\). Accordingly, the probability is calculated with respect to the FPUT Gibbs measure (2.5) or the Toda Gibbs measure (2.25).
Next we observe that the quantity \(\Phi := \sum _{j=1}^{N-1} {\widehat{g}}_j E_j \) defined in (2.22) can be written in the form
where \(\mathbf{g}\in {\mathbb R}^N\) is a m-admissible vector and \(G_2(\mathbf{p},\mathbf{r})\) is a m-admissible function of the second kind, as in Definition 3.8. As the inequality (2.29) is scaling invariant, proving (6.2) is equivalent to obtain that
Applying Proposition 5.3 we can estimate \(\sigma ^2_{G_2}\). We are then left to give an upper bound to \(\sigma ^2_{G_2(t) - G_2}\). By Lemma 3.10, there exists a unique sequence \(\{c_j\}_{j=0}^{{\widetilde{m}} -1}\), with \(\max _j |c_j| \) independent from N, such that \(G_2(p,r) = \sum _{l=0}^{{\widetilde{m}}-1} c_lJ_{2}^{(2l+2)}\), where \( J_{2}^{(2l+2)}\) are defined in (3.24). Hence we bound
Next we interpolate \(J_{2}^{(2l)}\) with the integrals \(J^{(2l)}\) and exploit the fact that they are adiabatic invariants for the FPUT flow and integrals of motion for the Toda flow. More precisely
By the invariance of the two measures with respect to their corresponding flow and Lemma 5.5, we get both for FPUT and Toda the estimate
for some constant \(\tilde{C}_1>0\) and for \(\beta >\beta _0\) and \(N>N_0\). As (6.6) is zero for the Toda flow (being \(J^{(2l)}(t)\) constant along the flow), we get
for some constant \(C_1>0\) and for \(\beta >\beta _0\) and \(N>N_0\). Combing Proposition 5.3 with (6.8) we conclude that
namely we have concluded the proof of Theorem 2.6.
We are left to estimate (6.6) for FPUT, but this is exactly the quantity bounded in Proposition 5.1. We conclude that
for some constant \(C_j>0\), \(j=1,2,3\) and for \(\beta >\beta _0\) and \(N>N_0\).
Combing Proposition 5.3 with (6.10) we obtain
Choosing \(\lambda =\beta ^{-\varepsilon }\) with \(0<\varepsilon <\frac{1}{4}\), (6.11) is equivalent to
for some redefine constant \(C_1>0\) and for every time t fulfilling (2.24).
We have thus concluded the proof of Theorem 2.5.
Notes
We recall that \(\gamma _d = \sum _{{\mathcal C}(d)} d!(-1)^{m_1+\ldots +m_d-1}\left( m_1+\ldots +m_d-1\right) !\prod _{l=1}^{d}\frac{\alpha _l^{m_l}}{m_l!(l!)^{m_l}}\) where \(\alpha _l\) is the lth moment of the random variable and \({\mathcal C}(d)\) is the set of all non-negative integer solution of \(\sum _l lm_l = d\).
References
Bambusi, D., Maspero, A.: Birkhoff coordinates for the Toda lattice in the limit of infinitely many particles with an application to FPU. J. Funct. Anal. 270(5), 1818–1887 (2016)
Bambusi, D., Carati, A., Maiocchi, A., Maspero, A.: Some analytic results on the FPU paradox. In Hamiltonian partial differential equations and applications, volume 75 of Fields Inst. Commun., pages 235–254. Fields Inst. Res. Math. Sci., Toronto, ON (2015)
Bambusi, D., Ponno, A.: On metastability in FPU. Commun. Math. Phys. 264(2), 539–561 (2006)
Benettin, G., Christodoulidi, H., Ponno, A.: The Fermi–Pasta–Ulam problem and its underlying integrable dynamics. J. Stat. Phys. 152(2), 195–212 (2013)
Benettin, G., Pasquali, S., Ponno, A.: The Fermi–Pasta–Ulam problem and its underlying integrable dynamics: an approach through Lyapunov exponents. J. Stat. Phys. 171(4), 521–542 (2018)
Benettin, G., Ponno, A.: Time-scales to equipartition in the Fermi–Pasta–Ulam problem: finite-size effects and thermodynamic limit. J. Stat. Phys. 144(4), 793–812 (2011)
Berchialla, L., Giorgilli, A., Paleari, S.: Exponentially long times to equipartition in the thermodynamic limit. Phys. Lett. A 321(3), 167–172 (2004)
Carati, A.: An averaging theorem for Hamiltonian dynamical systems in the thermodynamic limit. J. Stat. Phys. 128(4), 1057–1077 (2007)
Carati, A., Maiocchi, A.: Exponentially long stability times for a nonlinear lattice in the thermodynamic limit. Commun. Math. Phys. 314(1), 129–161 (2010)
Christodoulidi, H., Efthymiopoulos, C.: Stages of dynamics in the Fermi–Pasta–Ulam system as probed by the first Toda integral. Math. Eng. 1, mine–01–02–359 (2019)
Dubrovin, B.: On universality of critical behaviour in Hamiltonian PDEs. In: Buchstaber, V.M. (ed.) Geometry, Topology and Mathematical Physics. American Mathematical Society Translation Series 2, vol. 224, pp. 59–109. American Mathematical Society, Providence (2008)
Ferguson, W.E., Flaschka, H., McLaughlin, D.W.: Nonlinear normal modes for the Toda chain. J. Comput. Phys. 45(2), 157–209 (1982)
Fermi, E., Pasta, P., Ulam, S.: Studies of nonlinear problems. Lect. Appl. Math. 15, 143–156 (1974)
Fermi, E., Pasta, P., Ulam, S., Tsingou, M.: Studies of nonlinear problem, I. Los Alamos technical report, LA-1940 (1955). https://www.osti.gov/servlets/purl/4376203
Flaschka, H.: The Toda lattice II. Existence of integrals. Phys. Rev. B 9(4), 1924–1925 (1974)
Flaschka, H., McLaughlin, D.W.: Canonically conjugate variables for the Korteweg–de Vries equation and the Toda lattice with periodic boundary conditions. Prog. Theor. Phys. 55(2), 438–456 (1976)
Fucito, E., Marchesoni, F., Marinari, E., Parisi, G., Peliti, L., Ruffo, S., Vulpiani, A.: Approach to equilibrium in a chain of nonlinear oscillators. J. Phys. 43, 707–713 (1982)
Giorgilli, A., Paleari, S., Penati, T.: Extensive adiabatic invariants for nonlinear chains. J. Stat. Phys. 148(6), 1106–1134 (2012)
Giorgilli, A., Paleari, S., Penati, T.: An extensive adiabatic invariant for the Klein–Gordon model in the thermodynamic limit. Ann. Henri Poincaré 16(4), 897–959 (2015)
Goldfriend, T., Kurchan, J.: Equilibration of quasi-integrable systems. Phys. Rev. E 99, 022146 (2019)
Gray, R.: Toeplitz and circulant matrices: a review. Found. Trends Commun. Inf. Theory 2(3), 155–239 (2006)
Henon, M.: Integrals of the Toda lattice. Phys. Rev. B 3(9), 1921–1923 (1974)
Henrici, A., Kappeler, T.: Global action-angle variables for the periodic Toda lattice. Int. Math. Res. Not. (11):Art ID rnn031, 52 (2008)
Henrici, A., Kappeler, T.: Global Birkhoff coordinates for the periodic Toda lattice. Nonlinearity 21(12), 2731–2758 (2008)
Henrici, A., Kappeler, T.: Results on normal forms for FPU chains. Commun. Math. Phys. 278(1), 145–177 (2008)
Izrailev, F., Chirikov, B.: Statistical properties of a nonlinear string. Sov. Phys. Dokl. 11(1), 30–32 (1966)
Livi, R., Pettini, M., Ruffo, S., Sparpaglione, M., Vulpiani, A.: Relaxation to different stationary states in the Fermi–Pasta–Ulam model. Phys. Rev. A 28, 3544–3552 (1983)
Luke, Y.: The Special Functions and Their Approximations, vol. I. Mathematics in Science and Engineering, vol. 53. Academic Press, New York (1969)
Maiocchi, A., Bambusi, D., Carati, A.: An averaging theorem for FPU in the thermodynamic limit. J. Stat. Phys. 155(2), 300–322 (2014)
Maiocchi, A.: Freezing of the optical-branch energy in a diatomic FPU chain. Commun. Math. Phys. 372(1), 91–117 (2019)
Manakov, S.: Complete integrability and stochastization of discrete dynamical systems. Sov. Phys. JETP 40(2), 543–555 (1974)
Onorato, M., Vozella, L., Proment, D., Lvov, Y.: Route to thermalization in the \(\alpha \)-Fermi–Pasta–Ulam system. Proc. Natl. Acad. Sci. 112, 4208–4213 (2015)
Oste, R., Van der Jeugt, J.: Motzkin paths, Motzkin polynomials and recurrence relations. Electron. J. Comb. 22, 04 (2015)
Petrov, V.: Sums of Independent Random Variables. Springer, New York (1975)
Ponno, A., Christodoulidi, H., Skokos, C., Flach, S.: The two-stage dynamics in the Fermi–Pasta–Ulam problem: from regular to diffusive behavior. Chaos 21(4), 043127 (2011)
Rink, B.: Symmetry and resonance in periodic FPU chains. Commun. Math. Phys. 218(3), 665–685 (2001)
Sawada, K., Kotera, T.: Toda lattice as an integrable system and the uniqueness of Toda’s potential. Prog. Theor. Phys. Suppl. 59, 101–106 (1976)
Stanley, R.: Enumerative Combinatorics, vol. 1, 2nd edn. Cambridge University Press, New York (2011)
Toda, M.: Vibration of a chain with nonlinear interaction. J. Phys. Soc. Jpn. 22(2), 431–436 (1967)
Van Moerbeke, P.: The spectrum of Jacobi matrices. Invent. Math. 37(1), 45–81 (1976)
Zabuski, N., Kruskal, M.: Interaction of “solitons” in a collisionless plasma and the recurrence ofinitial states. Phys. Rev. Lett. 15, 240–243 (1965)
Zakharov, V.: On stochastization of one-dimensional chains of nonlinear oscillators. Sov. Phys. JETP 38(1), 108–110 (1974)
Acknowledgements
This manuscript was initiated during the research in pairs that took place in May 2019 at the Centre International des Rescontres mathématiques (CIRM), Luminy, France during the chair Morlet semester “Integrability and randomness in mathematical physics”. The authors thank CIRM for the generous support and the hospitality. This project has also received funding from the European Union’s H2020 research and innovation program under the Marie Skłowdoska–Curie Grant No. 778010 IPaDEGAN. Finally we are grateful to Miguel Onorato for very useful discussions.
Funding
Open access funding provided by Scuola Internazionale Superiore di Studi Avanzati - SISSA within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Liverani
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Proof of Lemma 3.7
In order to prove Lemma 3.7 we describe more specifically the Toda integrals and characterize their quadratic parts. Equation (3.15) follows by the explicit expression of \(h_j^{(m)}\) in (3.2), as the coefficients \(\rho ^{(m)}(\mathbf{n}, \mathbf{k})\) do not depend on the index j. We recall that \(h_1^{(m)}\) takes the form
with
In particular it is clear that \(h_1^{(m)}\) has diameter \(2{\widetilde{m}} \le m\).
Now we Taylor expand around \(\mathbf{r}=0\) the exponential with integral remainder:
and we substitute it in \(h_1^{(m)}\), obtaining an expansion of the form:
We can rewrite the above expression in the form
where \({\varphi }_\ell ^{(m)}\), \(\ell = 0,1,2\), are the Taylor polynomials at \((\mathbf{p}, \mathbf{r}) = (\varvec{0},\varvec{0})\). Their explicit expressions read
We deduce from these explicit formulas that if m is odd then \({\varphi }_0^{(m)} \equiv 0\) as well as the first sum defining \({\varphi }_1^{(m)}\) and the first and last one defining \({\varphi }_2^{(m)}\). Indeed the sums are carried on an empty set. If m is even the second sum defining \({\varphi }_1^{(m)}\) and the second one defining \({\varphi }_2^{(m)}\) are zero for the same reason. Concerning \({\varphi }_{\ge 3}^{(m)}\), it has a zero of order greater than 3 in the variables \((\mathbf{p},\mathbf{r})\), and it has the form
These, together with the explicit formula of \(\rho ^{(m)}(\mathbf{n},\mathbf{k})\), prove (3.21).
It is easy to see that defining
we immediately get that
Clearly \(J_0^{(m)}\) it is a constant that is zero for m odd; moreover thanks to the boundary condition (2.4) and the linearity of \(J_1^{(m)}\) we have that \(J_1^{(m)} = 0\). Further, \(J_{\ge 3}^{(m)}\) is clearly a cyclic function. In order to get (3.24) and (3.25) for \(J_2^{(m)}\) we have to split the proof in two different cases.
Case m odd. In this case thanks to the property of \({\varphi }_2^{(m)}\), the definition of \(J_2^{(m)}\) and (3.20) we get that there exists a cyclic and symmetric matrix \(B^{(m)}\) such that:
Moreover since the \(\mathrm{diam} (\mathbf{k}), \mathrm{diam }(\mathbf{n})\) defining \({\varphi }^{(m)}_2\) are at most \({\widetilde{m}}\) (see Remark 3.4) we have that the vector \({\mathtt b}^{(m)}\) representing the matrix \(B^{(m)}\) is m-admissible and from (3.4) we have that \({\mathtt b}^{(m)}_j = {\mathtt b}^{(m)}_{N-j}\) are positive integers for all \(j=0,\ldots , {\widetilde{m}}\).
Case m even. As before there exist two matrices \(A^{(m)}, D^{(m)}\) represented by m-admissible vectors such that:
We have just to prove that the two matrices are equal; to do this we exploit the involution property of the Toda integrals. Indeed we know that \(\left\{ J^{(j)}, J^{(k)}\right\} = 0, \) for any j, k. It follows easily that also their quadratic parts must commute:
To compute explicitly the Poisson bracket we change coordinates via the Hartley transform (2.18) getting that:
where \(\omega _j = 2\sin \left( \pi \frac{ j}{N}\right) \). As the Hartley transform is a symplectic map, by (A.1) we get
which implies that \({\widehat{a}}_j={\widehat{d}}_j\) for all \(j\ne 0\). To prove that also \({\widehat{a}}_0 = {\widehat{d}}_0\) we come back to the original variables getting that:
This means that \( {\mathtt a}^{(m)}_j - {\mathtt d}^{(m)}_j = \frac{{\widehat{a}}_0 - {\widehat{d}}_0}{\sqrt{N}}\) for all \(j=0,\dots ,N-1\). Since \({\mathtt a}^{(m)},{\mathtt d}^{(m)}\) are m-admissible it follows that \({\mathtt a}^{(m)}_{{\widetilde{m}} + 1}={\mathtt d}^{(m)}_{{\widetilde{m}} + 1}=0\) so that
which proves the statement.
Proof of Lemma 4.3
We prove the lemma for both the FPUT and Toda measure.
First of all we observe that for \(d,v=2,3\):
This means that we have actually to prove that for any fixed multi-index \(\mathbf{k},\mathbf{l},\mathbf{n}\in {\mathbb N}_0^{N}\) there exist two constants \(C_{\mathbf{k},\mathbf{l}}^{(1)} \in {\mathbb R}\) and \(C_{\mathbf{k},\mathbf{l}}^{(2)}>0\) such that:
Moreover since for the two measures \(\mathrm{d}\mu _{F,\theta }, \mathrm{d}\mu _{T,\theta }\) all \(\mathbf{p}\) and \(\mathbf{r}\) are independent random variables and moreover the \(p_j\) are independent and normally distributed according to \({\mathcal N}(0,\beta ^{-1})\), it follows
where
Here k!! denotes the double factorial. Instead the distribution of the \(r_j\) is different for the two measures, so we need to calculate it separately for the FPUT and Toda chain.
FPUT chain Let’s start considering \( \left\langle r^{l}\min \left( e^{-n r},1 \right) \right\rangle _\theta \):
Since for \(\beta \) large enough \(\theta (\beta )\) is uniformly bounded, it follows that there is a positive constant \(C_{l}\) such that:
We notice that if l is even then the right end side of (B.8) is positive. The proof for \(\left\langle r^{l}\max \left( e^{-n r},1 \right) \right\rangle _\theta \) follows in the same way so we get the claim for the FPUT chain. \(\square \)
Toda chain
For the Toda chain the computation is a little bit more involved, so we prefer to split it in different parts.
Lemma B.1
Consider the measure 4.2, then there exists a \(\beta _0> 0\) such that for all \(\beta >\beta _0\) there exists \(\theta \equiv \theta (\beta )\in [1/3, 2]\) such that
Proof
First we prove that, for any \(\beta \) large enough, we can chose \( \theta (\beta )\) in a compact interval \({\mathcal I}\) such that \(\left\langle r_j \right\rangle _\theta = 0\). We notice that:
where \(\Gamma (z)\) is the usual Gamma function and we used the following equality:
In the case \(k=1\) one obtains
Introducing the digamma function \(\psi (z)=\frac{\Gamma '(z)}{\Gamma (z)}\) [28] and using the inequality
it is easy to show that there exists \(\beta _0 >0\) such that \(\forall \beta > \beta _0\) one has
and
Since \(x \mapsto \psi (x)\) is continuous on \((1, + \infty )\), by the intermediate value theorem there exists \(\theta (\beta ) \in [1/3, 2]\) fulfilling \(\psi (\theta + \beta )=\log \beta \) which implies by (B.11) that
We will prove the remaining part of the claim by induction; (B.10) leads in the case \(k=2\) to:
where \(\psi ^{(s)}\) is the sth polygamma function defined as \(\psi ^{(s)}(z) := \dfrac{\partial ^s \psi (z) }{\partial z ^s}\). For \(x\in {\mathbb R}\) it has the following expansion as \(x\rightarrow +\infty \) :
where \(B_k\) are the Bernoulli number of the second kind. Therefore
So the first inductive step is proved. Next suppose the statement true for k and let us prove it for \(k+1\).
where we used (B.12) and (B.14).\(\square \)
We are now ready to prove the last part of Lemma 4.3 for the Toda chain:
The last integral can be estimated in the same way as in the previous lemma, moreover the lower bound follows in the same way, so we get the claim also for the Toda chain. \(\square \)
Measure Approximation
In this section we show how to approximate the measure \(\mathrm{d}\mu \), in which the variables are constrained, with the measure \(\mathrm{d}\mu _\theta \), where all variables are independent. The proof follows the construction of [29] (where it is done for Dirichlet boundary conditions) which applies both to the Gibbs measure of FPUT (2.5) and Toda (2.25). To simplify the construction we consider a general potential \(V:{\mathbb R}\rightarrow {\mathbb R}\) and make the following assumptions:
-
(V1)
There exist \(\beta _0 >0\) and a compact interval \({\mathcal I}\subset {\mathbb R}\) such that for any \(\beta > \beta _0\), there exists \(\theta \equiv \theta (\beta ) \in {\mathcal I}\) such that
$$\begin{aligned} \int _{{\mathbb R}} r \, e^{- \theta r - \beta V(r)} \, \mathrm{d}r = 0 . \end{aligned}$$(C.1) -
(V2)
There exist \(\beta _0, {\mathtt C}_1 , {\mathtt C}_2 >0\) such that for any \(\beta > \beta _0\), with \(\theta = \theta (\beta )\) of (V1), one has
$$\begin{aligned} \frac{{\mathtt C}_1}{\beta ^{k/2}}< \int _{{\mathbb R}} |r|^k \, e^{- \theta r - \beta V(r)} \, \mathrm{d}r < \frac{{\mathtt C}_2}{\beta ^{k/2}} , \qquad k = 0, \ldots , 4 . \end{aligned}$$(C.2)In particular the moments up to order 4 are finite.
-
(V3)
There exists \(\beta _0 >0\) such that \(\forall \beta > \beta _0\), with \(\theta = \theta (\beta )\) of (V1), one has
$$\begin{aligned} \inf _{r \in {\mathbb R}} \left| \theta r + \beta V(r) \right| > - \infty , \end{aligned}$$(C.3)namely the function \(r \mapsto \theta r + \beta V(r)\) is bounded from below.
Both the FPUT potential \(V_F(x)\) and the Toda potential \(V_T(x)\) satisfy the assumptions (V1)–(V3) by the results of “Appendix B”.
We define the constraint measure \(\mathrm{d}\mu ^V\) on the restricted phase space \({\mathcal M}\) as
and the unconstrained measure \(\mathrm{d}\mu ^V_{\theta }\) on the extended phase space \({\mathbb R}^N \times {\mathbb R}^N\) as
as usual \(Z_V(\beta )\) and \(Z_{V, \theta }(\beta )\) are the normalizing constants of \(\mathrm{d}\mu ^V, \,\mathrm{d}\mu ^V_\theta \) respectively. We denote the expectation of f with respect to the measure \(\mathrm{d}\mu ^V\) as \(\left\langle f \right\rangle _V\), and with respect to the measure \(\mathrm{d}\mu ^V_\theta \) as \(\left\langle f \right\rangle _{V, \theta }\).
We also denote by \(\displaystyle {\Vert f \Vert _{V, \theta }:= \left\langle f^2 \right\rangle _{V, \theta }^{1/2}}\) the \(L^2\) norm of f with respect to the measure \(\mathrm{d}\mu _\theta ^V\).
The main result is the following one:
Theorem C.1
Assume that (V1)–(V3) hold true. Fix \(K \in {\mathbb N}\) and assume that \(f :{\mathbb R}^N\times {\mathbb R}^N \rightarrow {\mathbb R}\) have support of size K (according to definition 3.11) and finite second order moment with respect to \(\mathrm{d}\mu ^V_\theta \). Then there exist \(C, N_0\) and \(\beta _0 \) such that for all \(N > N_0\), \(\beta > \beta _0\) one has
1.1 Proof of Theorem C.1
Introduce the structure function
The important remark is that \(\Omega _N(x)\) is N-times the convolution of the function \(e^{-\beta V(x)}\) with itself thus it is the density function of the sum of N iid random variables distributed as \(e^{-\beta V(x)}\).
Next, for \(\theta \in {\mathbb R}\), we define the conjugate distribution
As before, we remark that \(U^{(\theta )}_N(x)\) it is N-times the convolution of the function \(e^{-\beta V(x) - \theta x}\) with itself thus it is the density function of the sum of N iid random variables \(\{Y_n^{(\theta )}(\beta )\}_{1 \le n \le N}\) distributed as
moreover thanks to (C.1) we know that \(\left\langle Y^{(\theta )} \right\rangle = 0\).
The central limit theorem says that the rescaled random variable \(\displaystyle {\frac{1}{\sigma \sqrt{N}} \sum _{n=1}^N Y_n^{(\theta )}(\beta )}\) converges in distribution to a normal \({\mathcal N}(0,1)\). We want to apply a more refined version of this result, called local central limit theorem, which describes the asymptotic of this convergence.
In particular we will use a local central theorem whose proof can be found in [34, Theorem VII.15]; to state it, we first define the functions
where \({\mathtt H}_j\) is the j-th Hermite polynomial, \(\gamma _d\) is the d-th cumulantFootnote 1 of \( Y_n^{(\theta )}(\beta )\), and \({{\mathcal B}(\nu )}\) is the set of all non-negative integer solutions \(k_1, \ldots , k_\nu \) of the equalities \(k_1 + 2k_2 + \cdots + \nu k_\nu = \nu \), and \(s = k_1 + k_2 + \cdots +k_\nu \).
Theorem C.2
(Local central limit) Let \(\{X_n\}\) be a sequence of iid variables such that
-
(i)
For any \(1 \le n \le N\), one has \(\mathbf {E}\left[ {X_n}\right] = 0\).
-
(ii)
There exists \(k \ge 3\) such that \(\mathbf {E}\left[ {|X_n|^k}\right] < +\infty \) for all n. Moreover \(\sigma ^2:= \mathbf {E}\left[ {X_n^2}\right] >0\).
-
(iii)
The random variable \(\frac{1}{\sigma \sqrt{N}} \sum _{n=1}^N X_n \) has a bounded density \({\mathtt p}_N(x)\).
Then there exists \(C >0\) such that
where the \({\mathtt q}_\nu \)’s are defined in (C.10).
Applying this theorem in case \(X_n = Y_n^{(\theta )}(\beta )\) , one gets the following result:
Corollary C.3
Assume (V1)–(V3). There exist \(N_0, \beta _0, C >0\) such that for all \(N \ge N_0\), \(\beta > \beta _0\) one has
Proof
We verify that the assumptions of Theorem C.2 are met in case \(X_n = Y_n^{(\theta )}(\beta )\).
Item (i) and (ii) hold true thanks to assumptions (V1) and (V2), in particular (ii) is true with \(k=4\). To verify (iii), we note that \(\displaystyle {\frac{1}{\sigma \sqrt{N}}\sum _{n=1}^N Y_n^{(\theta )}(\beta )}\) has density given by \(\sigma \sqrt{N} \, U^{(\theta )}_N(\sigma \sqrt{N} x)\). This last function is N-times the convolution of \(g_\theta (r):= e^{-\theta r - \beta V(r)}\). By assumption (V3), \(g_\theta \in L^\infty ({\mathbb R})\) and by (V2) it belongs also to \(L^1({\mathbb R})\). So Young’s convolution inequality implies that \(\sigma \sqrt{N} \, U^{(\theta )}_N(\sigma \sqrt{N} x)\) is bounded uniformly in x, hence (iii) of Theorem C.2 is verified.
We apply Theorem C.2 with \({\mathtt p}_N(x) = \sigma \sqrt{N} \, U^{(\theta )}_N(\sigma \sqrt{N} x)\), then rescale the variable x to get (C.12).\(\square \)
We study also the structure function
and the normalized distribution
We have the following result:
Lemma C.4
For any \( N \ge 1\), any \(\beta >0\), one has
Proof
The function \({\widetilde{U}}_N\) is the N-times convolution of Gaussian functions of the form \(g(\xi ) := \sqrt{\frac{\beta }{2\pi }}\, e^{- \frac{\beta }{2} \xi ^2}\). Since convolution of Gaussians is a Gaussian whose variance is the sum of the variances, (C.13) follows.\(\square \)
We can finally prove Theorem C.1:
Proof of Theorem C.1
The proof follows closely [29]. We assume that f is supported on \(1, \ldots , K\), the other cases being analogous. Using that
and denoting \({\widetilde{\mathbf{p}}}:= (p_1, \ldots , p_K)\) and \({\widetilde{\mathbf{r}}}:= (r_1, \ldots , r_K)\), we write
where \(\mathrm{d}{\widetilde{\mu }}:= \exp \left( {-\beta \sum _{j=1}^K \frac{p_j^2}{2} - \beta \sum _{j=1}^K V(r_j)}\right) \mathrm{d}{\widetilde{p}} \mathrm{d}{\widetilde{r}}\). As, by (C.8) and (C.13),
we write the difference \(\left\langle f \right\rangle _V - \left\langle f \right\rangle _{V,\theta }\) as
where
Now we use that
so that we can write the difference \(\left\langle f \right\rangle _V - \left\langle f \right\rangle _{V,\theta }\) as
Using Cauchy-Schwartz we obtain that
so in order to prove (C.6) we are left to show that uniformly in N and \(\beta \) one has
Using (C.12) and (C.14), we have that
Next we use that \(|e^{-a^2 - b^2} - 1| \le a^2 + b^2\), the explicit expression
the estimate \(\displaystyle {\frac{\gamma _{3}}{6 \, \sigma ^{3}}} \le {\mathtt C}\) for some \({\mathtt C}\) independent of \(\beta \) (which follows by (C.2) as in our case \(\gamma _3 \le C \beta ^{-3/2}\)), to obtain that there exists \(C >0\) such that \(\forall N \ge N_0\), \(\forall \beta \ge \beta _0\),
Substituting \(x\equiv -\sum _{j=1}^K r_j\), \(\xi \equiv - \sum _{j=1}^K p_j\), and computing the \(L^2\) norm (with respect to \(\mathrm{d}\mu ^V_\theta \)) of the terms in the r.h.s. of the last formula give the claimed estimate (C.15). \(\square \)
Proof of Theorem 3.1
In this “Appendix” we prove Theorem 3.1. From the structure of the matrix Lax matrix L in (2.11), we immediately get
where \(S_{j}\) is the shift defined in (3.7), thus we have to prove formula (3.2) just for the case \(j=1\).
To accomplish this result we need to introduce the notion of super Motzkin path and super Motzkin polynomial, that generalize the notion of Motzkin path and Motzkin polynomial [33, 38].
Definition D.1
A super Motzkin path p of size m is a path in the integer plane \(\mathbb {N}_0\times \mathbb {Z}\) from (0, 0) to (m, 0) where the permitted steps from (0, 0) are: the step up (1, 1), the step down \((1,-1)\) and the horizontal step (1, 0). A similar definition applies to all other vertices of the path.
The set of all super Motzkin paths of size m will be denoted by \(s{\mathcal M}_m\).
In order to introduce the super Motzkin polynomial associated to these paths we have to define their weight. This is done in the following way: to each up step that occurs at height k, i.e. it joins the points (l, k) and \((l+1,k+1)\), we associate the weight \(a_k\), to a down step that joins the points (l, k) and \((l+1,k-1)\) we associate the weight \(a_{k-1}\), to each horizontal step from (l, k) to \((l+1,k)\) we associate the weight \(b_k\). Since \(k\in {\mathbb Z}\), the index of \(a_k\) and \(b_k\) are understood modulus N. At this point we can define the total weight w(p) of a super Motzkin path p to be the product of weights of its individual steps. So it is a monomial in the commuting variables \((\mathbf{b},\mathbf{a}) = (b_{-{\widetilde{m}}},\ldots ,b_{\widetilde{m}},a_{-{\widetilde{m}}},\ldots ,a_{{\widetilde{m}}})\), where \({\widetilde{m}} = \lfloor m/2\rfloor \). We remark that the total weight do not characterize uniquely the path. We are now ready to give the definition of Motzkin polynomial:
Definition D.2
The super Motzkin polynomial \(sP_m(\mathbf{a},\mathbf{b})\) is the sum of all weight of the elements of \(s{\mathcal M}_m\):
We are now ready to relate the Toda integrals to the super Motzkin polynomial \(sP_m(\mathbf{a},\mathbf{b})\).
Proposition D.3
Given the Lax matrix L in (2.11) then:
where the super Motzkin polynomial \(sP_m(\mathbf{a},\mathbf{b})\) is defined in (D.1) and \(a_j \equiv a_{j {\,\mathrm{mod}\,}N}, \, b_j \equiv b_{j {\,\mathrm{mod}\,}N}\).
Proof
In general we have that:
To every element of the sum we associate the path with vertices
where
This is a super Motzkin path \(p_{\mathbf{j}}\) and we can associate the weight \(w(p_{\mathbf{j}})\) as in the description above therefore we have
This is clearly a bijection. The sum of the weights of all possible super Motzkin paths, is defined to be the super Motzkin polynomial \(sP_m(\mathbf{a},\mathbf{b})\) and thus we get the claim.\(\square \)
Proceeding as in [33, Proposition 1], we are able to prove the following result, which together with Proposition D.3 proves Theorem 3.1:
Proposition D.4
The super Motzkin polynomial of size m is given explicitly as
where \({\mathcal A}^{(m)}\) is the set
where \({\widetilde{m}} = \lfloor m/2\rfloor \) and \(\rho ^{(m)}(\mathbf{n}, \mathbf{m}) \in {\mathbb N}\) is given by
Proof
For a give super Motzkin path p starting at (0, 0) and finishing at (0, m) let \(k_i\) be the number of horizontal steps at height i and let \(n_i\) be the number of step up from height i to \(i+1\). We remark the number \(n_i\) of step up from height i to \(i+1\) is equal to the number of step down from \(i+1\) to i. We define the vectors \(\mathbf{k}= (k_{-{\widetilde{m}}} , k_{-{\widetilde{m}} +1}, \ldots , k_{{\widetilde{m}}})\) and \(\mathbf{n}= (n_{-{\widetilde{m}}} , n_{-{\widetilde{m}}+1}, \ldots , n_{{\widetilde{m}}})\) and we associate the product
Next we need to sum over all possible super Motzkin path p of length m connecting (0, 0) to (0, m). Since the number of steps up is equal to the number of steps down, one necessarily have
Furthermore since the path is connected it follows that it is not possible to have a vertex at height \(i+1\) without have a vertex at height \(i>0\) and the other way round if \(i<0\). Therefore one has
This proves the definition of the set \({\mathcal A}^{(m)}\) in (D.5). The final step of the proof is to count the number of paths associated to the vectors \(\mathbf{k}= (k_{-{\widetilde{m}}} , k_{-{\widetilde{m}} +1}, \ldots , k_{{\widetilde{m}}})\) and \(\mathbf{n}= (n_{-{\widetilde{m}}} , n_{-{\widetilde{m}}+1}, \ldots , n_{{\widetilde{m}}})\). We want to show that this number is equal to \(\rho ^{(m)}(\mathbf{n},\mathbf{k}) \).
A horizontal step at height i can occur just after a step up to height i, another horizontal step at height i, or a step down to height i. This leaves a total of \(n_i + n_{i+1}\) different positions at which a horizontal step at height i can occur. Since we have \(k_i\) of horizontal steps, the number of different configurations with these step counts is the number of ways to choose \(k_i\) elements from a set of cardinality \(n_i + n_{i+1}\) with repetitions allowed, i.e.\(\left( {\begin{array}{c}n_i + n_{i+1} +k_i -1\\ k_i\end{array}}\right) \).
The number of different configurations with \(n_i\) steps at height i and \(n_{i+1}\) at height \(i+ 1\) is given by the number of multi-sets of cardinality \(n_{i+1}\) taken from a set of cardinality \(n_i\) and this number is equal to \(\left( {\begin{array}{c}n_i + n_{i+1} -1\\ n_{i+1}\end{array}}\right) . \)
For the horizontal steps at height 0, they can also occur at the beginning of the path, this increase the number of possible positions by 1, so the number of these configurations with these steps counts is \(\left( {\begin{array}{c}n_0 + n_{-1} + k_0\\ k_0\end{array}}\right) \). In this way we have obtained the coefficient \( \rho ^{(m)}(\mathbf{n},\mathbf{k}) \).\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grava, T., Maspero, A., Mazzuca, G. et al. Adiabatic Invariants for the FPUT and Toda Chain in the Thermodynamic Limit. Commun. Math. Phys. 380, 811–851 (2020). https://doi.org/10.1007/s00220-020-03866-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03866-2