Ordering and inventory reallocation decisions in a shared inventory platform with demand information sharing

Abstract

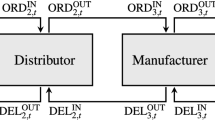
In this paper, we study the optimal ordering and inventory reallocation of the inventory service platform under the retailer demand information sharing. Due to the uncertainty of market demand, retailers’ demand information is likely to be inaccurate or even false. In this regard, retailers can reduce demand uncertainty by screening market signals. Therefore, based on the sharing of mean demand information and market signals, we explored the platform’s optimal ordering and inventory reallocation strategies, analyzed the retailer’s motivation for sharing false demand information, and proposed a corresponding penalty coordination mechanism. Our results show that the sharing of demand information and screening market signals reduces the uncertainty of market demand, thereby improving the accuracy of orders and increasing profit of the system. On the other hand, we find that the inventory reallocation strategy of the platform is affected by uncertain market information, but has nothing to do with the actual average demand and market signals shared by retailers. In this way, retailers will only share real information when the sharing system meets certain key conditions, otherwise they may share false demand information. The proposed punishment mechanism can encourage retailers to share their actual demand information with the platform.

Appendix: Proofs

1.1 Proof of Proposition 1

To explore the relationship between q_i^M* and d_i, we need to observe the first derivation бq_i^M*/бd_i. However, we do not know the explicit formula that q_i^M* satisfies, except the formula бSπ^M/бq_i^MI*. So, we use the derivation formula of implicit function to get our solution. Let the implicit function be Z = бSπ^M/бq_i^M*, then

$$ \frac{{\partial q_{i}^{M*} }}{{\partial d_{i} }} = - \frac{{Z_{{d_{i} }} }}{{Z_{{q_{i}^{MI*} }} }} = - {{\left(\frac{{\partial^{2} S\pi^{M*} }}{{\partial q_{i}^{M*} \partial d_{i} }}\right)} \mathord{\left/ {\vphantom {{\left(\frac{{\partial^{2} S\pi^{M*} }}{{\partial q_{i}^{M*} \partial d_{i} }}\right)} {\left(\frac{{\partial^{2} S\pi^{M*} }}{{\partial \left(q_{i}^{M*} \right)^{2} }}\right)}}} \right. \kern-\nulldelimiterspace} {\left(\frac{{\partial^{2} S\pi^{M*} }}{{\partial \left(q_{i}^{M*} \right)^{2} }}\right)}} $$

(A.1)

By taking the derivative of Eq. (12), we can obtain ${{\partial^{2} S\pi^{M} } \mathord{\left/ {\vphantom {{\partial^{2} S\pi^{M} } {(\partial q_{i}^{M*} \partial d_{i} )}}} \right. \kern-\nulldelimiterspace} {(\partial q_{i}^{M*} \partial d_{i} )}}$ and ${{\partial^{2} S\pi^{M} } \mathord{\left/ {\vphantom {{\partial^{2} S\pi^{M} } {(\partial q_{i}^{M*} )}}} \right. \kern-\nulldelimiterspace} {(\partial q_{i}^{M*} )}}^{2}$ as follows:

$$ \begin{gathered} \frac{{\partial^{2} S\pi^{M*} }}{{\partial q_{i}^{M*} \partial d_{i} }} = v_{i} \cdot f_{i} (q_{i}^{M*} - d_{i} ) - (v_{i} - r_{ji} ) \cdot \int\limits_{{ - a_{j} }}^{{q_{j}^{M*} - d_{j} }} {[f_{i} (q_{i}^{M*} - d_{i} ) - f_{i} (q_{i}^{M*} } \hfill \\ \qquad +\, q_{j}^{M*} - d_{i} - d_{j} - \varepsilon_{j} )]f_{j} (\varepsilon_{j} )d\varepsilon_{j} + (v_{j} - r_{ij} ) \cdot \int\limits_{{q_{j}^{M*} - d_{j} }}^{{a_{j} }} {[f_{i} (q_{i}^{M*} + q_{j}^{M*} } \hfill \\ \qquad -\, d_{i} - d_{j} - \varepsilon_{j} ) - f_{i} (q_{i}^{M*} - d_{i} )]f_{j} (\varepsilon_{j} )d\varepsilon_{j} + l \cdot f_{i} (q_{i}^{M*} + q_{j}^{M*} \hfill \\ \qquad -\, d_{i} - d_{j} - \varepsilon_{j} ) \hfill \\ \end{gathered} $$

(A.2)

$$ \begin{gathered} \frac{{\partial^{2} S\pi^{M*} }}{{\partial (q_{i}^{M*} )^{2} }} = - v_{i} \cdot f_{i} (q_{i}^{M*} - d_{i} ) - (v_{i} - r_{ji} ) \cdot \int\limits_{{ - a_{j} }}^{{q_{j}^{M*} - d_{j} }} {[f_{i} (q_{i}^{M*} + q_{j}^{M*} - d_{i} - d_{j} } \hfill \\ \qquad - \varepsilon_{j} ) - f_{i} (q_{i}^{M*} - d_{i} )]f_{j} (\varepsilon_{j} )d\varepsilon_{j} + (v_{j} - r_{ij} ) \cdot \int\limits_{{q_{j}^{M*} - d_{j} }}^{{a_{j} }} [ f_{i} (q_{i}^{M*} - d_{i} ) \hfill \\ \qquad - f_{i} (q_{i}^{M*} + q_{j}^{M*} - d_{i} - d_{j} - \varepsilon_{j} )]f_{j} (\varepsilon_{j} )d\varepsilon_{j} - l \cdot f_{i} (q_{i}^{M*} + q_{j}^{M*} \hfill \\ \qquad - d_{i} - d_{j} - \varepsilon_{j} ) \hfill \\ \end{gathered} $$

(A.3)

Comparing formula (A.2) and (A.3), we can know that $- {{(\frac{{\partial^{2} S\pi^{M*} }}{{\partial q_{i}^{M*} \partial d_{i} }})} \mathord{\left/ {\vphantom {{(\frac{{\partial^{2} S\pi^{M*} }}{{\partial q_{i}^{M*} \partial d_{i} }})} {(\frac{{\partial^{2} S\pi^{M*} }}{{\partial (q_{i}^{M*} )^{2} }})}}} \right. \kern-\nulldelimiterspace} {(\frac{{\partial^{2} S\pi^{M*} }}{{\partial (q_{i}^{M*} )^{2} }})}} = 1$, i.e., $\frac{{\partial q_{i}^{M*} }}{{\partial d_{i} }} = 1$. Thus, the relationship between q_i^MI* and d_i can be expressed as q_i^M* = d_i + CS_i^M, where CS_i^M is a constant.

Next, given that the mean market demand d_i and d_j shared by retailers to the platform, we can obtain q_i^M* = d_i + CS_i, which is substituted into Eq. (12) and simplify it to get

$$ \left\{ \begin{gathered} \frac{{v_{i} }}{w - s} \cdot \int\limits_{{CS_{i}^{M} }}^{{a_{i} }} {f_{i} (\varepsilon_{i} )d\varepsilon_{i} } - \frac{{v_{i} - r_{ji} }}{w - s} \cdot \int\limits_{{ - a_{j} }}^{{q_{j}^{M} - d_{j} }} {[\int\limits_{{CS_{i}^{M} }}^{\begin{subarray}{l} CS_{i}^{M} + q_{j}^{M} \\ - d_{j} - \varepsilon_{j} \end{subarray} } {f_{i} (\varepsilon_{i} )d\varepsilon_{i} } ] \cdot f_{j} (\varepsilon_{j} )d\varepsilon_{j} } + \frac{{(v_{j} - r_{ij} )}}{w - s} \hfill \\ \cdot \int\limits_{{q_{j}^{M} - d_{j} }}^{{a_{j} }} {[\int\limits_{\begin{subarray}{l} CS_{i}^{M} + q_{j}^{M} \\ - d_{j} - \varepsilon_{j} \end{subarray} }^{{CS_{i}^{M} }} {f_{i} (\varepsilon_{i} )d\varepsilon_{i} } ] \cdot f_{j} (\varepsilon_{j} )d\varepsilon_{j} } + \frac{l}{w - s} \cdot \int\limits_{\begin{subarray}{l} CS_{i}^{M} + q_{j}^{M} \\ - d_{j} - \varepsilon_{j} \end{subarray} }^{{a_{i} }} {f_{i} (\varepsilon_{i} )d\varepsilon_{i} } = 1 \hfill \\ \frac{{v_{j} }}{w - s} \cdot \int\limits_{{q_{j}^{M} - d_{j} }}^{{a_{j} }} {f_{j} (\varepsilon_{j} )d\varepsilon_{j} } - \frac{{v_{j} - r_{ij} }}{w - s} \cdot \int\limits_{{ - a_{i} }}^{{CS_{i}^{M} }} {[\int\limits_{{q_{j}^{M} - d_{j} }}^{\begin{subarray}{l} CS_{i}^{M} + q_{j}^{M} \\ - d_{j} - \varepsilon_{j} \end{subarray} } {f_{j} (\varepsilon_{j} )d\varepsilon_{j} } ] \cdot f_{i} (\varepsilon_{i} )d\varepsilon_{i} } + \frac{{(v_{i} - r_{ji} )}}{w - s} \hfill \\ \cdot \int\limits_{{CS_{i}^{M} }}^{{a_{i} }} {[\int\limits_{\begin{subarray}{l} CS_{i}^{M} + q_{j}^{M} \\ - d_{j} - \varepsilon_{j} \end{subarray} }^{{q_{j}^{M} - d_{j} }} {f_{j} (\varepsilon_{j} )d\varepsilon_{j} } ] \cdot f_{i} (\varepsilon_{i} )d\varepsilon_{i} } + \frac{l}{w - s} \cdot \int\limits_{\begin{subarray}{l} CS_{i}^{M} + q_{j}^{M} \\ - d_{j} - \varepsilon_{j} \end{subarray} }^{{a_{j} }} {f_{j} (\varepsilon_{j} )d\varepsilon_{j} } = 1 \hfill \\ \end{gathered} \right. $$

(A.4)

As show in Eq. (A.5), d_i and q_i^M* are eliminated, so q_j^M* is irrelevant to d_i and only related to d_j.

Thus, Proposition 1 is proved.

1.2 Proof of Proposition 2

Refer to the Proof of Proposition 1.

1.3 Proof of Proposition 3

When the retailer j shares its real market demand information, the individual optimality condition for the retailer i to maximize its own profit can be transformed from Eq. (26) into Eq. (A.5):

$$ \begin{gathered} \frac{{v_{i} }}{w - s} \cdot A_{i}^{f} (q_{i}^{f} ) - \frac{{p_{i} - c_{i} - t_{ji} - r_{ji} }}{w - s} \cdot B_{i}^{f} (q_{i}^{f} ,q_{j}^{r} ) + \frac{{t_{ij} - s}}{w - s} \cdot C_{i}^{f} (q_{i}^{f} ,q_{j}^{r} ) \hfill \\ + \frac{l}{w - s} \cdot M_{i}^{f} (q_{i}^{f} ,q_{j}^{r} ) = 1 \hfill \\ \end{gathered} $$

(A.5)

According to Eq. (23), when the shared inventory system is optimal, q_i^r = q_i^MS (d_i^r, S_i^r), the condition satisfied by the retailer i is

$$ \begin{gathered} \frac{{v_{i} }}{w - s} \cdot A_{i}^{MS} (q_{i}^{r} ) - \frac{{v_{i} - r_{ji} }}{w - s} \cdot B_{i}^{MS} (q_{i}^{r} ,q_{j}^{r} ) + \frac{{(v_{j} - r_{ij} )}}{w - s} \cdot C_{i}^{MS} (q_{i}^{r} ,q_{j}^{r} ) \hfill \\ + \frac{l}{w - s} \cdot E_{i}^{MS} (q_{i}^{r} ,q_{j}^{r} ) = 1 \hfill \\ \end{gathered} $$

(A.6)

For Eq. (A.5), if the retailer i share the real market demand information, i.e., d_i^r, S_i^r, it is not equal with Eq. (A.6), which indicates that global optimization is not consistent with the local optimization, and the retailer i will share false information in order to maximize its own private profit. Particularly, only when the above two optimality conditions are equal, that is,

$(t_{ji} - s) \cdot B_{i}^{MS} (q_{i}^{r} ,q_{j}^{r} ) = (p_{j} - c_{j} - t_{ij} - r_{ij} + l) \cdot C_{i}^{MS} (q_{i}^{r} ,q_{j}^{r} )$, retailer i will share the real information.

Thus, Proposition 3 is proved.

1.4 Proof of Proposition 4

When the retailer j shares the real market demand information to the platform, before the penalty mechanism is adopted, the private profit of the retailer i is

$$ \pi_{i}^{f} (q_{i}^{f} ,q_{j}^{r} ) = E[(p_{i} - c_{i} ) \cdot AS_{i}^{f} + t_{ij} \cdot TI_{ij}^{f} - (t_{ji} + r_{ji} ) \cdot TI_{ji}^{f} + s \cdot RI_{i}^{f} - l \cdot LS_{i}^{f} - w \cdot q_{i}^{f} ] $$

(A.7)

After the penalty mechanism is adopted, the retailer i’s private profit becomes

$$ \pi_{i}^{Pf} (q_{i}^{f} ,q_{j}^{r} ) = \pi_{i}^{f} (q_{i}^{f} ,q_{j}^{r} ) - \delta F_{i} w \cdot q_{i}^{f} $$

(A.8)

Next, when the shared inventory system is optimized, the expected profit of the retailer i is as follows

$$ \pi_{i}^{r} (q_{i}^{r} ,q_{j}^{r} ) = E[(p_{i} - c_{i} ) \cdot AS_{i}^{r} + t_{ij} \cdot TI_{ij}^{r} - (t_{ji} + r_{ji} ) \cdot TI_{ji}^{r} + s \cdot RI_{i}^{r} - l \cdot LS_{i}^{r} - w \cdot q_{i}^{r} ] $$

(A.9)

In order to induce retailers not to lie, we only need to make sure that the retailer i’s profit in the case of sharing real demand information is always higher than that in the case of lying. Thus, for Eq. (A.8) and Eq. (A.9), we make the inequality π_i^Pf(q_i^f,q_j^r) ≦ π_i^r(q_i^r,q_j^r) permanent, and the optimal unit penalty ceiling δ* can be obtained, i.e.

$\delta^{*} \ge \max \{ \mathop {\max }\limits_{{h_{i}^{f} \ne h_{i}^{r} }} \frac{{h_{i}^{r} \cdot [\pi_{i}^{f} (q_{i}^{f} ,q_{j}^{r} ) - \pi_{i}^{r} (q_{i}^{r} ,q_{j}^{r} )]}}{{w \cdot \left| {h_{i}^{f} - h_{i}^{r} } \right| \cdot q_{i}^{f} }},{ 0}\}$.

Thus, Proposition 4 is proved.