1 Introduction

The first principles description of nuclei, nuclear matter and reactions is one of the great challenges in contemporary physics with applications ranging from low-energy searches for physics beyond the Standard Model (SM) to properties of neutron stars and neutron star mergers. The currently most efficient and feasible approach along this line relies on the application of suitably tailored effective field theories (EFTs). In particular, an extension of chiral perturbation theory to multi-nucleon systems [1, 2], commonly referred to as chiral EFT, has been applied over the last two decades to derive nuclear forces at high orders in the EFT expansion in harmony with the spontaneously broken approximate chiral symmetry of QCD [3, 4]. See Refs. [5, 6] for the most accurate and precise chiral two-nucleon interactions at fifth order and Refs. [7,8,9,10,11] for a collection of review articles describing the current state-of-the-art in chiral EFT for nuclear forces and selected applications. In parallel with these developments, current operators describing the interactions of nuclear systems with external vector, axial-vector and pseudoscalar sources needed to study electroweak reactions driven by a single photon- or W/Z-boson exchange have been worked out completely through fourth order in the heavy-baryon formulation of chiral EFT with pions and nucleons as the only dynamical degrees of freedom, see Refs. [12, 13] for the pioneering studies by Park et al., Refs. [14,15,16,17] for our calculations using the method of unitary transformation [18,19,20] and Refs. [21,22,23,24] for an independent derivation by the Jlab-Pisa group in the framework of time-ordered perturbation theory. A direct comparison of the expressions for the current operators derived by different group is hindered by their scheme dependence. However, at least for the two-pion exchange axial-vector currents, our results [16] appear to be not unitarily equivalent to the ones of the Pisa-Jlab group [23], see Ref. [25] for a detailed discussion of the box diagram contribution. We further emphasize that off-shell consistency of the electroweak operators derived by our group [14,15,16,17] and the corresponding (unregularized) two- [26, 27] and three-nucleon forces [28, 29] has been verified explicitly by means of the corresponding continuity equations in Refs. [16, 17].

In this work we extend our earlier studies [14,15,16,17] and investigate the two-nucleon scalar current operators. Specifically, we consider the two-flavor QCD Lagrangian in the presence of external vector, axial-vector, scalar and pseudoscalar sources \(v_\mu (x)\), \(a_\mu (x)\), s(x) and p(x), respectively:

$$\begin{aligned} {\mathcal {L}} = {\mathcal {L}}_\mathrm{QCD}^0 + {\bar{q}} \gamma ^\mu (v_\mu + \gamma _5 a_\mu ) q - {\bar{q}} (s - i \gamma _5 p ) q, \end{aligned}$$
(1.1)

where q denotes the doublet of the up and down quark fields, while \({\mathcal {L}}_\mathrm{QCD}^0\) is the chirally invariant Lagrangian with massless up- and down-quarks. Throughout this work, we employ the SU(2) formulation of chiral EFT as done in our calculations of nuclear forces [5, 27,28,29,30,31,32,33,34] and current operators [14,15,16,17]. The external sources are represented by Hermitian 2\(\times \)2 matrices in the flavor space, and the original QCD Lagrangian is restored by setting \(v_\mu = a_\mu = p = 0\), \(s = \mathrm{diag} (m_u, \, m_d)\). Here and in what follows, we assume exact isospin symmetry with \(m_u = m_d \equiv m_q\). Embedded in the SM, the interactions between quarks and the external vector and axial-vector sources are probed in electroweak reactions involving hadrons or nuclei. Low-energy nuclear systems are nowadays commonly described by solving the many-body Schrödinger equation with the nuclear forces derived in chiral EFT [3, 4, 7]. An extension to electroweak processes with nuclei requires the knowledge of the corresponding nuclear current operators defined in terms of the functional derivatives of the effective nuclear Hamiltonian in the presence of external fields with respect to \(v_\mu (x)\) and \(a_\mu (x)\) [16]. For the vector, axial-vector and pseudoscalar sources, the corresponding expressions are already available up to fourth chiral order [14,15,16,17]. In this work we focus on the response of nuclear systems to the external scalar source s(x) and thus set \(v_\mu = a_\mu = p = 0\). While the scalar currents cannot be probed experimentally within the SM due to the absence of scalar sources, they figure prominently in dark matter (DM) searches in a wide variety of DM models such as e.g. Higgs-portal DM and weakly-interacting massive particles (WIMPs), see [35,36,37,38,39] for recent review articles. For example, the dominant interactions of a spin-1/2 Dirac-fermion DM particle \(\chi \) with the strong sector of the SM is given by the Lagrangian

$$\begin{aligned} {\mathcal {L}}_\chi = {{\bar{\chi }}} \chi \Big ( \sum _i c_i m_i \,{\bar{q}}_i q_i + c_G \,\alpha _s G_{\mu \nu }^a G^{\mu \nu \, a} \Big ), \end{aligned}$$
(1.2)

where i denotes the flavor quantum number, \(G_{\mu \nu }^a\) is the gluon field strength, \(\alpha _s\) is the strong coupling constant and the couplings \(c_i\) (\(c_G\)) determine the strength of the interaction between \(\chi \) and quarks of flavor i (gluons). Notice that the contributions from coupling to heavy quarks (charm, bottom and top) can be integrated out [40] and the sum in Eq. (1.2) can thus be taken only over the light quark flavors by replacing the coupling constants \(c_i\), \(c_G\) with the corresponding effective ones. Thus, the scalar nuclear currents derived in our paper can be used to describe the interactions of nuclei with DM particles emerging from their isoscalar coupling to the up- and down-quarks \(\propto (c_u + c_d)\).

Apart from their relevance for DM searches, the scalar currents are intimately related to quark mass dependence of hadronic and nuclear observables. For example, the pion-nucleon \(\sigma \)-term, \(\sigma _{\pi N}\), corresponds to the isoscalar scalar form factor of the nucleon at zero momentum transfer times the quark mass and determines the amount of the nucleon mass generated by the up- and down-quarks. Its value has been accurately determined from the recent Roy-Steiner-equation analysis of pion-nucleon scattering accompanied with pionic hydrogen and deuterium data to be \(\sigma _{\pi N} = (59.1 \pm 3.5)\) MeV [41, 42]. For the status of lattice QCD calculations of \(\sigma _{\pi N}\) see Ref. [43]. As pointed out, however, in Ref. [44], there is relation between the \(\sigma \)-term and the S-wave \(\pi N\) scattering lengths that so far has not been checked for the lattice calculations. Nuclear \(\sigma \)-terms and scalar form factors of light nuclei have also been studied in lattice QCD, albeit presently at unphysically large quark masses [45, 46]. Interestingly, the scalar matrix elements were found in these studies to be strongly affected by nuclear effects (in contrast to the axial-vector and tensor charges), which indicates that scalar exchange currents may play an important role. Last but not least, as will be shown below, the scalar isoscalar currents are directly related to the quark mass dependence of the nuclear forces, a subject that gained a lot of attention in the EFT community in connection with ongoing lattice QCD efforts in the multibaryon sector [47,48,49,50,51,52,53,54,55], a conjectured infrared renormalization group limit cycle in QCD [56, 57], searches for possible temporal variation of the light quark masses [58, 59] and anthropic considerations related to the famous Hoyle state in \(^{12}\)C [60,61,62,63].

Clearly, nuclear scalar currents have already been studied before in the framework of chiral EFT, see e.g. [64,65,66,67,68,69,70,71]. For the two-nucleon currents, only the dominant contribution at the chiral order \(Q^{-2}\) stemming from the one-pion exchange has been considered so far. Here and in what follows, \(Q \in \{ M_\pi /\Lambda _b, \, p/\Lambda _b \}\) denotes the chiral expansion parameter, \(M_\pi \) is the pion mass, p refers to the magnitude of three-momenta of external nucleons, while \(\Lambda _b\) denotes the breakdown scale of the chiral expansion. For a detailed discussion of the employed power counting scheme for nuclear currents see Ref. [16]. The two-body scalar current is suppressed by just one power of the expansion parameter Q relative to the dominant one-body contribution. Such an enhancement relative to the generally expected suppression of \((A+1)\)-nucleon operators relative to the dominant A-nucleon terms by \(Q^2\) can be traced back to the vertex structure of the effective Lagrangian and is not uncommon. For example, one- and two-nucleon operators contribute at the same order to the axial charge and electromagnetic current operators, see Table II of Ref. [16] and Table 1 of Ref. [17], respectively. For the scalar operator, the relative enhancement of the two-body terms is caused by the absence of one-body contributions at the expected leading order \(Q^{-4}\), see e.g. Table III of Ref. [16] for the hierarchy of the pseudoscalar currents. The first corrections to the scalar current appear at order \(Q^{-2}\) from the leading one-loop diagrams involving a single-nucleon line [66]. This relative enhancement of the two-body contributions might be responsible for the pattern found in the recent lattice QCD studies [45, 46], where strong nuclear effects were reported. Notice, however, that a conclusive statement is only possible once similar studies at physical quark masses will be available. In this paper we derive the subleading contributions to the two-nucleon scalar isoscalar current operators at order \(Q^0\). While the one-body current is not yet available at the same accuracy level, using empirical information on the scalar form factor of the nucleon from lattice QCD instead of relying on its strict chiral expansion may, in the future, provide a more reliable and efficient approach. Alternatively, one can use the dispersion theory of the single-nucleon scalar form factor [72, 73]. A similar strategy is, in fact, commonly used in studies of electromagnetic processes, see e.g. [74, 75] and Ref. [76] for a recent example. Concerning the two-nucleon scalar-isoscalar current, there appear only two additional short-range parameters at order \(Q^0\), which can be fixed in the studies of chiral extrapolations of the nuclear forces. Once they are known, it would be interesting to extend the studies of dark matter scattering of light nuclei [70] with the improved scalar-isoscalar current operator.

Our paper is organized as follows. In section 2, we briefly describe the derivation of the current operator using the method of unitary transformation and provide explicit expressions for the leading (i.e. order-\(Q^{-2}\)) and subleading (i.e. order-\(Q^{0}\)) two-body contributions. Next, in section 3, we establish a connection between the scalar currents at zero momentum transfer and the quark mass dependence of the nuclear force. The obtained results are briefly summarized in section 4, while some further technical details and the somewhat lengthy expressions for the two-pion exchange contributions are provided in appendices A and B.

2 Two-nucleon scalar operators

The derivation of the nuclear currents from the effective chiral Lagrangian using the method of unitary transformation is described in detail in Ref. [16]. The explicit form of the effective Lagrangian in the heavy-baryon formulation

$$\begin{aligned} {\mathcal {L}}_\mathrm{eff} = {\mathcal {L}}_{\pi }^{(2)} + {\mathcal {L}}_{\pi }^{(4)} + {\mathcal {L}}_{\pi N}^{(1)} + {\mathcal {L}}_{\pi N}^{(2)} + {\mathcal {L}}_{\pi N}^{(3)} + {\mathcal {L}}_{NN}^{(0)} + {\mathcal {L}}_{NN}^{(2)}\nonumber \\ \end{aligned}$$
(2.1)

can be found in Refs. [77] and [78] for the pionic and pion-nucleon terms, respectively. The relevant terms in \({\mathcal {L}}_{NN}\) will be specified in section 2.4. As already pointed out above, for the purpose of this study we switch off all external sources except the scalar one, s(x). To derive the scalar currents consistent with the nuclear potentials in Refs. [26,27,28,29, 31, 32] and electroweak currents in Refs. [14,15,16,17], we first switch from the effective pion-nucleon Lagrangian to the corresponding Hamiltonian H[s] using the canonical formalism and then apply the unitary transformations \(U_\mathrm{Okubo}\), \(U_\eta \) and U[s]. Here and in what follows, we adopt the notation of Ref. [16]. In particular, the Okubo transformations \(U_\mathrm{Okubo}\) [18] is a “minimal” unitary transformation needed to derive nuclear forces by decoupling the purely nucleonic subspace \(\eta \) from the rest of the pion-nucleon Fock space in the absence of external sources. However, as found in Refs. [31], the resulting nuclear potentials \(\eta U_\mathrm{Okubo}^\dagger H U_\mathrm{Okubo}^{} \eta \), with \(\eta \) denoting the projection operator onto the \(\eta \)-space, are non-renormalizable starting from next-to-next-to-next-to-leading order (N\(^3\)LO) \(Q^4\).Footnote 1 To obtain renormalized nuclear potentials, a more general class of unitary operators was employed in Refs. [31, 32] by performing additional transformations \(U_\eta \) on the \(\eta \)-space. The explicit form of the “strong” unitary operators \(U_\mathrm{Okubo}\) and \(U_\eta \) up to next-to-next-to-leading order (N\(^2\)LO) can be found in Refs. [28, 29, 31, 32]. Nuclear currents can, in principle, be obtained by switching on the external classical sources in the effective Lagrangian, performing the same unitary transformations \(U_\mathrm{Okubo} U_\eta \) as in the strong sector, and taking functional derivatives with respect to the external sources. However, similarly to the above mentioned renormalization problem with the nuclear potentials, the current operators obtained in this way can, in general, not be renormalized. A renormalizable formulation of the current operators requires the introduction of an even more general class of unitary transformation by performing subsequent \(\eta \)-space rotations with the unitary operators, whose generators depend on the external sources. In Refs. [16] and [17], such additional unitary operators \(U[a_\mu , \, p]\) and \(U[v_\mu ]\), subject to the constraints \(U[a_\mu , \, p ]_{a_\mu =p = 0} = U[v_\mu ]_{v_\mu = 0} = \eta \), are explicitly given up to N\(^2\)LO. Notice that such unitary transformations are necessarily time-dependent through the dependence of their generators on the external sources. This, in general, induces the dependence of the corresponding current operators on the energy transfer and results in additional terms in the continuity equations [16]. We now follow the same strategy for the scalar currents and introduce additional \(\eta \)-space unitary transformations U[s], \(U[s]_{s = m_q} = \eta \), in order to obtain renormalizable currents. The most general form of the operator U[s] at the chiral order we are working with is given in appendix A and is parametrized in terms of four real phases \(\alpha _i^s\), \(i = 0, \ldots , 3\). The nuclear scalar current is defined via

$$\begin{aligned} S(k)= & {} \int d^4 x \,\exp \left( -i k\cdot x\right) \frac{\delta }{\delta s(x)}\bigg |_{s=m_q}\nonumber \\&\times \bigg [U^\dagger [s]U^\dagger _\eta U_\mathrm{Okubo}^\dagger H[s] U_\mathrm{Okubo} U_\eta U[s] \nonumber \\&+\left( i\frac{\partial }{\partial t}U^\dagger [s]\right) U[s]\bigg ], \end{aligned}$$
(2.2)

see [16] for notation. While all the phases remain unfixed, they do not show up in the resulting expressions for the nuclear current given in the following sections. To the order we are working, we therefore do not see any unitary ambiguity.

Fig. 1
figure 1

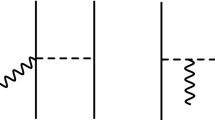
Diagram that leads to the dominant contribution of the 2N scalar isoscalar current operator \(S_\mathrm{2N}^{(Q^{-2})}\). Solid, dashed and wiggly lines denote nucleons, pions and external scalar sources, in order. Solid dots denote the leading-order vertices from the effective Lagrangians \({\mathcal {L}}_{\pi }^{(2)}\) and \({\mathcal {L}}_{\pi NN}^{(1)}\)

Full size image
Fig. 2
figure 2

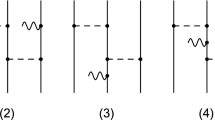
Non-tadpole one-loop one-pion-exchange diagrams contributing to \(S_\mathrm{2N}^{(Q^0)}\). For notation, see Fig. 1

Full size image
Fig. 3
figure 3

One-pion-exchange tadpole and tree-level diagrams that contribute to \(S_\mathrm{2N}^{(Q^0)}\). Filled squares denote the vertices from \({{{\mathcal {L}}}}_{\pi N}^{(3)}\) and \({{{\mathcal {L}}}}_{\pi }^{(4)}\) proportional to the low-energy constants \(d_i\) and \(l_i\), respectively. For remaining notation, see Fig. 1

Full size image

2.1 Contributions at order \(Q^{-2}\)

The chiral expansion of the 2N scalar isoscalar current starts at order \(Q^{-2}\). The dominant contribution is well known to emerge from the one-pion exchange diagram shown in Fig. 1 and has the form

$$\begin{aligned} S_\mathrm{2N}^{(Q^{-2})}= & {} -\frac{g_A^2 M_\pi ^2}{4 F_\pi ^2 m_{q}} \frac{ \vec {q}_1\cdot \vec {\sigma }_1 \vec {q}_{2}\cdot \vec {\sigma }_{2} }{ \left( M_\pi ^2+q_1^2\right) \left( M_\pi ^2+q_2^2\right) } {\varvec{\tau }}_{1}\cdot {\varvec{\tau }}_{2}\,, \end{aligned}$$
(2.3)

where \(g_A\) and \(F_\pi \) are the nucleon axial-vector coupling and pion decay constants, respectively, and \(\vec {q}_i = \vec {p}_i^{\, \prime } - \vec {p}_i\) denotes the momentum transfer of nucleon i. Further, \(\vec \sigma _i\) (\(\varvec{\tau }_i\)) refer to the spin (isospin) Pauli matrices of nucleon i. Here and in what follows, we follow the notation of our paper [16]. In terms of the Fock-space operator \({\hat{S}}_\mathrm{2N}\), the expressions we give correspond to the matrix elements

$$\begin{aligned}&\langle \vec {p}_1^{\, \prime } \vec {p}_2^{\, \prime } | {\hat{S}}_\mathrm{2N} | \vec p_1 \vec {p}_2 \rangle =: (2\pi )^{-3}\nonumber \\&\qquad \delta ^{(3)} ( \vec {p}_1^{\, \prime } + \vec {p}_2^{\, \prime } - \vec {p}_1 - \vec {p}_2 - \vec {k}\, ) S_\mathrm{2N} \,, \end{aligned}$$
(2.4)

where \(\vec {p}_i\) (\(\vec {p}_i^{\, \prime }\)) refers to the initial (final) momentum of nucleon i, \(\vec {k}\) is the momentum of the external scalar source and the nucleon states are normalized according to the nonrelativistic relation \(\langle \vec {p}_i^{\, \prime } | \vec p_i \rangle = \delta ^{(3)} (\vec {p}_i^{\, \prime } - \vec {p} \,)\). Finally, we emphasize that the dependence of the scalar currents on \(m_q\), which is renormalization-scale dependent, reflects the fact that in our convention, the external scalar source s(x) couples to the QCD density \({\bar{q}} q\) rather than \(m_q {\bar{q}} q\). Thus, only the combination \(m_q {\hat{S}}_\mathrm{2N} (k)\) is renormalization-scale independent. This is completely analogous to the pseudoscalar currents derived in Ref. [16], and we refer the reader to that work for more details.

2.2 One-pion-exchange contributions at order \(Q^0\)

Given that the first corrections to the pionic vertices are suppressed by two powers of the expansion parameter and the absence of vertices in \({\mathcal {L}}_{\pi N}^{(2)}\) involving the scalar source and a single pion, the first corrections to the two-nucleon current appear at order \(Q^0\). In Fig. 2 we show all one-loop one-pion-exchange diagrams of non-tadpole type that contribute to the scalar current at this order. Similarly, the corresponding tadpole and tree-level diagrams yielding nonvanishing contributions are visualized in Fig. 3.

It should be understood that the diagrams we show here and in what follows do, in general, not correspond to Feynman graphs and serve for the purpose of visualizing the corresponding types of contributions to the operators. The meaning of the diagrams is specific to the method of unitary transformation, see [16] for details. Using dimensional regularization, replacing all bare low-energy constants (LECs) \(l_i\) and \(d_i\) in terms of their renormalized values \({\bar{l}}_i\) and \({\bar{d}}_i\) as defined in Eq. (2.118) of [16], and expressing the results in terms of physical parameters \(F_\pi \), \(M_\pi \) and \(g_A\), see e.g. [15], leads to our final result for the static order-\(Q^0\) contributions to the 2N one-pion-exchange scalar current operators:

$$\begin{aligned} S_{\mathrm{2N:} \, 1\pi }^{(Q^0)}= & {} \frac{\vec {q}_1\cdot \vec {\sigma }_1}{q_1^2+M_\pi ^2}\bigg [\vec {q}_2\cdot \vec {\sigma }_2 \bigg (\frac{o_1(k)}{q_2^2+M_\pi ^2} + o_2(k)\bigg )\nonumber \\&+\vec {k}\cdot \vec {\sigma }_2 \Big (o_3(k)+q_2^2 o_4(k)\Big )\bigg ]\; + \; 1 \leftrightarrow 2\,, \end{aligned}$$
(2.5)

where the scalar functions \(o_i (k)\) are given by

$$\begin{aligned} o_1(k)= & {} \frac{g_A M_\pi ^2}{128\pi ^2 F_\pi ^4 m_q} \big [64\pi ^2\bar{d}_{18} F_\pi ^2 M_\pi ^2+g_A k^2\bar{l}_4\nonumber \\&-g_A L(k)\left( 2k^2+M_\pi ^2 \right) +g_A\left( k^2+M_\pi ^2\right) \big ],\nonumber \\ o_2(k)= & {} \frac{g_A M_\pi ^2}{64\pi ^2 F_\pi ^4 m_q} \bigg [32\pi ^2 F_\pi ^2\left( 2\bar{d}_{16} -\bar{d}_{18} \right) -g_A\bar{l}_4\nonumber \\&-\frac{4g_A^3 L(k)\left( k^2+3 M_\pi ^2\right) }{k^2+4M_\pi ^2} \bigg ], \nonumber \\ o_3(k)= & {} - \frac{g_A M_\pi ^2 }{128\pi ^2 F_\pi ^4 k^2 m_q} \nonumber \\&\times \bigg [128\pi ^2\bar{d}_{16} F_\pi ^2 k^2+g_A^3\left( -k^2+M_\pi ^2 \right) \nonumber \\&+2g_Ak^2 -\frac{4g_AL(k)}{k^2+4 M_\pi ^2}\left( \left( 2g_A^2+1 \right) k^4\right. \nonumber \\&+\left. \left( 5g_A^2+4\right) k^2 M_\pi ^2+g_A^2 M_\pi ^4\right) \bigg ],\nonumber \\ o_4(k)= & {} -\frac{g_A^4 M_\pi ^2}{128\pi ^2 F_\pi ^4 k^2 m_q} \frac{k^2+4 M_\pi ^2(1-L(k))}{k^2+4 M_\pi ^2} \,, \end{aligned}$$
(2.6)

and the loop function L(k) is defined as

$$\begin{aligned} L(k) = \frac{\sqrt{k^2 + 4 M_\pi ^2}}{k} \ln \bigg (\frac{\sqrt{k^2 + 4 M_\pi ^2}+k}{2 M_\pi } \bigg )\,. \end{aligned}$$
(2.7)

Finally, apart from the static contributions, we need to take into account the leading relativistic corrections emerging from tree-level diagrams with a single insertion of the 1/m-vertices from the Lagrangian \({\mathcal {L}}_{\pi N}^{(2)}\). Given our standard counting scheme for the nucleon mass \(m \sim \Lambda _b^2/M_\pi \), see e.g. [16], these contributions are shifted from the order \(Q^{-1}\) to \(Q^0\). However, the explicit evaluation of diagrams emerging from a single insertion of the 1/m-vertices into the one-pion-exchange graph in Fig. 1 leads to a vanishing result. Given the relation between the scalar current operator and the nuclear forces discussed in section 3, this observation is consistent with the absence of relativistic corrections in the (energy-independent formulation of the) nuclear forces at next-to-leading order.

Last but not least, there are no contributions proportional to the energy transfer \(k_0\) which may appear from the explicit time dependence of the unitary transformations in diagrams shown in Fig. 2.

Fig. 4
figure 4

Two-pion-exchange diagrams contributing to \(S_\mathrm{2N}^{(Q^0)}\). For notation, see Fig. 1

Full size image
Fig. 5
figure 5

Loop diagrams with contact interactions contributing to \(S_\mathrm{2N}^{ (Q^0)}\). Solid dots denote vertices from \({{{\mathcal {L}}}}_{\pi N}^{(1)}\), \({{{\mathcal {L}}}}_{\pi }^{(2)}\) or \(\mathcal{L}_{NN}^{(0)}\). Vertices from \(\mathcal{L}_{NN}^{(2)}\) are denoted by filled squares. For remaining notation see Fig. 1

Full size image

2.3 Two-pion-exchange contributions

We now turn to the two-pion exchange contributions. In Fig. 4, we show all diagrams yielding non-vanishing results for the scalar current operator with two exchanged pions. The final results for the two-pion exchange operators read

$$\begin{aligned}&S_{\mathrm{2N:} \, 2\pi }^{(Q^0)}= {\varvec{\tau }}_1\cdot {\varvec{\tau }}_2 \big [\vec {q}_1\cdot \vec {\sigma }_1\vec {k}\cdot \vec {\sigma }_2 t_1 + t_2\big ] + \vec {q}_1\cdot \vec {\sigma }_1\vec {q}_2\cdot \vec {\sigma }_2 t_3\nonumber \\&\quad + \vec {q}_2\cdot \vec {\sigma }_1\vec {q}_1\cdot \vec {\sigma }_2 t_4 \!+\!\vec {q}_1\cdot \vec {\sigma }_1\vec {q}_1\cdot \vec {\sigma }_2 t_5 \!+\!\vec {\sigma }_1\cdot \vec {\sigma }_2 t_6 + 1 \leftrightarrow 2\,,\nonumber \\ \end{aligned}$$
(2.8)

where the scalar functions \(t_i(k,q_1,q_2)\) are expressed in terms of the three-point function. Their explicit form is given in appendix B. Notice that the (logarithmic) ultraviolet divergences in the two-pion exchange contributions are absorbed into renormalization of the LECs from \({\mathcal {L}}^{(2)}_{NN}\) described in the next section.

2.4 Short-range contributions

Finally, we turn to the contributions involving short-range interactions. In Fig. 5, we show all one-loop and tree-level diagrams involving a single insertion of the contact interactions that yield non-vanishing contributions to the scalar current. The relevant terms in the effective Lagrangian have the form [32, 47]

$$\begin{aligned} {\mathcal {L}}_{NN}^{(0)}= & {} - \frac{{\overline{C}}_S}{2} (N^\dagger N)^2 + 2 {\overline{C}}_T N^\dagger S_\mu N N^\dagger S^\mu N,\nonumber \\ {\mathcal {L}}_{NN}^{(2)}= & {} -\frac{D_S}{8} \langle \!\chi _+\rangle (N^\dagger N)^2 \!+\! \frac{D_T}{2} \langle \chi _+\rangle N^\dagger S_\mu N N^\dagger S^\mu N \!+\! \dots \nonumber \\ \end{aligned}$$
(2.9)

where N is the heavy-baryon notation for the nucleon field with velocity \(v_\mu \), \(S_\mu = - \gamma _5 [\gamma _\mu , \, \gamma _\nu ] v^\nu /4 \) is the covariant spin-operator, \(\chi _+ = 2 B \left( u^\dagger (s + i p) u^\dagger + u (s - i p) u\right) \), B, \({\overline{C}}_{S,T}\) and \(D_{S,T}\) are LECsFootnote 2, \(\langle \ldots \rangle \) denotes the trace in the flavor space, \(u = \sqrt{U}\), and the 2\(\times \)2 matrix U collects the pion fields. Further, the ellipses refer to other terms that are not relevant for our discussion of the scalar current operator.

The total contribution of the diagrams of Fig. 5 can, after renormalization, be written in the form

$$\begin{aligned}&S_\mathrm{2N: \, cont}^{ (Q^0)}= \vec {\sigma }_1\cdot \vec {\sigma }_2 s_1(k) + \vec {k}\cdot \vec {\sigma }_1\vec {k}\cdot \vec {\sigma }_2 s_2(k) + s_3(k) \nonumber \\&\quad + \; 1 \leftrightarrow 2\,, \end{aligned}$$
(2.10)

with the scalar functions \(s_i(k)\) defined by

$$\begin{aligned} s_1(k)= & {} -\frac{M_\pi ^2}{8\pi ^2 F_\pi ^2 m_q} \left[ 2 g_A^2 {\overline{C}}_T-4\pi ^2 {\bar{D}}_T F_\pi ^2\right. \nonumber \\&+\left. \frac{g_A^2 {\overline{C}}_T L(k)\left( 3k^2+4M_\pi ^2\right) }{k^2+4M_\pi ^2} \right] ,\nonumber \\ s_2(k)= & {} \frac{3 g_A^2 {\overline{C}}_T M_\pi ^2}{8\pi ^2 F_\pi ^2 k^2 m_q} \frac{k^2-4 M_\pi ^2(L(k)-1)}{k^2+4M_\pi ^2}, \nonumber \\ s_3(k)= & {} \frac{M_\pi ^2}{16\pi ^2 F_\pi ^2 m_q} \left[ g_A^2 {\overline{C}}_T+8\pi ^2{\bar{D}}_S F_\pi ^2\right. \nonumber \\&\left. -\frac{2g_A^2 {\overline{C}}_T L(k)\left( 3k^2+8M_\pi ^2\right) }{k^2+4M_\pi ^2} \right] ~. \end{aligned}$$
(2.11)

The renormalized, scale-independent LECs \({\bar{D}}_{S}\), \({\bar{D}}_T\) are related to the bare ones \(D_{S}\), \(D_T\) according to

$$\begin{aligned} D_i={\bar{D}}_i+\frac{\beta _i^\mathrm{NN}}{F^4}\lambda +\frac{\beta _i^\mathrm{NN}}{16\pi ^2 F^4}\ln \left( \frac{M_\pi }{\mu }\right) , \end{aligned}$$
(2.12)

with the corresponding \(\beta \)-functions given by

$$\begin{aligned} \beta _S^\mathrm{NN}= & {} \frac{1}{2}\left( 1+6 g_A^2 - 15 g_A^4 + 24 F^2 g_A^2 {\overline{C}}_T\right) , \nonumber \\ \beta _T^\mathrm{NN}= & {} \frac{1}{4}\left( 1+6 g_A^2 - 15 g_A^4 + 48 F^2 g_A^2 {\overline{C}}_T\right) , \end{aligned}$$
(2.13)

and the quantity \(\lambda \) defined as

$$\begin{aligned} \lambda= & {} \frac{\mu ^{d-4}}{16\pi ^2}\bigg (\frac{1}{d-4}+\frac{1}{2}\big (\gamma _E-\ln 4\pi -1\big )\bigg ), \end{aligned}$$
(2.14)

where \(\gamma _E=-\Gamma ^\prime (1)\simeq 0.577\) is the Euler constant, d the number of space-time dimensions and \(\mu \) is the scale of dimensional regularization. Clearly, the \({\overline{C}}_T\)-independent parts of the \(\beta \)-functions emerge from the two-pion exchange contributions discussed in the previous section.

Notice that the LECs \({\overline{C}}_S\), \({\overline{C}}_T\), \({\bar{D}}_S\) and \({\bar{D}}_T\) also contribute to the 2N potential. However, experimental data on nucleon-nucleon scattering do not allow one to disentangle the \(M_\pi \)-dependence of the contact interactions and only constrain the linear combinations of the LECs [47]

$$\begin{aligned} C_S= & {} {\overline{C}}_S+M_\pi ^2{\bar{D}}_S, \quad C_T\,=\, {\overline{C}}_T+M_\pi ^2{\bar{D}}_T\;. \end{aligned}$$
(2.15)

The LECs \({\bar{D}}_S\) and \({\bar{D}}_T\) can, in principle, be determined once reliable lattice QCD results for two-nucleon observables such as e.g. the \(^3\)S\(_1\) and \(^1\)S\(_0\) scattering lengths at unphysical (but not too large) quark masses are available, see Refs. [63] and references therein for a discussion of the current status of research along this line.

Last but not least, we found, similarly to the one-pion exchange contributions, no 1/m-corrections and no energy-dependent short-range terms at the order we are working. Notice further that the loop contributions to the contact interactions are numerically suppressed due to the smallness of the LEC \(C_T\) as a consequence of the approximate SU(4) Wigner symmetry [79, 80].

3 Scalar current at zero momentum transfer

If the four-momentum transfer \(k_\mu \) of the scalar current is equal zero, one can directly relate the current to the quark-mass derivative of the nuclear Hamiltonian. To see this, we first rewrite the definition of the scalar current in Eq. (2.2) in the form

$$\begin{aligned} S(0)= & {} \left[ \left( \int d^4 x \frac{\delta }{\delta s(x)}\bigg |_{s=m_q} U^\dagger [s]\right) , H_\mathrm{eff}\right] \nonumber \\&+ U^\dagger _\eta U^\dagger _\mathrm{Okubo}\int d^4 x \frac{\delta H[s]}{\delta s(x)}\bigg |_{s=m_q} U_\mathrm{Okubo} U_\eta , \end{aligned}$$
(3.1)

where the nuclear Hamiltonian \(H_\mathrm{eff}\) is defined as

$$\begin{aligned} H_\mathrm{eff}= & {} U_\eta ^\dagger U_\mathrm{Okubo}^\dagger H[m_q] U_\mathrm{Okubo}^{} U_\eta ^{} \end{aligned}$$
(3.2)

and the unitary transformation U[s] satisfies by construction

$$\begin{aligned} U[m_q]=1. \end{aligned}$$
(3.3)

Notice that the last term in the brackets in Eq. (2.2) vanishes for \(k_0=0\). On the other hand, we obtain

$$\begin{aligned} \frac{\partial H_\mathrm{eff}}{\partial m_q}= & {} \left[ \left( \frac{\partial }{\partial m_q}U_\eta ^\dagger U_\mathrm{Okubo}^\dagger \right) U_\mathrm{Okubo}^{} U_\eta ^{}, H_\mathrm{eff}\right] \nonumber \\&+ U^\dagger _\eta U^\dagger _\mathrm{Okubo} \frac{\partial H[m_q]}{\partial m_q}U_\mathrm{Okubo}^{} U_\eta ^{}~. \end{aligned}$$
(3.4)

Given the trivial relation

$$\begin{aligned} \int d^4 x \frac{\delta }{\delta s(x)}\bigg |_{s=m_q} H_\mathrm{eff} [s]= & {} \frac{\partial }{\partial m_q} H_\mathrm{eff} [m_q]\,, \end{aligned}$$
(3.5)

the right-most terms in Eqs. (3.1) and (3.4) are equal, and we obtain the relation

$$\begin{aligned} S(0)= & {} \frac{\partial H_\mathrm{eff}}{\partial m_q} + \left[ \left( \int d^4 x \frac{\delta }{\delta s(x)}\bigg |_{s=m_q} U^\dagger [s]\right) \right. \nonumber \\&\left. - \left( \frac{\partial }{\partial m_q}U_\eta ^\dagger U_\mathrm{Okubo}^\dagger \right) U_\mathrm{Okubo}^{} U_\eta ^{}, H_\mathrm{eff}\right] . \end{aligned}$$
(3.6)

At the order we are working both commutators in this equation vanish (independently of the choice of unitary phases) leading to

$$\begin{aligned} S(0)= & {} \frac{\partial H_\mathrm{eff}}{\partial m_q} + {{{\mathcal {O}}}}(Q^1). \end{aligned}$$
(3.7)

In appendix C we demonstrate the validity of Eq. (3.7) for the two-nucleon potential at NLO, see Ref. [47] for the calculation of the quark mass dependence of nuclear forces using the method of unitary transformation.

It is important to emphasize that on the energy shell, i.e. when taking matrix elements in the eigenstates \(| i \rangle \) and \(| f \rangle \) of the Hamiltonian \(H_\mathrm{eff}\) corresponding to the same energy, all contributions from the commutator in Eq. (3.6) vanish leading to the exact relation

$$\begin{aligned} \langle f |S(0)| i \rangle= & {} \bigg \langle f \bigg | \frac{\partial H_\mathrm{eff}}{\partial m_q} \bigg | i \bigg \rangle . \end{aligned}$$
(3.8)

For eigenstates \(| \Psi \rangle \) corresponding to a discrete energy E, \(H_\mathrm{eff} | \Psi \rangle = E | \Psi \rangle \), the Feynman-Hellmann theorem allows one to interpret the scalar form factor at zero momentum transfer in terms of the eigenenergy slope with respect to the quark mass:

$$\begin{aligned} \langle \Psi |m_q S(0)| \Psi \rangle= & {} m_q \frac{\partial E(m_q)}{\partial m_q}. \end{aligned}$$
(3.9)

In particular, for \(|\Psi \rangle \) being a single-nucleon state at rest, the expectation value on left-hand side of Eq. (3.9) is nothing but the pion-nucleon sigma-term

$$\begin{aligned} \langle \Psi |m_q S(0)| \Psi \rangle \,=\, m_q \frac{\partial m_N(m_q)}{\partial m_q}\equiv & {} \sigma _{\pi N} \,, \end{aligned}$$
(3.10)

and for an extension to resonances \(|R\rangle \), see e.g. Ref. [81].

4 Summary and conclusions

In this paper we have analyzed in detail the subleading contributions to the nuclear scalar isoscalar current operators in the framework of heavy-baryon chiral effective field theory. These corrections are suppressed by two powers of the expansion parameter Q relative to the well-known leading-order contribution, see Eq. (2.3). They comprise the one-loop corrections to the one-pion-exchange and the lowest-order NN contact interactions as well as the leading two-pion exchange contributions. No three- and more-nucleon operators appear at the considered order. While the two-pion exchange terms do not involve any unknown parameters, the one-pion exchange contribution depends on a poorly known \(\pi N\) LEC \({\bar{d}}_{16}\) related to the quark mass dependence of the nucleon axial coupling \(g_A\). It can, in principle, be determined from lattice QCD simulations, see [82, 83] for some recent studies. The short-range part of the scalar current depends on two unknown LECs which parametrize the quark-mass dependence of the derivative-less NN contact interactions. In principle, these LECs can be extracted from the quark-mass dependence of, say, the NN scattering length, see Refs. [47,48,49, 51, 53,54,55] for a related discussion. Finally, we have explicitly demonstrated that the scalar current operator at vanishing four-momentum transfer is directly related to the quark-mass dependence of the nuclear force. The results obtained in our work are relevant for ongoing DM searches and for matching to lattice QCD calculations in the few-nucleon sector, see e.g. [45, 46] for recent studies along this line.

It is important to emphasize that our calculations are carried out using dimensional regularization. For nuclear physics applications, the obtained expressions for the scalar current operator need to be regularized consistently with the nuclear forces, which is a nontrivial task, see Refs. [7, 84] for a discussion. Work along these lines using the invariant higher derivative regularization [85] is in progress.