Introduction

With the application of genome-wide single-nucleotide polymorphism (SNP) markers, genomic selection (GS) or genomic prediction (GP) has emerged as a powerful method for animal and plant breeding (Hayes et al. 2009; VanRaden et al. 2009; Wolc et al. 2011; Garrick 2011). Effective utilization of marker information is vital in GP methods to accurately predict the genomic estimated breeding value (GEBV). Although a large number of GP methods have been proposed, the development of such methods is still ongoing, and so far, there is no consensus on the best approach (Misztal and Legarra 2017).

The methods available for GS can be classified broadly into two groups. The first group of methods is termed as the direct method (Zhang et al. 2011), in which markers covering the whole genome are used to derive the marker-based relationship matrix among individuals; the genetic merit is then predicted directly using the genomic best linear-unbiased prediction (GBLUP) model (VanRaden 2008). The total genetic effects of individuals are treated as random effects, with the variance structure defined by the genomic relationship matrix (G). This model can also be referred to as the breeding value model (Fernando et al. 2014). GBLUP has an equivalent relationship with ridge regression BLUP (RRBLUP) (Meuwissen et al. 2001), in which the marker effects are assumed to have a normal distribution with the same variance for all markers (Strandén and Garrick 2009; Meuwissen et al. 2001). Furthermore, a single-step GBLUP (ssGBLUP) (Legarra et al. 2009) approach has been developed, which can integrate all available information into a single model. An extension of the G matrix can be constructed in which genomic relationships are propagated to all individuals based on the pedigree relationship, resulting in a combined relationship matrix that can be used in a BLUP procedure (Legarra et al. 2009; Christensen and Lund 2010).

The second group of methods is termed as the indirect method (Zhang et al. 2011), in which all available genetic markers are fitted simultaneously as random effects to avoid the problem of model overfitting (Meuwissen et al. 2001). The estimates of all marker effects are then summed together to estimate an individual’s total genetic value; this is also called the marker-effect model (Fernando et al. 2014). To account for unknown marker effects with different prior distributions, various Bayesian methods have been developed, such as BayesA, B, Cπ, R, and LASSO, creating a series of analysis options, known as the Bayesian alphabet (Meuwissen et al. 2001; Habier et al. 2011; Gianola 2013).

In addition to Bayesian methods, genome-wide association study (GWAS) methods focusing on detecting QTLs can be used to estimate marker effects or to generate the test statistics for each marker (Zhang et al. 2010a; Liu et al. 2016; Wang et al. 2016; Runcie and Crawford 2019). Compared to GS methods, GWAS methods emphasize much more statistical power of QTL detection. Due to different purposes, GWAS and GS are often viewed as different subjects, but interdisciplinary communication may lead to unexpected and innovative outcomes (Marques et al. 2018); e.g., BayesC, a GS method, has been used in QTL fine mapping (van den Berg et al. 2013).

Many studies have been conducted to compare the prediction accuracy between Bayesian and GBLUP methods (van den Berg et al. 2015; Hayes et al. 2010). In general, Bayesian methods tend to perform better than GBLUP for traits controlled by loci with large effects. Otherwise, GBLUP has an advantage. This has been demonstrated in simulated studies (Daetwyler et al. 2010; Clark et al. 2011) and confirmed in real population (Rolf et al. 2015; Lee et al. 2017; Mehrban et al. 2017; Gao et al. 2015; Hayes et al. 2010). Nonetheless, GBLUP has the advantage of easily integrating into existing genetic evaluation infrastructure that uses pedigrees to derive the relationship matrix (Wang et al. 2018; Karaman et al. 2018). Therefore, developing methods within the BLUP framework for traits with various genetic architectures is highly desirable.

Various approaches have been used to combine the results from GWAS/GP methods into the GBLUP model. (a) The marker information from GWAS/GP methods was used to weight the markers to produce weighted GBLUP, like the BLUP|GA (Zhang et al. 2015) and the weighted ssGBLUP used in many studies (Fragomeni et al. 2017; Zhang et al. 2016). (b) The VanRaden’s G matrix (VanRaden 2008) was constructed with partial markers preselected by GWAS/GP methods to produce simplified GBLUP (sGBLUP) (Wang et al. 2018; Moser et al. 2010; Li et al. 2017; Veerkamp et al. 2016). (c) Markers were divided into genomic-feature (GF) set or the remaining set based on GWAS/GP methods, and two VanRaden’s G matrices were constructed with markers in the GF set and the remaining set, respectively, to establish the genomic-feature BLUP (GFBLUP) (Sarup et al. 2016). However, the research on this aspect is insufficient. On the one hand, the estimates of marker effects used in most studies were obtained by Bayesian methods (Tiezzi and Maltecca 2015) or RRBLUP (Zhang et al. 2015, 2016; Sarup et al. 2016), while GWAS methods were rarely used. On the other hand, only one weighted GBLUP method has been used to weight markers in most published studies (Calus et al. 2014; Zhang et al. 2015, 2016; Sarup et al. 2016; Wang et al. 2018); therefore, the most effective weighted GBLUP for a trait is not specified.

It can be assumed that the optimal weighting method for integrating the marker information into the GBLUP model can change with the genetic architecture of the trait being analyzed, and the GWAS/GP methods used to obtain marker information may also affect the prediction ability. The aim of (1) finding the most efficient weighted GBLUP methods for a variety of traits, and (2) analyzing the factors that affect the effectiveness of the various weighted GBLUP. Twelve GP strategies of three weighted GBLUPs by four different GWAS/GP methods were evaluated in traits with a broad spectrum of genetic architectures.

Materials and methods

Real data

Three publicly available data sets from cattle, pig, and loblolly pine were used in this study. The German dairy cattle population data were provided by Vereinigte Informationssysteme Tierhaltung w.V and available at https://www.g3journal.org/content/suppl/2015/02/09/g3.114.016261.DC1. This population comprises 5024 bulls, which were genotyped with the Illumina Bovine SNP50Beadchip; after quality control, 39,117 SNPs remained for our further analyses. Highly reliable conventional estimated breeding values (EBVs) of three traits were used in this study. The pig data set contains 3534 genotyped individuals with phenotypes and EBVs for five traits. The genotypes contain 45,385 SNPs after quality control (Cleveland et al. 2012). The loblolly pine data set includes 926 individuals genotyped with 4853 SNPs and 17 deregressed phenotypes from three studies (Resende et al. 2012).

Simulated data

We established a series of simulation studies to investigate factors that influence the prediction ability of weighted GBLUP methods. Phenotypes were simulated with different heritability and different numbers of QTL. The real pig genotypic information was used as a base for the simulations. Simulations were carried out in nine scenarios, with heritability of 0.15, 0.4, or 0.7 and 100, 500, or 1000 biallelic QTLs. The locations of the simulated QTLs were determined by random sampling of the existing SNPs in the real pig data set. The phenotypic variance \(\sigma _P^2\) was set as 100. The genetic variance of each QTL was drawn from a normal distribution N (0, 1), and the sum variance of all the QTLs rescaled to be equal to \(\sigma _P^2 \times h^2\). The allele substitution effect of the nth QTL (an) was calculated as \(a_n = \sqrt {{\it{\upsigma }}_n^2/2p_n(1 - p_n)}\), where \({\it{\upsigma }}_n^2\) represents the genetic variance explained by the nth QTL, and pn is the frequency of a given allele of the nth QTL. The simulated phenotype of an individual was calculated as the sum of its QTL effects and an environmental effect drawn from a normal distribution \(N(0,(1 - h^2)\sigma _P^2)\); each scenario was simulated ten times.

According to the assumption of marker-effect variance used in BayesR (Erbe et al. 2012), we divided the QTL into three groups based on the phenotypic variance occupied by the QTL, i.e., ≤0.09%, 0.09–0.45%, and ≥0.45%. We termed these QTL as loci with small, moderate, and large effects, respectively (Fig. S1).

General GBLUP

General GBLUP was used as a benchmark to evaluate the weighted GBLUP presented in this study. The model includes a single random genetic effect, and was expressed as follows:

$${\mathbf{y}} = {{\upmu }} + {\mathbf{Zg}} + {\mathbf{e}},$$
(1)

where y is the vector of phenotypic observations, μ is a vector of overall mean, g is a vector of individual genetic values captured by all genetic markers, Z is the design matrix of genetic values, and e is a vector of residuals. The random genetic and the residual values are assumed to be independent normally distributed values described as \({\mathbf{g}}\sim N({\mathbf{0}},{\mathbf{G}}\sigma _g^2)\) and \({\mathbf{e}}\sim N({\mathbf{0}},{\mathbf{I}}\sigma _e^2)\), \(\sigma _g^2\) and \(\sigma _e^2\) are the additive genetic and residual variance, respectively. In this study, all variance components were estimated using the average information-restricted maximum likelihood (AI-REML) algorithm in BLUPF90 (Misztal et al. 2002).

The additive G matrix, also called VanRaden’s G matrix (VanRaden 2008), was constructed using all genetic markers:

$${\mathbf{G}} = \frac{{{\mathbf{WW}}\prime }}{{2\mathop {\sum}\nolimits_{k = 1}^K {p_k\left( {1 - p_k} \right)} }},$$
(2)

where W = M − 2P is the centered genotype matrix, M is the genotype matrix with elements of 0, 1, and 2, P is a matrix of 1 × pk in the kth column, and pk is the frequency of a given allele of the kth marker. The solution of \({\hat{\mathbf g}}\) is equal to \({\mathbf{(Z}}^\prime {\mathbf{R}}^{ - {\mathbf{1}}}{\mathbf{Z}} + {\mathbf{G}}^{ - {\mathbf{1}}}{\mathbf{)}}^{ - {\mathbf{1}}}{\mathbf{Z}}^\prime {\mathbf{R}}^{ - {\mathbf{1}}}\left( {{\mathbf{y}} - {\hat{\mathbf \upmu }}} \right)\), where \({\mathbf{R = I}}\sigma _e^2\) is the covariance matrix of residuals.

Genomic-feature BLUP

The GF set is a set of markers selected by the corresponding test statistics of each GWAS/GP method. The posterior probabilities, t statistics, and Wald test statistics for BayesC, RRBLUP, and empirical Bayes (EB) were sorted in decreasing order, and the P values from fixed and random models circulating probability unification (FarmCPU) were sorted in increasing order. The first 100, 500, 1000, 1500, 2000, 5000, 10,000, 20,000, and 30,000 markers were selected to construct different GF set levels in the simulated study, and the residual markers were included in the remaining sets. For the loblolly pine data set, only the top 100, 500, 1000, and 2000 markers were used to construct GF sets, and for the cattle and pig data sets, only the top 100, 500, 1000, 2000, 5000, and 10,000 markers were used. The GFBLUP model originally proposed by Sarup et al. (2016) includes two random genetic effects and was expressed as follows:

$${\mathbf{y}} = {{\upmu }} + {\mathbf{Zf}} + {\mathbf{Zr}} + {\mathbf{e,}}$$
(3)

where f is a vector of genetic values captured by genetic markers in the GF set, r is a vector of genetic values captured by the remaining genetic markers, Z is the same as in Eq. (1), and e is a vector of residuals. The random genetic effects and the residuals were assumed to be independent and normally distributed with \({\mathbf{f}}\sim N({\mathbf{0}},{\mathbf{G}}_{\mathbf{f}}\sigma _f^2)\), \({\mathbf{r}}\sim N({\mathbf{0}},{\mathbf{G}}_{\mathbf{r}}\sigma _r^2)\), and \({\mathbf{e}}\sim N({\mathbf{0}},{\mathbf{I}}\sigma _e^2)\), where Gf and Gr are the VanRaden’s G matrices constructed with markers in the GF set and the remaining set, respectively, and \(\sigma _f^2\) and \(\sigma _r^2\) are the genetic variances captured by markers in the GF set and the remaining set, respectively.

The variance components \(\sigma _f^2\), \(\sigma _r^2\), and \(\sigma _e^2\) in Eq. (3) were estimated using the AI-REML algorithm. The heritability estimate is:

$$\hat h_{\rm{GFBLUP}}^2 = \frac{{\hat \sigma _f^2 + \hat \sigma _r^2}}{{\hat \sigma _f^2 + \hat \sigma _r^2 + \hat \sigma _e^2}}$$

and it can be partitioned into two ratios as \(\hat h_f^2 = \frac{{\hat \sigma _f^2}}{{\hat \sigma _f^2 + \hat \sigma _r^2}}\) and \(\hat h_r^2 = \frac{{\hat \sigma _r^2}}{{\hat \sigma _f^2 + \hat \sigma _r^2}}\), quantifying the genetic variances explained by the genetic markers in the GF set and the remaining set, respectively.

Methods for obtaining marker information

In this study, the marker information for constructing weighted G matrices was obtained by four methods: BayesC (Habier et al. 2011), EB (Wang et al. 2016), the FarmCPU (Liu et al. 2016), and RRBLUP (Meuwissen et al. 2001). The priors used in BayesC and EB aimed to shrink small effects to zero and maintain large effects, so we refer to them as local-shrinkage prior methods (van Erp et al. 2019). For FarmCPU, the marker effects were estimated by ordinary least squares (Liu et al. 2016), which is a ridge regression with the penalty parameter equal to zero (van Erp et al. 2019). The Bayesian counterpart of ridge regression is normal prior to marker effects. The normal prior in Bayesian methods shrinks all the coefficients to avoid model overfitting and is a global-shrinkage prior. Since the FarmCPU does not involve shrinkage, we refer to FarmCPU and RRBLUP as normal-prior methods. In these methods, the BayesC and RRBLUP are GP methods, and the EB and FarmCPU are GWAS methods; then the classification of methods is shown in Table 1.

Table 1 Methods used for QTL detection and marker-effect estimation.
Full size table

BayesC and RRBLUP

The estimation of marker effects based on BayesC or RRBLUP methods is performed using the GS3 software (http://snp.toulouse.inra.fr/~alegarra/manualgs3_last.pdf). The statistical model of both methods can be expressed as follows:

$$y_i = \mu + \mathop {\sum}\limits_{k = 1}^K {z_{ik}a_k} + e_i,$$
(4)

where yi is the phenotype for individual i, μ is the overall mean, K is the number of markers, zik is the genotype of individual i for marker k coded as 0, 1, or 2 depending on the number of copies of a given marker allele the individual carried, ak is the additive effect of the kth marker allele, and ei is the random residual for individual i.

For BayesC, all unknown parameters were assigned prior distributions and sampled with a Monte Carlo Markov chain (MCMC) using Gibbs sampling. The MCMC was run for 200,000 iterations, with a burn-in of 20,000 iterations and thin interval of 50. The prior used for ak was a mixture distribution that was expressed as follows:

$$a_k\left| {\pi ,\sigma _a^2\sim } \right.\left\{ {\begin{array}{*{20}{c}} {0\;{\rm{with}}\;{\rm{probility}}\;\pi ,} \\ {N(0,\sigma _a^2)\;{\rm{with}}\;{\rm{probability}}\;(1 - \pi ),} \end{array}} \right.$$

where \(\sigma _a^2\) is the marker-effect variance and 1 − π is the prior probability that the marker effect is nonzero. π was fixed at 0.95, 0.98, 0.99, or 0.995, respectively. The posterior probability that the marker is retained in the BayesC model was used to preselect markers to construct the GF set.

For RRBLUP, all the marker effects were assumed to have the same prior variance and normally distributed. The t statistic for a single genetic marker was computed as follows:

$$t_{\hat s_k} = \frac{{\hat s_k}}{{\sqrt {{\mathrm{Var}}(\hat s_k)} }},$$

where \(\hat s_k\) is the estimate of the kth marker effect, \({\mathrm{Var}}(\hat s_k)\) is the error variance of \(\hat s_k\), and \(t_{\hat s_k}\) was used to preselect markers as the GF set.

EB

EB method proposed by Wang et al. (2016) can selectively shrink marker effects and reduce the noise level to zero for nonassociated markers. The Wald test statistics used in EB method were computed as follows:

$$W_k = \frac{{\hat \gamma _k^2}}{{{\mathrm{Var}}(\hat \gamma _k)}},$$

where \(\hat \gamma _k\) is the estimate of the marker effect of the kth marker and \({\mathrm{Var}}(\hat \gamma _k)\) is the variance of the estimate, and Wk was used to preselect markers as the GF set.

FarmCPU

FarmCPU divided the mixed linear model into two parts: a fixed- and a random-effect item, and used them iteratively (Liu et al. 2016). The population structure is represented by three covariates, which were obtained by using the genome-association and prediction-integrated tool (Lipka et al. 2012). The P value of each marker produced in the last iteration was used as the test statistics to construct the GF set.

Weighted G matrices

The marker information obtained from GWAS/GP methods was used to construct three different weighted G matrices: (1) the genomic-feature-weighted G matrix (GFWG), (2) the estimated marker-variance-weighted G matrix (EVWG), and (3) the absolute value of the estimated marker-effect-weighted G matrix (AEWG).

Weights in the GFWG matrix

The GFWG matrix was constructed based on the GFBLUP model. The markers in the GF and the remaining set are assigned different weights based on \(\hat h_f^2\) and \(\hat h_r^2\), and the weights for markers in the GF and the remaining set were computed as follows:

$$w_f = \frac{{K\hat h_f^2}}{{K_f}}\;{\mathrm{and}}\;w_r = \frac{{K\hat h_r^2}}{{K_r}},$$
(5)

where wf and wr are the weights of markers in the GF and remaining set, respectively, and K is the same as in Eq. (4); Kf and Kr are the number of markers in the GF and the remaining set, separately.

Weights in the EVWG matrix

The EVWG matrix is constructed based on the estimated marker variance derived from the marker-effect estimates and the corresponding marker allele frequency. The weight for the kth marker is computed as follows:

$$w_k = \frac{{K2p_k(1 - p_k)\hat u_k^2}}{{\mathop {\sum}\nolimits_{k = 1}^K {2p_k(1 - p_k)\hat u_k^2} }} = \frac{{Kp_k(1 - p_k)\hat u_k^2}}{{\mathop {\sum}\nolimits_{k = 1}^K {p_k(1 - p_k)\hat u_k^2} }},$$
(6)

where pk is the same as in Eq. (2), and \(\hat u_k\) is the effect estimate of the kth marker. \(2p_k(1 - p_k)\hat u_k^2\) is the estimated genetic variance of the kth marker (Gianola et al. 2009; Zhang et al. 2010a, b).

Weights in the AEWG matrix

Compared to the EVWG matrix, the AEWG matrix only uses the absolute value of the marker-effect estimates to obtain the weight of each marker with:

$$w_k = \frac{{\rm{abs}(\hat u_k)K}}{{\mathop {\sum}\nolimits_{k = 1}^K {{\rm{abs}}(\hat u_k)} }},$$
(7)

where \({\rm{abs}}(\hat u_k)\) is the absolute value of the estimated effect for the kth marker.

Scaling factors

The \(\frac{K}{{K_f}}\) (or \(\frac{K}{{K_r}}\)), \(\frac{K}{{\mathop {\sum}\nolimits_{k = 1}^K {p_k(1 - p_k)\hat u_k^2} }}\), and \(\frac{K}{{\mathop {\sum}\nolimits_{k = 1}^K {{\rm{abs}}(\hat u_k)} }}\) used in Eqs. (5–7) are scaling factors following the recommendation in Gianola et al. (2020). Therefore, the sum of all weights is equal to K. Using these scaling factors, the weighted G matrices we proposed are similar to the additive genetic relationship matrix (A) (Appendix).

Construction of the weighted G matrix

The weighted G matrix was constructed as follows:

$${\mathbf{G}}_{\mathbf{w}} = \frac{{{\mathbf{WDW}}^\prime }}{{2\mathop {\sum}\nolimits_{k = 1}^K {p_k(1 - p_k)} }},$$
(8)

where D is a diagonal matrix with the diagonal elements corresponding to the weights of markers, W and pk are the same as in Eq. (2).

For VanRaden’s G matrix, all markers have the same weight of one; therefore, D is an identity matrix. For a specific trait, the genetic variance explained by each locus is different from each other, and the D matrix should reflect the genetic variance explained by each locus (Gianola et al. 2020). However, D may not be observable. For the EVWG matrix, the estimates (scaled) of genetic variance for each locus were used in the construction of the D matrix. For the GFWG matrix, a larger genetic variance was assigned to the loci in the GF set, and a smaller genetic variance was assigned to the loci in the remaining set. For the AEWG matrix, only the estimates of marker effect were used in the construction of the D matrix.

Weighted GBLUPs

The difference between the weighted and general GBLUP is that the weighted GBLUPs substitute VanRaden’s G matrix with weighted G (GFWG, EVWG, or AEWG) matrices. We also present an sGBLUP that only uses the markers in the GF set to construct VanRaden’s G matrix.

Evaluation of the accuracy of GEBV

For simulated traits, the first 3034 individuals with genotypes in the pedigree were used as the reference population and the residual 500 genotyped individuals as the validation population. The prediction accuracy is the average Pearson’s correlation coefficient of the true breeding value and GEBV of the validation individuals for ten repeats. For real data sets, a tenfold cross-validation procedure was conducted to compare the prediction ability of different methods. For real traits, the deregressed phenotypes of loblolly pine (Resende et al. 2012) and EBVs of bulls (Zhang et al. 2015) and pigs (Cleveland et al. 2012) were used to derive the GP. Marker effects were estimated based only on individuals in the reference group. The mean of the ten Pearson’s correlation coefficients between GEBVs and deregressed phenotypes/EBVs in the validation groups were used as prediction accuracies. For each trait, a one-way ANOVA was applied to determine whether there are any statistically significant differences in prediction accuracies between weighted GBLUPs; if the null hypothesis was rejected using the significance level of 0.05, the multiple paired t-tests were conducted between all GP methods, with P values adjusted by Bonferroni correction.

Results

Simulated QTL effects

The percentages of genetic variance explained by QTLs in different groups for simulated traits with different heritabilities and QTL numbers are summarized in Table 2. The QTL groups were defined by the classification criteria in Fig. S1. According to these percentages, we divided the simulated traits into five genetic architecture scenarios. Scenarios 1 and 2 correspond to traits mainly controlled by loci with large and moderate effects, respectively. Scenarios 3 and 4 correspond to traits controlled by loci with large and moderate effects simultaneously, with the moderate loci accounting for most of the genetic variance. However, the difference between these two scenarios is that there are fewer QTLs in scenario 3 than in scenario 4. Scenario 5 corresponds to traits mainly controlled by loci with small effects. This classification converts the two dimensions of genetic architecture (heritability and QTL number) into one dimension (QTL effect), thus simplifying the analysis of weighting methods. Scenario 5 is not shown in the following analysis because no weighting method was found superior to the general GBLUP in this scenario. The same trend was observed for all traits in each scenario. So, only the traits in the first row of scenarios 1–4 in Table 2 are presented in subsequent analyses.

Table 2 The percentages of genetic variance explained by QTL in different groups for simulated traits with different heritabilities and QTL numbers.
Full size table

Marker information from different GWAS/GP methods

Local-shrinkage (BayesC and EB) and normal-prior methods (RRBLUP and FarmCPU) were used in the estimation of marker effects. Table 3 shows the correlations between simulated and estimated QTL effects, which reflect the accuracy of QTL-effect estimates. The superiority of different GWAS/GP methods in accuracy varied with the change in genetic architectures. Local-shrinkage prior methods were superior to the corresponding normal-prior methods (i.e., EB was better than FarmCPU, and BayesC was better than RRBLUP) for traits mainly controlled by loci of the large effect (scenario 1). However, for traits mainly controlled by loci of moderate effect (scenarios 2 and 3), the normal-prior methods yielded more accurate estimates. For scenario 4, although there were only few loci of large effect, the local-shrinkage prior methods still had advantages. The estimates from GWAS methods were generally more accurate than those of the corresponding GS methods, i.e., FarmCPU was better than RRBLUP, and EB was better than BayesC.

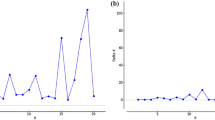
Table 3 The correlations between the simulated and estimated QTL effects based on different GWAS/GP methods for simulated traits with different genetic architectures.
Full size table

We also investigated the power of different methods in QTL detection, and the results are presented in Fig. 1. The π used in BayesC was 0.98. Overall, the local-shrinkage prior methods were better than normal-prior methods, and BayesC was the most powerful, followed by EB, RRBLUP, and FarmCPU. However, the detection efficiency of the methods varied with the scenarios analyzed. In scenario 1, QTLs were effectively detected, and the differences between the methods were obvious (Fig. 1a). In scenario 2, the QTL detection efficiency of all GWAS and GP methods was low (Fig. 1b). In scenario 3, all the GWAS and GP methods had good QTL detection results (Fig. 1c). In scenario 4, the differences between methods in QTL detection were obvious, and the local-shrinkage prior methods were better than normal-prior methods, except in the case of many markers in the GF set, in which the RRBLUP outperformed EB (Fig. 1d).

Fig. 1: The power to detect QTLs based on four GWAS/GP methods in different GF set levels for simulated traits with different genetic architectures.
figure 1

The power expressed as the percentage of the detected number of QTL in the GF set occupied the total number of QTL.

Full size image

Performance of GFWGBLUP

The prediction accuracies by GFBLUP, GFWGBLUP, and sGBLUP in different GF set levels are given in Fig. S2. The marker number in the GF set had an impact on the prediction accuracies of the three methods. When the number of markers was less than 500, GFWGBLUP performed a bit worse than GFBLUP, but better than sGBLUP. The poor performance of sGBLUP may be due to the loss of genetic variance caused by the simplified G matrix. GFWGBLUP almost equaled GFBLUP when the marker number was more than 500, and all three methods obtained similar results when the marker number was more than 2000. GFWGBLUP was superior or equal to the corresponding sGBLUP in the simulated study. Therefore, only GFWGBLUP was compared with other weighting methods. We also investigated the influence of hyperparameter π on the BayesC–GFWGBLUP (Fig. S3). Four different π values (0.95, 0.98, 0.99, and 0.995) were used. We found that the larger the π value, the better the prediction. Therefore, a larger π value (0.995) was used in BayesC for subsequent analyses.

To optimize the GFWGBLUP method for traits with different genetic architectures, two factors that affect the prediction accuracy of GFWGBLUP were investigated: the number of markers and the methods used to construct the GF set. Using the accuracy by GBLUP as a reference, the influences of these two factors varied under different scenarios of genetic architecture (Fig. 2). In scenario 1, good results were obtained by constructing a GF set with fewer top-ranked markers (100–2000) (Fig. 2a). The BayesC–GFWGBLUP (π equals to 0.995) achieved the best result (11.8% higher than GBLUP), followed by EB, RRBLUP, and FarmCPU-based GFWGBLUP. In scenario 2, normal-prior GFWGBLUP had very limited advantages over GBLUP when a large number of markers were included in the GF set (Fig. 2b). In scenario 3, optimal normal-prior GFWGBLUP performed better than GBLUP, and much better than local-shrinkage prior GFWGBLUP (Fig. 2c). In scenario 4, GFWGBLUP had very limited advantages over GBLUP (Fig. 2d).

Fig. 2: The accuracy of GFWGBLUP based on four GWAS/GP methods in different GF set levels for simulated traits with different genetic architectures.
figure 2

The dashed lines indicate the prediction accuracies of general GBLUP.

Full size image

Performance of EVWGBLUP and AEWGBLUP

In scenario 1, all the weighting methods outperformed the general GBLUP significantly (Fig. 3a). While EVWGBLUPs performed better than the corresponding AEWGBLUPs (e.g., BayesC–EVWGBLUP was better than BayesC–AEWGBLUP), local-shrinkage prior EVWGBLUPs performed better than the corresponding normal-prior EVWGBLUPs (i.e., BayesC–EVWGBLUP was better than RRBLUP–EVWGBLUP and EB-EVWGBLUP was better than FarmCPU–EVWGBLUP). Therefore, local-shrinkage prior EVWGBLUPs were best suited for this scenario. Meanwhile, BayesC–EVWGBLUP (14.8% higher than GBLUP) was better than EB-EVWGBLUP (9.3% higher than GBLUP), which may be due to the large π (0.995) used in BayesC. In fact, the prediction accuracy of EB-GFWGBLUP was similar to that of BayesC–GFWGBLUP when π was equal to 0.99. In scenario 2, AEWGBLUP was better than the corresponding EVWGBLUP (e.g., BayesC–AEWGBLUP was better than BayesC–EVWGBLUP), and normal-prior AEWGBLUPs performed better than local-shrinkage prior AEWGBLUPs (i.e., RRBLUP–AEWGBLUP was better than BayesC–AEWGBLUP, and FarmCPU–AEWGBLUP was better than EB-AEWGBLUP). Therefore, normal-prior AEWGBLUPs were best suited for this scenario (Fig. 3b). In scenario 3, FarmCPU–EVWGBLUP maximized the prediction accuracy (3.7% higher than GBLUP) (Fig. 3c) because of the higher accuracy of QTL-effect estimates from FarmCPU (Table 3). In scenario 4, BayesC–AEWGBLUP maximized the prediction accuracy (2.4% higher than GBLUP) (Fig. 3d) due to the advantages of BayesC in QTL detection (Fig. 1d) and effect estimation (Table 3). The comparisons mentioned above were conducted by paired t-test because the same simulated traits were used in different methods, and the statistical significance of the differences between methods is shown in Fig. 3.

Fig. 3: The accuracy of EVWGBLUP and AEWGBLUP based on four GWAS/GP methods for simulated traits with different genetic architectures.
figure 3

For the last group bars (the far right side of each plot), the weights are 1 for all markers, so these weighted GBLUPs are the same as the general GBLUP, and these groups of bars were used as the reference. The standard errors are indicated by the whiskers on the bars. ***indicates significant differences at P < 0.001, **indicates significant differences at 0.001 < P < 0.01.

Full size image

For traits mainly controlled by loci of large effect, the estimates of marker effects obtained by BayesB were also used in the construction of EVWGBLUP and AEWGBLUP models. However, there was no difference in prediction accuracy between BayeB-based EV/AEWGBLUP and BayeC-based EV/AEWGBLUP. Nevertheless, the prediction performances of the weighted GBLUPs were much better than that of BayesB and BayesC (Fig. S4).

In the simulated study, EVWGBLUP maximized the prediction accuracies for traits controlled by few QTLs. AEWGBLUP achieved the best results for traits mainly controlled by loci of moderate effect, except in scenarios where traits were controlled by fewer genes. Therefore, EV/AEWGBLUP are superior to GFWGBLUP for traits mainly controlled by loci with large or moderate effects. This suggests that the effect estimates of loci with large or moderate effects are meaningful in GP.

Superiority of GFWGBLUP

To explore the superiority of GFWGBLUP according to genetic architecture, we also simulated traits for which the GFWGBLUP was expected to achieve the best results (Fig. 4). The traits in scenarios 6a and 6b were mainly controlled by loci of a small effect; meanwhile, they were also influenced by some loci of a large effect; the GFWGBLUP was significantly better (P < 0.05) than other weighted GBLUPs. For traits mainly controlled by loci of a large effect, the superiority of GFWGBLUP disappeared (scenario 6c). GFWGBUP had no advantage across all combinations of moderate- and small-effect loci (scenarios 6d–f). Therefore, GFWGBLUP was advantageous for traits controlled by some loci with large effects (explain 25–50% genetic variance) and a range of loci with small effects.

Fig. 4: The performance of different weighted GBLUPs for traits controlled by loci with small and large/moderate effects simultaneously.
figure 4

The heritabilities and phenotypic variances for scenarios 6a–f were all 0.8 and 100, respectively. In scenarios 6a–c, loci of a large effect explained 20%, 40%, and 60% of the phenotypic variances, respectively; the remaining genetic variance was assigned to 5000 loci of a small effect evenly. In scenarios 6d–f, loci of a moderate effect explained 20%, 40%, and 60% of the phenotypic variances, respectively; the remaining genetic variance was assigned to 5000 loci of a small effect evenly. A single locus of a large effect in scenarios 6a–c accounts for 2% of the phenotypic variance, and each locus of moderate effect in scenarios 6d–f accounts for 0.4% of the phenotypic variance. All scenarios were replicated ten times. The standard errors are indicated by the whiskers on the bars. Paired t-test was applied to compare the difference between methods, with P values adjusted by Bonferroni correction. ***indicates significant differences at P < 0.001, **indicates significant differences at 0.001 < P < 0.01, NS indicates no statistically significant difference.

Full size image

Include or exclude QTLs

We examined the performance of different weighted GBLUPs based on genotypic data with or without QTLs for traits with different genetic architectures. The results indicated that the relationships between the prediction accuracy of weighted GBLUPs and the genetic architecture of traits were the same, regardless of whether QTLs were included in the genotypic data (Fig. S5).

Performance on real traits across species

We examined the performance of different weighted GBLUPs on 25 real traits from three species: loblolly pine (17), cattle (3), and pig (5). Overall, our weighted GBLUPs outperformed general GBLUP for 21 of 25 real traits (Fig. S6). Compared with the general GBLUP, the gains of weighting methods in terms of accuracy ranged from 44% to marginal for real traits. Table 4 lists nine traits for which the best weighted GBLUP performed significantly better than general GBLUP.

Table 4 The accuracies of different weighted GBLUPs for real traits in three data sets.
Full size table

Normal-prior AEWGBLUP maximized the prediction accuracies for milk yield and CWAL (crown width along the planting beds) (Fig. S7a, c). These results were consistent with that of simulated traits mainly controlled by loci of moderate effect (scenario 2); milk yield is mainly controlled by loci of moderate effect (Tiezzi and Maltecca 2015; Habier et al. 2011). FarmCPU–EVWGBLUP maximized the prediction accuracy for fat percentage (Fig. S7b), which is consistent with the results for simulated traits controlled by few loci of a large effect and some loci of moderate effect (scenario 3); fat percentage is controlled by one major gene and additional loci with moderate effects (Tiezzi and Maltecca 2015; Hayes et al. 2010). For Rust_gall_vol, which is controlled by few loci of a large effect (Resende et al. 2012), BayesC–AEWGBLUP achieved the best result (Fig. S7d), which is consistent with the results of simulated traits controlled by a few loci with large and many loci with moderate effects (scenario 4). For T1–5 from the pig data set, the BayesB always outperformed the ssGBLUP, indicating that some loci of large effect affect these traits (Cleveland et al. 2012). GFWGBLUP obtained the best results (Fig. S7e–i), which is consistent with the results of simulated traits controlled by some loci of large effect and a range of loci with small effects (scenarios 6a and b).

Discussion

The genomic relationship matrix is a crucial element in the GBLUP model. Ideally, the G matrix should precisely reflect the genetic relationship between individuals for a specific trait (Wang et al. 2018). However, this ideal situation is unrealistic in practice. A feasible method is to construct a weighted G matrix using marker information from GWAS or Bayesian methods (Fragomeni et al. 2017; Zhang et al. 2016). At the same time, the effective utilization of the marker information becomes crucial in the construction of the weighted G matrix (Fragomeni et al. 2017), and the optimal weighting method changes with the trait being analyzed. In this study, we developed a series of weighted methods that can be adapted to various genetic architectures of quantitative traits and assessed their relative performance in relation to trait genetic architecture and the number of markers considered.

QTL detection and marker-effect estimation

Published studies have shown that loci of a large effect are easier to be detected (Wimmer et al. 2013; van den Berg et al. 2013), which is consistent with our results (Fig. 1a). Meanwhile, the assumptions of marker effects used in GWAS/GP methods also influence the efficiency of QTL detection, like BayesC with larger π achieving better results (Lee et al. 2017; Mehrban et al. 2017; van den Berg et al. 2013; Zhang et al. 2016). These were consistent with the superiority of local-shrinkage prior methods used in our study.

In addition to the superiority of QTL detection, local-shrinkage prior methods can retain the effects of loci with large effects and shrink the effects of irrelevant loci (Hastie et al. 2015; van Erp et al. 2019). Therefore, local-shrinkage prior methods may be suitable for the estimation of marker effects for traits mainly controlled by loci of large effect. Detection of QTL is difficult for traits mainly controlled by loci of moderate effect (Fig. 1b), and local-shrinkage prior methods would shrink the effects of QTL that could not be detected (van Erp et al. 2019). Therefore, normal-prior methods may be appropriate in the estimation of marker effects for traits mainly controlled by loci of moderate effect.

EVWGBLUP

Most of the previously published weighted GBLUP methods are EVWGBLUP (Tiezzi and Maltecca 2015; Calus et al. 2014; Karaman et al. 2018; Fragomeni et al. 2017; Zhang et al. 2016). The EVWGBLUP improved the prediction accuracies for traits influenced by loci of large effect. However, this method had no advantage in traits mainly controlled by loci with small or moderate effects. These results are consistent with those of previous studies (Tiezzi and Maltecca 2015; Karaman et al. 2018). EVWGBLUP works to boost accuracies for traits mainly controlled by loci of large effect, especially when marker information was derived from local-shrinkage prior methods, for two reasons. First, local-shrinkage prior methods can detect and retain loci of a large effect effectively while shrinking the effects of irrelevant loci (Hastie et al. 2015; van Erp et al. 2019). Second, EVWGBLUP makes the most of the information of marker-effect estimates by using the estimated marker-effect variance to construct the G matrix. Therefore, the combination of local-shrinkage prior methods and EVWGBLUP is suitable for traits mainly controlled by loci of a large effect.

Compared to the general GBLUP, local-shrinkage prior EVWGBLUP improved the prediction accuracies for three real traits (i.e., rust_gall_vol, fat percentage, and T1) in this study (Table 4). Published studies have shown that these traits are more suitable to shrinkage prior Bayesian methods, such as BayesCπ performed better for fusiform rust resistance traits (Resende et al. 2012; Daetwyler et al. 2013) and fat percentage (Habier et al. 2011), and BayesB was superior to ssGBLUP for T1 (Cleveland et al. 2012). These results indicate that the local-shrinkage prior EVWGBLUP can improve the prediction accuracies for traits that are suitable for the shrinkage prior Bayesian methods. However, local-shrinkage prior EVWGBLUP did not have the highest prediction accuracies for these traits (Table 4) because loci of a large effect account for only a small part of the genetic variances, and most of the genetic variances are explained by loci of moderate or small effects (Resende et al. 2012; Habier et al. 2011; Cleveland et al. 2012).

Distinguishing causal variants or associated markers from irrelevant markers can be done more efficiently for traits controlled by fewer QTL, even for traits with lower heritabilities (Wang et al. 2018; van den Berg et al. 2013), which was also true for our study. For simulated traits with 100 QTLs and a heritability of 0.15 (scenario 3), 50–60% of the QTLs (and nearly 80% of the total genetic variance) were included in the 15% top-ranked markers, whichever GWAS/GP methods were used for the QTL detection (Fig. 1c). So, it is necessary to distinguish between predictive and irrelevant markers in constructing the G matrix. EVWGBLUP can be used to distinguish markers based on marker-effect estimates. Moreover, traits in scenario 3 are mainly controlled by loci of moderate effect, and the QTL-effect estimates from normal-prior methods were more accurate (Table 3). Therefore, the normal-prior EVWGBLUP achieved the best result (Fig. 3c). Similarly, fat percentage is controlled by one major gene (explaining about 30% of genetic variance) and some loci of moderate effect (Tiezzi and Maltecca 2015; Hayes et al. 2010). Consistent with the simulated results (scenario 3), FarmCPU–EVWGBLUP maximized the prediction accuracy for fat percentage (Table 4). Compared to a previously published study using the same cattle data set (Gao et al. 2015), the FarmCPU–EVWGBLUP performed better than all the Bayesian methods. This may be related to FarmCPU’s advantage in QTL-effect estimation (Table 3), and the EVWGBLUP used the advantage further.

AEWGBLUP

Weights of markers in the AEWG are proportional to the absolute value of marker-effect estimates. Therefore, the weights are not dependent on the estimates as heavily as that of EVWG, but the estimated effect information is still used. GWAS and GP methods are inefficient in QTL detection for traits mainly controlled by loci of moderate effect (van den Berg et al. 2013), and normal-prior methods should be used to avoid the effect shrinkage of QTL that could not be detected. Compared to EVWGBLUP, AEWGBLUP can reduce the negative impact of the inaccurate estimation of the marker effect. This is similar to the moderate weight used in the BLUP|GA for milk yield (Zhang et al. 2015). It is hard to find a Bayesian method that is better than the GBLUP for traits mainly controlled by loci of moderate effect, like milk yield (Habier et al. 2011; Gao et al. 2015). However, FarmCPU–AEWGBLUP improved the prediction accuracy significantly (Table 4). This may be due to the accurate QTL-effect estimates of GWAS methods (Table 3).

Most of the traits are actually with complex genetic backgrounds and may be influenced by loci with large, moderate, and small effects simultaneously. Like the simulated trait controlled by few loci with large and many loci with moderate effects simultaneously (scenario 4), BayesC–AEWGBLUP achieved the best result (Fig. 3d) for this case. The same trend was also observed in rust_gall_vol (Table 4), which is controlled by few loci of a large effect (Resende et al. 2012). In terms of genetic architecture, scenario 4 is a transition state from scenarios 1 to 2, while from the weighting methods, BayesC–AEWGBLUP is a transition state from local-shrinkage prior EVWGBLUP to normal-prior AEWGBLUP. Although BayesC–AEWGBLUP improved the prediction accuracies significantly for these traits, the combination (local-shrinkage prior methods and AEWGBLUP) seems to violate the pattern found in this study. BayesC is favorable for the detection and estimation of loci with large effects, but unfavorable for the loci of moderate effect. AEWGBLUP is suitable for loci of moderate effect, but not for loci of a large effect. As a result, the marker information from GWAS/GP methods may not be fully utilized. The combination of FarmCPU–EVWGBLUP used in scenario 3 also has the same problem. Therefore, Bayesian methods with mixture distribution priors for marker effects are needed. BayesR assumes that the true marker effects are derived from a series of normal distributions (Erbe et al. 2012; Wang et al. 2015; van den Berg et al. 2017). So a further study with a focus on the BayesR-weighted GBLUP is suggested.

GFWGBLUP

Compared to the RRBLUP used in Sarup et al. (2016), the local-shrinkage prior methods used in this study were more powerful in QTL detection (Fig. 1). One reason for the inconsistent results emerging from sGBLUP methods may be due to the different methods used in the detection of significant markers (Wang et al. 2018; Moser et al. 2010; Li et al. 2017; Veerkamp et al. 2016). Equal to the assumption used in GBLUP, each marker in the GF/remaining set evenly shares the genetic variances that were allocated to the GF/remaining set (Sarup et al. 2016; VanRaden 2008). For traits mainly controlled by loci of a small effect and influenced by some loci of a large effect simultaneously, loci of large and small effects can be treated differently in the GF and remaining sets, respectively. For the real pig traits that are influenced by some loci of a large effect (Cleveland et al. 2012), GFWGBLUP based on a powerful GWAS method, like FarmCPU, improved the prediction accuracies significantly (Table 4). Moreover, the FarmCPU–GFWGBLUP has better predictive performance than the BayesB method used in Cleveland et al. (2012) for all pig traits. From these results, the detection of loci with large effects may be crucial in the construction of the GFWG matrix and, therefore, powerful GWAS methods are needed.

The impact of genetic variance estimation

The estimates of genetic variance obtained by GBLUP are very close to the simulated values (Fig. S8) and were used as references. Local-shrinkage prior EVWGBLUP methods always had the problem of genetic variance overestimation (Fig. S8). The overestimation may be caused by the duplicate use of markers that are in linkage disequilibrium, which appeared on the same peaks in the GWAS results and had similar weights. The control of false positives is important in this situation. The GWAS methods used in this study can control the false-positive rate (Liu et al. 2016; Wang et al. 2016), and may explain the reasonable variance estimates from EB-EVWGBLUP (Fig. S8) and FarmCPU–GFWGBLUP (Fig. S9), and further explain the advantages of FarmCPU–GFWGBLUP in scenario 6 and real pig traits. The control of false positives in GWAS methods also seems to be related to the accurate QTL-effect estimates in Table 3. However, the control of false positives also compromises the detection of true positives (Fig. 1). Despite the problem of overestimation of genetic variance, BayesC–EVWGBLUP largely improved the performance of GP for traits mainly controlled by loci of a large effect (Fig. 3a). This finding is consistent with previous studies (Mathew et al. 2018; Zhang et al. 2010b).

For traits with low heritability, large numbers of genotyped and phenotyped individuals are needed to achieve even moderate GEBV accuracy (Goddard 2009). Alternatively, the heritability of the trait can be increased by using EBVs as phenotypes, in which case the effective heritability is proportional to the EBV accuracy (Garrick et al. 2009). The percentage of phenotypic variance explained by a single marker will increase with the increase in heritability. These increases will facilitate QTL detection and effect estimation and, in turn, improve the effectiveness of weighted GBLUP methods.

Conclusions

In this study, weighted G matrices were constructed in different ways to utilize the marker information from different GWAS/GP methods effectively, which can be used to adapt various genetic architectures. Local-shrinkage prior EVWGBLUP is superior for traits mainly controlled by loci of a large effect. Normal-prior AEWGBLUP performs well for traits mainly controlled by loci of moderate effect. For traits controlled by some loci of a large effect and a range of loci with small effects, GFWGBLUP based on powerful GWAS methods has advantages. Even for traits controlled by a combination of loci with large and moderate effects, which are common in real traits, our weighting methods can optimize the prediction accuracies by trading off the information of QTL detection and effect estimation. The strategies of constructing the weighted G matrix proposed in this study effectively improved the predictive ability of GBLUP by utilizing the marker information from GWAS/GP methods, and deserve further investigation in real data.