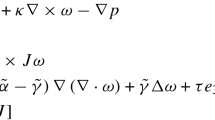Abstract
We study the asymptotic behavior of micropolar fluid flows in a thin domain of thickness \(\eta _\varepsilon \) with a periodic oscillating boundary with wavelength \(\varepsilon \). We consider the limit when \(\varepsilon \) tends to zero and, depending on the limit of the ratio of \(\eta _\varepsilon /\varepsilon \), we prove the existence of three different regimes. In each regime, we derive a generalized Reynolds equation taking into account the microstructure of the roughness.
Similar content being viewed by others
References
Allaire, G.: Homogenization of the Stokes flow in a connected porous medium. Asymp. Anal. 2, 203–222 (1989)
Anguiano, M., Suárez-Grau, F.J.: Nonlinear Reynolds equations for non-Newtonian thin-film fluid flows over a rough boundary. IMA J. Appl. Math. 84, 63–95 (2019)
Arbogast, T., Douglas, J.R.J., Hornung, U.: Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 21, 823–836 (1990)
Bayada, G., Chambat, M.: The transition between the Stokes equations and the Reynolds equation: a mathematical proof. Appl. Math. Opt. 14, 73–93 (1986)
Bayada, G., Chambat, M.: New models in the theory of the hydrodynamic lubrication of rough surfaces. J. Tribol. 110, 402–407 (1988)
Bayada, G., Chambat, M.: Homogenization of the Stokes system in a thin film flow with rapidly varying thickness. RAIRO Modél. Math. Anal. Numér. 23, 205–234 (1989)
Bayada, G., Chambat, M., Gamouana, S.R.: About thin film micropolar asymptotic equations. Quart. Appl. Math. 59, 413–439 (2001)
Bayada, G., Ciuperca, I., Jai, M.: Homogenized elliptic equations and variational inequalities with oscillating parameters. Application to the study of thin flow behavior with rough surfaces. Nonlinear Anal. Real World Appl. 7, 950–966 (2006)
Bayada, G., Lukaszewicz, G.: On micropolar fluids in the theory of lubrication. Rigorous derivation of an analogue of the Reynolds equation. Int. J. Eng. Sci. 34, 1477–1490 (1996)
Benhaboucha, N., Chambat, M., Ciuperca, I.: Asymptotic behaviour of pressure and stresses in a thin film flow with a rough boundary. Quart. Appl. Math. 63, 369–400 (2005)
Benterki, D., Benseridi, H., Dilmi, M.: On a non-stationary, non-Newtonian lubrication problem with Tresca fluid-solid law. J. Inverse Ill Posed Probl. 27, 719–730 (2019)
Bonnivard, M., Pazanin, I., Suárez-Grau, F.J.: Effects of rough boundary and nonzero boundary conditions on the lubrication process with micropolar fluid. Eur. J. Mech. B. Fluids 72, 501–518 (2018)
Boukrouche, M., Paoli, L.: Asymptotic analysis of a micropolar fluid flow in a thin domain with a free and rough boundary. SIAM J. Math. Anal. 44, 1211–1256 (2012)
Bresch, D., Choquet, C., Chupin, L., Colin, T., Gisclon, M.: Roughness-induced effect at main order on the Reynolds approximation. SIAM Multiscale Model. Simul. 8, 997–1017 (2010)
Boukrouche, M., Ciuperca, I.: Asymptotic behaviour of solutions of lubrication problem in a thin domain with a rough boundary and Tresca fluid–solid interface law. Quart. Appl. Math. 64, 561–591 (2006)
Cioranescu, D., Damlamian, A., Griso, G.: Periodic unfolding and homogenization. C.R. Acad. Sci. Paris Ser. I 335, 99–104 (2002)
Cioranescu, D., Damlamian, A., Griso, G.: The periodic unfolding method in homogenization. SIAM J. Math. Anal. 40, 1585–1620 (2008)
Chupin, L., Martin, S.: Rigorous derivation of the thin film approximation with roughness-induced correctors. SIAM J. Math. Anal. 44, 2041–3070 (2012)
Dupuy, D., Panasenko, G., Stavre, R.: Asymptotic solution for a micropolar flow in a curvilinear channel. ZAMM Z. Angew. Math. Mech. 88, 793–807 (2008)
Duvaut, G., Lions, J.L.: Les inequations en mechanique et en physique [The Inequations in Mechanics and Physics]. Dunod, Paris (1972)
Eringen, A.C.: Theory of micropolar fluids. J. Math. Mech. 16, 1–16 (1966)
Fabricius, J., Koroleva, Y.O., Tsandzana, A., Wall, P.: Asymptotic behaviour of Stokes flow in a thin domain with a moving rough boundary. Proc. R. Soc. A 470, 20130735 (2014)
Johnston, G.J., Wayte, R., Spikes, H.A.: The measurement and study of very thin lubricant films in concentrated contacts. Tribol. Trans. 34, 187–194 (1991)
Letoufa, Y., Benseridi, H., Dilmi, M.: Study of Stokes dynamical system in a thin domain with Fourier and Tresca boundary conditions. Asian Eur. J. Math. (2019). https://doi.org/10.1142/S1793557121500078
Lukaszewicz, G.: Micropolar Fluids, Theory and Applications. Modeling and Simulation in Science. Birkhaüser, London (1999)
Luo, J.B., Huang, P., Wen, S.Z.: Thin film lubrication part I: study on the transition between EHL and thin film lubrication using relative optical interference intensity technique. Wear 194, 107–115 (1996)
Luo, J.B., Huang, P., Wen, S.Z., Lawrence, L.: Characteristics of fluid lubricant films at nano-scale. J. Tribol. 121, 872–878 (1999)
Marusić-Paloka, E., Pazanin, I., Marusić, S.: An effective model for the lubrication with micropolar fluid. Mech. Res. Comm. 52, 69–73 (2013)
Mikelić, A.: Remark on the result on homogenization in hydrodynamical lubrication by G. Bayada and M. Chambat. RAIRO Modél. Math. Anal. Numér. 25, 363–370 (1991)
Mikelić, A., Tapiero, R.: Mathematical derivation of the power law describing polymer flow through a thin slab. Modélisation Math. Anal. Numér. 29, 3–21 (1995)
Pazanin, I., Suárez-Grau, F.J.: Analysis of the thin film flow in a rough thin domain filled with micropolar fluid. Comput. Math. Appl. 68, 1915–1932 (2014)
Singh, C., Sinha, P.: The three-dimensional Reynolds’ equation for micropolar fluid lubricated bearings. Wear 76, 199–209 (1982)
Suárez-Grau, F.J.: Asymptotic behavior of a non-Newtonian flow in a thin domain with Navier law on a rough boundary. Nonlinear Anal. 117, 99–123 (2015)
Tartar, L.: Incompressible fluid flow in a porous medium convergence of the homogenization process. In: Appendix to Lecture Notes in Physics, vol. 127. Springer, Berlin (1980)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Syakila Ahmad.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Computation of the Coefficients of the Micropolar Reynolds Equation
Appendix: Computation of the Coefficients of the Micropolar Reynolds Equation
In this appendix, we describe how to obtain the coefficient of the Reynolds equation
where \(b(x')= {h^3(z')\over 1-N^2}\varPhi (h(z'),N,R_c)f'(z')\) and \(\varPhi \) defined by (78), from the micropolar system posed in \(\varOmega =\{(z',z_3)\in \mathbb {R}^2\times \mathbb {R}:\,z'\in \omega ,\ 0<z_3<h(z')\}\), given by
together with
and boundary conditions
We note that \(({\bar{u}}_1, {\bar{w}}_2)\), with external forces \((\bar{f}',{\bar{g}}')\), and \(({\bar{u}}_2, -{\bar{w}}_1)\), with external forces \(({\bar{f}}',-{\bar{g}}')\), satisfy the same equations and boundary conditions. So we only describe the computation of \(({\bar{u}}_1, \bar{w}_2)\).
First, from the first equation of (105) we have
Putting this into the second equation of (105), we have
The solution is
where \(k=\sqrt{{4N^2(1-N^2)\over R_c}}\) and A and B are unknowns functions.
Putting this solution into equation (110), we can write \({\bar{u}}_1\) as follows
We rewrite C, D, as a function of A and B, using the boundary conditions. So, for \({\bar{u}}_1(z',0)={\bar{w}}_2(z',0)=0\), we, respectively, get
and so
Using the boundary conditions \({\bar{u}}_1(z',h(z'))=\bar{w}_2(z',h(z'))=0\), we get the following system
where Q is the matrix defined by
The solution of this system is given by
where \(A_1(z')\), \(B_1(z')\) and \(A_2(z')\), \(B_2(z')\) are solution of
Calculating \(A_i\), \(B_i\) for \(i = 1, 2\), we have
and then \({\bar{u}}_1\) and \({\bar{w}}_2\) are obtained by (113) as functions of \({\bar{p}}\), \({\bar{f}}_1\) and \({\bar{g}}_2\), by the following expressions
As it was pointed at the beginning, expressions for \({\bar{u}}_2,\bar{w}_1\) are obtained by using the expressions of \({\bar{u}}_2\), \(\bar{w}_1\), and so we have
We observe \({\bar{u}}'\) and \({\bar{w}}'\) can be rewritten as follows
and
Finally, integrating the expressions of \({\bar{u}}'\) and \({\bar{w}}'\) with respect to the variable \(z_3\), it holds that
for \(j=1,2\), with \(\varPhi \) and \(\varPsi \) defined by (78) and (79), respectively. Putting this in (107), we get the desired Reynolds equation (104).
Rights and permissions
About this article
Cite this article
Suárez-Grau, F.J. Analysis of the Roughness Regimes for Micropolar Fluids via Homogenization. Bull. Malays. Math. Sci. Soc. 44, 1613–1652 (2021). https://doi.org/10.1007/s40840-020-01027-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-020-01027-1