Differences in power law growth over time and indicators of COVID-19 pandemic progression worldwide

In this paper, we use error analysis and curve fitting to analyze the progression of COVID-19 [14–17]. In weighted least squares curve fitting for linear functions one finds the fit parameters, A, B, ..., which minimizes χ², which depends on the location of data points x_i, the measured values y_i, and the uncertainties in y_i given by σ_i.

$$\begin{equation*}{\chi }^{2}=\sum _{i=1}^{n}\frac{{\left[{y}_{i}-A-B{x}_{i}\right]}^{2}}{{\sigma }_{i}^{2}}.\end{equation*}$$

To fit a straight line model, one solves for A and B by calculating $\frac{\partial {\chi }^{2}}{\partial A}=0$ and $\frac{\partial {\chi }^{2}}{\partial B}=0$ and solving the resulting system of linear equations. We use the notation,

$$\begin{equation*}{S}_{wuv}=\sum _{i=1}^{N}{w}_{i}{u}_{i}{v}_{i}\quad {w}_{i}=\frac{1}{{\sigma }_{i}^{2}}.\end{equation*}$$

The uncertainties in the parameters can also be directly computed using propagation of error.

$$\begin{align*}\hfill A& =\frac{{S}_{wy}{S}_{wxx}.-{S}_{wx}{S}_{wxy}}{{S}_{w}{S}_{wxx}-{S}_{wx}^{2}}\qquad B=\frac{{S}_{w}{S}_{wxy}.-{S}_{wx}{S}_{wy}}{{S}_{w}{S}_{wxx}-{S}_{wx}^{2}}\hfill \\ \hfill {\sigma }_{A}& =\sqrt{\frac{{S}_{wxx}}{{S}_{w}{S}_{wxx}-{S}_{wx}^{2}}}\qquad {\sigma }_{B}=\sqrt{\frac{{S}_{w}}{{S}_{w}{S}_{wxx}-{S}_{wx}^{2}}}.\hfill \end{align*}$$

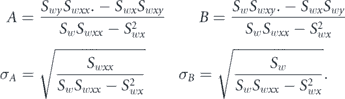
There are different methods to visualize the progression of the number of positive cases. Typically one uses linear plots, semilogarithmic plots, or log–log plots. Keep in mind several things when interpreting functions on a log–log plot. Exponential growth on a log–log plot appears exponential, and power-law growth on a log-log plot appears linear. If we define two transformations then we just have to fit linear functions. Transformation 1 is

$$\begin{equation*}{Y}_{i}=\mathrm{ln}\enspace {y}_{i}\qquad {X}_{i}=\mathrm{ln}\enspace {x}_{i}.\end{equation*}$$

For a power law function y = αx^β then

$$\begin{equation*}\mathrm{ln}\enspace {y}_{i}=\mathrm{ln}\enspace \alpha +\beta \enspace \mathrm{ln}\enspace {x}_{i}\to {Y}_{i}={A}_{1}+{B}_{1}{X}_{i}.\end{equation*}$$

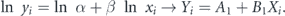
We refer repeatedly to β in this paper as the power-law exponent for the data region of interest.

If we define transformation 2

$$\begin{equation*}{Y}_{i}=\mathrm{ln}\enspace {y}_{i}\qquad {X}_{i}={x}_{i}.\end{equation*}$$

For an exponential function y = y(0)e^rx then

$$\begin{equation*}\mathrm{ln}\enspace {y}_{i}=\mathrm{ln}\enspace y\left(0\right)+r{x}_{i}\to {Y}_{i}={A}_{2}+{B}_{2}{X}_{i}.\end{equation*}$$

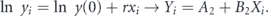
By propagation of error and the square root N rule, the weighting is ${\sigma }_{i}=1/\sqrt{{y}_{i}}$ in both transformations even though there are no explicit errorbars in reports of positive cases.

The logistic function is the solution to the differential equation, which models many different phenomena such as population growth.

$$\begin{equation*}\frac{\mathrm{d}N}{\mathrm{d}t}=rN\left(1-N/K\right).\end{equation*}$$

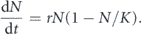
We write the solution in several ways that depend on three parameters.

$$\begin{equation*}N\left(t\right)=\frac{K}{1+{\mathrm{e}}^{-r\left(t-\tau \right)}}=\frac{KN\left(0\right)}{N\left(0\right)+\left(K-N\left(0\right)\right){\mathrm{e}}^{-rt}}.\end{equation*}$$

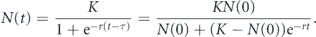
For short times, N increases exponentially. For long times, N is exponentially approaching a plateau. The logistic curve can be fitted by the Levenberg–Marquardt method.

Data was collected from Johns Hopkins [18], the European Centre for Disease Prevention and Control, and Wikipedia. The data files differed on the same days, probably due to how the start of a day is defined or lack of proper reporting. A small number of errors were found in all three data sources, such as the number of cases decreasing on a successive day. Some Wikipedia pages miss the death totals or recoveries, but we consider only positive cases in this paper.

Wikipedia data aggregation appeared to have the best-curated early time data, so it was the only data used for the analysis. Different countries have staggered outbreaks in time, and fitting power-laws depends on the origin of time. For synchronization between countries, an exponential fit to the first 1000 cases was performed. The initial time was an extrapolation of this curve to one case.

To visualize COVID-19 progress, we track the slope of the number of cases on a log–log plot, which is an exponent β. Using a 7 d or 14 d window did not result in much difference. In this visualization, when β nears zero, the disease is mitigated. When β is large, this indicates a country is going into more danger. If β drops significantly below one and then increases again, this can define a second wave.

A visualization method developed by Bhatia is simple to implement and surprisingly effective [11]. In this method, one plots points of the number of cases in the last week on the logarithmic y-axis versus the total number of cases on the logarithmic x-axis. The visualization is a parametric plot eliminating time. Most of the time, the data perfectly line up and progresses upwards and to the right as things get worse for a country. If the plot moves downwards, this indicates mitigation. The noise in actual measurements only modulates the spacing between points but does not impact the general shape of the visualization much.

Epidemiological mathematical models are only as good as their assumptions. Some more sophisticated models beyond SIR might include different compartments like frontline workers F in hospitals or supermarkets who have an increased rate of infectivity. Quarantined individuals Q could be isolated from infecting others after being detected by tests. Exposed individuals E could have a time delay before switching to infected. Super spreaders Z could infect at a higher rate because they do not know they are sick and do not go into quarantine. Adding more sophisticated compartments may seem more realistic, but comes at the cost of more complicated differential equations and more model parameters to be determined.

The SIA model introduced here is probably the most simple way of getting at the logistic equation, similar to what was observed in China. This is only intended to work during lockdowns or with effective social policies. S stands for susceptible, I stands for been infected in the past, and A stands for avoiders. Avoiders are good with hygiene, staying away from sick people, and wearing masks not to get infected. Using avoiders is similar to neglecting recoveries in the SIR model with a different population size.

$$\begin{equation*}S+I+A=P\quad S+I=P-A=K.\end{equation*}$$

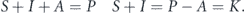
Then

$$\begin{equation*}\frac{\mathrm{d}I}{\mathrm{d}t}=\mu IS=\mu I\left(K-I\right).\end{equation*}$$

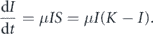
One can use r = μK which gives

$$\begin{equation*}\frac{\mathrm{d}I}{\mathrm{d}t}=rI\left(1-\frac{I}{K}\right).\end{equation*}$$

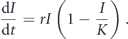
This derivation gives a logistic curve with reduced carrying capacity than the entire population, but does not suggest a way how to estimate K a priori.

In reality, there are probably different categories of people, depending on a complicated way of social interaction networks and behavior that cannot easily be quantified. This model provides a logistic curve, but many SIR model situations are also a similar form. Often in SIR, the effective value of K is of the same order of magnitude as P, whereas in SIA, one can easily achieve K ≪ P, which is different. Once restrictions are eased, then the curve would restart by not considering the previous cases anymore with new parameters in a possible second wave. Also, if there is significant travel between countries, one would expect this model to breakdown.

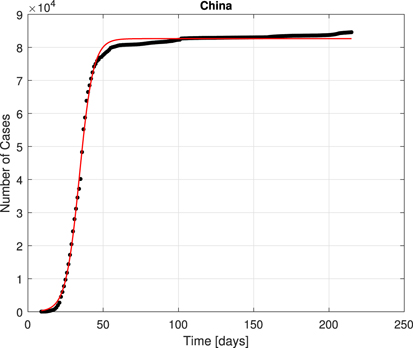
The SIA model may describe the logistic growth of positive cases in China. The reported cases follow a smooth curve once the correction for chest x-ray diagnoses is considered [13]. After the synchronization procedure, one finds in figure 1 the following parameter values.

$$\begin{equation*}\begin{gathered}{c}K=82\enspace 646{\pm}92\enspace \mathrm{p}\mathrm{e}\mathrm{o}\mathrm{p}\mathrm{l}\mathrm{e}\qquad r=0.219{\pm}0.003\enspace {\mathrm{d}}^{-\mathrm{1}}\\ \tau =34.26{\pm}0.08\enspace \mathrm{d}.\end{gathered}\end{equation*}$$

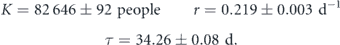
The fit seems reasonable on order 200 d. The genetic algorithm Eureqa also found a logistic curve for the simplest best fit function when running overnight. Most of the increase happens during a 15–20 d period, which may be why neglecting recoveries in SIR is reasonable. China is very strict on travel, but new cases trickle in at later times.

Zoom In Zoom Out Reset image size

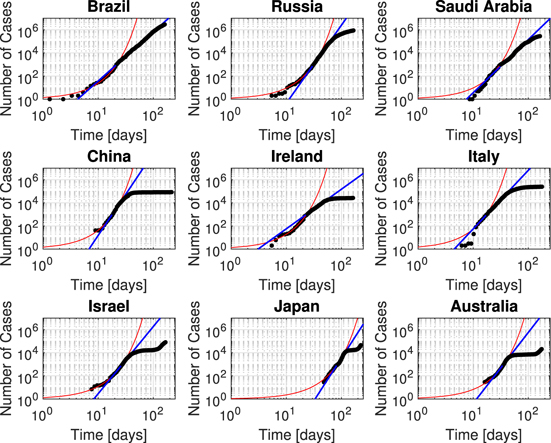
The number of positive cases was investigated with four analyses: early time exponential synchronization, overall power-law growth, the Bhatia visualization, and the β visualization. Nine representative countries are shown here in the results and all 27 in the supplementary materials (https://stacks.iop.org/PB/17/065005/mmedia). Brazil, Russia, and Saudi Arabia are examples of countries that are primarily still in the power-law phase or just exiting it. China, Ireland, and Italy have progressed to the logistic phase. Israel, Japan, and Australia are examples of a second wave after the logistic phase without a saturation.

Figure 2 illustrates the early time exponential phase and power-law growth. In no case does COVID-19 transmit like a pure runaway exponential function to the entire population. The power-law phase extends the longest for Brazil over many powers of 10 because they were slow to implement effective policies. The initial synchronization is not always possible in a satisfactory way due to a lack of data or irregularities. The mean initial exponential growth rate is about 0.25 ± 0.11 per day for 27 countries. An overall power-law exponent was computed for the region of cases that appears linear on the synchronized log–log plot in table 1. The mean overall power-law exponent for all 27 countries is 5.57 ± 0.98 suggesting there is a similarity in the cases' trajectories after synchronization.

Zoom In Zoom Out Reset image size

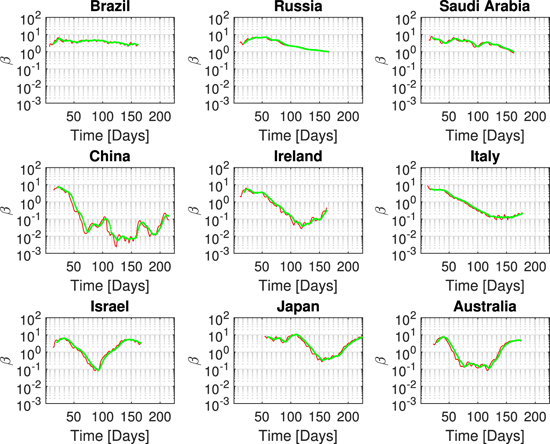
Figure 3 illustrates the β visualization for the same nine countries. Using a 7 d (red) or 14 d (green) window does not lead to much difference. The β always starts high then decreases. One can see the second wave as a decrease in the power-law exponent that later increases significantly above one. China seems to avoid a second wave due to strict policies, but second waves remain to be seen in several more months for most other countries.

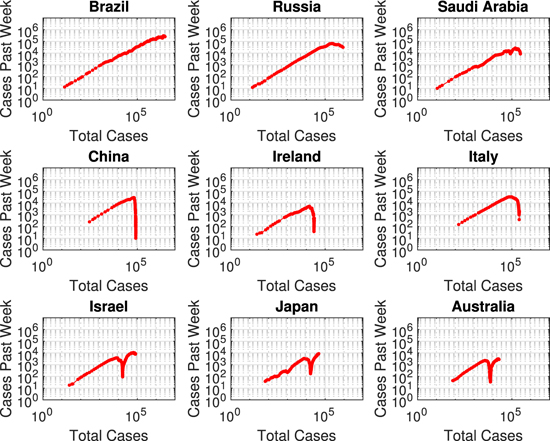
Zoom In Zoom Out Reset image size

Figure 4 illustrates the Bhatia visualization. There is no time parameter on the plots, but one sees the second wave as a drop then an increase in the curve. Most countries fall along the same initial line during the power-law phase. If the reopening of countries is only a delay in the progression, the curve will rise back up and continue along the same initial line. The β visualization is noisier than the Bhatia visualization because it depends explicitly on time.

Zoom In Zoom Out Reset image size