1 Introduction

Many engineering structures such as rotating blades of aircraft, high-rise buildings, wings of aircraft, spacecraft antenna, etc. can be modeled as a beam. Studying the vibration of a beam received a great deal of attention due to its usage in design and control of the mechanical systems. For instance, Woinowsky–Krieger (1950), Burgreen (1951), (Eisley 1964) and Srinivasan (1965) studied the nonlinear vibration of a simply supported beam. They showed that at large amplitude vibrations, the stretching of the beam’s mid-plane affects its dynamic behavior.

In the engineering systems, to suppress vibrations due to external excitation, it is common to use an absorber, spring–mass system attached to the main system. Özkaya et al. (1997) and Karlik et al. (1998) studied the nonlinear vibrations of beam–mass system under different boundary conditions. They demonstrated the effect of mass and its location as well as the effect of boundary conditions on the beam vibrations. Das et al. (2007) studied the out of plane free vibration of a rotating beam with nonlinear spring–mass system. In some applications, beam may be rested on an elastic foundation or it may have multiple supports. Yurddash et al. (2013) studied the nonlinear vibration and stability of an axially moving multi-supported string. They showed the effect of the non-ideal support on stability boundaries and vibration behavior. Pakdemirli and Boyacl (2003) investigated the nonlinear vibrations of a simply supported beam which has a non-ideal internal support. They computed natural frequencies for both ideal and non-ideal support, and also investigated the effect of the non-ideal support on the frequency response curve. Ghayesh (2012) studied free and forced vibrations of a simply supported viscoelastic beam with an intermediate nonlinear support. He used Newton’s second law and Euler–Bernoulli beam theory to obtain the governing equations of motion. He investigated the effect of the system parameters on the linear and nonlinear natural frequencies, vibration responses and frequency–response curves of the system.

Beams with axial motion have wide applications in many mechanical systems such as power transmission belts, conveyor belts, aerial cable tramways, cables of elevators, flexible arms of robots, band saws, pipes conveying fluid, etc. Because of their extensive usages and the requirement of high accuracy and stability, several studies have been conducted on vibrations of axially moving beams. Wickert (1992) studied free vibrations of a tensioned axially moving elastic beam over the sub- and supercritical transport speed ranges using the perturbation method. Mote (1968) obtained the natural frequencies of axially moving beam with constant speed by exactly solving its frequency equation. Chen and Yang (2005) studied the principal parametric resonance of viscoelastic beam with axial pulsating speed. Ghayesh and Khadem (2008) studied the nonlinear vibration of a beam with harmonic axial velocity to show the effects of the rotary inertia and temperature on the vibration response and stability regions. They concluded that as the rotary inertia increases, natural frequencies and critical velocity reduce whereas by increasing the temperature gradient, the critical velocity increases. Ghayesh and Balar (2008) studied the nonlinear parametric vibration of an axially moving beam and the effects of mechanical parameters on the vibration behavior, nonlinear resonance frequencies, stability and bifurcation points. Chang et al. (2010) studied the vibration and stability of an axially moving Rayleigh beam using the finite element method with variable-domain elements.

Park and Chung (2014) studied the vibrations of axially moving beam supported by rollers. They modeled the rollers as two parallel linear springs. Then, the mode shapes and natural frequencies were studied for different values of the spring stiffness and their locations. Considering the external excitation, Ghayesh and Amabili (2013) studied the nonlinear vibrations and stability of an axially moving Timoshenko beam on the internal support. They ignored internal damping and supposed that the axial velocity is constant. Recently, Bu Wang (2018) has studied the dynamic stability of axially moving viscoelastic Rayleigh beams and presented the effects of viscosity coefficients, mean speed, beam stiffness, and rotary inertia factor on the summation parametric resonance and principle parametric resonance. Hua et al. (2018) have studied the effects of retracting speed and static tip deflection on self-excited vibration of axially retracting cantilever beam using Galerkin method. Mokhtari et al. (2017) have investigated the effect of moving beam speed and axial tensile force on vibration and wave characteristics, and static and dynamic stabilities of moving beam by using Wavelet-based spectral finite element dynamic analysis.

In most of the conducted researches, the Euler–Bernoulli beam theory was used. However, for studying the lateral vibrations of beams with large amplitudes and high frequencies, the rotary inertia cannot be neglected. Therefore, by considering the Rayleigh’s beam theory, one can have a suitable dynamic model for the problem. Despite the dominant effect of the internal damping on the dynamic characteristics and wide applications of viscoelastic materials, the internal damping was not considered in most of the works done on axially moving beams. Moreover, although some researchers analyzed the dynamics of the axially moving beam considering constant velocity, in most applications the axial velocity is not constant and it may fluctuate about its mean-value which may lead to instability. Therefore, an intermediate support can be used to suppress the vibration of large-span moving beams and to increase the stability of the system.

According to the above-mentioned points, this paper is conducted to study the nonlinear vibration of axially moving viscoelastic Rayleigh beam with time-dependent velocity and equipped with an intermediate nonlinear support. For this purpose, considering the Kelvin–Voigt model for internal damping and applying the Hamilton’s principle, the governing equations of motion are derived. Then, the multiple scales method is applied to obtain the response of the system. Finally, the effects of the intermediate support parameters, the internal damping and the rotary inertia on the static and dynamic instability, natural frequencies, frequency response and time response of the system are investigated.

2 The Governing Equations of Motion

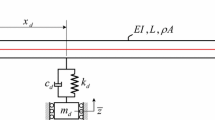
An axially moving beam with an intermediate support is considered as shown in Fig. 1. The beam moves with a time varying axial velocity of Γ. The beam has the length L, density \(\rho\), cross section A cross-sectional area moment of inertia I shearing modulus G, elastic modulus E. The intermediate nonlinear support is located at a distance of \(x_{s}\) from the origin of the fixed right-handed coordinate system \(xyz\) and the beam was considered to be under initial tension of P.

Fig. 1
figure 1

Schematic of an axially moving beam on the intermediate support

Full size image

For the vibration analysis, each of the beams section between a pair of supports is considered as a separate beam, namely the span 1, \(0 < x < x_{s}\), and the span 2, \(x_{s} < x < L\). As mentioned above, due to the importance of the rotary inertia in large amplitude and/or high frequency vibrations of beams, one may consider the Rayleigh’s beam theory to have a suitable dynamic model for the problem. Therefore, the kinetic energy of the beam can be expressed as Eq. 1 (Rezaee and Lotfan 2015).

$$\begin{aligned} T & = \frac{1}{2}\rho A\int_{0}^{{x_{s} }} {\left( {\dot{w}_{1} + \varGamma w_{1,x} } \right)^{2} {\text{d}}x} + \frac{1}{2}\rho A\int_{{\,x_{s} }}^{\,L} {\left( {\dot{w}_{2} + \varGamma w_{2,x} } \right)^{2} {\text{d}}x} \\ & \quad + \frac{1}{2}\rho I\int_{0}^{{x_{s} }} {\left( {\dot{w}_{1,x} + \varGamma w_{1,xx} } \right)^{2} {\text{d}}x} + \frac{1}{2}\rho I\int_{{\,x_{s} }}^{\,L} {\left( {\dot{w}_{2,x} + \varGamma w_{2,xx} } \right)^{2} {\text{d}}x} \\ \end{aligned}$$
(1)

where \(w_{i}\) is the transverse displacement of the ith span (i = 1, 2). \(w_{i,x} ,\,\,\,\,i = 1,2\) denotes the derivatives of \(w_{i}\) with respect to x and \(\dot{w}\) denotes the derivatives with respect to time, t.

In Eq. 1, the first and second terms are respectively the kinetic energy of the beam element in spans 1 and 2, due to the transverse vibration. The third and fourth terms are respectively the kinetic energy of the beam element in spans 1 and 2, due to its rotation about y axis.

The nonlinear strain–displacement relation and the constitutive equation of the viscoelastic material according to the Kelvin–Voigt model, for each span are as follows, respectively:

$$\varepsilon_{i} = \frac{1}{2}\left( {w_{i,x} } \right)^{2} - zw_{i,xx} \quad i = 1,2$$
(2)
$$\sigma_{i} = E\varepsilon_{i} + \eta \frac{{{\text{D}}\varepsilon_{i} }}{{{\text{D}}t}}\quad i = 1,2$$
(3)

where \(\eta\) is the viscosity coefficient, \(\sigma_{i}\) is the axial stress in span i and \(\varepsilon_{i}\) is the corresponding axial strain.

Using Eqs. (2) and (3), the stress resultants, namely the bending moment per unit length \(M_{i}\) and the axial force per unit length \(N_{i}\) can be obtained as

$$M_{i} = - \int\limits_{A} {z\sigma_{i} {\text{d}}A} = EIw_{i,xx} + \eta I\left( {\dot{w}_{i,xx} + \varGamma w_{i,xxx} } \right)$$
(4)
$$N_{i} = \int\limits_{A} {\sigma_{i} {\text{d}}A} = \frac{1}{2}EA\left( {w_{i,x} } \right)^{2} + \eta A\left[ {\dot{w}_{i,x} w_{i,x} + \varGamma w_{i,x} w_{i,xx} } \right]$$
(5)

The potential energy of the beam associated with the stress resultants and the work done by the intermediate support can be expressed as

$$\begin{aligned} U & = \frac{1}{2}\int_{0}^{{x_{s} }} {M_{1} w_{1,xx} {\text{d}}x} + \frac{1}{4}\int_{0}^{{x_{s} }} {\left( {P + N_{1} } \right)\left( {w_{1,x}^{2} } \right){\text{d}}x} + \frac{1}{2}\int_{{x_{s} }}^{L} {M_{2} w_{2,xx} {\text{d}}x} \\ & \quad + \frac{1}{4}\int_{{x_{s} }}^{L} {\left( {P + N_{2} } \right)\left( {w_{2,x}^{2} } \right){\text{d}}x} + \left. {\frac{1}{4}\alpha w_{1}^{4} } \right|_{{x = x_{s} }} + \left. {\frac{1}{2}\beta w_{1}^{2} } \right|_{{x = x_{s} }} \\ \end{aligned}$$
(6)

where \(\alpha\) and \(\beta\) are nonlinear coefficient and linear coefficient of the intermediate support, respectively.

Upon substituting Eqs. (1) and (6) into Hamilton’s principle, the governing equations of motion can be derived as

$$\begin{aligned} & \rho A\left( {\ddot{w}_{1} + 2\varGamma \dot{w}_{1,x} + \varGamma^{2} w_{1,xx} + \dot{\varGamma }w_{1,x} } \right) + EIw_{1,xxxx} + \eta I\left( {\dot{w}_{1,xxxx} + \varGamma w_{1,xxxxx} } \right) \\ & \quad - \left[ {\left( {EA\frac{1}{2}\left( {w_{1,x} } \right)^{2} + \eta A\left( {\dot{w}_{1,x} w_{1,x} + \varGamma w_{1,x} w_{1,xx} } \right)\, + P} \right)\,w_{1,x} } \right]_{,x} \\ & \quad - \rho I\left( {\ddot{w}_{1,xx} + \dot{\varGamma }w_{1,xxx} + 2\varGamma \dot{w}_{1,xxx} + \varGamma^{2} w_{1,xxxx} } \right)\, = 0 \\ \end{aligned}$$
(7)
$$\begin{aligned} & \rho A\left( {\ddot{w}_{2} + 2\varGamma \dot{w}_{2,x} + \varGamma^{2} w_{2,xx} + \dot{\varGamma }w_{2,x} } \right) + EIw_{2,xxxx} + \eta I\left( {\dot{w}_{2,xxxx} + \varGamma w_{2,xxxxx} } \right) \\ & \quad - \,\left[ {\left( {EA\frac{1}{2}\left( {w_{2,x} } \right)^{2} + \eta A\left( {\dot{w}_{2,x} w_{2,x} + \varGamma w_{2,x} w_{2,xx} } \right)\, + P} \right)\,w_{2,x} } \right]_{,x} \\ & \quad - \,\rho I\left( {\ddot{w}_{2,xx} + \dot{\varGamma }w_{2,xxx} + 2\varGamma \dot{w}_{2,xxx} + \varGamma^{2} w_{2,xxxx} } \right) = 0 \\ \end{aligned}$$
(8)

The boundary conditions are obtained as follows (Ghayesh et al. 2011).

at \(x = 0\)

$$\begin{aligned} & w_{1} = 0 \\ & EIw_{1,xx} + \eta I\left( {\dot{w}_{1,xx} + \varGamma w_{1,xxx} } \right) - \rho I\varGamma \left( {\dot{w}_{1,x} + \varGamma w_{1,xx} } \right) = 0 \\ \end{aligned}$$
(9)

at \(x = L\)

$$\begin{aligned} & w_{2} = 0 \\ & EIw_{2,xx} + \eta I\left( {\dot{w}_{2,xx} + \varGamma w_{2,xxx} } \right) - \rho I\varGamma \left( {\dot{w}_{2,x} + \varGamma w_{2,xx} } \right) = 0 \\ \end{aligned}$$
(10)

at \(x = x_{s}\)

$$\begin{aligned} & w_{1} = w_{2} ,4w_{1,x} = w_{2,x} , \\ & EIw_{1,xx} + \eta I\left( {\dot{w}_{1,xx} + \varGamma w_{1,xxx} } \right) - \rho I\varGamma \left( {\dot{w}_{1,x} + \varGamma w_{1,xx} } \right) = EIw_{2,xx} \\ & \quad \quad + \,\eta I\left( {\dot{w}_{2,xx} + \varGamma w_{2,xxx} } \right) - \rho I\varGamma \left( {\dot{w}_{2,x} + \varGamma w_{2,xx} } \right), \\ & \rho A\varGamma \left( {\dot{w}_{1} - \dot{w}_{2} } \right) + EI\left( {w_{1,xxx} - w_{2,xxx} } \right) + \eta I\left( {\dot{w}_{1,xxx} - \dot{w}_{2,xxx} + \varGamma w_{1,xxxx} - \varGamma w_{2,xxxx} } \right) \\ & \quad \quad - \,\rho I\left( {\ddot{w}_{1,x} - \ddot{w}_{2,x} + \dot{\varGamma }w_{1,xx} - \dot{\varGamma }w_{2,xx} + 2\varGamma \dot{w}_{1,xx} - 2\varGamma \dot{w}_{2,xx} + \varGamma^{2} w_{1,xxx} - \varGamma^{2} w_{2,xxx} } \right) \\ & \quad \quad - \,\eta A\left( {w_{1,x} \left( {\dot{w}_{1,x} w_{1,x} - \dot{w}_{2,x} w_{2,x} } \right) + \varGamma w_{1,x}^{2} \left( {w_{1,xx} - w_{2,xx} } \right)} \right) - \left( {\alpha w_{1}^{3} + \beta w_{1} } \right) = 0 \\ \end{aligned}$$
(11)

To obtain the dimensionless form of Eqs. (7) to (11), the following dimensionless parameters are defined:

$$\begin{aligned} w_{1}^{*} & = \frac{{w_{1} }}{L},\quad w_{2}^{*} = \frac{{w_{2} }}{L},\quad x^{*} = \frac{x}{L},\quad x_{s}^{*} = \frac{{x_{s} }}{L},\quad t^{*} = t\sqrt {\frac{P}{{\rho AL^{2} }}} , \\ \varGamma^{*} & = \varGamma \sqrt {\frac{\rho A}{P}} ,\quad I_{2} = \frac{I}{{AL^{2} }},\quad k_{1} = \sqrt {\frac{EI}{{PL^{2} }}} ,\quad k_{2} = \sqrt {\frac{EA}{P}} , \\ \gamma & = \frac{\eta I}{{PL^{3} }}\sqrt {\frac{P}{\rho A}} ,\quad \zeta = \frac{\eta A}{PL}\sqrt {\frac{P}{\rho A}} \\ \end{aligned}$$
(12)

where \(w_{1}^{*}\) and \(w_{2}^{*}\) are dimensionless transverse displacements, x* is dimensionless longitudinal coordinate, t* is dimensionless time, Γ* denotes dimensionless axial velocity, I2 is dimensionless rotary inertia, k1 is dimensionless bending stiffness of beam, k2 is dimensionless axial stiffness of the beam, γ is dimensionless linear viscosity coefficient, and ζ is dimensionless nonlinear viscosity coefficient. For simplicity, one may ignore the superscript, *, in dimensionless equations. Therefore, the dimensionless equations of motion become

$$\begin{aligned} & \ddot{w}_{1} + 2\varGamma \dot{w}_{1,x} + \left( {\varGamma^{2} - 1} \right)w_{1,xx} + \dot{\varGamma }w_{1,x} + k_{1}^{2} w_{1,xxxx} + \gamma \left( {\dot{w}_{1,xxxx} + \varGamma w_{1,xxxxx} } \right) \\ & \quad - \,1.5\,k_{2}^{2} \,w_{1,x}^{2} \,w_{1,xx} - I_{2} \left( {\ddot{w}_{1,xx} + \dot{\varGamma }w_{1,xxx} + 2\varGamma \dot{w}_{1,xxx} + \varGamma^{2} w_{1,xxxx} } \right) \\ & \quad - \,\zeta \left( {\dot{w}_{1,xx} w_{1,x}^{2} + 2\varGamma w_{1,x} w_{1,xx}^{2} + 2\dot{w}_{1,x} \,w_{1,x} \,w_{1,xx} + \varGamma w_{1,x}^{2} \,w_{1,xxx} } \right) = 0 \\ \end{aligned}$$
(13)
$$\begin{aligned} & \ddot{w}_{2} + 2\varGamma \dot{w}_{2,x} + \left( {\varGamma^{2} - 1} \right)w_{2,xx} + \dot{\varGamma }w_{2,x} + k_{1}^{2} w_{2,xxxx} + \gamma \left( {\dot{w}_{2,xxxx} + \varGamma w_{2,xxxxx} } \right) \\ & \quad - \,1.5\,k_{2}^{2} \,w_{2,x}^{2} \,w_{2,xx} - I_{2} \left( {\ddot{w}_{2,xx} + \dot{\varGamma }w_{2,xxx} + 2\varGamma \dot{w}_{2,xxx} + \varGamma^{2} w_{2,xxxx} } \right) \\ & \quad - \,\zeta \left( {\dot{w}_{2,xx} w_{2,x}^{2} + 2\varGamma w_{2,x} w_{2,xx}^{2} + 2\dot{w}_{2,x} \,w_{2,x} \,w_{2,xx} + \varGamma w_{2,x}^{2} \,w_{2,xxx} } \right) = 0 \\ \end{aligned}$$
(14)

and the dimensionless boundary conditions are derived as follows

at \(x = 0\)

$$\begin{aligned} & w_{1} = 0, \\ & \left( {k_{1}^{2} - I_{2} \varGamma^{2} } \right)w_{1,xx} + \gamma \left( {\dot{w}_{1,xx} + \varGamma w_{1,xxx} } \right) - I_{2} \varGamma \dot{w}_{1,x} = 0 \\ \end{aligned}$$
(15)

at \(x = x_{s}\)

$$\begin{aligned} & w_{1} = w_{2} ,\quad w_{1,x} = w_{2,x} \\ & \left( {k_{1}^{2} - I_{2} \varGamma^{2} } \right)w_{1,xx} + \gamma \left( {\dot{w}_{1,xx} + \varGamma w_{1,xxx} } \right) - I_{2} \varGamma \dot{w}_{1,x} = \left( {k_{1}^{2} - I_{2} \varGamma^{2} } \right)w_{2,xx} + \gamma \left( {\dot{w}_{2,xx} + \varGamma w_{2,xxx} } \right) - I_{2} \varGamma \dot{w}_{2,x} , \\ & \varGamma \left( {\dot{w}_{1} - \dot{w}_{2} } \right) + \,k_{1}^{2} \left( {w_{1,xxx} - w_{2,xxx} } \right) + \gamma \left( {\dot{w}_{1,xxx} - \dot{w}_{2,xxx} + \varGamma w_{1,xxxx} - \varGamma w_{2,xxxx} } \right) \\ & \quad - \,I_{2} \left( {\ddot{w}_{1,x} - \ddot{w}_{2,x} + \dot{\varGamma }w_{1,xx} - \dot{\varGamma }w_{2,xx} + 2\varGamma \dot{w}_{1,xx} - 2\varGamma \dot{w}_{2,xx} + \varGamma^{2} w_{1,xxx} - \varGamma^{2} w_{2,xxx} } \right) \\ & \quad - \,\zeta \left( {w_{1,x} \left( {\dot{w}_{1,x} w_{1,x} - \dot{w}_{2,x} w_{2,x} } \right) + \varGamma w_{1,x}^{2} \left( {w_{1,xx} - w_{2,xx} } \right)} \right) - \left( {\alpha^{*} w_{1}^{3} + \beta^{*} w_{1} } \right) = 0 \\ \end{aligned}$$
(16)

at \(x = 1\)

$$\begin{aligned} & w_{2} = 0, \\ & \left( {k_{1}^{2} - I_{2} \varGamma^{2} } \right)w_{2,xx} + \gamma \left( {\dot{w}_{2,xx} + \varGamma w_{2,xxx} } \right) - I_{2} \varGamma \dot{w}_{2,x} = 0\, \\ \end{aligned}$$
(17)

3 Extracting the System Response and Stability Analysis by Applying the Multiple Scales Method

In this study, it is assumed that the axial velocity of the beam fluctuates harmonically around the mean axial velocity Γ0 with an amplitude of εΓ1, i.e.,

$$\varGamma (t) = \varGamma_{0} + \varepsilon \,\varGamma_{1} \sin \varOmega t$$
(18)

where \(\varOmega\) is the frequency of fluctuations and \(\varepsilon\) is a small dimensionless positive parameter (\(\varepsilon \ll 1\)) (Rezaee and Lotfan 2015).

Based on the multiple scales method, the vibration response of the spans 1 and 2 are assumed as

$$w_{1} (x,t;\varepsilon ) = w_{10} (x,T_{0} ,T_{1} ) + \varepsilon w_{11} (x,T_{0} ,T_{1} ) + O(\varepsilon^{2} )$$
(19)
$$w_{2} (x,t;\varepsilon ) = w_{20} (x,T_{0} ,T_{1} ) + \varepsilon w_{21} (x,T_{0} ,T_{1} ) + O(\varepsilon^{2} )$$
(20)

where \(T_{0} = t\) is the fast time scale and \(T_{1} = \varepsilon t\) is the slow time scale (Karlik et al. 1998).

Substituting Eqs. (18) to (20), into weakly nonlinear form of Eqs. (13) to (17) obtained by letting \(w_{1} = w_{1} \sqrt \varepsilon\), \(w_{2} = w_{2} \sqrt \varepsilon\), \(\eta = \varepsilon \eta\), and considering the following relations:

$$\begin{aligned} \frac{\partial }{\partial t} & = \frac{\partial }{{\partial T_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} = D_{0} + \varepsilon D_{1} , \\ \frac{{\partial^{2} }}{{\partial t^{2} }} & = \frac{{\partial^{2} }}{{\partial T_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial T_{0} \partial T_{1} }} + O\left( {\varepsilon^{2} } \right) = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + O\left( {\varepsilon^{2} } \right) \\ \end{aligned}$$
(21)

and equating the coefficient of \(\varepsilon^{0}\) and \(\varepsilon^{1}\) on both sides, one obtains:

  1. (a)

    Order of \(\varepsilon^{0}\):

    $$\begin{aligned} & D_{0}^{2} w_{10} + 2\varGamma_{0} D_{0} w_{10,x} + \left( {\varGamma_{0}^{2} - 1} \right)w_{10,xx} + k_{1}^{2} w_{10,xxxx} \\ & \quad - \,I_{2} \left( {D_{0}^{2} w_{10,xx} + 2\varGamma_{0} D_{0} w_{10,xxx} + \varGamma_{0}^{2} w_{10,xxxx} } \right) = 0 \\ \end{aligned}$$
    (22)
    $$\begin{aligned} & D_{0}^{2} w_{20} + 2\varGamma_{0} D_{0} w_{20,x} + \left( {\varGamma_{0}^{2} - 1} \right)w_{20,xx} + k_{1}^{2} w_{20,xxxx} \\ & \quad - \,I_{2} \left( {D_{0}^{2} w_{20,xx} + 2\varGamma_{0} D_{0} w_{20,xxx} + \varGamma_{0}^{2} w_{20,xxxx} } \right) = 0 \\ \end{aligned}$$
    (23)

    and the corresponding boundary conditions are as follows:

    at \(x = 0\)

    $$\begin{aligned} & w_{10} = 0, \\ & \left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)w_{10,xx} - I_{2} \varGamma_{0} D_{0} w_{10,x} = 0 \\ \end{aligned}$$
    (24)

    at \(x = x_{s}\)

    $$\begin{aligned} & w_{10} = w_{20} ,\quad w_{10,x} = w_{20,x} ,\quad w_{10,xx} \, = \,w_{20,xx} , \\ & \left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)\,\left( {w_{10,xxx} - w_{20,xxx} } \right) - \beta w_{10} \, = \,0 \\ \end{aligned}$$
    (25)

    at \(x = 1\)

    $$\begin{aligned} w_{20} = 0, \hfill \\ \left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)w_{20,xx} - I_{2} \varGamma_{0} D_{0} w_{20,x} = 0 \hfill \\ \end{aligned}$$
    (26)
  2. (b)

    Order of \(\varepsilon^{1}\):

    $$\begin{aligned} & D_{0}^{2} w_{11} + 2\varGamma_{0} D_{0} w_{11,x} + \left( {\varGamma_{0}^{2} - 1} \right)w_{11,xx} + k_{1}^{2} w_{11,xxxx} - I_{2} \left( {D_{0}^{2} w_{11,xx} + 2\varGamma_{0} D_{0} w_{11,xxx} } \right) \\ & \quad - \,I_{2} \varGamma_{0}^{2} w_{11,xxxx} = 1.5k_{2}^{2} w_{10,x}^{2} w_{10,xx} - \varGamma_{1} \varOmega \,\cos \,\varOmega T_{0} \,w_{10,x} - 2D_{0} D_{1} w_{10} - 2\varGamma_{0} D_{1} w_{10,x} \\ & \quad - \,2\varGamma_{1} \sin \varOmega T_{0} \,D_{0} w_{10,x} - 2\varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} \,w_{10,xx} - \gamma \left( {D_{0} w_{10,xxxx} + \varGamma_{0} w_{10,xxxxx} } \right) \\ & \quad + \,I_{2} \left( {2\varGamma_{1} \sin \varOmega T_{0} \,D_{0} w_{10,xxx} + 2\varGamma_{0} D_{1} w_{10,xxx} + 2\varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} \,w_{10,xxxx} } \right) \\ & \quad + \,I_{2} \left( {2D_{0} D_{1} w_{10,xx} + \varGamma_{1} \varOmega \,\cos \,\varOmega T_{0} \,w_{10,xxx} } \right) \\ \end{aligned}$$
    (27)
    $$\begin{aligned} & D_{0}^{2} w_{21} + 2\varGamma_{0} D_{0} w_{21,x} + \left( {\varGamma_{0}^{2} - 1} \right)w_{21,xx} + k_{1}^{2} w_{21,xxxx} - I_{2} \left( {D_{0}^{2} w_{21,xx} + 2\varGamma_{0} D_{0} w_{21,xxx} } \right) \\ & \quad - \,I_{2} \varGamma_{0}^{2} w_{21,xxxx} = 1.5k_{2}^{2} w_{20,x}^{2} w_{20,xx} - \varGamma_{1} \varOmega \,\cos \,\varOmega T_{0} \,w_{20,x} - 2D_{0} D_{1} w_{20} - 2\varGamma_{0} D_{1} w_{20,x} \\ & \quad - \,2\varGamma_{1} \sin \varOmega T_{0} \,D_{0} w_{20,x} - 2\varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} \,w_{20,xx} - \gamma \left( {D_{0} w_{20,xxxx} + \varGamma_{0} w_{20,xxxxx} } \right) \\ & \quad + \,I_{2} \left( {2\varGamma_{1} \sin \varOmega T_{0} \,D_{0} w_{20,xxx} + 2\varGamma_{0} D_{1} w_{20,xxx} + 2\varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} \,w_{20,xxxx} } \right) \\ & \quad + \,I_{2} \left( {2D_{0} D_{1} w_{20,xx} + \varGamma_{1} \varOmega \,\cos \,\varOmega T_{0} \,w_{20,xxx} } \right) \\ \end{aligned}$$
    (28)

    and the corresponding boundary conditions are as follows:

    at \(x = 0\)

    $$\begin{aligned} & w_{11} = 0\, \\ & \left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)w_{11,xx} - I_{2} \varGamma_{0} D_{0} w_{11,x} = - \gamma \left( {D_{0} w_{10,xx} + \varGamma_{0} \,w_{10,xxx} } \right) + I_{2} \varGamma_{0} D_{1} w_{10,x} \\ & \quad + \,2I_{2} \varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} w_{10,xx} + I_{2} \varGamma_{1} \sin \varOmega T_{0} D_{0} w_{10,x} \\ \end{aligned}$$
    (29)

    at \(x = x_{s}\)

    $$\begin{aligned} & w_{11} = w_{21} ,\quad w_{11,x} = w_{21,x} , \\ & \left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)\left( {w_{11,xx} - w_{21,xx} } \right) = - \gamma D_{0} \left( {w_{10,xx} - w_{20,xx} } \right) - \gamma \varGamma_{0} \left( {w_{10,xxx} - w_{20,xxx} } \right), \\ & k_{1}^{2} \left( {w_{11,xxx} - w_{21,xxx} } \right) - 2I_{2} \varGamma_{0} D_{0} \left( {w_{11,xx} - w_{21,xx} } \right) - I_{2} \varGamma_{0}^{2} \left( {w_{11,xxx} - w_{21,xxx} } \right) - \beta w_{11} \\ & \quad = \,2I_{2} \varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} \left( {w_{10,xxx} - w_{20,xxx} } \right) + \alpha w_{10}^{3} \, - \gamma D_{0} \left( {w_{10,xxx} - w_{20,xxx} } \right) \\ & \quad - \,\gamma \varGamma_{0} \left( {w_{10,xxxx} - w_{20,xxxx} } \right) \\ \end{aligned}$$
    (30)

    at \(x = 1\)

    $$\begin{aligned} & w_{21} = 0 \\ & \left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)w_{21,xx} - I_{2} \varGamma_{0} D_{0} w_{21,x} = - \gamma \left( {D_{0} w_{20,xx} + \varGamma_{0} \,w_{20,xxx} } \right) + I_{2} \varGamma_{0} D_{1} w_{20,x} \\ & \quad + \,2I_{2} \varGamma_{0} \varGamma_{1} \sin \varOmega T_{0} w_{20,xx} + I_{2} \varGamma_{1} \sin \varOmega T_{0} D_{0} w_{20,x} \\ \end{aligned}$$
    (31)

One can assume the solutions of Eqs. (22) and (23) as (Ghayesh 2012; Ghayesh et al. 2011):

$$w_{10} (x,T_{0} ,T_{1} ) = \sum\limits_{n = 1}^{\infty } {\left[ {A_{n} (T_{1} )\,W_{1n} (x)e^{{i\omega_{n} T_{0} }} + \bar{A}_{n} (T_{1} )\bar{W}_{1n} (x)e^{{ - i\omega_{n} T_{0} }} } \right]}$$
(32)
$$w_{20} (x,T_{0} ,T_{1} ) = \sum\limits_{n = 1}^{\infty } {\left[ {A_{n} (T_{1} )\,W_{2n} (x)e^{{i\omega_{n} T_{0} }} + \bar{A}_{n} (T_{1} )\,\bar{W}_{2n} (x)e^{{ - i\omega_{n} T_{0} }} } \right]}$$
(33)

where \(\omega_{n}\) is the nth natural frequency,\(A_{n}\) and \(W_{in} \,\,\,i = 1,2\) are the nth complex function of vibration amplitude and mode shape, respectively. \(\bar{A}_{n}\) and \(\bar{W}_{in} \,\,\,\,i = 1,2\) are respectively the complex conjugate of \(A_{n}\) and \(W_{in} \,\,\,i = 1,2\). Assuming that one of the modes is more dominant in the response and using Eqs. (32) and (33) in Eqs. (22) and (23), the differential equations for mode-shape functions of each span are obtained as

$$\left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)W_{1n}^{(4)} - 2I_{2} \varGamma_{0} \omega_{n} iW^{\prime\prime\prime}_{1n} + \left( {\varGamma_{0}^{2} + I_{2} \omega_{n}^{2} - 1} \right)W^{\prime\prime}_{1n} + 2\varGamma_{0} \omega_{n} iW^{\prime}_{1n} - \omega_{n}^{2} W_{1n} = 0,\quad n = 1,2, \ldots$$
(34)
$$\left( {k_{1}^{2} - I_{2} \varGamma_{0}^{2} } \right)W_{2n}^{(4)} - 2I_{2} \varGamma_{0} \omega_{n} iW^{\prime\prime\prime}_{2n} + \left( {\varGamma_{0}^{2} + I_{2} - 1} \right)W^{\prime\prime}_{2n} + 2\varGamma_{0} \omega_{n} iW^{\prime}_{2n} - \omega_{n}^{2} W_{2n} = 0,\quad n = 1,2, \ldots$$
(35)

Then by applying power series method (Du et al. 1994) and using the boundary conditions, Eqs. (24)–(26), the natural frequencies and complex mode-shape functions will be obtained. The unknown complex function of vibration amplitude \(A_{n}\) will be obtained by using the solvability condition. For satisfying the solvability condition, the solution of \(w_{11}\) and \(w_{21}\) must be free of the secular terms. Therefore, substituting Eqs. (32), (33) and exponential expansion of \(\sin \varOmega t\) and \(\cos \varOmega t\) into Eqs. (27)–(31), two cases of \(\varOmega \ne 0,\;\varOmega \ne 2\omega_{n}\), and \(\varOmega \approx 2\omega_{n}\) will be investigated.

  1. (a)

    The Case of \(\varOmega \ne 0,\;\varOmega \ne 2\omega_{n}\):

In this case, the solvability condition is obtained as (Nayfeh and Mook 2008):

$$\varGamma_{1n} A_{n}^{2} \bar{A}_{n} + \varGamma_{2n} \dot{A}_{n} + \varGamma_{3n} A_{n} = 0$$
(36)

in which,

$$\begin{aligned} \varGamma_{1n} & = \int_{0}^{{x_{s} }} {\left( {3k_{2}^{2} \,W^{\prime\prime}_{1n} W^{\prime}_{1n} \bar{W^{\prime}}_{1n} + 1.5k_{2}^{2} \,\left( {W^{\prime}_{1n} } \right)^{2} \bar{W^{\prime\prime}}_{1n} } \right)\bar{W}_{1n} {\text{d}}x} - \left. {\left( {3\alpha W_{1n}^{2} \bar{W}_{1n}^{2} } \right)} \right|_{{x = x_{s} }} \\ & \quad + \,\int_{{x_{s} }}^{1} {\left( {3k_{2}^{2} \,W^{\prime\prime}_{2n} W^{\prime}_{2n} \bar{W^{\prime}}_{2n} + 1.5k_{2}^{2} \,\left( {W^{\prime}_{2n} } \right)^{2} \bar{W^{\prime\prime}}_{2n} } \right)\bar{W}_{2n} {\text{d}}x} \, = \varGamma_{1nr} + i\varGamma_{1ni} \\ \end{aligned}$$
(37)
$$\begin{aligned} \varGamma_{2n} & = \int_{0}^{{x_{s} }} {\left( { - 2i\omega_{n} W_{1n} - 2\varGamma_{0} W^{\prime}_{1n} + 2i\omega_{n} I_{2} W^{\prime\prime}_{1n} + 2I_{2} \varGamma_{0} W^{\prime\prime\prime}_{1n} } \right)\bar{W}_{1n} \,{\text{d}}x} \\ & \quad + \,\int_{{x_{s} }}^{1} {\left( { - 2i\omega_{n} W_{2n} - 2\varGamma_{0} W^{\prime}_{2n} + 2i\omega_{n} I_{2} W^{\prime\prime}_{2n} + 2I_{2} \varGamma_{0} W^{\prime\prime\prime}_{2n} } \right)\bar{W}_{2n} {\text{d}}x} \\ & \quad + \,\left. {\left( {I_{2} \varGamma_{0} \,Y^{\prime}_{1n} } \right)\bar{Y}_{1n} } \right|_{x = 0} + \left. {\left( {I_{2} \varGamma_{0} \,Y^{\prime}_{2n} } \right)\bar{Y}_{2n} \dot{A}_{n} } \right|_{x = 1} = \varGamma_{2nr} + i\varGamma_{2ni} \\ \end{aligned}$$
(38)
$$\begin{aligned} \varGamma_{3n} & = - \int_{0}^{{x_{s} }} {\left( {i\gamma \omega_{n} W_{1n}^{(4)} + \gamma \varGamma_{0} W_{1n}^{(5)} } \right)\bar{W}_{1n} {\text{d}}x} - \int_{{x_{s} }}^{1} {\left( {i\gamma \omega_{n} W_{2n}^{(4)} + \gamma \varGamma_{0} W_{2n}^{(5)} } \right)\bar{W}_{2n} {\text{d}}x} \\ & \quad - \,\left. {\gamma \varGamma_{0} W^{\prime\prime\prime}_{1n} \bar{W}_{1n} } \right|_{x = 0} + \left. {\gamma \varGamma_{0} W^{\prime\prime\prime}_{2n} \bar{W}_{2n} } \right|_{x = 1} - \left. {\gamma \varGamma_{0} \left( {W^{\prime\prime\prime}_{1n} - W^{\prime\prime\prime}_{2n} } \right)\bar{W}_{1n} } \right|_{{x = x_{s} }} \\ & \quad \left. { - \,\left( {\gamma i\omega_{n} \,\left( {W^{\prime\prime\prime}_{1n} - W^{\prime\prime\prime}_{2n} } \right) + \gamma \varGamma_{0} \,\left( {W_{1n}^{(4)} - W_{2n}^{(4)} } \right)} \right)\bar{W}_{1n} } \right|_{{x = x_{s} }} = \varGamma_{3nr} + i\varGamma_{3ni} \\ \end{aligned}$$
(39)

where, \(\varGamma_{jnr}\) and \(\varGamma_{jni}\) (j = 1,2,3) are the real and imaginary parts of \(\varGamma_{jn}\). The solution of Eq. (36) is assumed to be in polar form as

$$A_{n} \left( {T_{1} } \right) = \frac{1}{2}a_{n} \left( {T_{1} } \right)e^{{ib_{n} (T_{1} )}}$$
(40)

where \(a_{n}\) and \(b_{n}\) are functions of slow time scale with real values and denotes the real amplitude and phase of vibration, respectively. Using Eqs. (36) and (40), one will have:

$$a^{\prime}_{n} = - \upsilon_{1} a_{n}^{3} - \upsilon_{2} a_{n} = F_{1} \left( {b_{n} ,a_{n} } \right)$$
(41)
$$b^{\prime}_{n} = - \upsilon_{3} a_{n}^{2} - \upsilon_{4} = F_{2} \left( {b_{n} ,a_{n} } \right)$$
(42)

where \(\upsilon_{1}\), \(\upsilon_{2}\), \(\upsilon_{3}\), and \(\upsilon_{4}\) are

$$\upsilon_{1} = \frac{{\varGamma_{2ni} \varGamma_{1ni} + \varGamma_{2nr} \varGamma_{1nr} }}{{4\left( {\varGamma_{2nr}^{2} + \varGamma_{2ni}^{2} } \right)}}$$
(43)
$$\upsilon_{2} = \frac{{\varGamma_{2nr} \varGamma_{3nr} + \varGamma_{2ni} \varGamma_{3ni} }}{{\varGamma_{2nr}^{2} + \varGamma_{2ni}^{2} }}$$
(44)
$$\upsilon_{3} = \frac{{\varGamma_{2nr} \varGamma_{1ni} - \varGamma_{2ni} \varGamma_{1nr} }}{{4\left( {\varGamma_{2nr}^{2} + \varGamma_{2ni}^{2} } \right)}}$$
(45)
$$\upsilon_{4} = \frac{{ - \varGamma_{3nr} \varGamma_{2ni} + \varGamma_{3ni} \varGamma_{2nr} }}{{\varGamma_{2nr}^{2} + \varGamma_{2ni}^{2} }}$$
(46)

Solving the Bernoulli differential equation expressed in Eq. (41) gives

$$a_{n} = \pm \sqrt {\frac{{\upsilon_{2} }}{{a_{0n} \upsilon_{2} e^{{2\upsilon_{2} T_{1} }} - \upsilon_{1} }}}$$
(47)

where \(a_{0n}\) is a constant. Substituting Eq. (47) into Eq. (42) and solving the resulting differential equation gives,

$$b_{n} = - \frac{{\upsilon_{3} }}{{2\upsilon_{1} }}\ln \left( {a_{0n} \upsilon_{2} - \upsilon_{1} e^{{ - 2\upsilon_{2} T_{1} }} } \right) - \upsilon_{4} T_{1} + b_{0n}$$
(48)

where \(b_{0n}\) is a constant. Now, free responses of each span and nonlinear natural frequencies of the system can be expressed as

$$w_{10} (x,T_{0} ,T_{1} ) = \frac{1}{2}a_{n} \,W_{1n} (x)e^{{i\omega_{n} T_{0} + b_{n} }} + \frac{1}{2}a_{n} \,\bar{W}_{1n} (x)e^{{ - i\omega_{n} T_{0} - b_{n} }} \quad n = 1,2, \ldots$$
(49)
$$w_{20} (x,T_{0} ,T_{1} ) = \frac{1}{2}a_{n} \,W_{2n} (x)e^{{i\omega_{n} T_{0} + b_{n} }} + \frac{1}{2}a_{n} \,\bar{W}_{2n} (x)e^{{ - i\omega_{n} T_{0} - b_{n} }} \quad n = 1,2, \ldots$$
(50)
$$\omega = \omega_{n} + \varepsilon \frac{{{\text{d}}b_{n} }}{{{\text{d}}T_{1} }} = \omega_{n} - \varepsilon \left( {\frac{{\upsilon_{2} \upsilon_{3} }}{{\alpha_{0n} \upsilon_{2} e^{{2\upsilon_{2} T_{1} }} - \upsilon_{1} }} + \upsilon_{4} } \right)$$
(51)

To analyze the stability, eigenvalues of the Jacobian matrix of Eqs. (41) and (42) when \(a^{\prime}_{n} = b^{\prime}_{n} = 0\) is obtained as

$$\lambda = - \upsilon_{2} - 3\upsilon_{1} a_{0n}^{2}$$
(52)

Due to numerical results, \(\upsilon_{1}\) and \(\upsilon_{2}\) have real and positive values when the axial velocity is smaller than the critical speed. Therefore, the system is always stable.

  1. (b)

    ) The Case of \(\varOmega \approx 2\omega_{n}\):

In this case, we define the fluctuation frequency of the axial velocity as

$$\varOmega = 2\omega_{n} + \varepsilon \sigma$$
(53)

where \(\sigma\) is the detuning parameter. The equation for the solvability condition is

$$\varGamma_{1n} A_{n}^{2} \bar{A}_{n} + \varGamma_{2n} \dot{A}_{n} + \varGamma_{3n} A_{n} + \varGamma_{4n} \bar{A}_{n} e^{{i\sigma T_{1} }} = 0$$
(54)

where \(\varGamma_{1n}\), \(\varGamma_{2n}\) and \(\varGamma_{3n}\) are obtained as in Eqs. (37) to (39), respectively, and \(\varGamma_{4n}\) can be expressed as

$$\begin{aligned} \varGamma_{4n} & = \int_{0}^{{x_{s} }} {\left\{ {\left( { - \frac{1}{2}\varOmega \, + \omega_{n} \,} \right)\left( {\varGamma_{1} \bar{W^{\prime}}_{1n} - I_{2} \varGamma_{1} \,\bar{W^{\prime\prime\prime}}_{1n} } \right) - i\varGamma_{0} \varGamma_{1} \bar{W^{\prime\prime}}_{1n} + i\,I_{2} \varGamma_{0} \varGamma_{1} \bar{W}_{1n}^{(4)} } \right\}\bar{W}_{1n} {\text{d}}x} \\ & \quad + \,\int_{{x_{s} }}^{1} {\left\{ {\left( { - \frac{1}{2}\varOmega \, + \omega_{n} \,} \right)\left( {\varGamma_{1} \bar{W^{\prime}}_{2n} - I_{2} \varGamma_{1} \,\bar{W^{\prime\prime\prime}}_{2n} } \right) - i\varGamma_{0} \varGamma_{1} \bar{W^{\prime\prime}}_{2n} + i\,I_{2} \varGamma_{0} \varGamma_{1} \bar{W}_{2n}^{(4)} } \right\}\bar{W}_{2n} {\text{d}}x} \\ & \quad + \,\left. {\left\{ { - iI_{2} \varGamma_{0} \varGamma_{1} \bar{W^{\prime\prime}}_{1n} - 0.5I_{2} \varGamma_{1} \omega_{n} \,\bar{W^{\prime}}_{1n} } \right\}\bar{W}_{1n} \bar{A}_{n} e^{{i\sigma T_{1} }} } \right|_{x = 0} - \left. {i\,I_{2} \varGamma_{0} \varGamma_{1} \left( {\bar{W^{\prime\prime\prime}}_{1n} - \bar{W^{\prime\prime\prime}}_{2n} } \right)\bar{W}_{1n} } \right|_{{x = x_{s} }} \\ & \quad \left. { + \,\left\{ { - iI_{2} \varGamma_{0} \varGamma_{1} \bar{W^{\prime\prime}}_{2n} - 0.5I_{2} \varGamma_{1} \omega_{n} \,\bar{W^{\prime}}_{2n} } \right\}\bar{W}_{2n} \bar{A}_{n} e^{{i\sigma T_{1} }} } \right|_{x = 1} \, = \varGamma_{4nr} + i\varGamma_{4ni} \\ \end{aligned}$$
(55)

Using Eqs. (40) and (54) and making a transformation as \(\kappa_{n} = \sigma T_{1} - 2b_{n}\), one reaches:

$$a^{\prime}_{n} = - \upsilon_{1} a_{n}^{3} - \upsilon_{2} a_{n} - \upsilon_{5} a_{n} \cos \kappa_{n} + \upsilon_{6} a_{n} \sin \kappa_{n} = G_{1} \left( {\kappa_{n} ,a_{n} } \right)$$
(56)
$$a_{n} \kappa^{\prime}_{n} = \sigma a_{n} + 2\upsilon_{3} a_{n}^{3} + 2\upsilon_{4} a_{n} + 2\upsilon_{6} a_{n} \cos \kappa_{n} + 2\upsilon_{5} a_{n} \sin \kappa_{n} = G_{2} \left( {\kappa_{n} ,a_{n} } \right)$$
(57)

where \(\upsilon_{5}\), and \(\upsilon_{6}\) are

$$\upsilon_{5} = \frac{{\varGamma_{2nr} \varGamma_{4nr} + \varGamma_{2ni} \varGamma_{4ni} }}{{\varGamma_{2nr}^{2} + \varGamma_{2ni}^{2} }}$$
(58)
$$\upsilon_{6} = \frac{{\varGamma_{2nr} \varGamma_{4ni} - \varGamma_{2ni} \varGamma_{4nr} }}{{\varGamma_{2nr}^{2} + \varGamma_{2ni}^{2} }}$$
(59)

Assuming \(a^{\prime}_{n} = \kappa^{\prime}_{n} = 0\) and using Eqs. (56) and (57), the frequency response of the system can be stated as

$$\sigma_{1,2} = - 2\upsilon_{4} - 2\upsilon_{3} a_{n}^{2} \pm 2\sqrt {\left( {\upsilon_{6}^{2} + \upsilon_{5}^{2} } \right) - \left( {\upsilon_{1} a_{n}^{2} + \upsilon_{2} } \right)^{2} }$$
(60)

To investigate the stability of the response, the following Jacobian matrix is used:

$$\left[ {\begin{array}{*{20}c} {\frac{{\partial G_{1} }}{{\partial \alpha_{n} }}} & {\frac{{\partial G_{1} }}{{\partial \kappa_{n} }}} \\ {\frac{{\partial G_{2} }}{{\partial \alpha_{n} }}} & {\frac{{\partial G_{2} }}{{\partial \kappa_{n} }}} \\ \end{array} } \right]_{\begin{subarray}{l} \alpha_{n} = a_{0} \\ \kappa_{n} = b_{0} \end{subarray} } = \left[ {\begin{array}{*{20}l} { - 3\upsilon_{1} a_{0}^{2} - \upsilon_{2} - \upsilon_{5} \cos b_{0} + \upsilon_{6} \sin b_{0} } \hfill & {\quad \upsilon_{5} a_{0} \sin b_{0} + \upsilon_{6} a_{0} \cos b_{0} } \hfill \\ {4\upsilon_{3} a_{0} } \hfill & {\quad - 2\upsilon_{6} \sin b_{0} + 2\upsilon_{5} \cos b_{0} } \hfill \\ \end{array} } \right]$$
(61)

The singular points for which the eigenvalues of Jacobian matrix are real and negative are regarded as the stable points. Therefore, for stable points the following conditions are satisfied:

$$\begin{aligned} & \sigma_{1} :4\upsilon_{1} a_{0}^{2} + 2\upsilon_{2} > 0;\,\,4\left( {\upsilon_{1} a_{0}^{2} } \right)\left( {\upsilon_{1} a_{0}^{2} + \upsilon_{2} } \right) + 2\upsilon_{3} a_{0}^{2} \left( {2\sqrt {\upsilon_{6}^{2} + \upsilon_{5}^{2} - \left( {\upsilon_{1} a_{0}^{2} + \upsilon_{2} } \right)^{2} } } \right) > 0 \\ & \quad \quad \upsilon_{6}^{2} + \upsilon_{5}^{2} - \left( {\upsilon_{1} a_{0}^{2} + \upsilon_{2} } \right)^{2} > 0 \\ \end{aligned}$$
(62)
$$\begin{aligned} & \sigma_{2} :4\upsilon_{1} a_{0}^{2} + 2\upsilon_{2} > 0;\,\,4\left( {\upsilon_{1} a_{0}^{2} } \right)\left( {\upsilon_{1} a_{0}^{2} + \upsilon_{2} } \right) - 2\upsilon_{3} a_{0}^{2} \left( {2\sqrt {\upsilon_{6}^{2} + \upsilon_{5}^{2} - \left( {\upsilon_{1} a_{0}^{2} + \upsilon_{2} } \right)^{2} } } \right) > 0 \\ & \quad \quad \upsilon_{6}^{2} + \upsilon_{5}^{2} - \left( {\upsilon_{1} a_{0}^{2} + \upsilon_{2} } \right)^{2} > 0 \\ \end{aligned}$$
(63)

To evaluate the stability of trivial solution, the solution of Eq. (54) is supposed to be as

$$A_{n} = \frac{1}{2}\left( {p_{n} + iq_{n} } \right)e^{{i\left( {\frac{{\sigma T_{1} }}{2}} \right)}}$$
(64)

Substituting Eq. (64) into Eq. (54) and separating real and imaginary parts gives

$$\dot{p}_{n} = - \upsilon_{1} p_{n}^{3} - \upsilon_{1} p_{n} q_{n}^{2} + \upsilon_{3} q_{n}^{3} + \upsilon_{3} p_{n}^{2} q_{n} + \left( {\frac{\sigma }{2} + \upsilon_{4} - \upsilon_{6} } \right)q_{n} - \left( {\upsilon_{2} + \upsilon_{5} } \right)p_{n} = h_{1} \left( {p_{n} ,q_{n} } \right)$$
(65)
$$\dot{q}_{n} = - \upsilon_{3} p_{n}^{3} - \upsilon_{3} p_{n} q_{n}^{2} - \upsilon_{1} q_{n}^{3} - \upsilon_{1} p_{n}^{2} q_{n} - \left( {\frac{\sigma }{2} + \upsilon_{4} + \upsilon_{6} } \right)p_{n} + \left( { - \upsilon_{2} + \upsilon_{5} } \right)q_{n} = h_{2} \left( {p_{n} ,q_{n} } \right)$$
(66)

Forming Jacobian matrix for these two equations and setting \(p_{n} = q_{n} = 0\), the characteristic equation is obtained as

$$\lambda^{2} + 2\upsilon_{2} \lambda + \left( {\left( {\frac{\sigma }{2} + \upsilon_{4} } \right)^{2} - \upsilon_{6}^{2} + \upsilon_{2}^{2} - \upsilon_{5}^{2} } \right) = 0$$
(67)

Based on the Routh–Hurwitz criterion, trivial solution will be stable only if the following condition is held.

$$\begin{aligned} \sigma > - 2\upsilon_{4} + 2\sqrt {\upsilon_{6}^{2} + \upsilon_{5}^{2} - \upsilon_{2}^{2} } \hfill \\ \sigma < - 2\upsilon_{4} - 2\sqrt {\upsilon_{6}^{2} + \upsilon_{5}^{2} - \upsilon_{2}^{2} } \hfill \\ \end{aligned}$$
(68)

4 Numerical Case Studies

In this section, some numeric case studies are presented to illustrate the effect of variation of the system parameters on the vibration behavior. By taking into account the boundary conditions mentioned in Eqs. (24) to (26), and using the power series method, the natural frequencies and complex mode-shape functions are obtained through solving Eqs. (34) and (35), numerically. Before all, it is necessary to validate the accuracy of the presented solution method. So in the first case, a viscoelastic beam supported by an intermediate linear spring will be considered. Then, for several spring locations, variation of the first two natural frequencies versus linear stiffness coefficient of the spring were obtained and compared with those presented in Ghayesh (2012) (Fig. 2a, b). Secondly, by considering axially moving Euler–Bernoulli beam, the first two natural frequencies were obtained and compared with corresponding values in Öz and Pakdemirli (1999) (Table 1). According to Fig. 2a and b and Table 1, it is obvious that the results based on the present study are in good agreement with those reported in the mentioned references.

Fig. 2
figure 2

Variation of the a First natural, b Second natural frequency versus the linear stiffness coefficient of the intermediate support for different \(x_{s}\) (comparing results of Ghayesh (2012) to results of present method)

Full size image
Table 1 The first and the second natural frequencies for different mean axial velocities \(\varGamma_{0}\) and the beam bending stiffness \(k_{1}\)
Full size table

In the third case, the equations of motion for the present beam with the properties of \(I_{2} = 0.001\), \(k_{1} = 1\), \(k_{2} = 5\), \(\beta = 100\), \(x_{s} = 0.5\), \(\gamma = 0.008\), \(\varGamma_{0} = 1.01\) and \(\alpha = 1\) are solved using Wavelet-based spectral finite element method. According to Fig. 3, the vibration response of the beam is in good agreement with the corresponding results obtained by the presented method.

Fig. 3
figure 3

Vibration response of the beam obtained using presented method and wavelet-based spectral finite element method

Full size image

The first two natural frequencies versus the linear stiffness coefficient of the intermediate support for its different relative locations are shown in Fig. 4a and b. As seen in Fig. 4a and b, increasing the linear stiffness of the intermediate support, results in increasing the first and the second natural frequencies. It should be remarked that, for a stationary beam vibrating at the second mode for which the nodal point is located at its midpoint, placing the support at that point does not affect the second natural frequency (see Fig. 2b). However, in the presence of the axial velocity, the mode shapes become asymmetric, and this effect is observed more appreciable as the mean axial velocity increases. Therefore, at high axial velocities, the effect of the mid-support on the second natural frequency becomes more apparent (see Fig. 4b).

Fig. 4
figure 4

a Variation of the first natural frequency versus linear stiffness coefficient of the intermediate support for different \(x_{s}\) and \(\varGamma_{0} = 3\), \(I_{2} = 0\), \(k_{1} = 1\). b Variation of the second natural frequency versus linear stiffness coefficient of the intermediate support for different \(x_{s}\) and \(\varGamma_{0} = 5\), \(I_{2} = 0\), \(k_{1} = 1\)

Full size image

Figure 5a and b represents the effect of the rotary inertia and the mean axial velocity on the first natural frequency. Based on the comparison between Fig. 5a and Fig. 5b, although increasing the rotary inertia and mean axial velocity decreases the first natural frequency, the intermediate support has a dominant effect on increasing the first natural frequency.

Fig. 5
figure 5

a The first natural frequency versus mean axial velocity for different rotary inertia (without intermediate support). b The first natural frequency versus mean axial velocity for different rotary inertia (with intermediate support)

Full size image

Figure 6a and b is obtained to investigate the effect of intermediate support location on instability of the system within a wide range of mean axial velocity. According to these figures, as the mean axial velocity increases, the real parts of the natural frequencies decrease while their imaginary parts remain zero. For this range of mean axial velocities, all of the modes are stable. At the first critical velocity, the real part of the first natural frequency becomes zero and its imaginary part has two non-zero values. By more increasing the mean axial velocity, the imaginary part of the first natural frequency increases while its real part remains zero. In this condition, the first mode experiences the divergence instability, i.e., the amplitude of vibration increases statically while the rest of modes remain stable. As the axial velocity increases more, at a specific axial velocity, the first mode regains its stability and the real part of the first frequency begins to increase until the first mode merges to the second one, so that the system undergoes the coupled flutter instability. As it can be seen, by moving the intermediate support from one end of the beam to its midpoint, the region in which the first mode undergoes static instability, shrinks.

Fig. 6
figure 6

a Real part, b Imaginary part of the first and second natural frequencies versus mean axial velocity for different \(x_{s}\) and \(\beta = 100\), \(I_{2} = 0\), \(k_{1} = 1\)

Full size image

Based on Eq. (51), the first nonlinear resonance frequency is presented in Fig. 7a–d. Due to the internal damping, the nonlinear resonance frequency is time dependent, and it decreases from a higher value and tends toward linear natural frequency. According to Fig. 7a and b, as the intermediate support becomes closer to the beam midpoint and/or its stiffness coefficient increases, the nonlinear resonance frequency tends to the corresponding linear natural frequency more quickly.

Fig. 7
figure 7

a The nonlinear resonance frequency versus time for different locations of the intermediate support and \(\beta = 4\pi^{2}\), \(I_{2} = 0.001\), \(\gamma = 0.001\), \(\varGamma_{0} = 1.01\), \(k_{1} = 1\), \(k_{2} = 30\). b The nonlinear resonance frequency versus time for different linear stiffness coefficient of the intermediate support and \(x_{s} = 0.2\), \(I_{2} = 0.001\), \(\gamma = 0.001\), \(\varGamma_{0} = 1.01\), \(k_{1} = 1\), \(k_{2} = 30\). c The nonlinear resonance frequency versus time for different nonlinear stiffness coefficients of the intermediate support and \(\beta = 4\pi^{2}\), \(x_{s} = 0.2\), \(I_{2} = 0.001\), \(\gamma = 0.001\), \(\varGamma_{0} = 1.01\), \(k_{1} = 1\), \(k_{2} = 5\). d The nonlinear resonance frequency versus time for different axial stiffnesses and \(\beta = 4\pi^{2}\), \(x_{s} = 0.2\), \(I_{2} = 0.001\), \(\gamma = 0.001\), \(\varGamma_{0} = 1.01\), \(k_{1} = 1\)

Full size image

Figure 7c and d shows that for higher system nonlinearity, as time goes over, the nonlinear resonance frequency approaches the linear natural frequency very fast.

Supposing a specific initial amplitude, the time response for different \(x_{s}\) and the stiffness coefficient of the intermediate support are shown in Fig. 8a and b, respectively. In these figures, by increasing \(x_{s}\) or increasing the stiffness coefficient of the intermediate support, the natural and nonlinear resonance frequency increase and the vibration amplitude decreases quickly.

Fig. 8
figure 8

a The time response of the beam midpoint for different intermediate support locations and \(\beta = 4\pi^{2}\), \(I_{2} = 0.001\), \(\gamma = 0.0008\), \(\varGamma_{0} = 1.01\), \(k_{1} = 1\), \(k_{2} = 5\). b The time response of the beam midpoint for different linear stiffness coefficients of the intermediate support and \(x_{s} = 0.2\), \(I_{2} = 0.001\), \(\gamma = 0.0008\), \(\varGamma_{0} = 1.01\), \(k_{1} = 1\), \(k_{2} = 5\). c The time response of the beam midpoint for different axial velocities and \(\beta = 4\pi^{2}\),\(x_{s} = 0.2\), \(I_{2} = 0.001\), \(\gamma = 0.0008\), \(k_{1} = 1\), \(k_{2} = 5\)

Full size image

The effect of axial velocity on the time response is presented in Fig. 8c. Increasing the axial velocity strengthens the damping effect, so the vibration amplitude decreases fast.

As seen in Fig. 8a–c, when \(\Omega \ne 0,\Omega \ne 2\omega_{n}\), the response amplitude for axial velocity less than critical velocity is bounded in time.

Figure 9a and b demonstrates the vibration response of the system with axial velocity of 6.8 in which it is assumed that the frequency of velocity fluctuations is far from zero and two times the natural frequency. As seen in Fig. 9a, when \(x_{s} = 0.1\), the system undergoes coupled flutter instability and the vibration amplitude increases. However, for the same system parameters, by locating the intermediate support at \(x_{s} = 0.3\), the vibration amplitude remains bounded as time passes (see Fig. 9b).

Fig. 9
figure 9

a The time response of the beam midpoint for \(x_{s} = 0.1\) and \(\beta = 100\), \(I_{2} = 0\), \(\gamma = 0.001\), \(k_{1} = 1\), \(k_{2} = 12\). b The time response of the beam midpoint for \(x_{s} = 0.3\) and \(\beta = 100\), \(I_{2} = 0\), \(\gamma = 0.001\), \(k_{1} = 1\), \(k_{2} = 12\)

Full size image

Figure 10a–c shows the frequency response of the system for the case in which \(\Omega\) is near two times the first natural frequency. Due to the mentioned conditions in Eqs. (62), (63) and (68), it is observed that the trivial solution between two bifurcation points is unstable; the curve \(\sigma_{1}\) corresponding to nontrivial solution is stable and the curve \(\sigma_{2}\) corresponding to nontrivial solution is unstable. Therefore, according to Fig. 10a–c, if the detuning parameter,\(\sigma\) decreases from a large value, the trivial solution is stable, and upon reaching the bifurcation point where the trivial solution becomes unstable, there occurs a jump up to the curve \(\sigma_{1}\) and then the response amplitude begins to decrease through the curve \(\sigma_{1}\). Otherwise when \(\sigma\) increases from a small value, upon reaching the bifurcation point, the response amplitude begins to increase according to the curve \(\sigma_{1}\).

Fig. 10
figure 10

a The frequency response curve for different locations of the intermediate support and \(\beta = 4\pi^{2}\), \(I_{2} = 0.001\), \(\gamma = 0.0002\), \(k_{1} = 1\), \(k_{2} = 12\). b The frequency response curve for different nonlinear stiffness coefficients of the intermediate support and \(\beta = 4\pi^{2}\), \(x_{s} = 0.2\), \(I_{2} = 0.001\), \(\gamma = 0.0002\), \(k_{1} = 1\), \(k_{2} = 12\). c The frequency response curve for different stiffness coefficients of the intermediate support and \(x_{s} = 0.4\), \(I_{2} = 0.001\), \(\gamma = 0.0002\), \(k_{1} = 1\), \(k_{2} = 12\)

Full size image

The frequency response curve for different locations of the intermediate support is depicted in Fig. 10a. By moving the intermediate support from ends of the beam to its midpoint, the bifurcation points move toward each other, and therefore, the unstable region of the trivial solution decreases.

In Fig. 10b, the effect of the nonlinear stiffness coefficient of the intermediate support on the frequency response is shown. According to this figure, although the bifurcation points are not affected by the nonlinear stiffness, the curves bend more to the right as the nonlinear stiffness increases.

For various linear stiffness coefficient of the intermediate support, the frequency response of the system is depicted in Fig. 10c. As shown in Fig. 10c, the unstable region of the trivial solution decreases by increasing the linear stiffness coefficient.

5 Conclusion

The present study deals with the nonlinear parametric vibrations and stability of the axially moving Rayleigh viscoelastic beam equipped with a nonlinear intermediate support. For lateral vibrations of beams with large amplitude, the rotary inertia and the axial velocity impressively affect the vibration behavior and stability of the system. However, the intermediate support has dominant effect on increasing the natural frequencies, critical velocities and decreasing the unstable regions. Therefore, the system will remain stable within the wider range of axial velocities. In addition, the following results are obtained:

  • For the first mode, when the intermediate support is closer to the beam midpoint, the vibration amplitude decreases more quickly. Moreover, for this case, the region in which the first mode undergoes static instability shrinks.

  • In the presence of the axial velocity, the mode shapes become asymmetric. Increasing the axial velocity makes the mode shapes more asymmetric. Also, it is observed that the stiffness coefficient of intermediate support affect mode shapes in the same manner.

  • Due to the internal damping, the nonlinear resonance frequencies decrease to the corresponding linear natural frequencies, as time passes. As the viscosity coefficient increases, the nonlinear resonance frequencies tend quickly to the linear natural frequencies. Moreover, by increasing this parameter, amplitude vibration decreases quickly.

  • Investigating the influence of the intermediate support on nonlinear resonance frequencies shows that for higher stiffness coefficient of the intermediate support and/or by locating it closer to the beam midpoint, the nonlinear resonance frequencies tend faster to the corresponding linear natural frequencies.

  • As the dimensionless linear viscosity coefficient increases, the first nonlinear natural frequency tends to its corresponding linear natural frequency more quickly and amplitude vibration decreases fast. Additionally, the dimensionless linear viscosity coefficient has no effect on the linear natural frequency.

  • In the principal parametric resonance, by locating the intermediate support more close to the beam midpoint and/or increasing its linear stiffness coefficient, the unstable region of trivial solution decreases. Moreover, the nonlinearity only affects the curvature of the frequency response curves.