Stable Spatially Localized Configurations in a Simple Structure—A Global Symmetry-Breaking Approach

Abstract

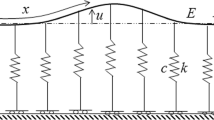
We revisit the classic stability problem of the buckling of an inextensible, axially compressed beam on a nonlinear elastic foundation with a semi-analytical approach to understand how spatially localized deformation solutions emerge in many applications in mechanics. Instead of a numerical search for such solutions using arbitrary imperfections, we propose a systematic search using branch-following and bifurcation techniques along with group-theoretic methods to find all the bifurcated solution orbits (primary, secondary, etc.) of the system and to examine their stability and hence their observability. Unlike previously proposed methods that use multi-scale perturbation techniques near the critical load, we show that to obtain a spatially localized deformation equilibrium path for the perfect structure, one has to consider the secondary bifurcating path with the longest wavelength and follow it far away from the critical load. The novel use of group-theoretic methods here illustrates a general methodology for the systematic analysis of structures with a high degree of symmetry.

Appendix: Group-Theoretic Considerations

The fundamental concept used to study the bifurcated equilibrium paths and their stability in any conservative elastic system is the existence of a group $G$ of transformations that leave its energy $\mathcal{E}(w;\lambda )$—defined in Eq. (2.2) for the problem at hand—unchanged, i.e., invariant under the action of all transformations $g \in G$. More specifically, to each element $g \in G$ we associate an orthogonal transformation $T_{g}$ (termed “representation” of $g$) acting on $w(x) \in H$ with image $T_{g}[w] \in H$ that satisfies

$$ \mathcal{E}(T_{g}[w];\lambda ) = \mathcal{E}(w ;\lambda ) \, ;\quad \forall \lambda \ge 0 \, , \ \forall w \in H \, , \ \forall g \in G\; , $$

(A.1)

where $\lambda$ is the scalar load parameter (assumed positive) and $H$ the space of admissible displacements.

It follows from Eq. (A.1) that the variation of ℰ with respect to its argument $w$ (first order functional derivative $\mathcal{E}_{,w}$) possess the property of “equivariance”

$$ T_{g}[\mathcal{E}_{,w}(w;\lambda )] \delta w = \mathcal{E}_{,w}(T_{g} [w] ;\lambda ) \delta w \, ; \quad \forall \lambda \ge 0 \, , \ \forall w, \delta w \in H \, ,\ \forall g \in G\; . $$

(A.2)

According to Eq. (2.3), the system’s equilibrium solutions $w(x ; \lambda )$ are found by extremizing its energy; consequently all solutions of the system $\mathcal{E}_{,w}(w;\lambda ) \delta w = 0$ must satisfy Eq. (A.2). It is more appropriate to talk about orbits of equilibrium paths since, in view of the equivariance described in (A.2), applying to an equilibrium solution $w$ the transformation $T_{g}$ automatically generates another equilibrium solution $T_{g}[w]$.

A subset of these equilibrium solutions, termed “principal solutions” and denoted by ${\stackrel{0}{w}}(x; \lambda )$, are invariant under all transformations $T_{g}$. These solutions belong to an invariant subspace of $H$, denoted ${\mathcal{S}}_{G}$ and called the “fixed-point space”

$$ \mathcal{E}_{,w}({\stackrel{0}{w}}(x; \lambda );\lambda ) \delta w = 0 \; , \ \forall \lambda \ge 0 \; ; \quad {\stackrel{0}{w}} \in { \mathcal{S}}_{G} := \{ w \in H \;|\; \ T_{g} [w] = {w} \; , \ \forall g \in G \} \; . $$

(A.3)

To determine the stability of a principal solution, one has to check the positive definiteness of the self-adjoint bilinear operator ${\mathcal{E}}^{0}_{,ww}$, evaluated on the principal path ${\stackrel{0}{w}}(x; \lambda )$, by finding its eigenvalues $\beta (\lambda )$

$$ ({\mathcal{E}}^{0}_{,ww}\Delta w)\delta w = \beta (\lambda ) < \Delta w, \delta w> \; ; \quad \forall \delta w \in H\; ; \ {\mathcal{E}}^{0}_{,ww} := {\mathcal{E}}_{,ww}({\stackrel{0}{w}}(x;\lambda );\lambda ) \; , $$

(A.4)

where $\Delta w$ is the corresponding eigenvector and $< \cdot \; ,\; \cdot >$ denotes an inner product in $H$. A stable solution corresponds to a positive minimum eigenvalue¹⁶$\beta _{min} > 0$ (the number of eigenvalues depends on the dimension of $H$). When ${\stackrel{0}{w}}(x;\lambda )$ is periodic, the Bloch-wave representation may be used, as described in Sect. 2.4. For a well-posed problem, its stress-free (unloaded) configuration at $\lambda =0$ is stable; as the load increases stability will be lost at the first bifurcation point encountered along the loading path at some $\lambda _{b}$.

It can be shown, e.g., [22, 40], that the existence of the group $G$ implies the existence of a symmetry basis with respect to which (i) the operator ${\mathcal{E}}^{0}_{,ww}$ defined in (A.4) can be block-diagonalized and (ii) the space of admissible functions $H=\oplus _{\mu =1}^{h} V^{\mu }$ can be uniquely decomposed into a direct sum of mutually orthogonal invariant subspaces $V^{\mu }$ (with $h$ being the number of equivalence, or conjugacy, classes for $G$). Each subspace $V^{\mu }$ is associated with an $n_{\mu }$-dimensional irreducible representation $\tau ^{\mu }$ of $G$, also termed “irrep” from which an appropriate projection operator can be constructed giving the $V^{\mu }$ component of any function in $H$.

Bifurcated equilibrium paths, termed primary, can emerge from the principal path at loads $\lambda _{b}$ corresponding to zero eigenvalues of ${\mathcal{E}}^{b}_{,ww}$. That is, $\beta (\lambda _{b})=0$ so that

$$ \begin{gathered} ({\mathcal{E}}^{b}_{,ww} {\stackrel{i}{w}})\delta w = 0 \; , \ { \stackrel{i}{w}} \in {\mathcal{N}}_{\mu }\; ,\ < {\stackrel{i}{w}},{ \stackrel{j}{w}}>=\delta _{ij}\; , \ i , j = 1,\dots ,n_{\mu }\; ; \\ \forall \delta w \in H\; ;\ {\mathcal{E}}^{b}_{,ww} := {\mathcal{E}}_{,ww}({\stackrel{0}{w}}(x; \lambda _{b});\lambda _{b}) \; , \end{gathered} $$

(A.5)

where the eigenmodes $\Delta w =\stackrel{i}{w}$ span ${\mathcal{N}}_{\mu }$, the $n_{\mu }$-dimensional null space of the operator ${\mathcal{E}}^{b}_{,ww}$. Some additional conditions, termed “transversality” conditions must also hold to ensure that $\lambda _{b}$ is a bifurcation and not a limit (i.e., turning) point:¹⁷

$$ ([d{\mathcal{E}}^{0}_{,ww}/d\lambda ]_{b}{\stackrel{1}{w}}){ \stackrel{1}{w}} \neq 0\; . $$

(A.6)

It can be shown that the null space ${\mathcal{N}}_{\mu }$ of the stability operator ${\mathcal{E}}^{b}_{,ww}$ is an $n_{\mu }$-dimensional subspace of the invariant subspace $V^{\mu }$ for some $\mu$, i.e. ${ \mathcal{N}}_{\mu } \subseteq V^{\mu }$, associated to the irreducible representation $\tau ^{\mu }$. The (primary) bifurcated paths ${\stackrel{b}{w}}(x; \lambda )$ emerging from ${\stackrel{0}{w}}(x; \lambda )$ at $\lambda _{b}$, can be represented with the following asymptotic expressions, resulting from the projection of the equilibrium equations onto the null space ${\mathcal {N}}_{\mu }$ and termed “Lyapunov–Schmidt–Koiter” asymptotics:

$$ \lambda (\xi )=\lambda _{b}+ \lambda _{1}\xi + {\frac{1}{2}} \lambda _{2} \xi ^{2} + O(\xi ^{3})\; , \qquad {\stackrel{b}{w}}(x; \xi ) = { \stackrel{0}{w}}(x; \lambda (\xi )) + \xi \sum _{i=1}^{n_{\mu }} \alpha _{i} {\stackrel{i}{w}}(x) + O(\xi ^{2})\; , $$

(A.7)

where $\xi$ is the path’s “bifurcation amplitude” parameter and $\alpha _{i}$ the components of the bifurcated path’s initial tangent vector. From knowledge of the bifurcation irrep $\tau ^{\mu }$, group theory results (such as the “lattice of isotropy subgroups” of $G$ [13]) allow the direct computation of the $\alpha _{i}$ tangents (one set for each bifurcating orbit) emerging at $\lambda _{b}$. Once the asymptotic expression of the primary bifurcating equilibrium path ${\stackrel{b}{w}}(x; \xi )$ is established, the global solution path may be computed efficiently by using the path’s isotropy group, i.e. the elements of the subgroup of $G$ satisfying $T_{g} [{\stackrel{b}{w}}]={\stackrel{b}{w}}$, to find its corresponding fixed-point space. Along this path there may occur (secondary) bifurcation points. In such cases, the above procedure begins once again with ${\stackrel{b}{w}}(x; \lambda )$ as the new principal path from which—secondary with respect to ${\stackrel{0}{w}}(x; \lambda )$—bifurcated orbits will emerge.

In order to determine the local (asymptotic) type—transverse or pitchfork—of the bifurcating paths (which may be different than the global type), we need to determine if $\lambda _{1} = 0$ or $\lambda _{1} \neq 0$ in Eq. (A.7)₁. From an asymptotic analysis (e.g., [47]) $\lambda _{1} = 0$ is guaranteed if

$$ \mathcal{E}_{ijk} := (([\mathcal{E}_{,www}({\stackrel{0}{w}}(x; \lambda _{b}); \lambda _{b})] {\stackrel{i}{w}}) {\stackrel{j}{w}}) { \stackrel{k}{w}} = 0, \qquad i,j,k = 1,\dots ,n_{\mu }. $$

(A.8)

To reiterate, the strategy followed in this work is to sequentially apply the above-described procedure to follow the bifurcating equilibrium orbits of the system by identifying, each time, their symmetry group and their corresponding fixed-point space. As we proceed from the principal solution to the primary bifurcations emerging from it, then to the secondary bifurcations emerging from the primary ones, the corresponding symmetry groups and fixed-point spaces change accordingly. Knowledge of the symmetries of a path allows for an efficient calculation of a unique solution in its own fixed-point space. The method adopted here follows the procedures introduced by [20, 23]. Moreover, following [13, 20], knowledge of the lattice of isotropy subgroups of the initial symmetry group guides the search for the bifurcated equilibrium paths in a systematic way and explains our findings.

1.1 A.1 Principal Solution, Irreps, and Bifurcations—Group $G = D_{\infty h}$

As described in Sect. 2.3, the fixed-point space of $D_{\infty h}$ for the beam–foundation system consists of only the trivial principal solution $\overset{0}{w}(x; \lambda ) = 0$. According to group theory (e.g., [32]) $D_{\infty h}$ has four 1-dimensional irreps (one being the trivial identity irrep). These provide the possibility of simple bifurcations to paths with symmetry groups of $C_{\infty v}$, $C_{\infty h}$ or $D_{\infty }$. There are also an infinity of 2-dimensional irreps, providing the possibility of double bifurcations. These correspond to bifurcating paths with symmetry groups $D_{nh}$ or $D_{nd}$, where $n\in \mathbb{N}$, as shown in Table 1. In Sect. 4.1.2 we find from Eq. (4.5) only double bifurcations at $\lambda _{n} \geq 2$ with corresponding eigenmodes ${\stackrel{ni}{w}}(x), i=1,2$—as expected from the 2-dimensional irreps of $D_{\infty h}$ of Table 1. Notice that no simple bifurcations exist, in spite of the existence of 1-dimensional irreps of this group. From the infinity of primary bifurcation paths, we follow next the bifurcation orbit emerging from the lowest load $\lambda _{c} = 2$ which corresponds to $n_{c}=q$ and $L_{c} = 2\pi$ (recall that the periodicity of the model is $L_{d}= L_{c} q$).

Table 1 Table of irreps and bifurcated orbit symmetries for $G = D_{\infty h}$. The first column gives the dimension $n_{\mu }$ of the corresponding irrep; the second column gives a standard label/name for the irrep; the third through fifth columns provide the corresponding irrep matrix for the generators $\tau ^{\mu }_{c(\phi )}$, $\tau ^{\mu }_{\sigma _{v}}$, and $\tau ^{\mu }_{\sigma _{h}}$, respectively; the sixth column gives the kernel of $\tau ^{\mu }$ (i.e., $G^{\mu } = \{ g \in G \;|\; \tau ^{\mu }_{g} = I\}$, where $I$ is the $n_{\mu }$-dimensional identity matrix); the seventh column gives the symmetry group of the corresponding bifurcating equilibrium path(s)

1.2 A.2 Primary Bifurcation Orbit at $\lambda _{c} = 2$, Irreps, and Bifurcations—Group $G = D_{qd}$

The bifurcated equilibrium paths emerging from the lowest critical load $\lambda _{c}$ correspond according to Eq. (4.4) to a double bifurcation with eigenmodes ${\stackrel{c1}{w}}(x) = \sin (x)$ and ${\stackrel{c2}{w}}(x) = \cos (x)$. Since every linear combination of these eigenmodes is left invariant by the elements of the group $S_{2q}$, the critical point corresponds to the $\mu = E_{2q}$ irrep, and according to the general theory (see Table 1) the symmetry group of the bifurcating orbit is $D_{qd}$. This symmetry group is finite and has the following two generators: $\sigma _{h} c(\pi /q)$ and $\sigma _{h}\sigma _{v}$.

As indicated in Table 2, this group has four 1-dimensional irreps (one being the trivial identity irrep). These provide the possibility of simple bifurcations to paths with symmetry groups of $S_{2q}$, $D_{q}$, or $C_{qv}$. There are also $(q-1)$ 2-dimensional irreps, providing the possibility of double bifurcations. These correspond to bifurcating paths with symmetry groups $D_{rd}$, $C_{rv}$ and $D_{r}$, where $r:=\mathrm{gcd}(j,q)$, with $j=1,\dots ,q-1$. The fixed-point space $\mathcal{S}_{ D_{qd}} := \{w(x) \in H \;|\; T_{g}[w(x)] = w(x), \; \forall g \in D_{qd}\}$ of the primary bifurcation solutions ${\stackrel{1}{w}}$ with $D_{qd}$ symmetry, as defined above, contains configurations $w(x)$ of the $L_{d}$-periodic beam that remain unaltered under the transformations of this group. The primary bifurcation path ${\stackrel{1}{w}}(x; \lambda )$ is contained within $\mathcal{S}_{D_{qd}}$ and a representative configuration along this path parameterized with respect to the bifurcation amplitude $\xi$ (see Sect. 4.1.2) is plotted in Fig. 3.

Table 2 Table of irreps and bifurcated orbit symmetries for $G = D_{qd}$. The first column gives the dimension $n_{\mu }$ of the corresponding irrep; the second column gives a standard label/name for the irrep; the third and fourth columns provide the corresponding irrep matrix for the generators $\tau ^{\mu }_{c(\pi /q)}$ and $\tau ^{\mu }_{\sigma _{h} \sigma _{v}}$, respectively; the fifth column gives the kernel of $\tau ^{\mu }$ (i.e., $G^{\mu } = \{ g \in G \;|\; \tau ^{\mu }_{g} = I\}$, where $I$ is the $n_{\mu }$-dimensional identity matrix); the sixth column gives the symmetry group of the corresponding bifurcating equilibrium path(s). The function $\gcd (a,b)$ is the greatest common divisor of $a$ and $b$

1.3 A.3 Secondary Bifurcation Orbits and Their Symmetry

Recall that for the numerical calculations reported here, we have selected $q=20$ which gives $L_{d} = L_{c} q = 40 \pi$. Due to the (energy-induced) symmetry of the dispersion curve discussed in Sect. 4.1.2, all bifurcations are double. Indeed, double bifurcation points corresponding to all of the 2-dimensional irreps $E^{j}$ of $D_{20d}$ are found along the primary bifurcation orbit ${\stackrel{1}{w}}(x; \lambda )$. The correspondence between the 2-dimensional irrep index $j$ of Table 2 and the Bloch-wave wavenumber $k$ is presented in Table 3, along with the symmetry group of each orbit bifurcating from a bifurcation point of this type. The $j$–$k$ correspondence is obtained by using standard group representation theory results to decompose the irreps of $D_{20d}$ into direct sums of the irreps of its subgroup $C_{20}$. In this way, we can find which wavenumbers $k$ (used in the Bloch-wave calculations of Sect. 3) correspond to each 2-dimensional irrep of $D_{20d}$. The global bifurcation type, either transverse or pitchfork, is obtained from a theorem in equivariant bifurcation theory [20], and indicates the nature of the global bifurcating equilibrium path. In particular, a globally transcritical path $w(x; \xi )$ will have $w(x; -\xi ) \neq w(x; \xi )$ for some value(s) of $\xi$, whereas a globally pitchfork path will have $w(x; -\xi ) = w(x; \xi )$ for all $\xi$. See Sect. 4 for some discussion of the different types of paths found in the present work.

Table 3 Correspondence between irreps of $D_{20d}$ and Bloch-wave wavenumber $k$. Also shown are the symmetries and global bifurcation type (transverse or pitchfork) of the corresponding bifurcating orbits

In addition to the group-theory results in Table 3, we can also show by group-theoretic calculation that all the secondary bifurcating paths are locally pitchfork, i.e. $\lambda _{1}=0$ in Eq. (A.7)₁ since all the coefficients $\mathcal{E}_{ijk}$ of Eq. (A.8) vanish. This result is obtained by constructing an appropriate tensor-product rep [40] for the vector space of third-order tensors to which the “vector” $\mathcal{E}_{ijk}$ belongs. Due to equivariance, $\mathcal{E}_{ijk}$ must be in the fixed-point space $\mathcal{S}_{D_{20d}}$ of this tensor-product space. Further, it is easily found that $\mathcal{S}_{D_{20d}} = \{0\}$. Thus, all paths bifurcating from the $D_{20d}$ primary orbit are locally pitchfork. However, as indicated in Table 3, not all such bifurcating paths are globally pitchfork. Again, see Sect. 4 for some discussion of this issue.

1.4 A.4 Critical Load and Eigenmodes for the Imperfect Beam (Amplitude: $\zeta < 0$)

We present here a calculation of the lowest load $\lambda _{cis}$ corresponding to a bifurcation with a symmetric (with respect to $x=0$) eigenmode ${\stackrel{is}{w}}(x)$ for an imperfect, periodic beam of length $L_{d}$. The calculation of the lowest load corresponding to a bifurcation with an antisymmetric (with respect to $x=0$) eigenmode is similar and gives a slightly higher critical load $\lambda _{cia}$; the corresponding calculation is omitted here since we are interested in the bifurcated equilibrium paths emerging from the lowest load $\lambda _{cis}$.

By taking the functional derivative of the equilibrium Eq. (2.7) and evaluating at $w(x)=0$ we obtain the equation for the symmetric with respect to $x=0$ eigenmode of the imperfect beam (${\stackrel{is}{w}}(x)={ \stackrel{is}{w}}(-x)$). The corresponding boundary conditions follow from Eq. (2.4) for $p=1, 3$ and hence

$$ \begin{gathered} \frac{d^{4} {\stackrel{is}{w}}}{d x^{4}} + \lambda \frac{d^{2} {\stackrel{is}{w}}}{d x^{2}} + [1+z(x)]{ \stackrel{is}{w}}= 0\; ,\ x \in (0,\frac{L_{d}}{2}) ;\\ \frac{d {\stackrel{is}{w}}}{d x} (0) = \frac{d {\stackrel{is}{w}}}{d x} ({\frac{L_{d}}{2}}) = 0 \; ,\ \frac{d^{3} {\stackrel{is}{w}}}{d x^{3}} (0) = \frac{d^{3} {\stackrel{is}{w}}}{d x^{3}} ({\frac{L_{d}}{2}}) = 0\; . \end{gathered} $$

(A.9)

Solving the problem in Eq. (A.9) with the constant coefficient ordinary differential equation in the intervals $(0, x_{0})$ and $(x_{0}, L_{d}/2)$, one has

$$ {\stackrel{is}{w}}(x) = \left \{ \textstyle\begin{array}{l@{\quad }l} \left . \textstyle\begin{array}{l} \eta \cos (a_{\zeta }x) + \theta \cos (b_{\zeta }x) \\ a_{\zeta }:= \displaystyle \left [{ \frac{\lambda +[\lambda ^{2}-4(1+\zeta )]^{1/2}}{2}}\right ]^{1/2}, \quad b_{\zeta }:= \left [{ \frac{\lambda -[\lambda ^{2}-4(1+\zeta )]^{1/2}}{2}}\right ]^{1/2} \end{array}\displaystyle \right \} \\ \quad x \in [0, x_{0}] \\ \left . \textstyle\begin{array}{l} \displaystyle \delta \cosh [a(x-\frac{L_{d}}{2})] \cos [b(x- \frac{L_{d}}{2})] + \epsilon \sinh [a(x-\frac{L_{d}}{2})] \sin [b(x- \frac{L_{d}}{2})] \\ a := \displaystyle {\frac{[2 -\lambda ]^{1/2}}{2}}, \quad b := { \frac{[2 +\lambda ]^{1/2}}{2}} \end{array}\displaystyle \quad \quad \ \ \right \} \\ \quad \displaystyle x \in [x_{0} ,{ \frac{L_{d}}{2}}] \end{array}\displaystyle \right . $$

(A.10)

where $a_{\zeta },\; b_{\zeta },\; a,\; b$ are all positive constants. Notice from Eq. (A.10) that the periodicity-imposed symmetry conditions at $L_{d}/2$ according to Eq. (A.9) are automatically satisfied.

Using the continuity condition at $x_{0}$ for ${\stackrel{is}{w}}(x)$ and its derivatives up to order three, one obtains a homogeneous linear system of four equations for the four constants $\eta , \theta , \delta , \epsilon$ appearing in Eq. (A.10). The vanishing of the determinant of the corresponding $4 \times 4$ matrix (not recorded here in view of the cumbersome expressions) provides the equation for the critical load $2(1+\zeta )^{1/2} < \lambda _{cis} < 2$ (guaranteed by $\zeta <0$), which is obtained numerically.