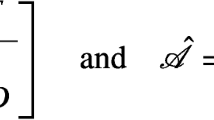Alternating positive semidefinite splitting preconditioners for double saddle point problems

Abstract

In this paper, an alternating positive semidefinite splitting (APSS) preconditioner is proposed for solving double saddle point problems. The corresponding APSS iteration method is proved to be convergent unconditionally. Moreover, to further improve its efficiency, a relaxed variant is established for the APSS preconditioner, which results in better spectral distribution and numerical performance. Numerical experiments with liquid crystal director models demonstrate the effectiveness of the APSS preconditioner and its relaxed variant when compared with other preconditioners. Comparison between the related numerical results shows that the proposed preconditioners are comparable with (though not really better than) the best existing preconditioners.

1 Introduction

We are concerned with iterative solution methods for the following double saddle point problems:

$$\begin{aligned} {\mathscr {A}}_+u\equiv \begin{bmatrix} A&B^T&C^T \\ B&0&0 \\ C&0&-D \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} f \\ g \\ h \end{bmatrix} \equiv b_+, \end{aligned}$$

(1)

where $A\in {\mathbb {R}}^{n\times n}$ and $D\in {\mathbb {R}}^{p\times p}$ are symmetric positive definite matrices, $B\in {\mathbb {R}}^{m\times n}$ is a matrix of full row rank, $C\in {\mathbb {R}}^{p\times n}$ is a rectangular matrix and $n\geqslant m+p$. Linear systems of the form (1) can be viewed as saddle point linear systems [4], which arise from many practical application backgrounds, for example, the mixed finite element approximation of fluid flow problems [7, 12], interior point methods for quadratic programming problems [10, 17] and so on.

Due to the block three-by-three structure of the saddle point matrix ${\mathscr {A}}_+$ in (1), it is generally difficult to analyze its spectral properties and design suitable solution methods for solving the double saddle point problem (1). Of course, we can decompose the two-fold saddle point matrix ${\mathscr {A}}_+$ into block two-by-two forms and choose solution methods for standard saddle point problems [4] to solve the corresponding double saddle point problems. However, owing to its more complex structure, straightforward application of the solution method for standard block two-by-two saddle point problems usually leads to poor numerical performance. In order to overcome such difficulties, some technical modifications for the corresponding solution methods are necessary to obtain satisfactory results. For example, by modifying the optimal block diagonal and block triangular preconditioners [8, 11] for standard saddle point problems, some efficient block diagonal and block triangular preconditioners are designed and analyzed in [1, 2] for solving the double saddle point problem (1).

Note that the augmented linear system (1) can equivalently be reformulated into

$$\begin{aligned} {\mathscr {A}}u\equiv \begin{bmatrix} D&-C&0 \\ C^T&A&B^T \\ 0&-B&0 \end{bmatrix} \begin{bmatrix} z \\ x \\ y \end{bmatrix} = \begin{bmatrix} -h \\ f \\ -g \end{bmatrix} \equiv b, \end{aligned}$$

(2)

which facilitates the possibility to apply certain specific iterative solution methods. In this paper, different from [1, 2], we exploit directly the block three-by-three structure of the double saddle point system (2) as the starting point to design solution methods. An alternating positive semidefinite splitting (APSS) is established for the matrix ${\mathscr {A}}$ in (2), which leads to an unconditionally convergent APSS iteration method for solving the linear system (2). Moreover, the APSS iteration method leads to an efficient alternating direct splitting preconditioner for solving the augmented linear system (2) within Krylov subspace acceleration [15]. Furthermore, based on an useful relaxation technique, we give an efficient modification of the APSS preconditioner to further improve its efficiency to solve double saddle point problems.

This paper is organized as follows. In Sect. 2, the new APSS preconditioner and its algorithmic implementation to accelerate the Krylov subspace methods are established. In Sect. 3, we analyze the convergence of the corresponding APSS iteration method. In Sect. 4, a relaxed variant of the APSS preconditioner is established, which leads to better spectral distribution and numerical performance than the original APSS preconditioner. Finally in Sect. 5, an example from the liquid crystal director model is used to test the numerical performance of the APSS preconditioner to accelerate the GMRES method [16] for solving double saddle point problems. Finally in Sect. 6, we end this paper with some conclusions.

2 The APSS preconditioner

For the double saddle point matrix ${\mathscr {A}}$ in (2), we can decompose it into

$$\begin{aligned} {\mathscr {A}}= \begin{bmatrix} D&-C&0 \\ C^T&0&0 \\ 0&0&0 \end{bmatrix} + \begin{bmatrix} 0&0&0 \\ 0&A&B^T \\ 0&-B&0 \end{bmatrix} \equiv {\mathscr {A}}_1+{\mathscr {A}}_2. \end{aligned}$$

(3)

Based on the splitting (3), we can obtain the following splittings for the matrix ${\mathscr {A}}$ in (2):

$$\begin{aligned} {\mathscr {A}} = (\alpha I+{\mathscr {A}}_1)-(\alpha I-{\mathscr {A}}_2) \quad \text {and} \quad {\mathscr {A}} = (\alpha I+{\mathscr {A}}_2)-(\alpha I-{\mathscr {A}}_1), \end{aligned}$$

where I denotes the identity matrix of proper size and the iteration parameter $\alpha$ is a positive number. It then directly leads to the following two-sweep iteration scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\alpha I+{\mathscr {A}}_1)u^{(k+\frac{1}{2})}=(\alpha I-{\mathscr {A}}_2)u^{(k)}+b,\\ (\alpha I+{\mathscr {A}}_2)u^{(k+1)}=(\alpha I-{\mathscr {A}}_1)u^{(k+\frac{1}{2})}+b, \end{array}\right. } \end{aligned}$$

(4)

where $u^{(k)}$ is the kth iteration vector with $k=0,1,2,\ldots$. It is easy to obverse that the matrices ${\mathscr {A}}_1$ and ${\mathscr {A}}_2$ in (3) are both positive semidefinite, so we abbreviate the corresponding iteration method based on iteration scheme (4) as the APSS iteration method.

By deleting the intermediate variable $u^{(k+\frac{1}{2})}$, we can alteratively rewrite the iteration scheme (4) as the following stationary form:

$$\begin{aligned} u^{(k+1)}={\mathscr {T}}_{\alpha }u^{(k)}+{\mathscr {P}}_{\alpha }^{-1}b, \end{aligned}$$

with

$$\begin{aligned} {\mathscr {T}}_{\alpha }=(\alpha I+{\mathscr {A}}_2)^{-1}(\alpha I-{\mathscr {A}}_1)(\alpha I+{\mathscr {A}}_1)^{-1}(\alpha I-{\mathscr {A}}_2) \end{aligned}$$

(5)

and

$$\begin{aligned} {\mathscr {P}}_{\alpha }=\frac{1}{2\alpha }(\alpha I+{\mathscr {A}}_1)(\alpha I+{\mathscr {A}}_2). \end{aligned}$$

(6)

Here, ${\mathscr {T}}_{\alpha }$ in (5) is the APSS iteration matrix and ${\mathscr {P}}_{\alpha }$ in (6) is served as an APSS preconditioner, which leads to the following matrix splitting for the double saddle point matrix ${\mathscr {A}}$ in (2):

$$\begin{aligned} {\mathscr {A}}={\mathscr {P}}_{\alpha }-{\mathscr {R}}_{\alpha } \quad \text {with} \quad {\mathscr {R}}_{\alpha }=\frac{1}{2\alpha }(\alpha I-{\mathscr {A}}_1)(\alpha I-{\mathscr {A}}_2). \end{aligned}$$

In practical implementation of the APSS preconditioner (6) within Krylov subspace acceleration, it involves the solution of the residual equation ${\mathscr {P}}_{\alpha }z=r$. By taking advantage of the matrix decompositions:

$$\begin{aligned} \alpha I+{\mathscr {A}}_1 = \begin{bmatrix} \alpha I+D&-C&0 \\ C^T&\alpha I&0 \\ 0&0&\alpha I \end{bmatrix} = \begin{bmatrix} \alpha I+D+\frac{1}{\alpha }CC^T&-C&0 \\ 0&\alpha I&0 \\ 0&0&\alpha I \end{bmatrix} \begin{bmatrix} I&0&0 \\ \frac{1}{\alpha }C^T&I&0 \\ 0&0&I \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} \alpha I+{\mathscr {A}}_2 = \begin{bmatrix} \alpha I&0&0 \\ 0&\alpha I+A&B^T \\ 0&-B&\alpha I \end{bmatrix} = \begin{bmatrix} \alpha I&0&0 \\ 0&\alpha I+A+\frac{1}{\alpha }B^TB&B^T \\ 0&0&\alpha I \end{bmatrix} \begin{bmatrix} I&0&0 \\ 0&I&0 \\ 0&-\frac{1}{\alpha }B&I \end{bmatrix}, \end{aligned}$$

we can obtain the following algorithmic implementation for the APSS preconditioner ${\mathscr {P}}_{\alpha }$.

Algorithm 1

Solution of ${\mathscr {P}}_{\alpha }w=r$ with $r=(r_1^T,r_2^T,r_3^T)^T$, $w=(w_1^T,w_2^T,w_3^T)^T$ and $r_1,w_1\in {\mathbb {R}}^p$, $r_2,w_2\in {\mathbb {R}}^n$, $r_3,w_3\in {\mathbb {R}}^m$, from the following steps:

• (1) solve $w_1$ from $(\alpha I+D+\frac{1}{\alpha }CC^T)w_1 = 2r_1+\frac{2}{\alpha }Cr_2$;

• (2) solve $w_2$ from $(\alpha I+A+\frac{1}{\alpha }B^TB)w_2 = 2r_2-C^Tw_1-\frac{2}{\alpha }B^Tr_3$;

• (3) compute $w_3=\frac{1}{\alpha }(2r_3+Bw_2)$.

3 Convergence analysis of the APSS iteration method

In this section, we analyze the convergence of the APSS iteration method for solving the double saddle point problem (2). Similar proof techniques as those in [5, 9, 13] are used for our analyses.

Theorem 1

Assume that $A\in {\mathbb {R}}^{n\times n}$ and $D\in {\mathbb {R}}^{p\times p}$ are symmetric positive definite, $B\in {\mathbb {R}}^{m\times n}$ is of full row rank, $C\in {\mathbb {R}}^{p\times n}$ is rectangular and $n\geqslant m+p$. Then the APSS iteration method for solving the double saddle point problem (2) is unconditionally convergent, i.e.,

$$\begin{aligned} \rho ({\mathscr {T}}_{\alpha })<1, \quad \forall \ \alpha >0. \end{aligned}$$

Proof

It is easy to verify that the APSS iteration matrix ${\mathscr {T}}_{\alpha }$ defined in (5) is similar to the following matrix:

$$\begin{aligned} {\hat{{\mathscr {T}}}}_{\alpha }= (\alpha I-{\mathscr {A}}_1)(\alpha I+{\mathscr {A}}_1)^{-1}(\alpha I-{\mathscr {A}}_2)(\alpha I+{\mathscr {A}}_2)^{-1}. \end{aligned}$$

Denote $\Vert \cdot \Vert$ as the Euclidean norm of a matrix. Then, it holds that

$$\begin{aligned} \rho ({\mathscr {T}}_{\alpha })=\rho (\hat{{\mathscr {T}}}_{\alpha })\leqslant \Vert (\alpha I-{\mathscr {A}}_1)(\alpha I+{\mathscr {A}}_1)^{-1}\Vert \cdot \Vert (\alpha I-{\mathscr {A}}_2)(\alpha I+{\mathscr {A}}_2)^{-1}\Vert \leqslant 1. \end{aligned}$$

Here, we have taken advantages of the positive semidefiniteness of the matrices ${\mathscr {A}}_1$ and ${\mathscr {A}}_2$. Thus, to obtain the unconditionally convergent result for the APSS iteration method, it only needs to verify that the iteration matrix ${\mathscr {T}}_{\alpha }$ has no unity eigenvalues.

Let $\lambda$ be an eigenvalue of the iteration matrix ${\mathscr {T}}_{\alpha }$, then $\lambda =1-\mu$ with $\mu$ being a generalized eigenvalue of the matrix pair $({\mathscr {A}},{\mathscr {P}}_{\alpha })$. Thus, there exists an nonzero eigenvector v such that

$$\begin{aligned} {\mathscr {A}}v=\mu {\mathscr {P}}_{\alpha }v=\frac{\mu }{2\alpha } ({\mathscr {A}}_1{\mathscr {A}}_2+\alpha {\mathscr {A}}+\alpha ^2I)v, \end{aligned}$$

which is equivalent to

$$\begin{aligned} (2-\mu ){\mathscr {A}}v=\alpha \mu \left( I+\frac{1}{\alpha ^2}{\mathscr {A}}_1{\mathscr {A}}_2\right) v. \end{aligned}$$

(7)

Due to the nonsingularity of the matrix ${\mathscr {A}}$, it is obvious that $\mu \ne 0$ from (7). Moreover, we have $\mu \ne 2$. Otherwise, from (7), it holds that the linear system $(I+\frac{1}{\alpha ^2}{\mathscr {A}}_1{\mathscr {A}}_2)v=0$ has a nonzero solution. However, it is impossible, due to the nonsingularity of the matrix:

$$\begin{aligned} {\mathscr {G}}_{\alpha }=I+\frac{1}{\alpha ^2}{\mathscr {A}}_1{\mathscr {A}}_2= \begin{bmatrix} I&-\frac{1}{\alpha ^2}CA&-\frac{1}{\alpha ^2}CB^T \\ 0&I&0 \\ 0&0&I \end{bmatrix}. \end{aligned}$$

Thus, the equation (7) can be reformulated as

$$\begin{aligned} {\mathscr {A}}v=\theta {\mathscr {G}}_{\alpha }v \quad \text {with} \quad \theta = \frac{\mu \alpha }{2-\mu }\ne 0, \end{aligned}$$

(8)

which is equivalently to

$$\begin{aligned} \mathscr {C}_{\alpha }v=\theta v \end{aligned}$$

(9)

with

$$\begin{aligned} \mathscr {C}_{\alpha }=\mathscr {G}_{\alpha }^{-1}\mathscr {A}= \begin{bmatrix} D+\frac{1}{\alpha ^2}CAC^T&-C+\frac{1}{\alpha ^2}CA^2-\frac{1}{\alpha ^2}CB^TB&\frac{1}{\alpha ^2}CAB^T \\ C^T&A&B^T \\ 0&-B&0 \end{bmatrix}. \end{aligned}$$

Then from (8), we have

$$\begin{aligned} |\lambda | = |1-\mu | = \Big |1 - \frac{2\theta }{\theta +\alpha }\Big | = \Big |\frac{\theta -\alpha }{\theta +\alpha }\Big |. \end{aligned}$$

Denote the real part of $\theta$ as $\text {Re}(\theta )$, then it is easy to verify that $|\lambda |=1$ if and only if $\text {Re}(\theta )=0$. Thus, in order to prove $\rho ({\mathscr {T}}_{\alpha })<1$, we only need to verify $\text {Re}(\theta )\ne 0$, i.e., $\theta$ is not a purely imaginary eigenvalue.

Let $v=[v_1^T,v_2^T,v_3^T]^T$, with $v_1\in {\mathbb {C}}^p$, $v_2\in {\mathbb {C}}^n$ and $v_3\in {\mathbb {C}}^m$ being the normalized eigenvector of the eigenproblem (9), then we have

$$\begin{aligned} {\left\{ \begin{array}{ll} (D+\frac{1}{\alpha ^2}CAC^T)v_1-(C-\frac{1}{\alpha ^2}CA^2+\frac{1}{\alpha ^2}CB^TB)v_2+\frac{1}{\alpha ^2}CAB^Tv_3=\theta v_1,\\ C^Tv_1+Av_2+B^Tv_3=\theta v_2,\\ -Bv_2=\theta v_3. \end{array}\right. } \end{aligned}$$

(10)

We now consider all the possible cases depending on $v_1$ and $v_2$:

• (i) If $v_1=0$, then the second equation of (10) reduces to

  $$\begin{aligned} Av_2+B^Tv_3=\theta v_2. \end{aligned}$$

  (11)

  Assume that $v_2=0$, then from (11), we have $B^Tv_3=0$. In consideration of that B is of full row rank, it holds that $v_3=0$. Then $v=0$, which contradicts the fact that v is an eigenvector. Thus $v_2\ne 0$. From the third equation of (10), we have $v_3=-\frac{1}{\theta }Bv_2$. Substituting it into the equation (11) and multiplying it form left by $v_2^*$, we can obtain

  $$\begin{aligned} v_2^*Av_2-\frac{1}{\theta }v_2^*B^TBv_2=\theta v_2^*v_2. \end{aligned}$$

  (12)

  If $\theta$ is a purely imaginary number, from (12) we have $v_2^*Av_2=0$, which leads to $v_2=0$ due to the symmetric positive definiteness of A. Then, it contradicts the fact that $v_2\ne 0$.

• (ii) If $v_2=0$, then from the third equation of (10), we know $v_3=0$. Therefore, $v_1\ne 0$. Furthermore, from the second equation of (10), we have $C^Tv_1=0$. So the first equation of (10) can be reduced to $Dv_1=\theta v_1$, which leads to $\theta >0$ due to the symmetric positive definiteness of D.

• (iii) If $v_1\ne 0$ and $v_2\ne 0$, it holds that $\text {Re}(\theta )=\frac{1}{2}v^*({\mathscr {C}}_{\alpha }+{\mathscr {C}}_{\alpha }^T)v$ with

  $$\begin{aligned} \begin{aligned}&\frac{1}{2}v^*({\mathscr {C}}_{\alpha }+{\mathscr {C}}_{\alpha }^T)v\\&\quad = v_1^*(D+\frac{1}{\alpha ^2}CAC^T)v_1+\frac{1}{2\alpha ^2}v_1^*C(A^2-B^TB)v_2+\frac{1}{2\alpha ^2}v_1^*CAB^Tv_3\\&\qquad +\frac{1}{2\alpha ^2}v_2^*(A^2-B^TB)C^Tv_1+v_2^*Av_2+\frac{1}{2\alpha ^2}v_3^*BAC^Tv_1 \\&\quad = v_1^*Dv_1+v_2^*Av_2+\frac{1}{2\alpha ^2}v_1^*CA(C^Tv_1+Av_2+B^Tv_3)\\&\qquad +\frac{1}{2\alpha ^2}(v_1^*C+v_2^*A+v_3^*B)AC^Tv_1-\frac{1}{2\alpha ^2}(v_1^*CB^TBv_2+v_2^*B^TBC^Tv_1). \\ \end{aligned} \end{aligned}$$

  Then, based on the second and third equations of (10), it further leads to

  $$\begin{aligned} \text {Re}(\theta )= & {} v_1^*Dv_1+v_2^*Av_2+\frac{\theta }{2\alpha ^2}v_1^*CAv_2+\frac{{\bar{\theta }}}{2\alpha ^2}v_2^*AC^Tv_1\\&+\frac{\theta }{2\alpha ^2}v_1^*CB^Tv_3+\frac{{\bar{\theta }}}{2\alpha ^2}v_3^*BC^Tv_1 \\= & {} v_1^*Dv_1+v_2^*Av_2+\frac{\theta }{2\alpha ^2}v_1^*C(A v_2+B^Tv_3) +\frac{{\bar{\theta }}}{2\alpha ^2}(v_2^*A+v_3^*B)C^Tv_1\\= & {} v_1^*Dv_1+v_2^*Av_2+\frac{\theta }{2\alpha ^2}v_1^*C(\theta v_2-C^Tv_1) +\frac{{\bar{\theta }}}{2\alpha ^2}({\bar{\theta }}v_2^*-v_1^*C)C^Tv_1\\= & {} v_1^*Dv_1+v_2^*Av_2+\frac{\theta ^2}{2\alpha ^2}v_1^*Cv_2+\frac{{\bar{\theta }}^2}{2\alpha ^2}v_2^*C^Tv_1 -\frac{\text {Re}(\theta )}{\alpha ^2}v_1^*CC^Tv_1. \end{aligned}$$

  If $\text {Re}(\theta )=0$, then

  $$\begin{aligned} v_1^*Dv_1+v_2^*Av_2+\frac{\theta ^2}{\alpha ^2}\text {Re}(v_2^*C^Tv_1) = 0 \quad \text {and} \quad \theta ^2<0. \end{aligned}$$

  Thus, it holds that $\text {Re}(v_2^*C^Tv_1)>0$. Moreover, from the second and third equations of (10), we have

  $$\begin{aligned} C^Tv_1+Av_2-\frac{1}{\theta }B^TBv=\theta v_2. \end{aligned}$$

  Then, we can verify that

  $$\begin{aligned} v_2^*C^Tv_1=\theta v_2^*v_2+\frac{1}{\theta }v_2^*B^TBv_2-v_2^*Av_2. \end{aligned}$$

  If $\theta$ is a purely imaginary number, then $\text {Re}(v_2^*C^Tv_1)=-v_2^*Av_2<0$, which contradicts $\text {Re}(v_2^*C^Tv_1)>0$.

Therefore, on account of the discussions in (i), (ii) and (iii), we can obtain the conclusion that $\text {Re}(\theta )\ne 0$. $\square$

Since ${\mathscr {P}}_{\alpha }^{-1}{\mathscr {A}}=I-{\mathscr {T}}_{\alpha }$, based on the unconditionally convergent result in Theorem 1, we can obtain the following eigenvalue distribution results for the APSS preconditioned matrix ${\mathscr {P}}_{\alpha }^{-1}{\mathscr {A}}$.

Theorem 2

Assume that the conditions of Theorem 1 are satisfied. Then the eigenvalues of the APSS preconditioned matrix ${\mathscr {P}}_{\alpha }^{-1}{\mathscr {A}}$ are located in the unit circle centered at (1, 0).

4 The relaxed APSS preconditioner

Following the construction ideas in [3, 6] for the relaxed dimensional factorization (RDF) preconditioners, to improve the performance of the APSS preconditioner (6), we propose a relaxed APSS (RAPSS) preconditioner, which is of the form

$$\begin{aligned} {\widetilde{\mathscr {P}}}_{\alpha } = \frac{1}{\alpha } \begin{bmatrix} D&-C&0 \\ C^T&\alpha I&0 \\ 0&0&\alpha I \end{bmatrix} \begin{bmatrix} \alpha I&0&0 \\ 0&A&B^T \\ 0&-B&\alpha I \end{bmatrix} = \begin{bmatrix} D&-\frac{1}{\alpha }CA&-\frac{1}{\alpha }CB^T \\ C^T&A&B^T \\ 0&-B&\alpha I \end{bmatrix}. \end{aligned}$$

(13)

Remark 1

For saddle point problem of the following form:

$$\begin{aligned} \begin{bmatrix} A_1&0&B_1^T \\ 0&A_2&B_2^T \\ -B_1&-B_2^T&0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} f \\ g \\ h \end{bmatrix}, \end{aligned}$$

(14)

which arises from the numerical discretization of the incompressible Navier-Stokes equations, a dimensional splitting (DS) preconditioner is designed in [5]:

$$\begin{aligned} {\mathscr {P}}_{\text {DS}} = \frac{1}{2\alpha } \begin{bmatrix} \alpha I + A_1&0&B_1^T \\ 0&\alpha I&0 \\ -B_1&0&\alpha I \end{bmatrix} \begin{bmatrix} \alpha I&0&0 \\ 0&\alpha I + A_2&B_2^T \\ 0&-B_2^T&0 \end{bmatrix}, \end{aligned}$$

(15)

following from a suitable alternating direction DS iteration scheme for solving the saddle point problem (14). As the factor $\frac{1}{2\alpha }$ of the DS preconditioner (15) has no effect on the corresponding preconditioned system, it can be replaced by $\frac{1}{\alpha }$. Then, by dropping the matrices $\alpha I$ in the blocks $\alpha I + A_1$ and $\alpha I + A_2$ of the DS preconditioner (15), a more efficient RDF preconditioner is introduced in [6]:

$$\begin{aligned} {\mathscr {P}}_{\text {RDF}} = \frac{1}{\alpha } \begin{bmatrix} A_1&0&B_1^T \\ 0&\alpha I&0 \\ -B_1&0&\alpha I \end{bmatrix} \begin{bmatrix} \alpha I&0&0 \\ 0&A_2&B_2^T \\ 0&-B_2^T&\alpha I \end{bmatrix}, \end{aligned}$$

(16)

which can be view as an improved relaxed variant of the DS preconditioner in [6]. See also [3] for the RDF preconditioner for block four-by-four saddle point problems with applications to hemodynamics.

In accordance to the discussions in Sect. 2, based on the decompositions:

$$\begin{aligned} \begin{bmatrix} D&-C&0 \\ C^T&\alpha I&0 \\ 0&0&\alpha I \end{bmatrix} = \begin{bmatrix} D+\frac{1}{\alpha }CC^T&-C&0 \\ 0&\alpha I&0 \\ 0&0&\alpha I \end{bmatrix} \begin{bmatrix} I&0&0 \\ \frac{1}{\alpha }C^T&I&0 \\ 0&0&I \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} \begin{bmatrix} \alpha I&0&0 \\ 0&A&B^T \\ 0&-B&\alpha I \end{bmatrix} = \begin{bmatrix} \alpha I&0&0 \\ 0&A+\frac{1}{\alpha }B^TB&B^T \\ 0&0&\alpha I \end{bmatrix} \begin{bmatrix} I&0&0 \\ 0&I&0 \\ 0&-\frac{1}{\alpha }B&I \end{bmatrix}, \end{aligned}$$

we can obtain the following algorithmic implementation for the RAPSS preconditioner (13).

Algorithm 2

Solution of $\widetilde{{\mathscr {P}}}_{\alpha }w=r$ with $r=(r_1^T,r_2^T,r_3^T)^T$, $w=(w_1^T,w_2^T,w_3^T)^T$ and $r_1,w_1\in {\mathbb {R}}^p$, $r_2,w_2\in {\mathbb {R}}^n$, $r_3,w_3\in {\mathbb {R}}^m$, from the following steps:

• (1) solve $w_1$ from $(D+\frac{1}{\alpha }CC^T)w_1 = r_1+\frac{1}{\alpha }Cr_2$;

• (2) solve $w_2$ from $(A+\frac{1}{\alpha }B^TB)w_2 = r_2-C^Tw_1-\frac{1}{\alpha }B^Tr_3$;

• (3) compute $w_3=\frac{1}{\alpha }(r_3+Bw_2)$.

For the RAPSS preconditioned matrix $\widetilde{{\mathscr {P}}}_{\alpha }^{-1}{\mathscr {A}}$, we have the following eigenvalue distribution results.

Theorem 3

Assume that the conditions of Theorem 1 are satisfied. Then the eigenvalues of the RAPSS preconditioned matrix $\widetilde{{\mathscr {P}}}_{\alpha }^{-1}{\mathscr {A}}$ are given by 1 with multiplicity at least p. The remaining eigenvalues are of the form $\mu$ or $1+\mu$ with $\mu$ being an eigenvalue of the matrix

$$\begin{aligned} Z_{\alpha } = \frac{1}{\alpha }S_{{\hat{D}}}-S_{{\hat{D}}}{\hat{A}}^{-1}-\frac{1}{\alpha }BB^T{\hat{A}}^{-1}, \end{aligned}$$

where ${\hat{A}}=A+\frac{1}{\alpha }B^TB$, ${\hat{D}}=D+\frac{1}{\alpha }CC^T$ and $S_{{\hat{D}}}=C^T{\hat{D}}^{-1}C$.

Proof

By direct calculations, we can verify that

$$\begin{aligned} {\widetilde{\mathscr {P}}}_{\alpha }^{-1} = \alpha \begin{bmatrix} \frac{1}{\alpha }I&0&0 \\ 0&{\hat{A}}^{-1}&-\frac{1}{\alpha }{\hat{A}}^{-1}B^T \\ 0&\frac{1}{\alpha }B{\hat{A}}^{-1}&\frac{1}{\alpha }I-\frac{1}{\alpha ^2}S_{{\hat{A}}} \end{bmatrix} \begin{bmatrix} {\hat{D}}^{-1}&\frac{1}{\alpha }{\hat{D}}^{-1}C&0 \\ -\frac{1}{\alpha }C^T{\hat{D}}^{-1}&\frac{1}{\alpha }I-\frac{1}{\alpha ^2}S_{{\hat{D}}}&0 \\ 0&0&\frac{1}{\alpha }I \end{bmatrix} \end{aligned}$$

(17)

with ${\hat{A}}=A+\frac{1}{\alpha }B^TB$, $S_{{\hat{A}}}=B{\hat{A}}^{-1}C^T$, ${\hat{D}}=D+\frac{1}{\alpha }CC^T$ and $S_{{\hat{D}}}=C^T{\hat{D}}^{-1}C$. Moreover, we know that ${\mathscr {A}}=\widetilde{{\mathscr {P}}}_{\alpha }-\widetilde{{\mathscr {R}}}_{\alpha }$ with

$$\begin{aligned} {\widetilde{\mathscr {R}}}_{\alpha } = \begin{bmatrix} 0&C-\frac{1}{\alpha }CA&-\frac{1}{\alpha }CB^T \\ 0&0&0 \\ 0&0&\alpha I \end{bmatrix}. \end{aligned}$$

(18)

Then, based on (17) and (18), we have $\widetilde{{\mathscr {P}}}_{\alpha }^{-1}{\mathscr {A}}=I-\widetilde{{\mathscr {P}}}_{\alpha }^{-1}\widetilde{{\mathscr {R}}}_{\alpha }$ with

$$\begin{aligned} \begin{aligned} \widetilde{{\mathscr {P}}}_{\alpha }^{-1}\widetilde{{\mathscr {R}}}_{\alpha }&= \begin{bmatrix} \frac{1}{\alpha }I&0&0 \\ 0&{\hat{A}}^{-1}&-\frac{1}{\alpha }{\hat{A}}^{-1}B^T \\ 0&\frac{1}{\alpha }B{\hat{A}}^{-1} \quad&\frac{1}{\alpha }I-\frac{1}{\alpha ^2}S_{{\hat{A}}} \end{bmatrix} \begin{bmatrix} 0&\alpha {\hat{D}}^{-1}C-{\hat{D}}^{-1}CA&-{\hat{D}}^{-1}CB^T \\ 0&-C^T{\hat{D}}^{-1}C+\frac{1}{\alpha }C^T{\hat{D}}^{-1}CA \quad&\frac{1}{\alpha }C^T{\hat{D}}^{-1}CB^T \\ 0&0&\alpha I \end{bmatrix} \\ ~&= \begin{bmatrix} 0&{\hat{D}}^{-1}C-\frac{1}{\alpha }{\hat{D}}^{-1}CA&-\frac{1}{\alpha }{\hat{D}}^{-1}CB^T \\ 0&-{\hat{A}}^{-1}S_{{\hat{D}}}+\frac{1}{\alpha }{\hat{A}}^{-1}S_{{\hat{D}}}A&\frac{1}{\alpha }{\hat{A}}^{-1}S_{{\hat{D}}}B^T-{\hat{A}}^{-1}B^T \\ 0&-\frac{1}{\alpha }B{\hat{A}}^{-1}S_{{\hat{D}}}+\frac{1}{\alpha ^2}B{\hat{A}}^{-1}S_{{\hat{D}}}A \quad&I-\frac{1}{\alpha }S_{{\hat{A}}}+\frac{1}{\alpha ^2}B{\hat{A}}^{-1}S_{{\hat{D}}}B^T \end{bmatrix}. \end{aligned} \end{aligned}$$

We can verify that

$$\begin{aligned} \begin{bmatrix} -{\hat{A}}^{-1}S_{{\hat{D}}}+\frac{1}{\alpha }{\hat{A}}^{-1}S_{{\hat{D}}}A&\frac{1}{\alpha }{\hat{A}}^{-1}S_{{\hat{D}}}B^T-{\hat{A}}^{-1}B^T \\ -\frac{1}{\alpha }B{\hat{A}}^{-1}S_{{\hat{D}}}+\frac{1}{\alpha ^2}B{\hat{A}}^{-1}S_{{\hat{D}}}A \quad&I-\frac{1}{\alpha }S_{{\hat{A}}}+\frac{1}{\alpha ^2}B{\hat{A}}^{-1}S_{{\hat{D}}}B^T \end{bmatrix} = \begin{bmatrix} 0&0 \\ 0&I \end{bmatrix} +{\hat{Z}}_{\alpha } \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} {\hat{Z}}_{\alpha }&= \begin{bmatrix} -{\hat{A}}^{-1}S_{{\hat{D}}}+\frac{1}{\alpha }{\hat{A}}^{-1}S_{{\hat{D}}}A&\frac{1}{\alpha }{\hat{A}}^{-1}S_{{\hat{D}}}B^T-{\hat{A}}^{-1}B^T \\ -\frac{1}{\alpha }B{\hat{A}}^{-1}S_{{\hat{D}}}+\frac{1}{\alpha ^2}B{\hat{A}}^{-1}S_{{\hat{D}}}A \quad&-\frac{1}{\alpha }S_{{\hat{A}}}+\frac{1}{\alpha ^2}B{\hat{A}}^{-1}S_{{\hat{D}}}B^T \end{bmatrix}\\ ~&= \begin{bmatrix} -{\hat{A}}^{-1} \\ -\frac{1}{\alpha }B{\hat{A}}^{-1} \end{bmatrix} \begin{bmatrix} S_{{\hat{D}}}-\frac{1}{\alpha }S_{{\hat{D}}}A \quad&-\frac{1}{\alpha }S_{{\hat{D}}}B^T+B^T \end{bmatrix} \equiv XY \end{aligned} \end{aligned}$$

and $Z_{\alpha }=YX$. Thus $Z_{\alpha }$ and ${\hat{Z}}_{\alpha }$ have same nonzero eigenvalues. Then, it directly leads to the eigenvalue distribution results in this theorem. $\square$

5 Numerical experiments

In this section, we use the double saddle point linear systems arising from the solution of liquid crystal problem [1, 12] to test the performance of the APSS and RAPSS preconditioners to accelerate the GMRES method [16] under right preconditioning. All the arising sublinear systems in Algorithms 1 and 2 are solved by Cholesky factorization in combination with an approximate minimum degree (AMD) reordering. The right hand side of the related double saddle point problem is chosen such that the exact solution is the vector with all its element being ones or the vector with randomly generated elements, which corresponds to ones(.,1) or rand(.,1) in matlab notations. Initial guesses of the preconditioned GMRES (PGMRES) methods are the zero vectors and the stopping tolerances for the relative error norm of the residuals of the tested PGMRES methods, denoted as RES, are set to be tol, i.e.,

$$\begin{aligned} \text {RES} = \frac{\Vert b-{\mathscr {A}}u^{(k)}\Vert _2}{\Vert b\Vert _2}<tol \end{aligned}$$

with $u^{(k)}$ the current approximation solution. Moreover, the relative errors of the computed approximations, denoted as ERR, i.e.,

$$\begin{aligned} \text {ERR} = \frac{\Vert u^{(k)}-u^*\Vert _2}{\Vert u^{*}\Vert _2} \end{aligned}$$

are also reported with $u^*$ the initially known exact solution.

We consider the solution of the liquid crystal director model, which involves the minimization of the the following free energy functional:

$$\begin{aligned} {\mathscr {F}}[u,v,w,U] = \frac{1}{2}\int _{0}^{1}\Big [(u_z^2+v_z^2+w_z^2)-\eta ^2(\beta +w^2)U_z^2\Big ]dz, \end{aligned}$$

(19)

where $\eta$ and $\beta$ are given positive parameters, u, v, w and U are functions of the space variable $z\in [0,1]$ satisfying suitable end-point conditions, $u_z$, $v_z$, $w_z$ and $U_z$ denote the first order derivation of the related functions with respective to z. By discretizing with uniform piecewise linear finite element with step size $h=\frac{1}{k+1}$, we minimize the functional (19) under the unit vector constraint. Then we use the Lagrange multiplier method to solve the discretized minimization problems, which involves the solution of a liner system with Hessian matrix at each Newton iteration. The related Hessian matrix has the double saddle point structure of the form (1) with $n=3k$ and $m=p=k$. In our numerical experiments, we choose $\eta =0.5\eta _c$ and $\beta =0.5$ with $\eta _c\thickapprox 2.721$, which is known as the critical switching value. For more details about this model, see [1, 12].

In Table 1, we list numerical results of the APSS and RAPSS preconditioned GMRES methods with stopping tolerance $tol=10^{-8}$. Problems of different sizes are tested in view of elapsed CPU times (denoted as “CPU”) and iteration steps (denoted as “IT”) and relative errors with respect to the exact solutions (denoted as “ERR”). Here, the right hand side of the related double saddle point problems are chosen as the vectors such that their exact solutions are the vector with all their elements being ones. For comparison, we also test the GMRES method accelerated by the following block triangular (BT) preconditioners [1, 2]:

$$\begin{aligned} {\mathscr {P}}_{\text {BT}\_\text {I}} = \begin{bmatrix} A&B^T&C^T \\ 0&-BA^{-1}B^T&-BA^{-1}C^T \\ 0&0&-(D+CA^{-1}C^T) \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} {\mathscr {P}}_{\text {BT}\_\text {II}} = \begin{bmatrix} A&B^T&C^T \\ \gamma B&0&0 \\ 0&0&-D \end{bmatrix} \end{aligned}$$

with $\gamma$ being a real parameter. Both of them are used as the right preconditioners of the GMRES method for solving the double saddle point problem of the form (1). The related numerical results are listed in Table 2. Moreover, we also list in Table 2 the numerical results of the GMRES method without preconditioning. For the implementation of the two BT preconditioners, in addition to the solutions of sublinear systems with matrices A and D, it also involves the solutions of those with matrices $BA^{-1}B^T$ and $D+CA^{-1}C^T$. As both $BA^{-1}B^T$ and $D+CA^{-1}C^T$ are full matrices, it is generally not practical, especially for large problems, to form them explicitly. Thus in Table 2, we only list the numerical results of the BT preconditioned GMRES methods for relatively smaller problems. Note that, following the strategies in [1, 2], we can also implement the BT preconditioned GMRES methods inexactly by using inner solvers, such as the PCG method, for solving the sublinear systems with matrices $BA^{-1}B^T$ and $D+CA^{-1}C^T$, which perform well for larger problems; see the numerical results in Table 3. Here, “inexactly” means that we should use the flexible GMRES (FGMRES) method [14]. In accordance to [1, 2], for the involved inner PCG methods, $BAB^T$ and $CD_A^{-1}C^T+D$ are used, respectively, as the preconditioners of $BA^{-1}B^T$ and $CA^{-1}C^T+D$, where $D_A$ is the diagonal part of A. Note that, as B has (nearly) orthogonal rows, $BAB^T$ can be used as a good approximation of $BA^{-1}B^T$; see the discussions in the parts of numerical experiments of [1, 2]. Moreover, the application of the preconditioner $CD_A^{-1}C^T+D$ is accomplished via a sparse Cholesky factorization with AMD recording. As for the stopping tolerance of the inner PCG solvers, it is $10^{-3}$ for systems with $BA^{-1}B^T$ and $10^{-1}$ for systems with $CD_A^{-1}C^T+D$. In Table 3, the average numbers to the nearest integers of the inner PCG iteration are displayed in brackets after the numbers of the related outer FGMRES iteration. Especially, for the BT-I preconditioned FGMRES method, the two inner PCG iteration numbers in the brackets are sequentially corresponding to the inner systems with matrices $BA^{-1}B^T$ and $CA^{-1}C^T+D$, respectively.

Table 1 Numerical results of the APSS and RAPSS preconditioned GMRES methods with exact inner solvers (the exact solution is the vector with all its element being ones, $tol=10^{-8}$)

Table 2 Numerical results of the GMRES method and the BT preconditioned GMRES methods with exact inner solvers (the exact solution is the vector with all its element being ones, $tol=10^{-8}$)

Table 3 Numerical results of the the BT preconditioned FGMRES methods with inexact inner solvers (the exact solution is the vector with all its element being ones, $tol=10^{-8}$)

From the numerical results in Tables 1, 2 and 3, we see that all the preconditioners improve the performance of the GMRES method significantly. The RAPSS preconditioned GMRES method outperforms the APSS preconditioned case in view of both elapsed CPU times and iteration steps. However, when the iteration parameter $\alpha$ is small, the differences between the two methods are not significant. Compared with the GMRES methods accelerated by the two BT preconditioners, the APSS and RAPSS preconditioned GMRES methods may have no advantages with respect to iteration steps and relative errors of the exact solutions. However, the APSS and RAPSS preconditioned GMRES methods are less time consuming than the BT preconditioned ones under exact implementations for the solutions of inner systems with matrices $BA^{-1}B^T$ and $CA^{-1}C^T+D$. Nevertheless, from the numerical results in Table 3, we observe that, by using inexact inner PCG solvers, the two BT preconditioned FGMRES methods exhibit fast and stable performance.

In Fig. 1, we plot the eigenvalue distributions of the original coefficient matrix and the APSS and RAPSS preconditioned matrices with $\alpha =0.01$. Here, we test the case with problem size of 5115. From this figure, it is easy to observe that the APSS and RAPSS preconditioners improve the eigenvalue distribution of the original coefficient matrix greatly. Moreover, the two preconditioned matrices have tight spectrums, which lead to stable numerical performances; see the numerical results in Table 1. It worths to indicate that the two BT preconditioners ${\mathscr {P}}_{\text {BT}\_\text {I}}$ and ${\mathscr {P}}_{\text {BT}\_\text {II}}$ can lead much nicer eigenvalue distributions than the APSS and RAPSS preconditioners; see, for example, the eigenvalue distributions depicted in Fig. 2 of [1]. Note that it is not difficult to imagine the better eigenvalue distribution results corresponding to the BT_II preconditioned matrices, as they resemble better to the coefficient matrix than the APSS and RAPSS preconditioners.

Fig. 1

Eigenvalue distributions of the original coefficient matrix and the APSS and RAPSS preconditioned matrices with $\alpha =0.01$

Fig. 2

Iterative plots of the APSS and RAPSS preconditioned GMRES methods with different $\alpha$

Fig. 3

Iterative plots of GMRES and the BT$\_$I and BT$\_$II preconditioned GMRES methods with different $\gamma$

In Fig. 2, we plot the convergence history of the the APSS and RAPSS preconditioned GMRES methods with iteration parameter $\alpha$. Here, we test the case with problem size of 20475, the exact solution being the vector of ones and the stopping tolerance being $\delta =10^{-8}$. For comparison, the corresponding plots for the GMRES method without preconditioning, the BT-I preconditioned GMRES method and the BT-II preconditioned GMRES method with different iteration parameter $\gamma$ are depicted in Fig. 3. From these figures, it can be observed that all preconditioners improve the performance of the GMRES method dramatically, which is in accordance with the numerical results in Tables 1, 2 and 3.

For comparison, we list the numerical results of the tested methods corresponding to the cases with randomly generated exact solutions in Tables 4 and 5 for stopping tolerances $tol=10^{-8}$ and $tol=10^{-10}$, respectively. Here, we test the APSS and RAPSS preconditioned GMRES methods with $\alpha =0.01$ and the BT-I and BT-II preconditioned FGMRES methods with $\gamma =1$ for the BT-II preconditioned case. It is observed that all tested methods perform well with respect to execution times and iteration steps. But, when the stopping tolerance tol is not small enough, the computed solutions by all tested methods are far from the initially given exact solutions, especially for the cases with large problem sizes. However, with the decreasing of tol, the relative errors of the computed solutions decrease, especially, those obtained by the two BT preconditioned FGMRES methods show significant improvements.

Table 4 Numerical results of the APSS, RAPSS and BT preconditioned GMRES methods (the exact solution is the vector with randomly generated elements, $tol=10^{-8}$)

Table 5 Numerical results of the APSS, RAPSS and BT preconditioned GMRES methods (the exact solution is the vector with randomly generated elements, $tol=10^{-10}$)

In summary, when used for accelerating the GMRES method to solve the double saddle point linear systems arising from the solution of the liquid crystal problem, the APSS and RAPSS preconditioners improve the performance of the GMRES method significantly. Though they are less efficient compared with the problem specific block triangular preconditioner in [1] within practical inexact implementation, especially in view of the accuracies of the computed solutions, their performances are satisfactory in view of iteration steps and elapsed CPU times. In the future, it is crucial to consider practical parameter choice strategies and efficient techniques to obtain more accurate approximations for the APSS and RAPSS preconditioners. Moreover, it is also interesting to test the performance of the two preconditioners to accelerate the GMRES method for solving the double saddle point problems arising from other application backgrounds.

6 Conclusions

In this paper, based on a positive semidefinite splitting of its coefficient matrix, an alternating semidefinite splitting preconditioner (APSS) is constructed for solving the double saddle point problem. Convergence analysis of the corresponding APSS iterative method shows that it can converge to the unique solution of the double saddle point problem unconditionally. Moreover, an useful relaxed variant of the APSS preconditioner, abbreviated as, RAPSS is established, which improves the APSS preconditioner in view of eigenvalue distribution of the preconditioned matrix and numerical performance of the preconditioned GMRES method. Numerical experiments for a liquid crystal model problem shows the efficiency of the proposed APSS and RAPSS preconditioners to accelerate the GMRES method for solving double saddle point problems. Comparison with the two block triangular (BT) preconditioners in [1, 2] indicates that the proposed APSS and RAPSS preconditioners are comparable with (though not really better than) them within Krylov subspace acceleration.