Introduction

To date, spaceborne telescope boom lengths have rarely exceeded 15 m, and achieving much greater separation distances in space between optics and detectors will likely require precise formation flying (PFF). The European Space Agency’s Proba-3 [1, 2], currently scheduled to be launched in 2022, attempts such a feat, with a coronograph spacecraft separated from a telescope spacecraft by a distance of ≈ 150 m in high Earth orbit. The Sun-coronograph-telescope alignment is planned to last about six hours during each \(\sim \)day-long length of the highly eccentric orbit. Besides an occulter-telescope pair, there are several other possible applications for such a concept. For example in the X-ray regime, the optics can be a Fresnel Zone Plate [3], a focusing optics mirror (the longer focal length enables shallower incidence angle on the mirrors, allowing higher energies to be reached), or a coded-mask or (rotating) grid allowing e.g. higher angular resolutions.

We are interested in the case of the Sun as a target, with the Optics spacecraft and Detector spacecraft in a “scopocentric” orbit around it (Fig.1), and we will use the term “Precise Formation Flying,” or PFF, to refer to the combination of Target-Optics-Detector alignment maintenance and Optics-Detector distance maintenance. This paper strives to make the case for scientists requiring large optics-to-detectors distances for the next generation of space instrumention that the time is nigh, and that a solar application is probably an easy first step.

Fig. 1
figure 1

Diagram and notations (here, a circular orbit). Throughout the orbit, target, Optics spacecraft and Detector spacecraft must remain aligned at all times, and the Optics-Detector separation must remain constant

Full size image

Section “Differential Accelerations” details the various forces acting on each spacecraft, Section “Simulations” describes the simulations done to confirm the theory, Section “Discussion” discusses the results and their possible applications with current or soon-to-be available launch capabilities for CubeSats and SmallSats. Finally, Section “Conclusions” summarizes and concludes this work.

Differential Accelerations

To maintain formation, either the Optics spacecraft or the Detector spacecraft must fight against the (often minute, but with long-term consequences) differences in the total accelerations they experience (solar radiation pressure, orbital/tidal effects from the orbited body/target, and tidal effects from nearby celestial bodies).

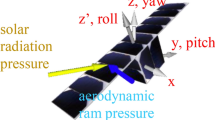
We will refer to the spacecraft closest to the the target as “Optics spacecraft”, and the spacecraft furthest away as “Detector spacecraft”. In many cases, the Optics spacecraft can be thought of as the spacecraft carrying the optics of the telescope, and the Detector spacecraft as the one carrying the detectors. Obviously, there can be variations: the Optics spacecraft can carry an occulter while the Detector spacecraft carries both optics and detectors (e.g. Proba-3). We present here simple analytical, acceleration budgets, mostly in the form of differential accelerations \(\vec {\delta a_{D}}\) that the Detector spacecraft must exert to maintain the formation. It has radial component δaD,r along the target-optics-detector axis, and tangential component δaD,t perpendicular to it, in the orbital plane. A negative δaD,r hence implies a sunward thrust requirement by the Detector spacecraft (or anti-sunward by the Optics spacecraft).

Most of the following is applicable when the target is any celestial body that can be orbited (e.g. a planet), but we will concentrate on the case of the Sun as a target. We will assume that the Optics spacecraft is in keplerian orbit, and that the Detector spacecraft does all the necessary thrusting to maintain the Target-Optics-Detector alignment and Optics-Detector distance throughout the orbit. The calculations and conclusions are of course almost completely interchangeable between the two spacecrafts, though considerations such as having a thruster in the optics path might constrain specific implementations.

Section “Thrust the Detector Spacecraft must Exert to Sustain its non-Keplerian (“NK”) Orbit” deals with compensating for the non-keplerian orbit of the Detector spacecraft, Section “Differential Acceleration due to Tidal Effects from Other Celestial Bodies” deals with compensating for the disruptive effects from other bodies than the one being orbited, and Section “Differential Acceleration due to Solar Radiation Pressure” deals with the effects of radiation pressure (which dominate when the formation-flying telescope is sufficiently far away from all celestial bodies). Finally, Section “Differential Acceleration due to Drag in Ram Direction” deals with interplanetary and atmospheric drags.

Thrust the Detector Spacecraft must Exert to Sustain its non-Keplerian (“NK”) Orbit

Linearized relative equation of motions in circular orbits have been presented by Clohessy-Wiltshire [4] for the case of circular orbits. We will jump directly to the elliptical case, using the linearized equations from [5] (or see Section 5.6 of [6]):

$$ \begin{array}{@{}rcl@{}} \delta a_{D,r} &=& \ddot x - 2 \dot \theta_{O} \dot y - \ddot \theta_{O} y - \left( {\dot\theta_{O}^{2}} + 2\frac{GM}{{r_{O}^{3}}} \right) x \end{array} $$
(1)
$$ \begin{array}{@{}rcl@{}} \delta a_{D,t} &=& \ddot y + 2 \dot \theta_{O} \dot x + \ddot \theta_{O} x - \left( {\dot \theta_{O}^{2}} + 2\frac{GM}{{r_{O}^{3}}} \right) y \end{array} $$
(2)
$$ \begin{array}{@{}rcl@{}} \delta a_{D,n} &=& \ddot z + \frac{GM}{{r_{O}^{3}}} z \end{array} $$
(3)

Where x, y, z are the radial, tangential, and normal components of the Detector spacecraft relative position with respect to the Optics spacecraft, and aD the thrust (acceleration) delivered by the Detector spacecraft. The Optics spacecraft is in Keplerian orbit, hence \({r_{O}^{2}} \dot \theta _{O} = h\), with \(h=\sqrt {GM a_{O} (1-{e_{O}^{2}})}\) the (constant) angular momentum, aO the semi-major axis, and eO the eccentricity. To maintain the Target-Optics-Detector alignment and Optics-Detector distance, \(\ddot x \equiv \ddot y \equiv \ddot z \equiv \dot x \equiv \dot y \equiv \dot z \equiv y \equiv z \equiv 0\), and x is a constant kept at Δr, leading to the thrust requirement on the Detector spacecraft:

$$ \begin{array}{@{}rcl@{}} \delta a_{D,r}^{\text{NK}} &=& -\frac{GM}{{r_{O}^{3}}} \left( 2 + \frac{r_{O} (1+e_{O} \cos \theta_{O})^{2}}{a_{O} (1-{e_{O}^{2}}) } \right) {\Delta} r \end{array} $$
(4)
$$ \begin{array}{@{}rcl@{}} &=& -\frac{GM}{{r_{O}^{3}}} {\Delta} r \left( \frac{1+e_{O} \cos \theta_{O}}{1-{e_{O}^{2}}} \right)^{3} (3+e_{O} \cos \theta_{O}) \end{array} $$
(5)
$$ \begin{array}{@{}rcl@{}} \delta a_{D,t}^{\text{NK}} &=& -2\frac{GM}{{r_{O}^{3}}} {\Delta} r e_{O} \sin \theta_{O} \end{array} $$
(6)

If the Detector spacecraft applies the above thrusts, then it will orbit the target with the same period as the Optics spacecraft, but Δr further away, and preserving the Target-Optics-Detector alignment. The Detector spacecraft orbit is faster than if it were freely-coasting. In the circular (eO = 0) case, \(\delta a_{D,r}^{\text {NK}}\) = -1.2× 10− 11 m/s2 = -0.38 mm/s/yr for aO= 1 AU, M = Msun, and Δr= 100 m.

The above equations are valid for Δr ≪ rO. As some applications requiring extremely large spacecraft separations are not inconceivable, though certainly technologically extremely difficult (e.g. a Fresnel lens for γ-rays observations), we also present exact solutions in Appendix A that are valid for any Δr < rO.

Figure 2 displays the orbital variation of the required accelerations for the case aO= 1 AU, eO= 0.1, and Δr= 100 m, compared to the circular (eO = 0) case. Figure 3 displays the minimum, average, and maximum accelerations for various eccentricities. Scaling for other parameters is simply given by the above equations. Equation (5) is maximum (in amplitude) at periapsis (𝜃O = 0), taking the value \(-GM\frac {{\Delta } r}{{p_{O}^{3}}}(1+e_{O})^{3} (3+e_{O})\), with the semilactus rectum of the Optics spacecraft \(p_{O}=a_{O}(1-{e_{O}^{2}})\). Equation (5) is minimum (in amplitude) at apoapsis (𝜃O = π), taking the value \(-GM\frac {{\Delta } r}{{p_{O}^{3}}}(1-e_{O})^{3} (3-e_{O})\). The minimum/maximum of Equation (6) are the same in absolute value, and found at \(\theta =\arccos (\frac {\sqrt {48e^{2}+1}-1}{8e})\) and \(\theta =2\pi -\arccos (\frac {\sqrt {48e^{2}+1}-1}{8e})\).

Fig. 2
figure 2

Radial and tangential accelerations required by Detector spacecraft to maintain the Target-Optics-Detector alignment, due to orbital eccentricity only. The dashed line denotes the time-average of δaD,r over a full orbit

Full size image
Fig. 3
figure 3

Maximal, minimal, and time-averaged radial and tangential acceleration needed to compensate for elliptical orbit of telescope, relative to circular case with same semi-major axis aO

Full size image

Generally, \(-3\frac {GM}{{r_{O}^{3}}}{\Delta } r\) (Equation (5) for eO = 0) is a good estimate for the amplitude of the tidal/orbital disruptive force for orbits with low to medium eccentricities, but also of the amplitude (though with direction varying with orbit phase) of the disruption that a telescope pointing at cosmic targets would have to overcome.

Differential Acceleration due to Tidal Effects from Other Celestial Bodies

Generally, any celestial body will exert a tidal disrupting force on the formation:

$$ \begin{array}{@{}rcl@{}} \delta a^{\text{tidal}} &=& GM\left( \frac{1}{{d_{O}^{2}}} -\frac{1}{{d_{D}^{2}}} \right) \end{array} $$
(7)
$$ \begin{array}{@{}rcl@{}} &\approx& -2 \frac{GM}{{d_{O}^{3}}} {\Delta} d_{\text{radial}} , {\Delta} d_{\text{radial}} \ll d_{O} \end{array} $$
(8)
$$ \begin{array}{@{}rcl@{}} &\approx& -1.4\times10^{-9} \left( \frac{M}{M_{Earth}}\right) \left( \frac{385 \text{Mm}}{d_{O}} \right)^{3} \left( \frac{{\Delta} d_{\text{radial}}}{100 \mathrm{m}}\right) \mathrm{[m/s^{2}]} \end{array} $$
(9)
$$ \begin{array}{@{}rcl@{}} &\approx& -44 \left( \frac{M}{M_{Earth}}\right) \left( \frac{385 \text{Mm}}{d_{O}} \right)^{3} \left( \frac{{\Delta} d_{\text{radial}}}{100 \mathrm{m}}\right) \mathrm{[mm/s/year]} \end{array} $$
(10)
$$ \begin{array}{@{}rcl@{}} &\approx& -0.25 \left( \frac{M}{M_{Sun}}\right) \left( \frac{1 \text{AU}}{d_{O}} \right)^{3} \left( \frac{{\Delta} d_{\text{radial}}}{100 \mathrm{m}}\right) \mathrm{[mm/s/year]} \end{array} $$
(11)

Where dO,D are the distances between the disruptive body and the Optics spacecraft and Detector spacecraft, and where Δdradial is the difference in radial distance to the disrupting mass (positive corresponding to the Optics spacecraft being closest). We here deliberately used the notation “d” instead of “r” to emphasize that it is not the distance to the telescope orbit’s center of mass. Note that the tidal disruptive effects due to the orbited target are already included in the results \(\delta a_{D}^{\text {NK}}\) of “Thrust the Detector Spacecraft must Exert to Sustain its non-Keplerian (“NK”) Orbit”.

Differential Acceleration due to Solar Radiation Pressure

The formation is influenced by the difference in solar radiation pressure experienced by the Optics spacecraft and the Detector spacecraft. In fact, far from celestial bodies, it is often the dominant effect disrupting the telescope formation.

The radiation pressure on a surface of cross-sectional area A is given by:

$$ F^{\text{RP}} = m \cdot a^{\text{RP}} = \frac{1}{c} \left( \frac{L}{4\pi D^{2}}\right) A \cdot (1+\alpha), $$
(12)

where D is the distance to the Sun, L the solar luminosity, and α the albedo coefficient. For clarity, α (as well as the squared cosine of the incidence angle) are thereon assumed folded in A. If the target is the Sun, the difference in solar pressure between distances rO and rD is compensated by:

$$ \begin{array}{@{}rcl@{}} \delta a_{D,r}^{\text{RP}} &=& \frac{L}{4\pi c} \left( \frac{A_{O}}{m_{O}} \frac{1}{{r_{O}^{2}}} - \frac{A_{D}}{m_{D}} \frac{1}{{r_{D}^{2}}} \right) \end{array} $$
(13)
$$ \begin{array}{@{}rcl@{}} &=& \frac{L}{4\pi {r_{O}^{2}} c} \left( \frac{A_{O}}{m_{O}} - \frac{A_{D}}{m_{D}} \frac{{r_{O}^{2}}}{{r_{D}^{2}}} \right) \end{array} $$
(14)
$$ \begin{array}{@{}rcl@{}} &=& \frac{L}{4\pi {r_{O}^{2}} c} {\Delta}\frac{1}{b} \end{array} $$
(15)
$$ \begin{array}{@{}rcl@{}} &=& 4.6\times10^{-8} \left( \frac{1 \text{AU}}{r_{O}} \right)^{2} \left( \frac{{\Delta}\frac{1}{b}}{1 \text{dm}^{2}\text{/kg}} \right) \mathrm{[m/s^{2}]} \end{array} $$
(16)
$$ \begin{array}{@{}rcl@{}} &=& 1.44 \left( \frac{1 \text{AU}}{r_{O}} \right)^{2} \left( \frac{{\Delta}\frac{1}{b}}{1 \text{dm}^{2}\text{/kg}} \right) \text{[m/s/year]} \end{array} $$
(17)

Where the modified inverse ballistic coefficient differential:

$$ \begin{array}{@{}rcl@{}} {\Delta}\frac{1}{b} &=& \frac{A_{O}}{m_{O}}-\frac{A_{D}}{m_{D}}\left( \frac{r_{O}}{r_{D}}\right)^{2} \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} &\approx& \frac{A_{O}}{m_{O}} - \frac{A_{D}}{m_{D}} \left( 1+\frac{2 {\Delta} r}{r_{O}} \right) \text{when} {\Delta} r \ll r_{O} \end{array} $$
(19)
$$ \begin{array}{@{}rcl@{}} \ &\approx& \left( \frac{A_{O}}{m_{O}}-\frac{A_{D}}{m_{D}}\right) \end{array} $$
(20)

and will likely lie in the 1–10 dm2/kg range for ordinary spacecraft pairs.

Nominally, if \(\frac {A_{O}}{m_{O}} > \frac {A_{D}}{m_{D}}\left (\frac {r_{O}}{r_{D}}\right )^{2}\), then \(a_{D,r}^{\text {RP}}>0\), i.e. an anti-sunward thrust by the Detector spacecraft is required to maintain formation (or a sunward thrust by the Optics spacecraft). However, a judicious choice for inverse ballistic coeffient differential can, in theory, lead to \(\delta a_{D,r}^{\text {RP}}\) being equal in amplitude but opposite in sign to \(\delta a_{D,r}^{\text {NK}}\), negating the need for any radial thrust requirement by either spacecraft to maintain formation, at least to first order (minor corrections due to perturbations, sensory input errors, thruster impulse bits accuracies, etc will of course be necessary). E.g., for Δr= 100 m and mD = mO = 1 kg, a 2.6 mm2 difference in cross-sectional area is enough to compensate for the Detector spacecraft’s excess centrifugal acceleration and maintain the PFF. (For Δr= 1 Mm, that would be 2.6 dm2; for Δr= 385 Mm (a lunar distance), that would be 1 dm2). Pointing errors can lead to a non-negligible sideways (tangential) thrust, which will have to be accounted for (“solar sail” effect).

Whatever avenue is chosen to compensate for the centrifugal force, it is likely that additional thrusters in the tangential and vertical directions will also be needed to keep the Target-Optics-Detector alignment and Optics-Detector distance as perfect as possible.

Differential Acceleration due to Drag in Ram Direction

$$ \begin{array}{@{}rcl@{}} \delta a_{D,t}^{\text{ram drag}} &=& \frac{\rho_{O}}{2} v_{t,O}^{2} \left( \frac{A_{O}^{\text{ram}}}{m_{O}} \right) - \frac{\rho_{D}}{2} v_{t,D}^{2} \left( \frac{A_{D}^{\text{ram}}}{m_{D}} \right) \end{array} $$
(21)
$$ \begin{array}{@{}rcl@{}} &=& \frac{GM}{r_{O}} \left[ \frac{\rho_{O}}{2}\frac{A_{O}^{\text{ram}}}{m_{O}} - \frac{\rho_{D}}{2}\frac{A_{D}^{\text{ram}}}{m_{D}} \frac{{r_{D}^{2}}}{{r_{O}^{2}}} \right] \end{array} $$
(22)
$$ \begin{array}{@{}rcl@{}} &=& \frac{\rho_{O}}{2} \frac{GM}{r_{O}} \left[ \frac{A_{O}^{\text{ram}}}{m_{O}} - \frac{A_{D}^{\text{ram}}}{m_{D}} \right] \end{array} $$
(23)
$$ \begin{array}{@{}rcl@{}} &\approx& 7.4\times10^{-15} \left( \frac{1 \text{AU}}{r_{O}}\right)^{3} \left( \frac{M}{M_{sun}}\right) \left( \frac{{\Delta}\frac{1}{b^{\text{ram}}}}{1 {dm^{2}/kg}} \right) \mathrm{[m/s^{2}]} \end{array} $$
(24)
$$ \begin{array}{@{}rcl@{}} &\approx& 0.23 \left( \frac{1 \text{AU}}{r_{O}}\right)^{3} \left( \frac{M}{M_{sun}}\right) \left( \frac{{\Delta}\frac{1}{b^{\text{ram}}}}{1 {dm^{2}/kg}} \right) \mathrm{[\mu m/s/year]} \end{array} $$
(25)

With, for interplanetary space and when rO is the distance to the sun, \(\rho _{O} \approx 1.67\times 10^{-24} \left (\frac {\text {1 AU}}{r_{O}}\right )^{2}\) g/cm3 and \(\rho _{D}=\rho _{O} (\frac {r_{O}}{r_{D}})^{2}\). As before, details of the the drag coefficient CD and exact incidence angle have been folded into Aram. This component is typically negligible far from planetary atmospheres or the Sun.

Simulations

Figure 4 summarizes differential acceleration effects on a Optics-Detector formation at 1 AU, in a heliocentric Earth-trailing orbit 90 degrees behind Earth. The crosses represent actual simulation points (note the excellent agreement with the theoretical curves), computed with the General Mission Analysis Tool (GMAT, https://opensource.gsfc.nasa.gov/projects/GMAT/index.php) developed by NASA’s Goddard Space Flight Center, which include effects from all planets and solar radiation pressure. The simulations were made assuming the Optics spacecraft orbits freely, while the Detector spacecraft is initially in the appropriate configuration (proper tangential velocity to maintain the Target-Optics-Detector alignment). All simulation results are summarized in Tables 1 and 2. Note that simulations 5a) and 5b) were made at the Earth-Sun L1 point, which requires additional station-keeping Delta-V expenditure (\(\sim \)14 m/s/year for each spacecraft) besides what is required purely to maintain the Target-Optics-Detector alignment (Fig. 5). (A set of simulations at 0.87 AU were also made, but are not shown here since they agree quantitatively with the 1 AU case discussed above.)

Fig. 4
figure 4

Differential accelerations (and Delta-V requirement to compensate) on an Optics-Detector pair around the Sun, trying to maintain the Target-Optics-Detector alignment and Optics-Detector distance. The two spacecrafts are at 1 AU, 90∘ behind Earth. Solid lines are theoretical computations from the equations presented in the main text for \({\Delta }\frac {1}{b}<0\), while dashed lines correspond to \({\Delta }\frac {1}{b}>0\) situations. The stars are the results of simulations 3a-f and 4a-c, all squarely falling on the theoretically-predicted curves. At low \({\Delta } \frac {1}{b}\), the curve branches out to various Δr

Full size image
Table 1 Simulation configurations and total Delta-V expenditure. A 0.8 coefficient of reflectivity was used for the computations of \({\Delta } \frac {1}{b}\). ∗: Earth-Sun L1 station-keeping requires an additional 14.2 m/s/year for each spacecraft
Full size table
Table 2 Simulations summary: Delta-V and deflections. To estimate constant acceleration values, divide the ΔV impulse bits presented here by the 2.4 hour time interval between them
Full size table
Fig. 5
figure 5

Similar to Fig. 4, for a formation at the Earth-Sun L1. Note that, in addition to the formation maintenance requirement shown in this plot, each spacecraft had to expend \(\sim \)14 m/s/year to be able to stay at L1

Full size image

The details of the simulations and the control algorithm used are detailed in Appendix B. They perform a sanity check on the analytical results displayed here, and provide coarse upper limits on Detector spacecraft deflections, which are sub-cm with the control algorithm used. A full control simulation, including sensor precision and actuator accuracy are beyond the scope of the present work.

Discussion

Simple simulations have corroborated analytical predictions on Delta-V expenditures, and have led to deflections of up to a few millimiters in either radial or tangential directions. It is likely that, given sufficiently precise sensory input, pointing and actuator control, a rigorous control algorithm coupled with a gentle constant-thrust or solar sailing approach could achieve even smaller deflections. In near-circular scopocentric orbits, the primary thrust to maintain PFF is uni-directional (either sunward or anti-sunward), while the secondary thrusting or solar sailing in the other five directions is required to correct tiny errors, and can be several orders of magnitude less in amplitudes (e.g. Table 2).

When sufficiently far from orbital and tidal effects, differences in inverse ballistic coefficient to incident solar radiation pressure between the two spacecrafts dominate the dynamics. Only in cases with extremely large spacecraft separation Δr (such as could be expected from e.g. a Fresnel lens-based telescopes for γ-rays) are orbital effects still the dominant disruptive forces on the formation.

Table 3 gives an overview of some currently accessible regions of space. Note that, currently or in coming years, CubeSats and SmallSats can be expected to be given regular rideshares to orbits more propitious to PFF telescopes, or to regions from which it is easier to get to such orbits: GTO, GEO, Mars Transfer Orbits, Earth-Sun L1/L2, and heliocentric.

Table 3 Some rideshare-accessible orbits and time-averaged formation maintenance thrust requirements for separation Δr= 100 m. Delta-V numbers in the second column are for impulsive maneuvers (low-thrust maneuvers often require in the neighborhood of twice as much)
Full size table

Table 4 gives an overview of typical thruster capabilities which could be used to precisely maintain the telescope formation, or even reach the favored orbit from the launcher or rideshare release point. A wide variety of possibilities exist. CubeSat cold-gas thrusters tend to leak and to have large minimum impulse bits, making precise formation maintenance more difficult than with a less impulsive approach. Weak but constant thrust propulsion will tend to have formation-keeping control mostly limited by other factors, such as attitude control & knowledge, accuracy of actuators, or minimum impulse bits. Note that S/C attitude control may not need to be extraordinary for the observations themselves, as most optical systems tend to follow the “thin lens” approximation to first order, and detector plates may also be somewhat tilted with little loss.

Table 4 Some example thrusters and spacecraft masses. All numbers approximate
Full size table

There are of course a host of other considerations, such as the bright Sun possibly complicating tracking of the Optics spacecraft by the Detector spacecraft (though a combination of an optical camera and radio direction-finding and ranging covers quite a bit of ground), or the shadowing of the Sun by the Optics spacecraft impacting the Detector spacecraft’s solar panels.

Within cislunar space, it appears that a thruster-based approach is necessary. Most tantalizing for remote-sensing solar physics and astrophysics is the possibility to have a Sun-orbiting telescope in trans-lunar orbits exclusively using solar sailing to maintain the PFF (Tables 3 & 4). A combination of flaps, rudders, or even solar panels with adjutable orientation and inclinations could maintain the PFF. Such a telescope would have no consumables. Drifting Earth-trailing or Earth-leading orbits are easier to reach than Earth-Sun L1/L2, and have been used by the Spitzer, Kepler, and STEREO missions (through Delta-II rocket launches). Such orbits should also be available to SmallSats in the coming years thanks in part to rideshares on the upcoming SLS (Artemis) launches to the Moon (“heliocentric disposal orbits”). Research into nullifying the drift, i.e. preserving the Earth-telescope distance (and downlink rate) over years, is presented in e.g. [7] and require in the neighborhood of \(\sim \)1 km/s Delta-V. Distant Retrograde Orbits (DRO) appear to be a robust alternative. They are accessible at a somewhat greater Delta-V cost. DROs have basically the same semi-major axis (and orbital period) as Earth and the same heliocentric orbital phase (anomaly), but with a slightly higher eccentricity, giving the impression the spacecrafts are orbiting the Earth-Moon system in a retrograde fashion. Stable DROs (requiring no station keeping) starting at a few percent of an AU away the from Earth-Moon system exist, but likely require a 0.5-1 km/s Delta-V to reach from Earth-Sun L1 or L2.

Conclusions

Through linearized relative equations of motion, we have gauged the feasibility of a Precise Formation Flying telescope, and have been particularly interested in the Sun as a target. We also present exact analytical equations in Appendix A.

Simulations spanning a wide range of parameters have fully supported both the cases of heliocentric and Earth-Sun L1 orbits. In most cases presented here, the Detector spacecraft drifts are sufficiently small that detector area does not need to be much larger than conventional, if at all (Table 2).

Translunar space is an ideal region to use PFF telescopes. They are already accessible to large payloads on heavy launchers, and becoming available to CubeSats and SmallSats via rideshares. We suggest putting such smaller payloads in heliocentric orbits, via Artemis and other rideshares to high-energy orbits, likely in the form of a single spacecraft that eventually separates into Optics spacecraft and Detector spacecraft. It is likely that in most cases, the payload will require a \(\sim \)1 km/s stage ot capability to complete the trip (e.g. L1 to DRO, or to nullify the drift away from Earth), but once in position, low-thrust propulsion and/or solar sailing can maintain the formation, potentially for years, and with 100% observation time throughout the orbit.

We shall conclude by stating that, while this study was oriented towards the Sun as target, it is relevant to any solar system target, such as planets. Cosmic targets should also be accessible for Astrophysics, with a slight increase in difficulty due to primary thrusting varying in both amplitude and direction with orbit phase.