1 Introduction

To successfully carry out flooding or enhanced oil recovery process, a good understanding of the reservoir fluid system and petrophysical characteristics of the rocks is desired. Most reservoir formations have a high degree of heterogeneity, and this usually results in reduced reliability of the reservoir information obtained from pressure transient analysis. Aside from the issues arising from the variation in petrophysical properties, for a long time, scientists have attempted to characterize these properties using the variation of pressure with time. This is based on the general belief that these properties are a function of time-dependent variables such as pressure. In highly heterogeneous formations such as naturally fractured and karst reservoirs, earlier methods of pressure transient analysis are expected to give unsatisfactory results because of the assumption of uniformity and homogeneity of reservoir pore structure.

Fractured reservoirs are known to be heterogeneous, with openings (fractures and fissures) of varying sizes which leads to the creation of vugs and interconnected channels within a reservoir. Fluid storage is mostly in the porous block of the reservoir which is characterized by low permeability, whereas the fracture has high permeability and low storage capacity. These systems have undergone extensive studies, and this work presents a critical review of such works to provide insights into what knowledge has been gained thus far and what limitations are inherent in the existing models and how best to improve them. Pollard was one of the first persons to publish a study in 1953 on pressure transient analysis, and in 1959, the first pressure transient analysis (PTA) models were made available for well test interpretation from a two-porosity system (Pollard 1959). Since then, the behavior of fractured reservoirs along with pressure transient analysis in such mediums has become a highly researched area in the field of reservoir engineering. Thus, this work will state all the models presented thus far and analyze their scope of coverage in predicting pressure changes in fractured mediums. The work is divided into several subheadings to enable clear comparison and analysis of the various sections considered.

2 Naturally fractured reservoirs

Fractures have different definitions depending on the point of view. However, from a geomechanics point of view, a fracture is said to be a surface phenomenon that could be vertical or horizontal and is caused by the loss of cohesion in the texture of a rock. Fracturing involves the formation of joints and fissures when rocks break up. Fractures are caused by stresses and are termed natural or induced depending on whether it was created purposely. Naturally fractured formations are those characterized by secondary porosities in addition to primary porosity (Gong and Rossen 2017; Odeh 1965, 1959). The induced porosity (secondary porosity) results from stresses or tensional forces that cause brittle formations to crack. Figure 1 shows a three-layered reservoir with layers labeled a, b and c. The layer with the weakest bonds (cohesion) would be the first to be fractured. Thus, in Fig. 1, layer b has weak cohesion and it is thus fractured while layers a and c can withstand further stress.

Fig. 1
figure 1

Three-layered reservoir (van Golf-Racht 1982)

Full size image

Naturally fractured reservoirs have been identified as some of the highly productive oil and gas reservoirs. Many fields containing naturally fractured reservoirs saw significant hydrocarbon production mainly during their primary recovery phases. Examples of such fields include the Asmari Formation in Iran (Alsharhan and Nairn 1997; Levorsen and Berry 1967), Ekofisk Maastrichtian chalk in the North Sea (Fritsen and Corrigan 1990; Owen and Thomas 2002), Gianitic Basement Formation (Areshev et al. 1992; Tandom et al. 1999), Permian Formation (Wilkinson and Hammond 1990) and Monterey Formation (Luthi 2001). In the majority of the studies involving these fields, the fracture networks were observed to have formed as a result of shearing and tensile forces acting on the rocks due to tectonic actions (Luthi 2001).

The origin of fractures has long been a topic of debate among researchers and professionals especially concerning its intensity and reservoir trapping significance (van Golf-Racht 1982). Friedman et al. (Friedman et al. 1976) classified fractures into two classes: those related to regional fractures and those related to folding. However, Hodgson (1961) had earlier postulated that there exists no genetic relationship between fold and fractures and asserted that joints are formed as a result of fatigue in the early diagenesis stage. Price (1966), on the other hand, asserted that even though joint could have been formed in the early stage of the diagenesis process as claimed by Hodgson (1961), it is impossible for it to have survived post-depositional compaction. Cook and Johnson (1970) concluded that joints could survive late diagenetic activities such as compaction, consolidation and burial. However, based on the analysis of fracture density and layer thickness by Harris et al. (1960), the authors affirmed the relationship between the two and it is safe to say, the origins of fractures could be structural and nonstructural related.

Due to the varying geological and structural configuration of various naturally fractured reservoirs, researchers have made several attempts at classifying them into different types with similar characteristics. Notably, van Golf-Racht (1982), Allan and Sun (2003), Bourbiaux (2010), Nelson (2001), Ng and Aguilera (1991) and others have attempted to use wide-ranging definitions with some similarities. The most acceptable definition is based on the relationship between fluid storage and flow capacity. The type of naturally fractured reservoirs (Fig. 2) identified under this category includes

  1. (A)

    Type 1: This type of formation has little or no matrix porosity and permeability. Here, the contribution of the matrix to flow could be negligibly small compared to that of fractures which serve as the primary pathway and storage for the reservoir fluid. An example of such formation can be found in the Keystone field in Texas with a characteristic average porosity of about 20% (Firoozabadi 2000).

  2. (B)

    Type 2: This type of reservoir has low matrix porosity and permeability with formation fluid flow due to the intensity of the fractures and its distribution dictating the production. An example of this type of formation can be found in Asmari limestone reservoirs with about 10%–20% matrix porosity (Saidi 1987).

  3. (C)

    Type 3: This type of reservoir has high matrix porosity and low permeability. Here, the bulk of the fluids are stored in the matrix. The pore volume of fractures is small compared to that of the matrix. Also, the flow capacity of the reservoir is fracture-dominated and this type of reservoir is commonly found in the North sea Ekofisk chalk formation with an average matrix porosity of about 35% (Hermansen et al. 1997).

  4. (D)

    Type 4: This type of formation is characterized by high matrix porosity and permeability with no additional porosity contribution from the fractured medium. In this type of reservoir, the fracture contributes less to the total available fluid flow and this typically enhanced permeability leads to increased anisotropy rather than improved fluid flow.

Fig. 2
figure 2

Types of fractures as a result of folding (van Golf-Racht 1982)

Full size image

3 Model development

The first fractured reservoir was discovered in 1880 (Willis and Hubbert 1955). However, the well-known well test analysis methods and models were not available until the 1950s and even at that, models were only available for homogeneous formations. One of the most practical models recognized in the literature was presented by Horner (1951), which produced graphs of wellbore flowing pressures and logarithmic time called Horner time \({{\left( {t_{\text{p}} + \text{d} t} \right)} \mathord{\left/ {\vphantom {{\left( {t_{\text{p}} + \text{d} t} \right)} {\text{d} t}}} \right. \kern-0pt} {\text{d} t}}\). However, this plot does not apply to formations with fractures. Based on the type of fissures found in the Middle East limestone reservoirs, Baker (1955) proposed a method of determining the sizes of the fissures and volume of fluid in a reservoir. The concept of fluid flow between two parallel plates was utilized as given by Lamb (1945) and Huitt (1956). The flow through such setup is given as

$$q = - \frac{{b\omega_{\text{f}}^{2} }}{12\mu }\frac{{\text{d} p}}{{\text{d} L}}$$
(1)

where q is the flow rate per unit length, ωf is the fracture width, b is the fracture depth, μ is the fluid viscosity and \({{\text{d} p} \mathord{\left/ {\vphantom {{\text{d} p} {\text{d} L}}} \right. \kern-0pt} {\text{d} L}}\) is the pressure gradient across the flow interval of length L.

3.1 Pressure transient analysis for fractured mediums

In describing the pressure transient analysis in a fractured medium, various modeling approaches have been applied. In the models, attempts have been made to account for the distinct porosity types within the formation by dividing the formation into two regions: that containing only formation matrix and the other containing only fractures. In this section, we present the various attempts at modeling the fluid flow through a naturally fractured reservoir.

Naturally fractured reservoirs have been characterized to exhibit two distinct forms of reservoir porosity types: matrix porosity and fracture porosity (Kazemi 1969; de Swaan 1976; Warren and Root 1963). The matrix region is a region having a high percentage of fine pores with characteristically high storage but low flow capability. The fracture region has a higher flow capacity but lower storage capacity as compared to the matrix region. Most studies aimed at characterizing flow in a naturally fractured reservoir typically consider the formation as having two distinct regions. One early work on flows in fractured formations was that carried out by Pollard (1959), in which the author evaluated the flow behavior of acid treatment operation using pressure transient analysis. Pollard proposed a method based on classifying naturally fractured reservoirs as being delineated into three regions, namely rock matrix, fracture and the damaged/improved region close to the wellbore. Further, Pollard posited that fluid flows typically from a high porosity region to the highly permeable fractures (Fig. 3), eventually reaching the wellbore through the damaged/improved region and that there exists no contact between the high porous region and the wellbore.

Fig. 3
figure 3

Flow pattern in fractured reservoir

Full size image

Also, the author observed that for all described regions, the average buildup pressure is approximately defined in the form of exponential time decay with different decay coefficients with each region occurring successively during the pressure buildup test. Pollard (1959) proposed an equation with three distinct terms each representing the pressure transient due to flow as shown in their earlier observed three distinct regions:

$$\begin{aligned} \left( {\overline{p} - p_{\text{w}} \left( {\Delta t_{\text{AD}} } \right)} \right) & = C_{\text{D}} \exp \left[ { - \alpha_{\text{1D}} \pi r_{\text{eD}}^{2}\Delta t_{\text{AD}} } \right] + D_{\text{D}} \exp \left[ { - \alpha_{\text{2D}} \pi r_{\text{eD}}^{2}\Delta t_{\text{AD}} } \right] \\ & \quad + \left( {p - p_{\text{w}} - C - D} \right)_{\text{D}} \exp \left[ { - \alpha_{\text{3D}} \pi r_{\text{eD}}^{2}\Delta t_{\text{AD}} } \right] \\ \end{aligned}$$
(2)

where CD and DD are the decay coefficients. This equation is applicable to estimate properties such as wellbore damage and fracture volume. A pseudo-steady-state assumption was made as well as two types of the void (fine voids and coarse void) during the mathematical development, which according to Dikkers (1964) found application in the La Paz field at that time. Barenblatt et al. (1960) laid the foundation of the physical principles of the mathematical modeling of fractured mediums based on the interaction between the matrix region and the fracture region. This interaction is expressed as Barenblatt et al. (1960)

$$q_{\text{mf}} = \rho \alpha \left( {p_{\text{m}} - p_{\text{f}} } \right)$$
(3)

where qmf is the flow rate from the matrix to fracture, α is the fissured medium characteristic parameter, pm is the pressure in the matrix and pf is the pressure in the fracture.

Applying the continuity equation and Darcy’s law and assuming a slightly compressible liquid of compressibility cl and matrix compressibility coefficient cm, Barenblatt et al. (1960) came up with a pressure diffusivity equation relating the matrix and fracture as

$$\frac{{\partial p_{\text{f}} }}{\partial t} - \frac{{k_{\text{f}} }}{\alpha }\frac{{\partial \Delta p_{\text{f}} }}{\partial t} = \frac{{k_{\text{f}} }}{{\mu (c_{\text{m}} + \phi_{\text{m}} c_{\text{l}} )}}\Delta p_{\text{f}}$$
(4)

Pirson and Pirson (1961) extended Pollard’s approach to estimating the volume of the matrix porosity and radius of well influence. In a further study developed for an infinite reservoir system, Warren and Root (1963) applied an approach different from earlier works by Pollard (1959) and Pirson and Pirson (1961). Here, the authors assumed that the reservoir pore system is having primary and secondary porosities. The primary porosity is composed of a set of rectangular building blocks called parallelepipeds which are homogeneous, isotropic and identical. The secondary porosity included in the coarse features with a uniform set of continuous fractures, each fraction having a property parallel to a principal axis of permeability. Warren and Root (1963)’s model depicts an overlapping arrangement of matrix and fractures (Fig. 4) with a quasi-steady-state flow assumed within the matrix at small times and unsteady-state flow within the fractures. The authors assumed a quasi-steady-state flow within the matrix at small times and unsteady-state flow within the fractures. The authors concluded that the behavior of this reservoir type will produce two parallel straight lines (Fig. 5) representing early and late times connected by a transition curve. These pressure signatures are controlled by two properties, ω, a measure of fluid flow capacity of the fracture porosity and λ, a measure of the level of reservoir heterogeneity.

Fig. 4
figure 4

Warren and Roots representation of fractured reservoirs (Warren and Root 1963)

Full size image
Fig. 5
figure 5

Typical pressure buildup curve for Warren and Roots reservoir description (Bahrami et al. 2012)

Full size image

Furthermore, Warren and Root (1963) presented a model utilizing the concept of mathematical superposition of two mediums as introduced by Barenblatt et al. (1960). The authors discussed the fluid flow equation by Barenblatt et al. (1960) that represents the flow in the matrix and fractures as represented in Eqs. (5)–(7).

$$- \nabla \cdot \left( {\rho \vec{u}_{\text{f}} } \right) + q^{\text{mf}} = \frac{{\partial \left( {\phi_{\text{f}} \rho } \right)}}{\partial t},$$
(5)

and

$$- \nabla \cdot \left( {\rho \vec{u}_{\text{m}} } \right) - q^{\text{mf}} = \frac{{\partial \left( {\phi_{\text{m}} \rho } \right)}}{\partial t}$$
(6)

where qmf is the pseudo-steady-state flow rate between the matrix and the fracture. qmf is given by

$$q^{\text{mf}} = \rho \frac{{\sigma k_{\text{m}} }}{\mu }\left( {p_{\text{f}} - p_{\text{m}} } \right)$$
(7)

The authors obtained the diffusivity equations in one dimension in both dimensional form:

$$\frac{{\sigma k_{\text{m}} }}{\mu }\left( {p_{\text{f}} - p_{\text{m}} } \right) + \phi_{\text{m}} c_{\text{m}} \frac{{\partial p_{\text{m}} }}{\partial t} = 0,$$
(8)
$$\frac{{k_{\text{f}} }}{\mu }\left[ {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial p_{\text{f}} }}{\partial r}} \right)} \right] + \phi_{\text{f}} c_{\text{f}} \frac{{\partial p_{\text{f}} }}{\partial t} - \phi_{\text{m}} c_{\text{m}} \frac{{\partial p_{\text{m}} }}{\partial t} = 0$$
(9)

and dimensionless form:

$$\left( {1 - \omega } \right)\frac{{\partial p_{{{\text{D}}_{\text{m}} }} }}{{\partial t_{\text{D}} }} - \lambda \left( {p_{{{\text{D}}_{\text{f}} }} - p_{{{\text{D}}_{\text{m}} }} } \right),$$
(10)
$$\frac{1}{{r_{\text{D}} }}\frac{\partial }{{\partial r_{\text{D}} }}\left( {r_{\text{D}} \frac{{\partial p_{{{\text{D}}_{\text{f}} }} }}{{\partial r_{\text{D}} }}} \right) - \omega \frac{{\partial p_{{{\text{D}}_{\text{f}} }} }}{{\partial t_{D} }} + \left( {1 - \omega } \right)\frac{{\partial p_{{{\text{D}}_{\text{m}} }} }}{{\partial t_{\text{D}} }} = 0.$$
(11)

The dimensionless variables in Eqs. (10) and (11) are given by

$$r_{\text{D}} = {r \mathord{\left/ {\vphantom {r {r_{\text{w}} }}} \right. \kern-0pt} {r_{\text{w}} }},$$
$$t_{\text{D}} = \frac{{k_{\text{f}} t}}{{\left( {\phi_{\text{m}} c_{\text{m}} + \phi_{\text{f}} c_{\text{f}} } \right)\mu r_{\text{w}}^{2} }},$$
$$p_{\text{D}} = \frac{2\pi rh}{\mu q}\left( {p - p_{\text{i}} } \right),$$
$$\lambda = \frac{{\sigma k_{\text{m}} r_{\text{w}}^{2} }}{{k_{\text{f}} }},$$
$$\omega = \frac{{\phi_{\text{f}} c_{\text{f}} }}{{\phi_{\text{f}} c_{\text{f}} + \phi_{\text{m}} c_{\text{m}} }}$$

The authors provided solutions to both finite-acting and infinite-acting reservoir systems. The dimensionless wellbore flow pressure for the infinite-acting reservoir was given as

$$p_{{{\text{D}}_{{{\text{f}}_{\text{w}} }} }} = \frac{1}{2}\left[ {0.80907 + \ln t_{\text{D}} + Ei\left( { - \frac{{\lambda t_{\text{D}} }}{\omega (1 - \omega )}} \right) - Ei\left( { - \frac{{\lambda t_{\text{D}} }}{1 - \omega }} \right)} \right]$$
(12)

This solution looks like the conventional solution to the single-porosity reservoir system with only a difference of Δ given by

$$\Delta = \frac{1}{2}\left[ {Ei\left( { - \frac{{\lambda t_{\text{D}} }}{\omega (1 - \omega )}} \right) - Ei\left( { - \frac{{\lambda t_{\text{D}} }}{1 - \omega }} \right)} \right]$$
(13)

The solution to the finite-acting naturally fractured reservoir system is given by

$$p_{{{\text{D}}_{{{\text{f}}_{\text{w}} }} }} = \left( {\frac{2}{{r_{{{\text{D}}_{\text{e}} }}^{2} }}} \right)\left[ {t_{\text{D}} + \frac{{\left( {1 - w} \right)^{2} }}{\lambda }\exp \left( { - \frac{{\lambda t_{\text{D}} }}{w(1 - w)}} \right) + \ln r_{{{\text{D}}_{\text{e}} }} - \frac{3}{4} + s} \right]$$
(14)

The difference between Eq. (14) and the solution to the single-porosity medium is given by

$$\Delta = \frac{{\left( {1 - w} \right)^{2} }}{\lambda }\exp \left( { - \frac{{\lambda t_{\text{D}} }}{w(1 - w)}} \right)$$
(15)

Based on these solutions, Warren and Root (1963) obtained a plot with a characteristic of three different regions. In the plot, the early time is represented by a straight line defining that stage where fracture depletion dominates. A transition zone describes the effect of the matrix-dominated flow period while the late time depicts the period when both porosity types influence production. The significance of Warren and Root’s model laid the foundation for future work on pressure transient analyses in naturally fractured reservoirs.

In another study, Odeh (1965) attempted to account for the failure of the Warren and Roots model in some field applications. In his research, he applied available field pressure data to mathematically analyze the behavior of reservoirs like that of Warren and Roots model but with an additional assumption of uniform flow capacity and degree of fracturing within the fractures typical of a reservoir with small grid block compared to the reservoir dimension. Odeh (1965)’s approach gave a general model expressed as

$$\Delta p = \frac{ - q\mu }{{4\pi k_{\text{f}} h\beta }}\left[ {\ln \left[ {\frac{{4tk_{\text{f}} V_{\text{f}} }}{{r^{2} \phi_{\text{f}} (c_{\text{f}} V_{\text{f}} + c_{\text{m}} V_{\text{m}} )}}} \right] - 0.5772 - Ei\left( { - C_{\text{t}} } \right) + Ei\left( { - C_{\text{t}} \left( {1 + \frac{{V_{\text{m}} c_{\text{m}} }}{{V_{\text{f}} c_{\text{f}} }}} \right)} \right)} \right]$$
(16)

Equation (16) can be approximated as

$$\Delta p = \frac{ - q\mu }{{4\pi k_{\text{f}} h\beta }}\left[ {Ei\left( {\frac{{ - r^{2} \mu \left( {c_{\text{f}} \beta \phi_{\text{f}} + c_{\text{m}} \left( {1 - \beta } \right)\phi_{\text{m}} } \right)}}{{4k_{\text{f}} \beta t}}} \right)} \right]$$
(17)

Equation (17) has a form similar to Horner’s buildup equation (Horner 1951) for a homogenous reservoir. His model has a characteristic property β that defines the entire fracture volume as a function of the studied core volume.

Odeh (1965) observed that both the pressure buildup (p vs. ln [(t + Δt)/Δt] and pressure drawdown plots (p vs. ln t) for a fractured reservoir give a characteristic straight-line plot similar to that of a homogenous reservoir. Thus, the author concluded that no specific model could be truly representative of every type of fractured reservoirs. In rebuttal within the same publication, Warren and Root observed that Odeh’s model was misleading and that the new parameters by Odeh can be adjusted to that resulting in the same model as Warren and Roots.

Kazemi (1969) observed some limitations in the widely used Warren and Roots model. In his study, Kazemi considered a radial flow in a well located at the center of a finite circular reservoir with horizontal fracture orientation as shown in Fig. 6. The author replaced Warren and Root’s assumption of quasi-steady-state flow with the unsteady-state flow and observed that there exists a considerable time difference between the disappearance time of the early-time plot in the Warren and Root model and the start of the quasi-steady state. This difference may result in a poor estimation of critical properties such as relative storage capacity. The author then concluded that for larger times, naturally fractured reservoirs tend to behave like a homogenous reservoir and that, the Warren and Roots model gives a substantially reasonable estimate but has limitations in formations with small fracture-matrix flow capacity difference. The differential equations of a reservoir undergoing unsteady-state flow with flow potential Φ, fracture thickness δ, fracture block thickness h, and compressibility c are

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \varPhi }{\partial r}} \right) + \frac{{\partial^{2} \varPhi }}{{\partial z^{2} }} = \frac{{\phi_{\text{m}} \mu c_{\text{m}} }}{{k_{\text{m}} }}\frac{\partial \varPhi }{\partial t}\,\,\, {\text{for}}\,\,\,\frac{\delta }{2} < z < \frac{h}{2},\,\,\,\,r_{\text{w}} < r < r_{\text{e}}$$
(18)

for flow in the matrix, and

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {k_{\text{f}} r\frac{\partial \varPhi }{\partial r}} \right) + \frac{{k_{\text{m}} }}{\delta /2}\left( {\frac{\partial \varPhi }{\partial z}} \right)_{{z = \delta^{ + } /2}} = \phi_{\text{f}} \mu c_{\text{f}} \frac{\partial \varPhi }{\partial t}\,\,\,{\text{for}}\,\,\, 0 {\text{ < z < }}\frac{\delta }{2},\,\,\,r_{\text{w}} < r < r_{\text{e}}$$
(19)

for flow in the fracture. The flow potential is given by

$$\varPhi = \rho \left( 0 \right)\left[ {\int_{0}^{p} {\frac{{\text{d} p}}{\rho \left( p \right)}} + gz} \right]$$
(20)

de Swaan (1976) presented a transient state model for slightly compressible flow with a flow from the matrix into the fracture using two geometries. The author based his findings on the fact that matrix blocks can be modeled as rectangular solids whose transient pressure models are similar to those from heat flow theory. Using convolution theory, the flow between the matrix and fractured medium is given as

$$q_{\text{m}} = \frac{ - 2}{{A_{\text{m}} h_{\text{f}} }}\int\limits_{0}^{t} {\frac{{\partial \Delta p_{\text{f}} }}{\partial r}q_{\text{m}} \left( {t - \tau } \right)\partial \tau }$$
(21)

This term is substituted in the diffusivity equation and the pressure equations defining flow within the fractured medium was obtained. Here, for a fractured medium having a constant wellbore flowing rate and uniform pressure at the initial condition, the governing pressure equation is given as:

$$\frac{{k_{\text{f}} }}{\mu }\frac{{\partial^{2} \Delta p_{\text{f}} }}{{\partial r^{2} }} = \phi_{\text{f}} c\frac{{\partial \Delta p_{\text{f}} }}{\partial r} - q_{\text{m}} \left( {\Delta p_{\text{f}} ,t} \right)$$
(22)

de Swaan (1976) provided a solution for early and long times without the transient period. Based on de Swans’ theory, Najurieta (1980) presented all the solutions of the radial distances with time (Figs. 7, 8).

Fig. 6
figure 6

Kazemi-fractured formation representation (Kazemi 1969)

Full size image
Fig. 7
figure 7

Typical buildup curve for Kazemi model (Kazemi 1969)

Full size image
Fig. 8
figure 8

The actual and idealized representation of the reservoir model by Engler and Tiab (1996)

Full size image

In a later attempt at getting a better insight into the flow behavior of a naturally fractured reservoir, other techniques such as pressure derivative solutions have been proposed (Bourdet et al. 1983; Escobar and Tiab 2002; Tiab 1994). This method gained prominence due to its ability to better capture the different flow regimes (Bourdet et al. 1983).

Engler and Tiab (1996) attempted to explore the benefits of applying derivative plots in fractured reservoirs. Here, the authors applied the Tiab direct synthesis (TDS) of a reservoir type with an idealized heterogeneous system of vugs, matrix and fractures. In modeling this, the authors assumed that the matrix element is separated by a uniformly continuous fractured region characterized by the pseudo-steady flow between it and the matrix as shown in Fig. 9. For a single-phase fluid flow, the pressure equation proposed by Warren and Root (1963) was employed. The authors obtained a pressure derivative equation for a formation with mechanical skin (Sm) as described by Eq. (23).

$$p_{{{\text{D}}_{\text{w}} }}^{'} t_{{{\text{D}}_{\text{w}} }} = \frac{1}{2}\left[ {1 - \text{e}^{{ - \frac{{\lambda t_{{{\text{D}}_{\text{w}} }} }}{1 - w}}} + \text{e}^{{ - \frac{{\lambda t_{{{\text{D}}_{\text{w}} }} }}{w(1 - w)}}} } \right]$$
(23)

The terms in Eq. (23) have the following forms.

$$p_{\text{D}} = \frac{{k_{\text{f}} h\Delta p}}{{141.2q\mu \beta_{\text{o}} }}$$
(24)
$$t_{{{\text{D}}_{\text{w}} }} = \frac{{0.0002637k_{\text{f}} t}}{{\left( {\phi_{\text{m}} c_{\text{m}} + \phi_{\text{f}} c_{\text{f}} } \right)\mu r_{\text{w}}^{2} }}$$
(25)
$$\omega = \frac{{\phi_{\text{f}} c_{\text{f}} }}{{\phi_{\text{m}} c_{\text{m}} + \phi_{\text{f}} c_{\text{f}} }}$$
(26)
$$\lambda = \alpha r_{\text{w}}^{2} \frac{{k_{\text{m}} }}{{k_{\text{f}} }}$$
(27)

Equation (23) as presented by Engler and Tiab (1996) gives a characteristic curve for the undamaged and damaged reservoir as shown in Fig. 10. With this curve, various parameters representative of the reservoir formation can be estimated.

Fig. 9
figure 9

Combined pressure and pressure derivative curve. a No skin or wellbore damage. b Skin damage (Engler and Tiab 1996)

Full size image
Fig. 10
figure 10

Vuggy reservoir transient analysis (Velazquez et al. 2005)

Full size image

The infinite-acting flow period is represented by a horizontal straight line on the pressure derivative-type curve. This region defines the period where only the fracture contributes to production. The pressure derivative (pDw′ · tDw) and fracture permeability (k2) during this period for a well experiencing no wellbore effect is given as

$$p_{\text{Dw}}^{'} t_{\text{Dw}} = \frac{1}{2}$$
(28)
$$S_{\text{m}} = \frac{1}{2}\left[ {\left( {\frac{{\Delta p}}{{\Delta p't}}} \right)_{{r_{1} }} - \ln \left( {\frac{{k_{\text{f}} t_{r1} }}{{s_{\text{T}} \mu r_{\text{w}}^{ 2} }}\frac{1}{w}} \right) + 7.43} \right]$$
(29)
$$k_{\text{f}} = \frac{{70.6q\mu \beta_{\text{o}} }}{{h\left( {\Delta p't} \right)}}$$
(30)

In a reservoir with a wellbore storage effect, the effect of early time represented by the straight line is nonexistent. After the early time, the transition period connects the early and late times. Here, the depth of the trough is dependent on the value of the Warren and Root storage coefficient (w) but not on the interporosity parameter (\(\lambda\)). The dimensionless terms depicting this timeline are defined as

$$\omega = 0.15866\left\{ {\frac{{\left( {\Delta p^{'} t} \right)_{\text{min} } }}{{\left( {\Delta p^{'} t} \right)_{\text{r}} }}} \right\} + 0.54653\left\{ {\frac{{\left( {\Delta p^{'} t} \right)_{\text{min} } }}{{\left( {\Delta p^{'} t} \right)_{\text{r}} }}} \right\}^{2}$$
(31)
$$\lambda = \frac{{42.5hs_{\text{T}} r_{\text{w}}^{2} }}{{q\beta_{\text{o}} }}\left( {\frac{\Delta p't}{t}} \right)_{\text{min} }$$
(32)

The late time of the Engler and Tiab (1996) pressure derivative plot exists in both the damaged and undamaged scenarios. Moreover, this period gives the idealistic representation of the mechanical skin (Sm) and the wellbore storage coefficient (C).

$$S_{\text{m}} = \frac{1}{2}\left[ {\left( {\frac{\Delta p}{{\Delta p^{'} t}}} \right)_{{r_{2} }} - \ln \left( {\frac{{k_{\text{f}} t_{r2} }}{{s_{\text{T}} \mu r_{\text{w}}^{2} }}} \right) + 7.43} \right]$$
(33)
$$C = \left\{ {_{{\left( {\frac{{q\beta_{\text{o}} }}{24}} \right)\frac{t}{{\Delta p^{'}* t}}}}^{{\left( {\frac{{q\beta_{\text{o}} }}{24}} \right)\frac{t}{\Delta p}}} } \right.$$
(34)

Rezk (2016) studied different pressure transient analysis techniques applicable in naturally fractured reservoirs. He considered PTA by Warren and Root (1963) model, Engler and Tiab (1996) and other types of type-curve matching. He concluded that the model proposed by Engler and Tiab offered various advantages compared to the conventional semi-log analysis by Warren and Root (1963). Most of the previous approaches at studying the behavior of fluid flow in naturally fractured reservoirs have strictly assumed no significant changes in the rock properties with pore pressure, effective stress and temperature (Berumen and Tiab 1997; Pedrosa 1986). As such these models are expected to fail when applied to a reservoir with stress-sensitive rock properties. Stress-dependent properties are typically associated with low-permeability formations, geopressured formations and fractured formations (Pedrosa 1986). Early works by various authors such as Cinco-Ley et al. (1985), Ostensen (1986), Pedrosa (1986), Raghavan et al. (1972), Samaniego et al. (1985) and Yilmaz et al. (1994) considered pressure-dependent rock properties in pressure transient analysis for both conventional rocks and naturally fractured rocks. In most modeling approaches, these authors applied numerical techniques in obtaining solutions to both the linear and radial flow diffusivity equations under the assumption of either constant flowing wellbore pressure or constant well flow rate.

Pedrosa (1986) applied a form of the Cole–Hopf transformation to convert the nonlinear diffusivity equation into a linear diffusivity equation that can be solved using an analytical technique. The nonlinear diffusivity equation is expressed in a dimensional form in Eq. (35) and in a dimensionless form in (36), for a well producing at a constant well rate in an infinite-acting radial system. These equations are

$$\frac{{\partial^{2} p}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial p}{\partial r} + \left( {C_{\text{L}} + \gamma } \right)\left( {\frac{\partial p}{\partial r}} \right)^{2} = \frac{\phi \mu }{k}\left( {C_{\text{L}} + C_{\text{m}} } \right)\frac{\partial p}{\partial t}$$
(35)

and

$$\frac{{\partial^{2} p_{\text{D}} }}{{\partial r_{\text{D}}^{2} }} + \frac{1}{{r_{\text{D}} }}\frac{{\partial p_{\text{D}} }}{{\partial r_{\text{D}} }} - \gamma_{\text{D}} \left( {\frac{{\partial p_{\text{D}} }}{{\partial r_{\text{D}} }}} \right)^{2} = {\text{e}}^{{\gamma_{\text{D}} p_{\text{D}} }} \frac{{\partial p_{\text{D}} }}{{\partial t_{\text{D}} }}$$
(36)

In the final model, the author proposed a key parameter known as γD to study the effect of pressure on the formation permeability. The reservoir model as described has an initial condition and inner and outer boundary conditions as expressed by Eqs. (37)–(39), respectively:

$$p_{\text{D}} \left( {r_{\text{D}} ,t_{\text{D}} = 0} \right) = 0$$
(37)
$$\mathop {\lim }\limits_{{r_{\text{D}} \to o}} \left( {r_{\text{D}} {\text{e}}^{{ - \gamma_{\text{D}} p_{\text{D}} }} \frac{{\partial p_{\text{D}} }}{{\partial t_{\text{D}} }}} \right) = - 1$$
(38)
$$\mathop {\lim }\limits_{{r_{\text{D}} \to \infty }} p_{\text{D}} (r_{\text{D}} ,t_{\text{D}} ) = 0$$
(39)

In Eqs. (37)–(39), the dimensionless terms are defined as

$$r_{\text{D}} = \frac{r}{{r_{\text{w}} }},\quad t_{\text{D}} = \frac{{k_{\text{i}} t}}{{\phi_{\text{i}} \mu \left( {C_{\text{L}} + C_{\text{m}} } \right)r_{\text{w}}^{2} }},\quad p_{\text{D}} = \frac{{2\pi k_{\text{i}} h}}{q\mu }\left( {p_{\text{i}} - p} \right),\quad \gamma_{\text{D}} = \frac{q\mu }{{2\pi k_{\text{i}} h}}\gamma$$

A limitation of the model as described by Pedrosa (1986) for flow in a stress-sensitive formation is the non-inclusion of properties representative of a naturally fractured formation. Berumen and Tiab (1997) studied the flow of a slightly compressible fluid of constant viscosity through a fracture located along the focal point/center of the reservoir. In the work, the authors assumed a high-velocity flow in both the fracture and formation. Such high-velocity flow could be represented by combining a Forchheimer transport equation

$$\vec{u} = - \delta \frac{k\left( p \right)}{\mu }\nabla p$$
(40)

with the continuity equation

$$- \nabla \cdot \left( {\rho_{\text{f}} \vec{u}} \right) + \frac{{q_{\text{f}} \left( {x,t} \right)}}{h} = \frac{{\partial \left( {\phi \rho_{\text{f}} } \right)}}{\partial t}$$
(41)

All the models presented so far have been for vertical well-types. However, fields with naturally fractured reservoirs have since witnessed the use of horizontal wells. Horizontal wells have gained wide acceptance in the industry, especially in the development of unconventional reservoirs because it accelerates production, increases recovery and minimizes pressure drop along the wellbore. Chen et al. (2019) developed a semi-analytical model for the pressure transient analysis of fractured horizontal well with natural fracture networks. This work highlights the behavior of the pressure derivative in formations with both natural and hydraulic fractures and networks. The authors identified six flow regimes and provided a guide to analyzing fracture networks.

3.2 Pressure transient analysis of vuggy reservoirs

Vuggy reservoirs are composed of many reservoir bodies each of which may exhibit distinct fluid and pressure systems (Chen et al. 2017). These are features created as a result of dissolution processes that result in discontinuities within the reservoir (Barros-Galvis et al. 2015). Reservoir engineers have referred to these discontinuities as a type of pore system regardless of its origin. Vugs are a type of pore system and can be classified differently based on pore space genesis (Choquette and Pray 1970). Petrophysical properties as well as pore size distribution are also used to classify vugs within a rock. Vuggy pore space is classified into two: touching and separate vuggy pores. Touching vugs form an interconnected pore system while separate vugs have larger pore space than the particle size and are interconnected only through the interparticle pore network. The permeability of vuggy porous media depends on its interconnection of the pore space.

Literature has shown that the development of vuggy carbonate reservoirs has received attention for over 25 years, with most activities in China (Yao 2010). Shengeli and Tahe oil fields have been developed for over 15 years. There are significant fracture networks in these fields and water injections have been implemented in both fields to increase production. It is reported that the field recovery factor of these vuggy reservoirs is between 13% and 15% and has thus received less attention compared with the conventional oil reservoirs. Also, a rapid annual decline rate of 25% is experienced due to a lack of adequate understanding of the flow mechanics in such reservoirs. Xiong et al. (2016) provided an explanation of observations on the pressure derivative curves for the vuggy-fractured reservoirs via an experimental technique. This was to highlight the governing characteristics of fluid exchange in vuggy reservoirs and to highlight some theoretical claims in the literature. The model developed was tested and had a reasonable accuracy level. However, comparison with other existing techniques was not made. Moreover, the fluid-rock material exchange had been observed to affect flow characteristics. This phenomenon was however not captured by the authors.

Vuggy reservoirs from a geological viewpoint have experienced multiple processes including hydrocarbon accumulation, karst superposition and tectonic movements, etc. and are characterized by permeability anisotropy and heterogeneity. Additionally, this type of reservoir exhibits different porosity types and fluid flow mechanisms (cavity-free fluid flow and flow within the matrix), with a laminar flow regime in low-permeability matrices and turbulent flow in cavities (Li et al. 2019). The complicated fluid flow patterns within the matrix and cavity make the understanding of the flow mechanism difficult.

Vuggy reservoirs are identified to have the following characteristics.

  1. 1.

    Vuggy reservoirs exhibit multiple storage categories including fractures, vugs, cavities and matrix.

  2. 2.

    The scale of variation (anisotropy) is wide.

  3. 3.

    High heterogeneity as a result of post-diagenesis activities.

The above characteristics of the vuggy reservoir are responsible for the complexity of the flow mechanism resulting in difficulty in modeling such reservoirs. Due to multiple storage mediums, there exist dual and triple-porosity models for the vuggy reservoir system. Vuggy reservoirs are known to consist of both vugs and matrix systems. The physical properties of the formation matrix are considerably different from those of vugs. Also, the vugs are dispersed within the matrix system. Several models have been proposed for vuggy reservoirs considering vug geometries, pressure distributions and fluid flow mechanisms. One of the early works on naturally fractured reservoirs was presented by Warren and Root in 1963. However, an abnormal change in well pressure test slope over the transient period was observed in some reservoir transient pressure data. This slope change is due to the flow assumption of the homogenous matrix system. Because some naturally fractured reservoirs matrices can also be vuggy, a pseudo-steady-state triple-porosity model was proposed to describe the fluid flow in such reservoirs.

Traditional pressure transient analysis has been used as a method in the identification of different flow regimes and the determination of appropriate reservoir and fractures parameters. The presence of a complex geometric pore system poses challenges when applying conventional PTA in naturally fractured and vuggy reservoirs. In recent times, several authors have proposed modifications to existing PTA models to better characterize this complex pore system. Researchers such as Fuentes-Cruz et al. (2004) applied PTA to partially penetrating wells in a naturally fractured vuggy system. The authors observed that the presence of vugs and/or caves may have a significant effect on the transient pressure and production curve behaviors. Fuentes-Cruz et al. (2004) studied the pressure behavior of naturally fractured vuggy reservoirs and the influence of secondary pore type on the shape of the production decline curve. The authors concluded that it is important to introduce the effect of the secondary porosity during type-curve matching. Guo et al. (2012) proposed a dual-permeability model to analyze the production behavior of a horizontal well in naturally fractured vuggy carbonate rocks. The authors assumed that the vugs are dispersed within the reservoir pore system implying the existence of only a two-pore system (matrix and fractures). They concluded that the type curve is strongly controlled by the interporosity flow characteristics, the existence of seven flow regimes for a constant-rate production and five flow regimes for a constant wellbore-pressure system. Nie et al. (2012) proposed a dual-porosity and dual-permeability approach to study flow behavior of a producing horizontal well in a naturally fractured reservoir formation. In contrast to the single-permeability modeling approach, the authors observed a significant difference in the type curve due to the addition of a direct flow link between the matrix and wellbore. Chen et al. (2016a, b) applied a numerical approach to study the flow behavior in a naturally fractured vuggy carbonate reservoir with large caves. The authors obtained pressure behavior using the Stehfest numerical inversion method. They observed that well radius affects the nature of the concavity and convexity of the curve.

Velazquez et al. (2005) proposed two models that describe the flow in naturally fractured vuggy carbonate reservoirs during transient and pseudo-steady-state interporosity flow. The first model considers flow from matrix and vugs to the fracture (triple-porosity/single-permeability), while the second model considers flow between interconnected vugs, in addition, to flow from matrix and vugs to fractures (triple-porosity/dual-permeability). The derivation of PDE for the triple-porosity/dual-permeability model presented by Velazquez et al. (2005) is shown hereunder.

The equation describing flow in the fracture system is given by

$$\kappa \frac{1}{{r_{\text{D}} }}\frac{\partial }{{\partial r_{\text{D}} }}\left( {r_{\text{D}} \frac{{\partial p_{\text{Df}} }}{{\partial r_{\text{D}} }}} \right) + \lambda_{\text{mf}} \left( {p_{\text{Dm}} - p_{\text{Df}} } \right) + \lambda_{\text{vf}} \left( {p_{\text{Dv}} - p_{\text{Df}} } \right) = \omega_{\text{f}} \frac{{\partial p_{\text{Df}} }}{{\partial t_{\text{D}} }}$$
(42)

while that describing flow in the matrix blocks is

$$- \lambda_{\text{mv}} \left( {p_{\text{Dm}} - p_{\text{Df}} } \right) - \lambda_{\text{mf}} \left( {p_{\text{Dm}} - p_{\text{Df}} } \right) = \left( {1 - \omega_{\text{f}} - \omega_{\text{v}} } \right)\frac{{\partial p_{\text{Dm}} }}{{\partial t_{\text{D}} }}$$
(43)

Furthermore, flow in the vugs is described by

$$\left( {1 - \kappa } \right)\frac{1}{{r_{\text{D}} }}\frac{\partial }{{\partial r_{\text{D}} }}\left( {r_{\text{D}} \frac{{\partial p_{\text{Dv}} }}{{\partial r_{\text{D}} }}} \right) + \lambda_{\text{mv}} \left( {p_{\text{Dm}} - p_{\text{Dv}} } \right) - \lambda_{\text{vf}} \left( {p_{\text{Dv}} - p_{\text{Df}} } \right) = \omega_{\text{v}} \frac{{\partial p_{\text{Dv}} }}{{\partial t_{\text{D}} }}$$
(44)

where

$$\begin{aligned} \lambda_{\text{mf}} & = \sigma_{\text{mf}} k_{\text{m}} r_{\text{w}}^{2} /\left( {k_{\text{f}} + k_{v} } \right),\,\,\,\,\lambda_{\text{mv}} = \sigma_{\text{mv}} k_{\text{m}} r_{\text{w}}^{2} /\left( {k_{\text{f}} + k_{\text{v}} } \right), \\ \lambda_{\text{vf}} & = \sigma_{\text{vf}} k_{\text{vf}} r_{\text{w}}^{2} /\left( {k_{\text{f}} + k_{\text{v}} } \right),\,\,\,\,\kappa = k_{\text{f}} /\left( {k_{\text{f}} + k_{\text{v}} } \right), \\ \end{aligned}$$
$$\begin{aligned} t_{\text{D}} & = \left( {k_{\text{f}} + k_{\text{v}} } \right)t/\phi_{\text{f}} \left( {k_{\text{f}} + k_{\text{v}} } \right),\,\,\,\,\omega_{\text{f}} = \phi_{\text{f}} c_{\text{f}} /\left( {\phi_{\text{f}} c_{\text{f}} + \phi_{\text{m}} c_{\text{m}} + \phi_{\text{v}} c_{\text{v}} } \right),\,\,\,{\text{and}} \\ \omega_{\text{v}} & = \phi_{\text{v}} c_{\text{v}} /\left( {\phi_{\text{f}} c_{\text{f}} + \phi_{\text{m}} c_{\text{m}} + \phi_{\text{v}} c_{\text{v}} } \right). \\ \end{aligned}$$

In the case of the triple-porosity/single-permeability model, kf and kv are set to zero (i.e., κ = 1) except in λvf. The Laplace-space solutions to the triple-porosity/single-permeability model are

$$\overline{{p_{\text{Dv}} }} = \overline{{p_{\text{Df}} }} \left[ {(b_{1} + b_{2} u} \right)/\left( {b_{3} + b_{4} u + b_{4} u^{2} } \right)]$$
(45)

and

$$\overline{{p_{\text{Dm}} }} = \overline{{p_{\text{Df}} }} \left( {\frac{{c_{1} + uc_{2} + u^{2} c_{3} }}{{d_{1} + ud_{2} + u^{2} d_{3} + u^{3} d_{4} }}} \right)$$
(46)

Applying boundary conditions, the solution at the wellbore is given by

$$\overline{{p_{\text{wD}} }} = \frac{{K_{0} \left[ {\sqrt {g\left( u \right)} } \right] + s\sqrt {g\left( u \right)} K_{1} \left[ {\sqrt {g\left( u \right)} } \right]}}{{u\sqrt {g\left( u \right)} K_{1} \left[ {\sqrt {g\left( u \right)} } \right] + C_{\text{D}} u\left\{ {K_{0} \left[ {\sqrt {g\left( u \right)} } \right] + s\sqrt {g\left( u \right)} K_{1} \left[ {\sqrt {g\left( u \right)} } \right]} \right\}}}$$
(47)

For the no-flow boundary condition,

$$\overline{p}_{\text{Df}} = \frac{{K_{1} \left[ {\sqrt {g\left( u \right)} r_{\text{eD}} } \right]I_{0} \left[ {\sqrt {g\left( u \right)} r_{\text{D}} } \right] + I_{1} \left[ {\sqrt {g\left( u \right)} r_{\text{eD}} } \right]K_{0} \left[ {\sqrt {g\left( u \right)} r_{\text{D}} } \right]}}{{u\sqrt {g\left( u \right)} \left\{ {K_{1} \left[ {\sqrt {g\left( u \right)} } \right]I_{1} \left[ {\sqrt {g\left( u \right)} r_{\text{eD}} } \right] - I_{1} \left[ {\sqrt {g\left( u \right)} } \right]K_{1} \left[ {\sqrt {{{g}}\left( {u} \right)} {{r}}_{\text{eD}} } \right]} \right\}}}$$
(48)

and

$$\bar{p}_{\text{wD}} = \frac{1}{{u^{2} \bar{q}_{\text{wD}} }}$$
(49)

The Laplace-space solutions to the triple-porosity/dual-permeability model are

$$\bar{p}_{\text{Df}} = \lambda_{1} A_{1} K_{0} \left( {\alpha_{1} r_{\text{D}} } \right) + \lambda_{2} A_{2} K_{0} \left( {\alpha_{2} r_{\text{D}} } \right) + \lambda_{3} B_{1} K_{0} \left( {\alpha_{1} r_{\text{D}} } \right) + \lambda_{4} B_{2} K_{0} \left( {\alpha_{2} r_{\text{D}} } \right)$$
(50)

and

$$\bar{p}_{\text{Dv}} = \lambda_{1} K_{0} \left( {\alpha_{1} r_{\text{D}} } \right) + \lambda_{2} K_{0} \left( {\alpha_{2} r_{\text{D}} } \right) + \lambda_{3} I_{0} \left( {\alpha_{1} r_{\text{D}} } \right) + \lambda_{4} I_{0} \left( {\alpha_{2} r_{\text{D}} } \right)$$
(51)

The pressure response for the triple-porosity/single-permeability (unconnected vugs) model is shown in Fig. 10 for different values of λmf, \(\lambda_{\text{vf}}\), λmv, ωf and ωv. A semi-log straight line appears at the early-time period which points to a fracture-controlled flow. Also, a similar semi-log straight line appears at the late time indicating a homogenous flow in the system components (fractures, vugs and matrix) where pressure is the same. The figure also shows anomalous slopes in the transient period with a slope ratio of around 2:1 of the early and late time. These slopes appear in this segment due to the presence of vugs. Also, these slopes are functions of λvf/λmf and λmv/λmf.

Velazquez et al. (2005) also examined the analytical decline curves of unconnected vugs at different values of λmf, \(\lambda_{\text{vf}}\), λmv, ωf and ωv in comparison with the double-porosity model proposed by Da Prat et al. (1981). The authors found significant differences between unconnected vugs and double-porosity behavior especially in the transient period as shown in Fig. 11. In some cases, the differences can also be observed in the boundary dominated periods.

Fig. 11
figure 11

Vuggy reservoir plot for dual-porosity (Velazquez et al. 2005)

Full size image

Unlike the case of unconnected vugs, the authors did not observe a straight line in the semi-log plot during the early transient period. The difference in pressure responses during the transient period becomes larger at bigger ωf values. However, the straight line is observed in the late time once the homogenous flow is attained. The authors also compared the rate responses of triple-porosity/single-permeability, triple-porosity/dual-permeability and double-porosity/double-permeability model of Da Prat et al. (1981). It was observed that differences in the rate occurred between the triple and double-porosity models during the boundary-dominated period, while differences in rate between the single and dual-permeability models were observed in the transient period (Fig. 12).

Fig. 12
figure 12

Single and dual permeability is observed in the transient segment (Velazquez et al. 2005)

Full size image

Although Velazquez et al. (2005) included the skin factor of a system in the transient flow solution of connected vugs, they did not discuss it in detail. The analysis of skin effect is important to realistically model production decline.

Nie et al. (2012) studied the pressure transient analysis of a naturally fractured vuggy reservoir with triple-porosity using a quadratic pressure gradient term. For an isotropic system, the diffusivity equation with the quadratic pressure gradient term included is

$$\frac{1}{r}\frac{\partial }{{{\text{d}}r}}\left( {r\frac{{\text{d} p}}{{\text{d} r}}} \right) + C_{\text{p}} \left( {\frac{{\text{d} p}}{{\text{d} r}}} \right)^{2} = \mu \phi C_{\text{t}} \frac{{\text{d} p}}{{\text{d} t}}$$
(52)

The authors utilized a model that idealizes the naturally fractured reservoir matrix block and vugs as spherical and unsteady interporosity flow from the matrix to fracture as well as from vugs to fracture, with no discharge from the matrix to vugs (Fig. 13). The assumptions made include a slightly compressible single-phase fluid, isotropic reservoir, no fluid storage in fractures.

Fig. 13
figure 13

Flow schematic of a porous vuggy reservoir (Jia et al. 2013)

Full size image

The partial differential equation of the vug system was given by the authors as

$$\left( {\frac{{\partial^{2} p_{\text{vD}} }}{{\partial r_{\text{vD}}^{2} }} + \frac{2}{{r_{\text{rD}} }}\frac{{\partial p_{\text{vD}} }}{{\partial r_{\text{vD}} }}} \right) + \beta \left( {\frac{{\partial p_{\text{vD}} }}{{\partial r_{\text{vD}} }}} \right)^{2} = \frac{{15\omega_{\text{v}} }}{{\lambda_{\text{v}} C_{\text{D}} }}\frac{{\partial p_{\text{vD}} }}{{\partial t_{\text{D}} }}$$
(53)

Their findings showed that the shapes of the pressure derivative curves are affected by the interporosity flow factor from vugs to fracture (λv) and interporosity flow factor from the matrix to fracture (λm). Similarly, the value of λ controls the concave-shape observed in the later period of interporosity flow.

Jia et al. (2013) studied a vuggy-matrix double-porosity carbonate reservoir system in the Tahe oilfield of China. Unlike other double-porosity models where a matrix-fracture continuum is considered, the model proposed by Jia et al. (2013) was developed with the assumption that the vugs are uniformly dispersed (not connect) and that vugs-matrix interporosity flow occurs under an unsteady state in non-fractured carbonate reservoirs. Thus, in such a model, fluid flow occurs from the vugs to the matrix and from the matrix to the wellbore as depicted in Fig. 14.

Fig. 14
figure 14

Flow schematic of the porous vuggy reservoir (Jia et al. 2013)

Full size image

Several assumptions were made to formulate the model describing the flow such as single-phase flow behavior, homogenous and isotropic system, slightly compressible system. The equation governing flow in the matrix system (in a cylindrical coordinate system) is

$$\frac{{\partial^{2} \bar{p}_{\text{mD}} }}{{\partial r_{\text{mD}}^{2} }} + \frac{1}{{r_{\text{mD}} }}\frac{{\partial \bar{p}_{\text{mD}} }}{{\partial r_{\text{mD}} }} - \frac{1}{5}\lambda_{\text{vm}} \exp ( - 2s)\left. {\left( {\frac{{\partial \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}} }}} \right)} \right|_{{r_{\text{vD}} = 1}} = z\omega_{\text{m}} \exp ( - 2s)\bar{p}_{\text{mD}}$$
(54)

while that governing flow in the vug system (in a spherical coordinate system) is

$$\frac{{\partial^{2} \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}}^{2} }} + \frac{2}{{r_{\text{vD}} }}\frac{{\partial \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}} }} = \frac{{15z\omega_{\text{v}} }}{{\lambda_{\text{v}} }}\bar{p}_{\text{vD}} \,\,\,\,(0 < r_{\text{vD}} < 1)$$
(55)

The authors solved the dimensionless differential equations using Laplace transforms and inverted to real-space via Stephfest numerical inversion. This model was tested by matching real data to the log–log type-curves from the model.

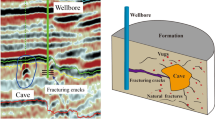
3.3 Pressure transient analysis for caves

Although many well testing models have been developed for triple-porosity systems, such models lack a reasonable approximation of volumes and connectivity of large caves with the radius as big as tens of meters (Pang et al. 2019). Thus, Pang et al. (2019) developed a pressure transient model for a well that penetrates through a cave. The model introduces fluid flow and pressure wave propagation concept and diagnoses the cave’s volume. Moreover, the model defines three parameters that affect the pressure response in the log–log plot. These parameters are wave coefficient, damping coefficient and cave shape factor. The model is given as follows.

Darcy flow in matrix outside wellbore:

$$\frac{1}{{r_{\text{D}} }}\frac{\partial }{{\partial r_{\text{D}} }}\left( {r_{\text{D}} \frac{{\partial p_{{ 1 {\text{D}}}} }}{{\partial r_{\text{D}} }}} \right) = \frac{{\partial p_{{1{\text{D}}}} }}{{\partial t_{\text{D}} }}$$
(56)

Darcy flow in the matrix outside the cave:

$$\frac{1}{{r_{\text{D}} }}\frac{\partial }{{\partial r_{\text{D}} }}\left( {r_{\text{D}} \frac{{\partial p_{{ 2 {\text{D}}}} }}{{\partial r_{\text{D}} }}} \right) = \frac{{\partial p_{{2{\text{D}}}} }}{{\partial t_{\text{D}} }}$$
(57)

The wellbore flow is modeled by

$$p_{\text{wfD}} = \left( {p_{{1{\text{D}}}} - s_{\text{w}} r_{\text{D}} \frac{{\partial p_{{ 1 {\text{D}}}} }}{{\partial r_{\text{D}} }}} \right)|_{{r_{\text{D}} = 1}} ,$$
(58)

while the flow in the cave is modeled by

$$p_{\text{vD}} = \left( {p_{{2{\text{D}}}} - s_{\text{v}} r_{\text{D}} \frac{{\partial p_{{ 2 {\text{D}}}} }}{{\partial r_{\text{D}} }}} \right)|_{{r_{\text{vD}} }}$$
(59)

The inner boundary condition is given by

$$1 = C_{\text{wD}} \frac{{\partial p_{\text{wfD}} }}{{\partial t_{\text{D}} }} + C_{\text{vD}} \frac{{\partial p_{\text{vD}} }}{{\partial t_{\text{D}} }} - \left[ {\lambda \frac{{\partial p_{{ 1 {\text{D}}}} }}{{\partial r_{\text{D}} }}|_{{r_{\text{D}} = 1}} + \left( {1 - \lambda } \right)r_{\text{vD}} \frac{{\partial p_{{ 2 {\text{D}}}} }}{{\partial r_{\text{D}} }}|_{{r_{\text{vD}} }} } \right]$$
(60)

Outer boundary:

$$\frac{{\partial \overline{{p_{{ 1 {\text{D}}}} }} }}{{\partial r_{\text{D}} }}|_{{r_{{{\text{eD}}1}} }} = \frac{{\partial \overline{{p_{{ 2 {\text{D}}}} }} }}{{\partial r_{\text{D}} }}|_{{r_{{{\text{eD}}2}} }} = 0$$
(61)

Also, the relation between dimensionless bottomhole pressure and dimensionless cave pressure is

$$\overline{{p_{\text{wfD}} }} = \overline{{p_{\text{vD}} }} - C_{\text{pD}} t_{\text{D}}^{\alpha - 1} {\text{e}}^{{ - C_{\text{aD}} t_{\text{D}} }}$$
(62)

where CaD is the dimensionless wave coefficient that describes the wave flow in caves while CpD is the dimensionless damping coefficient which describes pressure drop in caves. Also, α is the cave shape factor that accounts for the difference in shape between the actual cave and an ideal cylindrical cave. The authors obtained the solution to the set of equations in (56)–(61) in the Laplace domain. Using this solution, the authors studied the effect of key parameters on the log–log pressure and pressure derivative-type curves. The plot was divided into four regions starting with wellbore storage followed by a transition period from wellbore storage to cave storage, full cave storage stage and finally, the formation-dominated transient flow. Figure 15 shows that the wave coefficient affects the pressure response. The higher the CaD the longer wellbore storage effect and subsequently the later wellbore/cave storage transition. Also, the bigger the CaD the less pressure drop is observed in the full cave storage period. The matrix-dominated transient flow is the only segment that is not affected.

Fig. 15
figure 15

Impact of wave coefficient on the pressure response (Ye et al. 2016)

Full size image

The effect of CpD on the wellbore storage period is lesser than that of CaD (Fig. 16). CpD also affects the sharpness of the trough seen on the pressure derivative curve beyond the wellbore storage period. It is observed that the time at which the trough appears is the same for all values of CpD as shown in Fig. 16. Finally, the effect of the shape factor α on the pressure and pressure derivative curves is shown in Fig. 17. It is observed that the shape factor affects the cave storage period.

Fig. 16
figure 16

Influence of wave coefficient on wellbore storage (Ye et al. 2016)

Full size image
Fig. 17
figure 17

Dimensionless plot with the effect of the shape factor (Ye et al. 2016)

Full size image

4 Field applications

Olarewaju (1997) applied pressure transient analysis to the Hanifa reservoir to provide insight into the abnormally high flow rates recorded by the flow meters. Also, the permeability derived from well test was observed to be 40 times greater than the permeability determined from core plugs. To resolve this, the author applied analytical pressure transient analysis to confirm the existence of naturally fractures. The findings confirmed the existence of a dual-permeability system in place. The author further asserted that the use of a dual-porosity model to analyze this reservoir will lead to error in interpretation, as significant portions of the reservoir have little or no fracture and the matrix block contributes to the production.

5 Comparison of different pressure transient analysis models

5.1 Naturally fractured reservoirs

In this section, analysis is made of the differences and similarities between the models developed for naturally fractured reservoirs, with emphasis laid on the applications of the models. It appears that in the early days of well test analysis, the geological model of a reservoir received much attention. For instance, Baker (1955) presented a method based on a geological model in which natural fissures of great extent characterized the formation. Pollard (1959) method was as a result of the fact that, from a geological point of view, the reservoir void space consisted of two types of voids. In a way, it was a pragmatic approach to solving the problem. However, the drawback of this approach was that it seems to apply only to that geological model. On the other hand, from a production viewpoint, Barenblatt et al. (1960) are the first to present a mathematical fluid flow model to describe flow dynamics in fissured formations based on fundamental laws of fluid mechanics. In his model, a homogeneous parallel system was set up to mimic primary porosity and fissures. This captured adequately the concept of property averaging as Darcy law is said to be valid for both the matrix and fissures in this setup. The Barenblatt et al. (1960) theory served as the fundamental basis upon which the Warren and Root (1963) model were developed, and their model accounting for different fractured reservoir types, with fluids either in the matrix or fissures.

The nature of the interaction between the matrix and the fissures is reflected by ω and A. However, the introduction of w and X to describe the fracture types has been a subject open to so many criticisms for years. Also, the presence of two parallel lines on the buildup test has received criticism as well for the wellbore storage that could have obscured the semi-log straight line. However, with the development of type curves, this concern was overcome.

Bourdet and Gringarten (1980) presented a method in which w and X can be determined by type-curve matching techniques, showing a practical and applicable method that can be used to analyze fractured reservoir’s pressure buildup test. Warren and Root’s model has been studied by several authors (Mavor and Ley 1979; Kazemi 1969; Bourdet and Gringarten 1980). The model has been extended to include transient interporosity flow and wellbore storage effects. According to the literature, it can be said that Warren and Root’s model laid the foundation for many practical applications. The development of models by Barenblatt et al. (1960) and Warren and Root (1963) was based on the internal source concept. Kazemi (1969) and Streltsova (1984) models are conceptually different models. These authors utilized a multilayered system for fracture modeling and solved the system of equations, with the source as a boundary condition which shows that there is no basis for comparison between Kazemi (1969), Streltsova’s model and Warren and Root (1963). Speaking from a geological viewpoint, a multilayer system is quite different from a vuggy, fissured/fractured one-layer reservoir, due to high permeability contrast.

From the practical viewpoint, the answer to the question of which model to use lies in the integration of pressure with geological models. An approach suggested by Ramey and Agarwal (1972) was to start with a simple homogenous system with conventional analysis and then build up from there as a basis to enable the achievement of pragmatic analysis.

5.2 Vuggy reservoirs

5.2.1 Triple-porosity model

To model fluid dynamics in vuggy reservoirs, reference is often made to models for naturally fractured reservoirs, such as dual-porosity and triple-porosity models and their extensions. The dual-porosity model was first developed by Barenblatt et al. (1960). Subsequently, Warren and Root proposed a complete dual-porosity model that has gained acceptance in naturally fractured reservoir modeling (Warren and Root 1963). Additionally, these models focused on the fluid flow between formation matrix and fractures (Kazemi et al. 1976; Coats 1989; Ueda et al. 1989; Saidi 1987; Thomas et al. 1983). Based on the classical dual-porosity model, a model which subdivided the fracture grids into sections and accounting for the multiple interactions was proposed (Wu and Pruess 1988; Wu et al. 2011).

In the development of models for vuggy reservoirs, flow behavior was encountered which could not be explained by the dual-porosity model. Thus, the triple-porosity model was proposed, and this has found application in several fields. The triple-porosity effect has been shown by several authors (Yao et al. 2010) to be distinguishable in well test and has recently been extended by Kang et al. (2006) and Wu et al. (2011). The triple-porosity model can account for mass exchange between matrix, fracture and vug systems as well as the preferential flow phenomena. However, the triple-porosity model does not account for full-physics and thus is still an approximation to the actual flow behavior of naturally fractured vuggy systems.

5.2.2 Equivalent-medium model

This concept is different from the dual and triple-porosity models in that it assumes a fracture-vuggy reservoir as a continuous porous media with its heterogeneity represented by equivalent parameters. This model is simple and has a far-reaching application in rock hydraulics (Yao et al. 2010), with high calculation efficiency. Single-phase flow has its theoretical basis established over the decades with limited theories that account for multiphase flow and calculated the equivalent properties such as permeability and capillary curves (Yao et al. 2010; Kang et al. 2006). The theoretical basis for the equivalent flow model is aimed at reducing the order of the flow governing equation on a fine scale which is pivoted on scale theory. Thus, this is a macroscopic approach that reduces the heterogeneity effect and may lead to loss of signatures of vugs and fractures. Jia et al. (2013) presented an oversampling methodology to account for the macroscopic heterogeneity and connectivity in fracture-vuggy mediums at a coarse grid scale. His model proved to be more accurate and efficient as compared to the equivalent-medium model. However, the model showed significant error in multiphase flow prediction due to its failure to capture the physics of flow at a fine scale in vugs and fractures (Yao et al. 2010).

5.2.3 Discrete medium model

Discrete surfaces of varying properties may result from a long period of geologic processes on carbonate rocks. A discrete vuggy system is often a result of washouts at varying periods. Thus, it is presumed that all formations growing with vugs are discrete and are categorized under the discrete medium model. This concept was first proposed for rock hydraulics by Snow (1969). However, what is currently used is a model proposed by Noorishad and Mehran (1982). The authors utilized the upstream technique to solve a 2D-solute diffusivity problem using finite-element analysis. In their approach, 2D and 1D surfaces were used for rock and fracture, respectively, with both of these coupled using the principle of superposition. However, the model had limited application in the petroleum industry prior to 1999, when it was applied to simulate a two-phase flow (Kim and Deo 1999). Since then, several methods (Galerkin finite-element method; finite-volume method; finite-difference method, etc.) have been proposed and have served as an extension of the discrete model technique (Yao et al. 2010). Explicit description of vugs has been achieved by the discrete model using flux equivalent principal considering flows in fractures as seepages. These models have a good representation of reality as well as high precision and can be used to solve dual and triple-porosity problems as well as the equivalent-medium problems. Pulido et al. (Pulido et al. 2011) developed a similar approach with the inclusion of skin factor impact analysis. Additionally, Velazquez et al. (2005) made no distinction between channel, vugs or caves. The authors considered all additional porosity generated by dissolution in carbonate as vuggy porosity. This assumption may not be valid for caves with a large radius.

6 Conclusion and recommendations

In this work, we considered various methods describing highly heterogeneous forms of reservoir formations, with classification into the naturally fractured reservoirs with and without vugs and caves serving as the basis for model analysis and comparison. In describing the pattern of fluid flow within these formations, modeling attempts have been made to use either the porosity or permeability types to correct the changes in the pressure diffusivity equations. Most of the models reviewed have pros and cons depending on the condition under which each model is applied. For example, to model flow in formations with natural fractures or vugs, it is important to characterize the different porosity or permeability systems due to the varying relationships between the properties of the multiple media that make up the reservoir. Furthermore, in modeling flow in naturally fractured mediums, only Warren and Roots model have found wide-spread applications in many formation types. Thus, most of the recent techniques of pressure transient analysis in naturally fractured and vuggy reservoirs are based on the Warren and Roots model.

Furthermore, models for vuggy reservoirs have been based on the models developed for naturally fractured reservoirs, with the resulting models classified into equivalent-medium models and discrete medium models. These models differ from the dual and triple-porosity models in their assumption of the vuggy system as a continuum. Explicitly, the choice of models highly depends on the uniqueness or peculiarity of the candidate reservoir in question, how much information is available and what inference can be made of its data. Research in this area is still very active as there are ongoing efforts to improve the interpretation of data from these formations.