Introduction

Detrimental mineral deposition in formations that are operated to produce oil is known as one of the most problematic issues in the petroleum industry, especially when scales of barium and calcium sulfate cause a significant reduction in permeability due to pore throat plugs in reservoir rocks. Besides, these scales can adversely affect the productivity of wells through blocking tubing and casings (Boon et al. 1983; Cusack et al. 1987; Ahmed 2004). A mineral deposition is heavily and strongly influenced by a variety of parameters such as temperature fluctuation, pressure reduction, and getting mixed incompatible waters (Bertero et al. 1988; BinMerdhah et al. 2010; Moghadasi 2004).

Moreover, deposition of sulfate scales is mainly caused by the injection of seawater saturated with sulfate anion into a formation containing high calcium, strontium, and barium cations for water flooding (Crabtree et al. 1999; Moghadasi et al. 2004; Frenier and Ziauddin 2008; Khatami et al. 2010; McElhiney 2001; Collins 2005). As for water incompatibility, barium sulfate scales are also formed with changes in the pressure, temperature, and concentration of relevant ions (BinMerdhah et al. 2010; Crabtree et al. 1999; Frenier and Ziauddin 2008; Liu et al. 2009). Based on the experiments done by Mitchell et al. (1980), taking inhibitor selection as the main topic results in concluding barium sulfate scale precipitations as the particular major problem of North Sea fields (Mitchell et al. 1980). The acquired result was later shown by Read and Ringen, who injected a mixture of seawater and North Sea formation water to synthetic alumina cores under special conditions, and a considerable reduction in permeability was observed due to scaling (Read and Ringen 1982). The possibility of calcium sulfate and strontium sulfate scaling due to seawater injection was experimentally evaluated on samples gathered from an Arab-D reservoir in the northern area of the Ghawar field. Lindlof and Stoffer (1983) finalized that the amounts of strontium sulfate precipitation certified their already calculations, and a mixture of seawater and Arab-D formation water caused the existence of scale formation in the wellbore when the flow was turbulent.

Scale formation as a result of incompatibility between injected seawater and formation water once again turned into a topic that investigated the Namorado field in Brazil. Precipitation stopping procedures were accompanied by a high rate of water production to block formations of strontium and barium sulfate, studied by Bezerra et al. (1990). Aliaga et al. (1992) showed the wavy behavior of dissolution and precipitation in the reservoir. They conducted flooding experiments in sand packs to study and quantify a permeability reduction and inferred that geochemical flow models can be employed in a case of having solid migration. Considerable scale deposition can occur when two incompatible waters were injected concurrently into a rock core, a result that was deduced when a sensitivity analysis was run to observe the effect of temperature on barium and strontium sulfate scale formation. According to tests performed to investigate scale formation kinetics, Wat (1992) proposed that the kinetics of scale formation  plays a significant role in modeling of formation damage. Furthermore, mixing in situ-based synthetic seawater with formation water that has a significant amount of dissolved barium ions leads to making the precipitation of barium sulfate happen. It was observed by McElhiney (2001) when they studied the in situ precipitation of barium sulfate during core flooding experiments. Moghaddasi et al., who proposed a diversity of mechanisms for scale formation as a result of water injection, developed a model to predict correctly scaling deposition as a strong function of hydrodynamic and kinetic conditions in Iranian oil fields (Wat 1992; Moghadasi 2002, 2003a, b; Strachan 2004). CaSO4 precipitation was modeled to be slightly affected by pressure and notably impacted by temperature and a flood velocity, a result presented experimentally and theoretically through studying a permeability reduction as a consequence of mixing two incompatible solutions consisting of Ca2+ and SO42− ions. Strachan (2004) determined the effects of wettability alterations and permeability damages extracted from using aqueous-based polymeric and phosphonate precipitation inhibitors. Bedrikovetsky (2005) have observed that a flow velocity usually influences a reaction rate coefficient, and their studies led to the development of an analytical model to treat data generated with quasi-steady-state tests and later be extended by formulating a formation damage coefficient based on pressure drop measurements during core flooding. Merdhah and Yassin (2007, 2009) reported that increasing temperature, pressure head, and brine concentration had an unfavorable impact on the permeability reduction and reaction rate constant. Clarifying the constant for each model of scale deposition, more accurate for artificial cores than for natural reservoir cores based on a series of core flooding tests dependent on pressure measurements, was done by Carageorgos et al. (2010). Figuring the interaction between reservoir lithology and a scale inhibitor has recently turned into researchers’ interest like Todd (2012), who did some tests within modern phosphorus inhibitors that have some advantages in comparison with the conventional types. A comparison between these kinds of inhibitors alongside a number of other available P-containing polymers was also made. Ahmadi et al. (2017) used data analytics methods to develop a gray-box predictive tool for estimating the permeability reduction in the reservoir. They revealed that the hybrid of evolutionary optimizers could significantly improve the efficacy of the data-driven model.

This study aims to provide a simple machine learning model for estimating permeability reduction due to the scale deposition in a water injection process. Two different types of machine learning methods are employed to fulfill the aim of this paper; ANN and GA-LSSVM methods are those intelligent models used in the current paper. To develop and examine those machine learning models, high accuracy with infinitesimal uncertainty real data from the previous studies (BinMerdhah et al. 2010; Moghadasi et al. 2004; Merdhah and Yassin 2007, 2009; Merdhah et al. 2008; Zabihi et al. 2011) is used. Comparing those experimental results and those correlated with machine learning models in terms of statistical performance indexes provides appropriate information to make a decision on which methods work better.

Least squares support vector machine (LSSVM)

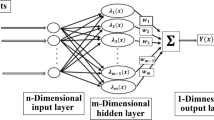
Suykens and Vandewalle (1999) proposed the original LSSVM model in 1999 for function estimation and regression. Overfitting problems may occur through classical SVM and feed-forward neural networks. The objective of the LSSVM is to overcome this hurdle. Consider given inputs Xi (flow rate, pressure difference, temperature, initial permeability, and ions concentration in formation water such as Sr2+, Ba2+, Ca2+, and SO42−) and output Yi (permeability reduction due to formation damage) time series. Table 1 reports the statistical properties of those input data samples employed for developing intelligent models in the current paper. A LSSVM nonlinear function can be represented as follows (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b):

$$\varvec{f}(\varvec{x}) = \varvec{w}^{T} \varvec{\varphi} (\varvec{x}) + \varvec{b}$$
(1)

where f expresses the connection between the target variable (permeability reduction ratio) and input variables (flow rate, pressure difference, temperature, initial permeability, and ions concentration in formation water such as Sr2+, Ba2+, Ca2+, and SO42−), w acts as an m-dimensional weight vector, φ plays a mapping function which maps x into the m-dimensional characteristic vector, and b represents the bias term (Kisi 2012; Ahmadi et al. 2014a).

Table 1 Statistical properties of the input parameters
Full size table

To minimize the risk of LSSVM structure, we have to solve the following problem (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b):

$${\text{Min}}\; {\mathcal{J}} (w,e) = \frac{1}{2}w^{T} w + \gamma \sum\limits_{k = 1}^{m} {e_{k}^{2} }.$$
(2)

But, the following limits should be considered (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b):

$$y_{k} = w^{T} \varphi (x_{k} ) + b + e_{k} \quad k = 1,2, \ldots,m$$
(3)

where γ and ek represent the margin parameter and loose variable for xk, respectively (Ahmadi and Pournik 2016; Ahmadi et al. 2015a, b, 2016; Ahmadi and Bahadori 2015).

Developing the limited issue into an unlimited issue and suggesting the Lagrange multipliers αi to figure out the objective function is a robust and effective way that can be used to find the solution of the optimization problem given in Eq. (2) which presents the following expression (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b):

$${\mathcal{L}}(w,b,e,\alpha) = {\mathcal{J}}(w,e) - \sum\limits_{k = 1}^{N} {\alpha_{k} \{ w^{T} \phi (x_{k} ) + b + e_{k} - y_{k}\}}.$$
(4)

According to the Karush–Kuhn–Tucker (KKT) investigation, the optimal states can be obtained by conducting the partial derivatives of Eq. (4) with respect to the parameters such as w, b, e, and α, respectively, as follows (Ahmadi et al. 2015a, b, 2016; Ahmadi and Pournik 2016; Ahmadi and Bahadori 2015; Ayatollahi et al. 2016; Hajirezaie et al. 2015, 2017a, b):

$$\frac{\partial {\mathcal{L}}(w,b,e,\alpha )}{\partial w} = 0 \to w = \sum\limits_{k = 1}^{N} {\alpha_{k} \varphi (x_{k} )}$$
(5)
$$\frac{\partial {\mathcal{L}}(w,b,e,\alpha )}{\partial b} = 0 \to \sum\limits_{k = 1}^{N} {\alpha_{k} } = 0$$
(6)
$$\frac{\partial {\mathcal{L}}(w,b,e,\alpha )}{{\partial e_{k} }} = 0 \to \alpha_{k} = \gamma e_{k} ,\quad k = 1, \ldots,N$$
(7)
$$\frac{\partial {\mathcal{L}}(w,b,e,\alpha )}{{\partial \alpha_{k} }} = 0 \to y_{k} = w^{T} \varphi (x_{k} ) + b + e_{k} ,\quad k = 1, \ldots ,N.$$
(8)

Thus, the linear equations are determined as follows: (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b):

$$\left[ {\begin{array}{*{20}l} 0 \hfill & { - Y^{T} } \hfill \\ Y \hfill & {ZZ^{T} + \frac{I}{\gamma }} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ \alpha \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]$$
(9)

where Y = Y1,…, Yym; Z = φ(X1)TYi,…, φ(Xm)TYm, I = [1,….,1], and α = [α1,…,α1]. By involving the kernel function K(X,Xk) = φ(X)Tφ(Xk), i = 1,2,…,m, the least squares SVM regression is expressed as follows (Ahmadi and Pournik 2016; Ahmadi et al. 2015a, b, 2016; Ahmadi and Bahadori 2015; Ayatollahi et al. 2016; Hajirezaie et al. 2015, 2017a, b; Ahmadi 2015, 2016):

$$f(x) = \sum\limits_{k = 1}^{N} {\alpha_{k} K(x,x_{k} ) + b}.$$
(10)

One of the well-known kernels is the radial basis function (RBF) kernel; in this paper, the RBF kernel is employed. It can be formulated as the following equation (Ahmadi and Pournik 2016; Ahmadi et al. 2015a, b, 2016; Ahmadi and Bahadori 2015; Ayatollahi et al. 2016; Hajirezaie et al. 2015, 2017a, b; Ahmadi 2015, 2016):

$$K(x,x_{k} ) = \exp ( - \left\| {x_{k} - x} \right\|^{2} /\sigma^{2} )$$
(11)

where \(\sigma^{2}\) represents the squared bandwidth that has to optimize using a robust optimization algorithm, genetic algorithm (GA), during calculations (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b). The objective function of the optimization approach is the mean squared error (MSE) between the results of the least squares SVM method and the corresponding experimental data samples which can be expressed as (Suykens and Vandewalle 1999; Suykens et al. 2002; Kisi 2012; Pelckmans et al. 2002; Ahmadi and Ebadi 2014; Ahmadi et al. 2014a, b):

$${\text{MSE}} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {{\text{scale}}_{{m_{i} }} - {\text{scale}}_{{f_{i} }} } \right)^{2} } }}{n}$$
(12)

where Scale, subscripts est, and act are the forecasted and measured formation damage values, respectively, and ns is the number of data banks from the initial population.

Genetic algorithm (GA)

A genetic algorithm (GA) is an evolutionary optimization algorithm which is developed on the basis of the Darvin hypothesis. According to this hypothesis, each generation of a possible solution is produced by different GA operators, including mutation and crossover of the previous set of solutions. After each generation, a predefined function, called fitness function, is evaluated, and according to this evaluation, possible solutions will be sorted (See Fig. 1) (Niazi et al. 2008). The main advantage of the GA algorithm is that the optimization process is free of derivatives. Hence, it can apply to a broad range of non-linear problems without trapping in local extremums (Reihanian et al. 2011).

Methodology

Data points employed in this paper were divided into two phases, including the testing and training phases. Those that belong to the training phase are employed for training a machine learning model; this phase contains 80% of the whole data bank. Those data points that belong to the testing phase are used to verify the performance and accuracy of the constructed machine learning model; this phase comprises 20% of the whole data bank.

RBF kernel as a simple to use and robust kernel function provides only two hyperparameters to be optimized by GA (Liu et al. 2005a, b). According to Eqs. (9)–(11), optimization of these two hyperparameters, including γ and σ2, plays a vital role in developing an efficient LSSVM model. γ stands for the regularization factor, and σ2 denotes the variance of the kernel (Vong et al. 2006).

As demonstrated in the previous section, to gain optimum values of the LSSVM parameters such as γ and σ2, GA was utilized to minimize the mean squares error (MSE) of the output results of the evolved least squares SVM. The procedure of the GA-LSSVM algorithm is illustrated in Fig. 1. Finally, the values of the global optima, which include σ2 and γ, have been determined as 1.24934 and 0.08245, correspondingly.

Fig. 1
figure 1

The flowchart of hyperparameters selection based on GA

Full size image

Results and discussion

The gained outcomes from the LSSVM method are demonstrated in Figs. 2, 3, 4, and 5. Figure 2 depicts the comparison between the least squares SVM outputs and the corresponding measured permeability reduction ratio versus the relevant data index. As illustrated in Fig. 2, the obtained results of the least squares SVM covered the relevant experimental permeability reduction ratio. In other words, the outputs of the LSSVM approach have the same behavior as the actual measured data. Figure 3 depicts the scatter or regression plot of the LSSVM output results versus the corresponding experimental formation damage data. As depicted in Fig. 3, the LSSVM outputs follow the red dash line Y = X; this means that the outputs gained from the least squares SVM are the same as the measured permeability reduction data samples. The extracted correlation coefficient from Fig. 3 again shows the high degree of efficiency and accuracy of the LSSVM in monitoring a permeability reduction due to scale deposition during water flooding. Also, to depict the robustness of the LSSVM, the relative deviations of the LSSVM model outcomes from the corresponding actual formation damage are demonstrated in Figs. 4 and 5. Figure 4 exhibits the relative deviation of the least squares SVM outputs versus the relevant experimental data. As can be seen from Fig. 4, the maximum deviation of the LSSVM results is observed in the early boundary. In other words, the maximum deviation of the LSSVM outputs is observed for a permeability reduction between 0.3 and 0.8. One of the possible reasons is the number of training data points for those boundaries were limited, and consequently, the machine learning model is not trained very well for those. Also, as shown in Fig. 4, the maximum relative deviation of the LSSVM outcomes is about 18%. Figure 5 depicts the relative deviation of the LSSVM output results versus the corresponding measured permeability reduction data.

Fig. 2
figure 2

Comparison between the proposed LSSVM model outputs and measured permeability reduction versus data index

Full size image
Fig. 3
figure 3

Scatter plot of the proposed LSSVM model results against relevant experimental permeability reduction data

Full size image
Fig. 4
figure 4

Relative deviation of the LSSVM outcomes versus relevant measured permeability reduction data

Full size image
Fig. 5
figure 5

Relative deviation of the LSSVM outcomes versus relevant data index

Full size image

To certify the ability of the developed least squares SVM method in monitoring a permeability reduction due to scale deposition, a conventional back-propagation (BP) neural network is also implemented to tackle this obstacle. The interested readers can find more information about ANN in the Refs. (Ahmadi and Chen 2019a, b; Ahmadi and Shadizadeh 2012; Ahmadi 2011). Due to the limitation on the available experimental data in the open literature and the possibility of overfitting in architectures with more than one hidden layer, we decided to use only one hidden layer in our study. In this case, artificial neural network (ANN) performance is highly dependent on various parameters like a number of neurons in the hidden layer. To overcome this hurdle, a sensitivity analysis of ANN model performance versus a number of neurons in the hidden layer was investigated systematically. Owing to this fact, the dependence of the correlation coefficient (R2) and the mean squares error (MSE) of the output results of ANN versus a relevant number of neurons in the hidden layer is demonstrated in Figs. 6 and 7, respectively. Figure 6 depicts the sensitivity of the ANN correlation coefficient versus the corresponding hidden neurons. According to this figure, the best correlation coefficient is achieved for seven hidden neurons. Also, the dependency of the mean squares error (MSE) on a number of neurons in the hidden layer is demonstrated in Fig. 7. Figure 7 certifies that the optimum number of neurons in the hidden layer is equal to 7. The obtained results of the optimized neural network are illustrated in Figs. 8, 9, 10, and 11. Figure 8 exhibits the comparison between ANN results and actual formation damage against the relevant data index. As shown in Fig. 8, the ANN results did not follow the trend of the measured permeability reduction data. Figure 9 demonstrates the correlation between ANN outcomes and the corresponding measured formation damage data. As can be seen from Fig. 9, the outcomes of the network approach deviated from a diagonal line; this means that the ANN model predicts permeability reduction ratio with higher error compared to those predicted by the LSSVM approach. Finally, the relative deviation of the network outputs from the actual permeability reduction data versus the corresponding experimental data and the data index is illustrated in Figs. 10 and 11, respectively. As shown in Fig. 10, the maximum deviation occurred in the early boundary of the permeability reduction ratio. Also, the maximum error of the network approach is about 100 percent, which is not acceptable in any scientific area. Figure 11 demonstrates the relative error of the network model versus the relevant data index for both the training and testing phases. Finally, to wrap up the previous results, Table 2 reports the determined statistical criteria of the least squares SVM and ANN models. According to Table 2, the least squares SVM has a high efficiency compared to the ANN model.

Fig. 6
figure 6

Sensitivity of correlation coefficient versus the number of neurons for permeability reduction monitoring

Full size image
Fig. 7
figure 7

Sensitivity of mean square error (MSE) versus number neurons for permeability reduction monitoring

Full size image
Fig. 8
figure 8

Comparison between proposed ANN model outputs and measured formation damage versus data index

Full size image
Fig. 9
figure 9

Scatter plot of the proposed ANN model results against relevant experimental formation damage data

Full size image
Fig. 10
figure 10

Relative deviation of the ANN outcomes versus relevant measure permeability reduction data

Full size image
Fig. 11
figure 11

Relative deviation of the network outcomes versus relevant data index

Full size image
Table 2 Analysis of the outputs predicted by machine learning models
Full size table

Figure 12 shows the relative importance of those input parameters employed in the current paper for developing the machine learning models predicts permeability impairment due to scale deposition. As illustrated in Fig. 12, the initial permeability has the highest impact on the permeability reduction ratio.

Fig. 12
figure 12

Relative importance of the input variables on the permeability impairment using Pearson’s correlation

Full size image

Conclusions

The following main conclusions can be drawn from this study:

  1. 1.

    The traditional feed-forward ANN with a back-propagation training algorithm fails to represent formation damage owning to scale deposition through water flooding in oil reservoirs, but the obtained data from the LSSVM approach are closest to the real formation damage data samples.

  2. 2.

    LSSVM model has only two hyperparameters to be optimized rather than the weight and bias of each input variable in the ANN. This feature of the LSSVM data-driven model makes it easy to use. However, the performance of such a model cannot always be above the ANN model; it depends on the quality, quantity, and the behavior of the system in terms of linearity.

  3. 3.

    The quality and quantity of the data samples play a vital role in the efficacy of the data-driven model. Tuning the proposed machine learning model, including LSSVM and BP-ANN, with new high-quality data samples, can make these predictive tools more reliable, and provide an opportunity for broader applications, especially in industrial scale.