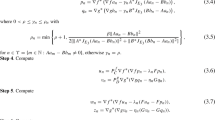Abstract
Passive discrete-time systems in Pontryagin space setting are investigated. In this case the transfer functions of passive systems, or characteristic functions of contractive operator colligations, are generalized Schur functions. The existence of optimal and \(^*\)-optimal minimal realizations for generalized Schur functions are proved. By using those realizations, a new definition, which covers the case of generalized Schur functions, is given for defects functions. A criterion due to D.Z. Arov and M.A. Nudelman, when all minimal passive realizations of the same Schur function are unitarily similar, is generalized to the class of generalized Schur functions. The approach used here is new; it relies completely on the theory of passive systems.
Similar content being viewed by others
1 Introduction
An operator colligation\(\Sigma =(T_{\Sigma };{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) consists of separable Pontryagin spaces \({{\mathcal {X}}}\) (the state space), \({{\mathcal {U}}}\) (the incoming space), and \({{\mathcal {Y}}}\) (the outgoing space) and the system operator\(T_{\Sigma } \in {{\mathcal {L}}}({{\mathcal {X}}}\oplus {{\mathcal {U}}},{{\mathcal {X}}}\oplus {{\mathcal {Y}}}),\) the space of bounded operators from \({{\mathcal {X}}}\oplus {{\mathcal {U}}}\) to \({{\mathcal {X}}}\oplus {{\mathcal {Y}}},\) where \({{\mathcal {X}}}\oplus {{\mathcal {U}}},\) or \(\begin{pmatrix} {{\mathcal {X}}}\\ {{\mathcal {U}}}\end{pmatrix} \), means the direct orthogonal sum with respect to the indefinite inner product. The symbol \(\kappa \) is reserved for the finite negative index of the state space. The operator \(T_{\Sigma }\) has the block representation of the form
where \(A \in {{\mathcal {L}}}({{\mathcal {X}}})\) (the main operator), \(B \in {{\mathcal {L}}}({{\mathcal {U}}},{{\mathcal {X}}})\) (the control operator), \(C \in {{\mathcal {L}}}({{\mathcal {X}}},{{\mathcal {Y}}})\) (the observation operator), and \(D \in {{\mathcal {L}}}({{\mathcal {U}}},{{\mathcal {Y}}})\) (the feedthrough operator). If needed, the colligation is written as \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ).\) It is always assumed in this paper that \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) have the same negative index.
All notions of continuity and convergence are understood to be with respect to the strong topology, which is induced by any fundamental decomposition of the space in question.
The colligation (1.1) will be called as a system since it can be seen as a linear discrete time system of the form
where \(\{h_k\}\subset {{\mathcal {X}}}\), \(\{\xi _k\}\subset {{\mathcal {U}}}\) and \(\{\sigma _k\}\subset {{\mathcal {Y}}}.\) In what follows, the “system” is identified with the operator expression appearing in (1.1). When the system operator \(T_{\Sigma }\) in (1.1) is contractive (isometric, co-isometric, unitary), with respect to the indefinite inner product, the corresponding system is called passive (isometric, co-isometric, conservative). In literature, conservative systems are also called unitary systems. The transfer function of the system (1.1) is defined by
whenever \(I-z A\) is invertible. Especially, \(\theta _\Sigma \) is defined and holomorphic in a neighbourhood of the origin. The values \(\theta _{\Sigma }(z)\) are bounded operators from \({{\mathcal {U}}}\) to \({{\mathcal {Y}}}.\) Conversely, if \(\theta \) is an operator valued function holomorphic in a neighbourhood of the origin, and transfer function of the system \(\Sigma \) coinsides with it, then \(\Sigma \) is a realization of \(\theta .\) In some sources, transfer functions of the systems are also called characteristic functions of operator colligations.
The adjoint or dual of the system \(\Sigma \) is the system \(\Sigma ^*\) such that its system operator is the indefinite adjoint \(T_{\Sigma }^*\) of \(T_\Sigma .\) That is, \(\Sigma ^*=(T_{\Sigma }^*;{{\mathcal {X}}},{{\mathcal {Y}}},{{\mathcal {U}}};\kappa ).\) In this paper, all the adjoints are with respect to the indefinite inner product. For an operator valued function \(\varphi ,\) the notation \({\varphi }^*({z})\) is used instead of \(\left( \varphi ({z})\right) ^*, \) and the function \(\varphi ^\#(z)\) is defined to be \(\varphi ^*({\bar{z}}).\) With this notation, for the transfer function \(\theta _{\Sigma ^*}\) of \(\Sigma ^*,\) it clearly holds \( \theta _{\Sigma ^*}(z)={\theta _{\Sigma }}^\#(z). \) Since contractions between Pontryagin spaces with the same negative index are bi-contractions (cf. eg. [24, Corollary 2.5]), \(\Sigma ^*\) is passive whenever \(\Sigma \) is.
In the case where all the spaces are Hilbert spaces, the result that the transfer function of a passive system belongs to the Schur class has been established by Arov [4, Proposition 8]. In the case where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces and the state space \({{\mathcal {X}}}\) is a Pontryagin space, Saprikin showed in [30, Theorem 2.2] that the transfer function of the passive system (1.1) is a generalized Schur function. It will be proved later in Proposition 2.4 that this result holds also in the case when all the spaces are Pontryagin spaces. The generalized Schur class\({{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})\), where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index, is the set of \(\mathcal {L}({{\mathcal {U}}},{{\mathcal {Y}}})\)-valued functions S(z) holomorphic in a neighbourhood \(\Omega \) of the origin such that the Schur kernel
has \(\kappa \) negative squares (\(\kappa =0,1,2,\ldots \)). This means that for any finite set of points \(w_1,\ldots ,w_n\) in the domain of holomorphy \(\rho (S)\) of S and set of vectors \(\{f_1,\ldots ,f_n\} \subset {{\mathcal {Y}}},\) the Hermitian matrix
where \(\left\langle \cdot , \cdot \right\rangle _{{{\mathcal {Y}}}}\) is the indefinite inner product of the space \({{\mathcal {Y}}},\) has no more than \(\kappa \) negative eigenvalues, and there exists at least one such matrix that has exactly \(\kappa \) negative eigenvalues. A function S belongs to \({{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) if and only if \(S_\kappa ^\# \in \mathbf {S}({{\mathcal {Y}}},{{\mathcal {U}}})\); see [1, Theorem 2.5.2]. The class \(\mathbf {S}_0({{\mathcal {U}}},{{\mathcal {Y}}})\) coinsides with the ordinary Schur class, and it is written as \(\mathbf {S}({{\mathcal {U}}},{{\mathcal {Y}}}).\) The generalized Schur class was first studied by Kreĭn and Langer; see [26] for instance.
The direct connection between the transfer functions of passive systems of the form (1.1) and the generalized Schur functions allows to study the properties of generalized Schur functions by using passive systems, and vice versa. Therefore, a fundamental problem of the subject is, for a given \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) find a realization \(\Sigma \) of \(\theta \) with the desired minimality or optimality properties (observable, controllable, simple, minimal, optimal, \(^*\)-optimal); for details, see Theorems 2.6 and 3.5 and Lemma 2.8. The described problem is called a realization problem. In the standard Hilbert space setting, realizations problems, as well as other properties of passive systems, were studied, for instance, by Arov [4, 5], Arov et al. [6,7,8], Ball and Cohen [13], de Branges and Rovnyak [20, 21], Helton [25] and Nagy and Foias [29]. The case where the state space is a Pontryagin space while incoming and outgoing spaces are still Hilbert spaces, unitary systems were studied, for instance, by Dijksma et al. [22, 23], and passive systems by Saprikin [30], Saprikin and Arov [10], Saprikin et al. [9] and by the author in [27]. The case where all the spaces are Pontryagin spaces, theory of isometric, co-isometric and conservative systems is considered, for instance, in [1, 2, 24].
Especially, Arov [5] proved the existence of so-called optimal minimal realizations of an ordinary Schur function; for definitions, see Sect. 3. The proof was based on the existence (right) defect functions. For an ordinary Schur function \(S(\zeta )\), the (right) defect function \(\varphi \) of S is, roughly speaking, the maximal analytic minorant of \(I-S^*(\zeta )S(\zeta ).\) More precicely, this means that for almost everywhere (a.e.) \(\zeta \) on the unit circle \({{\mathbb {T}}},\) it holds
and for every other operator valued analytic function \({\widehat{\varphi }}\) with similar property, it holds
For the existence of defect functions, see [29, Theorem V.4.2], and for a detailed treatise, see [17,18,19]. Another names of defect functions are “spectral factors”, see [12]. Arov et al. [6] constructed (\(^*\)-)optimal minimal passive systems in the Hilbert space setting without using defect functions. The construction can be done by taking an appropriate restriction of some system. In the indefinite setting, if one uses a suitable definition of optimality, a similar method as was used by Arov et al. still produces a (\(^*\)-)optimal minimal passive system. In Pontryagin state space case, this was proved by Saprikin [30]. It will be shown in Theorem 3.5 that the same result still holds in the case where all the spaces are Pontryagin spaces.
The study of the class of generalized Schur functions \({{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) was continued in [9, 10], in the case where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces and the state space is a Pontryagin space. Saprikin and Arov [10] used the right Kreĭn–Langer factorization of the form \(S=S_rB_r^{-1}\) for \(S \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) and proved that the existence of the optimal minimal realization of S is equivalent to the existence of the right defect function of \(S_r.\) However, they did not define the defect functions for the generalized Schur functions. This was done by the author in [27] by using the Kreĭn–Langer factorizations. With the definition given therein, the main results of [3] were generalized to the Pontryagin state space setting. The main subjects of [27] include some continuation of the study of products of systems and the stability properties of passive systems, subjects treated earlier by Saprikin et al. [9]. In the present paper, it will be shown that a concept of defect functions can be defined in the case where all the spaces are Pontryagin spaces. The key idea here is to use optimal minimal passive realizations and conservative embeddings. By using such a definition, it is shown that one can generalize and improve some of the main results from [3], using different proofs than those given in [3] or [27], see Theorem 4.8. Furthermore, in Theorem 4.10, the main results from [7, 8] concerning the criterion when all the minimal realizations of a Schur function are unitarily similar, is generalized to the present indefinite setting. The proof will be carried out entirely by using the theory of passive systems, without applying Hardy space theory or the theory of Hankel operators as in the proof provided in [8].
The paper is organized as follows. In Sect. 2 basic facts of linear systems, Julia operators, dilations and embeddings are recalled. Moreover, Lemma 2.8 gives some usefull representations and restrictions of passive systems. That lemma will be used extensively later on in this paper.
In Sect. 3, the existence and basic properties of (\(^*\)-)optimal minimal realizations are established. The main result of this section is Theorem 3.5.
The generalized defect functions are introduced in Sect. 4. In particularly, Theorem 4.10 in this section can be seen as the main result of the paper.
2 Linear Systems, Dilations and Embeddings
Let \(\Sigma =(T_{\Sigma };{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be a linear system as in (1.1). The following subspaces
are called, respectively, controllable, observable and simple subspaces. The system is said to be controllable (observable, simple) if \({{\mathcal {X}}}^c={{\mathcal {X}}}({{\mathcal {X}}}^o={{\mathcal {X}}},{{\mathcal {X}}}^s={{\mathcal {X}}})\) and minimal if it is both controllable and observable.
When \(\Omega \ni 0\) is some symmetric neighbourhood of the origin, that is, \({\bar{z}} \in \Omega \) whenever \(z\in \Omega ,\) then also
The system (1.1) can be expanded to a larger system without changing the transfer function. It can be done by using the so-called defect operator and Julia operator, see, respectively, (2.7) and (2.8) below. For a proof of the following theorem and more details about the defects operators and Julia operators, see [24]. The basic information about the indefinite inner product spaces and their operators can be recalled from [11, 15, 24].
Theorem 2.1
Suppose that \({{\mathcal {X}}}_1\) and \({{\mathcal {X}}}_2\) are Pontryagin spaces with the same negative index, and let \(A: {{\mathcal {X}}}_1 \rightarrow {{\mathcal {X}}}_2\) be a contraction. Then there exist Hilbert spaces \({{\mathfrak {D}}}_{A}\) and \({{\mathfrak {D}}}_{A^*},\) linear operators \(D_A: {{\mathfrak {D}}}_{A}\rightarrow {{\mathcal {X}}}_1, D_{A^*}: {{\mathfrak {D}}}_{A^*} \rightarrow {{\mathcal {X}}}_2 \) with zero kernels and a linear operator \(L:{{\mathfrak {D}}}_{A} \rightarrow {{\mathfrak {D}}}_{A^*} \) such that it holds
and the operator
is unitary. Moreover, \(D_{A}, D_{A^*}\) and \(U_A\) are unique up to unitary equivalence.
The notion of dilation of a discrete time-invariant system has been introduced by Arov [4]. A dilation of a system \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is any system of the form \({\widehat{\Sigma }}=({\widehat{A}},{\widehat{B}},{\widehat{C}},D;{\widehat{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ),\) where
The spaces \({{\mathcal {D}}}\) and \({{\mathcal {D}}}_*\) are required to be Hilbert spaces. The system operator \(T_{{\widehat{\Sigma }}}\) of \({\widehat{\Sigma }}\) is of the form
The system \(\Sigma \) is called a restriction of \({\widehat{\Sigma }}.\) Recall that subspace \({{\mathcal {N}}}\) of the Pontryagin space \({{\mathcal {H}}}\) is regular if it is itself a Pontryagin space with the inherited inner product of \(\langle \cdot ,\cdot \rangle _{{{\mathcal {H}}}}.\) The subspace \({{\mathcal {N}}}\) is regular precicely when \({{\mathcal {N}}}^\perp \) is regular, where \(\perp \) refers to orthogonality with respect to the indefinite inner product of \({{\mathcal {H}}}\). Since \({{\mathcal {X}}}\) clearly is a regular subspace of \({\widehat{{{\mathcal {X}}}}},\) there exists the unique orthogonal projection \(P_{{{\mathcal {X}}}}\) from \({\widehat{{{\mathcal {X}}}}}\) to \({{\mathcal {X}}}.\) Let \({\widehat{A}}{\upharpoonright }_{{{\mathcal {X}}}}\) be the restriction of \({\widehat{A}}\) to the subspace \({{\mathcal {X}}}.\) Then, the system \(\Sigma \) can be represented as \( \Sigma =(P_{{{\mathcal {X}}}}{\widehat{A}}{\upharpoonright }_{{{\mathcal {X}}}},P_{{{\mathcal {X}}}}{\widehat{B}},{\widehat{C}}{\upharpoonright }_{{{\mathcal {X}}}},D;P_{{{\mathcal {X}}}}{\widehat{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ).\) A calculation show that the transfer functions of the original system and its dilation coincide. Moreover, if \(\Sigma \) is passive, then is any retriction of it. The following proposition states that a passive system has a conservative dilation. For the Hilbert space case, this result is from [4], and for the Pontryagin state space case, see [30]. The similar proof as in [4] and [30] can be applied. For details, see the proof in [28, Proposition 2.3].
Proposition 2.2
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be a passive system. Then there exists a conservative dilation \({\widehat{\Sigma }}=({\widehat{A}},{\widehat{B}},{\widehat{C}},D;{\widehat{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\Sigma \).
It is possible that \({{\mathcal {D}}}=\{0\}\) or \({{\mathcal {D}}}_*=\{0\}\) in (2.9). In those cases, the zero space and the corresponding row and column will be left out in (2.10). In particular, if the system \(\Sigma \) with the system operator T as in (1.1) is isometric (co-isometric), then \(D_T=0\) (\(D_{T^*}=0\)).
There is also an another way to expand the system (1.1), and it is called an embedding. In this expansion, the state space and the main operator will not change. The embedding of the system (1.1) is any system determined by the system operator
where \({{\mathcal {U}}}'\) and \({{\mathcal {Y}}}'\) are Hilbert spaces. The transfer function of the embedded system is
where \(\theta _{\Sigma }\) is the transfer function of the original system. The embedded systems will be needed in Sect. 4.
It will be proved in Proposition 2.4 below that the transfer function of any passive system (1.1) is a generalized Schur function with index not larger than the negative index of the state space. For a special case where incoming and outcoming spaces are Hilbert spaces, this result is due to [30, Theorem 2.2]. The proof of the general case follows the lines of Saprikin’s proof of the special case.
Lemma 2.3
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be a passive system with the transfer function \(\theta \). Denote the system operator of \(\Sigma \) as T. If
are defect operators of T and \(T^*\), respectively, then the identities
with
hold for every z and w in a sufficiently small symmetric neighbourhood of the origin.
Proof
By applying the results from [1, Theorem 1.2.4] and the identities in (2.7), the results follow by straightforward calculations. For details, see the proof in [28, Lemma 2.4]. \(\square \)
Note that if \(\Sigma \) in Lemma 2.3 is isometric (co-isometric), then \(D_T=0\) (\(D_{T^*}=0\)) and therefore \(\varphi \equiv 0\) (\(\psi \equiv 0\)).
Proposition 2.4
If \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is a passive system, the transfer function \(\theta \) of \(\Sigma \) belongs to \( \mathbf {S}_{\kappa '}({{\mathcal {U}}},{{\mathcal {Y}}}),\) where \(\kappa '\le \kappa .\)
Proof
Denote the system operator of \(\Sigma \) as T. By Lemma 2.3, the kernel \( K_\theta \) defined as in (1.2) has a representation
where G(z) and \(\psi (z)\) are defined as in (2.13). Since the negative index of \({{\mathcal {X}}}\) is \(\kappa \) and the negative index of the Hilbert space \({{\mathfrak {D}}}_{T^*}\) is zero, it follows from [1, Lemma 1.1.1.], that for any finite set of points \(w_1,\ldots ,w_n\) in the domain of holomorphy of \(\theta \) and the set of vectors \(\{y_1,\ldots ,y_n \}\subset {{\mathcal {Y}}},\) the Gram matrices
have, respectively, at most \(\kappa \) and zero negative eigenvalues.
The kernel \((1 -z{\bar{w}}) ^{-1}\) has no negative square, since it is the reproducing kernel of the classical Hardy space \(H^2({{\mathbb {D}}}).\) The Schur product theorem shows that the kernel \((1 -z{\bar{w}}) ^{-1}\psi (z) \psi ^*(w)\) has no negative square. Then it follows from [1, Theorem 1.5.5] that the kernel \(K_{\theta }\) has at most \(\kappa \) negative square. That is, \( \theta \in \mathbf {S}_{\kappa '}({{\mathcal {U}}},{{\mathcal {Y}}}),\) where \(\kappa '\le \kappa ,\) and the proof is complete. \(\square \)
Definition 2.5
A passive realization \(\Sigma \) of a generalized Schur function \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) is called \(\kappa \)-admissible if the negative index of the state space of \(\Sigma \) coinsides with the negative index \(\kappa \) of \(\theta .\)
In what follows, this paper deals mostly with the \(\kappa \)-admissible realizations. It will turn out that the \(\kappa \)-admissible realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are well behaved is some sense; they have many similar propeties than the standard passive Hilbert space systems.
The following realizations theorem is well known, see [1, Theorems 2.2.1, 2.2.2 and 2.3.1].
Theorem 2.6
For a generalized Schur function \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) there exist realizations \(\Sigma _k=(T_k;{{\mathcal {X}}}_k,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ), k=1,2,3,\) of \(\theta \) such that
- (i)
\(\Sigma _1\) is observable co-isometric;
- (ii)
\(\Sigma _2\) is controllable isometric;
- (iii)
\(\Sigma _3\) is simple conservative.
Conversely, if the system \(\Sigma \) has some of the properties (i)–(iii), then \(\theta _{\Sigma }\in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) where \(\kappa \) is the negative index of the state space of \(\Sigma .\)
Recall that a Hilbert subspace of the Pontryagin space \({{\mathcal {X}}}\) is a regular subspace such that its negative index is zero. Conversely, anti-Hilbert subspace is a regular subspace such that its positive index is zero. When \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) happens to be Hilbet spaces, the transfer function \(\theta \) of the passive system \(\Sigma =(T_{\Sigma };{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) belongs to class \({{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) (with \(\kappa =\mathrm {ind}_{-}{{\mathcal {X}}}\)) if and only if \(({{\mathcal {X}}}^s)^\perp \) is a Hilbert subspace [27, Lemma 3.2]. In the case when \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index, the transfer function \(\theta \) of the isometric (co-isometric, conservative) system \(\Sigma =(T_{\Sigma };{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) belongs to class \({{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) if and only if \(({{\mathcal {X}}}^c)^\perp \) (\(({{\mathcal {X}}}^o)^\perp \),\(({{\mathcal {X}}}^s)^\perp \)) is a Hilbert subspace [1, Theorem 2.1.2]. For a passive system, one has the following result.
Proposition 2.7
For a passive realization \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) spaces \({{\mathcal {X}}}^c,\)\({{\mathcal {X}}}^o\) and \({{\mathcal {X}}}^s \) are regular and their orthogonal complements are Hilbert subspaces.
Proof
Let \(\Omega \) be a symmetric neighbourhood of the origin such that \((I-zA)^{-1}\) and \((I-zA^*)^{-1}\) exist for every \(z \in \Omega .\) Represent the kernel \(K_\theta \) as in (2.14). Since \(K_\theta \) has \(\kappa \) negative square, a similar argument used in the proof of 2.4 shows that the kernel \( K_1(z,w)= G(z)G^*(w),\) where \( G(z)=C(I-zA)^{-1}, \) has \(\kappa \) negative square. It follows now from [1, Lemma 1.1.1’] that \( \mathrm {span}\{\mathrm{ran\,}(I-{\overline{w}}A^*)^{-1}C^*, {\overline{w}} \in \Omega \}\) contains a \(\kappa \)-dimensional maximal anti-Hilbert subspace \({{\mathcal {X}}}_\kappa .\) Then, \({{\mathcal {X}}}_\kappa \oplus ({{\mathcal {X}}}_\kappa )^\perp ={{\mathcal {X}}}\) is a fundamental decomposition of \({{\mathcal {X}}}.\) Especially, \( ({{\mathcal {X}}}_\kappa )^\perp \) is a Hilbert subspace of \({{\mathcal {X}}}.\) But
which implies that \(\left( {{\mathcal {X}}}^o\right) ^\perp \) is a Hilbert subspace, and therefore its orthocomplement \({{\mathcal {X}}}^o\) is regular.
By duality argument, the space \({{\mathcal {X}}}^c\) is a regular subspace and the space \(({{\mathcal {X}}}^c)^\perp \) is a Hilbert subspace. It easily follows from (2.1)–(2.3) that \(({{\mathcal {X}}}^s)^\perp =({{\mathcal {X}}}^c)^\perp \cap ({{\mathcal {X}}}^o)^\perp ,\) and therefore \(({{\mathcal {X}}}^s)^\perp \) is also a Hilbert subspace and \({{\mathcal {X}}}^s\) is regular. \(\square \)
It follows from the Proposition 2.7 above that the state space \({{\mathcal {X}}}\) of a \(\kappa \)-admissible realization \(\Sigma \) of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) can be decombosed to the controllable, observable and simple parts. Using this fact, the lemma below, which will be used extensively, can be proved.
Lemma 2.8
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be a passive system such that the spaces \(({{\mathcal {X}}}^o)^\perp \), \(({{\mathcal {X}}}^c)^\perp \) and \(({{\mathcal {X}}}^s)^\perp \) are Hilbert subspaces of \({{\mathcal {X}}}.\) Then the system operator T of \(\Sigma \) has the following representations
The restrictions
of \(\Sigma \) are passive, and \(\Sigma _o\) is observable, \(\Sigma _c\) is controllable, \(\Sigma _s\) is simple, and \(\Sigma '\) and \(\Sigma ''\) are minimal. For any \(n \in {{\mathbb {N}}}_0\) and any z in a sufficiently small symmetric neighbourhood of the origin, it holds
Moreover, if \(\Sigma \) is co-isometric (isometric), then so are \(\Sigma _o\) and \(\Sigma _s \) (\(\Sigma _c\) and \(\Sigma _s\)).
Proof
Since \(({{\mathcal {X}}}^o)^\perp \), \(({{\mathcal {X}}}^c)^\perp \) and \(({{\mathcal {X}}}^s)^\perp \) are Hilbert spaces, the spaces \({{\mathcal {X}}}^o\), \({{\mathcal {X}}}^c\) and \({{\mathcal {X}}}^s\) are regular subspaces with the negative index \(\kappa .\) It follows from the identities (2.1)–(2.3) that
and the representations (2.15)–(2.17) follow. That is, \(\Sigma _o,\Sigma _c\) and \(\Sigma _s\) are restrictions of the passive system \(\Sigma ,\) ans therefore they are passive.
Let \(T_{\Sigma _k}\) be the system operator of \(\Sigma _k\) where \(k=o,c,s\), and let \({\hat{x}} \in {{\mathcal {X}}}^k \oplus {{\mathcal {U}}}\) and \(\breve{{x}} \in {{\mathcal {X}}}^k \oplus {{\mathcal {Y}}}.\) Calculation show that \(T_{\Sigma _k}{\hat{x}}=T{\hat{x}}\), where \( k=c,s\) and \( T_{\Sigma _k}^*\breve{x}=T^*\breve{x}\) where \( k=o,s. \) It follows that if \(\Sigma \) is co-isometric (isometric), then so are \(\Sigma _o\) and \(\Sigma _s \) (\(\Sigma _c\) and \(\Sigma _s\)).
Suppose \(x \in { {{\mathcal {X}}}}^o \) such that \(C_{o}A_{o}^nx=0\) for every \(n=0,1,2,\ldots \). Then
and the identity (2.2) implies that \(x \in { {{\mathcal {X}}}}^o \cap ({{\mathcal {X}}}^o)^\perp =\{0\}. \) Thus \(x=0,\) and it can be deduced that \( \Sigma _{o}\) is observable. Similar arguments show that \( \Sigma _{c}\) is controllable and \( \Sigma _{s}\) is simple, the details will be omitted.
Let \(u \in {{\mathcal {U}}},\) and \(n \in {{\mathbb {N}}}_0.\) Then, by (2.16) and (2.17),
and (2.25) holds. By Neumann series, \((I-zA)^{-1}B=\sum _{n=0}^\infty z^nA^nB\) holds for all z in a sufficiently small symmetric neighbourhood of the origin, and (2.26) follows now from (2.25). The equalities (2.27) and (2.28) can be deduced similarly.
Since the orthocomplements \(({{\mathcal {X}}}^o)^\perp \) and \(({{\mathcal {X}}}^c)^\perp \) are Hilbert subspaces, it follows from [30, Lemma 3.1] that \(\overline{P_{{{\mathcal {X}}}^o}{{\mathcal {X}}}^c}\) and \( \overline{P_{{{\mathcal {X}}}^c}{{\mathcal {X}}}^o}\) are regular subspaces, and it holds
Since \( ({{{\mathcal {X}}}^o})^\perp \subset (P_{{{\mathcal {X}}}^o}{{\mathcal {X}}}^c)^\perp , ({{{\mathcal {X}}}^c})^\perp \subset (P_{{{\mathcal {X}}}^c}{{\mathcal {X}}}^o)^\perp \) and all the spaces are regular, simple calculations show that
Therefore,
and similarly, \( {{\mathcal {X}}}=({{\mathcal {X}}}^c \cap ({{\mathcal {X}}}^o)^\perp ) \oplus \overline{P_{{{\mathcal {X}}}^c}{{\mathcal {X}}}^o} \oplus ({{\mathcal {X}}}^c)^\perp . \) Since \(({{\mathcal {X}}}^o \cap ({{\mathcal {X}}}^c)^\perp \) and \({{\mathcal {X}}}^c \cap ({{\mathcal {X}}}^o)^\perp \) are also Hilbert spaces, the spaces \( \overline{P_{{{\mathcal {X}}}^o}{{\mathcal {X}}}^c}\) and \( \overline{P_{{{\mathcal {X}}}^c}{{\mathcal {X}}}^o}\) are Pontryagin spaces with the negative index \(\kappa .\) By considering the properties in (2.29), the representations (2.18) and (2.19) follow now easily. That is, \(\Sigma '\) and \(\Sigma ''\) are restrictions of \(\Sigma \), and therefore passive.
Denote \({{\mathcal {X}}}':= \overline{P_{{{\mathcal {X}}}^o}{{\mathcal {X}}}^c} .\) Represent the system operator T of \(\Sigma \) as in (2.18). Then
and similarly \(A'^{*n}C^{'*} =P_{{{\mathcal {X}}}'}A^{*n}C^*.\) Therefore,
and similarly \({{{\mathcal {X}}}'}^{o}=P_{{{\mathcal {X}}}'}{{\mathcal {X}}}^o={{\mathcal {X}}}'\), which implies that \(\Sigma '\) is minimal. A similar argument shows that \(\Sigma ''\) is minimal, and the proof is complete. \(\square \)
Note that in particular, Lemma 2.8 implies the existence of a minimal passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\)
Definition 2.9
The restrictions \(\Sigma _o,\Sigma _c,\Sigma _s,\Sigma ',\) and \(\Sigma ''\) in Lemma 2.8 are called, respectively, the observable, the controllable, the simple (or proper), the first minimal and the second minimal restrictions of \(\Sigma .\)
The first minimal and the second minimal restrictions will be considered later in Sects. 3 and 4.
Two realizations \(\Sigma _1=(A_1,B_1,C_1,D_1;{{\mathcal {X}}}_1,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa _1)\) and \(\Sigma _2=(A_2,B_2,C_2,D_2;{{\mathcal {X}}}_2,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa _2)\) of the same function \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are called unitarily similar if \(D_1=D_2\) and there exists a unitary operator \(U: {{\mathcal {X}}}_1 \rightarrow {{\mathcal {X}}}_2 \) such that
In that case, it easily follows that \(\kappa _1=\kappa _2.\) Unitary similarity preserves dynamical properties of the system and also the spectral properties of the main operator. If two realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) both have the same property (i), (ii) or (iii) of Theorem 2.6, then they are unitarily similar [1, Theorem 2.1.3].
The realizations \(\Sigma _1\) and \(\Sigma _2\) above are said to be weakly similar if \(D_1=D_2\) and there exists an injective closed densely defined possible unbounded linear operator \(Z: {{\mathcal {X}}}_1 \rightarrow {{\mathcal {X}}}_2\) with the dense range such that
where \({{\mathcal {D}}}(Z)\) is the domain of Z. In Hilbert state space case, a result of Helton [25] and Arov [4] states that two minimal passive realizations of \(\theta \in {{{\mathbf {S}}}( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are weakly similar. However, weak similarity preserves neither dynamical properties of the system nor the spectral properties of its main operator.
Helton’s and Arov’s statement holds also in case where all the spaces are indefinite. This result is stated for reference purposes. Similar argument as Hilbert space case can be applied, definiteness of the inner product play no role. For a proof of special cases, see [14, Theorem 7.1.3], [31, p. 702] and [27, Theorem 2.5]. Note that the realizations are not assumed to be \(\kappa \)-admissible or passive.
Proposition 2.10
Two minimal realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are weakly similar.
3 Optimal Minimal Systems
For \(\kappa \)-admissible realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\), where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index, one can form the similar theory of optimal minimal passive systems as represented in the standard Hilbert space case in [6] and the Pontryagin state space case in [30]. Techniques, definitions and notations to be used here are similar to what appears in those papers.
Denote \(E_{{{\mathcal {X}}}}\left( x \right) =\langle x,x \rangle _{{{\mathcal {X}}}}\) for a vector x in an inner product space \({{\mathcal {X}}}.\) Following [6, 10, 30], a passive realization \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) is called optimal if for any passive realization \(\Sigma '=(A',B',C',D';{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta ,\) the inequality
holds. On the other hand, the system \(\Sigma \) is called *-optimal if it is observable and
holds for every observable passive realization \(\Sigma '\) of \(\theta .\) The requirement for observability must be included for avoiding trivialities, since otherwise every isometric realization of \(\theta \) would be \(^*\)-optimal; see Lemma 3.3 below and [6, Proposition 3.5 and example on page 144].
In the definition of optimality and \(^*\)-optimality, the requirement that the considered realizations are \(\kappa \)-admissible is essential, as the example below shows.
Example 3.1
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) and \(\Sigma '=(A',B',C',D';{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa '),\) where \(\kappa <\kappa ',\) be passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Suppose that (3.1) holds. By Lemma 2.8, if (3.1) holds for \(\Sigma \), it holds also for the controllable restriction \(\Sigma _c=(A_c,B_c,C_c,D';{{\mathcal {X}}}^c,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\Sigma .\) For any vector x of the form \(x=\sum _{n=0}^{M}A_c^nB_cu_n\) where \( \{u_n\}\subset {{\mathcal {U}}}\) and \( M \in {{\mathbb {N}}}_0, \) define
It is easy to deduce that R is a linear relation. Moreover, since \(\Sigma _c\) is controllable by Lemma 2.8, R is densely defined. Since (3.1) holds, R is contractive. It follows now from [1, Theorem 1.4.2] that R can be extended to be everywhere defined contractive linear operator. Since \(\mathrm {ind}_- {{\mathcal {X}}}^c=\kappa < \kappa '=\mathrm {ind}_- {{\mathcal {X}}}',\) it follows from [24, Theorem 2.4] that linear operator from \({{\mathcal {X}}}^c\) to \({{\mathcal {X}}}'\) cannot be contractive, and hence (3.1) cannot hold.
It will be shown in Theorem 3.5 below that an optimal (\(^*\)-optimal) minimal realization exists, and it can be constructed by taking the first (second) minimal restriction, introduced in Definition 2.9, of simple conservative realizations. More lemmas will be needed before that.
Lemma 3.2
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is a passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) and let \(\Sigma _s=(A_s,B_s,C_s,D;{{\mathcal {X}}}^s,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be the restriction of \(\Sigma \) to the simple subspace. Then, the first (second) minimal restrictions of \(\Sigma \) and \(\Sigma _s\) coinside.
Proof
Only the proof of the statement concerning about the second minimal restrictions is provided, since the other case is similar. To make the notation less cumbersome, write \({{\mathcal {X}}}^s={{\mathcal {X}}}_p,\) where p refers to proper part. By Lemma 2.8, the equalities (2.25) and (2.27) hold, and it easily follows that it holds \( {{\mathcal {X}}}^o = {{\mathcal {X}}}_p^o,\)\({{\mathcal {X}}}^c = {{\mathcal {X}}}_p^c,\)\(({{\mathcal {X}}}^o)^\perp = ({{\mathcal {X}}}^s)^\perp \oplus ({{\mathcal {X}}}_p^o)^\perp \) and \( ({{\mathcal {X}}}^c)^\perp = ({{\mathcal {X}}}^s)^\perp \oplus ({{\mathcal {X}}}_p^c)^\perp ,\) where orthogonal complements \( ({{\mathcal {X}}}_p^o)^\perp \) and \(({{\mathcal {X}}}_p^c)^\perp \) are taken with respect to the space \({{\mathcal {X}}}_p.\) Therefore \( P_{{{\mathcal {X}}}^c}{{\mathcal {X}}}^o = P_{ {{\mathcal {X}}}_p^c}{{\mathcal {X}}}_p^o \subset {{\mathcal {X}}}^s={{\mathcal {X}}}_p, \) and consequently,
which shows that the second minimal restrictions of \(\Sigma \) and \(\Sigma _s\) co-inside. \(\square \)
To prove the (\(^*\)-)optimality of a system, the following lemma is helpful.
Lemma 3.3
Let \({\Sigma }=({A},{B},{C},D;{{{\mathcal {X}}}},{{\mathcal {U}}},{{\mathcal {Y}}},\kappa )\), \({\widehat{\Sigma }}=({\widehat{A}},{\widehat{B}},{\widehat{C}},D;{\widehat{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}},\kappa )\) and \( \Sigma '=(A',B',C',D;{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ) \) be realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) such that \(\Sigma \) is passive, \({\widehat{\Sigma }}\) is a passive dilation of \(\Sigma \) and \(\Sigma '\) is the first minimal restriction of \({\widehat{\Sigma }}.\) Then
Moreover, for any isometric realization \( {\breve{\Sigma }}=({\breve{A}_1},{\breve{B}_1},{{\check{C}}_1},D;{\breve{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}},\kappa )\) of \(\theta ,\) it holds
Note that Proposition 2.2 guarantees the existence of a passive dilation \(\widehat{{\Sigma }}\) of \(\Sigma \) with the properties described above.
Proof
Since \({\widehat{\Sigma }}\) is a dilation of \(\Sigma ,\) the system operator \(T_{{\widehat{\Sigma }}}\) has a representation
where \({{\mathcal {D}}}\) and \({{\mathcal {D}}}^*\) are Hilbert spaces. On the other hand, by Lemma 2.8, \({\widehat{\Sigma }}\) can also be represented as
where \({{\mathcal {X}}}_1=({\widehat{{{\mathcal {X}}}}}^o)^\perp , {{\mathcal {X}}}'= \overline{P_{{\widehat{{{\mathcal {X}}}}}^o}{\widehat{{{\mathcal {X}}}}}^c}\) and \({{\mathcal {X}}}_3={\widehat{{{\mathcal {X}}}}}^o \cap ({\widehat{{{\mathcal {X}}}}}^c)^\perp .\) The spaces \({{\mathcal {X}}}_1\) and \({{\mathcal {X}}}_3\) are Hilbert spaces, and \({{\mathcal {X}}}'\) is a Pontryagin space with the negative index \(\kappa .\) Let \(n \in {{\mathbb {N}}}_0\) and \(\{u_k \}_{k=0}^n \subset {{\mathcal {U}}}.\) Since \({{\mathcal {X}}}_3 \subset ({\widehat{{{\mathcal {X}}}}}^c)^\perp ,\) it holds
With \({{\mathcal {D}}}\) and \({{\mathcal {D}}}^*\) as in (3.5), the identities in (2.9) hold. Therefore, it follows from the identities (2.1) and (2.2) that \({{\mathcal {D}}}_* \subset ({\widehat{{{\mathcal {X}}}}}^c)^\perp \) and \({{\mathcal {D}}}\subset ({\widehat{{{\mathcal {X}}}}}^o)^\perp = {{\mathcal {X}}}_1. \) A similar calculation as above yields then
The inclusion \({{\mathcal {D}}}\subset {{\mathcal {X}}}_1 \) and the fact that \({{\mathcal {D}}}\) and \({{\mathcal {X}}}_1\) are Hilbert spaces now implies the inequality \(E_{{\widehat{{{\mathcal {X}}}}}}\left( P_{{{\mathcal {D}}}} \sum _{k=0}^{n}{\widehat{A}}^k{\widehat{B}}u_k \right) \le E_{{\widehat{{{\mathcal {X}}}}}}\left( P_{{{\mathcal {X}}}_1} \sum _{k=0}^{n}{\widehat{A}}^k{\widehat{B}}u_k \right) . \) It follows now from the Eqs. (3.6) and (3.7) that \(E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}A'^kB'u_k \right) \le E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}A^kBu_k \right) , \) and the inequality (3.3) is proved.
Assume that \(\widehat{{\Sigma }}\) is isometric. Since \({{\mathcal {D}}}\) is a Hilbert space, it follows from (3.7) that
By Lemma 2.8, the controllable restriction \({{\widehat{\Sigma }}_c}=({{\widehat{A}}_c},{{\widehat{B}}_c},{{\widehat{C}}_c},D;{{\widehat{{{\mathcal {X}}}}}^c},{{\mathcal {U}}},{{\mathcal {Y}}},\kappa )\) of \({\widehat{\Sigma }}\) is controllable isometric, and for every \(n=0,1,2,\ldots ,\) it holds \( {\widehat{A}}^n{\widehat{B}}={\widehat{A}}_c^n{\widehat{B}}_c. \) Therefore
Similar argument show that if \( {\breve{\Sigma }^c}=({\breve{A}_c},{\breve{B}_c},{\breve{C}_c},D;{\breve{{{\mathcal {X}}}}^c},{{\mathcal {U}}},{{\mathcal {Y}}},\kappa )\) is the controllable restriction of the isometric system \( {\breve{\Sigma }}=({\breve{A}},{\breve{B}},{{\check{C}}},D;{\breve{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}},\kappa ),\) then \(\breve{\Sigma }^c\) is controllable isometric and it holds
But \({{\widehat{\Sigma }}^c}\) and \({\breve{\Sigma }^c}\) are unitarily similar, and therefore
By combining (3.8)–(3.11), the inequality (3.4) follows. \(\square \)
Remark 3.4
It follows from the inequality (3.4) of Lemma 3.3 that if there exists an observable isometric realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) then it is \(^*\)-optimal.
In the standard Hilbert space case, results of Arov [5] show that there exist optimal minimal realizations of a Schur function. The construction was based on the existence of the defect functions, see Sect. 4. Arov et. all provided new geometric proofs of these results in [6]. Saprikin used those new proofs and generalized Arov’s results to Pontryagin state space case in [30]. It will be proved next that Arov’s results holds in the case when all spaces are Pontryagin spaces. The geometric proofs in [6] can still be applied in the present setting with few appropriate changes.
Theorem 3.5
Let \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\), where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index. Then:
- (i)
The first minimal restriction of a simple conservative realization of \(\theta \) is optimal minimal;
- (ii)
The minimal passive system \(\Sigma ^*\) is optimal if and only if the dual system \(\Sigma \) is *-optimal minimal;
- (iii)
The second minimal restriction of a simple conservative realization of \(\theta \) is *-optimal minimal;
- (iv)
Optimal (*-optimal) minimal systems are unique up to unitary similarity, and every optimal (*-optimal) minimal realization of \(\theta \) is the first minimal restriction (second minimal restriction) of some simple conservative realization of \(\theta .\)
Proof
-
(i)
Let \(\Sigma '=(A',B',C',D;{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be the first minimal restriction of a simple conservative realization \({\widehat{\Sigma }}'=({\widehat{A}}',{\widehat{B}}',{\widehat{C}}',D;{\widehat{{{\mathcal {X}}}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be the first minimal restriction of some conservative realization of \(\theta \) such that its state space has negative index \(\kappa .\) To prove that \(\Sigma '\) is optimal, Lemma 3.3 shows that it is enough to prove
$$\begin{aligned} E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}A'^kB'u_k \right) \le E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}A^kBu_k \right) , \qquad n \in {{\mathbb {N}}}_0, \quad u_k \in {{\mathcal {U}}}. \end{aligned}$$(3.12)By Lemma 3.2, it can be assumed that \(\Sigma \) is the first minimal restriction of some simple conservative realization \({\widehat{\Sigma }}=({\widehat{A}},{\widehat{B}},{\widehat{C}},D;{\widehat{{{\mathcal {X}}}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta .\) Since \({\widehat{\Sigma }}\) and \({\widehat{\Sigma }}'\) are both simple conservative, they are unitarily similar, so there exists a unitary operator \(U: {\widehat{{{\mathcal {X}}}}} \rightarrow {\widehat{{{\mathcal {X}}}}}'\) such that \( {\widehat{A}}=U^{-1}{\widehat{A}}'U,\)\( {\widehat{B}}=U^{-1}{\widehat{B}}'\) and \( {\widehat{C}}={\widehat{C}}'U. \) Easy calculations shows that \({\widehat{{{\mathcal {X}}}}}^{'o} =U{\widehat{{{\mathcal {X}}}}}^{o},\)\({\widehat{{{\mathcal {X}}}}}^{'c} =U{\widehat{{{\mathcal {X}}}}}^{c},\)\(({\widehat{{{\mathcal {X}}}}}^{'o})^\perp =U({\widehat{{{\mathcal {X}}}}}^{o})^\perp ,\)\(({\widehat{{{\mathcal {X}}}}}^{'c})^\perp =U({\widehat{{{\mathcal {X}}}}}^{c})^\perp \) and \(P_{{\widehat{{{\mathcal {X}}}}}^{'o}}{\widehat{{{\mathcal {X}}}}}^{'c} = U P_{{\widehat{{{\mathcal {X}}}}}^{o}}{\widehat{{{\mathcal {X}}}}}^{c}.\) In particular,
$$\begin{aligned} P_{{{\mathcal {X}}}}=P_{P_{{\widehat{{{\mathcal {X}}}}}^{o}}{\widehat{{{\mathcal {X}}}}}^{c}}= U^{-1} P_{P_{{\widehat{{{\mathcal {X}}}}}^{'o}}{\widehat{{{\mathcal {X}}}}}^{'c}}U =U^{-1} P_{{{\mathcal {X}}}'} U, \end{aligned}$$which implies
$$\begin{aligned}&A= P_{{{\mathcal {X}}}} {\widehat{A}} {\upharpoonright }_{{{\mathcal {X}}}} = U^{-1} P_{{{\mathcal {X}}}'} {\widehat{A}}'U {\upharpoonright }_{{{\mathcal {X}}}} = (U{\upharpoonright }_{{{\mathcal {X}}}})^{-1} P_{{{\mathcal {X}}}'} {\widehat{A}}' {\upharpoonright }_{{{\mathcal {X}}}'} U{\upharpoonright }_{{{\mathcal {X}}}}= (U{\upharpoonright }_{{{\mathcal {X}}}})^{-1} {A}' U{\upharpoonright }_{{{\mathcal {X}}}}\\&B=(U{\upharpoonright }_{{{\mathcal {X}}}})^{-1}{B}', \qquad C= C'U{\upharpoonright }_{{{\mathcal {X}}}}. \end{aligned}$$It follows that \(\Sigma \) and \(\Sigma '\) are unitarily similar and the corresponding unitary operator is \(U_0=U{\upharpoonright }_{{{\mathcal {X}}}}.\) Then
$$\begin{aligned} E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}A^kBu_k \right) = E_{{{\mathcal {X}}}}\left( U_0^{-1} \sum _{k=0}^{n}A'^kB'u_k \right) = E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}A'^kB'u_k \right) . \end{aligned}$$Therefore (3.12) holds, and \(\Sigma '\) is an optimal minimal system.
-
(ii)
Let \(\Sigma ^*=(A^*,C^*,B^*,D^*;{{\mathcal {X}}},{{\mathcal {Y}}},{{\mathcal {U}}};\kappa )\) be an optimal minimal passive realization of \({\theta }^\# \in \mathbf {S}_{\kappa }({{\mathcal {Y}}},{{\mathcal {U}}}).\) Then \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is a minimal passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Consider an arbitrary observable passive realization \({\Sigma '}=({A'},{B'},{C'},{D};{{{\mathcal {X}}}'},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Then \({\Sigma }^{'*} = (A^{'*},C^{'*},B^{'*},D^*;{{\mathcal {X}}}',{{\mathcal {Y}}},{{\mathcal {U}}};\kappa ) \) is a controllable passive realization of \({\theta ^\#}.\) For a vector of the form \(x'= \sum _{k=0}^{n}{{A^{'*}}}^k{C}^{'*}y_k,\) where \( n \in {{\mathbb {N}}}_0\) and \( y_k \in {{\mathcal {Y}}},\) define
$$\begin{aligned} Sx'= \sum _{k=0}^{n}{(A^*)}^kC^*y_k. \end{aligned}$$Since \(\Sigma ^{'*}\) is controllable and \(\Sigma ^{*}\) is optimal, the domain of S is dense, and it holds
$$\begin{aligned} E_{{{\mathcal {X}}}}(Sx)= E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}{(A^*)}^kC^*y_k \right) \le E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}{{A^{'*}}}^k{C}^{'*}y_k \right) =E_{{{\mathcal {X}}}'}(x). \end{aligned}$$That is, S is a contractive linear relation with the dense domain. Then [1, Theorem 1.4.4] shows that the closure of S, which is still denoted as S, is contractive everywhere defined linear operator from \({{\mathcal {X}}}' \rightarrow {{\mathcal {X}}}.\) Since \({{\mathcal {X}}}'\) and \({{\mathcal {X}}}\) are Pontryagin spaces with the same negative index, \(S^*: {{\mathcal {X}}}\rightarrow {{\mathcal {X}}}',\) is contractive as well. The transfer functions of the \(\Sigma \) and \(\Sigma '\) coincide, and therefore \(CA^mB=C'{A'}^kB'\) for every \(m \in {{\mathbb {N}}}_0.\) By definition, \(S({A^{'*}})^mC^{'*}=({A^{*}})^mC^{*},\) or what is the same thing, \(C'{A'}^mS^*=CA^m,\) for every \(m \in {{\mathbb {N}}}_0.\) Then also
$$\begin{aligned} C'{A'}^{m+k}B'=C{A}^{m}{A}^{k}B=C'{A'}^mS^*A^{k}B \quad \text {for}\quad m,k\ge 0. \end{aligned}$$This implies \({A'}^{k}B'=S^*A^{k}B\) and moreover \( S^*\left( \sum _{k=0}^{n}{A}^kBu_k\right) = \sum _{k=0}^{n}{A'}^kB'u_k, \) since the system \(\Sigma '\) is observable. Therefore,
$$\begin{aligned} E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}{A'}^kB'u_k \right) = E_{{{\mathcal {X}}}'}\left( S^* \left( \sum _{k=0}^{n}{A}^kBu_k\right) \right) \le E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}{A}^kBu_k \right) , \end{aligned}$$since \(S^*\) is contractive. This proves that \(\Sigma \) is \(^*\)-optimal.
Suppose then that \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is minimal passive \(^*\)-optimal realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Then \(\Sigma ^*\) is a minimal passive realization of \({\theta }^\# \in \mathrm {\mathbf {S}}_{\kappa }({{\mathcal {Y}}},{{\mathcal {U}}}).\) To prove the optimality of \(\Sigma ^*\), it suffices to consider all the minimal passive realizations of \({\theta }^\#\); see Lemma 3.3. Let \(\Sigma ^{'*}=(A^{'*},C^{'*},B^{'*},D^{*};{{\mathcal {X}}}',{{\mathcal {Y}}},{{\mathcal {U}}};\kappa )\) be a minimal passive realization of \({\theta ^\#}.\) Then \(\Sigma '\) is a minimal passive realization of \(\theta . \) Since \(\Sigma \) is \(^*\)-optimal, the inequality
$$\begin{aligned} E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}A^kBu_k \right) \ge E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}A'^kB'u_k \right) , \qquad n \in {{\mathbb {N}}}_0, \quad u_k \in {{\mathcal {U}}}, \end{aligned}$$holds. Define \(Kx=\sum _{k=0}^{n}A'^kB'u_k\) for \( x=\sum _{k=0}^{n}A^kBu_k. \) Using similar techniques as above, K can be extended to be a contractive operator from \({{\mathcal {X}}}\rightarrow {{\mathcal {X}}}'\) such that
$$\begin{aligned} K^*(A^{'*})^kC^{'*}=(A^{*})^kC^{*}. \end{aligned}$$Since \(K^*\) is contractive,
$$\begin{aligned} E_{{{\mathcal {X}}}}\left( \sum _{k=0}^{n}{A^{*}}^k C^*y_k \right) = E_{{{\mathcal {X}}}}\left( K^* \sum _{k=0}^{n}{A^{'*}}^k C^{'*}y_k \right) \le E_{{{\mathcal {X}}}'}\left( \sum _{k=0}^{n}{A^{'*}}^k C^{'*}y_k \right) , \end{aligned}$$for \(\{ y_k\}\subset {{\mathcal {Y}}}.\) This shows that \(\Sigma ^*\) is optimal.
-
(iii)
Let \(\Sigma \) be a simple conservative realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Then \(\Sigma ^*\) is a simple conservative realization of \({\theta ^\#},\) and the first minimal restriction \({\Sigma ^*}'\) of \(\Sigma ^*\) is optimal minimal by the part (i). By using the representations (2.18) and (2.19) from Lemma 2.8, it is easy to deduce that the dual system of \({\Sigma ^*}'\) is the second minimal restriction \(\Sigma ''\) of \(\Sigma \), and it follows from the part (ii) that \(\Sigma ''\) is \(^*\)-optimal.
-
(iv)
Only the proofs of the claims considering optimal minimal realizations will be given, since the claims considering \(^*\)-optimal minimal realizations can be proved analogously. Let \(\Sigma _j=(A_j,B_j,C_j,D;{{\mathcal {X}}}_j,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) for \(j=1,2,\) be optimal minimal realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) In a sufficiently small neighbourhood of the origin, the transfer functions \(\theta _{\Sigma _1}\) and \(\theta _{\Sigma _2}\) of the systems \(\Sigma _1\) and \(\Sigma _2\) have the Neumann series and they coincide, so \(C_1A_1^kB_1=C_2A_2^kB_2\) for \(k=0,1,2,\ldots \) Define
$$\begin{aligned} Ux=\sum _{k=0}^N A_2^k B_2 u_k \end{aligned}$$(3.13)for a vector x of the form \(x=\sum _{k=0}^N A_1^k B_1 u_k,\) where \( \{u_k\} \in {{\mathcal {U}}}.\) Since \(\Sigma _1\) is controllable, such vectors are dense in \({{\mathcal {X}}}_1.\) Because \(\Sigma _2\) is controllable as well, vectors of the form Ux are dense in \({{\mathcal {X}}}_2.\)
Since \(\Sigma _1\) and \(\Sigma _2\) both are optimal realizations, \(E_{{{\mathcal {X}}}_1} (x) = E_{{{\mathcal {X}}}_1} (Ux),\) and therefore U is an isometric linear relation with the dense domain and the dense range. It follows now from [1, 1.4.2] that the closure of U is a unitary operator, which is still denoted as U. Then, trivially \(B_1=U^{-1}B_2.\) For vector x in (3.13), it holds
$$\begin{aligned} UA_1x= U \sum _{k=0}^N A_1^{k+1} B_1 u_k = \sum _{k=0}^N A_2^{k+1} B_2 u_k =A_2Ux. \end{aligned}$$It follows that \(UA_1x=A_2Ux\) holds in a dense set, and therefore by continuity, everywhere. Thus \(A_1=U^{-1}A_2U.\) Moreover, for \(k = 0,1,2,\ldots ,\) one concludes \(C_1A_1^kB_1=C_2A_2^kB_2 = C_2UA_1^kB_1. \) Since \(\mathrm {span}_{k \in {{\mathbb {N}}}_0}A_1^k B_1\) is dense in \({{\mathcal {X}}}_1,\) it must be \(C_1=C_2U.\) It has been shown that the unitary operator U has all the properties of (2.30), and therefore \(\Sigma _1\) and \(\Sigma _2\) are unitarily similar.
Suppose then that \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is an optimal minimal realization of \(\theta .\) Let \({\widehat{\Sigma }}_0=({\widehat{A}}_0,{\widehat{B}}_0,{\widehat{C}}_0,D;{\widehat{{{\mathcal {X}}}}}_0,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be some simple conservative realization of \(\theta .\) Lemma 2.8 shows that the system operator of \({\widehat{\Sigma }}\) can be represented as
$$\begin{aligned} T_{{\widehat{\Sigma }}_0} =\begin{pmatrix} \begin{pmatrix}A_{11}' &{} \quad A_{12}' &{} \quad A_{13}'\\ 0 &{} \quad A' &{} \quad A_{23}' \\ 0 &{} \quad 0 &{} \quad A_{33}' \end{pmatrix} &{} \begin{pmatrix} B_1' \\ B' \\ 0 \end{pmatrix} \\ \begin{pmatrix} 0 &{}\quad C' &{} \quad C_1' \end{pmatrix}&D \end{pmatrix} :\begin{pmatrix} \begin{pmatrix} {{\mathcal {X}}}_1 \\ {{\mathcal {X}}}' \\ {{\mathcal {X}}}_2 \end{pmatrix} \\ {{\mathcal {U}}}\end{pmatrix} \rightarrow \begin{pmatrix} \begin{pmatrix} {{\mathcal {X}}}_1 \\ {{\mathcal {X}}}' \\ {{\mathcal {X}}}_2 \end{pmatrix} \\ {{\mathcal {Y}}}\end{pmatrix}, \end{aligned}$$where \( {{\mathcal {X}}}_1=({\widehat{{{\mathcal {X}}}}}^o)^\perp , {{\mathcal {X}}}'=\overline{P_{{\widehat{{{\mathcal {X}}}}}^o}{\widehat{{{\mathcal {X}}}}}^c}\) and \({{\mathcal {X}}}_2= {\widehat{{{\mathcal {X}}}}}^o \cap ({\widehat{{{\mathcal {X}}}}}^c)^\perp .\) Now \(\Sigma '=(A',B',C',D;{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is the first minimal restriction of \({\widehat{\Sigma }},\) and it follows from part (i) that \(\Sigma '\) is optimal minimal, and moreover, as proved above, unitarily similar with \(\Sigma .\) Therefore, there exists a unitary operator \(U: {{\mathcal {X}}}\rightarrow {{\mathcal {X}}}'\) such that \(A =U^{-1}A'U ,B=U^{-1}B' \) and \(C=C'U.\) Define
$$\begin{aligned} T_{{\widehat{\Sigma }}} =\begin{pmatrix} \begin{pmatrix}A_{11}' &{} \quad A_{12}'U &{} \quad A_{13}'\\ 0 &{} \quad A &{} \quad U^{-1}A_{23}' \\ 0 &{} \quad 0 &{} \quad A_{33}' \end{pmatrix} &{} \begin{pmatrix} B_1' \\ B \\ 0 \end{pmatrix} \\ \begin{pmatrix} 0 &{} \quad C &{} \quad C_1' \end{pmatrix}&D \end{pmatrix} :\begin{pmatrix} \begin{pmatrix} {{\mathcal {X}}}_1 \\ {{\mathcal {X}}}\\ {{\mathcal {X}}}_2 \end{pmatrix} \\ {{\mathcal {U}}}\end{pmatrix} \rightarrow \begin{pmatrix} \begin{pmatrix} {{\mathcal {X}}}_1 \\ {{\mathcal {X}}}\\ {{\mathcal {X}}}_2 \end{pmatrix} \\ {{\mathcal {Y}}}\end{pmatrix}, \end{aligned}$$and let \({\widehat{\Sigma }}\) be the system corresponding the system operator \(T_{{\widehat{\Sigma }}} \). Easy calculations show that \({\widehat{\Sigma }}\) and \({\widehat{\Sigma }}_0\) are unitarily similar and
$$\begin{aligned} {\widehat{U}}=\begin{pmatrix} I &{} \quad 0 &{}\quad 0 \\ 0 &{} \quad U &{} \quad 0\\ 0 &{} \quad 0 &{} \quad I \end{pmatrix}:\begin{pmatrix} {{\mathcal {X}}}_1 \\ {{\mathcal {X}}}\\ {{\mathcal {X}}}_2 \end{pmatrix} \rightarrow \begin{pmatrix} {{\mathcal {X}}}_1 \\ {{\mathcal {X}}}' \\ {{\mathcal {X}}}_2 \end{pmatrix} \end{aligned}$$is the corresponding unitary operator. Therefore \({\widehat{\Sigma }}\) is a simple conservative system. Now \({\widehat{U}}\) maps \(P_{{{\mathcal {X}}}^o}{{\mathcal {X}}}^c\) to \(P_{{{{\mathcal {X}}}'}^o}{{{\mathcal {X}}}'}^c,\) and \({\widehat{U}}{{{\mathcal {X}}}'}=U{{{\mathcal {X}}}'}={{\mathcal {X}}}.\) It follows that \(\Sigma \) is the first minimal restriction of \({\widehat{\Sigma }}.\)\(\square \)
4 Generalized Defect Functions
If \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces, it is well known that \(S \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {Y}}})\) is holomorphic in the unit disk and it has non-tangential contractive strong limit values almost everywhere (a.e.) on the unit circle \({{\mathbb {T}}}.\) Therefore, S can be extended to \(L^{\infty }({{\mathcal {U}}},{{\mathcal {Y}}})\) function, that is, the class of weakly measurable a.e. defined and essentially bounded \(\mathcal {L}({{\mathcal {U}}},{{\mathcal {Y}}})\)-valued functions on \({{\mathbb {T}}}.\) Then it follows from [29, Theorem V.4.2] that there exist a Hilbert space \({{\mathcal {K}}}\) and an outer function \(\varphi _S \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {K}}})\) such that
a.e. on \({{\mathbb {T}}}\), and if a function \({\widehat{\varphi }}\in \mathbf {S}({{\mathcal {U}}},{\widehat{{{\mathcal {K}}}}})\), where \({\widehat{{{\mathcal {K}}}}}\) is a Hilbert space, has this same property, then
a.e. on \({{\mathbb {T}}}.\) The function \(\varphi _S\) is called the right defect function of S. For the notions of the outer functions, \(^*\)-outer functions, inner functions and \(^*\)-inner functions, see [29, Chapter V]. From [29, Theorem V.4.2] it is also easy to deduce that there exists a Hilbert space \({{\mathcal {H}}}\) and a \(^*\)-outer function \(\psi _S \in \mathbf {S}({{\mathcal {H}}},{{\mathcal {Y}}})\) such that
a.e. \(\zeta \in {{\mathbb {T}}}\) and if a Schur function \({\widehat{\psi }} \in \mathbf {S}({\widehat{{{\mathcal {H}}}}},{{\mathcal {Y}}})\) has this same property, then
The function \(\psi _S\) is called the left defect function of S. Both \(\varphi _S\) and \(\psi _S\) are unique up to a unitary constant.
The theory of the defect functions is considered, for instance, in [17,18,19]. Various connections of defect functions and passive realizations can be found in [3, 7, 8]. The definition of the defect functions was generalized for functions \(S \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) in [27] by using the Kreĭn–Langer factorizations and the fact that all functions in \({{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) have also contractive strong limit values a.e. on \({{\mathbb {T}}}.\) If \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces such that their negative index is not zero, the defect functions cannot be defined similarly as in the Hilbert space setting, since the boundary values of \(S \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) may not be Hilbert space contractions. However, in the Hilbert state space case, Arov and Saprikin showed in [10] that for a function \(S=S_rB_r^{-1} \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\), where \(S_rB_r^{-1}\) is the right Kreĭn–Langer factorization of S, the existence of the optimal minimal realization of S is connected with the existence of the right defect function of \(S_r.\) In general, similar connections exist with certain functions constructed by embedded systems, and those function are called defect functions; this is the approach taken here.
Suppose that \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is a passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) Denote the system operator of \(\Sigma \) by T. Theorem 2.1 shows that T has a Julia operator of the form
where \( {{\mathfrak {D}}}_{T^*}\) and \( {{\mathfrak {D}}}_{T}\) are Hilbert spaces, \( D_{T^*}D_{T^*}^*=I-TT^*\) and \( D_{T}D_{T}^*=I-T^*T \) such that \(D_{T}\) and \(D_{T^*}\) have zero kernels. Then, one can form the Julia embedding\(\widetilde{\Sigma }\) of the system \(\Sigma ;\) recall the embeddings from page 5. That is, the corresponding system operator \({T}_{\widetilde{\Sigma }}\) of the embedding \(\widetilde{\Sigma }\) is a Julia operator of T, and it is of the form
where \( D_{T^*} = \begin{pmatrix} D_{T_{,1}^*}\\ D_{T_{,2}^*} \end{pmatrix} \) and \( D_{T} = \begin{pmatrix} D_{T_{,1}}\\ D_{T_{,2}} \end{pmatrix}. \) The transfer function of the Julia embedding is
Moreover, the identities (2.11) and (2.12) of Lemma 2.3 hold for the system \(\Sigma \) and its transfer function \(\theta \). If \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces, similar arguments as used in the proof of Proposition 2.4 and in the proof of [27, Lemma 3.2] show that \(\varphi \), \(\psi \) and \(\chi \) are generalized Schur functions with the index not larger than \(\kappa \).
Definition 4.1
Let \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) be Pontryagin spaces with the same negative index. Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be an optimal minimal passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) and let \(\widetilde{\Sigma }\) be the Julia embedding of it, represented as in (4.6). Then the function \(\varphi \) in (4.7) is defined to be the right defect function \(\varphi _\theta \) of \(\theta .\)
Moreover, let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be a \(^*\)-optimal minimal passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) and let \(\widetilde{\Sigma }\) be the Julia embedding of it, represented as in (4.6). Then the function \(\psi \) in (4.7) is defined to be the left defect function \(\psi _{\theta }\) of \(\theta .\)
Remark 4.2
Since optimal (\(^*\)-optimal) minimal realizations are unitarily similar by Theorem 3.5, and Julia operators for contractive operator are essentially unique by Theorem 2.1, it can be deduced that the defect functions are essentially uniquely defined by \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}.\) The definition above is also slightly different from the one given in [27] for functions in the class \({{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces.
The right defect function of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) and the left defect function of \(\theta ^\#\) are closely related to each other.
Lemma 4.3
For \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) it holds \(\varphi _{\theta }^\#=\psi _{\theta ^\#}\) and \(\psi _\theta ^\#=\varphi _{\theta ^\#}\)
Proof
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be an optimal (\(^*\)-optimal) minimal realization of \(\theta .\) Denote the system operator of \(\Sigma \) as T, and the Julia operator \(T_{\widetilde{\Sigma }}\) of T as in (4.6). By Theorem 3.5, the system \(\Sigma ^*\) is \(^*\)-optimal (optimal) minimal, and a calculation shows that \(T_{\widetilde{\Sigma }}^*\) is the Julia operator of \(T^*.\) Now the results follow means of (4.7). \(\square \)
In the Hilbert space setting, \(S \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {Y}}}) \) has factorizations of the form
where \(S_i \in \mathbf {S}({{\mathcal {Y}}}',{{\mathcal {Y}}}) \) is inner, \(S_o \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {Y}}}') \) is outer, \(S_{*o} \in \mathbf {S}({{\mathcal {U}}}',{{\mathcal {Y}}}) \) is \(^*\)-outer, \(S_{*i} \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {U}}}') \) is \(^*\)-inner, and \({{\mathcal {Y}}}'\) and \({{\mathcal {U}}}'\) are Hilbert spaces [29, p. 204]. The next proposition shows that for an ordinary Schur function \( \theta \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {Y}}}), \) the outer factor of \(\varphi _\theta \) and the \(^*\)-outer factor of \(\psi _\theta \) defined above coincide essentially with the usual definition of defect functions.
Proposition 4.4
Let \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces. Then
a.e. on \({{\mathbb {T}}}\), and if a generalized Schur function \({\widehat{\varphi }}\in \mathbf {S}_{\kappa '}({{\mathcal {U}}},{\widehat{{{\mathcal {K}}}}})\), where \({\widehat{{{\mathcal {K}}}}}\) is a Hilbert space and \(\kappa '\) does not depend on \(\kappa \), has this same property, then
a.e. on \({{\mathbb {T}}}.\) If \(\kappa =0,\) denote the inner and outer factors of \(\varphi _\theta \) as \(\varphi _{\theta _i}\) and \(\varphi _{\theta _o},\) respectively. Then, \(\varphi _{\theta _i}\) is an isometric constant, and if \(\varphi '\) is an outer function with properties (4.1) and (4.2), then it holds \(U\varphi _{\theta _o}=\varphi ',\) where U is a unitary operator.
Moreover,
a.e. \(\zeta \in {{\mathbb {T}}}\) and if a generalized Schur function \({\widehat{\psi }} \in \mathbf {S}_{\kappa '}({\widehat{{{\mathcal {H}}}}},{{\mathcal {Y}}})\), where \({\widehat{{{\mathcal {K}}}}}\) is a Hilbert space and \(\kappa '\) does not depend on \(\kappa \), has this same property, then
a.e. \(\zeta \in {{\mathbb {T}}}. \)If \(\kappa =0,\) denote the \(^*\)-inner and \(^*\)-outer factors of \(\psi _\theta \) as \(\psi _{\theta _{^*i}}\) and \(\psi _{\theta _{^*o}},\) respectively. Then, \(\psi _{\theta _{^*i}}\) is a co-isometric constant, and if \(\psi '\) is a \(^*\)-outer function with properties (4.3) and (4.4), then it holds \(\psi _{\theta _{^*o}}U'=\psi ',\) where \(U'\) is a unitary operator.
Proof
Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be an optimal minimal realization of \(\theta .\) Denote the system operator of \(\Sigma \) as T, the Julia operator \(T_{\widetilde{\Sigma }}\) of T as in (4.6) and the function \(\varphi =\varphi _\theta \) as in (4.7). Since \(T_{\widetilde{\Sigma }}\) is unitary, the operator
must be isometric, and therefore the system
is an isometric realization of the function \(\begin{pmatrix}\theta \\ \varphi _\theta \end{pmatrix} \) . Since \(\Sigma '\) is an embedding of the minimal system \(\Sigma ,\) the system \(\Sigma '\) is also minimal. It follows from Theorem 2.6 that \(\begin{pmatrix}\theta \\ \varphi _\theta \end{pmatrix}\)\(\in \mathbf {S}_\kappa \left( {{\mathcal {U}}}, {{\mathcal {Y}}}\oplus {{\mathfrak {D}}}_{T} \right) .\) Since contractive boundary values of generalized Schur functions exist for a.e. \(\zeta \in {{\mathbb {T}}},\) it holds
for a.e. \(\zeta \in {{\mathbb {T}}}.\)
Suppose that a function \({\widehat{\varphi }}\in \mathbf {S}_{\kappa '}({{\mathcal {U}}},{\widehat{{{\mathcal {K}}}}})\), where \({\widehat{{{\mathcal {K}}}}}\) is a Hilbert space, has the property \( {\widehat{\varphi }}^* (\zeta ) {\widehat{\varphi }}(\zeta ) \le I-\theta ^* (\zeta ) \theta (\zeta ) \) for a.e. \(\zeta \in {{\mathbb {T}}}.\) Since the function \({\widehat{\varphi }}\) has the left Kreĭn–Langer factorization of the form \({\widehat{\varphi }}= B^{-1}_{{\widehat{\varphi }}} {\widehat{\varphi }}_{l} ,\) where \({\widehat{\varphi }}_{l} \) is an ordinary Schur function, it holds \( {\widehat{\varphi }}^* (\zeta ) {\widehat{\varphi }}(\zeta ) = {\widehat{\varphi }}_{l}^* (\zeta ) {\widehat{\varphi }}_{l}(\zeta ) \) for a.e. \(\zeta \in {{\mathbb {T}}}.\) Then the function
belongs to the Schur class \(\mathbf {S}_\kappa \left( {{\mathcal {U}}}, {{\mathcal {Y}}}\oplus {\widehat{{{\mathcal {K}}}}} \right) ,\) and it has a controllable isometric realization \(\breve{{\Sigma }}\) with the system operator
That is,
It follows that
is a realization of \(\theta ,\) and since \({\breve{\Sigma }}\) is isometric and \({\widehat{{{\mathcal {K}}}}}\) is a Hilbert space, the system \(\Sigma _1\) is passive. Since \(T_{\breve{\Sigma }}\) is isometric, the defect operator \(D_{T_{\breve{\Sigma }}}\) of \(T_{\breve{\Sigma }}\) is zero, and it follows from Lemma 2.3 that
whenever the expressions are meaningful. By combining the identities (2.12) and (4.11) for optimal minimal realization \(\Sigma ,\) one gets
for every z in a sufficiently small symmetric neighbourhood \(\Omega \) of the origin. Since the system \(\Sigma \) is optimal, if follows by using Neumann series that
for every \(z \in \Omega \) and for every \(u \in {{\mathcal {U}}}.\) Then it follows from (4.12) that \( {\widehat{\varphi }}_{l}^* (z) {\widehat{\varphi }}_{l}(z) \le {\varphi _\theta }^* (z){\varphi _\theta }(z)\) for every \( z \in \Omega . \) By continuity,
for a.e. \(\zeta \in {{\mathbb {T}}}.\)
Next suppose that \(\kappa =0.\) By combining (4.2) and (4.13), it can be deduced that
for a.e. \(\zeta \in {{\mathbb {T}}}.\) Then it follows from [29, Proposition V.4.1] that \(\varphi '=U\varphi _{\theta _o},\) where U is a unitary operator. If one puts an outer function \( {\widehat{\varphi }}_{l}=\varphi _{\theta _{o}}=U^{-1}\varphi '\) in (4.8) and constructs the operator \(T_{\breve{\Sigma }}\) as in (4.9) , the construction of an optimal minimal system used in the proof of [5, Theorem 7] shows that the associated system \(\Sigma _1\) in (4.10) is optimal. Since \(\Sigma \) is also optimal, for every \(z \in {{\mathbb {D}}},\) it holds
Then it follows from (4.12) that \(\Vert {\varphi _{\theta _i}} (z){\varphi _{\theta _o}}(z)u \Vert = \Vert {\varphi _{\theta _o}}(z)u \Vert \) for every \(z \in {{\mathbb {D}}}\) and every \(u \in {{\mathcal {U}}}.\) The outer function \({\varphi _{\theta _o}}(z)\) has a dense range for every \(z \in {{\mathbb {D}}}\) [29, Proposition V.2.4]. This implies that \( {\varphi _{\theta _i}} (z)\) is an isometry for every \(z \in {{\mathbb {D}}},\) and arguing as in the proof of [29, Proposition V.2.1] one deduces that \( {\varphi _{\theta _i}} \) is an isometric constant. The claims involving \( {\varphi _{\theta }} \) are proved.
The claims involving \( {\psi _{\theta }} \) follow now directly by applying Lemma 4.3. \(\square \)
Lemma 4.5
Let \(\Sigma _0=(A_0,B_0,C_0,D;{{\mathcal {X}}}_0,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) and \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be passive realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) such that \(\Sigma _0\) is optimal. If for every z and w in a sufficiently small symmetric neighbourhood \(\Omega \) of the origin the equality
holds, then \(\Sigma \) is optimal.
Proof
It follows from Lemma 2.8 that the system operator \(T_\Sigma \) of \(\Sigma \) can be represented as in (2.16), the restriction \(\Sigma _c=(A_c,B_c,C_c,D;{{\mathcal {X}}}^c,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\Sigma \) to the controllable subspace \({{\mathcal {X}}}^c\) is controllable passive, and (2.25) and (2.26) hold.
Define \(Rx=\sum _{j=1}^M A_0^j B_0u_j\) for the vectors of the form \( x=\sum _{j=1}^M A_c^j B_cu_j,\) where \( M \in {{\mathbb {N}}}\) and \( \{u_j\}_{j=1}^M \subset {{\mathcal {U}}}.\) Since \(\Sigma _c\) is controllable, the domain of R is dense. Moreover, \(\Sigma _0\) is optimal, and therefore \( E_{{{\mathcal {X}}}_0} \left( Rx \right) \le E_{{{\mathcal {X}}}^c} \left( x \right) . \) That is, R is contractive, and it follows from [1, Theorem 1.4.2] that the closure of R is everywhere defined contractive linear operator. It is still denoted by R. Since
holds for every z in a sufficiently small symmetric neighbourhood \(\Omega \) of the origin, it follows by continuity that \( R\left( (I-zA_c)^{-1}B_cu\right) =(I-zA_0)^{-1}B_0u \) for every \(z\in \Omega \) and \(u\in {{\mathcal {U}}}.\) Then
for all \( M \in {{\mathbb {N}}}, \{z_j \}_{j=1}^M \subset \Omega , \) and \( \{u_j \}_{j=1}^M \subset {{\mathcal {U}}}.\) Equalities (2.26) and (4.14) imply now
This implies that R is isometric in \(\mathrm {span}\{\mathrm{ran\,}(I-zA_1)^{-1}B_1, z \in \Omega \},\) which is a dense set, since \(\Sigma _1\) is controllable. Since R is bounded, it is now isometric everywhere, and it follows that \(\Sigma _c\) is optimal. Then it follows from (2.25) that \(\Sigma \) is optimal, and the proof is complete. \(\square \)
The main results of [3, Theorem 1.1] were generalized to the Pontryagin state space setting in [27, Theorem 4.4]. By using Definition 4.1, it can be shown that parts of this result, as well as [8, Theorem 1], hold also in the case when all the spaces are indefinite. Moreover, certain parts of [3, Theorem 1.1], [8, Theorem 1] and [27, Theorem 4.4] can be improved. Before stating these results, some lemmas are needed.
Lemma 4.6
Let \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\). Then the following statements are equivalent:
- (i)
all \(\kappa \)-admissible minimal passive realizations of \(\theta \) are unitarily similar;
- (ii)
there exists a minimal passive realization of \(\theta \) such that it is both optimal and \(^*\)-optimal;
- (iii)
all \(\kappa \)-admissible minimal passive realizations of \(\theta \) are both optimal and \(^*\)-optimal.
Proof
(i) \(\Rightarrow \) (iii). Suppose (i). Let the systems \(\Sigma _1=(A_1,B_1,C_1,D;{{\mathcal {X}}}_1,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ) \) and \( \Sigma _2=(A_2,B_2,C_2,D;{{\mathcal {X}}}_2,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be, respectively, minimal passive and optimal (\(^*\)-optimal) minimal passive realizations of \(\theta .\) Let U be the unitary operator from \({{\mathcal {X}}}_1\) to \({{\mathcal {X}}}_2\) with the properties described in (2.30). An easy calculation shows that
for every \(u \in {{\mathcal {U}}}\) and for every \(n=0,1,2,\ldots \) which implies that \(\Sigma _1\) is actually optimal (\(^*\)-optimal), and therefore (iii) holds.
(iii) \(\Rightarrow \) (ii). The claim (iii) trivially implies (ii).
(ii) \(\Rightarrow \) (i). Suppose (ii). Let the systems \(\Sigma _1=(A_1,B_1,C_1,D;{{\mathcal {X}}}_1,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ) \) and \( \Sigma _2=(A_2,B_2,C_2,D;{{\mathcal {X}}}_2,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be, respectively, optimal and \(^*\)-optimal minimal passive realizations of \(\theta .\) Let Z be the weak similarity mapping from \({{\mathcal {X}}}_1\) to \({{\mathcal {X}}}_2\) with the properties described in (2.31). It follows from (2.31) that all elements of the form \(\sum _{k=0}^nA_1^kB_1u_k\) belongs to the domain of Z, and \(Z\left( \sum _{k=0}^nA_1^kB_1u_k\right) =\sum _{k=0}^nA_2^kB_2u_k\). Recall also here the construction of Z in the proof of [27, Theorem 2.5]. Since \(\Sigma _1\) is both optimal and \(^*\)-optimal,
Then it follows from [1, Theorem 1.4.2] that the operator Z has a unitary extension, and the properties in (2.30) follow by continuity. Therefore \(\Sigma _1\) and \(\Sigma _2\) are unitarily similar. Since unitary similarity clearly is a transitive property, (i) holds, and the proof is complete. \(\square \)
Lemma 4.7
If the system \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is an optimal passive realization of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) then \({{\mathcal {X}}}^c \subset {{\mathcal {X}}}^o.\)
Proof
According to Proposition 2.7, the spaces \({{\mathcal {X}}}^o\) and \(({{\mathcal {X}}}^o)^\perp \) are regular subspaces and \(({{\mathcal {X}}}^o)^\perp \) is a Hilbert space. It follows from Lemma 2.8 that the system operator T of \(\Sigma \) can be represented as in (2.15), and the restriction \(\Sigma _o=(A_o,B_o,C_o,D;{{\mathcal {X}}}^o,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\Sigma \) to the observable subspace \({{\mathcal {X}}}^o\) is observable passive realization of \(\theta .\) For \(n=0,1,2,\ldots \), it holds
where f(n) is an operator depending on n. Then for any \(N\in {{\mathbb {N}}}_0\) and any \(\{u_n \}_{n=0}^N \subset {{\mathcal {U}}},\) it holds
This implies
But since \(\Sigma \) is optimal and \(({{\mathcal {X}}}^o)^\perp \) is a Hilbert space, one deduces \( P_{({{\mathcal {X}}}^o)^\perp }\left( \sum _{n=0}^{N} A^nBu_n\right) =0.\) That is, \(\mathrm {span}\{ A^nB : n=0,1,\ldots \} \subset {{\mathcal {X}}}^o\) and since \({{\mathcal {X}}}^o\) is closed, also \(\overline{\mathrm {span}}\{ A^nB : n \in {{\mathbb {N}}}_0 \} = {{\mathcal {X}}}^c \subset {{\mathcal {X}}}^o.\)\(\square \)
The next Theorem contains promised extensions for some results of [3]. In particular, the fact that statements (I)(b), (II)(b) and (III)(b) implies the other statements, respectively, in parts (I), (II) and (III), is new also in the Hilbert space setting.
Theorem 4.8
Let \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})},\) where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index.
- (I)
The following statements are equivalent:
- (a)
\(\varphi _\theta \equiv 0\);
- (b)
all \(\kappa \)-admissible controllable passive realizations of \(\theta \) are minimal isometric;
- (c)
there exists an observable conservative realization of \(\theta ;\)
- (d)
all simple conservative realization of \(\theta \) are observable;
- (e)
all observable co-isometric realizations of \(\theta \) are conservative.
- (a)
- (II)
The following statements are equivalent:
- (a)
\(\psi _\theta \equiv 0\);
- (b)
all \(\kappa \)-admissible observable passive realization of \(\theta \) are minimal co-isometric;
- (c)
there exists a controllable conservative realization of \(\theta ;\)
- (d)
all simple conservative realization of \(\theta \) are controllable;
- (e)
all controllable isometric realizations of \(\theta \) are conservative.
- (a)
- (III)
The following statements are equivalent:
- (a)
\(\varphi _\theta \equiv 0\) and \(\psi _\theta \equiv 0\);
- (b)
all \(\kappa \)-admissible simple passive realization of \(\theta \) are minimal conservative;
- (d)
there exists a minimal conservative realization of \(\theta .\)
- (a)
Proof
(I) (a) \(\Rightarrow \) (b). Suppose (a). Let the systems \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) and \(\Sigma _0=(A_0,B_0,C_0,D;{{\mathcal {X}}}_0,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be, respectively, a controllable passive and an optimal minimal passive realizations of \(\theta .\) Represent the Julia embeddings of \(\Sigma \) and \(\Sigma _0\) as in (4.6). Then, (2.12) holds for \(\Sigma \). Since \(\varphi _\theta \equiv 0,\) if follows from the definition of \(\varphi _\theta \) that
holds for every z and w in a sufficiently small symmetric neighbourhood \(\Omega \) of the origin. Since \(\Sigma _0\) is optimal, by considering the Neuman series of \((I-zA_0)^{-1}B_0\) and \((I-zA_0)^{-1}B_0,\) one deduces that
Then it holds \(\varphi ^*(z) \varphi (z) \le =0 \) for every \(z \in \Omega \). But since \(\varphi (z)\) is an operator whose range belongs to the Hilbert space \(\mathfrak {D}_T,\) this implies \(\varphi (z)= D_{T_{,2}}^* +zD_{T_{,1}}^*(I-zA)^{-1}B = 0\) for \( z \in \Omega .\) It follows that \( D_{T_{,2}}^*=0.\) Since \(\Sigma \) is controllable, \(\mathrm {span}\{(I-zA)^{-1}B; z \in \Omega \}\) is dense in \({{\mathcal {X}}}\) by the identity (2.4) and therefore also \(D_{T_{,1}}^*=0.\) Then \(D_T=0,\) so T is isometric, and \(\Sigma \) is a controllable isometric system. In particular, if \(\Sigma \) is chosen to be minimal passive; for the existence, see Lemma 2.8, the previous argument shows that \(\Sigma \) is a minimal isometric realization of \(\theta .\) Since all controllable isometric realizations of \(\theta \) are unitarily similar, they are now also minimal, and (b) holds.
(b) \(\Rightarrow \) (c). Suppose (b). Let \(\Sigma '=(A',B',C',D;{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ) \) be an optimal minimal passive realization of \(\theta .\) The existence of \(\Sigma '\) follows from Theorem 3.5 (i). By assumption, \(\Sigma '\) is isometric. It follows from Theorem 3.5 (iv) that \(\Sigma '\) is the first minimal restriction of the simple conservative system \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\). By Lemma 2.8, the system operator \(T_{\Sigma }\) of \(\Sigma \) can be represented as in (2.18), where now \({{\mathcal {X}}}'=\overline{P_{{{\mathcal {X}}}^o}{{\mathcal {X}}}^c}\).
\(T_{\Sigma '}\) of \(\Sigma '\) is isometric and \(T_{\Sigma }\) is unitary, an easy calculation using the fact that the range space \(({{\mathcal {X}}}^o)^\perp \) is a Hilbert space shows that \(B_1'=0\) and \(A_{12}'=0\) in (2.18). But then for every \(x \in ({{\mathcal {X}}}^o)^\perp \) and every \(n=0,1,2,\ldots \),
That is, \(({{\mathcal {X}}}^o)^\perp \subset ({{\mathcal {X}}}^c)^\perp \) and therefore \({{\mathcal {X}}}^c \subset {{\mathcal {X}}}^o\). Since \(\Sigma \) is simple, this implies now \({{\mathcal {X}}}^o={{\mathcal {X}}}.\) Then \(\Sigma \) is observable, and (c) holds.
(c) \(\Rightarrow \) (a). Suppose (c). Let \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) be an observable conservative realization of \(\theta .\) By Lemma 2.8, \(\Sigma \) can be represented as in (2.18). The first minimal restriction (2.23) of \(\Sigma \) is an optimal minimal realization of \(\theta \) by Theorem 3.5 (i). But since \(\Sigma \) is observable, \({{\mathcal {X}}}^o={{\mathcal {X}}}\) and \(({{\mathcal {X}}}^o)^\perp =\{0\}.\) It follows that the reprentations (2.16) and (2.18) coinsides. That is, the first minimal restriction \(\Sigma '\) is just a restriction to the controllable subspace of \(\Sigma .\) By Lemma 2.8, \(\Sigma '\) is now isometric. Thus if one constructs a Julia operator of \(T_{\Sigma '}\) as in (4.5), \(D_{T_{\Sigma '}}=0,\) and then it follows from the definition of \(\varphi _{\theta }\) and (4.7) that \(\varphi _{\theta }\equiv 0,\) and (a) holds.
The equivalences of the statements (c), (d) and (e) follow easily from the facts that all observable co-isometric realizations of \(\theta \) are unitarily similar, all simple conservative realization of \(\theta \) are unitarily similar and unitary similarity preserves the structural properties of the system and system operator. The part (I) is proven.
(II) The proof is analogous to the proof of the part (I), and the details are omitted.
(III) (a) \(\Rightarrow \) (b). Suppose (a). By combining the parts (I) and (II), it follows that all controllable or observable passive realizations of \(\theta \) are minimal conservative. Consider a simple passive realization \(\Sigma \!=(A.B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\theta .\) It follows from Lemma 2.8 that the contractive system operator T of \(\Sigma \) can be represented as in (2.15), where the restriction \(\Sigma _o\) in (2.20) is observable passive, and therefore now minimal conservative. Then the system operator \(T_{\Sigma _o}\) of \({\Sigma _o}\) is unitary. Let \(x\in {{\mathcal {X}}}^o.\) Then, by contractivity of T and unitarity of \(T_{\Sigma _o}\)
Since \(A_{2} x \in ({{\mathcal {X}}}^o)^\perp \) and \(({{\mathcal {X}}}^o)^\perp \) is a Hilbert space, it follows that \(A_{2} =0.\) If one chooses \(u \in {{\mathcal {U}}},\) a similar argument as above shows that \(B_1=0.\) Then for any \(n \in {{\mathbb {N}}}\), it holds
This is only possible if \(({{\mathcal {X}}}^o)^\perp =0,\) since \(\Sigma \) is simple. But then the systems \(\Sigma _0\) and \(\Sigma \) coincide, so the system \(\Sigma \) is minimal conservative, and (b) holds.
Now (b) trivially implies (c), and the fact that (c) implies (a) follows by combining the parts (I) and (II). The proof is complete. \(\square \)
Remark 4.9
If \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Hilbert spaces, it follows from [27, Lemma 3.2] that simple passive realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are \(\kappa \)-admissible. Therefore, in that case it is not necessary to assume the considered systems to be \(\kappa \)-admissible in Lemma 4.6 and Theorems 4.8 and 4.10, since the other assumptions already guarantee it. However, if \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index, it is not known that are all simple passive, or even all minimal passive, realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\)\(\kappa \)-admissible.
If \(\varphi _{\theta }\equiv 0\) (\(\psi _{\theta }\equiv 0\)), then Theorem 4.8 shows that all \(\kappa \)-admissible minimal passive realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are minimal isometric (co-isometric). In particular, they are controllable isometric (observable coisometric), and it follows from Theorem 2.6 that they are unitarily similar. This situation can occur also when the defect functions do not vanish identically. In what follows, the range of \(\varphi _{\theta }\) and the domain of \({\psi _{\theta }}\) will be denoted, respectively, by \(\mathfrak {D}_{\varphi _{\theta }}\) and \(\mathfrak {D}_{\psi _{\theta }}\). In the Hilbert space setting, it is well known [18, 19] that for a standard Schur function \(\theta \in \mathbf {S}({{\mathcal {U}}},{{\mathcal {Y}}}), \) there exists a function \(\chi _{\theta } \in L^\infty (\mathfrak {D}_{\psi _{\theta }},\mathfrak {D}_{\varphi _{\theta }})\) such that the function
has contractive values for a.e. \(\zeta \in {{\mathbb {T}}}.\) Under certain normalizing conditions for the functions \( \varphi _{\theta }\) and \( \psi _{\theta }\), the function \(\chi _{\theta }\) is unique. In the Hilbert space setting, the important properties of the function \(\chi _{\theta }(\zeta )\) established by Boiko and Dubovoj, were bublished without proof in the paper [16]. In general, \(\chi _{\theta }\) may has negative Fourier coefficients and therefore it is not a Schur function. In that case the function \(\Theta \) in (4.15) is not a Schur function either. However, Arov and Nudelmann showed in [7, 8] that \(\Theta \) is a Schur function if and only if all minimal passive realizations of \(\theta \) are unitarily similar. This result will be generalized to the indefinite setting in the following theorem. The proof uses optimal and \(^*\)-optimal realizations as in [7, 8], but it is more elementary.
Theorem 4.10
Let \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\), where \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Pontryagin spaces with the same negative index, and let \(\varphi _\theta \) and \(\psi _\theta \) be defect functions of \(\theta .\) Then all \(\kappa \)-admissible minimal passive realizations of \(\theta \) are unitarily similar if and only if there exist an \({{\mathcal {L}}}(\mathfrak {D}_{\psi _{\theta }},\mathfrak {D}_{\varphi _{\theta }})\)-valued function \(\chi _{\theta }\) analytic in a neighbourhood of the origin such that
Proof
Suppose that all \(\kappa \)-admissible minimal passive realizations of \(\theta \in {{{\mathbf {S}}}_{\kappa }( {{\mathcal {U}}},{{\mathcal {Y}}})}\) are unitarily similar. Then it follows from Lemma 4.6 that every \(\kappa \)-admissible minimal passive realization is optimal and \(^*\)-optimal. Take any \(\kappa \)-admissible minimal passive realization \(\Sigma \) of \(\theta \) and consider its Julia embedding as in (4.6). Then the transfer function (4.7) of the Julia embedding belongs to the class \(\mathbf {S}_{\kappa }\left( {{\mathcal {U}}}\oplus {{\mathfrak {D}}}_{T^*} , {{\mathcal {Y}}}\oplus {{\mathfrak {D}}}_{T} \right) ,\) and since \(\Sigma \) is both optimal and \(^*\)-optimal, the upper right corner and lower left corner of (4.7) are defect functions of \(\theta .\) Choose \(\chi _{\theta }=\chi \) in (4.7), and the necessity is proven.
Suppose then that there exists an \({{\mathcal {L}}}(\mathfrak {D}_{\psi _{\theta }},\mathfrak {D}_{\varphi _{\theta }})\)-valued function \(\chi _\theta \) such that \(\Theta \) in (4.16) belongs to the class \(\mathbf {S}_{\kappa }\left( {{\mathcal {U}}}\oplus {{\mathfrak {D}}}_{\psi _{\theta }} , {{\mathcal {Y}}}\oplus {{\mathfrak {D}}}_{\varphi _{\theta }} \right) .\) It suffices to show that there exists minimal passive realization \(\Sigma \) of \(\theta \) such that it is both optimal and \(^*\)-optimal; see Lemma 4.6. Let
be a simple conservative realization of \(\Theta \in \mathbf {S}_{\kappa }\left( {{\mathcal {U}}}\oplus {{\mathfrak {D}}}_{\psi _{\theta }} , {{\mathcal {Y}}}\oplus {{\mathfrak {D}}}_{\varphi _{\theta }} \right) . \) Then the system operator \(T_\Theta \) of \(\Sigma _\Theta \) can be represented as
In a sufficiently small symmetric neighbourhood \(\Omega \) of the origin, it holds
The spaces \({{\mathfrak {D}}}_{\varphi _{\theta }}\) and \({{\mathfrak {D}}}_{\psi _{\theta }}\) are Hilbert spaces, and therefore it follows that the system \(\Sigma =(A,B,C,D;{{\mathcal {X}}},{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) is a passive realization of \(\theta .\) Since \(\Sigma _\Theta \) is conservative, Lemma 2.3 shows that
That is,
An easy calculation and Lemma 4.3 show that the Eq. (4.17) is equivalent to
Let \(\Sigma '=(A',B',C',D;{{\mathcal {X}}}',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) and \( \Sigma ''=(A'',B'',C'',D;{{\mathcal {X}}}'',{{\mathcal {U}}},{{\mathcal {Y}}};\kappa ) \) be, respectively, an optimal minimal and a \(^*\)-optimal minimal realizations of \(\theta \). It follows from Theorem 3.5 (ii) that \({\Sigma ''}^* \) is an optimal minimal realization of \(\theta ^\#.\) Then, by the definition of \(\varphi _{\theta }\) and \(\varphi _{\theta ^\#},\) it holds
It follows that
By using Lemma 4.5, it can be deduced that \(\Sigma \) and \(\Sigma ^*\) are optimal systems. Then it follows from Lemma 4.7 that \({{\mathcal {X}}}^c={{\mathcal {X}}}^o\) and therefore \({{\mathcal {X}}}^s={{\mathcal {X}}}^c={{\mathcal {X}}}^o.\) By Lemma 2.8, the restriction \(\Sigma _s=(A_s,B_s,C_s,D;{{\mathcal {X}}}^s,{{\mathcal {U}}},{{\mathcal {Y}}};\kappa )\) of \(\Sigma \) to the simple subspace \({{\mathcal {X}}}^s\) is simple, and it holds \(A^nB=A_s^nB_s\) and \({A^*}^nC^*={A_s^*}^nC_s^*\) for every \(n \in {{\mathbb {N}}}_0.\) That is, \(\Sigma _s\) and \(\Sigma _s^*\) also are optimal systems. Moreover, they are minimal since \({{\mathcal {X}}}^s={{\mathcal {X}}}^c={{\mathcal {X}}}^o.\) It follows now from Theorem 3.5 (ii) that \(\Sigma _s\) is also \(^*\)-optimal, and the proof is complete. \(\square \)
References
Alpay, D., Dijksma, A., Rovnyak, J., de Snoo, H.S.V.: Schur Functions, Operator Colligations, and Pontryagin Spaces. Operator Theory: Advances and Applications, 96. Birkhäuser Verlag, Basel-Boston (1997)
Alpay, D., Azizov, T.Y., Dijksma, A., Rovnyak, J.: Colligations in Pontryagin Spaces with a Symmetric Characteristic Function. Linear Operators and Matrices, 55–82, Operator Theory: Advances and Applications, 130. Birkhäuser, Basel (2002)
Arlinskiĭ, YuM, Hassi, S., de Snoo, H.S.V.: Parametrization of contractive block operator matrices and passive discrete-time systems. Complex Anal. Oper. Theory 1(2), 211–233 (2007)
Arov, D.Z.: Passive linear steady-state dynamical systems. Sibirsk. Mat. Zh. 20(2), 211–228 (1979). (Russian); English transl. in Siberian Math. J. 20(2), 149–162 (1979)
Arov, D.Z.: Stable dissipative linear stationary dynamical scattering systems. J. Oper. Theory 2(1), 95–126 (1979). (Russian); English transl. in Oper. Theory Adv. Appl., 134, Interpolation theory, systems theory and related topics (Tel Aviv, Rehovot, : 99–136, p. 2002. Birkhäuser, Basel (1999)
Arov, D.Z., Kaashoek, M.A., Pik, D.P.: Minimal and optimal linear discrete time-invariant dissipative scattering systems. Integr. Equ. Oper. Theory 29, 127–154 (1997)
Arov, D.Z., Nudel’man, M.A.: A criterion for the unitary similarity of minimal passive systems of scattering with a given transfer function. Ukraïn. Mat. Zh. 52(2), 147–156 (2000). (Russian); English transl. in Ukrainian Math. J. 52 (2000), no. 2, 161–172
Arov, D.Z., Nudel’man, M.A.: Conditions for the similarity of all minimal passive realizations of a given transfer function (scattering and resistance matrices). Mat. Sb. 193(6), 3–24 (2002). (Russian); English transl. in Sb. Math. 193 (2002), no. 5-6, 791–810
Arov, D.Z., Rovnyak, J., Saprikin, S.M.: Linear passive stationary scattering systems with Pontryagin state spaces. Math. Nachr. 279(13–14), 1396–1424 (2006)
Arov, D.Z., Saprikin, S.M.: Maximal solutions for embedding problem for a generalized Shur function and optimal dissipative scattering systems with Pontryagin state spaces. Methods Funct. Anal. Topol. 7(4), 69–80 (2001)
Azizov, T.I.A., Iokhvidov, I.S.: Foundations of the Theory of linear operators in spaces with indefinite metric, Nauka, Moscow, 1986; English transl. Wiley, Chichester (1989)
Bakonyi, M., Constantinescu, T.: Schur’s Algorithm and Several Applications. Pitman Research Notes in Mathematics Series, 261. Longman Scientific & Technical, New York (1992)
Ball, J.A., Cohen, N.: de Branges–Rovnyak Operator Models and Systems Theory: A Survey. Topics in matrix and operator theory (Rotterdam, 1989), 93–136, Oper. Theory Adv. Appl., 50, Birkhäuser, Basel (1991)
Bart, H., Gohberg, I.Z., Kaashoek, M.A., Ran, A.C.M.: Factorization of Matrix and Operator Functions: The State Space Method. Operator Theory: Advances and Applications, 178, Linear Operators and Linear Systems. Birkhäuser Verlag, Basel (2008)
Bognár, J.: Indefinite Inner Product Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 78. Springer, New York (1974)
Boiko, S.S., Dubovoj, V.K.: On some extremal problem connected with the suboperator of the scattering through inner channels of the system. Dopov. Nats. Akad. Nauk Ukr. Mat. Prirodozn. 4, 7–11 (1997)
Boiko, S.S., Dubovoj, V. K., Fritzsche, B., Kirstein, B.: Models of contractions constructed from the defect function of their characteristic function. Operator theory, system theory and related topics (Beer-Sheva/Rehovot, 1997), 67-87, Operator Theory: Advances and Applications, 123, Birkhäuser, Basel (2001)
Boiko, S.S., Dubovoj, V.K.: Defect functions of holomorphic contractive operator functions and the scattering suboperator through the internal channels of a system. Part I. Complex Anal. Oper. Theory 5(1), 157–196 (2011)
Boiko, S.S., Dubovoj, V.K., Kheifets, A.Ya.: Defect functions of holomorphic contractive operator functions and the scattering suboperator through the internal channels of a system: part II. Complex Anal. Oper. Theory 8(5), 991–1036 (2014)
de Branges, L., Rovnyak, J.: Square Summable Power Series. Holt, Rinehart and Winston, New York (1966)
de Branges, L., Rovnyak, J.: Appendix on square summable power series, Canonical models in quantum scattering theory, Perturbation Theory and its Applications in Quantum Mechanics (Proc. Adv. Sem. Math. Res. Center, U.S. Army, Theoret. Chem. Inst., Univ. of Wisconsin, Madison, Wis., 1965), pp. 295–392, Wiley, New York (1966)
Dijksma, A., Langer, H., de Snoo, H.S.V.: Characteristic functions of unitary operator colligations in \(\pi _{\kappa }\)-spaces. Operator theory and systems (Amsterdam, 1985), 125–194, Operator Theory: Advances and Applications, 19, Birkhäuser, Basel (1986)
Dijksma, A., Langer, H., de Snoo, H.S.V.: Unitary colligations in \(\Pi _{\kappa }\)-spaces, characteristic functions and Štraus extensions. Pac. J. Math. 125(2), 347–362 (1986)
Dritschel, M.A., Rovnyak, J.: Operators on Indefinite Inner Product Spaces. Lectures on operator theory and its applications (Waterloo, ON, 1994), 141–232, Fields Inst. Monogr., 3, Amer. Math. Soc., Providence, RI (1996)
Helton, J.W.: Discrete time systems, operator models, and scattering theory. J. Funct. Anal. 16, 15–38 (1974)
Kreĭn, M.G., Langer, H.: Über die verallgemeinerten Resolventen und die charakteristische Funktion eines isometrischen Operators im Raume \(\Pi _\kappa \) (German), Hilbert space operators and operator algebras (Proc. Internat. Conf., Tihany, 1970), pp. 353–399, Colloq. Math. Soc. János Bolyai, 5. North-Holland, Amsterdam (1972)
Lilleberg, L.: Isometric discrete-time systems with Pontryagin state space. Complex Anal. Oper. Theory 13(8), 3767–3793 (2019)
Lilleberg, L.: Minimal passive realizations of generalized Schur functions in Pontryagin spaces. arXiv:1910.11053, 37 pp (2019)
Nagy, B.S., Foias, C.: Harmonic Analysis of Operators on Hilbert Space. North-Holland, New York (1970)
Saprikin, S.M.: The theory of linear discrete time-invariant dissipative scattering systems with state \(\pi _\kappa \)-spaces, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 282 (2001), Issled. po Lineĭn. Oper. i Teor. Funkts. 29, 192–215, 281 (Russian); English transl. in J. Math. Sci. (NY) 120 (2004), no. 5, 1752–1765
Staffans, O.J.: Well-Posed Linear Systems. Encyclopedia of Mathematics and its Applications, 103. Cambridge University Press, Cambridge (2005)
Acknowledgements
Open access funding provided by University of Vaasa (UVA). I wish to thank Seppo Hassi for helpful discussions while preparing this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Bernd Kirstein.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lilleberg, L. Minimal Passive Realizations of Generalized Schur Functions in Pontryagin Spaces. Complex Anal. Oper. Theory 14, 35 (2020). https://doi.org/10.1007/s11785-020-00993-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11785-020-00993-5
Keywords
- Operator colligation
- Passive system
- Transfer function
- Defect functions
- Generalized Schur class
- Contractive operator