Abstract
Iterative methods with certified convergence for the computation of Gauss–Jacobi quadratures are described. The methods do not require a priori estimations of the nodes to guarantee its fourth-order convergence. They are shown to be generally faster than previous methods and without practical restrictions on the range of the parameters. The evaluation of the nodes and weights of the quadrature is exclusively based on convergent processes which, together with the fourth-order convergence of the fixed point method for computing the nodes, makes this an ideal approach for high-accuracy computations, so much so that computations of quadrature rules with even millions of nodes and thousands of digits are possible on a typical laptop.






Similar content being viewed by others
Notes
It is interesting to observe that, as we discuss later, also the Golub-Welsch algorithm appears to suffer from some loss of accuracy for these parameter values
Observe that we need to compute Kn,α,β only if α < 0 (and Kn,β,α only if β < 0), and in this case, in practical terms the constant does not overflow/underflow as n becomes large (it does so algebraically). However, the gamma functions do become huge. For computing this it is preferable to compute the logarithm of the constant and exponentiate afterwards. The logarithm of the gamma function is a widely available computation, for example through the command gammaln in MATLAB or with the Fortran function loggam of [12]
The Maple worksheet (Gauss-Gegenbauer) and the MATLAB code (Gauss-Jacobi) mentioned in this paper can be found at https://personales.unican.es/segurajj/gaussian.html, together with the codes corresponding to the Gauss–Hermite and Gauss–Laguerre cases of [14]. None of these codes should be considered as final versions of our algorithms.
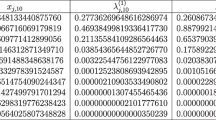
Absolute errors do not make much sense as an error measure for the weights, because the magnitude of the weights depends strongly on the parameters and the corresponding nodes, particularly for large values of the parameters (see (15)). It is more reasonable to consider absolute errors relative to the maximum value of the weight, as we do here.
References
Bogaert, I.: Iteration-free computation of Gauss-Legendre quadrature nodes and weights. SIAM J. Sci. Comput. 36(3), A1008–A1026 (2014). https://doi.org/10.1137/140954969
Bogaert, I., Michiels, B., Fostier, J.: \(\mathcal {O}\)(1) computation of Legendre polynomials and Gauss-Legendre nodes and weights for parallel computing. SIAM J. Sci. Comput. 34(3), C83–C101 (2012). https://doi.org/10.1137/110855442
Bremer, J., Yang, H.: Fast algorithms for Jacobi expansions via nonoscillatory phase functions. IMA J. Numer. Anal. 40(3), 2019–2051 (2020). https://doi.org/10.1093/imanum/drz016
Davis, P.J., Rabinowitz, P.: Some geometrical theorems for abscissas and weights of Gauss type. J. Math. Anal. Appl. 2, 428–437 (1961). https://doi.org/10.1016/0022-247X(61)90021-X
Deaño, A., Segura, J.: Global Sturm inequalities for the real zeros of the solutions of the Gauss hypergeometric differential equation. J. Approx. Theory 148(1), 92–110 (2007). https://doi.org/10.1016/j.jat.2007.02.005
Deaño, A., Gil, A., Segura, J.: New inequalities from classical Sturm theorems. J. Approx. Theory 131(2), 208–230 (2004). https://doi.org/10.1016/j.jat.2004.09.006
Driscoll, T.A., Hale, N., Trefethen, L.N.: Chebfun Guide. Pafnuty Publications, Oxford (2014)
Elaydi, S.: An Introduction to Difference Equations, 3rd edn. Undergraduate Texts in Mathematics. Springer, New York (2005)
Gil, A., Segura, J., Temme, N.M.: Asymptotic expansions of Jacobi polynomials and of the nodes and weights of Gauss-Jacobi quadrature for large degree and parameters in terms of elementary functions. Submitted. arXiv:2007.10748
Gil, A., Segura, J., Temme, N.M.: Numerical Methods for Special Functions. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2007). https://doi.org/10.1137/1.9780898717822
Gil, A., Segura, J., Temme, N.M.: Numerically satisfactory solutions of hypergeometric recursions. Math. Comput. 76(259), 1449–1468 (2007). https://doi.org/10.1090/S0025-5718-07-01918-7
Gil, A., Segura, J., Temme, N.M.: GammaCHI: a package for the inversion and computation of the gamma and chi-square cumulative distribution functions (central and noncentral). Comput. Phys. Commun. 191, 132–139 (2015). https://doi.org/10.1016/j.cpc.2015.01.004
Gil, A., Segura, J., Temme, N.M.: Asymptotic approximations to the nodes and weights of Gauss-Hermite and Gauss-Laguerre quadratures. Stud. Appl. Math. 140(3), 298–332 (2018). https://doi.org/10.1111/sapm.12201
Gil, A., Segura, J., Temme, N.M.: Fast, reliable and unrestricted iterative computation of Gauss–Hermite and Gauss–Laguerre quadratures. Numer. Math. 143(3), 649–682 (2019). https://doi.org/10.1007/s00211-019-01066-2
Gil, A., Segura, J., Temme, N.M.: Noniterative computation of Gauss-Jacobi quadrature. SIAM J. Sci. Comput. 41(1), A668–A693 (2019). https://doi.org/10.1137/18M1179006
Glaser, A., Liu, X., Rokhlin, V.: A fast algorithm for the calculation of the roots of special functions. SIAM J. Sci. Comput. 29(4), 1420–1438 (2007). https://doi.org/10.1137/06067016X
Golub, G.H., Welsch, J.H.: Calculation of Gauss quadrature rules. Math. Comput. 23, 221–230 (1969). addendum, ibid. 23(106, loose microfiche suppl), A1? A10
Hale, N., Townsend, A.: Fast and accurate computation of Gauss-Legendre and Gauss-Jacobi quadrature nodes and weights. SIAM J. Sci. Comput. 35(2), A652–A674 (2013). https://doi.org/10.1137/120889873
Johansson, F., Mezzarobba, M.: Fast and rigorous arbitrary-precision computation of Gauss-Legendre quadrature nodes and weights. SIAM J. Sci. Comput. 40(6), C726–C747 (2018). https://doi.org/10.1137/18M1170133
Koornwinder, T.H., Wong, R., Koekoek, R., Swarttouw, R.F.: Orthogonal polynomials. In: NIST Handbook of Mathematical Functions, pp 435–484. U.S. Dept. Commerce, Washington, DC (2010)
Opsomer, P: Asymptotics for orthogonal polynomials and high-frequency scattering problems. PhD thesis, KU Leuven. https://lirias.kuleuven.be/retrieve/493748(2018)
Segura, J.: Reliable computation of the zeros of solutions of second order linear ODEs using a fourth order method. SIAM J. Numer. Anal. 48(2), 452–469 (2010). https://doi.org/10.1137/090747762
Swarztrauber, P.N.: On computing the points and weights for Gauss-Legendre quadrature. SIAM J. Sci. Comput. 24(3), 945–954 (electronic) (2002). https://doi.org/10.1137/S1064827500379690
Trefethen, L.N.: Is Gauss quadrature better than Clenshaw-Curtis? SIAM Rev. 50(1), 67–87 (2008). https://doi.org/10.1137/060659831
Yakimiw, E.: Accurate computation of weights in classical Gauss-Christoffel quadrature rules. J. Comput. Phys. 129(2), 406–430 (1996). https://doi.org/10.1006/jcph.1996.0258
Acknowledgments
The authors thank the anonymous referees for their constructive comments and suggestions. NMT thanks CWI for scientific support.
Funding
This work was supported by Ministerio de Ciencia, Innovación y Universidades, Spain, projects MTM2015-67142-P (MINECO/FEDER, UE) and PGC2018-098279-B-I00 (MCIU/AEI/FEDER, UE).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix. On the conditioning of the recurrence for computing derivatives
Appendix. On the conditioning of the recurrence for computing derivatives
We briefly discuss the conditioning of the computation of the derivatives with the recurrence relation (26). This is a five term recurrence relation, with a space of solutions of dimension four. For studying the conditioning as \(j\rightarrow \infty \) we can divide all terms of the recurrence by j2 and then all the coefficients have finite limit as \(j\rightarrow +\infty \). We have
with
Then it is known (see, for instance, [8], Theorem 8.11) that the solutions of the recurrence satisfy
where W is the modulus of one of the solutions of the characteristic polynomial
which, upon dividing by δ4 and denoting μ = 1/δ we can write
And because Q is a polynomial of degree four (Q(x) = 4(1 − x2)2) this equation is the same as Q(x + μ) = 0, which, solving for μ gives two double roots μ = x ± 1. This means that the possible values of W in (45) are W1 = 1/|1 − x| and W2 = 1/|1 + x| and there is a subspace of dimension 2 satisfying (45) with W = W1 and a second subspace with W = W2; the first space will be dominant over the second when W1 > W2 and the opposite when W1 < W2 (the case W1 = W2 is the degenerate case, in which no solution is exponentially dominant over the rest).
In our case, we have \(a_{j}=\tilde {Y}^{(j)}(x)\) with \(\tilde {Y}(x)\) given by (10). We notice that for α and β odd, \(\tilde {Y}(x)\) is a polynomial of degree N = n + (α + β + 2)/2 = (L + 1)/2, and then aj = 0 if j > N. The Taylor series have a finite number of terms in this case and the analysis of stability for aj as \(j\rightarrow \infty \) is not needed. Let us now consider that neither α nor β are odd, and we leave for later the case in which only one of the parameters (α or β) is odd.
When neither α nor β are odd, then Taylor series at x ∈ (− 1, 1) has an infinite number of terms. Because \(\tilde {Y}(x)\) is a polynomial times (1 − x)(α+ 1)/2(1 + x)(β+ 1)/2 the radius of convergence of the series for \(\tilde {Y}(x+t)\) centered at x,
is \(R=\min \limits \{1-x,1+x\}\) (which we could expect because the ODE satisfied by \(\tilde {Y}\) has singularities at x = ± 1) and then
Therefore in this case the sequence {aj}, \(a_{j}=\tilde {Y}^{(j)}(x)/j!\) is in the dominant subspace of solutions of the recurrence.
The case when either α or β is odd but not both is different. Let us for instance consider that α is odd, but not β. In this case, the convergence of the series is limited by the singularity at − 1 (but not at + 1); the radius of convergence in this case is therefore R = 1 + x and then
Therefore, {aj} is in the dominant subspace only if x ∈ (− 1, 0). In this case for large enough j the forward computation of aj would be unstable for positive x. However, even for this case we have not observed inaccuracies in the computation of the series. For a given accuracy claim, the number of terms in the series needed are not high enough to produce stability issues.
Rights and permissions
About this article
Cite this article
Gil, A., Segura, J. & Temme, N.M. Fast and reliable high-accuracy computation of Gauss–Jacobi quadrature. Numer Algor 87, 1391–1419 (2021). https://doi.org/10.1007/s11075-020-01012-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-020-01012-6