1 Introduction

The Navier–Stokes equations for the flow of a linearly viscous, incompressible fluid are well known throughout the fields of applied mathematics and engineering. For a Navier–Stokes fluid the response of stress to change in the velocity gradient is instantaneous. This special response is not enjoyed by all real life fluids and, in particular, by many classes of viscoelastic and complex fluids. These fluids possess a stress which does not react instantaneously and instead they remember the velocity gradient history. Typically such fluids possess fading memory where the history dependence diminishes as the time advances into the past. Theoretical work on such fluids is vast, see e.g. Amendola and Fabrizio [1], Amendola et al. [2], Anand et al. [3], Anand and Christov [4], Christov and Christov [5], Fabrizio et al. [6], Franchi et al. [7,8,9], Gatti et al. [10], Jordan and Saccomandi [11], Jordan et al. [12, 13], Payne and Straughan [14], Yang et al. [15].

Recent work (arising from the Russian literature) is focussing on a very interesting class of complex (viscoelastic) materials associated with the names of Kelvin and of Voigt, cf. Chirita and Zampoli [16], Berselli and Bisconti [17], Layton and Rebholz [18]. Models for Kelvin–Voigt fluids have been presented by Oskolkov [19, 20], and the references therein. Of particular relevance to the present article are the generalizations of the Kelvin–Voigt models to incorporate thermal effects as presented by Sukacheva and Matveeva [21], Kondyukov [22], Sukacheva and Kondyukov [23]. A special class of the thermal Kelvin–Voigt models are the so called Navier–Stokes–Voigt equations which are analysed here.

Thermal convection when a salt is simultaneously dissolved in the fluid is a very rich area within the Navier–Stokes setting, see e.g. Barletta and Nield [24], Capone et al. [25], Galdi et al. [26], Harfash and Hill [27], Nield [28], Matta et al. [29], Mulone [30], Straughan [31,32,33], Straughan and Hutter [34].

We are interested in the thermosolutal convection problem where the layer is heated from below and simultaneously salted from below resulting in a hard mathematical problem where the heat effect encourages the fluid to rise whereas salting below has the opposite effect and creates a competition between the physical attributes of heating and salting. This is the configuration of the promising method of generating renewable energy through electricity with a solar pond, see e.g. Abdullah et al. [35], and the present work may have a bearing on how to add an additive to stabilize the solar pond and ensure it functions in an optimal way.

The goal of this work is to develop a model and analyse thermosolutal convection in a layer of Navier–Stokes–Voigt fluid heated and salted from below, generalizing the models of Sukacheva and Matveeva [21] and Sukacheva and Kondyukov [23]. We believe this is the first analysis of this problem.

2 The Navier–Stokes–Voigt Equations for Thermosolutal Convection

Let \(\mathbf{v}(\mathbf{x},t),\) \(T(\mathbf{x},t),\) \(C(\mathbf{x},t)\), \(p(\mathbf{x},t)\) be the velocity, temperature, concentration of a dissolved salt, and pressure at position \(\mathbf{x}\) and time t of a body of fluid. The Navier–Stokes–Voigt equations for thermosolutal convection may be derived from Sukacheva and Matveeva [21], by incorporating the concentration effect, cf. Straughan [36, Sect. 14.1]. The appropriate system of equations may be written as

$$\begin{aligned} \begin{aligned}&(1-{\hat{\lambda }}\Delta )v_{i,t}+v_jv_{i,j}=-\frac{1}{\rho _0}p_{,i}+\nu \Delta v_i+\alpha Tgk_i-\gamma Cgk_i\,,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \Delta T\,,\\&C_{,t}+v_iC_{,i}=\kappa _s\Delta C\,. \end{aligned} \end{aligned}$$
(1)

Here \({\hat{\lambda }},\nu ,\rho _0,\alpha ,\gamma ,g,\kappa \) and \(\kappa _s\) are the Kelvin–Voigt coefficient, the kinematic viscosity, a reference density, the coefficient of thermal expansion of the fluid, the coefficient of concentration in the density, gravity, thermal diffusivity, and salt diffusivity. The symbol \(\Delta \) denotes the Laplacian, \(\mathbf{k}=(0,0,1)\), and standard indicial notation together with the Einstein summation convention is employed throughout. For example, if \(\mathbf{v}=(v_1,v_2,v_3)\equiv (u,v,w)\) and \(\mathbf{x}=(x_1,x_2,x_3)\equiv (x,y,z)\), then we write the divergence of the velocity field in the forms

$$\begin{aligned} v_{i,i}\equiv \sum _{i=1}^3v_{i,i}=&\frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3}\\ =&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z} \end{aligned}$$

For an example involving a nonlinearity, we write

$$\begin{aligned} v_iT_{,i}\equiv \sum ^3_{i=1}v_iT_{,i}= u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y} +w\frac{\partial T}{\partial z}. \end{aligned}$$

To derive Eq. (1) a Boussinesq approximation has been employed whereby the density in the buoyancy force is written as \(\rho =\rho _0[1-\alpha (T-T_0)+\gamma (C-C_0)]\) for a reference temperature \(T_0\) and reference concentration \(C_0\). This gives rise to the \(\alpha gTk_i\) and \(\gamma gCk_i\) terms. Details are similar to those in Sect. 14.1 of Straughan [36] where the Navier–Stokes analogue is analysed.

As Oskolkov [19, 20] notes, the Kelvin–Voigt \(\hat{\lambda }\) term in (1) arises from a stress relation like

$$\begin{aligned} \sigma _{ij}=2\rho _0{\hat{\lambda }}\frac{\partial d_{ij}}{\partial t}+2\mu d_{ij}\,, \end{aligned}$$
(2)

where \(\mu (=\nu \rho _0)>0\) is a constant, \(d_{ij}\) is the symmetric part of the velocity gradient, and \(\sigma _{ij}\) is the Cauchy extra stress tensor, related to the stress tensor \(t_{ij}\) by \(t_{ij}=-p\delta _{ij}+\sigma _{ij}\). Then Eq. (1)\(_1\) follows from the balance of linear momentum equation

$$\begin{aligned} \rho _0(v_{i,t}+v_jv_{i,j})=t_{ji,j}+\rho f_i\,, \end{aligned}$$

with \(f_i\) being the body force term. Equation (2) is a linear relationship and as such is compatible with a linear instability analysis. One should perhaps consider an objective derivative in (2), as discussed in another context by Christov [37]. However, we here follow the procedure of Sukacheva and Matveeva [21], Sukacheva and Kondyukov [23].

Equations (1) are sometimes called the Navier–Stokes–Voigt equations, cf. Layton and Rebholz [18], or alternatively they can be called the Kelvin–Voigt equations of order zero, or the Oskolkov equations, see Oskolkov [20].

3 Thermosolutal Convection, Heated and Salted Below

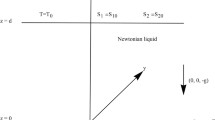
We shall suppose the Navier–Stokes–Voigt fluid occupies the horizontal layer \(0<z<d\) with gravity acting downward. Equations (1) are defined on the spatial region \(\mathbb {R}^2\times \{z\in (0,d)\}\), for \(t>0\).

The boundary conditions on the planes \(z=0\) and \(z=d\) are given by

$$\begin{aligned} \begin{aligned}&v_i=0,\quad z=0,d;\\&T=T_L,\quad z=0,\qquad T=T_U,\quad z=d;\\&C=C_L,\quad z=0,\qquad C=C_U,\quad z=d; \end{aligned} \end{aligned}$$
(3)

for prescribed constant values \(T_L,T_U,C_L,C_U\), with \(T_L>T_U>0\) and \(C_L>C_U\) where \(T_L,T_U\) are in \(^{\circ }\)K.

The steady solution in whose stability we are interested is given by

$$\begin{aligned} {\bar{v}}_i\equiv 0,\quad {\bar{T}}=-\beta z+T_L\,,\quad {\bar{C}}=-\beta _s z+C_L\,, \end{aligned}$$
(4)

where the temperature and concentration gradients, \(\beta ,\beta _s\), are given by

$$\begin{aligned} \beta =\frac{T_L-T_U}{d}\,, \qquad \beta _s=\frac{C_L-C_U}{d}\,. \end{aligned}$$

The steady pressure \(\bar{p}\) is a quadratic in z which may then be derived from Eq. (1)\(_1\).

To investigate stability of the conduction solution (4) we introduce perturbations \((u_i,\theta ,\phi ,\pi )\) by

$$\begin{aligned} v_i={\bar{v}}_i+u_i,\quad T={\bar{T}}+\theta ,\quad C={\bar{C}}+\phi ,\quad p={\bar{p}}+\pi \,. \end{aligned}$$

The equations for the perturbations are then derived and non - dimensionalized with the scalings, cf. details in Sect. 14.1 of Straughan [36],

$$\begin{aligned}&\qquad U=\frac{\kappa }{d}\,,\qquad {\mathcal T}=\frac{d^2}{\kappa }\,,\\&P=\frac{\rho _0\nu U}{d}\,, \qquad T^{\sharp }=U\sqrt{\frac{\beta \nu }{\kappa g\alpha }}\,, \qquad C^{\sharp }=U\sqrt{\frac{\beta _s\nu }{\gamma g\kappa _s}}\,, \end{aligned}$$

where \(d,{\mathcal T},U,C^{\sharp }\) and \(T^{\sharp }\) are the scales for length, time, velocity, concentration, and temperature, respectively. Define the Rayleigh number, \(Ra=R^2\), the salt Rayleigh number \(Rs={\mathcal C}^2\), the Lewis number Le, and the Prandtl number Pr, by

$$\begin{aligned} Ra=\frac{\alpha g\beta d^4}{\nu \kappa }\,,\quad Rs=\frac{\beta _s g\gamma d^4}{\kappa _s\nu }\,, \quad Le=\frac{\kappa }{\kappa _s}\,,\quad Pr=\frac{\nu }{\kappa }\,. \end{aligned}$$

The Kelvin–Voigt parameter \(\hat{\lambda }\) is rescaled as

$$\begin{aligned} \lambda ={\hat{\lambda }}\frac{{\mathcal T}}{\nu }\,. \end{aligned}$$

Now drop the *s and treat \(x_i\) and t as the non-dimensional variables. The non-dimensional form of the perturbation equations to (1) is

$$\begin{aligned} \begin{aligned}&\frac{1}{Pr}\Bigl (u_{i,t}-\lambda \Delta u_{i,t}+u_ju_{i,j}\Bigr )=-\pi _{,i}+\Delta u_i+Rk_i\theta -{\mathcal C}\phi k_i\,,\\&u_{i,i}=0,\\&\theta _{,t}+u_i\theta _{,i}=Rw+\Delta \theta \,,\\&Le(\phi _{,t}+u_i\phi _{,i})={\mathcal C}w+\Delta \phi , \end{aligned} \end{aligned}$$
(5)

where \(w=u_3\).

Equations (5) are defined on the domain \(\mathbb {R}^2\times \{z\in (0,1)\}\times \{t>0\}\) and the boundary conditions are

$$\begin{aligned} u_i=0,\quad \phi =0,\quad \theta =0,\qquad z=0,1, \end{aligned}$$
(6)

together with the fact that \(u_i,\phi ,\theta \) and \(\pi \) satsify a plane tiling periodicity in the x, y plane.

To analyse linear instability we linearize (5) and seek solutions of the form \(u_i=u_i(\mathbf{x},t)e^{\sigma t},\) \(\phi =\phi (\mathbf{x},t)e^{\sigma t},\) \(\theta =\theta (\mathbf{x},t)e^{\sigma t},\) \(\pi =\pi (\mathbf{x},t)e^{\sigma t}.\) Equations (5) may then be reduced to

$$\begin{aligned} \begin{aligned}&\frac{\sigma }{Pr}\Bigl (1-\lambda \Delta \Bigr )u_i=-\pi _{,i}+\Delta u_i+Rk_i\theta -{\mathcal C}k_i\phi ,\\&u_{i,i}=0,\\&\sigma \theta =Rw+\Delta \theta \,,\\&Le\sigma \phi ={\mathcal C}w+\Delta \phi \,. \end{aligned} \end{aligned}$$
(7)

Next take \(curl\,curl\) of Eq. (7)\(_1\) and retain the third component of the resulting equation to reduce Eq. (7) to

$$\begin{aligned} \begin{aligned}&\frac{\sigma }{Pr}\Bigl (1-\lambda \Delta \Bigr )\Delta w=\Delta ^2w+R\Delta ^*\theta -{\mathcal C}\Delta ^*\phi ,\\&\sigma \theta =Rw+\Delta \theta \,,\\&Le\sigma \phi ={\mathcal C}w+\Delta \phi \,, \end{aligned} \end{aligned}$$
(8)

where \(\Delta ^*= \partial ^2/\partial x^2 +\partial ^2/\partial y^2\) is the horizontal Laplacian. Introduce now the forms \(w=w(z)h(x,y),\) \(\theta =\theta (z)h(x,y)\), \(\phi =\phi (z)h(x,y)\), where h(x, y) is a planform which reflects the shape of the instability cell, cf. Chandrasekhar [38, pp. 43–52], and \(\Delta ^*h=-a^2h\), for a wavenumber a. Then Eq. (8) are rewritten as

$$\begin{aligned} \begin{aligned}&\frac{\sigma }{Pr}\Bigl (D^2-a^2\Bigr )w-\sigma \frac{\lambda }{Pr}\Bigl (D^2-a^2\Bigr )^2w=(D^2-a^2)^2w -a^2R\theta +{\mathcal C}a^2\phi ,\\&\sigma \theta =Rw+(D^2-a^2)\theta \,,\\&Le\sigma \phi ={\mathcal C}w+(D^2-a^2)\phi \,, \end{aligned} \end{aligned}$$
(9)

where \(D=d/dz\) and Eq. (9) hold on \(z\in (0,1)\).

We must specify further information on boundary conditions. We already have

$$\begin{aligned} w=0,\quad \theta =0,\quad \phi =0,\qquad z=0,1. \end{aligned}$$
(10)

We believe this is the first analysis to address the thermosolutal convection problem for a Navier–Stokes–Voigt fluid. Thus we restrict attention to two stress free surfaces and so we additionally require

$$\begin{aligned} D^2w=0,\qquad z=0,1. \end{aligned}$$
(11)

The equations lead to even derivatives being zero on the surfaces \(z=0,1\), and then we may write w, \(\phi \) and \(\theta \) as a \(\sin \) series in z of form \(\sin (n\pi z)\), \(n=1,2,\ldots \) We take \(n=1\) since computations show this yields the lowest value of the Rayleigh number. With the \(\sin \) representation of solutions, Eq. (9) then yield a determinant equation which leads to the following expression for \(R^2\),

$$\begin{aligned} R^2={\mathcal C}^2\biggl (\frac{\Lambda +\sigma }{\Lambda +Le\sigma }\biggr ) +\Bigl [\frac{\sigma }{Pr}(\Lambda +\lambda \Lambda ^2)+\Lambda ^2\Bigr ]\frac{1}{a^2}(\Lambda +\sigma )\,, \end{aligned}$$
(12)

where \(\Lambda =\pi ^2+a^2\).

The stationary convection threshold follows from (12) and takes the form

$$\begin{aligned} R^2={\mathcal C}^2+\frac{\Lambda ^3}{a^2}\,. \end{aligned}$$
(13)

Upon minimization in \(a^2\) we find the critical wave number value is \(a_c^2=\pi ^2/2\) and inserting this in (13) it follows that

$$\begin{aligned} Ra_{stat}=\frac{27\pi ^4}{4}+{\mathcal C}^2. \end{aligned}$$
(14)

Further analysis requires us to take the real and imaginary parts of (12) and recollect that \(R^2\) is real. To find the oscillatory convection curve we put \(\sigma =i\omega \), \(\omega \in \mathbb {R}\), and then the real part of (12) yields

$$\begin{aligned} R^2=\Bigl (\frac{\Lambda ^2+Le\omega ^2}{\Lambda ^2+Le^2\omega ^2}\Bigr ){\mathcal C}^2+\frac{\Lambda ^3}{a^2} -\frac{\omega ^2}{a^2}\Bigl (\frac{\Lambda +\lambda \Lambda ^2}{Pr}\Bigr )\,. \end{aligned}$$
(15)

From the imaginary part of (12) we may show that

$$\begin{aligned} \omega ^2=\frac{(Le-1){\mathcal C}^2a^2-\Lambda ^3(1+Pr^{-1})-\lambda Pr^{-1}\Lambda ^4}{Le^2[(1+Pr^{-1})\Lambda +\lambda Pr^{-1}\Lambda ^2]}\,. \end{aligned}$$
(16)

The critical value of the oscillatory convection threshold \(R^2\) is found by employing (16) in (15) and then minimising \(Ra=R^2\) in \(a^2\) for fixed values of \(\lambda ,Le\) and Pr. This we do numerically and report the findings in Sect. 4.

Remark 1

It is possible to add a Rayleigh friction term to the right hand side of equation (5)\(_1\) as do Di Plinio et al. [39] for the isothermal and non concentration case. In this situation the perturbation equations (5) are replaced by

$$\begin{aligned} \begin{aligned}&\frac{1}{Pr}\Bigl (u_{i,t}-\lambda \Delta u_{i,t}+u_ju_{i,j}\Bigr )=-\pi _{,i}+\Delta u_i-\xi u_i+Rk_i\theta -{\mathcal C}\phi k_i\,,\\&u_{i,i}=0,\\&\theta _{,t}+u_i\theta _{,i}=Rw+\Delta \theta \,,\\&Le(\phi _{,t}+u_i\phi _{,i})={\mathcal C}w+\Delta \phi , \end{aligned} \end{aligned}$$
(17)

for a constant \(\xi >0\). By proceeding as outlined above one may perform a stationary convection and an oscillatory convection analysis for system (17).

Remark 2

One could also consider a Soret effect upon the convection threshold for a Navier–Stokes–Voigt fluid, cf. Straughan and Hutter [34]. In this case the perturbation equations (5) are replaced by

$$\begin{aligned} \begin{aligned}&\frac{1}{Pr}\Bigl (u_{i,t}-\lambda \Delta u_{i,t}+u_ju_{i,j}\Bigr )=-\pi _{,i}+\Delta u_i+Rk_i\theta -{\mathcal C}\phi k_i\,,\\&u_{i,i}=0,\\&\theta _{,t}+u_i\theta _{,i}=Rw+\Delta \theta \,,\\&Le(\phi _{,t}+u_i\phi _{,i})={\mathcal C}w+\Delta \phi +S\Delta \theta , \end{aligned} \end{aligned}$$
(18)

for a constant Soret coefficient \(S>0\). Again, one may proceed as outlined above to perform a stationary convection and an oscillatory convection analysis for system (18).

4 Numerical Results

We report on numerical solutions to Eqs. (14), (15) and (16). To do this we require values for the Prandtl and Lewis numbers. The Prandtl number for water at \(20^{\circ }\)C is 6.99 and for vegetable oils Rodenbush et al. [40] report values in the range 25-400. For the thermal and solute diffusivities we employ values from Caldwell [41], Ozbek and Phillips [42], Yanez Limon et al. [43] and from Engineering Toolbox. These articles suggest values of \(\kappa =1.43\times 10^{-7}\,\,m^2\,\,s^{-1}\) and \(\kappa _s=1.286\times 10^{-9}\,\,m^2\,\,s^{-1}\) at \(20^{\circ }\)C, or \(\kappa _s\) in the range

$$\begin{aligned} 1.33\times 10^{-9}\le \kappa _s\le 2.03\times 10^{-9}\,\,m^2\,\,s^{-1}. \end{aligned}$$

This leads to Lewis number values of \(Le=111.2\) or in the range \(70.44\le Le\le 107.5\), for primarily water based solvent. However, for commerical cooking oils \(\kappa \) is in the range \(4.4\times 10^{-8} - 8\times 10^{-8}\,\,m^2\,\,s^{-1}\), see Yanez Limon et al. [43], and this leads to Lewis number values in the range 21.67–60.15.

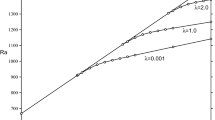
We have computed values of the Rayleigh number and critical wave number versus the salt Rayleigh number for various combinations of Pr, Le and \(\lambda \). For the many values we examined the qualitative behaviour is always the same and resembles that of Fig. 1, where \(Pr=50,Le=21.67\), although the quantitative values at the transitions depend on the parameters Pr, Le and \(\lambda \). We here report on values for \(Pr=50,Le=21.67\), for \(Pr=6.99,Le=70.44\), and for \(Pr=6.99,Le=111.2\). The pattern of instability in all cases follows that of Fig. 1 in that the stationary convection curve begins at \(Ra=27\pi ^4/4\) for \(Rs=0\) and is then the straight line E–S as Rs increases. Depending on the value of the Kelvin–Voigt parameter \(\lambda \) there is a transition from stationary to oscillatory convection as shown in Fig. 1, where the 0–0 curve denotes the oscillatory convection threshold when \(\lambda =0\), 1–1 curve denotes the oscillatory convection threshold when \(\lambda =1\), and the 2–2 curve denotes the oscillatory convection threshold when \(\lambda =2\). The basic conduction solution (4) is unstable when the (Ra, Rs) values lie above the linear instability curve, and convective motion ensues. For example, when \(\lambda =1\), the solution is unstable above the straight line E–1, but for \(Rs={\mathcal C}^2\) values greater than the transition the instability is oscillatory when \(Ra=R^2\) lies above the curve 1–1.

Observe that \(\lambda \) increasing raises the instability threshold, and as we might expect \(\lambda \) is a stabilizing influence.

Table 1 yields the transition values for the values of Pr and Le as indicated. The \(a^2\) values reported in this table are the critical values for oscillatory convection. We observe that the critical oscillatory wave number values are smaller as \(\lambda \) increases indicating that the convection cells become wider for increasing \(\lambda \). The Lewis number effect is to lower the critical Rayleigh number as Le increases.

5 Nonlinear Stability Considerations for Thermal Convection in a Navier–Stokes–Voigt fluid

Let \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert \) denote the inner product and norm on the Hilbert space \(L^2(V)\), where V is a period cell for the solution.

To develop a nonlinear stability analysis a classic approach to nonlinear energy stability will multiply (5)\(_1\) by \(u_i\), (5)\(_2\) by \(\theta \) and (5)\(_3\) by \(\phi \), and integrate each in turn over the period cell V using the boundary conditions. In this manner we obtain the identities

$$\begin{aligned} \frac{d}{dt}\Bigl (\frac{1}{2Pr}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2Pr}\Vert \nabla \mathbf{u}\Vert ^2\Bigr )= -\Vert \nabla \mathbf{u}\Vert ^2+R(\theta ,w)-{\mathcal C}(\phi ,w), \end{aligned}$$
(19)

and

$$\begin{aligned} \frac{d}{dt}\frac{1}{2}\Vert {\theta }\Vert ^2 =R(\theta ,w)-\Vert \nabla \theta \Vert ^2\,, \end{aligned}$$
(20)

together with

$$\begin{aligned} \frac{d}{dt}\frac{Le}{2}\Vert {\phi }\Vert ^2 ={\mathcal C}(\phi ,w)-\Vert \nabla \phi \Vert ^2. \end{aligned}$$
(21)

We may add these equations to derive the energy equation

$$\begin{aligned} \frac{dE}{dt}=RI-D, \end{aligned}$$
(22)

where the energy function is given by

$$\begin{aligned} E(t)=\frac{1}{2Pr}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2Pr}\Vert \nabla \mathbf{u}\Vert ^2+\frac{1}{2}\Vert \theta \Vert ^2 +\frac{Le}{2}\Vert \phi \Vert ^2, \end{aligned}$$
(23)

the production term I is defined by

$$\begin{aligned} I(t)=2R(\theta ,w), \end{aligned}$$
(24)

and the dissipation is

$$\begin{aligned} D(t)=\Vert \nabla \mathbf{u}\Vert ^2+\Vert \nabla \theta \Vert ^2+\Vert \nabla \phi \Vert ^2 \end{aligned}$$
(25)

From this one computes the value

$$\begin{aligned} \frac{1}{R_E}=\max _{H}\,\frac{I}{D}\,, \end{aligned}$$
(26)

where H is the space of admissible solutions, cf. Straughan [36]. Since the \({\mathcal C}\) terms disappear from I the Euler–Lagrange equations which arise from (26) yield the global nonlinear stability threshold of \(R_E=27\pi ^4/4\), i.e. the straight line E–E in Fig. 1. This means that values of Ra, Rs below this threshold yield a globally stable nonlinear solution. However, there is still the possibility of sub-critical convection in the region above E–E and below the linear instability threshold.

If one is prepared to employ a generalized energy functional by introducing \(\psi =\theta -\delta \phi \) where \(\delta ={\mathcal C}/R\), and work with the function

$$\begin{aligned} {\mathcal E}(t)=\frac{1}{2Pr}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2Pr}\Vert \nabla \mathbf{u}\Vert ^2 +\frac{\omega _1}{2}\Vert \theta \Vert ^2 +\frac{\omega _2Le}{2}\Vert \psi \Vert ^2\,, \end{aligned}$$

then see Joseph [44], Mulone [30], it is possible with a lot of analysis and much effort, employing numerical optimization on the parameters \(\omega _1>0\), \(\omega _2>0\), while also minimizing in the wavenumber, see Straughan [45], to increase the global nonlinear stability boundary into the region in Fig. 1 denoted by E–0–0–E. However, a lot of analytical and computational effort is required. The threshold so obtained does not coincide with the linear instability one and so there remain regions of possible sub-critical instability. However, for the Navier–Stokes–Voigt fluid the coupling parameter generalized energy method must involve \(\lambda \) in the maximization, Euler–Lagrange process, to be able to achieve a global nonlinear stability boundary which will exceed the 0–0 curve when \(\lambda >0\). We believe at present this problem is open.

In the present situation because the energy in (23) involves \(\lambda \Vert \nabla \mathbf{u}\Vert ^2\), the rate of decay obtained is better than that observed in classical Bénard convection. This faster decay rate is also observed by Layton and Rebholz [18], in their Kelvin vortex solutions, see also numerical computations of Matveeva [22].

Table 1 Transition from stationary to oscillatory convection values
Full size table
Fig. 1
figure 1

Graph of Ra against C with \(Le=21.67\), \(Pr=50\). The diagonal solid line (E–S) represents the stationary convection curve. The curves 00, 11, 22 are the oscillatory convection thresholds for \(\lambda =0,\) 1, 2. The horizontal dashed line (E–E) is the global nonlinear stability boundary

Full size image

6 Conclusions

We have developed an analysis for the thermosolutal convection problem for a Navier–Stokes–Voigt viscoelastic fluid. We concentrate on the problem where the layer of fluid is heated from below and simultaneously salted from below. The thermal convection problem for a Navier–Stokes–Voigt fluid without a salt field was suggested by Sukacheva and Matveeva [21], Sukacheva and Kondyukov [23]. The isothermal model for a Navier–Stokes–Voigt fluid is explained at length by Oskolkov [19, 20].

We have shown that for small enough salt Rayleigh number the onset of thermally driven motion is by stationary convection. There is then a transition to oscillatory convection. The transition values are calculated for several realistic values of Prandtl and Lewis numbers. We have shown that the transition to oscillatory convection occurs at higher Rayleigh and salt Rayleigh numbers as the Kelvin - Voigt parameter \(\lambda \) increases. The fact that the convective motion instability threshold is increased when the Kelvin–Voigt parameter increases is very useful for solar pond design. A solar pond is a mechanism whereby solar energy is harnessed through a thermosolutal process and converted into renewable electric energy, cf. Abdullah et al. [35]. A solar pond consists of a layer of salt water approximately 1–2   m thick in a horizontal configuration with direct access to solar radiation. The salt field is arranged so that the salt concentration decreases approximately linearly from the base of the layer. The base of the layer is chosen to absorb solar radiation and this configuration can achieve temperatures close to 100 \(^{\circ }\)C in the solution near the base. The naturally heated brine solution is drawn out and passed through a heat exchanger to generate renewable electricity. It is important that convective motion does not commence otherwise the solution mixes and so it is key that the conditions remain in the stable case for the problem studied herein. Our work suggest that adding a suitable additive to the salt solution which increases the Kelvin - Voigt parameter will ensure the solar pond does not commence overturning instability and will, therefore greatly improve the efficiency of the device.