A presmooth estimator of unbiased distributions with length-biased data

Abstract

In this paper, we propose a presmooth product-limit estimator to draw statistical inference on the unbiased distribution function representing the population of interest. The strong consistency of the estimator proposed is investigated. The finite sample performance of the proposed estimator is evaluated using simulation studies. It is observed that the proposed estimator exhibits greater efficiency in comparison with the alternative method in de Uña-Álvarez (Test 11(1):109–125, 2002).

Introduction

In practical studies, it is not feasible sometimes to collect a random sample from the population of interest, called the target population. In such occasions, a biased or weighted sample from the underlying population is obtained. In other words, the data are collected from another distribution, which may induce a type of bias to our inferences. Thus, the biased sampling problem is to make inference about the target population, while our samples are generated from another distribution function. The most common case, called length-biased, is when the biased data are collected according to the chance proportional to their value (measures, lengths, etc.), arising in many types of sampling. There can be found many examples of such situations in various articles and books from different disciplines, e.g., biology, biotechnology, genetics, forestry, economics, industry and medical science. For more information, we refer readers to the following studies: Rao [19, 20], Patil and Ord [18], Zelen and Feinleib [28], Song et al. [22] and Kvam [12].

Wicksell [26] found in the study blood cells microscope that only those cells which are bigger than a threshold are detectable and the existing smaller cells are not visible. At that point in time, he called this phenomenon corpuscle problem, which was later known as the length-biased sampling. McFadden [15], Blumenthal [2] and Cox [5] are of the first scientists who address this phenomenon in statistics. In the past two decades, many more studies have been performed to extend the statistical inferences in regard to the problem of length-biased sampling [21, 14, 17].

For example, Efromovich [8] attempted to draw statistical inference for the police investigation, in which they looked at the ratio of alcohol in liquor-intoxicated drivers. Since there is a higher chance for drunker drivers to be suspected by the police, their data collection suffers from the length-biased problem.

Definition 1

Suppose that F(·) is an absolutely continuous cumulative distribution function. The random variable Y has the length-bias distribution corresponding to F(·), if it satisfies the following distribution function.

$$G(t)=\mu^{-1} \int_{0}^{t} u\,{\rm d}F(u), \quad t \ge 0,$$

(1.1)

where $\mu = \int_{0}^{\infty }u\,{\rm d}F(u)$.

It is easy to obtain Eq. (1.1) for the distribution function F(·) as follows

$$F(t)=\frac{ \int_{0}^{t} u^{-1}\,{\rm d}G(u)}{ \int_{0}^{\infty } u^{-1}\,{\rm d}G(u)}, \quad t \ge 0.$$

(1.2)

Here, the problem is to draw statistical inference about the underlying population (F(·)), while the available data are collected from length-bias distribution G(·). Accordingly, when encountering the length-biased sampling problem, we obtain a data collection which may be used to estimate the distribution function G(·) empirically. Having obtained the empirical estimation of G(·), the distribution function F(·) can be estimated using Eq. (1.2). For a sample consisting of complete observations (excluding censored data), the nonparametric estimation of the distribution function F(·) under length bias has been investigated by Vardi et al. [25], Vardi [24], Horváth et al. [9] and Jones [10].

The other obstacle commonly faced, specially in survival analysis, is that some of the subjects are not completely observed owing to right censoring. There have been many studies in the literature concerning length-biased and right-censored data. Let $Y_{1}, Y_{2}, \ldots , Y_{n}$ denote iid random variables with distribution function G(·). Also, suppose that $C_{1}, C_{2}, \ldots , C_{n}$ are iid random variables from the distribution function ${\tilde{G}}(\cdot )$ and independent from $Y_{1}, Y_{2}, \ldots , Y_{n}$. Define I(A) as the indicator function of the event A. Under the right random censorship model, observations are $\{(Z_{i}, \delta_{i})\,;\, i=1,2,\ldots ,n\}$ in which the variables $Z_{i}=\min (Y_{i}, C_{i})$ are iid copies of distribution function H(·) and $\delta_{i}=I(Y_{i}\le C_{i})$. $C_ {i}$ denotes the censored random variable, and $\delta_{i}=0$ indicates that the ith subject is censored, while $\delta_{i} = 1$ denotes for the uncensored observations. We are interested in estimating the distribution function F(·) based on the pair of observations $(Z_{i}, \delta_ {i})$.

In the presence of length bias and right censoring, Winter and Földes [27] introduced a conditional method to estimate the distribution function F(·). Their proposed estimator is applicable under the left-truncation of observations in general, when the values of truncation variable for each subject are specified. de Uña-Álvarez [6] showed that ignoring the extra information of the length-bias model (unconditional approach) in the structure of conditional estimators, like Winter and Földes [27], results in lower efficiency.

When a sample only includes censored data, but not length-biased or truncated observations, the nonparametric maximum likelihood product-limit estimator [11] may be used. The Kaplan–Meier estimator of distribution function F(·) is defined as follows

$$F_{n}^{\rm KM}(t)=1- \prod_{i=1:Z_{(i)}\le t}^{n}\,\left[ 1-\frac{\delta_{[i]}}{n-i+1}\right] ,$$

(1.3)

where the $Z_{(i)}$ variables are the ordered observations of $Z_{i}$ and $\delta_{[i]}$ is the responsible value of $\delta_{i}$ for the variable $Z_{(i)}$. Equation (1.3) could be simply rewritten as follows

$$F_{n}^{\rm KM}(t)= \sum_{i=1}^{n}\,w_{i}\,I_{\left( Z_{(i)}\le t \right) },$$

(1.4)

where

$$w_{i} = \frac{\delta_{[i]}}{n-i+1}\,\prod_{j=1}^{i-1}\,\left[ 1-\frac{\delta_{[j]}}{n-j+1}\right] .$$

To study the statistical properties of the estimator $F_ {n}^{\rm KM}(\cdot )$, we refer readers to Andersen et al. [1]. It is deduced from Eq. (1.4) that the Kaplan–Meier estimator is a step function with jumps at the non-censored observations. The sizes of jumps in each step depend not only on the complete observations, but also on the number of censored observations prior to the step. It can be easily checked that when the sample does not consist of any censored data, the Kaplan–Meier estimator is equivalent to the empirical distribution function estimator.

de Uña-Álvarez [6] first estimated the distribution function G(·) on the basis of biased observations using the Kaplan–Meier estimator. Afterward, by substituting the estimator for G(·) in Eq. (1.2), they have obtained the following estimator, called the length-bias-corrected product-limit estimator, for the target distribution.

$${\widehat{F}}_{n}(t)=\frac{ \int_{0}^{t}\,u^{-1}{\rm d}G_{n}^{\rm KM}(u)}{ \int_{0}^{\infty }\,u^{-1}{\rm d}G_{n}^{\rm KM}(u)}, \quad t \ge 0.$$

(1.5)

It is simply followed from (1.5) that

$$\begin{aligned} {\widehat{F}}_{n}(t)= & \frac{\sum_{i=1}^{n}w_{i}Z_{(i)}^{-1}I_{\left( Z_{(i)}\le t\right) }}{\sum_{i=1}^{n}w_{i}Z_{(i)}^{-1}} \\= & \sum_{i=1}^{n}\,{\widetilde{w}}_{i}I_{\left( Z_{(i)}\le t\right) }, \end{aligned}$$

(1.6)

where

$${\widetilde{w}}_{i}=\frac{w_{i}Z_{(i)}^{-1}}{\sum_{i=1}^{n}w_{i}Z_{(i)}^{-1}}.$$

${\widetilde{w}}_{i}$ is calculated applying the jumps of Kaplan–Meier estimator in (1.4).

In the rest of this study, we first introduce the presmooth estimator in “The presmooth estimator” section. Next, by substituting the presmooth estimator for the estimator $G_{n}^{\rm KM}(\cdot )$ in Eq. (1.5), we obtain a smoother method for the distribution function F(·), which is expected to possess higher efficiency in predicting the true distribution function. In “Strong consistency” section, the strong consistency of the proposed estimator is investigated. Finally, the simulations studies for two estimators are presented and their behaviors are discussed in “Simulation” section.

The presmooth estimator

In this section, inspired by the expression of the product-limit estimator of de Uña-Álvarez [6], we will propose the presmooth estimator for the distribution function using length-biased right-censored data.

Presmooth estimator in LB distribution

Suppose that

$$p(z):=P(\delta =1\,|\,Z=z)=E(\delta \,|\,Z=z)$$

denote the conditional probability of non-censored event given the observation Z = z. Cao et al. [4] introduced a presmooth estimator by substituting the nonparametric regression estimator proposed in Nadaraya [16] for the censoring indicator variables. Following that, Cao and Jácome [3] assessed the limit distribution and the asymptotic mean squared error of the estimator presented in Cao et al. [4]. Stute and Wang [23] discussed the significance of p(·) to prove the consistency of an integral $\int \varphi \, {\rm d}F_{n}^{\rm KM}$ where $\varphi$ is a measurable function over $\mathbb {R}$ and $F_{n}^{\rm KM}$ is the Kaplan–Meier estimator. Given the pairs observations $\{ (Z_i, \delta_i ); \, i= 1,2, \ldots , n\}$, we propose the following estimator for p(z),

$$p_{n}(z)=\sum_{i=1}^{n} \frac{ K_{b}\left( z- Z_{i}\right) \delta_{i}}{ \sum_{i=1}^{n} K_{b}\left( z- Z_{i}\right) },$$

(2.1)

where K(·) is a kernel function and $K_{b}(\cdot ) = \left( {\frac{1}{b}}\right) K \left( {\frac{\cdot }{b}}\right)$, in which $\{b \equiv b_{n}, \, n = 1,2, \ldots \}$ is the sequence of bandwidth.

By replacing $\delta_{[\cdot ]}$ in Eq. (1.4) with $p_{n}(\cdot )$, the presmooth estimator of the distribution function F(·) is defined as follows:

$$F_{n}^{P}(t)= \sum_{i=1}^{n}\,\nu_{i}\,I_{\left( Z_{(i)}\le t\right) },$$

(2.2)

where

$$\nu_{i}= \frac{p_{n}(Z_{(i)})}{n-i+1}\,\prod_{j=1}^{i-1}\,\left[ 1-\frac{p_{n}(Z_{(j)})}{n-j+1}\right] .$$

Remark 1

Even though the proposed presmooth estimator seems similar to the Kaplan–Meier estimator in (1.4), they mainly differ in $\delta_{[\cdot ]}$ which has been replaced with the smoothing function $p_{n}(Z_{(\cdot )})$ in (2.2). Adapting the Kaplan–Meier estimator to the smoother method by plugging in $p_{n}(Z_{(\cdot )})$ might be invaluable, as the presmooth estimators exhibit superior accuracy in estimating the distribution function. By contrast, the Kaplan–Meier estimator only assigns equal jumps to all of the complete observations, excluding the censored data.

Remark 2

It is of note that when $n\rightarrow \infty$, the bandwidth defined in (2.1) decreases and converges to 0, and very small values of $b \simeq 0$ implies $p_n(Z_i)\simeq \delta_i$. Accordingly, when $n\rightarrow \infty$, the presmooth and the Kaplan–Meier estimators become equal.

The presmooth estimator of the unbiased distribution

In this section, we present a presmooth product-limit estimator for a distribution function in the length-biased and random right-censored sampling. For this purpose, we substitute the presmooth estimator of the right-censored data, say $G_{n}^{P}(\cdot )$, for the distribution function G(·) in Eq. (1.5). Hence, we obtained the presmooth product-limit estimator through

$${\widehat{F}}_{n}^{P}(t)=\frac{ \int_{0}^{t} u^{-1}{\rm d}G_{n}^{P}(u)}{ \int_{0}^{\infty }u^{-1}{\rm d}G_{n}^{P}(u)}, \quad t \ge 0.$$

(2.3)

Given Eq. (2.3), it can be deduced that

$$\begin{aligned} {\widehat{F}}_{n}^{P}(t)= & \frac{\sum_{i=1}^{n}\nu_{i}Z_{(i)}^{-1}I_{\left( Z_{(i)}\le t\right) }}{\sum_{i=1}^{n}\,\nu_{i}Z_{(i)}^{-1}} \\= & \sum_{i=1}^{n}\,{\widetilde{\nu }}_{i}I_{\left( Z_{(i)}\le t\right) }, \end{aligned}$$

(2.4)

with

$${\widetilde{\nu }}_{i}=\frac{\nu_{i}Z_{(i)}^{-1}}{\sum_{i=1}^{n}\,\nu_{i}Z_{(i)}^{-1}}.$$

${\widetilde{\nu }}_{i}$ is calculated from the jumps of a presmooth estimator of distribution function in Eq. (2.2).

Corollary 1

Cumulative hazard rate function ofF(·) is defined as

$$\Lambda (t)= \int_{0}^{t}\frac{1}{1-F(u^{-})}\,{\rm d}F(u).$$

(2.5)

By plugging in${\widehat{F}}_{n}^{P}{(\cdot )}$in Eq. (2.5), the presmooth estimator of the cumulative hazard rate can be obtained by means of

$$\begin{aligned} {\widehat{\Lambda }}_{n}^{P}(t)= & \int_{0}^{t}\frac{1}{1-{\widehat{F}}_{n}^{P}(u^{-})}\,{\rm d}{\widehat{F}}_{n}^{P}(u) \\= & \sum_{i=1}^{n}\frac{{\tilde{\nu }}_{i}}{1-{\widehat{F}}_{n}^{P}(Z_{(i)}^{-})}\,I_{\left( Z_{(i)}\le t\right) } \\= & \sum_{i=1}^{n}\frac{\nu_{i}Z_{(i)}^{-1}}{\sum_{j=1}^{n}\nu_{j}Z_{(j)}^{-1}I_{\left( Z_{(i)}\le Z_{(j)}\right) }}\,I_{\left( Z_{(i)}\le t\right) }. \end{aligned}$$

(2.6)

Strong consistency

In this section, we study the strong consistency of ${\widehat{F}}_ {n}^{P}(\cdot )$. For this purpose, we define

$$\tau_{F}=\inf \{{t\,:\,F(t)=1}\}.$$

Similarly, $\tau_{G}$, $\tau_{{\widetilde{G}}}$ and $\tau_{H}$ are defined for the distribution functions G(·), ${\tilde{G}}(\cdot )$ and H(·). Apparently, it could be claimed that $\tau_{F} =\tau_{G}$ and $\tau_H = \min ( \tau_F, \tau_{{\widetilde{G}} } )$.

Theorem 1

Let$\varphi (\cdot )$be a measurable function, $\varphi_{1}(x) = x^{- 1}$and$\varphi_{2}(x) = x^{-1}\varphi (x)$areG(·)-integrable. Assuming that$\tau_{H} = \tau_{F}$is reasonable, then we have

$$\lim_{n\rightarrow \infty } \int \varphi (x)\,{\rm d}{\widehat{F}}_{n}^{P}(x)= \int \varphi (x)\,{\rm d}F(x) \quad a.s.$$

(3.1)

Proof

Suppose

$${\widehat{S}}_{\varphi } = \int \varphi (x)\,{\rm d}{\widehat{F}}_{n}^{P}(x),$$

and

$$S_{\varphi } = \int \varphi (x)\,{\rm d}F(x).$$

Using Eq. (2.4), it is obtained that

$$\begin{aligned} {\widehat{S}}_{\varphi }= & \sum_{i=1}^{n}\,{\widetilde{\nu }}_{i}\varphi \left( Z_{(i)}\right) \\= & \frac{\sum_{i=1}^{n}\nu_{i}Z_{(i)}^{-1}\varphi \left( Z_{(i)}\right) }{\sum_{i=1}^{n} \nu_{i}Z_{(i)}^{-1}}\cdot \end{aligned}$$

(3.2)

According to Theorem 2.1 of de Uña-Álvarez and Rodríguez-Campos [7], regardless of the presence of covariates in this case, when $n \rightarrow \infty$, we have

$${\widetilde{\mu }}=\frac{1}{\sum_{i=1}^{n}\nu_{i}Z_{(i)}^{-1}}{\mathop {\longrightarrow }\limits^{a.s.}}\dfrac{1}{E(\varphi_{1}(Y))}=\dfrac{1}{ \int \varphi_{1}(y)\,{\rm d}G(y)}=\mu ,$$

(3.3)

and

$$\sum_{i=1}^{n}\nu_{i}Z_{(i)}^{-1}\varphi (Z_{(i)}){\mathop {\longrightarrow }\limits^{a.s.}}E(\varphi_{2}(Y))= \int \varphi_{2}(y)\,{\rm d}G(y).$$

(3.4)

Now, considering Eqs. (3.2)–(3.4), it can be deduced that

$${\widehat{S}}_{\varphi }{{\mathop {\longrightarrow }\limits^{a.s.}}}S_{\varphi }.$$

Therefore, the proof of Theorem 1 is completed. $\square$

Corollary 2

Let$0<\mu <\infty$. Using Theorem1, we have

$${\widehat{F}}_{n}^{P}(t){{\mathop {\longrightarrow }\limits^{a.s.}}}{F}(t)$$

for any$t>0$, when$n\rightarrow \infty$.

Moreover, given the relation$\Lambda (t)= - \ln (1- F(t))$, if$n\rightarrow \infty$, we have

$$\Lambda_{n}^{P}(t){{\mathop {\longrightarrow }\limits^{a.s.}}} \Lambda (t).$$

Simulation

In this section, simulation studies are carried out to inspect the finite sample performance of the presmooth limit-product estimator. For better illustration, we have examined the proposed estimator behavior (2.3) in comparison with the product-limit estimator introduced in (1.5). For this purpose, we have studied the relative efficiency of the two estimators (RE) through the ratio of their values of MSE(·), which is defined as follows.

$${\rm RE}(t)=\frac{\hbox{MSE}({\widehat{F}}_{n}(t))}{\hbox{MSE}({\widehat{F}}_{n}^{P}(t))},$$

(4.1)

where

$$\hbox{MSE}({\widehat{F}}_{n}(t))=E({\widehat{F}}_{n}(t)- E({\widehat{F}}_{n}(t)))^{2},$$

and

$$\hbox{MSE}({\widehat{F}}^{P}_{n}(t))=E({\widehat{F}}_{n}^{P}(t)- E({\widehat{F}}_{n}^{P}(t)))^{2}.$$

We have approximated the value of RE in (4.1) using Monte Carlo simulations. The amounts of RE are calculated based on B = 5000 replications of estimations using samples sizes n = 20, 50 and 100. Suppose distribution F(·) is a member of gamma family with density

$$f(t)=\frac{1}{\Gamma (\alpha )\beta^{\alpha }}\, t^{\alpha -1}e^{-\frac{t}{\beta }},\quad \alpha>0,\,\beta >0,\, t\ge 0.$$

Given Eq. (1.1), it can be easily deduced that if the distribution of target population is $Gamma(\alpha , \beta )$, the resulting length-biased distribution is $Gamma (\alpha +1,\beta )$. Similarly, the corresponding length-biased distribution to the $Weibull(p,\lambda )$ is a generalized gamma distribution, $G(\mu ,\sigma ,\nu )$, with the probability density function:

$$f(y) = {\nu y^{\nu -1}\over (\sigma /\mu )^{\nu \mu }\Gamma (\mu )} y^{\nu (\mu -1)} \exp (-(y \mu /\sigma )^\nu ),$$

where $\mu =1+1/p$, $\sigma =1/\lambda$, and $\nu =p$ are the shape, scale and family parameters, respectively.

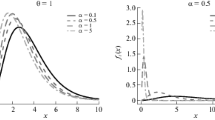
Figure 1 compares the performance of the presmooth estimator with that of the product-limit estimator in predicting the survival function of the U(0, 4) distribution. The figure consists in 5000 iterations for the moderate sample scenario (n = 50). It can be observed that applying the proposed method has considerably reduced the amount of deviations from the true survival function by comparison with the product-limit estimator.

Fig. 1

Presmooth estimator versus PL-estimator for Exp(1) with n = 50 and $C\sim U (0,4)$

Figures 2 and 3 illustrate the approximated values of RE(·) for the Weibull(0.5, 1) and Gamma(1, 1) (the exponential distribution, EXP(1)) unbiased distributions, respectively. The diagrams were estimated based on 5000 iterations of the different sample sizes generated from the corresponding length-biased observations. The U(0, 4) distribution was considered as the censoring distribution, resulting in about 24% incomplete data in all surveys. Considering the sample sizes n = 20 and 50 in the both diagrams, it can be observed that the proposed method for all values of t exhibited superiority over the product-limit estimator in terms of MSE. Similarly, the proposed presmooth estimator indicated much better results for the large sample scenario (n = 100) of the Weibull(0.5, 1) target population (Fig. 2). However, turning to the large sample scenario (n = 100) of the Gamma(1, 1) unbiased population, while for the values of t smaller than roughly 0.5 the product-limit estimator performed better, the proposed method revealed better efficiency for t larger than 0.5.

Fig. 2

Curves obtained for simulated AR with different sample size taken from Weibull(0.5, 1) and 24% censoring

Fig. 3

Curves obtained for simulated AR with different sample size and 32% censoring

For better illustration, we have compared the efficiency of the estimators under different levels of censoring via RE in Fig. 4. For this purpose, we calculated the values of RE based on 5000 replications of the large sample scenario (n = 100). The data were generated from the length-biased distribution corresponding to the Exp(1) target population. The censoring times were generated from the $U(0, \beta )$ distribution, in which the values of 3, 2 and 1 were chosen for $\beta$ resulting in 63%, 43% and 32% incomplete observations, respectively. Accordingly, it can be obtained that although for the small values of t the product-limit estimator exhibited better results, the presmooth estimator has significantly reduced the amount of MSE in all levels of censoring as the value of t increased. Broadly, the presmooth estimator exhibited superior efficiency in comparison with the product-limit method.

Fig. 4

Efficiency comparison for Exp(1) with n = 100 and different values of censoring rate

It has been revealed in the all above RE diagrams that the figures have become closer to the line RE = 1 by rising in the sample sizes. This increasing tendency for the two methods to perform similar as the sample size increased is clearly justified by Remark 2.

To calculate the estimated ${\widehat{F}}_{n}^{P}(\cdot )$, the Nadaraya–Watson estimator method, presented in Eq. (2.1), has been used to estimate p(·). Thus, it is crucial to select the bandwidth properly as it plays a key role the Nadaraya–Watson estimator. For this purpose, Cao and Jácome [3] and Cao et al. [4] obtained an optimal bandwidth for their presmooth pug-in method by minimizing the asymptotic mean integrated squared error, avoiding any bias in results. Later, the simulation results for this estimator was studied through the Simpson’s rule using the survPresmooth package López-de Ullibarri and Jácome Pumar [13].

Conclusion

In this paper, we have proposed a presmooth estimator by adapting the product-limit estimator of de Uña-Álvarez [6] for length-biased and (random) right-censored data. The limit properties of the proposed estimator have been investigated. To inspect the performance of the method, simulations studies were conducted to make comparisons between the proposed estimator and the product-limit estimator of de Uña-Álvarez [6]. As mentioned, it is very important to select the bandwidth for the Nadaraya–Watson regression estimation appropriately. We have overcome this issue by applying the MISE(·) estimator.