Semi-Analytical Solution of Chemical Flooding in Heterogeneous Non-Communicating Layers with a Focus on Low Salinity Water Flooding

Abstract

Chemical flooding has been implemented intensively for some years to enhance sweep efficiency in porous media. Low salinity water flooding (LSWF) is one such method that has become increasingly attractive. Historically, analytical solutions were developed for the flow equations for water flooding conditions, particularly for non-communicating strata. We extend these to chemical flooding, more generally, and in particular for LSWF where salinity is modeled as an active tracer and changes relative permeability. Dispersion affects the solutions, and we include this also. Using fractional flow theory, we derive a mathematical solution to the flow equations for a set of layers to predict fluid flow and solute transport. Analytical solutions tell us the location of the lead (formation) waterfront in each layer. We extend a correlation that we previously developed to predict the effects of numerical and physical dispersion. We used this correction to predict the location of the second waterfront in each layer which is induced by the chemical’s effect on mobility. We show that in multiple non-communicating layers, mass conservation can be used to deduce the interlayer relationships of the various fronts that form. This is based on similar analysis developed for water flooding although the calculations are more complex because of the development of multiple fronts. The result is a predictive tool that we compare to numerical simulations and the precision is very good. Layers with contrasting petrophysical properties and wettability are considered. We also investigate the relationship between the fractional flow, effective salinity range, salinity dispersion and salinity retardation. The recovery factor and vertical sweep efficiency are also very predictable. The work can also be applicable to other chemical EOR processes if they alter the fluid mobility. This includes polymer and surfactant flooding.

1 Introduction

Multi-phase flow in porous media is studied in many disciplines and has a number of engineering applications including contaminant transport, ground water movement in water aquifers and prediction of the behavior of oil and gas reservoirs. Chemical flooding in porous media has broad application where it can be used to reduce the effect of greenhouse emissions by injecting captured CO₂ as carbonated water in reservoirs (Sari et al. 2020), improve production from gas hydrate formations (Hassanpouryouzband et al. 2018), enable nuclear waste storage and remediation of water aquifers (Zheng and Bennett 2002) and is a significant part of enhanced oil recovery (EOR) (Lake et al. 2014). In the oil and gas industry, such chemical flooding is often used to change fluid mobility properties (e.g., Lake 1989; Lake et al. 1981; Sheng 2013a, b). For instance, polymers have long since been used to alter the viscosity of injected water, and surfactants are known to change the interfacial tension between oil and water. More recently, it has been accepted that rock wettability can be altered due to reactive transport of active ions such as low salinity and engineered water flooding (Tripathi and Mohanty 2008; Jackson et al. 2016; Khaledialidusti and Kleppe 2017; Mahani et al. 2017; Maes and Geiger 2018). LSWF mainly depends on injecting a diluted brine and/or manipulating the active ion concentration, such as cations and sulfate so that a chemical reaction between fluid–fluid and fluid–rock causes the improvement in the displacement efficiency. However, the underlying physical or chemical mechanism is still under debate. Moreover, LSWF experiments show even further improvement in the sweep efficiency by combining LSWF with other EOR components, e.g., with polymer (Alfazazi et al. 2019), surfactant (Tavassoli et al. 2016) and nanoparticles (Ali et al. 2019). In this paper, we focus on low salinity effects that change wettability and model it by altering relative permeability. Additional effects such as fines migration are often considered to depend on fluid velocity as well as salinity (e.g., Chequer et al. 2019), and we ignore these processes in this paper.

The equations that describe chemical flooding can be solved numerically so that we can approximate fluid flow of active and passive tracers in various systems. Passive tracers can be tracked through the reservoir but have no effect on the flow. Active tracers (Schlumberger 2018) will influence flow either through changes to relative permeability or more directly through explicit reactions. Representing changes to wettability simply by changing relative permeability (Jerauld et al. 2008, see also “Appendix”) offers an effective tool for reservoir-scale simulations. Modeling reaction kinetics is more appropriate for core-scale modeling where the rates should be captured more precisely. Analytical solutions can be obtained for traditional water flooding provided that certain assumptions apply such as flow in sets of non-communicating layers. We show elsewhere (Al-Ibadi et al. 2019a) that, under some conditions, flow in strongly communicating layers is quite similar such that there would be great value in deriving analytical solutions to obtain good approximations.

In 1D homogeneous models of water flooding where gravity, capillary pressure and compressibility are ignored, a single shock front of the displacing phase is predicted, as described by Buckley and Leverett (1942). For chemical flooding in these conditions, the analytical solution predicts that changes to the relative permeability (i.e., mobility) will result in two shock fronts forming (Patton et al. 1971; Pope 1980). We have shown more recently that this solution can be extended to account for numerical or physical dispersion (Al-Ibadi et al. 2019a, b). We now develop this analysis to reservoirs with non-communicating layers. The observed well behavior will be more complex due to variations between the layers as each will have its own fluid velocity, displacement performance and breakthrough time. This is because the wells see the combined effect of various fronts arriving over time. Note that the fluid velocity in each layer is a function of petrophysical properties, rock wettability and fluid viscosities, and all these factors are the subject of this study.

In 2D non-communicating layered reservoirs, there exist mathematical solutions to the flow equations based on specific assumptions. For single-phase flow, the relative flow capacity (the product of permeability and layer thickness) can be applied to allocate the total flux in each layer. This will be discussed later. Also, there exists an analytical solution of solute transport for single-phase flow in non-communicating layers (Lake and Hirasaki 1981; Shen et al. 2016). For two-phase flow, there is an analytical solution for piston-like displacement that can be used to predict the location of the shock front (Stiles 1949; Dykstra and Parsons 1950; Lake 1989) in each layer. However, there is no clear analysis of solute transport in such a system. Similarly, for a Buckley–Leverett displacement in which there are two phases flowing behind a single formation water shock front, the velocity can be estimated mathematically (El-khatib 2001). This solution does not represent solute transport in such a system, however. Here, we present an analytical solution for models that predict two shock fronts in non-communicating layers (Lake et al. 2014). We also extend the work to include the impact of dispersion (either physical or numerical) which makes the fronts non-shock like (Al-Ibadi et al. 2019d) and introduces retardation as a physical phenomenon. These processes are particularly relevant to LSWF due to the relatively sharp way in which the change in salinity alters wettability.

Retardation is a significant process in chemical flooding and affects its performance. It has been observed both in laboratory and in simulation studies. For instance, in models that simulate the alteration of wettability due to the injection of low salinity or engineered water, various mechanisms result in adsorption of active ions such as Ca²⁺ and Mg²⁺ (Lager et al. 2006; Sharma and Mohanty 2018; Al-Shalabi and Sepehrnoori 2017) which slows down the front as a chemical retardation. Further, there is evidence that dispersion and diffusion can retard the active ion or salinity front as well (Al-Ibadi et al. 2019d) causing the displacing fronts to be either accelerated or retarded as a function of the effective concentration range (Al-Ibadi et al. 2018, 2019b). This creates a physical retardation. All these effects will be considered in this study in order to develop an analytical solution.

Earlier work on waterflooding only accounted for heterogeneity in static petrophysical properties, while in this work we include for the first time the additional impact of variations in wettability between layers, as represented by changes to the relative permeability curves. In order to derive an analytical solution of chemical flooding in such systems, first we calculate the relative location of formation water in each layer compared to that in the other layers. We focus on the breakthrough time of the whole reservoir, primarily, but these calculations can be extended to other times. Then, we calculate the location of the following chemical front relative to the formation waterfront in each layer. Afterward, we calculate the time at which the fronts reach their location and hence the velocities of the chemical front, which are needed to calculate solute transport.

The results of our paper can also be applied to the broader class of chemical flooding as part of EOR. Polymer flooding involves the modification of the injected fluid’s viscosity by tracking the concentration of the polymer. Similarly, surfactant floods additional result in a change from immiscible to miscible flow requiring additional changes to relative permeability. The approaches discussed here can be applied to any displacement process where relative permeability is modified by tracking a solute that is dissolved in water.

In this paper, we do the following. First, we give a brief description of mathematical equations that govern two-phase flow in 1D porous media for conventional water flooding and for chemical flooding. Then, we consider water flooding in 2D non-communicating layers, where we derive the mathematical terms that describe the location of the shock front of the displacing phase relative to that in the other layers. After that, we consider chemical flooding in 2D non-communicating layers, where we derive mathematical equations to calculate the location of the chemical front relative to the formation waterfront in the same layer. We calculate the dimensionless time using pore volumes injected (PVI) at any given location of these fronts. Then, we generalize this work to a multilayer system.

2 Problem Statement and Model Set Up

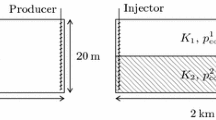
We considered a stratified porous medium in which each layer was aligned to the horizontal, of equal area and constant thickness. Each layer was homogeneous at the model scale, but petrophysical properties and thickness were often distinct from the other layers. We focused on permeability contrast primarily in numerical experiments but generalized the equations which include all these variables. Each layer was separated from the others by a barrier, e.g., shale or marl beddings, so that vertical communication was zero, as shown in Fig. 1 for two layers. We ignore gravity and capillary effects. Diffusion and physical dispersion that was induced by fine-scale heterogeneity were replaced by numerical dispersion. This was a two-step process. First, we assumed that a heterogeneous medium was replaced by a homogeneous one at the model scale where the effect of variations in petrophysical properties was represented by dispersion terms in the continuum-scale mathematical model. This is a classical approach and required that the heterogeneities had a limited length scale of variability. Then, we assumed that the dispersion terms could be represented via numerical dispersion by choosing an appropriate size of grid cell and time step. For a more detailed discussion, see Al-Ibadi et al. (2019b). This has been discussed for some time in the literature (Jerauld et al. 2008, discussed it in the context of LSWF). Details about replacing this kind of physical dispersion by equivalent numerical dispersion can be found in Ghanbari et al. (2018) and Garmeh and Johns (2010). A sector-scale model was considered in which we defined a producer and injector, as displayed in Fig. 2a.

Fig. 1

Sketch of non-communicating stratified model where there are two layers, the upper layer was the high permeability layer and the lower layer was low permeability layer. Petrophysical and mobility variables and functions were constant within the layers but variable between them

Fig. 2

Fluid flow in a non-communicating stratified models for a LSWF showing a water saturation distribution indicating separate fronts and b pressure variation along each layer which would result in crossflow if layers were in communication. The pressure changes slope suddenly at the formation water front and more slowly over the low salinity front

Flow in the layers was strongly affected by the contrast in permeability. Figure 2 illustrates that in each layer there were two shock fronts, the first was the formation waterfront and the second was the chemical (low salinity) front. Figure 2b shows the pressure profile in two layers illustrating the potential for crossflow if the barriers were removed. Individual layers behaved as if they were in isolation except for the flow rates which depended on behavior at the wells. A larger volume of injected fluid went to the high permeability layer. In single-phase flow, this was controlled by the flow capacity (the product of permeability and layer thickness). In two-phase flow, the dynamic variation in mobility altered the flow rates in the layers over time such that flow capacity gave inaccurate prediction. This resulted in the high permeability layer having an earlier breakthrough. In contrast, porosity variations had the opposite effect such that the high porosity layer had a late breakthrough though both had the same flux. This was because the interstitial velocity was affected by porosity. This in turn affected the displacement efficiency and the performance of the injected compound. These types of relationships are understood well for single-phase flow. In this work, we addressed the interactions of these factors in the presence of two-phase flow, which depended on fluid mobility factors. We will answer the following questions:

• How much does the contrast in petrophysical properties affect the fractional flow in each layer?

• How will retardation affect the fractional flow in each layer compared to 1D models?

• How will the results be affected if different relative permeability curves are used (e.g., for a change of wettability)?

• How will solute be transported in such a system?

We will answer all these questions by finding a mathematical equation that describes fluid flow, to help evaluate the performance and the productivity of this flooding process.

A black oil simulator (Schlumberger 2018) was used to compare the analysis versus the numerical result. For the base case, ∆x = 1 ft (3500 cells in x-direction), ∆z = 75 ft (2 layers in z-direction) and ∆y = 1800 ft (1 cell in y-direction). The grid cell size in the x-direction was then modified for various coarse models to examine the effect of numerical dispersion, which can be used to mimic the physical dispersion that may be induced in a heterogeneous system, where both spread out the salinity front and the water saturation. The similarity between numerical and physical dispersion has been known for some time (Lantz 1971) and we have previously discussed using the former to represent the latter in some detail (Al-Ibadi et al. 2019b). Two sets of relative permeability were then used, one set to simulate fluid flow behavior for high salinity formation water and another to simulate fluid flow after the salinity has been reduced. Moving from one set to another is salinity dependent where interpolations take place as shown in “Appendix.” Further details of the models and fluid properties are given in Table 1.

Table 1 Parameters of the reservoir model

3 Two Phase Flow Equations in 1D Models

We considered two-phase flow in a porous medium in which the fluids were immiscible and incompressible. The models consisted of layers that were isothermal and isotropic and had homogenous petrophysical properties at the model scale and the rocks were incompressible. Properties could vary between layers, however. We assumed the fluids flowed in one direction. For thin layers, capillary effects may dominate vertical flow, generally, producing near one-dimensional flow. An assumption of thinner layers also allows us to ignore viscous fingering effects within a layer for higher viscosity oil. Meanwhile for thicker layers, gravity effects may be ignored if the vertical permeability is low but viscous fingering may become an issue for high viscosity oils. We ignored horizontal capillary effects, setting P_c = 0. The mathematical model for this equation consisted of mass conservation equations for the oil and water phases. Salinity was modeled as an active tracer dissolved in the water phase. There was no adsorption nor absolute change to permeability which may occur from the movement of fines. The flow equations were defined by:

$$\emptyset \frac{{\partial S_{\text{w}} }}{\partial t} + \frac{{\partial u_{\text{w}} }}{\partial x} = \alpha_{\text{w}} u_{\text{w}} \frac{{\partial^{2} S_{\text{w}} }}{{\partial x^{2} }} + q_{\text{wi}} - q_{\text{wp}}$$

(1a)

$$\emptyset \frac{{\partial S_{\text{o}} }}{\partial t} + \frac{{\partial u_{\text{o}} }}{\partial x} = \alpha_{\text{o}} u_{\text{o}} \frac{{\partial^{2} S_{\text{o}} }}{{\partial x^{2} }} - q_{\text{op}}$$

(1b)

$$\emptyset \frac{\partial }{\partial t}\left( {S_{\text{w}} C_{\text{S}} } \right) + \frac{\partial }{\partial x}\left( {C_{\text{S}} u_{\text{w}} } \right) = \alpha_{\text{c}} u_{\text{w}} \frac{{\partial^{2} S_{\text{w}} C_{\text{S}} }}{{\partial x^{2} }} + C_{\text{S}}^{\text{inj}} q_{\text{wi}} - C_{\text{S}} q_{\text{wp}}$$

(1c)

$$S_{\text{w}} + S_{\text{o}} = 1$$

(1d)

The above model contains an explicit representation of dispersion processes through the dispersivity terms multiplying the second-order spatial derivatives. Physically, these terms represent the influence of heterogeneity at a scale below that represented by the mathematical model. Usually, this is negligible in the mathematical model for waterflooding. The terms also arise from the numerical representation of the equations even when the physical dispersion is missing (Lantz 1971). In that case, the cell size and time steps define the dispersivity.

The flux is given by Darcy’s Law:

$$\begin{aligned} & u_{\text{w}} =- K\frac{{k_{\text{rw}} \left( { S_{\text{w}} ,C_{\text{S}} } \right)}}{{\mu_{\text{w}} }}\frac{{\partial P_{\text{w}} }}{\partial x} \\ & u_{\text{o}} =- K\frac{{k_{\text{ro}} \left( { S_{\text{w}} ,C_{\text{S}} } \right)}}{{\mu_{\text{o}} }}\frac{{\partial P_{\text{o}} }}{\partial x} \\ & P_{\text{c}} = P_{\text{o}} - P_{\text{w}} = 0 \\ \end{aligned}$$

(2)

The reservoir models were assumed to be in hydrostatic equilibrium at t = 0 such that the pressure was uniform horizontally and pressure potential was uniform across all layers. The saturations are given by the irreducible water saturation of the high salinity relative permeability curves. No flow boundary conditions were assumed and a source term, $q_{\text{wi}}$, was added for a water injector at x = 0 and sink terms ($q_{\text{wp}}$ and $q_{\text{op}}$ for water and oil production, respectively) were added at x = L for a producer. Constant rate injection and constant rate liquid production were applied to each well. The model also represented flow in an open well in which a bottom hole pressure, P_bhp was defined. For N^layer multiple layers, the total flow into and out of the reservoir was

$$\begin{aligned} q_{\text{Ti}} = & \mathop \sum \limits_{j = 1}^{{N^{\text{layer}} }} q_{\text{wi}}^{j} = \mathop \sum \limits_{j = 1}^{{N^{\text{layer}} }} \frac{{{\text{PI}}_{\text{wi}}^{j} }}{\Delta V}\left( {P_{\text{bhp}} - P_{\text{w}}^{j} \left( {x = 0} \right)} \right) \\ q_{\text{Tp}} = & \mathop \sum \limits_{j = 1}^{{N^{\text{layer}} }} \left( {q_{\text{wp}}^{j} + q_{\text{op}}^{j} } \right) = \mathop \sum \limits_{j = 1}^{{N^{\text{layer}} }} \frac{{{\text{PI}}_{\text{wp}}^{j} }}{\Delta V}\left( {P_{\text{bhp}} - P_{\text{w}}^{j} \left( {x = L} \right)} \right) \\ & + \,\mathop \sum \limits_{j = 1}^{{N^{\text{layer}} }} \frac{{{\text{PI}}_{\text{op}}^{j} }}{\Delta V}\left( {P_{\text{bhp}} - P_{\text{o}}^{j} \left( {x = L} \right)} \right) \\ \end{aligned}$$

(3)

where

$${\text{PI}}_{\text{fp}}^{j} = \frac{{2\pi K^{j} h^{j} }}{{\mu_{\text{f}} \ln \left( {\frac{{r_{\text{e}} }}{{r_{\text{w}} }}} \right)}}k_{\text{rf}} \left( {S_{\text{w}} \left( {x = L} \right)} \right)$$

(4)

The equations were solved numerically using a decoupled implicit scheme (Schlumberger 2018). The oil and water phases were solved first implicitly, and then, the salinity was solved for the new time step, n + 1 in cell i:

$$\begin{aligned} & S_{\text{w}}^{i,n + 1} = S_{\text{w}}^{i,n} - \frac{\Delta t}{\emptyset \Delta x}\left( { u_{\text{w}}^{i,n + 1} \left( {S_{\text{w}}^{i,n + 1} ,C_{\text{S}}^{i,n } } \right) - u_{\text{w}}^{i - 1,n + 1} \left( {S_{\text{w}}^{i - 1,n + 1} ,C_{\text{S}}^{i - 1,n} } \right)} \right) \\ & S_{\text{o}}^{i,n + 1} = S_{\text{o}}^{i,n} - \frac{\Delta t}{\emptyset \Delta x}\left( { u_{\text{o}}^{i,n + 1} \left( {S_{\text{o}}^{i,n + 1} ,C_{\text{S}}^{i,n} } \right) - u_{\text{w}}^{i - 1,n + 1} \left( {S_{\text{o}}^{i - 1,n + 1} ,C_{\text{S}}^{i - 1,n} } \right)} \right) \\ & (S_{\text{w}} C)_{{}}^{i,n + 1} = (S_{\text{w}} C)_{{}}^{i,n} - \frac{\Delta t}{\emptyset \Delta x}\left( { u_{\text{w}}^{i,n + 1} \left( {S_{\text{w}}^{i,n + 1} ,C_{\text{S}}^{i,n + 1} } \right)C_{{}}^{i,n + 1} - u_{\text{w}}^{i - 1,n + 1} \left( {S_{\text{w}}^{i - 1,n + 1} ,C_{\text{S}}^{i - 1,n + 1} } \right)C_{{}}^{i - 1,n + 1} } \right) \\ & C_{\text{S}}^{i,n + 1} = \frac{{(S_{\text{w}} C_{\text{S}} )_{{}}^{i,n + 1} }}{{S_{\text{w}}^{i,n + 1} }} \ldots \\ \end{aligned}$$

(5)

In the above numerical equations, there is no explicit representation of dispersion. Equation (5) is usually used as the discretized version of Eq. (1) where there is no dispersion. However, Eq. (5) is a more precise representation of Eq. (1) where dispersivity is numerical and $\alpha_{{}} = v\Delta t + \Delta x$. Injector and producer wells were indicated by a source and sink term, respectively, in the cells for i = 1 and i = N_x. The scaling factor of ΔV was set to the volume of the grid cell to calculate injection rates.

First, we considered that there was no compositional variation, i.e., a single relative permeability function is used. The Buckley and Leverett (1942) equations were solved for waterflooding using the method of characteristics and the Welge tangent (Welge 1952) to derive the velocity of the saturation, $S_{\text{w}}^{\text{F}}$, at the front as:

$$\left. {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right|_{{S_{\text{w}}^{\text{F}} }} = \frac{{v_{\text{t}} }}{\emptyset }\left. {\frac{{\partial f_{\text{w}} }}{{\partial S_{\text{w}} }}} \right|_{{S_{\text{w}}^{\text{F}} }}$$

(6)

where $v_{\text{t}}$ is the total fluid flux for oil and water and f_w is the fractional flow. $S_{\text{w}}^{\text{F}}$ was derived from the fractional flow curve, plotted versus saturation, and a line was drawn from the minimum mobile water saturation to the fractional flow curve as a tangent (Welge 1952). The fractional flow at the front, $f_{\text{w}}^{\text{F}}$, was also obtained from this curve.

For chemical flooding on the other hand, two sharp fronts were formed. In normal and chemical waterflooding, the formation water is pushed ahead of the injected water and a front forms. In low salinity water flooding, the solute in the injected water releases oil and also for a given saturation, the formation water tends to be more mobile than the injected water. Thus, a second front occurred in the simulations which was coincident with the front of the injected solute in the absence of dispersion, capillary pressure and other spreading effects. The salinity front followed the advection equation but remained as a sharp front. This is the case for a typical sharp transition where the effective salinity range is narrow. If the effective salinity range is broad and there is dispersion (i.e., the salinity has a mixing zone), then the second front will be smoothed out.

Fractional flow theory has been extended for chemical flow. We ignore the details of the analysis here and refer to Patton et al. (1971) and Pope (1980) who derived the velocity of the concentration front:

$$\left. {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right|_{{S_{\text{w}}^{\text{C}} }} = \frac{{v_{\text{t}} }}{\emptyset } \times \frac{{f_{\text{w}}^{\text{C}} }}{{S_{\text{w}}^{\text{C}} + D}}$$

(7)

$S_{\text{w}}^{\text{C}}$ and $f_{\text{w}}^{\text{C}}$ are the saturation and fractional flow at the second front. D is a retardation effect accounting for a slowdown of the front. The impact of chemical retardation on fractional flow in 1D models has been discussed previously (Pope 1980; Borazjani et al. 2016; Khorsandi et al. 2017). This is usually due to some chemical reaction such as adsorption which depletes the transporting fluid of the active component. This occurs at the head of the injected water front. Once the active component has been reduced, a proportion of injected water then behaves more like the formation water. This results in a slowdown of the effective front and this retardation is then an effect of adsorption. This is not the only process that can cause the effective injected water front to be retarded. Purely physical processes such as dispersion may induce a similar retardation effect. Dispersion of the solute may occur as a result of fine-scale heterogeneity and capillary pressure, for example. In numerical models, we may also have significant numerical dispersion. We have presented evidence of this dispersion-induced retardation previously for LSWF simulations where salinity caused a change in wettability. (More details can be found in Al-Ibadi et al. 2018, 2019b.) The key to this effect is the range of chemical concentrations over which the wettability changes relative to the mixing zone created by dispersion. In LSWF, for example, the salinity must drop to a certain level before any effect is seen. If that level is below the midpoint of the formation and injected water salinities (i.e., it is in the trailing part of the mixing zone), then dispersion effectively slows down the effect of salinity. The critical salinity is reached after the time taken for an advection-dominated shock front to pass a point in the reservoir. The low salinity front is effectively retarded even though there is no removal of the solute. This is because a significant volume of the injected water has high enough salinity that it behaves like formation water. In such conditions, Eq. (7) may be used to predict the effective salinity front with D > 0. As a consequence to this, the volume of water with the properties of the formation water is increased, effectively, leading to a faster moving formation water front. On the other hand, if the critical salinity required to change wettability lies in the advanced part of the dispersion induced mixing zone, the effect is one of acceleration. Then, D < 0 in Eq. (7). In that case, the formation water front is slowed down. In this paper, we ignore adsorption of the salinity but this could be added to affect retardation. We leave verification of this to further work.

The saturations and velocity of the fronts were obtained by a similar solution to the waterflood problem (Fig. 3). The fractional flow curves of the formation water and the injected solution were plotted against saturation. If D is known, we can start at $S_{\text{w}}^{{}} = - D$ and draw a line as a tangent to the fractional flow curve for the injected solution. The point of contact gives $S_{\text{w}}^{\text{C}}$ and $f_{\text{w}}^{\text{C}}$. The line passes through the fractional flow curve for the formation water to give the saturation, $S_{\text{w}}^{\text{F}}$, and fractional flow, $f_{\text{w}}^{\text{F}}$, for the formation water front. If D is not known, then we can infer it by plotting fractional flow against saturation and then drawing the same tangent through the highest fractional flow and saturation value reached on the high salinity curve to the saturation axis. D is then given by the intercept with the saturation axis.

Fig. 3

a Relative permeability versus water saturation for LSWF as an example of chemical flooding and b the corresponding fractional flow. This can be used as a graphical method to estimate f_w and S_w at the formation waterfront and second chemical front. The gray, black and green lines are for cases with retardation (D > 0), zero retardation (D = 0) and acceleration, (D < 0), respectively

The velocity of the second waterfront is the same as for the solute as in Eq. (7) while the formation waterfront velocity is given as:

$$\left. {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right|_{{S_{\text{w}}^{\text{F}} }} = \frac{{v_{\text{t}} }}{\emptyset } \times \frac{{f_{\text{w}}^{\text{F}} }}{{S_{\text{w}}^{\text{F}} - S_{\text{wi}} }}$$

(8)

where $S_{\text{wi}}$ is the initial (irreducible) water saturation.

In LSWF, it is often observed that the change in wettability occurs over a relatively narrow range of salinity. The injected salinity must be less than the minimum of the range for the optimal results while the formation water salinity is often much larger. Thus, the midpoint of the effective salinity range, $C_{\text{d}}^{\text{mid-eff}}$, can be expressed in dimensionless form as the fractional distance between the injected salinity and the formation water salinity. If it is less than halfway, then dispersion therefore slows down the change of wettability relative to the shock front condition that is usually assumed in the analytical solution. This gives a physical retardation as described just above. In the case of numerical and physical retardation, D can be obtained (Al-Ibadi et al. 2019b) from the input data as:

$$D = \frac{{f_{\text{w}}^{\text{C}} }}{{\frac{{f_{\text{w}}^{\text{C}} }}{{S_{\text{w}}^{\text{C}} }} - \left( {\frac{\emptyset }{{v_{\text{t}} }}} \right) \left( {v_{\text{ref}}^{{}} - \left( {v_{\text{A}}^{\text{Mid}} + \left( {\left( {1 - C_{\text{d}}^{\text{mid-eff}} } \right)^{3} \times \frac{{\left( {v^{{{\text{F}}*}} - v^{{{\text{C}}*}} } \right)}}{{\sqrt {N_{\text{pe}} } }} } \right)} \right)} \right)}} - S_{\text{w}}^{\text{C}}$$

(9)

where $v_{\text{ref}}^{{}}$ is the velocity of the solute front for a reference case in which there is zero retardation;$v_{\text{A}}^{\text{Mid}}$ is the velocity that the true concentration, $C_{\text{d}}^{\text{mid-eff}}$, would travel in an imaginary situation where $C_{\text{d}}^{\text{mid-eff}}$ = 1 (in which case the wettability changes instantaneously). The advantage of this hypothetical condition is that we can obtain the solution analytically (for details, see Al-Ibadi et al. 2019b). $v^{{{\text{C}}*}} \,{\text{and}}\,v^{{{\text{F}}*}}$ are injected and formation water velocities, respectively, for the analytical solution with D = 0 in Eqs. (2) and (3) above, respectively; $N_{\text{pe}}$ is the Peclet number which reflects the ratio of advection rate to the dispersion rate. Thus, the advection velocity of the chemical waterfront for any given $C_{\text{d}}^{\text{mid-eff}}$ is as follows:

$$\left. {\frac{{{\text{d}}C_{\text{s}} }}{{{\text{d}}t}}} \right|_{{C_{\text{o}}^{{}} }} = \frac{{v_{\text{t}} }}{\emptyset }\frac{{f_{\text{w}}^{\text{C}} }}{{S_{\text{w}}^{\text{C}} }} - \left( {v_{\text{ref}}^{{}} - \left( {v_{\text{A}}^{\text{Mid}} + \left( {\left( {1 - C_{\text{d}}^{\text{mid-eff}} } \right)^{3} \times \frac{{\left( {v^{{{\text{F}}*}} - v^{{{\text{C}}*}} } \right)}}{{\sqrt {N_{\text{pe}} } }} } \right)} \right)} \right)$$

(10)

The impact of D on the graphical representation is illustrated in Fig. 3.

4 Analytical Solution of Fractional Flow Behavior in 2D Models

As we mentioned in the introduction, for single-phase flow in a non-communicating layered system, the flow capacity can be used to calculate the volumetric flow rate, $q_{\text{wi}}^{j}$, entering each layer, as follows:

$$q_{\text{wi}}^{j} = \frac{{\left( {kh} \right)^{j} }}{{\mathop \sum \nolimits_{j = 1}^{N} \left( {kh} \right)^{j} }} q_{\text{Ti}}$$

(11)

For two-phase flow cases, Lake (1989) present an equation to describe piston-like displacement for traditional water flooding. This is based on the work of Stiles (1949) and also Dykstra and Parsons (1950). In this case, we discuss the case of variable permeability and porosity such that high permeability layers will have earlier breakthrough indicating “faster layers.” Based on this (for details see Lake 1989), we can determine the frontal position of the low permeability layer at the time the fastest layer has breakthrough:

$$x_{\text{D2}}^{0} = \frac{{\left\{ {\left( { M^{\text{F}} } \right)^{2} + \frac{{1 - \left( { M^{\text{F}} } \right)^{2} }}{R}} \right\}^{{\frac{1}{2}}} - M^{\text{F}} }}{{1 - M^{\text{F}} }}$$

(12)

This was derived for models with the same relative permeability functions in each layer with:

$$R = \frac{{k_{1} \phi_{2} }}{{k_{2} \phi_{1} }}$$

(13)

$M^{\text{F}}$ is the ratio of total mobility across the shock front, since Eq. (12) was derived for piston-like displacement, such that $M^{\text{F}} = M^{\text{Fe}}$ where $M^{\text{Fe}}$ is the endpoint mobility ratio and can be calculated as:

$$M^{\text{Fe}} = \frac{{k_{\text{w}}^{\text{e}} \mu_{\text{o}} }}{{\mu_{\text{w}} k_{\text{o}}^{\text{e}} }}$$

(14)

Figure 4 shows the validity of these equations against the simulator results for two scenarios of permeability contrast at breakthrough time in the fast layer. The simulator result was obtained with a fine-scale grid which produced negligible dispersion. We see that the analytical solution matches the numerical result very well. Please note that in the results that follow where we compare the analytical solutions to the numerical models, the plots are obtained at the time of breakthrough in the fastest layer. This was defined based on the visual detection of a rise in saturation in the grid cells at the producer. It means that when we consider changing permeability contrast, the graphs are shown at different PVI.

Fig. 4

Numerical result against analytical solution to determine the location of waterfront (saturation) of the low permeability layer where the high permeability layer = 200 md and the low permeability layer was a 20 mD and b 100 mD. The results are shown at the time of breakthrough in the fast layer for each case

In order to extend this work to non-piston-like displacement, we use the term $M^{\text{Fe}}$ to be the ratio of total mobility across the formation water shock front for Buckley–Leverett displacement. For chemical flooding displacements, $M^{\text{F}}$ will be the ratio of total mobility across the formation waterfront. Thus, $M^{\text{F}}$ in Eq. (7) is:

$$M^{\text{F}} = \frac{{\lambda_{\text{t}}^{\text{F}} }}{{\lambda_{\text{t}}^{\text{o}} }}$$

(15)

where $\lambda_{\text{t}} \left( {S_{\text{w}} } \right)$ is the total mobility for any saturation:

$$\lambda_{\text{t}} \left( {S_{\text{w}} } \right) = \frac{{k_{\text{rw}} \left( {S_{\text{w}} } \right)}}{{\mu_{\text{w}} }} + \frac{{k_{\text{ro}} \left( {S_{\text{w}} } \right)}}{{\mu_{\text{o}} }}$$

(16)

and where $\lambda_{\text{t}}^{\text{F}} \equiv \lambda_{\text{t}} \left( {S_{\text{w}}^{\text{F}} } \right)$, the total mobility at the saturation of the formation waterfront and $\lambda_{\text{t}}^{\text{o}} \equiv \lambda_{\text{t}} \left( {S_{\text{wc}}^{{}} } \right)$, the total mobility ahead of the formation water for secondary recovery. $\lambda_{\text{t}}^{\text{o}}$ is simply the mobility of oil as the water mobility is zero for this saturation.

The next step is to determine the location of the chemical front in each layer. The fractional flow theory in 1D tells us that the velocities of the chemical and formation water shock fronts ($v^{\text{C}}$ and $v^{\text{F}}$, respectively) are related to each one other. We will use this principle to extend it to a 2D model by dividing Eq. (7) by Eq. (8) to get:

$$\frac{{\left. {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right|_{{S_{\text{w}}^{\text{C}} }} }}{{\left. {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right|_{{S_{\text{w}}^{\text{F}} }} }} = \frac{{v^{\text{C}} }}{{v^{\text{F}} }} = \frac{{\frac{{f_{\text{w}}^{\text{C}} }}{{S_{\text{w}}^{\text{C}} + D}}}}{{\frac{{f_{\text{w}}^{\text{F}} }}{{S_{\text{w}}^{\text{F}} - S_{\text{wi}} }}}}$$

(17)

We can eliminate the time in the velocity term above (since we calculate the location of each front at the same time). Thus, using dimensionless distance Eq. (17) will become:

$$x_{\text{Dl}}^{\text{C}} = \frac{{v^{\text{C}} }}{{v^{\text{F}} }}x_{\text{Dl}}^{\text{F}}$$

(18)

A similar form can be derived to predict the rarefaction wave, (i.e., the saturation distribution behind the chemical front) as follows:

$$x_{\text{Dl}}^{\text{R}} \left( {S_{\text{w}}^{\text{R}} } \right) = \frac{{\frac{{f_{\text{w}}^{\text{R}} }}{{S_{\text{w}}^{\text{R}} - S_{\text{w}}^{*} }}}}{{\frac{{f_{\text{w}}^{\text{F}} }}{{S_{\text{w}}^{\text{F}} - S_{\text{wi}} }}}}x_{\text{Dl}}^{\text{F}}$$

(19)

where $f_{\text{w}}^{\text{R}}$ is the fractional flow for any given saturation, $S_{\text{w}}^{\text{R}}$, behind the chemical front, and $S_{\text{w}}^{*}$ is given by intersect the tangent of $\left( {f_{\text{w}}^{\text{R}} , S_{\text{w}}^{\text{R}} } \right)$ in the $S_{\text{w}}$-axis. The graphical method of fractional flow can be used to estimate the fractional flow and saturations for both formation and chemical fronts (Al-Ibadi et al. 2019b) where $x_{\text{Dl}}^{\text{F}}$ is already calculable using Eq. (12) with $M^{\text{F}}$ obtained from Eq. (15).

We checked the precision and validity of these derived equations using the simulator to investigate both frontal velocities. Figure 5 shows the validity of using the mobility defined by Eqs. (15), (16) and (19) and substituted in Eq. (12) for water flooding as a Buckley–Leverett displacement. Figure 6 indicates the validity of using $M^{\text{F}}$ in chemical flooding to be defined as the ratio of total mobility across the formation shock front, i.e., the lead front in Fig. 6.

Fig. 5

Saturation along the model for Buckley–Leverett type displacement, plotted at the time of breakthrough in the faster layer. The numerical simulation result is compared to the analytical solution. All models had a high permeability of 200 mD while low permeability was a 20 mD and b 100 mD

Fig. 6

Saturation as a function of dimensionless distance along the model comparing numerical simulations and the analytical solution of the waterfronts for chemical flooding (low salinity water) and formation water. The high permeability layer is 200 mD while the low permeability is a 100 mD, b and c 20 mD. Results are shown at the time of breakthrough in the fast layer for each model. The timings are different for (a) compared to (b) and (c). Solid and dashed lines indicate the simulation results in the high and low permeability, respectively. Dotted lines indicate the analytical solution. In (c) the numerically defined dispersion coefficients were varied by changing cell size as indicated by different colored solid and dashed lines

For the chemical flooding cases, we first ran the simulator with zero chemical retardation, i.e., zero adsorption or desorption, and negligible physical retardation. The latter was achieved by assuming that wettability was altered along the active ion front. In other words, the effective salinity range was symmetric about the midpoint salinity of the injected and formation waters. We simulated wettability changes as a function of salinity but could have considered Ca²⁺ or Mg²⁺ directly just as easily. This approach is also applicable for any sort of chemical flooding such, as polymers or surfactants, in which the chemicals change the relative permeability. Figure 6 compares frontal positions for the numerical results as well as the analytical solutions obtained from Eqs. (18) and (19) for the chemical fronts (low salinity front in this case) and rarefaction wave, respectively. Equations (12) and (15) were used to obtain the formation waterfront. The match was good for the various scenarios of permeability contrast. The simulated formation water fronts were sharp. There is some spread in the salinity front, as a combination of the finite width of the effective salinity range combined with dispersion. The main location of the front was matched well though. The dispersion was varied by changing cell size (Fig. 6c) and in the absence of physical retardation, there was a good match for the midpoint of the various dispersed water fronts.

The equations above can be used to calculate the fronts in models with variable cross-sectional area, i.e., different width or height. This is because the location of the chemical front in each layer relative to the formation water location is solely affected by the relative mobility as defined by Eq. (18). Moreover, the location of the formation waterfront relative to the position of the formation water in the other layer is merely a function of petrophysical and wettability contrast that are defined by Eq. (12). The impact of changing thickness or width is to alter the flow capacity. Once we have adjusted that and we know the volumetric injection rate and total flux, then the rest of the equations can be applied. The result of changing the thickness alters the volumetric rate assigned to each layer and slows down the fronts. However, the relative effect is shared across fronts equally so that the ratio of velocities is unchanged. In Fig. 7, we examine a scenario where each layer was given a different thickness. We see that: (1) the analytical solution is still applicable, and (2) the frontal locations were the same as that in Fig. 6b. Figure 7 is shown at a different time compared to Fig. 6, but both were obtained at breakthrough in the fastest layer.

Fig. 7

Saturation plotted against dimensionless distance along the model comparing the simulator results to the analytical solution for models with different layer thickness where the thickness of high and low permeability layers was 100 and 50 ft, respectively. The results are shown at the time of breakthrough in the fastest layer. The high and low permeability values were 200 and 100 mD, respectively. Note that the front locations are identical to the models in Fig. 6a

5 Considering the Retardation Effect

We introduced the concept of the retardation or acceleration of the low salinity front in the text above along with the acceleration or retardation of the formation water front which may arise various chemical (e.g., adsorption) and physical (e.g., dispersion) processes. So far, we have examined models that had zero chemical or physical retardation effects. We now investigate this retardation or acceleration effect due to dispersion in the 2D model. We first show that the analytical model the fails to predict the simulated behavior (Fig. 8) then we show that we can amend these (Fig. 9) using the results observed previously (Al-Ibadi et al. 2019c). Changes to the velocity of the flood fronts are derived using the corrective term, D.

Fig. 8

Simulator results and analytical prediction of water front location for models with a various effective salinity ranges and Peclet number, $N_{\text{pe}}$ = 1000, b various $N_{\text{pe}}$ values but the same effective salinity range = [1000, 7000 mg/L] with apparent retardation and c the same effective salinity range [194,000, 200,000 mg/L] and various $N_{\text{pe}}$ which resulted in acceleration. Once again, the results are shown at the time of breakthrough in the fastest layer

Fig. 9

Saturation versus dimensionless distance comparing simulator results versus the analytical solution obtained by Eq. (18). Lines are organized as in Fig. 7, the high permeability has 200 mD, while low permeability has a 20 mD and b 100 mD. The results are shown at the time of breakthrough in the fast layer

Figure 8 shows simulations where the wettability was changed due to chemical flooding (LSWF) under various scenarios of effective salinity range. We reported previously that for models with a low midpoint concentration of the effective salinity range, a numerical and physical retardation effect was apparent (Al-Ibadi et al. 2018, 2020). On the other hand, acceleration was observed when the midpoint of the effective salinity range was close to the formation water salinity. We see this for the set of models in Fig. 8. For models where interaction happens across the whole of the salinity front, i.e., the effective salinity range covers all of the solute profile, there was negligible retardation or acceleration effect. Figure 8b represents various cases of dispersion coefficients where all have the same limited range of effective salinity range, i.e., 1000–7000 mg/L. We note that the retardation effect grew as dispersion was increased. Over all, the retardation effect in the 2D models was similar to that in the 1D model as described by (Al-Ibadi et al. 2019b). However, it is clear from Fig. 8 that retardation and acceleration render the calculation of the fronts by the analytical methods unreliable.

In order to better describe models affected by retardation analytically, Eq. (18) can be used to account for the retardation factor, D. We will now explore this approach with a particular case. We used the numerical result to give us the velocity ratio in Eq. (17) and applied this in Eq. (19). We then compared that to the analytical equivalent of Eq. (18). Table 2 shows the calculations from the simulator. $x_{\text{Dl}}^{\text{F}}$ and $M^{\text{F}}$ were obtained from Eqs. (12) and (18), respectively. In Table 3, we show the calculations for Eq. (18) to estimate the analytical values of the same data. f_w and S_w for each front were obtained graphically as in Fig. 3 and D was calculated using Eq. (9). The calculated positions match very well. Figure 9 shows the analytical solution of water saturation distribution that was obtained using Eq. (18). A good match with the numerical result was observed. However, for more dispersion-dominated coarse models (i.e., low N_pe) the saturation fronts tended to more spread out. The spreading was milder for the formation waterfront while dispersion combined with the finite width of the effective salinity front added to the spreading of the low salinity front. While this spreading was largely numerical in nature in this simulation, we consider the results to be fairly precise as we are using numerical dispersion to emulate physical equivalence. The main point, however, is that the fronts were predicted reasonably well by the analytical model even if their precise nature is not.

Table 2 Calculations of the location of the second fronts using Eq. (18) and velocities obtained directly from the simulator

Table 3 Calculations of the location of the second fronts using the analytical solution combined with the graphical method as illustrated by Eq. (15)

6 Application to Interlayer Variations in Relative Permeability

In this section, we consider models where the relative permeability was varied between layers in addition to the static petrophysical properties. This was equivalent to a situation where the wettability conditions were layer dependent. The numerical Peclet number, N_pe, was 1060 as for the base case. Figure 10 shows the various cases and the corresponding fractional flow curves are given in Fig. 11. In this part of the study, the relative permeability curves in Fig. 3a were always used to model wettability effects in the upper (high permeability) layer, in which there was zero retardation, i.e., the case with the black line in Fig. 3a. Relative permeability in Fig. 10a and b was used in various cases to represent the wettability change in the lower (low permeability) layer. The shape of the relative permeability curves is chosen carefully in order to examine several conditions as follows. First, we considered a scenario where both layers had the same ratio of total mobility, $M^{\text{F}}$, across the formation waterfront, but different mobility ratios on the chemical fronts in each layer. This was obtained by setting one layer to have relative permeability as in Fig. 3a and the other in Fig. 10a. Second, we investigated cases where relative permeability variations affected for both fronts in each layer. The relative permeability curves in Fig. 10b were used for the low permeability layers. These two approaches allow us to determine whether or not the ratio of total mobility is a key driver in the flow behavior. In the first case, the ratio of total mobility, $M^{\text{F}}$, is only varying between layers for the low salinity front. The relative permeability for the low salinity injection in Fig. 10b was chosen to represent a very strong change in wettability. The residual oil saturation was almost zero in this case to exaggerate the variation. Table 4 shows mobility across the formation water and chemical front under these scenarios.

Fig. 10

Relative permeability curves that were used to mimic alternative wettability behavior in the low permeability layer. The curves in Fig. 3a were used in the high permeability layer. The ratio of total mobility, $M^{\text{F}}$, across the formation waterfront is a the same as for Fig. 3a b different. The ratio of total mobility across the chemical induced front is different in both cases

Fig. 11

Fractional flow for the relative permeability shown in a Fig. 10a and b Fig. 10b

Table 4 Calculated front location for models interlayer variations in relative permeability

For the upper layer, the curves in Fig. 3a were used. Scenario 1 in Table 4 was obtained by using relative permeability curves in Fig. 10a and Scenario 2 using relative permeability in Fig. 10b. We first consider Scenario 1. At this point, for illustration, we also considered a situation where the layers had the same porosity and permeability. We note in Fig. 12a that the formation water in both layers had the same interstitial velocity while the chemical fronts did not. We consider this to be a coincidence. We then took the same model and used the relative permeabilities in Fig. 10b and examined the simulation output (Fig. 12b). In that case, all the fronts have different velocities.

Fig. 12

Simulator result of water saturation obtained at $x_{\text{D}}$ = 0.5 for both upper and lower layers where the relative permeability of the high permeability layer is given in Fig. 3a and the low permeability has relative permeability as in a Fig. 10a and b Fig. 10b

The ratio of total mobility across the formation waterfront, $M^{\text{F}}$, is the factor that should be considered in order to calculate the location of formation water in the low permeability layer relative to that in high permeability layer. Thus, Eq. (13) can be modified as:

$$R = \frac{{k_{1} M^{\text{F1}} \phi_{2} \Delta s_{\text{w2}} }}{{k_{2} M^{\text{F2}} \phi_{1} \Delta s_{\text{w1}} }}$$

(20)

where $M^{\text{F1}}$ and $M^{\text{F2}}$ are the ratio of total mobility of the formation waterfront, $M^{\text{F}}$, for each of the high and low permeability layers, respectively, as in Eq. (15). $\Delta s_{\text{w}}$ is the water saturation change which is $s_{\text{wf}} - s_{\text{wi}}$. We examined the validity of this form of the equation against the numerical results for models with the same relative permeability curve in each layer as well as petrophysical properties, as shown in Fig. 13. The ratios of total mobility across the shock fronts are obtained in graphical from Fig. 11 and are documented in Table 4. From Fig. 13 we see that the analytical solution matches the simulator results in both scenarios of the relative permeability functions.

Fig. 13

Simulator result versus analytical solutions for models with variations in relative permeability as well as contrasting petrophysical properties. The high and low permeability layers were 200 and 100 mD, respectively. The relative permeability for the low permeability layer was the same as in a Fig. 10a and b Fig. 10b

7 Generalizing the Frontal Locations for Multiple Layers

So far, the calculation of frontal locations has been shown for two-layer models. Here we extend the demonstration to multiple layers. This was done by redefining Eq. (20) to represent the heterogeneity contrast between any two layers in a multiple layer system, as follows:

$$R = \left( {\frac{{k M^{\text{F}} }}{{\phi \Delta s_{\text{w}} }}} \right)_{\text{h}} \left( {\frac{{ \phi \Delta s_{\text{w}} }}{{k M^{\text{F}} }}} \right)_{\text{l}}$$

(21)

the subscripts h and l are for high and low permeability layers, respectively. Equation (21) was used to calculate the locations of the fronts for any chosen layers. The high permeability layer had already seen water breakthrough in order to calculate the locations as given by Eq. (12). Figure 14 displays a model with five layers, each with unique permeability values. In such a model the water saturation profile, at the breakthrough time, will be as shown in Fig. 15.

Fig. 14

Sketch of a model with five non-communicating layers. Each layer has a unique horizontal permeability (k_x). All layers have the same relative permeability curves. As above, the layers are in communication via the wells

Fig. 15

Model with five non-communicating layers. The petrophysical properties are given in Fig. 14. The figure shows a the vertical permeability distribution and b simulated water profile at the breakthrough time

We could now perform the necessary calculation for such a multilayer model to predict the water profile and front locations at breakthrough time for the top layer. We used Eq. (21) to calculate R. Using Eq. (12) we calculated the corresponding location of the formation water in each layer, by using $M^{F}$ from Eq. (15). The chemical (second) shock front was calculated using Eq. (18). The analytical result is compared versus the numerical outcome are given in Fig. 16, where both are matched very well.

Fig. 16

Water saturation from simulator results (red solid lines) versus analytical solution (green dashed lines) for models represented in Figs. 14 and 15. In this case, there is no retardation effect as the effective salinity range spanned the injected to in situ salinities

8 Calculations of Breakthrough Time

Above, we calculated the location of each front in each layer. We also calculated the time that was required to achieve the frontal locations. In other words, the time of first breakthrough was derived along with other times such as breakthrough in each layer. Thus, we were able to calculate the velocity of the fronts in each layer using the frontal location and the time required to get there. Using the volumetric method, we calculated the dimensionless injection time, $t_{\text{D}}$, by using the following form:

$$t_{\text{D}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mathop \smallint \nolimits_{0}^{{x_{{{\text{D}}i}}^{\text{C}} }} S_{\text{w}} \phi A {\text{d}}x_{\text{D}} } \right)_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\phi A} \right)_{i} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\phi A x_{\text{D}}^{\text{C}} \bar{S}_{\text{w}}^{\text{C}} } \right)_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\phi A} \right)_{i} }}$$

(22)

where $t_{\text{D}}$ is the number of injected pore volumes (PVI), $\bar{S}_{\text{w}}^{\text{C}}$ is the average water saturation behind the chemical front as defined by (Welge 1952). By including the retardation effect, Eq. (21) was modified to:

$$t_{\text{D}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\phi A x_{\text{D}}^{\text{C}} \left( { \bar{S}_{\text{w}}^{\text{C}} + D} \right)} \right) _{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\phi A} \right)_{i} }}$$

(23)

where $D$ is the retardation factor that can be induced due to adsorption/desorption of the injected chemical component, such as in polymer and surfactant flooding, or due to the dispersion of the active ion as in LSWF. This led to a certain amount of the injected water retaining the mobility of the formation water, which is equivalent, in turn, to the amount lost or gained across the secondary waterfront. We examine the precision of these equations as shown in Table 5 for the two-layer models shown before where permeability was set to 200 and 20 mD in the upper and lower layers, respectively. It is observed that this analytical solution gave a good match to the numerical result even for complicated scenarios where there is a retardation effect and dispersion, with fractional error less than 6%. This minor misfit could be due to various sources including measurement error in detecting breakthrough in the fastest layer, precision of the calculation of D as well as precision of the calculation of fractional flows and saturations from the model and so on, in addition to small variations in the simulation result. Figure 17 shows a bar chart of the total difference between the calculated injected pore volume and the simulator result where we see a good match between them.

Table 5 Calculations of time breakthrough using the volumetric method

Fig. 17

Comparison of injected pore volume between the analytical solution using Eq. (23) and the numerical result

Calculations of breakthrough time can be used to predict the fractional flow profile versus time. The fractional flow change of each given saturation can be estimated graphically as in Fig. 3b, which will give the fractional flow of each layer. In order to obtain the total flow rate of the whole system, the fractional flow of each layer should be scaled to the ratio of total mobility at the formation water front, $M^{\text{F}}$. Thus, the total fractional flow of the system can be given as:

$$f_{\text{w}}^{\text{T}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {f_{\text{w}} Q_{\text{T}} } \right) _{i} }}{{Q_{\text{T,total}} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {f_{\text{w}} K A \bar{\lambda }_{\text{T}}^{{}} } \right) _{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( { K A \bar{\lambda }_{\text{T}}^{{}} } \right) _{i} }}$$

(24)

where ${\text{PV}}_{i}$ is the pore volume of i layer, $Q_{\text{T,total}}$ is the total flow across all layers (known), while $Q_{\text{T}}$ is the total flow rate within a given layer.$\bar{\lambda }_{\text{T}}^{{}}$ is derived based on Darcy’s law so that:

$$\bar{\lambda }_{\text{T}}^{{}} = \frac{L}{{\mathop \smallint \nolimits_{0}^{\text{L}} \lambda_{\text{Ti}} {\text{d}}x}}$$

(25)

Equation (23) can be utilized to estimate the time of the front progression. Figure 18 displays a comparison between calculated Fw and the simulator output for the model that is shown in Fig. 6a.

Fig. 18

Fractional flow versus time dimensionless for model given in Fig. 6a. The calculated F_w is shown in black dashed line while the simulator result is in red solid line

9 Solute transport—analytical solution

In addition to predicting the waterfront locations analytically, we predicted the solute mixing zone for cases with dispersion. In a 1D, homogenous, semi-infinite medium, solute transport in a single fluid can be predicted according to the advection–dispersion equation (e.g., Brigham 1974):

$$C_{\text{D}} = 1 - \frac{1}{2} {\text{erfc}}\left( {\frac{{x_{\text{D}} - t_{\text{D}} }}{{2\sqrt {\frac{{t_{\text{D}} }}{{N_{\text{pe}} }}} }}} \right)$$

(26)

This normalized concentration was 1.0 initially and zero in terms of injection. Other properties are dimensionless also. However, for chemical flooding such as LSWF, we accounted for two phases flowing, but also the effect of the physical retardation (Al-Ibadi et al. 2019d) as in Eqs. (4) and (5). In each layer, the solute transport was similar to that in 1D models (Shen et al. 2016), since there was no mix between layers due to crossflow. Thus, Eq. (26) can be updated for non-communicating layers to give the concentration at the producer in the ith layer:

$$C_{{{\text{D}},i}} = 1 - \frac{1}{2}{\text{erfc}}\left( {\frac{{x_{\text{D}} \left( {1 - S_{{{\text{or}},i}} } \right) - \left\{ { {\text{PVI}}_{i} + \Delta {\text{PVI}}_{i} \times \frac{{ \left( {1 - C_{{{\text{d}},i}}^{\text{mid-eff}} } \right)^{3} }}{{\sqrt {N_{{{\text{pe}},i}} } }} } \right\}}}{{\sqrt {\frac{{4\left( {1 - S_{{{\text{or}},i}} } \right){\text{PVI}}_{i} }}{{N_{{{\text{pe}},i}} }}} }}} \right)$$

(27)

We refer the reader to the (Al-Ibadi et al. 2019c) for explanation of this equation. It was assumed that residual oil affected flow by reducing the available pore space. PVI is the pore volume injected and equivalent to t_D assuming piston-like displacement. ΔPVI is the difference in pore volume injected between breakthrough of the formation and chemical fronts. $C_{\text{d}}^{\text{mid-eff}}$ will be zero for a passive tracer, and 0 < $C_{\text{d}}^{\text{mid-eff}}$ ≤ 1 for an active ion.

All factors in Eq. (27) were calculable and similar to that in 1D, while $v_{i}^{\text{C}}$ is the interstitial velocity of the chemical front. $v_{i}^{\text{C}}$ and $v_{i}^{\text{F}}$ can be calculated from fractional flow theory since we are able to calculate the location of chemical front in each layer using Eqs. (18) and (12), respectively. The time of breakthrough was calculated using Eq. (23).

To calculate $v_{i}^{\text{C}}$, we used the same method that was used in the 1D model, and as follows: $v_{i}^{\text{C}}$ and $v_{i}^{\text{F}}$ are the velocity of the reference case where $C_{\text{d}}^{\text{mid-eff}} = 0.5$, this was achieved by setting the effective salinity range to be $C_{\text{D}}^{\text{R-eff}} = \left[ {0, 1} \right]$. Calculations were made at breakthrough time as shown in Table 5. Figure 19 shows a good match of the analytical solution using Eq. (27) compared with the simulator results. The location of the midpoint of the effective salinity range,$C_{\text{d}}^{\text{mid-eff}}$, was also consistent with the low salinity water front that was determined analytically. We note here that the saturations are somewhat harder to match than above. First, dispersion has disturbed the saturation at the front. We presented previously (Al-Ibadi et al. 2018) that retardation can be so extreme that the formation water front can behave almost as if there is no low salinity effect. In such a situation, the saturation at the front tends to the Buckley–Leverett solution from the high salinity fractional flow curve. In the case in Fig. 19, this effect is small but barely noticeable in the fast layer. However, in the slow layer, the effect is stronger due to the lower Peclet number. The effect of dispersion is also time dependent diminishing as fronts approach the producer. The retardation correction term of Eq. (9) was determined at the producer well and may not be perfectly calibrated for the time at which the slow layer front is shown, adding to the further difference between the analytical and numerical results. We still consider approximation of the analytical solution to be a useful prediction though we acknowledge that it is at the limit of its application.

Fig. 19

Analytical solution of the salinity mixing zone versus simulator results for models affected by retardation and dispersion, where $N_{\text{pe}}$ = 66 and effective salinity range = [1000, 7000 mg/L]. The high permeability was 200 mD and the low permeability was a 20 mD and b 100 mD. Solid red and green lines indicate the water saturation in the low and high permeability layers, respectively. Analytical predictions of the fronts are indicated as dashed lines. The black and purple lines indicate the analytical solution for the mixing front, and these lie virtually on top of the lines from the simulator

10 Discussion

In this work we, considered models in which the petrophysical properties of the layers can vary in terms of both the static single-phase and two-phase properties, including the effect of salinity. We also considered the effect of physical and numerical retardation on fractional flow. We have developed an extension of the analytical solution of solute transport under such conditions. First, we have developed a mathematical formulation that can be used to calculate the location of formation waterfront in the lower permeability layers at the breakthrough time of the formation water in the layer of highest permeability. Then, we derived a mathematical formulation that can be used to predict the location of the chemical waterfront and the rarefaction wave relative to the formation waterfront. For many layers, the frontal positions can be derived as each layer sees water breakthrough to build up a picture of how the reservoir behaves. The analytical formulations were compared against a number of simulations with reasonably good results. A good approximation to the relative arrival time of the various fronts was obtained although some smearing of the fronts could not be matched. The arrival times required representation of the physical retardation that occurs due to dispersion.

The results of our model can be compared to those of Bedrikovetsky (1993), Hussain et al. (2012), Schmid et al. (2012). Those previous papers presented analytical solutions that enabled the tracking of the shock fronts by reducing the problem to a steady-state problem. In those cases, dispersion of the oil and water phases was represented by capillary pressure effects. Khorsandi et al. (2017) have extended these approaches to simulate chemically induced retardation with explicit representation of the chemical reactions in the equations. A major difference between those approaches and the ones shown here in this paper, however, is the existence of the effect of retardation on the salinity front as a result of the dispersion effect. While the other authors considered adsorption as a potential retarding process, dispersion has different effects which are harder to account for.

This work shows clearly the effect of interaction of factors that affect fluid movement, such as heterogeneity, fluid mobility, retardation effects that induced by adsorption, desorption, dispersion and diffusion hence predicting sweeping performance and invaded zone in each layer, where the need of such work is observed (Lake et al. 2014; Luo et al. 2017).

Based on the literature, there is a clear need to have analytical tools to predict fluid behavior. For example, we need to predict fluid flow behavior in EOR processes (Lake et al. 2014; Al-Shalabi et al. 2017) and to predict solute transport (De Zwart et al. 2011; Shen et al. 2016). This work can be used as a bench mark to extend work that has been done for 1D chemical flooding so that it is applicable in 2D non-communicating models, e.g., multi-component gas flooding (Johns et al. 1994), surfactant flooding (Walsh and Lake 1989), polymer flooding (Borazjani et al. 2016; AlSofi and Blunt 2013), low salinity and engineered water flooding (Jerauld et al. 2008; Al-Ibadi et al. 2019b), combined low salinity with polymer injection (Khorsandi et al. 2017), thermal flooding (Pope 1980) and other similar applications. This kind of analysis helps to analyze uncertainty for these processes at the reservoir scale, especially for emerging methods that are still under debate even at the core scale. For example, in low salinity water flooding, we may wish to estimate the impact of certain parameter such as effective salinity, adsorption, fluid mobility and heterogeneity. All of these factors are included in the analysis of this work, see Eqs. (7), (10), (15) and (18).

The analytical methods can also be used to assess the effect of crossflow in models with communicating layers (Alshawaf et al. 2017; Al-Ibadi et al. 2019a) which are perhaps more common. Further, evidence indicates that with fully communicating layers, when the mobility ratio across the formation water front, $M^{\text{F}} > 1$, then the flow is approximately similar to that in the non-communicating case (Al-Ibadi et al. 2019a). On the other hand for $M^{\text{F}} < 1$, the communicating and non-communicating layer cases are quite different. We leave the test of the analytical model in these cases to another paper.

One question is: can we extend this work to radial flow or a useful model that is more three dimensional in nature? Craig et al. (1955) used the Buckley–Leverett solution with the Welge tangent combined with an empirical model of areal sweep efficiency, obtained empirically, to predict breakthrough and subsequent flow for pattern floods of single and multiple layers. This was known as the Craig–Geffen–Morse method. More recently, Ling (2016) developed a radial fractional flow analysis and has been extended by Prakasa et al. 2019 for non-communicating layers. We then need to decide what is needed to extend this to chemical flooding. We would need to consider the fractional flow analysis more deeply. We would also need to calibrate the effect of dispersion on the physical retardation. The correction factor calculated for linear flow can be applied to the whole model while its behavior would be quite different for radial flow. This would obviously require some additional work.

Chemical flooding usually consists of a slug of solution chased by sea water. Continuous injection of the chemical is expensive. Optimizing the slug size requires suitable simulation or mathematical modeling tools (Attar and Muggeridge 2018). Given that fast models are often preferred, the analytical model derived here would serve as a suitable proxy model. For example, we were able to predict the amount of injected water in each layer as shown in Table 5 and the location of the salinity front as appears in Eq. (27) and shown in Fig. 19, where both those parameters can be important to predict the slug size in each layer. This could be extended to optimize the injected properties and is an area of interest for future work. Of course, slug flow is likely to experience dispersion at both ends of the displacement. The optimization may therefore require verification with a more sophisticated and precise full simulation. Otherwise, this extra effect may require calibration.

This work also has the potential to be used to create pseudo-relative permeabilities for coarsened grid models to mitigate the impact of numerical error. We have already investigated this for single-layer flow with good results (Al-Ibadi et al. 2018). The value of the model is that it can be applied quickly once set up and can then be used to create representative models for a range of scenarios and for uncertainty testing. Such approaches have been applied in the past for waterfloods but here we include some of the major effects on chemical waterflooding. This can be done by understanding the related fractional flow of each layer, as given in Fig. 11, thus one can create pseudo-relative permeability to ensure that fractional flow for the coarse grid scenario is similar to that in the fine case scenario, more details can be seen in (Al-Ibadi et al. 2018).

11 Conclusions

We present the following conclusions of this work.

• We have extended analytical models for waterflooding to include the effects of chemicals on wettability in reservoirs consisting of non-communicating layers.

• This models accounted for variations in static and dynamic petrophysical properties between layers.

• Models were tested against numerical simulations for various combinations of interlayer porosities, permeabilities and relative permeabilities as well as properties associated with the chemical flooding

• The distribution and arrival time of fronts was predicted quite well over a stack of layers while local smearing of the fronts was less well matched.

• Physical retardation via dispersion must be accounted for to obtain good predictions. We used a correction factor derived previously.

• Salinity profiles can be predicted analytically using a modified form of the solution to the one-dimensional advection dispersion model.

Appendix

Here we set out the model used for controlling wettability variation for LSWF that was used in this paper. Two sets of relative permeability tables (Fig. 3) were used to simulate fluid flow. One set was for the initial reservoir salinity condition which is more oil wet and the other set was to simulate reservoir conditions for the zone that was swept by low salinity water, which was more water wet. Moving from one set to another is salinity dependent and controlled using the “weighting function” which is expressed in linear form by:

$$\theta = 1 - \frac{{C_{\text{S}} - C_{\text{S}}^{\text{LS}} }}{{C_{\text{S}}^{\text{HS}} - C_{\text{S}}^{\text{LS}} }}\;\; {\text{for}}\;\;C_{\text{S}}^{\text{LS}} \le C_{\text{S}} \le C_{\text{S}}^{\text{HS}}$$

(A1a)

$$\theta = 1\;\;{\text{for}}\;\;C_{\text{S}} \le C_{\text{S}}^{\text{LS}}$$

(A1b)

$$\theta = 0\;\;{\text{for}}\;\;C_{\text{S}} \ge C_{\text{S}}^{\text{HS}}$$

(A1c)

where C^LS_S and C^HS_S define the effective salinity range. We define the midpoint of the effective salinity range as:

$$C_{\text{S}}^{\text{mid-eff}} = \frac{{C_{\text{S}}^{\text{LS}} + C_{\text{S}}^{\text{HS}} }}{2}$$

(A2)

and the domain of the salinity weighting function of Eq. (A1a) as:

$$C_{\text{S}}^{\text{R-eff}} = \left[ {C_{\text{S}}^{\text{LS}} , C_{\text{S}}^{\text{HS}} } \right]$$

(A3)

It is convenient to express the concentration or salinity in normalized units relative to C^formation_S and C^inj_S , the formation and injected water salinities, respectively:

$$C_{\text{d}} = \frac{{C_{\text{S}} - C_{\text{S}}^{\text{inj}} }}{{C_{\text{S}}^{\text{formation}} - C_{\text{S}}^{\text{inj}} }}$$

(A4)

We use subscript “d” in place of “S” to refer to normalized saturations for the threshold values and the midpoint salinities in Eq. (A1c). Thus,

$$C_{\text{d}}^{\text{mid-eff}} = \frac{{C_{\text{S}}^{\text{mid-eff}} - C_{\text{S}}^{\text{inj}} }}{{C_{\text{S}}^{\text{formation}} - C_{\text{S}}^{\text{inj}} }}$$

(A5)

$$C_{\text{d}}^{\text{LS}} = \frac{{C_{\text{S}}^{\text{LS}} - C_{\text{S}}^{\text{inj}} }}{{C_{\text{S}}^{\text{formation}} - C_{\text{S}}^{\text{inj}} }}$$

(A6)

$$C_{\text{d}}^{\text{HS}} = \frac{{C_{\text{S}}^{\text{HS}} - C_{\text{S}}^{\text{inj}} }}{{C_{\text{S}}^{\text{formation}} - C_{\text{S}}^{\text{inj}} }}$$

(A7)

C^LS_S and C^HS_S are defined in Eq. (A1) as upper and lower limits of the effective salinity range. Equation (A3) becomes:

$$C_{\text{d}}^{\text{R-eff }} = \left[ {C_{\text{d}}^{\text{LS}} , C_{\text{d}}^{\text{HS}} } \right]$$

(A8)

While Eq. (A1a) is linear, simulators allow nonlinear forms by inputting θ at each salinity as a table. We have examined nonlinear forms of this in (Al-Ibadi et al. 2019b). Based on Eq. (1), the salinity dependence of water relative permeability (k_rw) and oil relative permeability (k_ro) are given as:

$$k_{\text{rw}} = \, (1 \, - \theta )k_{\text{rw}}^{\text{HS}} \left( {S^{*} } \right) + \theta k_{\text{rw}}^{\text{LS}} \left( {S^{*} } \right)$$

(A9)

$$k_{\text{ro}} = \, (1 \, - \theta )k_{\text{ro}}^{\text{HS}} \left( {S^{*} } \right) + \theta k_{\text{ro}}^{\text{LS}} \left( {S^{*} } \right)$$

(A10)

where $k_{\text{rw}}^{\text{HS}}$ and $k_{\text{rw}}^{\text{LS}}$ are high and low salinity water relative permeabilities. Although ignored here, capillary pressure also depends on salinity as follows:

$$P_{\text{cow}} = \, (1 \, - \theta )P_{\text{COW}}^{\text{HS}} \left( {S^{*} } \right) + \theta P_{\text{COW}}^{\text{LS}} \left( {S^{*} } \right)$$

(A11)

water saturation at each concentration will be:

$$S^{*} = \frac{{S_{\text{w}} - S_{\text{or}} }}{{1 - S_{\text{wi}} - S_{\text{or}} }}$$

(A12)

S_or and S_wi are the effective residual oil and irreducible water saturations. These are also weighted in a similar fashion to Eqs. (A9)–(A11) and based on the low and high salinity values such that the relative permeabilities are end point shifted, effectively.