Introduction

The problem of chiral symmetry breaking in live matter or why life forms use only L enantiomers of amino acids and D enantiomers of sugars has been the subject of great scientific interest and extensive research since the discovery of enantiomers by Louis Pasteur more than 150 year ago. Many theoretical and experimental works were performed in this area, for example Frank 1953; Joyce et al. 1984; Kondepudi et al. 1985; Kauffman 1986; Avetisov and Goldanskii 1996; Steel 2000; Sandars 2003; Plasson et al. 2004; Saito and Hyuga 2004; Wattis and Coveney 2005; Weissbuch et al. 2005; Brandenburg et al. 2007; Plasson et al. 2007; Gleiser et al. 2008; van der Meijden et al. 2009; Kafri et al. 2010; Noorduin et al. 2010; Blackmond 2011; Blanco and Hochberg 2011; Hordijk et al. 2011; Coveney et al. 2012; Hein et al. 2012; Ribó et al. 2013; Konstantinov and Konstantinova 2014, 2018; Sczepanski and Joyce 2014; Brandenburg 2019.

One of the first and probably the most often cited theoretical works is Frank’s model (Frank 1953) where it was shown that autocatalytic synthesis coupled with mutual inhibition does result in chiral symmetry breaking. Later, the models based on catalytic networks (Sandars 2003; Wattis and Coveney 2005; Blanco and Hochberg 2011) were created. They advanced Frank’s model further into the world of polymers. These models are also based on a single chiral substance, which could form some longer polymer chains and where the longest homochiral polymer or some combination of homochiral polymers would catalyze the creation of the chiral substance from which the homochiral polymers are created. Mutual inhibition occurs when the enantiomer binds to some perfect homochiral polymer made from molecules of the opposite chirality.

Kauffman (Kauffman 1986; Steel 2000; Hordijk et al. 2011) introduced the notion of catalytic sets, where the set is autocatalytic as a whole, but each individual molecule in the set is not. This shows that mutual cooperation of molecules was also important in the early history of life on Earth. Further research with RNA molecules also showed that (Higgs and Lehman 2015). The most important difference between catalytic set models and symmetry breaking catalytic network models is that catalytic set models assume that there is small probability that any given molecule in the system might catalyze some arbitrary reaction and then apply statistical analysis to investigate the results, whereas catalytic network models explicitly set all rate coefficients. Hordijk et al. 2011 considered some estimates of probability that a random peptide is a catalyst and showed that for the value of probability p = 2 × 10−6 it is sufficient that each catalyst would catalyze 15 reactions for the autocatalytic set to emerge. The overall number of molecules in the whole set that they considered was 65,534. However, catalytic set models did not consider chiral symmetry breaking. Kafri et al. 2010 employed a catalytic set-like model (called C-GARD) with 100 enantiomer pairs of substances to study symmetry breaking. They used a lognormal distribution for enantiodiscrimination factor α Eq. (9) below and showed that when a standard deviation of such distribution increases, that results in higher enantiodiscrimination and subsequently in larger chances of broken chiral symmetry. However, they concluded that there might be some stochastic effect in play and that high enantiodiscrimination is necessary but not sufficient.

There are several statistical biases baked in into models of chiral symmetry breaking discussed above because there is an assumption that chiral substances “favor their kind” – a perfect chiral catalyst is more likely to create an amino acid (or, in general a chiral substance) of the same chiral symmetry and that attachment of the opposite chirality molecule to a perfect homochiral polymer of the opposite chirality effectively “kills” (or deactivates) it. While both phenomena are observed in Life now, we find it hard to justify them for early prebiotic Earth and especially when many substances are involved. In fact, Sczepanski and Joyce 2014, developed cross-chiral RNA polymerase where D-RNA enzyme catalyzes joining of L-mono or oligonucleotide substrates on a complimentary L-RNA template. This experiment is completely opposite to the assumption used in polymerization network-based models because the catalyst is made of molecules of opposite chirality.

Consider Sandar’s model in its modern form (as described e.g. in Blanco and Hochberg 2011) where most of the reactions are considered reversible. This model is based on the following set of reactions:

Synthesis:

$$ S\rightleftharpoons {L}_1,\kern0.5em S\rightleftharpoons {R}_1 $$
(1)

Catalytic synthesis:

$$ S+Q\rightleftharpoons {L}_1+Q,\kern0.5em S+P\rightleftharpoons {R}_1+P $$
(2)

and

$$ S+P\rightleftharpoons {L}_1+P,\kern0.5em S+Q\rightleftharpoons {R}_1+Q $$
(3)

where, S is some achiral “food” molecule, L1 and R1 are left and right enantiomers, and depending on the model, Q = LN, P = RN or \( Q=\sum \limits_{n=1}^Nn\ {L}_n \), \( P=\sum \limits_{n=1}^Nn\ {R}_n \) are some measures of left and right handed enantiopure polymers in the system and N is the maximum polymer length.

The polymerization in this model is described as follows.

$$ {L}_n+{L}_1\rightleftharpoons {L}_{n+1},\kern0.5em {R}_n+{R}_1\rightleftharpoons {R}_{n+1} $$
(4)

and chain-end termination as follows:

$$ {L}_n+{R}_1\rightleftharpoons {RL}_n,\kern0.5em {R}_n+{L}_1\rightleftharpoons {LR}_n $$
(5)

where 1 ≤ n ≤ N − 1. It is then interesting that Frank’s model can be “recovered” from the model above by setting N = 2, all rate coefficients in Eq. (4) equal to zero, and making Eq. (5) irreversible.

This model is powered by several explicitly chosen enantioselectivity coefficients. The first one is enantioselectivity of forward catalytic synthesis of amino acid (L1 and R1). It is often called fidelity of feedback (f) in polymerization network models.

$$ {\eta}_1\equiv f=\frac{k\left(S+Q\to {L}_1+Q\right)-k\left(S+P\to {L}_1+P\right)}{k\left(S+Q\to {L}_1+Q\right)+k\left(S+P\to {L}_1+P\right)} $$
(6)

where k(S + Q → L1 + Q) and k(S + P → L1 + P) are the rates of forward reactions Eqs. (2) and (3) correspondingly and the model assumes global Z2 symmetry, that is the system is left-right symmetric. Parameter f, which we here denote as η1 is the fidelity of the feedback, or, in other words, the enantioselectivity of the catalytic pair. Sandar’s model assumed that k(S + P → L1 + P) ≡ 0 and, therefore, η1 ≡ 1. Other models allowed imperfect enantioselectivity η1 < 1. However, this parameter may actually take values between −1 and 1. And if η1 < 0 (or even below some positive threshold number between 0 and 1) then symmetry breaking cannot possibly occur.

Experimental results show that the energy difference between catalytic reaction with two enantiomer catalysts is on the order of a few KJ/mol, which translates that enantiospecificity (the ratio of rate coefficients for reactions catalyzed by enantiomers) is ~ 1.5, which after substituting this value into Eq. (6) results that η1 ≈ 0.2 (Gellman and Ernst 2018). However, it was shown (Wattis and Coveney 2005) that larger values of η1 are required even when mutual inhibition reaction rate is twice as large as polymerization rate of same chirality polymers (\( \chi =\frac{k\left({L}_n+{R}_1\to {RL}_n\right)}{k\left({L}_n+{L}_1\to {L}_{n+1}\right)}=2 \)). Such a large value seems to be ruled out by experimental results (Hitz and Luisi 2004) where it was shown that polymerization of hydrophobic NCA racemates yields oligopeptides with higher degree of homochiral sequences than expected from binomial distribution. That implies that χ < 1, which, in turn, requires even larger value of η1. This experiment also confirms that attaching opposite chirality monomer to a polymer chain of opposite chirality does not deactivate it and the chain can continue to grow.

The second enantioselectivity coefficient is hidden in mutual inhibition reactions Eq. (5). The polymers RLn, LnR, RLnR (and their enantiomers) are treated as inert and that they do not participate in any reactions. There are several assumptions in that. First, amino acids may form several types of bonds. If peptide bond is considered, then L and R can be easily mixed in a peptide (Hitz and Luisi 2004). Thus, we would have to consider all possible combinations that can be formed from L and R and that some of them could be catalysts as well. The models considered above usually deal with that by assuming that polymerization happens on some surface or template. While simple chiral templates, like quartz are known to increase the likeliness of same chirality polymerization (Hitz and Luisi 2004) they seem to have far from perfect enantioselectivity. In addition, left-handed quartz is less than 1% more abundant than right-handed quartz and both are usually located at the same place, often in the form of various so-called twins. So, while that difference might help to account for the direction of the symmetry breaking, it cannot be the source of it. On another side, even more advanced organic templates (Rohatgi et al. 1996) are not completely perfect, but they would have to exist first before such template induced polymerization could occur.

Even if we assume that apart from peptide bond, L and R can form some other type of bond and that that bond deactivates the polymer, then concentrations of such deactivated polymers will keep increasing over time until the point that the assumption that they do not participate in any further reactions can no longer hold. In other words, we must account for deactivated polymers. It is possible, for example, to consider that these polymers are insoluble and leave the reaction area by e.g. falling to the ocean floor. However, only 5–10% of amino acids form highly insoluble diastereomeric salts. Serine is probably one of the best-known examples. A mixture of two solutions of L and D serine with approximate total quantities results in nearly 98% enantiopure solution of serine enantiomer with larger quantity (Blackmond 2011). Other amino acids do not exhibit such a large enantioselectivity. That means that apart from polymerization reaction, we would have to consider e.g. sedimentation reactions which, in an extremely simplified form, could be written as follows and with the assumption that sediment falls into the ocean floor with lower temperature and thus leaves the reaction area:

$$ {\displaystyle \begin{array}{c}R+{L}_n\to {C}_{RL_n}\downarrow \\ {}L+{L}_n\to {C}_{LL_n}\downarrow \end{array}} $$
(7)

where \( {C}_{RL_n} \) and \( {C}_{LL_n} \) are formed using some different type of bond than the bond used in polymerization and that they possess different solubility. We can then calculate enantioselectivity of this process as:

$$ {\eta}_2=\frac{k\left(R+{L}_n\to {C}_{RL_n}\downarrow \right)-k\left(L+{L}_n\to {C}_{LL_n}\downarrow \right)}{k\left(R+{L}_n\to {C}_{RL_n}\downarrow \right)+k\left(L+{L}_n\to {C}_{LL_n}\downarrow \right)} $$
(8)

To the best of our understanding, most catalytic network models assumed that \( k\left(L+{L}_n\to {C}_{LL_n}\downarrow \right)\equiv 0 \) making η2 ≡ 1. And while it is likely that a catalytic network made from only serine amino acids could have η2 ≈ 1, we are not aware of any catalyst made only out of serine amino acids of the same chirality and which would catalyze the production of serine of the same chirality. We shall note that the sedimentation process is far more complicated than described by Eq. (7). If only a handful of substances were involved, then we could use solubility product constants to determine which pairs of reagents would form a precipitate. However, if the number of substances measures in many thousands (if not many orders of magnitude more as in prebiotic soup) then describing sedimentation using solubility product constants becomes challenging even theoretically. First, the number of pairs to consider grows proportionally to the square of the number of substances in the solution. As the numbers are so large, it seems no longer possible to consider pairs as separate. Most likely some complex mixture would form a sediment. In addition, unless some pairs form nearly completely insoluble conglomerates, it is important to consider that solubility product constants of some pair, e.g. R + Ln exceeds some threshold. It was shown (Konstantinov and Konstantinova 2014) that enantioselectivity due to sedimentation in a more realistic scenario where all pairs are more or less soluble (not many order of magnitude soluble as in typical chemical problems involving a handful of solubility product constants) can work only in some window of concentrations.

Kafri et al. 2010 used enantiodiscrimination factor α instead of enantioselectivity factor η1:

$$ \alpha =\frac{k\left(S+Q\to {L}_1+Q\right)}{k\left(S+P\to {L}_1+P\right)} $$
(9)

It appears that the procedure used in their work to generate values of α based on the values of k(S + Q → L1 + Q) might have resulted in substantial bias because strong catalysts (catalysts with k(S + Q → L1 + Q) > μ + σ, where μ and σ are mean and standard deviation of the distribution of k(S + Q → L1 + Q)) were also very likely to be strongly and favorably enantioselective.

Therefore, it is important to note that such extended Frank’s models are powered by a bias in two enantioselectivity coefficients. The necessary though insufficient condition is that both must be positive for the symmetry breaking to have a chance to occur. We will call a chiral reaction (reaction involving chiral substances) favorable if it contributes to symmetry breaking (e.g. reaction Eqs. (2 and 3) with η1 > 0, reaction Eq. (7) with η2 > 0) and unfavorable if it inhibits it (e.g. η1 < 0). That means that if we randomly and with equal probability choose positive or negative values of η1 and η2, then we will get a model where symmetry breaking can occur only in 25% of the cases.

Another interesting phenomenon to consider is that long-term chiral term symmetry breaking can only occur in thermodynamically open systems (Plasson et al. 2007). If we consider a thermodynamically closed system, then a racemic state is the only possible stable state because it is the state with the maximum number of microstates and subsequently entropy. This can be easily illustrated considering backward reactions in Eq. (2 and 3). We can calculate the enantioselectivity of backward reaction as follows:

$$ {\overset{\sim }{\eta}}_1=\frac{k\left(S+{L}_n\leftarrow {R}_1+{L}_n\right)-k\left(S+{L}_n\leftarrow {L}_1+{L}_n\right)}{k\left(S+{L}_n\leftarrow {L}_1+{L}_n\right)+k\left(S+{L}_n\leftarrow {R}_1+{L}_n\right)} $$
(10)

The necessary condition for the symmetry breaking is that \( {\overset{\sim }{\eta}}_1>0 \), which means that when a backward catalytic reaction “destroys” an amino acid, it should destroy more molecules of the opposite kind. However, thermodynamic constraints require that equilibrium does not change in the presence of a catalyst, which leads to \( {\overset{\sim }{\eta}}_1\equiv -{\eta}_1 \) and, therefore, combined contribution of forward and backward reactions toward symmetry breaking is exactly zero when the system is in thermodynamic equilibrium. Consider reversible reactions Eq. (2 and 3). If the system is far from equilibrium (e.g. a pass-through system), then products of reaction (L1 and R1) participate in further reactions until some matters eventually leaves the reaction area due to mutual inhibition. That makes forward rate of synthesis and catalytic synthesis reactions higher (and in some cases even much higher) than a backward rate. Subsequently, we can ignore the contribution due to backward rate coefficient and set it to zero to simplify the analysis of the models, as was done in the original Frank’s and Sandar’s models.

The situation changes drastically when we consider that the number of substances and possible reactions among them during formation of life and transition to biological homochirality was extremely large. Subsequently, the choice of coefficients made by all models with a limited number of substances / reactions cannot be justified: unless we assume that all reactions are biased in some very specific way, once we consider a very large number of them, then favorable and unfavorable reactions should be on average statistically possible. In simple words, the necessary condition that the symmetry breaking could have a chance to occur can be written as:

$$ {\eta}_1>0,\kern0.5em {\eta}_2>0 $$
(11)

Our main concern and the ground of the current work is that this assumption is statistically biased. In other words, if we assume that η1 and η2 could independently take positive and negative values with equal probabilities then only one out of four randomly chosen values of η1 and η2 could potentially result in chiral symmetry breaking, as mentioned above. We will discuss this in more details further.

Another important factor to consider is that biological reactions include not only synthesis of amino acids but also their destruction. For example, amino acids, which are not used to build proteins, may be broken down. A typical process usually starts from deamination and then breaks amino acid in one of the several metabolic intermediaries. These reactions require several organic catalysts (enzymes). Zepik et al. 2001 constructed a model of minimal autopoietic “unit” where both synthesis and destruction reactions play equally important role to describe the evolution of the unit. Therefore, it seems important to accommodate catalytic destruction reactions into the models of symmetry breaking.

The Problem of Large Numbers

As discussed in the introduction, all models of chiral symmetry breaking, which consider a very limited number of substances and reactions, have to choose some favorable combination of parameters. What we mean is easier to illustrate using an example. Consider some organic catalytic reaction. As discussed in the introduction, such reactions (for example catalytic synthesis of amino acids) were considered in many works related to chiral symmetry breaking:

$$ X+\Gamma \rightleftharpoons Z+\Gamma $$
(12)

where Γ is some chiral catalyst, X is some achiral substance (food) and Z is some chiral substance, e.g. amino acid. We shall note that the actual amino acid synthesis reaction is not that simple, but this simplified consideration is used in most models and it is sufficient for illustrative purposes. As mentioned, the backward reaction may be effectively “turned off” due to inflow of energy and subsequent participation of the products of forward reactions in further reactions, so in order for the symmetry breaking to occur, such a reaction must have a chiral catalyst, which would have more chiral centers of the same chirality as the amino acid, which is produced by that reaction.

The main problem comes from the fact that, given the reaction Eq. (12), the following reaction must also be considered:

$$ X+\gamma \rightleftharpoons Z+\gamma $$
(13)

where \( \gamma \equiv \hat{E}\left(\Gamma \right) \) is the enantiomer of Γ. Subsequently, if reaction Eq. (12) does contribute to symmetry breaking, then reaction Eq. (13) is its inhibitor. The difference comes from rate multipliers. If catalyst Γ has larger or, better, much larger rate multiplier than catalyst γ:

$$ {k}_{\Gamma}>{k}_{\gamma } $$
(14)

then this pair is contributing to symmetry breaking, but if it is the other way around:

$$ {k}_{\Gamma}<{k}_{\gamma } $$
(15)

then the pair inhibits it. When we consider that the number of substances and reactions is very large, then the natural assumption is that favorable (inequality (14)) and unfavorable (inequality (15)) pairs of catalysts should occur nearly equally likely. Unfortunately, it is not possible to argue that all or at least a substantially larger number of catalytic pairs should be favorable. And, in fact, some of the well-known catalysts can be classified as unfavorable. Subsequently, with the absence of any arguments or experimental support that catalytic pairs are statistically biased toward favorable ones, the only reasonable assumption that we can make is that the mean enantioselectivity of a catalytic pair among all possible catalysts should be near zero.

We can then calculate the effective enantioselectivity of a collection of catalytic pairs present in the system near stationary (symmetric) point for some amino acid Z as follows:

$$ {\eta}_{eff}=\frac{\sum_{\Gamma}{\rho}_{\Gamma}\left(k\left(X+\Gamma \to Z+\Gamma \right)-k\left(X+\gamma \to Z+\gamma \right)\right)}{\sum_{\Gamma}{\rho}_{\Gamma}\left(k\left(X+\Gamma \to Z+\Gamma \right)+k\left(X+\gamma \to Z+\gamma \right)\right)} $$
(16)

where ρΓ ≡ ργ is the concentration of a catalyst Γ (and its enantiomer) and we sum over all available catalytic pairs. The situation gets even more interesting once we consider longer and longer peptides. If we consider that all ligation reactions have the same forward and the same backward rates, then, as discussed in e.g. Konstantinov and Konstantinova 2018, the distribution of sum of concentrations of peptides by length forms a geometric progression with some common ratio α < 1. However, the concentration of individual peptides falls much faster. If m is the number of amino acids and n is peptide length, then concentration of individual peptides of length n is on the order of:

$$ {\rho}_{m,n}\sim {\left(\frac{\alpha }{2\ m}\right)}^n $$
(17)

and if we consider mere 50 amino acids to account for some competition in the primordial “soup”, then increasing peptide length by one results in the drop in concentrations of individual peptides by at least two orders of magnitude. Given that catalysts have physical limit of the rate multiplier, that leads to a conclusion that contribution from very short catalysts is critical for the symmetry breaking or, in general, for any catalytic reactions, which were crucial for starting the transition from chemical to biological evolution. If we truncate the sum in Eq. 16 at peptides of length 3, then there are (2 × 50)3 = 106 potential catalysts and that number goes to 1010 for peptides of length 5. Taking an estimate of probability that random peptide is a catalyst as used by Hordijk et al. 2011: p~10−6 ÷ 10−5 leads to an estimate of the number of possible catalysts as ~100 ÷ 101 for peptides of length 3 and ~104 ÷ 105 for peptides of length 5.

Therefore, there are several completely different scenarios in regard to Eq. 16:

  1. 1.

    The value of α is small and the number of catalysts is very small as well. The contribution from very short peptides is important whereas longer peptides will make only very small contribution. Since the number of catalysts is very small, then some amino acids may have substantial positive effective enantioselectivity just “by chance”. For example, if we consider 4 random catalytic pairs with random enantioselectivity ±1 each, then there is a 31.25% chance that sum of these random catalytic pairs with the same concentrations would produce effective enantioselectivity of 0.5 or more. That number falls to 3.84% if there are 16 pairs of catalysts.

  2. 2.

    The value of α is small but the number of catalysts is large. Same as above, the contribution from very short peptides is important whereas longer peptides will make only very small contribution. However, since the number of catalysts is large, Central Limit Theorem (CLT) is likely to be applicable and that should result in expected value of ηeff ≈ 0.

  3. 3.

    The value of α ≈ 1 for short peptides. In fact, α ≡ 1 for short peptides was considered in a number of works. This is the regime where CLT is also likely to be applicable. While the concentrations of individual peptides in this regime falls \( \sim {\left(\frac{1}{2\ m}\right)}^n \) as peptide length m increases, the number of peptides of length m grows as (2 m)n. Therefore, contribution to denominator of Eq. 16 does not fall, whereas contribution to numerator becomes close to zero, as the length of peptides increases. Subsequently, expected value of ηeff should be close to zero as well, regardless the abundance of catalysts.

The first scenario seems to be the most interesting for the problems of chiral symmetry breaking and it the basis of research in the current work. There are two parameters that we varied.

The first one controls the chances that some peptide is a catalyst. We will call this parameter abundance rather than scarcity in the models considered below to maintain the meaning that if the value of parameter is small then the number of catalysts is small.

Catalytic set models (Hordijk et al. 2011) showed that catalysts must work on several reactions and, therefore, exhibit mutual cooperation. In fact, this is also observed in Life: a catalyst / resolving agent / enzyme / etc.… often works not just for a single reaction, but for some class (or a set) of similar reactions and / or organic substances. We will call this parameter similarity in the models considered below.

Symmetry Breaking among Amino Acids

Another interesting phenomenon, which can only be observed when the number of amino acids is large, is the symmetry breaking among amino acid themselves. When some subset of amino acids has favorable catalysts to support symmetry breaking between left and right ones, that results in higher concentrations of these amino acids, which, in turn, makes them better suited to compete for scarce substances, e.g. “food”. As a result, the concentrations of “unlucky” amino acids should decrease. To better see if this works as expected we made all linear coefficients (e.g. synthesis coefficients) the same for all amino acids.

Description of Models

The models that we run for the current work had 20 amino acids and maximum peptide length of 3. That makes the total number of amino acids and peptides equal to 65,640 once we account that each amino acid comes in two enantiomers (40 + 402 + 403 = 65,640). That, in turn, required solving system of ordinary differential equations (ODE) with 65,642 variables once we account for “food” and “waste”.

We will use:

  • Capital letters from A to T to describe left amino acids,

  • Small letters from a to t to describe right amino acids,

  • X to describe food,

  • W to describe waste,

  • Sequences of letters, e.g. AB, cdE, FgH to describe peptide chains,

  • Z and z to describe any left and right amino acid,

  • U or V to describe any peptide chain (amino acid, dipeptide, or tripeptide).

  • Γ to describe any catalyst and \( \hat{E}\left(\Gamma \right)\equiv \upgamma \) to describe its enantiomer. We considered that catalysts can only have length 3 and that any combination of three amino acids chosen from all 40 left and right ones could be a catalyst. Therefore, the total number of possible catalytic pairs is \( \frac{40^3}{2}=\mathrm{32,000} \).

A model is determined by various parameters of statistical distributions used to generate all coefficients and a random seed value. We called a collection of such parameters (without a random seed value) a default set. Subsequently, for each default set that we are interested in, we generated and ran many models using different seed values. Then we could compare, which default set was “better” by calculating how often symmetry breaking occurred within models produced by each set. In other words, a default set allows building different chemical reaction networks (models) randomly using some specific statistical distributions of all coefficients used in the model. However, once the model was built, we then solved it deterministically to check if the symmetry breaking can occur.

We shall note that, contrary to the common approach, it is not possible to provide all equations for each kinetic constant and it is also not possible to provide a name for each parameter because the number of such reactions and parameters is too large. Given that we used 20 amino acids (40 when accounted for left and right ones), there are 129,600 distinct reactions responsible for formation of peptide chains (half of that if we count only unique ones and then impose a global symmetry to get matching enantiomeric reaction) and there are potentially 2,560,000 catalytic synthesis reactions to choose from, of which the distributions “choose” somewhere between 200 to 2000 depending on the parameters. All rate coefficients are controlled by distributions. We used several simple standardized distributions and then we applied parameters, called threshold (p), scale (k), and shift (b) to transform them. Threshold parameter is effectively a success rate in binomial trials. It was used when we needed to choose pairs of amino acid and catalyst out of all possible pairs. Scale and shift transform a random value x generated by distribution as:

$$ y=k\ x+b $$
(18)

The following reactions were considered in the current work:

Synthesis and Catalytic Synthesis of Amino Acids

$$ X\rightleftharpoons Z,\kern0.5em X\rightleftharpoons z $$
(19)

and

$$ X+\Gamma \rightleftharpoons Z+\Gamma, \kern0.5em X+\upgamma \rightleftharpoons Z+\upgamma, \kern0.5em X+\Gamma \rightleftharpoons z+\Gamma, \kern0.5em X+\upgamma \rightleftharpoons z+\upgamma $$
(20)

where X is a food substance, Z is some amino acid, Γ is some chiral catalyst, and \( \upgamma \equiv \hat{E}\left(\Gamma \right) \) is its enantiomer. This is one of the reaction types, which we considered irreversible. If amino acids participate further in some other reactions, then they leave the reaction area thus making synthesis / catalytic synthesis effectively irreversible. Such a condition is easy to fulfill in the experiments and on a geological scale.

We used fixed value of 10−3 for forward reaction rate and 0 for backward reaction rate of reaction Eq. (19) and triangular distribution (with parameters a = c = 0, b = 3) and scale μ = 105 for the catalytic rate multiplier for the reaction Eq. (20). The value of threshold parameter (which is the same as abundance) was varied. Once a pair of amino acid + catalyst was chosen we then needed to choose the enantioselectivity of that catalyst and its enantiomer. In the current work we considered a simplified model that enantioselectivity can take values of ±0.95 with equal probability.

As a starting point we considered the following base values of abundance: a = 10 × 10−6 and similarity: s = 0.2. That value of a means that the average number of successes (pairs of amino acid + catalyst) was around 6.4. Since the symmetry multiplier is 4 (there are 4 reactions for each chosen pair), that means that the average number of catalytic reactions was about 26 in a given model with this value of abundance parameter and before similarity parameter was applied.

The similarity parameter controls how many other amino acids synthesis or destruction reactions (on average) a chosen catalytic pair can catalyze. Base value of similarity above means that there are on average 20% extra amino acids, which are similarly affected by a chosen catalytic pair. This means that average number of catalytic reactions was about 120–140 for the base value of similarity parameter. We used two different distributions for controlling the number of additional amino acids based on similarity parameter: binomial distribution and delta distribution. If delta distribution was used, then we choose exact number of similar amino acids (though the choice of actual amino acids was still random). And if binomial distribution was used then we performed Bernoulli trials with the success rate equal to similarity parameter. Delta distribution makes dependencies on similarity more precise, whereas binomial distribution seems to be better suited to model real course of events.

Finally, we needed to fix catalytic rates for all similar reactions. In the current work we consider that they all have the same values as the primary reaction. It is straightforward to consider more general models by replacing delta distribution used in current work by some other distributions.

Ligation

$$ U+V\rightleftharpoons UV $$
(21)

where U and V are some amino acid chains and UV is a longer chain. We used fixed values of 0.1 and 0.1 for all forward and all backward reaction rates. These values along with other parameters of the models make most of the matter accumulate at peptide length 3. That makes current consideration incomplete, as peptides would grow much longer with these values of parameters. While this is understandable, it was not the purpose of current research. On top of that it would be impossible to consider longer chains of 20 amino acids without exponentially increasing computation time.

Destruction and Catalytic Destruction of Amino Acids

$$ Z\rightleftharpoons W,\kern0.5em z\rightleftharpoons W $$
(22)

and

$$ Z+\Gamma \rightleftharpoons W+\Gamma, \kern0.5em Z+\upgamma \rightleftharpoons W+\upgamma, \kern0.5em z+\Gamma \rightleftharpoons W+\Gamma, \kern0.5em z+\upgamma \rightleftharpoons W+\upgamma $$
(23)

where W is some substance, which we can call “waste”, Z is some amino acid and Γ is some catalyst. This seems to be identical to the synthesis of amino acids. However, it is not the same. The main differences are as follows: we consider that the “waste” leaves the reaction area either as a gas or as a sediment and that it is possible to “destroy” an amino acid in many different ways while synthesis is just one very specific process. The fact that a “waste” substance leaves the reaction area makes originally reversible reactions Eq. (22) and (23) effectively irreversible. To complete the process, we also need to model how the waste is removed. There are two ways to do that. First, we can model that W actually leaves the reaction area:

$$ {\displaystyle \begin{array}{c}W\to W\uparrow \\ {}\mathrm{or}\\ {}W\to W\downarrow \end{array}} $$
(24)

That, in turn, would require introducing a constant inflow of food, as otherwise all food would be eventually consumed and transformed into waste. If this approach is taken, then the total amount of all substances in the system starts to depend significantly on the values of parameters. That has many drawbacks. First, if the total amount goes too high or too low, then either the solution time becomes too large or the symmetry breaking cannot possibly occur due to very small concentrations of reagents. Second, it becomes hard to compare the models because they will have different nonlinearity. Finally, as the total amount of matter in the system changes over time it becomes hard to come up with the integral(s) of motion and we need at least one to perform a sanity check that the numerical algorithm did not blow up. An alternative approach is to close the model by “recycling” the waste:

$$ W\to X $$
(25)

That creates an integral of motion – the total amount of matter in the system. We used this approach in the current work. The base values for all coefficients of reactions described by Eq. (22) and (23) used in the current work are the same as for synthesis / catalytic synthesis reaction described by Eq. (19) and (20), and the value for recycling coefficient was 0.1. In addition, this reaction takes the system into far from equilibrium state.

The system core can also handle catalytic ligation, racemization, catalytic racemization, and several other reaction types. None of that was included in the current work as we wanted to consider the simplest possible scenarios.

Description of Model Generation Process

We now illustrate the process using one of the default sets used in the current work. It is a set with the number 1000021002 (the reference to the code is: ClmFSharp (default set 1,000,021,002)). This set has the following parameters defined:

  • Synthesis of amino acids, Eq. (19) uses delta distribution (a distribution which generates only 0) with shift parameter equal to 0.001 for forward rate and 0 for backward rate. That will generate all k(X → Z) = k(X → z) = 10−3 and all k(X ← Z) = k(X ← z) = 0.

  • Catalytic synthesis of amino acids, Eq. (20) was not used for this default set.

  • Ligation, Eq. (21) uses delta distributions with shift parameters equal to 0.1 for both forward and backward rate. That will generate all k(U + V → UV) = 0.1 and all k(U + V ← UV) = 0.1 for all 129,600 reactions of peptide chain formations.

  • Destruction of amino acids, Eq. (22) uses delta distribution with shift parameter equal to 0.001 for forward rate and 0 for backward rate. That will generate all k(Z → W) = k(z → W) = 10−3 and all k(Z ← W) = k(z ← W) = 0.

  • Catalytic destruction, Eq. (23) uses triangular distribution, threshold value p = 0.0005 (abundance a = p · 106 = 50), scale equal to 100,000, similarity equal to 0.2 for rate multiplier, and bi-delta distribution (distribution, which generates ±1 with equal probability) with scale = 0.95 for enantioselectivity distribution. That means that \( \frac{p\ {N}_a\ {N}_c}{4}=\frac{0.0005\cdotp 40\cdotp {40}^3}{4}=32 \) of random pairs of amino acids (Na) and peptides of length 3 (Nc) was chosen for each generated model. The denominator 4 is used to account for enantiomers of amino acids and catalysts.

Let’s say that one of such chosen pairs was (a + Bcd) and that rate multiplier distribution generated value m = 50,000. The enantioselectivity distribution means that a random value of ±0.95 will be chosen with equal probability for that chosen pair of amino acid and catalyst. Let’s say that a value f =  − 0.95 was chosen. Then rate coefficients will be calculated as follows:

$$ {\displaystyle \begin{array}{c}k\left(a+ Bcd\to W+ Bcd\right)=k\left(a\to W\right)\cdotp m\cdotp \left(1+f\right)={10}^{-3}\cdotp \mathrm{50,000}\cdotp 0.05=2.5\\ {}k\left(a+ bCD\to W+ bCD\right)=k\left(a\to W\right)\cdotp m\cdotp \left(1-f\right)={10}^{-3}\cdotp \mathrm{50,000}\cdotp 1.95=97.5\\ {}\begin{array}{c}k\left(A+ bCD\to W+ bCD\right)\equiv k\left(a+ Bcd\to W+ Bcd\right)=2.5\\ {}k\left(A+ Bcd\to W+ Bcd\right)\equiv k\left(a+ bCD\to W+ bCD\right)=97.5\ \end{array}\end{array}} $$
(26)

The similarity parameter s = 0.2 means that \( \frac{s\ {N}_a}{2}=4 \) random additional amino acids of the same chirality will be chosen and that a chosen catalytic pair will catalyze their synthesis similarly as it does with the chosen amino acid. The distribution that controls rate multipliers for these similar reactions was also a delta distribution with shift = 1 which means all rate will be the same as for the chosen catalyst and its enantiomer correspondingly. Let’s say that amino acids e, g, h, and q were chosen. Then:

$$ k\left(e+ Bcd\to W+ Bcd\right)=k\left(g+ Bcd\to W+ Bcd\right)=k\left(h+ Bcd\to W+ Bcd\right)=k\left(q+ Bcd\to W+ Bcd\right)=k\left(a+ Bcd\to W+ Bcd\right) $$
(27)

and similarly, for all relevant enantiomer combinations.

Waste recycling, Eq. (25) uses rate coefficient k(W → X) = 0.1. This is just a single reaction, so no distribution was needed.

Solution Method

Due to statistical and computational challenges of dealing with large number of amino acids and reactions, we would like also to talk about solution method, algorithms, and the choice of computer languages used in the system.

The system of chemical equations has two scaling parameters: we are free to choose in which units we measure the concentration of substances and we are free to choose in which units we measure time. However, numerical calculations “behave” better when the values are centered near 1 (and a few orders of magnitude smaller or larger) and without extremes. That reduces the number of numerical rounding errors. Subsequently we found it convenient to “fix” the total scaled (dimensionless) concentration at around 10 and, given values of all other parameters, that resulted in a scaled (dimensionless) evolution time of around 250,000. This time was chosen by trials and errors and it allows the symmetry breaking to occur if it can occur in a model.

The system core was written in F#. It uses open source C# ALGLIB library (Bochkanov 2019) as a vector ODE solver, open source F# Plotly wrapper (Muhlhaus 2019) for generating interactive html charts, MSSQL Express Edition as a database, and local disk to store generated html charts. The code of the system is available as an open source: (Konstantinov and Konstantinova 2020a, b). We also tested vector ODE solver of ALGLIB library with up to a million variables and it seems to have a decent speed and precision. ALGLIB vector ODE solver implements Cash-Karp adaptive method, which is an explicit method. While it is sometimes argued that implicit methods are better for chemical equations, that, unfortunately, cannot work for the models that we considered. Using implicit methods would require inverting huge matrices (about 65,000 × 65,000 for the models used in the current work). So that would be approximately 65,000 times slower per step in comparison to explicit methods. In addition, as the number of computations is much larger (again it would be about 65,000 times larger) for implicit methods, the machine noise will increase substantially. We had a chance to work with reasonably smaller matrices (around 10,000 × 10,000) for some other projects in the past and such matrices required pushing the precision of calculations up to about 50–100 digits from natively supported of about 17 in order to achieve meaningful results. Given that such large precision is not directly supported by current processors, that would slow down implicit methods even further.

We used sparce matrices to describe models. For simpler models (3 amino acids and peptides up to length 3) we also generated F# code of the model and then compared that all the relevant calculations (vector derivative for the ODE and some totals) using the code and sparce matrices based approach used in the calculations are the same. We also examined the code of such smaller models by sight to ensure that it has correct global symmetry and for larger models we imported the model code into SQL table and run some queries to ensure that generated code has correct symmetries. While we can generate the code for models used in the current work, that results in huge files with typical file size of about 70-90 MB and somewhere between 1.5 to 1.8 millions of lines of code per model file. Such files cannot be compiled with the current compilers.

Once the model was generated, we used vector ODE solver provided by ALGLIB to solve the model for some small random initial values of all substances and some values of total initial concentration (called y0) and evolution time. The ODE solver is not very well parallelizable and so the only way to achieve maximum possible performance was to run many models in parallel while each model was running in a single thread. The models that we run for the current work had 20 amino acids and maximum peptide length of 3. A typical model run time for these parameters and chosen values of other parameters was from about a few hours to over a month with most of the models taking between one and three days to complete. We performed 50 runs for each default set that we used in this work.

Description of Results

Figures 1 through 4 below show the percentage of the models where symmetry breaking occurred for a given default set adjusted to use Wilson score interval with 95% confidence level (Wilson 1927):

$$ \frac{1}{1+\frac{z^2}{n}}\left(\hat{p}+\frac{z^2}{2\ n}\right)\pm \frac{z}{1+\frac{z^2}{n}}\sqrt{\frac{\hat{p}\left(1-\hat{p}\right)}{n}+\frac{z^2}{4\ {n}^2}} $$
(28)
Fig. 1
figure 1

Dependence of percentage of the models with symmetry breaking on abundance parameter ×106 for models with catalytic destruction (D), catalytic synthesis (S), both (DS), and sum of statistically independent catalytic destruction and synthesis (D + S)

Full size image
Fig. 2
figure 2

Dependence of percentage of the models with symmetry breaking on similarity for models with catalytic destruction (D), catalytic synthesis (S), and both (DS) for the value of abundance parameter a = 20 × 10−6

Full size image
Fig. 3
figure 3

Dependence of percentage of the models with symmetry breaking on similarity for models with catalytic destruction (D), catalytic synthesis (S), and both (DS) for the value of abundance parameter a = 50 × 10−6

Full size image
Fig. 4
figure 4

Dependence of percentage of the models with symmetry breaking on similarity for models with catalytic destruction (D), catalytic synthesis (S), and both (DS) for the value of abundance parameter a = 100 × 10−6

Full size image

where z ≈ 1.96 is the value that corresponds to 95% confidence interval, n = 50 is the number of trials (the number of models that we generated for each default set), and \( \hat{p}=\frac{n_s}{n} \) is the percentage of the models that have symmetry breaking (ns) out of number of trials (n). The bar shows the middle of the interval and the error bar shows lower and upper confidence limits. When lower confidence limit of Wilson score is zero that means that symmetry breaking has never been observed in that class of models.

Abundance Parameter

Figure 1 shows dependence of percentage of the models with symmetry breaking on abundance parameter ×106 for models with catalytic destruction (D – used Eq. 19, 21, 22, 23, 25 but did not use Eq. 20), catalytic synthesis (S – used Eq. 19, 20, 21, 22, 25 but did not use Eq. 23), and both (DS – used Eq. 19, 20, 21, 22, 23, 25). The similarity parameter was 0.2 and we used binomial distribution for controlling the number of additional amino acids in all models used to calculate the data for this figure. For comparison we also calculated a hypothetical scenario if D and S models were independent, and we consider the system with both. To do so we use the following formula:

$$ {p}_{D+S}=1-\left(1-{p}_D\right)\left(1-{p}_S\right) $$
(29)

where pD, pS, pD + S are the probabilities that S model, D model, and a model with independent S and D results in symmetry breaking.

There Are Several Interesting Observations:

First, the averaging of enantioselectivity does not occur only within some small range of abundance parameter. If the abundance parameter is too small, then the number of catalysts is (on average) too close to zero and since a linear system (a system without catalysts) cannot produce a symmetry breaking, then it just does not happen. However, if the abundance parameter becomes too large (and it seems that 200 × 10−6 is near that too large threshold for the models that we considered), then averaging kicks in and ensures that chiral symmetry breaking cannot occur.

Second, the models with both catalytic destruction and synthesis produce symmetry breaking more often than models with just catalytic synthesis or catalytic destruction. This was expected. However, what is more interesting is that curve where DS models can produce symmetry breaking seems to be slightly shifted to the right and has substantially higher maximum than a sum of statistically independent D and S models. This leads to a hypothesis that if the system has several non-linear channels of symmetry breaking (like D and S above), then it may have a higher chance of symmetry breaking in comparison to a sum of statistically independent channels.

Similarity Parameter

Figures 2, 3 to 4 below show dependency of the percentage of the models with symmetry breaking on the similarity parameter for models with catalytic destruction, catalytic synthesis, and both catalytic destruction and catalytic synthesis for different values of abundance parameter. The similarity parameters for D and S parts of DS models were changed simultaneously, and we used delta distribution for controlling the number of additional amino acids for all considered here models.

The Following Observations Can Be Made Analyzing these Figures:

When the value of parameter a is small (a = 20 × 10−6), the dependency on similarity looks like a wide bell curve with zero or nearly zero percentage of symmetry breaking models at values s = 0 and s = 1. The statistical resolution does not seem sufficient to perform conclusion about the peak (which can be called the most suitable similarity value for symmetry breaking). It looks that the value of around 0.4–0.5 corresponds to that peak.

The situation changes as the value of a increases. For a = 50 × 10−6, DS models seem to have a reasonably clear peak at around s = 0.2, which changes to around s = 0.1 for a = 100 × 10−6. We were unable to perform sufficient statistical resolution for a = 200 × 10−6 due to prohibitive computation times of these models. However, approximate results show that the curve keep shifting toward s = 0 until symmetry breaking completely disappears.

As parameter a increases, S models seem to be running faster toward s = 0, followed by D models and then followed by DS models. Which mean that DS models benefit from having some groups of similar reactions in a larger interval of similarity parameter and over a larger interval of abundance parameter. In other words, adding the second nonlinear channel of potential symmetry breaking increased the range of parameter space and the probability that the symmetry breaking can occur as well as made it more beneficial to have groups of similar reactions.

Best Similarity Value

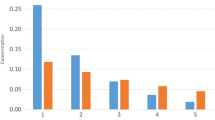
All charts on the Figs. 2 to 4 above (with the exception of S model, which seems to have two peaks for a = 20 × 10−6) look like bell shapes defined on the interval [0, 1]. It is therefore interesting to ask a question about what are the best similarity value and the width of the peak for a given class of model and some value of abundance parameter. To do so we calculated weighted average of the similarity and width:

$$ \overline{s}=\frac{\sum_{s_i}{s}_i\ {p}_i}{\sum_{s_i}{p}_i},\kern0.5em {\sigma}_s=\sqrt{\frac{\sum_{s_i}{\left({s}_i\right)}^2\ {p}_i}{\sum_{s_i}{p}_i}-{\left(\overline{s}\right)}^2} $$
(30)

Where si = 0.0, 0.1, 0.2, …1.0 are the values of similarity parameter for which we performed the calculations and pi is the probability estimate that the symmetry breaking occurred for a given value of si. Each pi is just the ratio of the models where we observed the symmetry breaking to the total number of models with a given value of si. The results are shown on Fig. 5.

Fig. 5
figure 5

Dependence of best similarity value (weighed average) and width of the peak (shown as error bars) for models with catalytic destruction (D), catalytic synthesis (S), and both (DS) for different values of abundance parameter

Full size image

When the abundance parameter is small (a = 20 × 10−6), the best similarity value is around 0.5. This means that catalysts are very scarce and due to a statistical chance some models just happen to have symmetry breaking. However, as the abundance parameter increases it becomes beneficial to form smaller and smaller groups. For example, for a = 50 × 10−6 the best result is achieved if catalysts are split in approximately 4 groups for DS models. The most favorable number of groups goes up to about 6 for a = 100 × 10−6. It is then interesting that real amino acids do form groups due to some similar properties.

Sample Runs

Figures 6 and 7 below show a sample run for the model where symmetry breaking occurred. It is a DS model with both similarity parameters equal to 0.2 and both abundance parameters equal to 50 ×10−6. The letters A through T and a through t on the figures are concentrations of left and right amino acids.

Fig. 6
figure 6

Dependence of enantiomeric excess over time for all 20 amino acids in one of the sample models

Full size image
Fig. 7
figure 7

Dependence of total concentration over time for all 20 amino acids in one of the sample models

Full size image

The following can be noted. The symmetry breaking results in different enantiomeric excess for different amino acids with some having positive and some having negative sign. This was standard and it was observed in almost all, if not all models that we calculated and which had symmetry breaking.

Amino acids called A and I had the highest concentrations prior to the symmetry breaking. However, after it occurred, amino acid B started to have the highest concentration. Other amino acids also experienced significant change up or down near symmetry breaking point. This is very interesting because it shows that symmetry breaking also affects the ability of groups of amino acids to cooperate and then compete for scarce resources as a group. It looks that B amino acid along with several others formed a group, which was better suited to “fight” against other amino acids. Subsequently, that group stated to have higher concentrations after symmetry breaking point, which means that they would be able to build longer peptides and then find better catalysts so that to drive others to extinction. Such calculations would require considering longer peptides and it is currently beyond our reach.

Conclusion

It was argued that the number of different organic molecules, including organic catalysts must have been very large on prebiotic Earth. Average enantioselectivity of catalysts was considered and it was shown that there are several scenarios in which Central Limit Theorem is likely to be applicable and that in such scenarios chiral symmetry breaking is very unlikely to occur. A scenario when good catalysts (among all possible catalysts) are very scarce and they act similarly on some subsets of amino acids was considered. It was argued that some amino acids could have substantial positive effective enantioselectivity just “by chance” in such a scenario.

Far from equilibrium models with 20 amino acids and peptides up to length three were considered. It was shown that when the catalysts are very scarce, such systems do exhibit chiral symmetry breaking, though not in 100% cases. It was shown that having two channels of catalytic reactions substantially increases the chances of symmetry breaking in such systems. It was shown that such models have a range of abundance and similarity parameters where symmetry breaking can occur. It was also shown that if the number of catalysts increases, then effective averaging becomes too strong and symmetry completely disappears. It was argued and then shown that when the enantiomeric symmetry breaking occurs in large systems it should also result in the symmetry breaking among amino acids themselves due to cooperation among some amino acids and competition among some groups of amino acids.