The vibro-impact capsule system in millimetre scale: numerical optimisation and experimental verification

Abstract

The vibro-impact capsule system has been studied extensively in the past decade because of its research challenges as a piecewise-smooth dynamical system and broad applications in engineering and healthcare technologies. This paper reports our team’s first attempt to scale down the prototype of the vibro-impact capsule to millimetre size, which is 26 mm in length and 11 mm in diameter, aiming for small-bowel endoscopy. Firstly, an existing mathematical model of the prototype and its mathematical formulation as a piecewise-smooth dynamical system are reviewed in order to carry out numerical optimisation for the prototype by means of path-following techniques. Our numerical analysis shows that the prototype can achieve a high progression speed up to 14.4 mm/s while avoiding the collision between the inner mass and the capsule which could lead to less propulsive force on the capsule so causing less discomfort on the patient. Secondly, the experimental rig and procedure for testing the prototype are introduced, and some preliminary experimental results are presented. Finally, experimental results are compared with the numerical results to validate the optimisation as well as the feasibility of the vibro-impact technique for the potential of a controllable endoscopic procedure.

1 Introduction

Inspired from inchworm’s locomotion, self-propelled mobile mechanisms driven by autogenous internal force and environmental resistance have attracted great attention from applied mathematicians, experimentalists and engineers because of their theoretical challenges as piecewise-smooth dynamical systems and broad applications in robotics, e.g. [1]. The original idea of the self-propelled driving was pioneered by Chernousko [2, 3]. He proposed a two-mass system to move progressively in a resistive medium when the two bodies performed periodic motions relative to each other [4]. By adopting this idea, the small body can be encapsulated in the large body and is excited in a controlled manner. Once the net force of their interaction is greater than the environmental resistance, rectilinear motion of the entire system can be obtained. To implement this, various driving means for the small body were proposed by researchers, such as vibration-driven [5, 6], vibro-impact driven [7,8,9,10], and pendulum-like driven [11,12,13]. The common feature of these methods is that the small body needs to be controlled precisely in order to obtain a desired motion for the entire system. However, to control the motion of the small body within such a limited traveling space is extremely challenging if the entire system is in millimetre or micro scale.

The vibro-impact capsule system studied in the present work was proposed to address the precise control issue in a limited space. The basic idea is to simplify the motion control of its inner mass (i.e. the small body) by employing a harmonic or a square-wave excitation, while fully understanding the dynamics of the system to ensure an efficient performance in terms of its progression direction and speed. Since the vibro-impact capsule involves two nonlinearities, namely friction and impact, its near-grazing dynamics and friction-induced oscillations may induce abundant coexisting attractors and cause complex phenomena. This has driven the research work of the capsule system to two major directions. For one hand, to consider it as a piecewise-smooth dynamical system, many researchers studied the complex dynamics of the capsule system. For example, Páez Chávez et al. studied the dynamical response of a piecewise-linear capsule system by means of path-following techniques [14]. Liu and Páez Chávez [15] explored the multistability and applied a position feedback controller for directional control of the vibro-impact capsule system. Fang and Wang [16] investigated the resonance and bistability of two piezoelectric vibration-driven locomotion systems. In [17], Gu and Deng studied the dynamical response of a vibro-impact capsule system with Hertzian contact and random environmental perturbation. On the other hand, a lot of studies have focused on the prototype development of the vibro-impact capsule system for some specific practical applications, such as pipeline inspection [18,19,20], gastrointestinal capsule endoscopy [21], and ground moling [22]. The present study in this paper is to report our recent progress on scaling down the prototype design of the vibro-impact capsule system to a standard dimension for gastrointestinal capsule endoscopy, which is 26 mm in length and 11 mm in diameter. This dimension refers to the market-leading capsule endoscope, $\hbox {PillCam}^{\mathrm {TM}}$ SB 3 Capsule [23].

The principle of our proposed driving method is that the rectilinear motion of the capsule can be generated using a periodically driven internal mass interacting with the main body of the capsule as a “hammer”, in the presence of external resistances. Inspired from the “hammer” drilling [24, 25], the entire capsule will be progressing at its maximum during the resonance of the “hammer”. The merit of such a capsule is its simplicity in mechanical design and control which does not require any external driving accessories, while allowing independent movements in a complex environment. The study of this method was initiated from mathematical modelling [7, 8, 26, 27], early proof-of-concept investigation [28], multistable dynamics control [15, 29], to our recent capsule-intestine contact modelling [30], intestinal friction study [31] and mesoscale demonstration [32, 33]. Since the mathematical model of the system belongs to the class of piecewise-smooth dynamical systems, for this type of systems, the state space can be divided into disjoint subregions [34]. Therefore, path-following methods [14] by using the specialised continuation tool COCO was employed in the current work for the numerical study of the system, and then with experimental verification.

The numerical investigation in the present work will be carried out using the path-following software COCO (short form of Computational Continuation Core [35]). This is an analysis and development platform for the numerical treatment of continuation problems using MATLAB. A notably useful feature of COCO is its set of toolboxes that covers, to a large extent, the functionality of classical continuation packages, such as AUTO [36] and MATCONT [37]. In particular, in this work we will make extensive use of the COCO capability for the numerical continuation and bifurcation treatment of periodic orbits for non-smooth dynamical systems. In this way, we will be able to locate codimension-1 bifurcations of limit cycles and then trace such bifurcations in two parameters. This approach has been extensively used in previous works, for instance in [14], where the authors utilise path-following techniques to unveil the complex bifurcation scenario of a preliminary capsule model, with focus on multistability and directional control.

The contributions of this paper are threefold: (1) The prototype of the vibro-impact capsule system was developed at the standard millimetre scale to prove the feasibility of utilising the vibro-impact self-propulsion technique for small-bowel endoscopy; (2) A generic mathematical model and the computational platform COCO were adopted to analyse the dynamics of the prototype and to optimise its progression speed and propulsive force; (3) Experimental results demonstrated the validity of the mathematical model and the numerical optimisation, so an optimum parametric regime in terms of the excitation frequency and duty cycle was obtained.

The rest of the paper is organised as follows. In the next section, the components and the physical model of the prototype are introduced, and its mathematical formulation as a piecewise-smooth dynamical system is studied in order to carry out numerical analysis by means of path-following techniques. In Sect. 3, numerical optimisation of the prototype in terms of its progression speed and propulsive force is carried out. In Sect. 4, experimental setup and procedure are introduced, and experimental verification of the mathematical model is presented. Finally, in Sect. 5 some concluding remarks are drawn.

Fig. 1

(Colour online) a External and b internal views of the prototype [31]

2 Mathematical modelling

2.1 Prototype

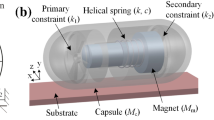
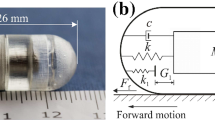
The standard-sized capsule prototype, which is 26 mm in length and 11 mm in diameter, is shown in Fig. 1a where a capsule was manufactured by using a stereolithography 3D printer to produce a high-quality inner structure, including two impact constraints and a linear bearing. The linear bearing holds a T-shaped NdFeB magnet made up by two small magnets in different lengths and diameters as shown in Fig. 1b, and restricts the motion of the magnet in a linear manner. A helical spring connecting the magnet and the bearing was used to push the magnet back to its original position after each external excitation. The two impact constraints, namely the primary and the secondary constraints, restrict the linear motion of the magnet in a limited distance, as well as magnify the propulsive force on the capsule.

2.2 Equations of motion

Conceptual design and physical model of the prototype are presented in Fig. 2, where $M_\mathrm {c}$ and $M_\mathrm {m}$ are the masses of the capsule and the magnet, respectively. k and c represent the stiffness of the helical spring connecting the magnet and the capsule and the damping coefficient of the energy dissipation led by the relative speed between the capsule and the magnet, respectively. The springs with stiffness $k_1$ and $k_2$ represent the primary and the secondary constraints, and their gaps between the magnet and the constraints are $G_1$ and $G_2$, respectively. $X_\mathrm {c}$ and $X_\mathrm {m}$ are the displacements of the capsule and the magnet, and their velocities are $V_\mathrm {c}$ and $V_\mathrm {m}$, respectively. The friction between the capsule and the synthetic small intestine is modelled as a Coulomb friction with the friction coefficient $\mu$. It is worth noting that although the intestinal friction when the capsule moved on a flat cut-open intestine was identified experimentally as a function of capsule’s velocity in [31], i.e. $8.778V_{\mathrm {c}}^{0.25}+2.518$, the dynamics of the prototype under this friction model was almost the same as the one under the Coulomb friction. So we will use the latter in the present work for simplicity in optimisation by means of path-following techniques.

Fig. 2

a Conceptual design and b physical model of the prototype

The considered system operates in bidirectional stick-slip phases which contain the following four modes: stationary capsule without impact, moving capsule without impact, stationary capsule with impact and moving capsule with impact. All these modes can be modelled via the following equations of motion

$$\begin{aligned} \left\{ \begin{array}{lll} M_\mathrm {m}{\ddot{X}}_\mathrm {m}&{}=&{}F_\mathrm {e}-F_\mathrm {i},\\ M_\mathrm {c}{\ddot{X}}_\mathrm {c}&{}=&{}F_\mathrm {f}+F_\mathrm {i}, \end{array} \right. \end{aligned}$$

(1)

where $F_\mathrm {e}$ is the external excitation, $F_\mathrm {f}$ is the friction acting on the capsule, and $F_\mathrm {i}$ represents the interaction force between the capsule and the magnet written as

$$\begin{aligned} F_\mathrm {i}=\left\{ \begin{array}{ll} kX_\mathrm {r}+cV_\mathrm {r}+F_2, &{\quad} X_\mathrm {r} \le -G_2,\\ kX_\mathrm {r}+cV_\mathrm {r}, &{\quad} -G_2 \le X_\mathrm {r} \le G_1,\\ kX_\mathrm {r}+cV_\mathrm {r}+F_1, &{\quad} X_\mathrm {r} \ge G_1. \end{array} \right. \end{aligned}$$

(2)

Here, $X_\mathrm {r}=X_\mathrm {m}-X_\mathrm {c}$ and $V_\mathrm {r}=V_\mathrm {m}-V_\mathrm {c}$ represent the relative displacement and velocity between the magnet and the capsule, $F_1=k_1(X_\mathrm {r}-G_1)$ and $F_2=k_2(X_\mathrm {r}+G_2)$ represent the interaction forces for the front and back impacts, respectively. In this study, the frictional force between the capsule and the synthetic small intestine is given as

$$\begin{aligned} \left\{ \begin{array}{lrl} F_\mathrm {f}\in [-P_\mathrm {f},\,P_\mathrm {f}],&{} &{}V_\mathrm {c}=0,\\ F_\mathrm {f}=-\mathrm {sign}(V_\mathrm {c})P_\mathrm {f},&{} &{}V_\mathrm {c}\ne 0, \end{array} \right. \end{aligned}$$

(3)

where $P_\mathrm {f}=\mu (M_\mathrm {m}+M_\mathrm {c})g$ is the static friction of the prototype, and g is the gravitational acceleration. The external excitation, $F_\mathrm {e}$, is a rectangular waveform signal written as

$$\begin{aligned} F_\mathrm {e}(t)=\left\{ \begin{array}{ll} P_\mathrm {d}, &{} t \in [nT,\,nT+DT], \\ 0, &{} t \in (nT+DT,\,nT+T), \end{array} \right. \end{aligned}$$

(4)

where n is the period number, $P_\mathrm {d}$, T and $D \in (0,1)$ are the amplitude, period and duty cycle ratio of the signal, respectively.

It should be noted that the above model has been reported in [32] where a mesoscale capsule prototype, 56.9 mm in length and 19.4 mm in diameter, was studied. The model was verified on different contact surfaces, and thanks to the relative large dimension of the prototype, direct measurement was made to its inner mass and capsule, so an accurate observation of its dynamics was carried out. In the present work, due to the dimension of the current prototype, direct measurement to the inner mass was impossible, so only the displacement of the capsule was recorded by video camera for dynamic analysis. A similar model was also studied in [31] for magnifying the propulsive force of the prototype. However, only a one-sided constraint was considered for the model, and its external excitation was a sinusoidal signal. The reason that the rectangular waveform signal (i.e. the PWM signal in experiment) was used in the present study is due to its simplicity in experimental implementation and calibration.

2.3 Mathematical formulation as a piecewise smooth dynamical system

Let us denote by $\beta =(T,D,P_\mathrm {d},G_{1}, G_{2},M_\mathrm {c},M_\mathrm {m},k,k_{1},$ $k_{2},c,\mu )\in \left( {\mathbb {R}}^+_{0}\right) ^5\times \left( {\mathbb {R}}^+\right) ^7$ and $u=(V_{\mathrm {m}},X_{\mathrm {r}},V_{\mathrm {r}},s)^T\in {\mathbb {R}}^4$ the parameters and state variables of the system, respectively, with ${\mathbb {R}}^+_{0}$ being the set of nonnegative numbers. In this setting, the equations of motion of the capsule model (1) can be represented by a first-order system as follows

$$\begin{aligned} {\dot{u}}&=\left( \begin{array}{l} P_\mathrm {d} f_{\mathrm {e}}-f_{0}-H_{\mathrm {k_{1}}}f_{1}-H_{\mathrm {k_{2}}}f_{2} \\ V_{\mathrm {r}}\\ P_\mathrm {d} f_{\mathrm {e}}-f_{0}-H_{\mathrm {k_{1}}}f_{1}-H_{\mathrm {k_{2}}}f_{2} \\ +\dfrac{M_\mathrm {m}}{M_\mathrm {c}} \left| H_{\mathrm {vel}}\right| \left( H_{\mathrm {vel}}P_\mathrm {f}-f_{0}-H_{\mathrm {k_{1}}}f_{1}-H_{\mathrm {k_{2}}}f_{2}\right) \\ 1\end{array}\right) \nonumber \\&=f_{\text {\tiny CAP}}(u,\beta ,H_{\mathrm {k_{1}}},H_{\mathrm {k_{2}}},H_{\mathrm {vel}},f_{\mathrm {e}}), \end{aligned}$$

(5)

where $f_{0}=kX_{\mathrm {r}}+cV_{\mathrm {r}}$, $f_{1}=k_{1}(X_{\mathrm {r}}-G_{1})$ and $f_{2}=k_{2}(X_{\mathrm {r}}+G_{2})$. Note that in model (5) we have introduced an additional variable s, whose purpose is to map the time into the state space. This variable will be allowed to vary within the excitation period $I=[0,T]$, due to which we will implement the reset procedure

$$\begin{aligned} s(t^+)=s(t^-)-T, \text{ whenever } s(t)=T, \end{aligned}$$

(6)

assuming that s has started in I. On the other hand, model (5) includes some flags $H_{\mathrm {k_{1}}}$ ,$H_{\mathrm {k_{2}}}$, $H_{\mathrm {vel}}$, and $f_{\mathrm {e}}$, which represent discrete variables used to determine the operation modes of the system, defined as

$$\begin{aligned} H_{\mathrm {k_{1}}}={\left\{ \begin{array}{ll} 1, &{\quad} X_{\mathrm {r}}-G_{1}\ge 0, \text{(contact } \text{ with } k_{1}\text{) },\\ 0, &{\quad} X_{\mathrm {r}}-G_{1}<0, \text{(no } \text{ contact) }, \end{array}\right. }\end{aligned}$$

(7)

$$\begin{aligned} H_{\mathrm {k_{2}}}={\left\{ \begin{array}{ll} 1, &{} X_{\mathrm {r}}+G_{2}\le 0, \text{(contact } \text{ with } k_{2}\text{) },\\ 0, &{} X_{\mathrm {r}}+G_{2}>0, \text{(no } \text{ contact) }, \end{array}\right. } \end{aligned}$$

(8)

$$\begin{aligned} H_{\mathrm {vel}}={\left\{ \begin{array}{ll} 0, &{} V_{\mathrm {c}}=0 \text{ and } \left| f_{0}+H_{\mathrm {k_{1}}}f_{1}+H_{\mathrm {k_{2}}}f_{2}\right| \\ &{} \le P_\mathrm {f} , \text{(capsule } \text{ stationary) },\\ 1, &{} V_{\mathrm {c}}>0 \text{ or } (V_{\mathrm {c}}=0 \text{ and } f_{0}+H_{\mathrm {k_{1}}}f_{1}\\ &{} +H_{\mathrm {k_{2}}}f_{2}>P_\mathrm {f}), \text{(forward } \text{ motion) },\\ -1, &{} V_{\mathrm {c}}<0 \text{ or } (V_{\mathrm {c}}=0 \text{ and } f_{0}+H_{\mathrm {k_{1}}}f_{1}\\ &{} +H_{\mathrm {k_{2}}}f_{2}<-P_\mathrm {f}), \text{(backward } \text{ motion) }, \end{array}\right. }\end{aligned}$$

(9)

$$\begin{aligned} f_{\mathrm {e}}={\left\{ \begin{array}{ll} 1, &{} 0\le s<DT,\quad \text{(forcing } \text{ on) },\\ 0, &{} DT\le s<T, \quad\text{(forcing } \text{ off) }. \end{array}\right. } \end{aligned}$$

(10)

Note that the motion of the capsule strongly depends on the term

$$\begin{aligned} f_{\mathrm {mc}}=f_{0}+H_{\mathrm {k_{1}}}f_{1}+H_{\mathrm {k_{2}}}f_{2}, \end{aligned}$$

(11)

which represents the force acting between the capsule and the internal mass. Therefore, if the capsule is stationary, the capsule will move whenever $f_{\mathrm {mc}}$ exceeds the threshold of dry friction. Following the notation introduced in [33], each operation regime of the capsule will be represented by a triple $\left\{ \varSigma ,\varDelta ,\varTheta \right\}$, where $\varSigma \in \left\{ \text{ NC },\text{ Ck1 },\text{ Ck2 }\right\}$ (no contact, contact with $k_{1}$, contact with $k_{2}$), $\varDelta \in \left\{ \text{ Vc0 },\text{ Vcp },\text{ Vcn }\right\}$ (capsule stationary, forward motion, backward motion) and $\varTheta \in \left\{ \text{ ON },\text{ OFF }\right\}$ (forcing on, forcing off). Therefore, the capsule system presents a total of 18 different operation regimes, as given in Table 1. It should be noted that the mathematical arrangement in [33] is nondimensional, while the one in this subsection is dimensional.

Table 1 Operation regimes of the capsule system and the corresponding values of the flags $H_{\mathrm {k_{1}}}$, $H_{\mathrm {k_{2}}}$, $H_{\mathrm {vel}}$ and $f_{\mathrm {e}}$ defined in (7)–(10) [33]

2.4 Solution measures

In the following sections we will study the behavior of the capsule model under parameter variations. For this analysis, it is convenient to introduce suitable solution measures that allow us to monitor any negative impact that the capsule may have on an individual, as well as the device’s performance. The average velocity per period of the capsule will be then given by

$$\begin{aligned} V_{\text{ avg }}=\frac{1}{T}(X_{\mathrm {c}}(T)-X_{\mathrm {c}}(0)), \end{aligned}$$

(12)

whose sign indicates whether the capsule moves forwards ($V_{\text{ avg }}>0$) or backwards ($V_{\text{ avg }}<0$). Note that system (5) does not include an equation describing explicitly the capsule motion $X_{\mathrm {c}}$. This variable, however, can be recovered from system (5) via

$$\begin{aligned} X_{\mathrm {c}}(t)=X^*_{\mathrm {c}}+\int \limits _{0}^{t}V_{\mathrm {c}}(t)\,dt= X^*_{\mathrm {c}}+\int \limits _{0}^{t}(V_{\mathrm {m}}(t)- V_{\mathrm {r}}(t))\,dt, \end{aligned}$$

where $X^*_{\mathrm {c}}\in {\mathbb {R}}$ represents the position of the capsule at $t=0$.

The second measure that will be considered in our study is the maximum propulsive force, defined as

$$\begin{aligned} A_{f}=\max _{0\le t\le T}\left| f_{0}+H_{\mathrm {k_{1}}}f_{1}+H_{\mathrm {k_{2}}}f_{2}\right| , \end{aligned}$$

(13)

whose value should be as low as possible in order to minimize any harm to an individual’s body. These solution measures will allow us to gain more insight into the dynamics of the capsule from a practical perspective, as will be seen in the following sections.

3 Numerical optimisation

Identified system and control parameters of the prototype are summarised in Table 2, and the detailed introduction of experimental apparatus and procedures for parameter identification is given in Sect.4.2.

Table 2 Identified parameters of the prototype

Fig. 3

Numerical continuation of the periodic response of the capsule system (1) with respect to the excitation period T, computed for the parameter values given in Table 2, with $D=0.8$ and $P_\mathrm {d}=6.8$ mN. Panel (a) shows the behavior of the average capsule velocity $V_{\text{ avg }}$, while panel (b) displays the variation of the maximum propulsive force $A_{f}$. The labels Fi, PDi and GRi denote fold, period-doubling and grazing bifurcations of limit cycles, respectively. In both panels, dashed and solid lines represent unstable and stable solutions, respectively. Similarly, the red and blue curves represent periodic solutions for which $V_{\text{ avg }}=0$ and $V_{\text{ avg }}>0$, respectively. Panels (c), (e) and (d), (f) depict system responses at the test points P1 ($T=26.8390$ ms, with $A^{1}_{f}=64.6633$ mN) and P2 ($T=32.4958$ ms, with $A^{2}_{f}=11.5282$ mN), respectively. In both cases, the resulting average capsule velocity is 5 mm/s. The propulsive force in panels (c) and (d) is calculated from formula (11), via the relation $F_{\mathrm {mc}}=P_\mathrm {f}f_{\mathrm {mc}}$. In panels (c)–(f), grey and blank areas indicate that the excitation is on and off, respectively

Fig. 4

Panels a and b show enlargements of the boxed regions shown in Fig. 3a and b, respectively. Panels c–e depict phase plots of periodic solutions computed at the grazing points GR3 ($T\approx 32.0298$ ms) and GR4 ($T\approx 45.3868$ ms), and the test point P1 ($T=38.7$ ms). Here, the vertical red line stands for the impact boundary $X_{\mathrm {r}}=0$

To begin our analysis, we will investigate the periodic behavior of the capsule model (1) as the period of external excitation T varies. The result is shown in Fig. 3. In this figure, panels (a) and (b) show in the vertical axis the variation of the average capsule velocity $V_{\text{ avg }}$ and the maximum propulsive force $A_{f}$, respectively. Starting from low values of T (i.e. on the red curve) we observe that the capsule remains stationary, that is $V_{\text{ avg }}=0$, with the internal mass oscillating inside the capsule without making any contact with the constraints $k_{1}$, $k_{2}$. If T increases, then a critical point GR1 ($T\approx 22.5481$ ms) is found, corresponding to a grazing bifurcation of limit cycles, after which the capsule starts moving forward (i.e. $V_{\text{ avg }}>0$). From this point onwards, a rapid increase of the capsule average velocity can be observed. Further increment of the excitation period leads to a second grazing bifurcation (GR2, $T\approx 25.9963$ ms), after which the internal mass makes intermittent contact with the secondary constraint $k_{2}$. For this reason, as observed in Fig. 3b, the maximum propulsive force $A_{f}$ rises significantly after this grazing bifurcation occurs. Very close to this point, another bifurcation is detected, corresponding to a fold bifurcation of limit cycles, due to which the periodic solution becomes unstable. This branch of unstable periodic solutions terminates at the fold point F2 ($T\approx 25.0433$ ms), where the periodic solution recovers stability. If T grows further, a period-doubling bifurcation of limit cycles is found (PD1, $T\approx 28.7431$ ms), where a branch of stable period-2 solutions is born, while the original period-1 orbit becomes unstable. This solution becomes stable again at a second period-doubling bifurcation (PD2, $T\approx 32.0298$ ms), after which we find a grazing bifurcation GR3, very close to PD2. For T beyond this GR3 point, we encounter a window of periodic solutions with no impacts with the internal constraints, due to which the maximum propulsive force remains low. This window, however, finishes at the grazing bifurcation GR4 ($T\approx 45.3868$ ms), after which impacts can be observed again (see Fig. 4). Right after this point, another short branch of unstable periodic solutions is found, between the fold bifurcation points F3 (very close to GR4) and F4 ($T\approx 44.5951$ ms).

Fig. 5

a Two-parameter continuation of the grazing solutions found in Fig. 4 with respect to the excitation period T and duty cycle D. The resulting curve divides locally the parameter space into two regions corresponding to impacting and non-impacting solutions. Panels b–e show phase plots of periodic solutions computed at the test points P1 ($D=0.837$, $T=47$ ms), P2 ($D=0.77$, $T=44$ ms), P3 ($D=0.76$, $T=38$ ms) and P4 ($D=0.775$, $T=33$ ms), respectively

Note that in Fig. 3 two test points P1 ($T=26.8390$ ms) and P2 ($T=32.4958$ ms) have been chosen, in such a way that in both cases the capsule moves with the same average velocity $V_{\text{ avg }}=5$ mm/s. There is, however, a significant difference regarding the behavior of the propulsive force, as shown in the panels (c) and (d). In one case, the maximum propulsive force is $A_{f}=11.5282$ mN (at P2), while at the other test point we have that $A_{f}=64.6633$ mN, that is, more than 5 times the value at P2. This test indicates that for a desired capsule average velocity we should look for those operation points producing the smallest possible propulsive force. According to the numerical study carried out in Fig. 3, it can be seen that the parameter window between the grazing points GR3 ($T\approx 32.0298$) and GR4 ($T\approx 45.3868$ ms) provides a suitable operation interval, where no impacts occur, while showing relatively high progression rates with low propulsive force (due to the non-impacting motion). Via two-parameter continuation of the grazing orbits shown Fig. 4 we can identify a parameter region in the D-T plane for which non-impacting solutions can be found, see Fig. 5a. In this diagram, the blue curve corresponds to (D, T)-values producing a grazing bifurcation with respect to the impact boundary $X_{\mathrm {r}}=0$ (i.e. impact with the constraint $k_{2}$). This curve then divides locally the parameter space into two regions, corresponding to impacting and non-impacting behavior, as shown at the test points displayed in panels (b)–(e). In this way, we are able to choose operation points (D, T) leading to non-impacting behavior (hence with low maximum propulsive force), with $V_{\text{ avg }}>0$.

Fig. 6

Two-parameter continuation of the periodic solution shown in Fig. 4d with respect to the excitation period T and duty cycle D, keeping the maximum propulsive force $A_{f}$ constant. Panel (a) shows the behavior of the average capsule velocity $V_{\text{ avg }}$, computed for fixed $A_{f}=11.55$ mN ($c_{1}$), $A_{f}=11.45$ mN ($c_{2}$), $A_{f}=11.35$ mN ($c_{3}$), $A_{f}=11.25$ mN ($c_{4}$), $A_{f}=11.15$ mN ($c_{5}$) and $A_{f}=11.05$ mN ($c_{6}$). Panel (b) shows the computed curves on the D-T plane. The point P0 ($D=0.74$, $T=25.3853$ ms) stands for a test point, while P1 ($D\approx 0.8665$, $T\approx 28.8876$ ms), P2 ($D\approx 0.8611$, $T\approx 28.9971$ ms), P3 ($D\approx 0.8585$, $T\approx 28.7412$ ms), P4 ($D\approx 0.8537$, $T\approx 28.7742$ ms), P5 ($D\approx 0.8488$, $T\approx 28.8006$ ms) and P6 ($D\approx 0.8439$, $T\approx 28.8265$ ms) are points at which the average capsule velocity is maximized, for the corresponding fixed values of $A_{f}$. Panels (c), (e) and (d), (f) depict system responses at the points P6 (with $V_{\text{ avg }}=4.5550$ mm/s) and P0 (with $V_{\text{ avg }}=2.6624$ mm/s), respectively. In both cases, the maximum propulsive force is $A^{0}_{f}=11.05$ mN

Let us now assume that for safety requirements we need to restrict the maximum propulsive force $A_{f}$ to certain predefined fixed values. Given this constraint, we will investigate how to obtain optimal values of average capsule velocity $V_{\text{ avg }}$ by choosing the main control parameters D, T in a suitable manner. For this purpose, we are going to carry a two-parameter continuation of periodic solutions within the suitable parameter window identified before (between the grazing points GR3 and GR4, see Fig. 4). In this way, we can obtain a family of curves in the D-T plane yielding (D, T)-values for which $A_{f}$ is constant. The result of this procedure is shown in Fig. 6. Panel (b) shows a family of curves corresponding to the fixed values $A_{f}=11.55$ mN ($c_{1}$), $A_{f}=11.45$ mN ($c_{2}$), $A_{f}=11.35$ mN ($c_{3}$), $A_{f}=11.25$ mN ($c_{4}$), $A_{f}=11.15$ mN ($c_{5}$) and $A_{f}=11.05$ mN ($c_{6}$). In panel (a) we can observe the behavior of $V_{\text{ avg }}$ along the curves $c_{1}$–$c_{6}$. With this information we can identify (D, T)-points (labeled P1–P6) for which $V_{\text{ avg }}$ is maximum. Hence, given the restriction on the maximum propulsive force, we can determine optimal operation points for the capsule system. To illustrate this, Fig. 6 shows the capsule behavior at one of the optimal points (P6, with $D\approx 0.8439$, $T\approx 28.8265$ ms) and a test point P0 ($D=0.74$, $T=25.3853$ ms). As can be observed in Fig. 6, in both cases we have that $A_{f}=11.05$ mN, however, the resulting average velocity is $V_{\text{ avg }}=4.5550$ mm/s for P6, while $V_{\text{ avg }}=2.6624$ mm/s at the test point P0. A similar scenario is analyzed in Fig. 7. In this case, however, we fix some desired average capsule velocities and find, via two-parameter continuation, a family of curves in the D-T plane yielding the desired velocities. Similarly as before, we now monitor the resulting maximum propulsive force and identify (D, T)-values with the lowest $A_{f}$.

Fig. 7

Two-parameter continuation of the periodic solution shown in Fig. 4d with respect to the excitation period T and duty cycle D, keeping the average capsule velocity $V_{\text{ avg }}$ constant. Panel (a) shows the behavior of the maximum propulsive force $A_{f}$, computed for fixed $V_{\text{ avg }}=4.74$ mm/s ($c_{1}$), $V_{\text{ avg }}=4.48$ mm/s ($c_{2}$), $V_{\text{ avg }}=4.22$ mm/s ($c_{3}$), $V_{\text{ avg }}=3.96$ mm/s ($c_{4}$) and $V_{\text{ avg }}=3.70$ mm/s ($c_{5}$). Panel (b) shows the computed curves on the D-T plane. The points P1 ($D\approx 0.8617$, $T\approx 28.8583$ ms), P2 ($D\approx 0.8680$, $T\approx 28.9615$ ms), P3 ($D\approx 0.8746$, $T\approx 29.0283$ ms), P4 ($D\approx 0.8808$, $T\approx 29.1677$ ms) and P5 ($D\approx 0.8875$, $T\approx 29.2241$ ms) are parameter values at which the maximum propulsive force is minimized, for the corresponding fixed values of $V_{\text{ avg }}$

4 Experimental verification

4.1 Powering system and experimental setup

The schematic of the experimental setup is presented in Fig. 8a, and a photograph of the testing platform is shown in Fig. 8b. As can be seen from the figure, the T-shaped NdFeB magnet was driven by an external electromagnetic coil. The dimension of the coil with regard to its turns, diameter and thickness has been optimised to achieve the maximal excitation on the magnet. This was done through numerical simulation using ANSYS MAXWELL as presented in Fig. 9, and then was winded using an automatic winding machine. The coil was made by a 26AWG wire with a total of 912 turns. The magnet can vibrate inside the capsule through an on-off electromagnetic field and the helical spring to generate forward and backward impact motion, so leading to the locomotion of the entire system. As illustrated in Fig. 8a, the on-off excitation was generated using a signal generator producing the pulse width modulation (PWM) signal via a power amplifier OPA544, and the amplifier can control the voltage applied to the coil by adjusting a DC power supply between 0.6 V and 25 V. In this work, three control parameters, the frequency, amplitude and duty cycle ratio of the electromagnetic excitation, were optimised. Here, the duty cycle ratio is the fraction of one period in which the on-off excitation is active.

Fig. 8

(Colour online) a Schematic and c photograph of the experimental setup. The T-shaped magnet inside the capsule prototype was excited through an on-off electromagnetic field $\mathop {B}\limits ^{\rightarrow }$ and the helical spring to generate forward and backward impact motion, leading to the locomotion of the prototype. The on-off external excitation was generated using a signal generator producing a pulse width modulation (PWM) signal via a power amplifier, and the amplifier can control the voltage applied to the coil by adjusting a DC power supply. The prototype was put on a piece of cut-open synthetic small intestine supported by a halved black plastic tube, which was placed along the axis centre of the coil. On the top of the experimental setup, a video camera was used to record the motion of the capsule, and recorded videos were analysed by using an open source software to generate the time history of capsule’s displacement and velocity

Fig. 9

(Colour online) Numerical simulation of flux density of the coil and the magnet using ANSYS MAXWELL

4.2 Experimental apparatus and procedure for parameter identification

The dimensions of the prototype and its inner components are presented in Fig. 10. The total weight of the T-shaped magnet provides the value of the inner mass $M_\mathrm {m}$, and the weight of the remaining parts, including the capsule shell and the helical spring, gives the mass of the capsule $M_\mathrm {c}$. Both of the weights were kept constant throughout the experiments.

Fig. 10

(Colour online) Dimension of the prototype

Fig. 11

(Colour online) a Experimental set-up [31] and force-deflection curves for static testing of b the primary and c the secondary constraints

The stiffness of the primary and the secondary constraints, $k_1$ and $k_2$, were determined through static tests using an Instron machine as shown in Fig. 11a. The constraint was put on a holder fixed onto a supporting platform, and a continuous loading force acting on the constraint was applied from the Instron machine through a rod with the same diameters of both magnet’s heads. To validate the experimental results, a finite element (FE) model of static testing was also developed in ANSYS WORKBENCH by using the static structural module, where a magnet applied continuous force on a fixed constraint. A detailed description of the FE model can be found from [31]. FE and experimental results of the static testing are presented in Figs. 11b and c for the primary and the secondary constraints, respectively. It should be noted that the dimensions of the primary and the secondary constraints are the same, while the only difference that causes their different stiffness is the diameters of the T-shaped magnet impacting the constraints. It is also worth noting that the targeted thickness of the 3D printed constraints is 0.6 mm. However, the thickness of the real constraints is slightly different due to the inaccuracy of the 3D printer, which led to different values of stiffness for the constraints. In order to compensate this inaccuracy, the constraints with different thicknesses were simulated using the FE model, and the averaged values of the stiffness for the primary and the secondary constraints, $k_1=27.9$ and $k_2=53.5$ kN/m, were adopted.

Fig. 12

(Colour online) a Force-deflection curve for static testing of the helical spring. b Schematic and c the sample graph of the free vibration test, where $c=2\sqrt{m_vk}\tfrac{\delta }{2\pi }$, $m_v$ is the mass of the vibrating block, $\delta =\frac{1}{n}\mathrm {ln}\frac{X_0}{X_n}$, $n=1, 2, 3, \ldots$

The stiffness of the helical spring k was determined through static tests using the Instron machine, and the experimental results are shown in Fig. 12a. To measure the value of the coefficient c, free vibration tests were carried out by fixing one end and attaching a free vibrating block to the other end of the helical spring as presented in Fig. 12b, where an optical laser sensor was used to measure the displacement of the block. Then the coefficient c was calculated by using the logarithmic decrement method as illustrated in Fig. 12c.

Fig. 13

(Colour online) Experimental set-up for identification of the friction coefficient $\mu$

Identification of the friction coefficient $\mu$ was carried out by lifting one side of the supporting surface slowly until the stationary capsule started to move as illustrated in Fig. 13. Therefore, the friction coefficient was determined by the angle of the surface slope at that moment, $\mu =\arctan \theta =h/l$.

To calibrate the amplitude of the excitation force $P_\mathrm {d}$, as shown in Fig. 14a, the coil was left above the magnet, and the magnet was put on a lab scale recording its electromagnetic forces at different positions of the coil. A comparison of analytical solutions, numerical simulation (obtained by ANSYS MAXWELL) and experimental results is presented in Fig. 14b to demonstrate the accuracy of this calibration. It is worth noting that the analytical solutions were calculated by using the Biot–Savart law, and a detailed derivation of the electromagnetic force will be studied in another publication in due course.

Fig. 14

(Colour online) a Experimental set-up for calibration of coil’s electromagnetic force generated on the magnet. b Comparison of analytical solutions (calculated by using the Biot–Savart law), numerical simulation (obtained by ANSYS MAXWELL) and experimental results

4.3 Experimental procedure and data processing

During the experiment, the coil was fixed at a permanent location and created a magnetic field gradient exciting the T-shaped magnet inside the capsule. As presented in Fig. 8b, the prototype was tested on a piece of cut-open synthetic small intestine [38] supported by a halved black plastic tube, which was placed along the axis centre of the coil. On the top of the experimental setup, a video camera was fixed to record the motion of the capsule, and recorded videos were analysed by using an open source software Tracker [39]. Displacement of the capsule was recorded, and the average velocity of the prototype in a specific time interval was calculated using

$$\begin{aligned} V_{\mathrm {avg}}^{\mathrm {exp}}=\frac{X_{\mathrm {c}}(t_0+\varDelta t)-X_{\mathrm {c}}(t_0)}{\varDelta t}, \end{aligned}$$

(14)

where $X_{\mathrm {c}}$ represents capsule’s displacement along the axis of the coil, $t_0$ is the starting time, and $\varDelta t$ is the time interval.

4.4 Experimental results

Experimental and numerical results are compared in this section to validate the effectiveness of the proposed mathematical model. It is worth noting that since the position of the coil for exciting the magnet was fixed in experiment, the amplitude of excitation $P_\mathrm {d}$ may vary with the progression of the capsule. In order to compensate this variation, our experimental measurement was taken from a small range of capsule’s displacement ensuring the actual amplitude of excitation and the calibration as close as possible, i.e. $P_\mathrm {d}$ can be reasonably approximated as a constant during the measurement.

Fig. 15

a Comparison of capsule’s average velocity as a function of the period of external excitation between numerical simulation (blue dots) and experiment (grey dots) at $D=0.8$ and $P_\mathrm {d}=6.8$ mN. Numerical (blue lines) and experimental (red-dot lines) time histories of capsule’s displacement at b $T=35$ ms in simulation, $T=33$ ms in experiment, $D=0.8$ and $P_\mathrm {d}=6.8$ mN, c $T=55$ ms in simulation, $T=62.5$ ms in experiment, $D=0.8$ and $P_\mathrm {d}=6.8$ mN, and d $T=50$ ms, $D=0.3$ and $P_\mathrm {d}=5.8$ mN. (Color figure online)

Figure 15a compares the average velocity of the prototype as a function of the period of the rectangular waveform signal between numerical simulation and experiment. For the experimental work, we repeated four times of tests for each period between $T\in [20,\,71.43]$ ms, and an average velocity of the prototype was obtained. It can be seen from the figure that the average velocities obtained from numerical simulation and experiment have a similar trend. Both results indicate that the capsule has a fast forward progression in the regime of $T\in (25,\,45)$ ms. However, peak forward progression was recorded at $T=30.15$ ms in simulation while $T=35.71$ ms in experiment and $T=38.46$ ms for experimental average. This small deviation may be caused by the inaccuracy of the signal generator which always introduces some extra noise in nature in the waveform signal. On the other hand, both numerical and experimental results suggest that the capsule has slow progression when the period is chosen at $T>45$ ms or $T<25$ ms, which is consistent with our finding in the mesoscale prototype (see Figs. 9 and 14 in [32]).

Figures. 15b–d exemplify time histories of capsule’s displacement obtained from numerical simulation and experiment where both forward and backward progressions were observed. In Fig. 15b, the capsule had a forward progression without any backward motion, and there was a slight difference in the period of excitation between simulation and experiment ($T=35$ ms in simulation and $T=33$ ms in experiment). The same duty cycle $D=0.8$ and amplitude of excitation $P_\mathrm {d}=6.8$ mN but a small difference in the period of excitation, $T=55$ ms in simulation and $T=62.5$ ms in experiment, were used in Fig. 15c where the capsule had an overall forward progression but with obvious backward motion. In Fig. 15d, backward progression of the capsule was presented where a smaller amplitude of excitation, $P_\mathrm {d}=5.8$ mN, and a shorter duty cycle, $D=0.3$, were used. Through observing a single period of this progression, it shows that the capsule had a fast forward progression followed by a fast backward progression leading capsule’s overall progression to backward. This was caused by the helical spring (represented by k and c) in the capsule and the secondary constraint (represented using $k_2$). When the magnet in the capsule moved forward, the helical spring was compressed, and its elastic force on the capsule overcame the intestinal friction, so resulting in a fast forward motion of the capsule. While the magnet moved back to its original position, it hit the secondary constraint which led to a fast backward motion of the capsule. Here, a faster overall backward progression of the capsule can be achieved in experiment by reducing the stiffness of the helical spring, i.e. replacing it using a softer one, causing less elastic force on the capsule, so less forward motion can be generated.

Fig. 16

Left panel compares experimental results with the grazing solutions numerically found in Fig. 4 with respect to the excitation period T and duty cycle D. The grazing curve denoted by blue dots divides the parameter space into two regions corresponding to impacting and non-impacting solutions. Experimental results for impacting and non-impacting solutions are marked by green triangles and red squares, respectively. Right panels show experimental time histories of displacement of the capsule for impacting and non-impacting solutions. (Color figure online)

Fig. 17

Left panel presents capsule’s average velocity as a function of the duty cycle of external excitation obtained for $T=50$ ms, $D\in [0.1,\,0.9]$, $P_\text {d}=6.8$ mN (green triangles) and $P_\text {d}=8$ mN (blue dots) by numerical simulation, and $P_\text {d}=28$ mN (red squares) from experiment. Internal windows show phase trajectories of the capsule computed for $P_\text {d}=28$ mN in different duty cycles. Red lines indicate the impact boundary of the secondary constraint $k_2$. Right panels show experimental time histories of displacement of the capsule under different duty cycle. (Color figure online)

In order to test the grazing boundary for impacting and non-impacting solutions experimentally, we further extended the parameter region of Fig. 5a and plotted the experimental data points in the D-T plane in Fig. 16. In the figure, we distinguished impacting and non-impacting solution by using green triangles and red squares, respectively, and presented their corresponding time histories of capsule’s displacement on the right panels of Fig. 16. Although displacement of the inner mass was not measured in experiment, back impact between the inner mass and the secondary constraint can be identified from where backward or stationary motion of the capsule is observed. Since back impact can encourage backward motion or cause less forward progression for the capsule, this observation can be used as the evidence of impacting and non-impacting solutions.

Figureefdutyfit presents the numerical and experimental confirmation of the optimisation carried out in Figs. 6 and 7 by varying the duty cycle of external excitation. Comparing the numerical ($P_\text {d}=6.8$ mN and $P_\text {d}=8$ mN) and the experimental results ($P_\text {d}=28$ mN) in the left panel of Fig. 17, there is an obvious difference in the amplitude of excitation $P_\text {d}$, which could be caused by imperfect experimental environment and measurement errors, e.g. the friction between the magnet and the bearing was omitted. However, their trends are similar such that capsule’s forward progression became much faster when $D>0.6$. Internal windows in the left panel which were obtained from numerical simulation calculated for $P_\text {d}=28$ mN reveal that when $D<0.6$, excitation duration was short, and multiple impacts between the magnet and the secondary constraint were encountered which restricted capsule’s forward progression. When $D>0.6$, excitation duration became long, and the number of the impact between the magnet and the secondary constraint was decreased, so leading to a faster progression. Right panels in the figure also confirm that the capsule had more impact solutions when $D<0.6$ causing less progression of the capsule. When the duty cycle was $D>0.6$, the number of impact decreased clearly and forward progression of the capsule was improved significantly. When $D=0.8$, very few impacts can be identified, so producing the fastest forward progression ($V_\text {avg}=14.4$ mm/s).

5 Conclusions

This paper studied the optimisation of a vibration-driven capsule robot for small-bowel endoscopy with respect to maximising its progression speed and minimising propulsive force through a numerical analysis and experimental investigation. The driving principle of the capsule robot is to employ a periodically driven internal mass interacting with the main body of the capsule as a “hammer” in the presence of intestinal resistances. “Hammer” effect may occur once the internal mass contacts with the primary or the secondary constraint of the capsule. Therefore, a magnified propulsive force could be generated during the impact to overcome the intestinal resistances.

Due to the dimensional restriction of our capsule prototype, 26 mm in length and 11 mm in diameter, it was difficult for us to equip any portable sensors on the capsule. So direct measurement of the internal mass and the capsule was not possible, and only a video camera was used for tracking the progression of the capsule. Another restriction of our experiment was that the internal mass of the prototype was excited by an external magnetic field, and to employ an untethered non-magnetic sensor on the capsule was challenging. Therefore, a mathematical model of the capsule system studied in [32] was adopted in this work for understanding the dynamics of the prototype.

Our numerical investigation reveals that the impact between the internal mass and the constraint of the capsule was not required actually to propel the capsule, since the interactive force generated between the internal mass and the capsule via the helical spring was sufficiently large to overcome the intestinal friction in the current experimental setup. Therefore, our optimisation focused on identifying a parametric regime where only non-impacting motion existed by using path-following techniques. Based on our numerical continuation through following a periodic non-impacting response, a grazing boundary for impacting (with the secondary constraint) and non-impacting solutions was found, which was consistent with our experimental results. We also confirmed in both numerical simulation and experimental testing that the optimum duty cycle of the prototype was about $80\%$ of the external excitation at where a fast progression but less propulsive force can be generated.

Our future work will concentrate on numerical and experimental investigation of dynamics of the capsule robot in a more complicated intestinal environment, e.g. a naturally twisted intestine, identification of dynamic friction on the capsule during progression, closed-loop control system design, ex vivo and in vivo tests.