Skip to main content
SpringerLink
Log in

The RBF partition of unity method for solving the Klein-Gordon equation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

A Correction to this article was published on 13 November 2020

This article has been updated

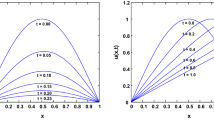
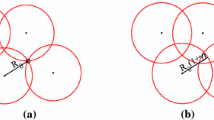
Abstract

In this paper, a localized radial basis function (RBF) method is applied to obtain a global approximation of the solution of two dimensional Klein-Gordon equation on a given bounded domain. We use the RBF partition of unity (RBF-PU) method which is based on partitioning the original domain to several patches and using the RBF approximation on each local domain. Low computational cost and well conditioned final linear system are the main advantages of this method comparing with the original (global) RBF techniques. Numerical experiments show that the given problem could be solved successfully with a reasonable accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Change history

References

  1. Argyris J, Haase M, Heinrich JC (1991) Finite element approximation to two-dimensional sine-gordon solitons. Comput Methods Appl Mech Eng 86:1–26

    Article  MathSciNet  Google Scholar 

  2. Bogolyubskiǐ IL (1976) Oscillating particle-like solutions of the nonlinear Klein-Gordon equation. JETP Lett 24(10):535–538

    Google Scholar 

  3. Bogolyubskiǐ IL (1977) Dynamics of spherically symmetrical pulsons of large amplitude. JETP Lett 25(2):107–110

    Google Scholar 

  4. Bogolyubskiǐ IL, Makhankov VG (1976) Lifetime of pulsating solitons in certain classical models. JETP Lett 24(1):12–14

    Google Scholar 

  5. Bratsos AG (2007) The solution of the two-dimensional sine-gordon equation using the method of lines. J Comput Appl Math 206:251–277

    Article  MathSciNet  Google Scholar 

  6. Bratsos AG (2007) A third order numerical scheme for the two-dimensional sine-gordon equation. Math Comput Simul 76:271–282

    Article  MathSciNet  Google Scholar 

  7. Christiansen PL, Lomdah PS (1981) Numerical study of \(2+1\) dimensional sine-gordon solitons. Physica 2D(3):482–491

    MathSciNet  MATH  Google Scholar 

  8. Darani MA (2017) Direct meshless local Petrov-Galeckin method for the two-dimensional klein-gordon equation. Eng Anal Bound Elem 74:1–13

    Article  MathSciNet  Google Scholar 

  9. Davydov AS (1976) Quantum mechanics. Pergamon, Elmsford

    Google Scholar 

  10. Davydov O, Schaback R (2017) Optimal stencils in Sobolev spaces. IMA J Numer Anal 39(1):398–422

    MathSciNet  MATH  Google Scholar 

  11. Djidjeli K, Price WG, Twizell EH (1995) Numerical solutions of a damped sine-gordon equation in two space variables. J Eng Math 29:347–369

    Article  MathSciNet  Google Scholar 

  12. Drazin PG, Johnson RS (1983) Solitons: an introduction. Cambridge University Press, Cambridge

    Book  Google Scholar 

  13. Ebaid A (2009) Exact solutions for the generalized Klein-Gordon equation via a transformation and Exp-function method and comparison with Adomian’s method. J Comput Appl Math 223:278–290

    Article  MathSciNet  Google Scholar 

  14. Floater MS, Iske A (1996) Multistep scattered data interpolation using compactly supported radial basis functions. J Comput Appl Math 73:65–78

    Article  MathSciNet  Google Scholar 

  15. Fornberg B, Larsson E, Flyer N (2011) Stable computations with Gaussian radial basis functions. SIAM J Sci Comput 33:869–892

    Article  MathSciNet  Google Scholar 

  16. Guo BY, Pascual PJ, Rodriguez MJ, Vzquez L (1986) Numerical solution of the sine-gordon equation. Appl Math Comput 18:1–14

    MathSciNet  MATH  Google Scholar 

  17. Heryudono A, Larsson E, Ramage A, Von Sydow L (2016) Preconditioning for radial basis function partition of unity methods. J Sci Comput 67:1089–1109

    Article  MathSciNet  Google Scholar 

  18. Iske A (2002) On the approximation order and numerical stability of local lagrange interpolation by polyharmonic splines. Mod Dev Multivar Approx 145:153–165

    MathSciNet  MATH  Google Scholar 

  19. Kivshar Yu S, Malomed BA (1989) Dynamics of solitons in nearly integrable systems. Rev Mod Phys 61:763–915

    Article  Google Scholar 

  20. Larsson E, Lehto E, Heryudono ARH, Fornberg B (2013) Stable computation of differentiation matrices and scattered node stencils based on gaussian radial basis functions. SIAM J Sci Comput 35:1–22

    Article  MathSciNet  Google Scholar 

  21. Larsson E, Shcherbakov V, Heryudono A (2017) A least squares radial basis function partition of unity method for solving PDEs. SIAM J Sci Comput 39:538–563

    Article  MathSciNet  Google Scholar 

  22. Malomed BA (1987) Decay of shrinking solitons in multidimensional sine-gordon equation. Phys D 24(1):155–171

    MathSciNet  MATH  Google Scholar 

  23. Melenk JM, Babuska I (1996) The partition of unity finite element method: basic theory and applications. Comput Meth Appl Mech Eng 139:289–314

    Article  MathSciNet  Google Scholar 

  24. Mirzaei D, Dehghan M (2009) Boundary element solution of the two-dimensional sine-gordon equation using continuous linear elements. Eng Anal Bound Elem 33:12–24

    Article  MathSciNet  Google Scholar 

  25. Mirzaei D, Dehghan M (2009) Implementation of meshless LBIE method to the 2D nonlinear SG problem. Int J Numer Meth Eng 79:1662–1682

    Article  Google Scholar 

  26. Mirzaei D, Dehghan M (2010) Meshless local Petrov-Galerkin (MLPG) approximation to the two dimensional sine-Gordon equation. J Comput Appl Math 233:2737–2754

    Article  MathSciNet  Google Scholar 

  27. Safdari-Vaighani A, Heryudono A, Larsson E (2015) A radial basis function partition of unity collocation method for convection-diffusion equations arising in financial applications. J Sci Comput 64:341–367

    Article  MathSciNet  Google Scholar 

  28. Schaback R (1995) Creating surfaces from scattered data using radial basis functions. Mathematical methods for curves and surfaces. University Press, Oxford, pp 477–496

    MATH  Google Scholar 

  29. Shepard D (1968) A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23th National Conference ACM, pp. 517–523

  30. Shokri A, Dehghan M (2010) A not-a-knot meshless method using radial basis functions and predictor-corrector scheme to the numerical solution of improved boussinesq equation. Comput Phys Commun 181:1990–2000

    Article  MathSciNet  Google Scholar 

  31. Shokri A, Dehghan M (2012) Meshless method using radial basis functions for the numerical solution of two-dimensional complex ginzburg-landau equation. CMES-Comput Model Eng Sci 84:333–358

    MathSciNet  MATH  Google Scholar 

  32. Stevens D, Power H, Meng CY, Howard D, Cliffe KA (2013) An alternative local collocation strategy for high-convergence meshless pde solutions using radial basis functions. J Comput Phys 254:52–75

    Article  MathSciNet  Google Scholar 

  33. Wendland H (1998) Error estimates for interpolation by compactly supported radial basis functions of minimal degree. J Approx Theory 93:258–272

    Article  MathSciNet  Google Scholar 

  34. Wendland H (2002) Fast evaluation of radial basis functions: methods based on partition of unity. Approximation theory X: wavelets, splines and applications. Vanderbilt University Press, Nashville, pp 473–483

    Google Scholar 

  35. Wendland H (2005) Scattered data approximation. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  36. Wendland H (2010) Multiscale analysis in Sobolev spaces on bounded domains. Numer Math 116:493–517

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Special thanks go to Dr. Davoud Mirzaei for his helpful comments and suggestions that improved the quality of the paper. Supports from IPM-Isfahan are greatly acknowledged. The author is very grateful to reviewers for carefully reading this paper and for their comments and suggestions which have improved the paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics Faculty of Mathematical Sciences, Shahrekord University, P. O. Box 115, Shahrekord, Iran

    Mohammadreza Ahmadi Darani

Authors
  1. Mohammadreza Ahmadi Darani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohammadreza Ahmadi Darani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original version of this article was revised due to a retrospective Open Access cancellation

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (rar 2121 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmadi Darani, M. The RBF partition of unity method for solving the Klein-Gordon equation. Engineering with Computers 38 (Suppl 1), 679–691 (2022). https://doi.org/10.1007/s00366-020-01171-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01171-z

Keywords

Search

Navigation