Abstract
In this work, we deal with Truncated Newton methods for solving large scale (possibly nonconvex) unconstrained optimization problems. In particular, we consider the use of a modified Bunch and Kaufman factorization for solving the Newton equation, at each (outer) iteration of the method. The Bunch and Kaufman factorization of a tridiagonal matrix is an effective and stable matrix decomposition, which is well exploited in the widely adopted SYMMBK (Bunch and Kaufman in Math Comput 31:163–179, 1977; Chandra in Conjugate gradient methods for partial differential equations, vol 129, 1978; Conn et al. in Trust-region methods. MPS-SIAM series on optimization, Society for Industrial Mathematics, Philadelphia, 2000; HSL, A collection of Fortran codes for large scale scientific computation, http://www.hsl.rl.ac.uk/; Marcia in Appl Numer Math 58:449–458, 2008) routine. It can be used to provide conjugate directions, both in the case of \(1\times 1\) and \(2\times 2\) pivoting steps. The main drawback is that the resulting solution of Newton’s equation might not be gradient–related, in the case the objective function is nonconvex. Here we first focus on some theoretical properties, in order to ensure that at each iteration of the Truncated Newton method, the search direction obtained by using an adapted Bunch and Kaufman factorization is gradient–related. This allows to perform a standard Armijo-type linesearch procedure, using a bounded descent direction. Furthermore, the results of an extended numerical experience using large scale CUTEst problems is reported, showing the reliability and the efficiency of the proposed approach, both on convex and nonconvex problems.
Similar content being viewed by others
1 Introduction
In this paper we consider the unconstrained optimization problem
where \(f : {\mathbb {R}}^n\longrightarrow {\mathbb {R}}\) is a possibly nonconvex real valued function, n is large and we solve (1.1) by means of an iterative method which generates the sequence \(\{x_h\}\). We consider the standard assumptions that f is twice continuously differentiable, and that \(\{x_h\}\subset \Omega \), where \(\Omega \subset {\mathbb {R}}^n\) is compact. Furthermore, no sparsity pattern is assumed for the Hessian matrix \(\nabla ^2 f(x)\). Then, we approach the solution of (1.1) by means of the iterative process
being  a search direction and \(\alpha _h>0\) a steplength. Dealing with large scale problems, Truncated Newton methods are often considered a good choice for their solution. Truncated Newton methods are also called Newton–Krylov methods, since a Krylov subspace method is usually used, for iteratively (approximately) solving the Newton equation at each iteration. In [21] a general description of a Truncated Newton method is reported. As well known, given an initial guess \(x_h\), a Truncated Newton method for problem (1.1) is based on two nested loops:
a search direction and \(\alpha _h>0\) a steplength. Dealing with large scale problems, Truncated Newton methods are often considered a good choice for their solution. Truncated Newton methods are also called Newton–Krylov methods, since a Krylov subspace method is usually used, for iteratively (approximately) solving the Newton equation at each iteration. In [21] a general description of a Truncated Newton method is reported. As well known, given an initial guess \(x_h\), a Truncated Newton method for problem (1.1) is based on two nested loops:
-
The outer iterations, where the current estimate of the solution \(x_{h+1}\) is updated using \(x_h\);
-
The inner iterations, where an iterative algorithm is used for computing, at each outer iteration h, the approximate solution \(p_h\) of the Newton equation
$$\begin{aligned} \nabla ^2 f(x_h) p = - \nabla f(x_h). \end{aligned}$$(1.3)
The Conjugate Gradient (CG) method is among the most commonly used iterative algorithms (see e.g. [1, 17]) for solving (1.3). The main drawback of CG method is that it is well-posed only in case \(\nabla ^2f(x_h)\) is positive definite. Conversely, if matrix \(\nabla ^2f(x_h)\) is indefinite, the CG algorithm could break down and some difficulties may arise to define an approximate solution \(p_h\) of (1.3). In order to cope also with indefinite linear systems, some modified CG algorithms have been proposed in [8, 9, 11, 12, 14]. In particular, if the CG breaks down when solving (1.3), we can take as Newton–type direction \(p_h\) in the recursion (1.2):
-
A scaled steepest descent direction (i.e., \(p_h = -C \nabla f(x_h)\), with C positive definite);
-
A suitable gradient–related adaptation of the current best approximate solution of (1.3);
-
A suitable (descent) negative curvature direction.
Moreover, in [18] a non-standard approach is proposed in order to build a gradient–related direction, by separately accumulating positive and negative curvature directions computed by the CG.
Considering a different standpoint, the CG algorithm may be also used in the indefinite case, as proposed in [13, 18], where a suitable combination of conjugate directions proves to yield a gradient–related direction.
In this work we are interested to compare the quality of the search direction obtained by both CG and SYMMBK algorithms (the latter being proposed by Chandra in [5]), when solving (1.3), in order to provide eventually the gradient–related direction \(p_h\) in (1.2). On this guideline, we first need to prove that both these solvers yield a gradient–related direction to the optimization framework. I.e., the direction \(p_h\) in (1.2) is eventually bounded and of sufficient descent, namely for any \(h \ge {\bar{h}} \ge 1\) the next definition holds.
Definition 1.1
Given the direction \(p_h\) in (1.2), which approximately solves (1.3), let \({\bar{h}}\), \(\sigma _1\), \(\sigma _2\) and M be finite positive values independent of h, with \({\bar{h}} \ge 1\). Then, we say that \(p_h\) is gradient–related at \(x_h\) if for any \(h\ge {\bar{h}}\) the next couple of conditions hold:
For this purpose, as regards the CG, the reader may refer to [11, 12, 18]. On the other hand, we also need to analyze the Lanczos process, adopted inside SYMMBK algorithm. As well known, one of the advantages of using the Lanczos process in place of CG algorithm is that it does not break down in the indefinite case. We recall that in the case the matrix \(\nabla ^2f(x_h)\) is positive definite, from a theoretical point of view, using the Lanczos process or CG algorithm is to a large extent equivalent [23, 24].
The paper is organized as follows. In Sect. 2 some preliminaries on Truncated Newton method and Lanczos process are reported; then, the Bunch and Kaufman decomposition, as well as some basics on SYMMBK (see also [6]), are detailed. In Sect. 3 we show how to compute a gradient–related direction by using the Bunch and Kaufman decomposition. Section 4 details numerical experiments. Finally, Sect. 4 reports some concluding remarks.
We indicate by \(\Vert \cdot \Vert \) the Eclidean norm of real vectors and matrices. Moreover, \(\lambda _\ell (C)\) represents the \(\ell \)th eigenvalue of the real symmetric matrix C. Finally, \(e_i\) is the ith real unit vector.
2 Preliminaries
In this section we report some basics we will use in the sequel. In particular, first we recall a general scheme of a linesearch–based Truncated Newton algorithm. Afterwards, we report the well known Lanczos process. Finally, we detail the Bunch and Kaufman factorization in order to decompose the tridiagonal matrix provided by the Lanczos process.
2.1 Truncated Newton method
A practical linesearch–based Truncated Newton algorithm can be described as follows (see e.g. [21]).

In large scale settings, iterative methods like the CG algorithm can be used in the inner iterations. In the case the Hessian matrix in (1.3) is indefinite, then the Lanczos algorithm may successfully be used as an alternative to the CG method, since it does not suffer for a possible pivot breakdown. We remark that within the Truncated Newton methods, the importance of an efficient truncation criterion for the inner iterations was pointed out in [8, 9, 22]. More recently, an adaptive truncation rule, in order to enhance the residual–based criterion, was proposed in [3, 4].
Assumption 2.1
Given the function  in (1.1), with \(f \in C^2({\mathbb {R}}^n)\), the sequence \(\{x_h\}\) in (1.2) is such that \(\{x_h\} \subset \Omega \), with \(\Omega \subset {\mathbb {R}}^n\) compact.
in (1.1), with \(f \in C^2({\mathbb {R}}^n)\), the sequence \(\{x_h\}\) in (1.2) is such that \(\{x_h\} \subset \Omega \), with \(\Omega \subset {\mathbb {R}}^n\) compact.
For completeness we close this section by recalling a very general result of global convergence for Truncated Newton methods (see any textbook on Continuous Optimization).
Proposition 2.2
Let us consider the sequences \(\{x_h\}\) and \(\{p_h\}\) in (1.2). Assume \(\{x_h\}\) satisfies Assumption 2.1and \(\{p_h\}\) fulfills Definition 1.1. If the steplength \(\alpha _h\) in (1.2) is computed by an Armijo-type linesearch procedure, then
-
The sequence \(\{f(x_k)\}\) converges;
-
The sequence \(\{\nabla f(x_k)\}\) satisfies \(\lim _{k \rightarrow \infty } \Vert \nabla f(x_k)\Vert = 0.\)
2.2 Basics of the Lanczos process
As well known, the Lanczos process (see [6]) is an efficient tool to transform the symmetric indefinite linear system (1.3) into a symmetric tridiagonal one. On this guideline, consider the Newton equation (1.3) and rewrite it as follows (here we drop for simplicity the dependency on the subscript h):
where
-
\(A = \nabla ^2 f(x_h)\) is a symmetric (possibly dense) nonsingular matrix;
-
\(b = -\nabla f(x_h)\) is a constant (bounded) vector.
A practical implementation of the Lanczos process applied to (2.1), which generates the orthogonal Lanczos vectors \(q_i\), \(i \ge 1\), is reported in the scheme below.

Suppose the Lanczos process has performed k iterations; then,
-
The k vectors \( q_1, \ldots , q_k\), namely the Lanczos vectors, were generated;
-
The k scalars \(\delta _1, \ldots , \delta _k\) and the \(k-1\) nonzero scalars \(\gamma _2, \ldots , \gamma _k\) were generated.
Defining  as the matrix whose columns are the Lanczos vectors, that is
as the matrix whose columns are the Lanczos vectors, that is
and the symmetric tridiagonal matrix 
the Lanczos process generates \(T_k\) from (2.1) in \(k\le n\) steps. On the other hand, after \(k \le n\) iterations the next additional relations also hold for the Lanczos process:
In particular, if \(\gamma _{k+1} = 0\) in (2.4), then from (2.4)–(2.8) we have (see also [5])
Relations (2.9) also reveal that, since \(T_k\) is nonsingular, as long as \(\gamma _{k+1} \ne 0\) in (2.4) then computing the vector \(y_k\) from \(T_ky_k = \Vert b\Vert e_1\) may easily yield \(d_k = Q_ky_k\), being \(d_k\) an approximate solution of the linear system in (2.1).
2.3 Bunch and Kaufman decomposition
As reported in Sect. 2.1, unlike the CG method, the Lanczos process does not break down if matrix A in (2.1) is indefinite nonsingular. Furthermore, by (2.5)–(2.6) the nonsingularity of A also yields the nonsingularity of matrix \(T_k\). On the other hand, observe that a suitable decomposition of the tridiagonal matrix \(T_k\) in (2.3) is mandatory, in order to easily compute \(y_k\) by solving the tridiagonal system \(T_k z=\Vert b\Vert e_1\). However, in the case the matrix A is indefinite, the Cholesky factorization of \(T_k\) may not exist. In this regard, the Bunch and Kaufman decomposition of \(T_k\) may be adopted, as in SYMMBK algorithm. We detail now for \(T_k\) the Bunch and Kaufman decomposition (see [2])
where \(B_k\) is a block diagonal matrix with \(1\times 1\) or \(2\times 2\) diagonal blocks, and \(S_k\) is a unit lower triangular matrix, such that its non-zeroes are restricted to three main diagonals. The diagonal blocks of \(B_k\) represent pivoting elements in the factorization (2.10). In particular, in order to control the growth factor when computing the decomposition (2.10), the scalar
is selected (see [5]), and the choice of \(1\times 1\) pivot or \(2\times 2\) pivot for \(B_k\) is based on the following rule (which only refers, without loss of generality, to the first step of the decomposition (2.10)):
-
If \(|\delta _1| > \eta (\gamma _2)^2\), then \(\delta _1\) in (2.3) is used as a \(1\times 1\) pivot to generate the factorization (2.10) of \(T_k\). Namely, we have \(T_k = S_kB_kS_k^T\) with
$$\begin{aligned} T_k \ = \ S_k B_k S_k^T \ = \ \left( \begin{array}{c|c} 1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline S_{2,1} &{}\quad \\ 0 &{}\quad {{I}} \\ \vdots &{}\quad \\ 0 &{}\quad \\ \end{array} \right) \left( \begin{array}{l|l} \delta _1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline 0 &{}\quad \\ 0 &{}\quad {{{\tilde{T}}_{k-1}}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) \left( \begin{array}{c|cc} 1&S_{2,1}&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline 0 &{} &{} \\ 0 &{} &{} {{I}} \\ \vdots &{} &{} \\ 0 &{} &{} \\ \end{array} \right) . \qquad \end{aligned}$$(2.11)After a brief computation we have
$$\begin{aligned} T_k= & {} \left( \begin{array}{c|c} 1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline S_{2,1} &{} \\ 0 &{} {{I}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) \left( \begin{array}{c|c} \delta _1&\delta _1 S_{2,1} \ \ \begin{matrix}0 \cdots 0 \end{matrix} \\ \hline 0 &{} \\ 0 &{} {{{\tilde{T}}_{k-1}}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) \\= & {} \left( \begin{array}{c|c} \delta _1&\delta _1 S_{2,1} \ \ \begin{matrix}0 \cdots \cdots \cdots \cdots \cdots 0 \end{matrix} \\ \hline \begin{array}{c} \delta _1 S_{2,1} \\ \vdots \\ \vdots \\ 0 \end{array}&\left( \begin{array}{c|c} \delta _1 S_{2,1}^2 &{} \begin{matrix}0 \cdots 0\end{matrix} \\ \hline 0 &{} \\ 0 &{} {{\emptyset }} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) + {{{\tilde{T}}_{k-1}}} \end{array} \right) , \end{aligned}$$so that \({\tilde{T}}_{k-1}\) is itself a tridiagonal matrix with
$$\begin{aligned} {\tilde{T}}_{k-1} \ = \ T_k[2:k,2:k] - \left( \begin{array}{c|c} \delta _1 S_{2,1}^2&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline 0 &{} \\ 0 &{} {{\emptyset }} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) \end{aligned}$$(2.12)and \(T_k[2:k,2:k]\) is the \((k-1)\times (k-1)\) submatrix of \(T_k\) corresponding to the last \(k-1\) rows and \(k-1\) columns.
-
If \(|\delta _1| \le \eta (\gamma _2)^2\), then the \(2\times 2\) block
$$\begin{aligned} \left( \begin{array}{cc} \delta _1 &{} \gamma _2\\ \gamma _2 &{} \delta _2\\ \end{array} \right) \end{aligned}$$(2.13)is used as a \(2\times 2\) pivot, to generate the factorization (2.10), so that
$$\begin{aligned} T_k = S_k B_k S_k^T = \left( \begin{array}{cc|c} 1&0&\begin{matrix}0 \ldots 0\end{matrix} \\ 0 &{} 1 &{} \begin{matrix}0 \ldots 0\end{matrix} \\ \hline S_{3,1} &{} S_{3,2} &{} \\ 0 &{} 0 &{} {{I}} \\ \vdots &{} \vdots &{} \\ 0 &{} 0 &{} \\ \end{array} \right) \left( \begin{array}{cc|c} \delta _1&\gamma _2&\begin{matrix}0 \ldots 0\end{matrix} \\ \gamma _2 &{} \delta _2 &{} \begin{matrix}0 \ldots 0\end{matrix} \\ \hline 0 &{} 0 &{} \\ 0 &{} 0 &{} {{{\tilde{T}}_{k-2}}} \\ \vdots &{} \vdots &{} \\ 0 &{} 0 &{} \\ \end{array} \right) \left( \begin{array}{cc|cc} 1&0&S_{3,1}&\begin{matrix}0 \ldots 0\end{matrix} \\ 0 &{} 1 &{} S_{3,2} &{} \begin{matrix}0 \ldots 0\end{matrix} \\ \hline 0 &{} 0 &{} &{} \\ 0 &{} 0 &{} &{} \\ \vdots &{} \vdots &{} &{} {{I}} \\ 0 &{} 0 &{} &{} \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$(2.14)being now
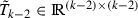 a tridiagonal matrix satisfying $$\begin{aligned} {\tilde{T}}_{k-2} \ = \ T_k[3:k,3:k] - \left( \begin{array}{c|c} \left( \begin{array}{c} S_{3,1} \\ S_{3,2} \end{array} \right) ^T \left( \begin{array}{cc} \delta _1 &{} \gamma _2 \\ \gamma _2 &{} \delta _2 \end{array} \right) \left( \begin{array}{c} S_{3,1} \\ S_{3,2} \end{array} \right)&\begin{matrix} 0 \cdots 0 \end{matrix} \\ \hline 0 &{} \\ 0 &{} {{\emptyset }} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) . \end{aligned}$$(2.15)
a tridiagonal matrix satisfying $$\begin{aligned} {\tilde{T}}_{k-2} \ = \ T_k[3:k,3:k] - \left( \begin{array}{c|c} \left( \begin{array}{c} S_{3,1} \\ S_{3,2} \end{array} \right) ^T \left( \begin{array}{cc} \delta _1 &{} \gamma _2 \\ \gamma _2 &{} \delta _2 \end{array} \right) \left( \begin{array}{c} S_{3,1} \\ S_{3,2} \end{array} \right)&\begin{matrix} 0 \cdots 0 \end{matrix} \\ \hline 0 &{} \\ 0 &{} {{\emptyset }} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) . \end{aligned}$$(2.15)
Following a simple recursion, the tridiagonal matrices \(\tilde{T}_{k-1}\) in (2.12) and \({\tilde{T}}_{k-2}\) in (2.15) can be similarly decomposed, so that the entries of \(S_k\) in (2.10) can be fully computed after m pivoting steps of the Bunch and Kaufman decomposition, with \(m \le k\) (see [5] and relations (2.19)–(2.20) or (2.25)–(2.26)).
2.4 Basics of SYMMBK
Here we report some basics of the SYMMBK algorithm (first proposed by Chandra in [5]), that uses the Bunch and Kaufman factorization in (2.10) to compute \(d_k\) in (2.9). Technicalities in this section are needed to provide formulae (2.22)–(2.24) and (2.28)–(2.30), which are essential to prove properties for our proposal in Sect. 3. To this aim, recalling (2.10) we introduce the \(n\times k\) matrix \(W_k = \left[ w_1 ~ ~ \vdots ~ ~ \vdots ~ ~ w_k \right] \) and the vector \(\zeta ^{(k)} = (\zeta _1, \ldots , \zeta _k)^T\) such that
By (2.10), (2.16) and (2.17), the equations in (2.9) can be rewritten as follows:
Then, to calculate the vector \(d_k\) of (2.9), we equivalently need to compute both \(W_k\) and \(\zeta ^{(k)}\). In this regard, we must provide in (2.18) the matrices \(S_k\) and \(B_k\), distinguishing between the cases where either a \(1\times 1\) or a \(2\times 2\) pivoting step was performed for their computation. This can be easily done by considering that the first step is performed as in (2.11) (\(1 \times 1\) pivot) or (2.14) (\(2 \times 2\) pivot). Then, for any successive step we use information from the previous pivot, as reported hereafter (we assume that applying the rule (j)–(jj) in Sect. 3 the Bunch and Kaufman decomposition performed m steps, with \(m \le k\)). To preserve the notation used by Chandra [5], here we simply focus on the last pivot; then, we infer results for the intermediate pivots, too.
If the last pivot performed is \(1\times 1\) (i.e. according with the rule (j) we have \(\delta _{k}\) large enough), then from Sect. 2.3 the first relation \(S_kB_k\zeta ^{(k)} = \Vert b\Vert e_1\) in (2.18) is equivalent to
where \(s_1\), \(s_2\), \(b_1\), \(b_2\), \(b_3\), \(b_4\) are computed from the second last step. In particular, if the second last pivot was \(1\times 1\), then \(s_1 = b_2 = b_3 = 0\). From (2.19) we have
where
After some computations, replacing the expressions of \(B_k\) and \(S_k\) in (2.18) we obtain the following formulae
With an obvious generalization the formulae (2.22)–(2.24) hold replacing the step k with the step \(i \le k\), whenever a \(1 \times 1\) pivot is performed by the Bunch and Kaufman decomposition.
Similarly, if the last pivot performed is now \(2\times 2\) (i.e. according with the rule (jj) we have \(\delta _{k-1}\) relatively small and \(|\delta _{k-1} \delta _k - \gamma _k^2|\) large enough), then \(S_kB_k\zeta ^{(k)} = \Vert b\Vert e_1\) in (2.18) is equivalent to
where \(s_1\), \(s_2\), \(b_1\), \(b_2\), \(b_3\), \(b_4\) are computed from the second last step. In particular, if the second last pivot was \(1\times 1\), then \(s_1 = b_2 = b_3 = 0\). By multiplying in (2.25) we have
where now
After some computations, replacing again the expressions of \(B_k\) and \(S_k\) in (2.18), we obtain the following formulae
As for (2.22)–(2.24), the formulae (2.28)–(2.30) hold replacing the step k with the step \(i \le k\), as long as at step i a \(2 \times 2\) pivot is used. In the end, we conclude that SYMMBK algorithm generates the vectors \(z_i\), \(i=1,\ldots ,k\), which represent a sequence of approximations of the vector \(d_k\) satisfying (2.18). Moreover, the direction \(d_k=z_k\) satisfies (2.18) (or equivalently (2.9)).
3 Our proposal
As detailed in Sect. 2.3, the Bunch and Kaufman decomposition used within the SYMMBK algorithm is able to cope with Newton’s equation (2.1), also in the indefinite case. However, the search direction provided by (2.9) might not be gradient–related, at the hth outer iteration. In this section we aim at suitably adapting SYMMBK algorithm, in order to guarantee that, using the computed approximate solution of (1.3), we can yield a gradient–related direction. For this purpose, first of all we need to slightly modify the partial pivoting rule used for choosing \(1\times 1\) or \(2\times 2\) pivot in the Bunch and Kaufman decomposition. In particular, given \(\omega \in (0,1)\) the choice for \(1\times 1\) pivot or \(2\times 2\) pivot in Sect. 2.3, in order to obtain (2.11) or (2.14), is replaced by the following rule (again for simplicity we refer only to the first step of the decomposition):
- (j):
-
if \(|\delta _1| > \omega \eta (\gamma _2)^2\), then \(\delta _1\) is used as a \(1\times 1\) pivot;
- (jj):
-
if \(|\delta _1| \le \omega \eta (\gamma _2)^2\), then the \(2\times 2\) block (2.13) is used as a \(2\times 2\) pivot.
Now we show that the novel condition \(|\delta _1| > \omega \eta (\gamma _2)^2\) in (j) (which yields (2.11)), along with the novel condition \(|\delta _1| \le \omega \eta (\gamma _2)^2\) in (jj) (which yields (2.14)), allow to use an adapted SYMMBK algorithm for the construction of a gradient–related direction. To this aim, we recall that repeatedly performing the factorizations (2.11) and (2.14) we finally obtain for \(T_k\) the decomposition (2.10), where (\(m \le k\))
Moreover, by (2.6) the columns of \(Q_k\) are orthogonal unit vectors, and from Assumption 2.1 then b in (2.1) has a bounded norm. Thus, according to (1.4) and (1.5) of Definition 1.1, \(p_h\) in (1.2) is gradient–related at \(x_h\) as long as the next two conditions are satisfied:
-
(i)
The matrix \(T_k\) in (2.9) is nonsingular with the vector \(y_k=T_k^{-1}(\Vert b\Vert e_1)\) bounded;
-
(ii)
\(p_h\) is a descent direction at \(x_h\) and (1.5) holds.
Of course, since the matrix A in (2.1) is possibly indefinite, the direction \(d_k\) in (2.9) might be of ascent and/or not gradient–related. However, we show how to possibly modify \(d_k\) in order to obtain the gradient–related direction \(p_h\), to be used in (1.2).
3.1 How SYMMBK can provide a gradient–related direction
Here we prove that both adopting the rule (j)–(jj) in the Bunch and Kaufman decomposition, and slightly adapting the SYMMBK algorithm for the solution of Newton’s equation (2.1), we can provide a gradient–related direction \(p_h\) at \(x_h\) for the optimization problem (1.1). In this regard, we first refer the reader to Sect. 2.4, which shows that pairing (j)–(jj) with SYMMBK, to iteratively compute the vector \(d_k\) in (2.9), we generate the sequence of vectors \(z_i\), \(i\le k\), such that
-
If at step i a \(1\times 1\) pivot is performed by the Bunch and Kaufman decomposition in SYMMBK, then the vector \(z_i = z_{i-1} + \zeta _i w_i\) is generated,
-
If at step i a \(2\times 2\) pivot is performed by the Bunch and Kaufman decomposition in SYMMBK, then the vector \(z_i = z_{i-2} + \zeta _{i-1} w_{i-1} + \zeta _i w_i\) is generated,
-
When \(i=k\) we have \(d_k=z_k\),
and the quantities \(\{\zeta _i\}\), \(\{w_i\}\) are computed using the entries of matrices \(S_k\) and \(B_k\) in (2.10). As regards the vectors \(\{z_i\}\), the next result gives a relevant property of these vectors.
Proposition 3.1
Let the matrix A in (2.1) be nonsingular, and let \(z_i\), \(i \le k\) be the directions generated by the SYMMBK algorithm when solving (2.9). Assume that the Bunch and Kaufman decomposition (2.10) is adopted according with the rule (j)–(jj). Then, for proper values of the parameter \(\omega \) in (j)–(jj) we have that
-
Any direction in the finite sequences \(\zeta _1 w_1, \ldots ,\zeta _k w_k\) and \(z_1, \ldots ,z_k\) is bounded;
-
The vector \(d_k\) in (2.9) coincides with \(z_k\) (and is bounded).
Proof
In order to obtain the overall proof, without loss of generality it suffices to assume \(k>1\) and separately consider only the first step in the cases (2.11) and (2.14), since a similar reasoning holds for any step i (see Sect. 2.4). Indeed, since \({\tilde{T}}_{k-1}\) in (2.12) and \({\tilde{T}}_{k-2}\) in (2.15) are tridiagonal, then we can apply for them the same reasoning adopted, at the first step, for \(T_k\). In this regard we have:
-
If the first step is a \(1\times 1\) pivot step, comparing \(T_k\) in (2.11) and \(T_k\) in (2.3) we get
$$\begin{aligned} \delta _1S_{2,1} = \gamma _2, \end{aligned}$$(3.2)that is
$$\begin{aligned} S_{2,1} = \frac{\gamma _2}{\delta _1}. \end{aligned}$$(3.3)Since \(\gamma _2 \ge \varepsilon \) (see the Lanczos process) and \(|\delta _1| > \omega \eta (\gamma _2)^2\) we have
$$\begin{aligned} |S_{2,1}| = \frac{|\gamma _2|}{|\delta _1|} < \frac{1}{\omega \eta |\gamma _2|} \le \frac{1}{\omega \eta \varepsilon }, \end{aligned}$$(3.4)i.e. in case of \(1\times 1\) pivot, we obtain in (2.11) that \(|\delta _1| = |q_1^TAq_1| \le \max _{\ell } \{|\lambda _{\ell }(A)|\}\) and \(|S_{2,1}|\) is bounded;
-
If the first step is a \(2\times 2\) pivot step, comparing \(T_k\) in (2.14) and \(T_k\) in (2.3) we get
$$\begin{aligned} \left\{ \begin{array}{l} S_{3,1}\delta _1 + S_{3,2}\gamma _2 = 0 \\ S_{3,1}\gamma _2 + S_{3,2}\delta _2 = \gamma _3, \end{array} \right. \end{aligned}$$(3.5)that is
$$\begin{aligned} \left\{ \begin{array}{l} S_{3,1} = -\displaystyle \frac{\gamma _3\gamma _2}{\delta _1\delta _2 - (\gamma _2)^2} \\ S_{3,2} = \displaystyle \frac{\gamma _3\delta _1}{\delta _1\delta _2 - (\gamma _2)^2}. \end{array} \right. \end{aligned}$$(3.6)Now observe that
$$\begin{aligned} \gamma _2= & {} \Vert Aq_1 - \delta _1 q_1\Vert \ \le \ \Vert Aq_1\Vert + \Vert (q_1^TAq_1)q_1\Vert \nonumber \\\le & {} \max _{\ell } \{ |\lambda _{\ell }(A)|\}\Vert q_1\Vert + \left( \max _{\ell } \{ |\lambda _{\ell }(A)|\} \right) \Vert q_1\Vert ^3 \ \le \ 2 \left[ \max _{\ell } \{ |\lambda _{\ell }(A)|\}\right] , \nonumber \\ \gamma _3= & {} \Vert Aq_2 - \delta _2 q_2-\gamma _2 q_1\Vert \ \le \ 4 \left[ \max _{\ell } \{ |\lambda _{\ell }(A)|\}\right] , \nonumber \\&\vdots&\nonumber \\ \gamma _{k+1}= & {} \Vert Aq_k - \delta _k q_k - \gamma _k q_{k-1}\Vert \ \le \ 2 k \cdot \left[ \max _{\ell } \{ |\lambda _{\ell }(A)|\} \right] , \end{aligned}$$(3.7)which implies that since \(k \le n\) then \(\gamma _j\) is bounded, for any \(j \ge 1\). Moreover, in case \(\delta _1=0\) or \(\delta _2=0\) then \(|\delta _1\delta _2 - (\gamma _2)^2| = |-(\gamma _2)^2| > \varepsilon ^2\), and by (3.6)–(3.7), along with \(|\delta _1| \le \omega \eta (\gamma _2)^2\), we obtain that both \(S_{3,1}\) and \(S_{3,2}\) are bounded by a constant,
$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle |S_{3,1}| \le \frac{| \gamma _3 \gamma _2|}{(\gamma _2)^2}=\frac{|\gamma _3|}{\gamma _2} \le \frac{4 \max _{\ell } \left\{ |\lambda _{\ell }(A)|\right\} }{\varepsilon } \\ \displaystyle |S_{3,2}| \le \gamma _3\omega \eta \le 4 \omega \eta \max _{\ell } \left\{ |\lambda _{\ell }(A)| \right\} . \end{array} \right. \end{aligned}$$(3.8)On the other hand, in case \(\delta _1 \ne 0\) and \(\delta _2 \ne 0\) in (3.6), recalling that \(\gamma _2 \ge \varepsilon \) and using the condition \(|\delta _1| \le \omega \eta (\gamma _2)^2\) we distinguish two subcases:
-
\(\delta _2 > 0\) which implies \(\delta _1\delta _2-(\gamma _2)^2 \le -(\gamma _2)^2 (1-\omega \eta \delta _2)\), so that imposing \(1> 1-\omega \eta \delta _2 > \xi \), for a given \(0< \xi < 1\), we obtain \(\omega < (1-\xi )/(\eta \delta _2)\) and \(|\delta _1\delta _2-(\gamma _2)^2|> \varepsilon ^2 \xi \). Thus, if in the test (j)–(jj) we finally set
$$\begin{aligned} 0< \omega< \min \left\{ 1 \ , \ \frac{1-\xi }{\eta \delta _2} \right\} , \qquad \ \text {for some } 0< \xi < 1, \end{aligned}$$then, \(S_{3,1}\) and \(S_{3,2}\) in (3.5)–(3.6) are bounded;
-
\(\delta _2 < 0\) which implies \(\delta _1\delta _2-(\gamma _2)^2 \le -(\gamma _2)^2 (1+\omega \eta \delta _2)\), so that imposing now \(1> 1+\omega \eta \delta _2 > \xi \), for a given \(0< \xi < 1\), we obtain \(\omega < (\xi -1)/(\eta \delta _2)\) and \(|\delta _1\delta _2-(\gamma _2)^2|> \varepsilon ^2 \xi \). Thus, if in the test (j)–(jj) we finally set
$$\begin{aligned} 0< \omega< \min \left\{ 1 \ , \ \frac{\xi -1}{\eta \delta _2} \right\} , \qquad \ \text {for some } 0< \xi < 1, \end{aligned}$$then, again \(S_{3,1}\) and \(S_{3,2}\) in (3.5)–(3.6) are bounded.
Thus, in both the above subcases \(S_{3,1}\) and \(S_{3,2}\) in (3.6) are evidently bounded by a constant value, with
$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle |S_{3,1}| \le \frac{8 \max _{\ell } \left\{ |\lambda _{\ell }(A)| \right\} ^2}{\varepsilon ^2 \xi } \\ \displaystyle |S_{3,2}| \le \frac{4 \max _{\ell } \left\{ |\lambda _{\ell }(A)| \right\} ^2}{\varepsilon ^2 \xi }. \end{array} \right. \end{aligned}$$(3.9) -
Finally, iterating the above procedure for any step, by (3.2), (3.6), (3.8), (3.9) and using the test (j)–(jj) in the Bunch and Kaufman decomposition to decide pivoting \(1 \times 1\) or \(2 \times 2\), we obtain that
- (a):
-
By (2.11)–(2.12) and (2.14)–(2.15), any pivoting element \(B_k^j\) in (3.1) has a determinant which is bounded away from zero;
- (b):
-
All the entries of the matrix \(S_k\) in (2.11) and (2.14) are bounded by constant values independent of k.
This implies (see Sect. 2.4) that any vector in the sequences \(\zeta _1 w_1, \ldots , \zeta _k w_k\) and \(z_1, \ldots , z_k\) is bounded. Moreover, the vector \(d_k=z_k\) fulfilling (2.9) is unique and bounded.
Observe that by the previous result, the condition (i) in Sect. 3 is partly guaranteed to hold. However, using SYMMBK algorithm, the direction \(d_k\) computed in Proposition 3.1 might not be a direction of sufficient descent. To guarantee also the fulfillment of (ii), we propose to suitably use the information collected by the sequence \(\{\zeta _i w_i\}\), in order to compute \(p_h\) endowed with descent property.
From Proposition 3.1 and Sect. 2.4, the real vector \(\zeta _i w_i = z_i-z_{i-1}\) (respectively the vector \(\zeta _{i-1} w_{i-1} + \zeta _i w_i = z_i-z_{i-2}\)) is bounded. Thus, we propose to compute the search direction \(p_h\), at the outer iteration h of the Truncated Newton method, in accordance with the next scheme:

We remark that in case the matrix A in (2.1) is positive definite, and the parameter \(\omega \) in (j)–(jj) is sufficiently small (i.e. no \(2\times 2\) pivot is performed), then the vector \(p_h\) computed by the Reverse–Scheme coincides with Newton’s direction.
Now, in the next proposition we prove that the direction \(p_h\), obtained by Reverse–Scheme at any iterate of the sequence \(\{x_h\}\) of the Truncated Newton method, is gradient–related. This result is not an immediate consequence of Proposition 3.1, since the latter proposition merely guarantees the simple boundedness of the direction \(d_k\), for a given \(k \ge 1\). Conversely, the next result proves that, under mild additional assumptions, all the vectors in the sequence \(\{p_h\}\) are of sufficient descent and eventually are uniformly bounded by a positive finite constant.
Proposition 3.2
Let Assumption 2.1hold. Assume that Proposition 3.1holds with \(A=\nabla ^2f(x_h)\) and \(b=-\nabla f(x_h)\). Let the search direction \(p_h\) in (1.2) be computed as in Reverse–Scheme. Then, for any \(k \ge 1\) the direction \(d_k\) in (2.9) is bounded, namely it satisfies \(\Vert d_k\Vert < \mu \), for some positive value of \(\mu \), and \(p_h\) is a gradient–related direction as in (1.5).
Proof
The statement trivially holds if in Proposition 3.1 the Lanczos process performs just one iteration, being \(\gamma _2 < \varepsilon \). In all the other cases (i.e. the Lanczos process has performed at least 2 iterations), we first prove that \(p_h\) is of sufficient descent for f(x) at \(x_h\). In this regard, it suffices to prove the sufficient descent property for \(p_h\) after the first step of the Bunch and Kaufman decomposition in SYMMBK, since the Reverse–Scheme accumulates only non-ascent directions in \(p_h\). To this aim, we distinguish between two cases, which may occur at iterate \(x_h\), when applying the Bunch and Kaufman decomposition to matrix \(T_k\) in (2.9):
-
The first step corresponds to a \(1 \times 1\) pivot. Then, by (2.16) and (2.22)–(2.24), we have for the vector uu in Reverse–Scheme
$$\begin{aligned} uu= & {} -sgn[\nabla f(x_h)^T(\zeta _1 w_1)] \zeta _1 w_1 = -sgn[\nabla f(x_h)^T(\zeta _1 q_1)] \zeta _1 q_1 \nonumber \\= & {} -sgn[-\zeta _1 \Vert \nabla f(x_h)\Vert ] \zeta _1 \left( - \frac{\nabla f(x_h)}{\Vert \nabla f(x_h)\Vert } \right) = -sgn[\zeta _1]\zeta _1 \frac{\nabla f(x_h)}{\Vert \nabla f(x_h)\Vert } \nonumber \\= & {} - |\zeta _1| \frac{\nabla f(x_h)}{\Vert \nabla f(x_h)\Vert }, \end{aligned}$$(3.10)so that
$$\begin{aligned} \nabla f(x_h)^Tp_h= & {} - \frac{|\zeta _1|}{\Vert \nabla f(x_h)\Vert } \Vert \nabla f(x_h)\Vert ^2 +\nonumber \\&\quad \sum _{i\ge 2}-sgn \left[ \nabla f(x_h)^T (\zeta _i w_i) \right] \nabla f(x_h)^T(\zeta _i w_i) \nonumber \\\le & {} - |\zeta _1| \Vert \nabla f(x_h)\Vert . \end{aligned}$$(3.11)More explicitly, by (2.17) and relations (2.9)–(2.11) we have
$$\begin{aligned} \zeta ^{(k)}= & {} S_k^T y_k \ = \ S_k^T T_k^{-1}\Vert b\Vert e_1 \ = \ B_k^{-1}S_k^{-1}\Vert b\Vert e_1 \\= & {} \left( \begin{array}{c|c} \delta _1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline 0 &{} \\ 0 &{} {{{\tilde{T}}_{k-1}}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) ^{-1} \left( \begin{array}{c|c} 1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline S_{2,1} &{} \\ 0 &{} {{I}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) ^{-1} \Vert b\Vert e_1 \\= & {} \left( \begin{array}{c|c} 1/\delta _1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline 0 &{} \\ 0 &{} {{{\tilde{T}}_{k-1}^{-1}}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) \left( \begin{array}{c|c} 1&\begin{matrix}0 \cdots 0\end{matrix} \\ \hline -S_{2,1} &{} \\ 0 &{} {{I}} \\ \vdots &{} \\ 0 &{} \\ \end{array} \right) \Vert b\Vert e_1 \ = \ \Vert b\Vert \left( \begin{array}{c} \displaystyle \frac{1}{\delta _1} \\ *\\ \vdots \\ *\end{array} \right) , \end{aligned}$$where the asterisks represent irrelevant entries. Then, \(\zeta _1 = \Vert b\Vert /\delta _1\). Moreover, by Assumption 2.1 the set \(\Omega \) is compact, so that \(|\zeta _1| = \Vert b\Vert /|\delta _1| \ge \Vert b\Vert /\max _{\ell } \left| \lambda _{\ell } [\nabla ^2 f(x_h)] \right| \ge \Vert b\Vert /\lambda _M\), for some \(0< \lambda _M < +\infty \). Thus, relation (3.11) becomes
$$\begin{aligned} \nabla f(x_h)^Tp_h \le - |\zeta _1| \Vert \nabla f(x_h)\Vert \le - \frac{1}{\lambda _M} \Vert \nabla f(x_h)\Vert ^2. \end{aligned}$$(3.12) -
The first step corresponds to a \(2 \times 2\) pivot. Then, recalling (2.28) we have \(w_2=q_2\), so that by (3.10) for the vectors uu and vv in Reverse–Scheme the next relations hold
$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle uu = -sgn[\nabla f(x_h)^T(\zeta _1 w_1)] \zeta _1 w_1 = -|\zeta _1| \frac{\nabla f(x_h)}{\Vert \nabla f(x_h)\Vert }, \\ \displaystyle vv = -sgn[\nabla f(x_h)^T(\zeta _2 w_2)] \zeta _2 w_2 = -sgn[\nabla f(x_h)^T(\zeta _2 q_2)] \zeta _2 q_2. \end{array} \right. \end{aligned}$$(3.13)Now, again by (2.17) and relations (2.9)–(2.10), (2.14) we get

where again the asterisks represent irrelevant entries. Thus, it results
$$\begin{aligned} \begin{array}{c} \displaystyle \zeta _1 = \frac{\delta _2}{\delta _1\delta _2 - (\gamma _2)^2} \Vert b\Vert , \\ \displaystyle \zeta _2 = \frac{-\gamma _2}{\delta _1\delta _2 - (\gamma _2)^2} \Vert b\Vert . \end{array} \end{aligned}$$Finally, similarly to (3.11), recalling that \(\nabla f(x_h)^Tq_2=-\Vert \nabla f(x_h)\Vert q_1^T q_2 = 0\), we have by (3.13) and Reverse–Scheme the relation
$$\begin{aligned} \nabla f(x_h)^Tp_h= & {} -sgn[\nabla f(x_h)^T({{\tilde{\zeta }}}_1 q_1)] \nabla f(x_h)^T ({{\tilde{\zeta }}}_1 q_1) \nonumber \\&+ \sum _{i > 2}-sgn \left[ \nabla f(x_h)^T (\zeta _i w_i) \right] \nabla f(x_h)^T(\zeta _i w_i) \nonumber \\\le & {} - |{{\tilde{\zeta }}}_1| \Vert \nabla f(x_h)\Vert \ \le \ - \phi \Vert \nabla f(x_h)\Vert ^2. \end{aligned}$$(3.14)
Relations (3.12) and (3.14) prove that for any \(h \ge 1\) the condition (1.5) is eventually fulfilled, with
As regards the boundedness of \(d_k\) in (2.9) and \(p_h\), for any \(h \ge 1\), observe that by (2.9) we first have
Then, \(\Vert d_k\Vert = \Vert y_k\Vert \le \Vert T_k^{-1}\Vert \cdot \Vert \nabla f(x_h)\Vert \le \Vert S_k^{-T} B_k^{-1}S_k^{-1}\Vert \Vert \nabla f(x_h)\Vert \le \Vert S_k^{-1}\Vert ^2 \cdot \Vert B_k^{-1}\Vert \cdot \Vert \nabla f(x_h)\Vert \). Now, let \(m_1\) be the number of steps where the test (j) is fulfilled (i.e. \(m_1\) is the number of \(1 \times 1\) pivot steps), so that \((k-m_1)/2\) is the number of \(2 \times 2\) pivot steps. Also observe that the inverse \(S_k^{-1}\) of \(S_k\) in (2.11) is given by
and the inverse \(S_k^{-1}\) of \(S_k\) in (2.14) is given by
Thus, the bound (3.4) on \(S_{2,1}\), along with the bounds (3.8) and (3.9) on \(S_{3,1}\) and \(S_{3,2}\) yield
where
Moreover, as regards the diagonal blocks of \(B_k^{-1}\) (see (2.11) and (2.14)), for any \(i \ge 1\) we have by the proof of Proposition 3.1 and the compactness of \(\Omega \) the following bounds:
Finally, by Assumption 2.1 we have that \(\Vert \nabla f(x_h)\Vert \) is bounded on \(\Omega \) by a constant value, showing that the direction \(d_k\) is bounded by a constant value independent of h. To complete the proof we show the boundedness of vectors \(\{\zeta _i w_i\}\) in Reverse–Scheme, by a constant value independent of h. From relation \(\Vert d_k\Vert =\Vert y_k\Vert \le \mu \), for any \(k \ge 1\), and recalling (3.15) along with relation \(S_k^T=[-S_k^{-1}]^T\), we immediately infer (using (2.17))
where \(\beta \) is given in (3.15). Similarly, by (2.18) we have \(W_k=Q_kS_k^{-T}\), so that any column \(w_i\) of \(W_k\) satisfies (see (3.15))
This implies, by (3.16) and the boundedness of vectors \(\zeta _1 w_1, \ldots ,\zeta _k w_k\) (see Proposition 3.1), that also \(\Vert uu\Vert \) and \(\Vert vv\Vert \) in Reverse–Scheme are bounded by a positive constant, for any \(x_h \in \Omega \). Thus, \(\Vert p_h\Vert \) is bounded by a positive constant independent of h.
4 Numerical experiments
In order to assess the effectiveness of the approach proposed in this paper, we performed an extensive numerical testing. We used the HSL_MI02 Fortran routine available from the HSL Mathematical Software Library [19] which implements the SYMMBK algorithm, where we modified the pivoting rule as described in Sect. 3, namely (j)–(jj) on page 9. Then, we embedded this routine within a standard implementation of a linesearch based Truncated Newton method, namely the one proposed in [15] (we refer to this paper for any implementation details), without considering any preconditioning strategy. Moreover, we replaced the CG used as iterative solver by the Truncated Newton method in [15] with the modified SYMMBK algorithm. It is worthwhile to note that in [15], in order to handle the indefinite case, the inner CG iterations are not terminated whenever a negative curvature direction is encountered. Indeed, by drawing inspiration from [18], positive and negative curvature CG directions \(\{d_i\}\) are separately accumulated, and then suitably combined to obtain the search direction. We report the following scheme of the CG method adopted in [15], in order to briefly describe the latter strategy.

In particular, at the kth CG inner iteration, the following vectors are defined
where for a given \( \epsilon \in (0 , 1) \)
\(|I_k^+|+|I_k^-|=k\). Then, the vector \(p_k^{P}+p_k^{N}\) is used as search direction. This choice has several advantages for which we refer to [15]. In particular, it can be proved that \(p_k^{P}+p_k^{P}\) is a gradient–related direction. However, as shown in [7], the use of \(p_k^{P}\) and \(p_k^{N}\) obtained by separating the contribution of negative and positive curvature directions actually corresponds to considering a modified positive definite linear system, in place of the original indefinite one. For this reason, in our numerical experiments, in order to avoid unfair conclusions, we prefer not to use the modified search direction \(p_k^{P}+p_k^{N}\) and adopt a more standard approach in the literature. Therefore, in our implementation we use the approximate solution of the original linear system as search direction. An additional safeguard is needed whenever the Hessian matrix is nearly singular at the hth iterate of the Truncated Newton method. In this case, the steepest descent direction is considered as “alternative” direction (both when the CG or the modified SYMMBK algorithms are adopted). As regards the termination criterion of the inner iteration, the standard residual–based criterion is used (see e.g. [3, 4, 21]), which we make slightly tighter (with respect to that in [15]) by multiplying the tolerance of the criterion by \(10^{-2}\). In this manner, a more accurate solution of the Newton system at each outer iteration of the methods is required, and possibly a more significant comparison between the use of the modified SYMMBK in place of the standard CG can be obtained. Finally, the parameter \(\xi \) in the proof of Proposition 3.1 is set as \(\xi = \max \{(1-\eta |\delta _2|), 10^{-1}\}\), so that we consequently chose \(\omega = \min \{1, (1-\xi )/ (\eta |\delta _2|)\}\) in (j)–(jj). In addition, the parameter \(\phi \) in Reverse–Scheme was set as \(\phi = 10^{-10}\): in this regard we strongly remark that in our numerical experience we always observed \({{\tilde{\zeta }}}_{i-1} \equiv \zeta _{i-1}\) in the Reverse–Scheme.
As regards the test problems, we selected all the large scale unconstrained test problems in the CUTEst collection [16], including both convex and nonconvex functions. In particular, we considered 112 problems whose dimension ranges from 1000 to 10,000. We report the results obtained in terms of number inner iterations, number of function evaluations and CPU time. The comparison between the use of the CG algorithm and the modified SYMMBK, when performing the inner iterations, is reported by using performance profiles [10]. Here the abscissa axis details values of the positive parameter \(\tau \ge 1\). In particular, for a given value \({\bar{\tau }}\) of the parameter \(\tau \), each profile represents the percentage of problems solved by the corresponding method, using at most \({\bar{\tau }}\) times the resource (inner iterations/function evaluations/CPU time) used by the best method.
Figure 1 reports the comparison in terms of inner iterations. By observing these plots, the performance of the two approaches seems to be similar and the use of the modified SYMMBK is slightly preferable in terms of robustness. The profiles in terms of function evaluations are reported in Fig. 2. In this case, the superiority of using the modified SYMMBK algorithm is more evident. Finally, as regards the comparison in terms of CPU, Fig. 3 indicates that the use of the standard CG leads to a slight improvement in terms of efficiency, but it is definitely less performing in terms of robustness. We recall indeed that though the CG can easily provide a gradient–related search direction in convex problems, it might prematurely stop in nonconvex problems.
Now, in order to better assess the quality of the search direction obtained by using the modified SYMMBK algorithm, we performed further numerical experiments. In particular we computed the normalized directional derivative of the search direction \(p_h\) in (1.2), namely \(\nabla f(x_h)^T p_h / \Vert \nabla f(x_h)\Vert \Vert p_h\Vert \), at each outer iteration of the CG and the modified SYMMBK method respectively, for some test problems. As an example, we report in Fig. 4 the normalized directional derivative obtained as the number of outer iterations increases, for the test problems DIXMAANJ-1500 (upper-left), DIXMAANK-3000 (upper-right), DIXMAANL-1500 (mid-left), DIXMAANL-3000 (mid-right), DIXMAANJ-3000 (lower-left), SPARSINE-1000 (lower-right), where the number indicates the dimension of the test problem.
Plot of the normalized directional derivative, when our proposal with the modified SYMMBK is used (+), and when the CG is used (empty squares). The plot refers to DIXMAANJ-1500 (upper-left), DIXMAANK-3000 (upper-right), DIXMAANL-1500 (mid-left), DIXMAANL-3000 (mid-right), DIXMAANJ-3000 (lower-left), SPARSINE-1000 (lower-right)
On these problems the method based on the modified SYMMBK algorithm outperforms the one based on the standard CG (a much smaller number of iterations is required to achieve convergence). Plots reveal that this is due to the fact that the quality of the Newton–type direction, obtained by means of the modified SYMMBK algorithm, is definitely better. Indeed, on one hand the use of the modified SYMMBK algorithm for computing the search direction enables to discard the steepest descent direction more frequently than the use of the standard CG. On the other hand, the introduction of the parameter \(\omega \) in the modified SYMMBK algorithm (see (j)–(jj)) allows to have values of the directional derivative which are more likely bounded away from zero. Similar behaviour is evidenced when solving many other test problems of the CUTEst collection. Note also that in the plots of Fig. 4, both the compared methods tend to initially select the steepest descent method as a search direction. This should not be surprising, inasmuch as in the early outer iterations the truncation criterion of the Truncated Newton method is less tight.
5 Conclusions
In this work, which deals with an efficient Truncated Newton method for solving large scale unconstrained optimization problems, we considered the use of an adapted Bunch and Kaufman decomposition for the solution of Newton’s equation. By slightly modifying the test performed at each iteration of the Bunch and Kaufman decomposition, we were able to ensure that the Newton–type direction computed by our proposal is gradient–related. Extensive numerical testing, on both convex and nonconvex problems, highlights the effectiveness and robustness of a Truncated Newton framework, where our modified SYMMBK algorithm is used in place of the CG method.
We remark that the enhanced robustness of our proposal, with respect to the CG method, is not only the consequence of the possible premature stopping of the CG on nonconvex problems. On the contrary, we often tend to generate at the current outer iteration an approximate Newton’s direction which yields a more effective directional derivative with respect to the CG.
Note that a comparison of the standard SYMMBK and our modified SYMMBK routines, within the same Truncated Newton method, yields to large extent, similar numerical results. However, the standard SYMMBK routine is unable to provide essential theoretical properties, which are sought for the search direction of the optimization framework.
Finally, we are persuaded that the modified test (j)–(jj) in SYMMBK might be worth investigating, also to construct a suitable negative curvature direction (see [14]), in nonconvex problems. This issue plays a keynote role in case the adopted Truncated Newton method is asked to provide also convergence to stationary points, where second order optimality conditions hold.
Furthermore, there is the chance that adaptively updating the parameter \(\omega \) in (j)–(jj) may further enhance the performance of our method, preserving the theory developed in Sect. 3.
References
Barret, R., Berry, M., Chan, T., Demmel, J., Donato, J., Dongarra, J., Eijkhout, V., Pozo, R., Romine, C., Van der Vorst, H.: Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods. SIAM, Philadelphia, PA (1994)
Bunch, J., Kaufman, L.: Some stable methods for calculating inertia and solving symmetric linear equations. Math. Comput. 31, 163–179 (1977)
Caliciotti, A., Fasano, G., Nash, S.G., Roma, M.: An adaptive truncation criterion, for linesearch-based truncated Newton methods in large scale nonconvex optimization. Oper. Res. Lett. 46, 7–12 (2018)
Caliciotti, A., Fasano, G., Nash, S.G., Roma, M.: Data and performance profiles applying an adaptive truncation criterion, within linesearch-based truncated Newton methods, in large scale nonconvex optimization. Data Brief 17, 246–255 (2018)
Chandra, R.: Conjugate gradient methods for partial differential equations, Ph.D. thesis, Yale University, New Haven. Research Report 129 (1978)
Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust-Region Methods. MPS-SIAM Series on Optimization. Society for Industrial Mathematics, Philadelphia (2000)
De Leone, R., Fasano, G., Sergeyev, Y.: Planar methods and grossone for the conjugate gradient breakdown in nonlinear programming. Comput. Optim. Appl. 71, 73–93 (2018)
Dembo, R., Eisenstat, S., Steihaug, T.: Inexact Newton methods. SIAM J. Numer. Anal. 19, 400–408 (1982)
Dembo, R., Steihaug, T.: Truncated-Newton algorithms for large-scale unconstrained optimization. Math. Program. 26, 190–212 (1983)
Dolan, E.D., Moré, J.: Benchmarking optimization software with performance profiles. Math. Program. 91, 201–213 (2002)
Fasano, G.: Planar-conjugate gradient algorithm for large-scale unconstrained optimization, part 1: theory. J. Optim. Theory Appl. 125, 523–541 (2005)
Fasano, G.: Planar-conjugate gradient algorithm for large-scale unconstrained optimization, part 2: application. J. Optim. Theory Appl. 125, 543–558 (2005)
Fasano, G.: Lanczos-conjugate gradient method and pseudoinverse computation, in unconstrained optimization. J. Optim. Theory Appl. 132, 267–285 (2006)
Fasano, G., Roma, M.: Iterative computation of negative curvature directions in large scale optimization. Comput. Optim. Appl. 38, 81–104 (2007)
Fasano, G., Roma, M.: Preconditioning Newton–Krylov methods in nonconvex large scale optimization. Comput. Optim. Appl. 56, 253–290 (2013)
Gould, N.I.M., Orban, D., Toint, P.L.: CUTEst: a constrained and unconstrained testing environment with safe threads. Comput. Optim. Appl. 60, 545–557 (2015)
Greenbaum, A.: Iterative Methods for Solving Linear Systems. SIAM, Philadelphia (1997)
Grippo, L., Lampariello, F., Lucidi, S.: A truncated Newton method with nonmonotone linesearch for unconstrained optimization. J. Optim. Theory Appl. 60, 401–419 (1989)
HSL, A collection of Fortran codes for large scale scientific computation. http://www.hsl.rl.ac.uk/
Marcia, R.: On solving sparse symmetric linear systems whose definiteness is unknown. Appl. Numer. Math. 58, 449–458 (2008)
Nash, S.: A survey of truncated-Newton methods. J. Comput. Appl. Math. 124, 45–59 (2000)
Nash, S., Sofer, A.: Assessing a search direction within a truncated-Newton method. Oper. Res. Lett. 9, 219–221 (1990)
Nocedal, J., Wright, S.: Numerical Optimization, 2nd edn. Springer, New York (2006)
Stoer, J.: Solution of large linear systems of equations by conjugate gradient type methods. In: Bachem, A., Grötschel, M., Korte, B. (eds.) Mathematical Programming. The State of the Art, pp. 540–565. Springer, Berlin (1983)
Acknowledgements
The authors wish to thank both the reviewers and the Associate Editor for their fruitful and constructive comments. G. Fasano thanks the National Research Council - Marine Technology Research Institute (CNR-INSEAN), Italy, along with the working group GNCS of IN\(\delta \)AM (Istituto Nazionale di Alta Matematica), Italy, for the support received.
Funding
Open access funding provided by Università Ca’ Foscari Venezia within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Caliciotti, A., Fasano, G., Potra, F. et al. Issues on the use of a modified Bunch and Kaufman decomposition for large scale Newton’s equation. Comput Optim Appl 77, 627–651 (2020). https://doi.org/10.1007/s10589-020-00225-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-020-00225-8




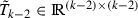 a tridiagonal matrix satisfying
a tridiagonal matrix satisfying 



