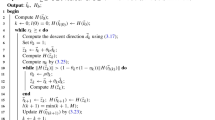A Lagrange multiplier method for semilinear elliptic state constrained optimal control problems

Abstract

In this paper we apply an augmented Lagrange method to a class of semilinear elliptic optimal control problems with pointwise state constraints. We show strong convergence of subsequences of the primal variables to a local solution of the original problem as well as weak convergence of the adjoint states and weak-* convergence of the multipliers associated to the state constraint. Moreover, we show existence of stationary points in arbitrary small neighborhoods of local solutions of the original problem. Additionally, various numerical results are presented.

1 Introduction

In this paper, the solution of an optimal control problem subject to a semilinear elliptic state equation and pointwise control and state constraints will be studied. The control problem is non-convex due to the nonlinearity of the state equation. The problem under consideration is given by

$$ \min \ J(y,u):=\frac{1}{2}||y-y_d||_{L^2(\Omega )}^2+\frac{\alpha }{2}||u||_{L^2(\Omega )}^2 $$

(1)

subject to

$$ \begin{array}{lll} Ay + d(y) &{}=u &{} \text { in }\Omega , \\ \quad \quad \partial _{\nu _A} y&{}= 0 &{} \text { on }\Gamma ,\\ \quad \quad \quad \; y &{}\le \psi &{}\text { in } \Omega ,\\ \quad \quad \quad \; u&{}\in U_{\mathrm {ad}}.&{} \end{array} $$

(2)

Here, A denotes a second-order elliptic operator, while d(y) is a nonlinear term in y. The setting of the optimal control problem will be made precise in Sect. 2.

Optimal control problems with pointwise state constraints suffer from low regularity of the respective Lagrange multipliers, see [4, 6] for Dirichlet problems and [5] for Neumann problems. The multiplier ${\bar{\mu }}$ associated to the state constraint is a Borel measure. Under additional assumptions it has been proven in [8] that the multiplier satisfies $H^{-1}(\Omega )$-regularity. These assumptions are satisfied, e.g., for $\psi$ constant.

In contrast to non-convex problems, convex state constrained optimal control problems allow a much simpler convergence analysis of optimization algorithms and have therefore been studied extensively during the last years. To give just a brief insight into the literature of convex problems, we want to mention the common approaches given by penalization based methods [13,14,15,16, 19] possibly with fixed shift, interior point methods [27, 36] or the investigation of mixed control-state-constraints [10, 17, 33]. The monograph [20] discusses augmented Lagrange methods for convex problems in Hilbert spaces, which are not applicable to state constrained problems.

Let us emphasize that the nonlinear state Eq. (2) gives rise to a nonlinear solution operator, which turns problem (1) into a non-convex optimization problem. However, the convergence analysis of solution algorithms of non-convex optimal control problems suffers significantly from non-uniqueness of local and global solutions and only few contributions can be found in the literature. Let us mention the so-called virtual control approach [25], Lavrentiev regularization [34], and Moreau–Yosida regularization [32]. All of these publications discuss under which conditions local solutions of the unregularized problem can be approximated by sequences of local solutions of the regularized problems, but do not provide convergence results for the overall iterative solution method. The convergence analysis of safe-guarded augmented Lagrange method has been considered in [3, 21].

The goal of the present paper is to extend the augmented Lagrange method presented in [23], and to provide the corresponding convergence analysis in order to solve (1). By penalizing the state constraint, one has to solve subproblems that are control constrained only. These subproblems are of the form

$$ \begin{aligned} \underset{y,u}{\text {minimize}}&\quad J(y,u) +\frac{1}{2\rho }\left\Vert (\mu +\rho (y-\psi ))_+\right\Vert ^2_{L^2(\Omega )}\\ \text {subject to}&\quad y=S(u) \quad \text {and } \quad u\in U_{\mathrm {ad}}, \end{aligned}$$

(3)

where $\mu$ is a function given in $L^2(\Omega )$ and S denotes the solution operator of the semilinear partial differential equation given in (1). Given penalty parameters $\rho _k$ and multiplier estimates $\mu _k$, new iterates $(y_{k+1},u_{k+1})$ of the algorithm are computed as stationary points of (3) for $(\rho ,\mu ):=(\rho _k,\mu _k)$.

The question of convergence of the algorithm is linked to the question of feasibility of limit points of iterates that are only stationary points of the augmented Lagrange subproblem. In particular, the subproblem may have stationary points that are located arbitrarily far from the feasible set and there is no rule to determine which stationary points have to be chosen in the solution process of the subproblem in order to guarantee convergence. Specifically for augmented Lagrange methods, feasibility of limit points is not guaranteed, see for instance [22]. Consequently, feasibility is either imposed as an additional assumption [11, 12, 21] or is an implication of a constraint qualification [3, 21]. Let us mention that the classical quadratic penalty method is contained in [3, 21] as a special case, and the comments regarding feasibility of limit points apply equally to this method.

The crucial point of augmented Lagrange methods is the questions when and how to update the penalty parameter and multiplier. In this paper we use an update rule that performs the classical augmented Lagrange update only if a sufficient decrease of the maximal constraint violation and the violation of the complementarity condition is achieved. Accordingly, during all other steps the penalty parameter is increased, but the multiplier remains unchanged. This allows us to conclude feasibility of a weak limit point if and only if an infinite number of multiplier updates is executed, see Theorem 3.3. This type of update rule has its predecessors in finite dimensional nonlinear optimization [11, 12, 28]. It would be favorable if the penalty parameter is increased only finitely many times. This cannot be expected in general for infinite dimensional optimization problems. In this case, the penalty parameter is only bounded in exceptional situations, i.e., if the multiplier is a function in $L^2(\Omega )$, see Theorem 4.9 and [23, Thm. 3.14].

In practice, solutions of the augmented Lagrange subproblems are obtained by iterative methods, which naturally use the previous iterate as starting point. Thus, it is realistic to expect that the iterates stay in a neighbourhood of a local solution of the original problem. One main result of this paper is to prove that such a situation can occur, i.e., for each iteration, we provide existence of a stationary point of the subproblem in exactly this neighborhood. Therefore, we investigate the auxiliary problem

$$\begin{aligned} \underset{y,u}{\text {minimize}}&\quad J(y,u) +\frac{1}{2\rho }\left\Vert (\mu +\rho (y-\psi ))_+\right\Vert ^2_{L^2(\Omega )}\\ \text {subject to}&\quad y=S(u) \quad \text {and } \quad u\in U_{\mathrm {ad}},\quad \left\Vert {{\bar{u}}}-u\right\Vert _{L^2(\Omega )}\le r \end{aligned}$$

that possesses solutions that are close enough to a local solution ${{\bar{u}}}$ of (1). We will prove under a quadratic growth condition that for $\rho$ large enough global solutions of this auxiliary problem are local solutions of the augmented Lagrange subproblem. Moreover, if we assume that the algorithm chooses the global solutions of the auxiliary problem as KKT points of the augmented Lagrange subproblem and the penalty parameter remains bounded, then the multiplier is a function in $L^2(\Omega )$.

The outline of this paper is as follows: In Sect. 2 we start collecting results about the unregularized optimal control problem. Next, in Sect. 3 we present the augmented Lagrange method. Section 3.3 is dedicated to show that every weak limit point of the sequence generated by our algorithm is a KKT point of the original problem. Further, in Sect. 4 we construct an auxiliary problem that claims solutions near a local solution of the original problem. Exploiting appropriate properties of this auxiliary problem we prove that for $\rho$ sufficiently large solutions of the auxiliary problem are local solutions of the augmented Lagrange subproblem. In Sect. 5 we consider second-order sufficient conditions. To illustrate our theoretical findings we present numerical examples in Sect. 6.

Notation Throughout the article we will use the following notation. The inner product in $L^2(\Omega )$ is denoted by $(\cdot ,\cdot )$. Duality pairings will be denoted by $\langle \cdot ,\cdot \rangle$. The dual of $C({\overline{\Omega }})$ is denoted by ${\mathcal {M}}({\overline{\Omega }})$, which is the space of regular Borel measures on ${\overline{\Omega }}$. Further $(\cdot )_+:=\max (0,\cdot )$ in the pointwise almost-everywhere sense.

2 The optimal control problem

Let Y denote the space $Y:= H^1(\Omega )\cap {C({\overline{\Omega }})}$, and set $U:={L^2(\Omega )}$. We want to solve the following state constrained optimal control problem: Minimize

$$ J(y,u):=\frac{1}{2}||y-y_d||_{L^2(\Omega )}^2+\frac{\alpha }{2}||u||_{L^2(\Omega )}^2 $$

over all $(y,u)\in Y\times U_{\mathrm {ad}}$ subject to the semilinear elliptic equation

$$ \begin{array}{ll} (Ay)(x) +d(x,y) = u(x) &{} \text {in } \Omega , \\\quad \quad \quad(\partial _{\nu _A}y)(x) =0 &{} \text {on } \Gamma , \end{array} $$

and subject to the pointwise state constraints

$$ \begin{array}{lll} \quad \quad \quad \;y(x)\le \psi (x) &{}\quad &{} \text {in } {\overline{\Omega }},\\ u_a(x)\le u(x)\le u_b(x)&{}&{}\text {in } \Omega . \end{array} $$

In the sequel, we will work with the following set of standing assumptions.

Assumption 1

(Standing assumptions)

• (a) Let $\Omega \subset {\mathbb {R}}^N$, $N=\lbrace 2,3\rbrace$ be a bounded domain with $C^{1,1}$-boundary $\Gamma$ or a bounded, convex domain with polygonal boundary $\Gamma$.

• (b) The given data satisfy $y_d\in L^2(\Omega )$, $u_a,u_b\in L^\infty (\Omega )$, $\psi \in {C({\overline{\Omega }})}$.

• (c) The differential operator A is given by

  $$ (Ay)(x) := -\sum _{i,j=1}^N \partial _{x_j}(a_{ij}(x)\partial _{x_i} y(x)) + a_0(x)y(x) $$

  with $a_{ij} \in C^{0,1}({\overline{\Omega }}), a_{ij}=a_{ji}$ and $a_0\in L^\infty (\Omega )$. Further, $a_0(x)\ge 0$ a.e. $x\in \Omega$ and $a_0\ne 0$. The operator A is assumed to satisfy the following ellipticity condition: There is $\delta >0$ such that

  $$ \sum _{i,j=1}^N a_{ij}(x)\xi _i\xi _j\ge \delta |\xi |^2 \quad \forall \xi \in {\mathbb {R}}^N, \text { a.e. on } \Omega . $$

• (d) The co-normal derivative $\partial _{\nu _A}y$ is given by

  $$ \partial _{\nu _A}y=\sum _{i,j=1}^N a_{ij}(x)\partial _{x_i}y(x)\nu _j(x), $$

  where $\nu$ denotes the outward unit normal vector on $\Gamma$.

• (e) The function $d(x,y):\Omega \times {\mathbb {R}}$ is measurable with respect to $x\in \Omega$ for all fixed $y\in {\mathbb {R}}$ and twice continuously differentiable with respect to y for almost all $x\in \Omega$. Moreover, for $y=0$ the function d and its derivatives with respect to y up to order two are bounded, i.e. there exists $C>0$ such that

  $$ \left\Vert d(\cdot ,0)\right\Vert _\infty +\left\Vert \frac{\partial d}{\partial y}(\cdot ,0)\right\Vert _\infty +\left\Vert \frac{\partial ^2d}{\partial y^2}(\cdot ,0)\right\Vert _\infty \le C $$

  is satisfied. Further

  $$ d_y(x,y)\ge 0 \quad \text { for almost all } x\in \Omega . $$

  The derivatives of d with respect to y are uniformly Lipschitz up to order two on bounded sets, i.e, there exists a constant M and a constant L(M), that is dependent of M such that

  $$ \left\Vert \frac{\partial ^2d}{\partial y^2}(\cdot ,y_1)-\frac{\partial ^2d}{\partial y^2}(\cdot ,y_2)\right\Vert _\infty \le L(M)|y_1-y_2| $$

  for almost every $x\in \Omega$ and all $y_1,y_2 \in [-M,M]$. Finally, there is a subset $E_\Omega \subset \Omega$ of positive measure with $d_y(x,y)>0$ in $E_\Omega \times {\mathbb {R}}$.

2.1 Analysis of the optimal control problem

2.1.1 The state equation

A function $y\in H^1(\Omega )$ is called a weak solution of the state equation (2) if for all $v\in H^1(\Omega )$ there holds

$$ \int _\Omega \sum _{i,j=1}^N a_{ij}(x)\partial _{x_i}y(x)\partial _{x_j} v(x) +a_0(x)y(x)\,\mathrm {d}x+ \int _\Omega d(x,y) v(x) \,\mathrm {d}x= \int _\Omega u(x) v(x) \,\mathrm {d}x. $$

Theorem 2.1

(Existence of solution of the state equation) Let Assumption 1be satisfied. Then for every $u \in L^2(\Omega )$, the elliptic partial differential equation

$$ \begin{array}{ll} Ay + d(y)=u &{} \text {in }\Omega ,\\ \quad \quad \partial _{\nu _A} y = 0 &{} \text {on }\Gamma \end{array} $$

(4)

admits a unique weak solution $y\in H^1(\Omega )\cap {C({\overline{\Omega }})}$, and it holds

$$ \left\Vert y\right\Vert _{H^1(\Omega )}+\left\Vert y\right\Vert _{{C({\overline{\Omega }})}}\le c\left\Vert u\right\Vert _{L^2(\Omega )} $$

with $c>0$ independent of u. If in addition $(u_n)_n$ is such that $u_n\rightharpoonup u\in L^2(\Omega )$ then the corresponding solutions $(y_n)_n$ of (4) converge strongly in ${H^1(\Omega )\cap {C({\overline{\Omega }})}}$ to the solution y of (4) to data u.

Proof

The proof stating existence of a solution, its uniqueness, and the estimates of the norm can be found in [5, Thm. 3.1]. The compact inclusion $L^2(\Omega )\subset H^{-1}(\Omega )$ and the fact that $u\in L^2(\Omega )$ provides solutions in $H^2(\Omega )$ [24, Thm. 5], which can be embedded compactly in ${C({\overline{\Omega }})}$ [1, Thm. 5.4], imply the additional statement. $\square$

We introduce the control-to-state operator

$$ S\,{\colon}\,{L^2(\Omega )}\rightarrow {H^1(\Omega )\cap {C({\overline{\Omega }})}},\quad u\mapsto y. $$

It is well known [37, Thm. 4.16] that S is Lipschitz continuous from $L^2(\Omega )$ to $H^1(\Omega )\cap {C({\overline{\Omega }})}$, i.e., there exists a constant L such that

$$ \left\Vert y_1-y_2\right\Vert _{H^1(\Omega )}+\left\Vert y_1-y_2\right\Vert _{{C({\overline{\Omega }})}}\le L\left\Vert u_1-u_2\right\Vert _{L^2(\Omega )} $$

(5)

is satisfied for all $u_i\in L^2(\Omega )$, $i=1,2$ with corresponding states $y_i=S(u_i)$. We define the following sets

$$ \begin{array}{l} U_{\mathrm {ad}}=\lbrace u\in L^\infty (\Omega )\ |\ u_a(x)\le u(x)\le u_b(x) \text { a.e. in } \Omega \rbrace ,\\ Y_{\mathrm {ad}}=\lbrace y\in C({\overline{\Omega }})\quad\ |\ y(x)\le \psi (x)\ \forall x\in {\overline{\Omega }}\rbrace . \end{array} $$

The feasible set of the optimal control problem is denoted by

$$ F_{\mathrm {ad}}= \lbrace (y,u)\in Y\times U\ |\ (y,u)\in Y_{\mathrm {ad}}\times U_{\mathrm {ad}},\ y=S(u)\rbrace . $$

Using this notation the reduced formulation of problem (P) is given by

$$ \begin{array}{ll} \underset{u\in L^2(\Omega )}{\text {minimize}} &{}\quad f(u):= \frac{1}{2}\left\Vert Su-y_d\right\Vert ^2_{L^2(\Omega )}+\frac{\alpha }{2}\left\Vert u\right\Vert ^2_{L^2(\Omega )}, \\ \text {subject to} &{}\quad (S(u),u)\in F_{\mathrm {ad}}. \end{array} \qquad {(P)} $$

For further use we want to recall a result concerning differentiability of the nonlinear control-to-state mapping S.

Theorem 2.2

(Differentiability of the solution mapping) Let Assumption 1be satisfied. Then the mapping $S\,{\colon}\,L^2(\Omega ) \rightarrow {H^1(\Omega )\cap {C({\overline{\Omega }})}}$, that is defined by $S(u)=y$, is twice continuously Fréchet differentiable. Furthermore for all $u,h\in L^2(\Omega )$, $y_h=S'(u)h$ is defined as solution of

$$ \begin{array}{llll} Ay_h+d_y(y)y_h &{}= h &{}\quad &{}\text {in }\Omega ,\\ \quad \quad \quad\;\; \partial _{\nu _A}y_h &{}= 0 &{}&{}\text {on } \Gamma . \end{array} $$

Moreover, for every $h_1,h_2\in L^2(\Omega ),\ y_{h_1,h_2}= S''(u)[h_1,h_2]$ is the solution of

$$ \begin{array}{llll} Ay_{h_1,h_2}+d_y(y)y_{h_1,h_2} &{}= -d_{yy}(y)y_{h_1}y_{h_2} &{}\quad &{}\text {in }\Omega ,\\ \quad \quad \quad \quad\; \partial _{\nu _A}y_{h_1,h_2} &{}= 0 &{}&{}\text {on } \Gamma , \end{array} $$

where $y_{h_i}=S'(u)h_i, i=1,2$.

Proof

The proof for the first derivative of $S \,{\colon}\,L^r(\Omega )\rightarrow {H^1(\Omega )\cap {C({\overline{\Omega }})}}, r>N/2$ can be found in [37, Thm. 4.17]. We refer to [37, Thm. 4.24] for the proof of second-order differentiability of $S\,{\colon}\,L^\infty (\Omega )\rightarrow {H^1(\Omega )\cap {C({\overline{\Omega }})}}$ which is also valid for $S\,{\colon}\,L^2(\Omega )\rightarrow {H^1(\Omega )\cap {C({\overline{\Omega }})}}$. $\square$

2.1.2 Existence of solutions of the optimal control problem

Under the standing assumptions we can show existence of solutions of the reduced control problem (P). By standard arguments we get the following theorem.

Theorem 2.3

(Existence of solution of the optimal control problem) Let Assumption 1be satisfied. Assume that the feasible set $F_{\mathrm {ad}}$ is nonempty. Then there exists at least one global solution ${{\bar{u}}}$ of (P).

Proof

The proof can be found in [18, Thm. 1.45]. $\square$

Due to non-convexity, global solutions of problem (P) are not unique in general. Also, in addition there might be local solutions.

Definition 2.1

(Local solution) A control ${{\bar{u}}}\in U_{\mathrm {ad}}$ satisfying $S({{\bar{u}}}) \le \psi$ in ${\overline{\Omega }}$ is called a local solution of problem (P) in the sense of $L^2(\Omega )$ if there exists a $\zeta >0$ such that

$$ f({{\bar{u}}})\le f(u) \quad \text {for all } u\in U_{\mathrm {ad}}\text { with } S(u)\le \psi \text { in }{\overline{\Omega }}\text { and } \left\Vert {{\bar{u}}}-u\right\Vert _{L^2(\Omega )}\le \zeta . $$

2.1.3 First-order optimality conditions

The existence of Lagrange multipliers to state constrained optimal control problems is not guaranteed without some regularity assumption. In order to formulate first-order necessary optimality conditions we will work with the following linearized Slater condition.

Assumption 2

(Linearized Slater condition) A feasible point ${{\bar{u}}}$ satisfies the linearized Slater condition, if there exists ${\hat{u}}\in U_{\mathrm {ad}}$ and $\sigma >0$ such that

$$ S({{\bar{u}}})(x)+S'({{\bar{u}}})({\hat{u}}-{{\bar{u}}})(x) \le \psi (x)-\sigma \quad \forall x\in {\overline{\Omega }} $$

holds.

Next, we state a regularity result concerning linear partial differential equations with measures on the right-hand side, see [5, Thm. 4.3].

Theorem 2.4

(Existence of solution of the adjoint equation) Let $\mu$ be a regular Borel measure with $\mu =\mu _\Omega +\mu _\Gamma \in {{\mathcal {M}}({\overline{\Omega }})}$. Then the elliptic partial differential equation

$$ \begin{array}{llll} A^*p + d_y(y)p&{}=y-y_d +\mu _\Omega &{}\quad &{} \text {in }\Omega ,\\ \quad \quad \quad \partial _{\nu _{A^*}} p&{}= \mu _\Gamma &{}&{} \text {on }\Gamma \end{array} $$

admits a unique weak solution $p\in W^{1,s}(\Omega ),s\in (1,N/(N-1))$ and it holds

$$ \left\Vert p\right\Vert _{W^{1,s}(\Omega )}\le c\left( \left\Vert y\right\Vert _{L^2(\Omega )}+\left\Vert y_d\right\Vert _{L^2(\Omega )}+\left\Vert \mu \right\Vert _{{\mathcal {M}}({\overline{\Omega }})}\right) $$

with $c>0$ independent of the right hand side of the partial differential equation.

Based on the linearized Slater condition first-order necessary optimality conditions for problem (P) can be established.

Theorem 2.5

(First-order necessary optimality conditions) Let ${{\bar{u}}}$ be a local solution of problem (P) that satisfies Assumption 2. Let ${\bar{y}}=S({{\bar{u}}})$ denote the corresponding state. Then there exists an adjoint state ${\bar{p}}\in W^{1,s}(\Omega )$, $s\in (1,N/(N-1))$ and a Lagrange multiplier ${\bar{\mu }}\in {{\mathcal {M}}({\overline{\Omega }})}$ with ${\bar{\mu }}={\bar{\mu }}_{\Omega }+{\bar{\mu }}_{\Gamma }$ such that the following optimality system

$$ \begin{array}{ll} A{\bar{y}}+d({\bar{y}})={{\bar{u}}} &{}\text {in } \Omega ,\\ \quad \quad \partial _{\nu _A}{\bar{y}} = 0 &{}\text {on } \Gamma , \end{array} $$

(6a)

$$ \begin{array}{ll} A^*{\bar{p}}+d_y({\bar{y}}){\bar{p}}= {\bar{y}}-y_d +{\bar{\mu }}_\Omega &{}\text {in } \Omega ,\\ \quad \quad \quad \partial _{\nu _{A^*}}{\bar{p}} = {\bar{\mu }}_\Gamma &{}\text {on } \Gamma , \end{array} $$

(6b)

$$ ( {\bar{p}}+\alpha {{\bar{u}}},u-{{\bar{u}}}) \ge 0\quad \forall u\in U_{\mathrm {ad}}, $$

(6c)

$$ \langle {\bar{\mu }},{\bar{y}}-\psi \rangle _{{{\mathcal {M}}({\overline{\Omega }})},{C({\overline{\Omega }})}}=0,\quad {\bar{\mu }}\ge 0,\quad {\bar{y}}(x)\le \psi (x),\ \forall x\in {\overline{\Omega }} $$

(6d)

is fulfilled. Here, the inequality ${\bar{\mu }}\ge 0$ means $\langle {\bar{\mu }},\varphi \rangle _{{{\mathcal {M}}({\overline{\Omega }})},{C({\overline{\Omega }})}}\ge 0$ for all $\varphi \in {C({\overline{\Omega }})}$ with $\varphi \ge 0$.

Proof

The proof can be done by adapting the theory from [5, Thm. 5.3] to Neumann boundary conditions. $\square$

Let us emphasize that due to the presence of control as well as state constraints, the adjoint state ${\bar{p}}$ and the Lagrange multiplier ${\bar{\mu }}$ need not to be unique.

3 The augmented Lagrange method

Like in [23] we eliminate the explicit state constraint $S(u)\le \psi$ from the set of constraints by adding an augmented Lagrange term to the cost functional. Let $\rho >0$ denote a penalization parameter and $\mu$ a fixed function in $L^2(\Omega )$. Then in every step k of the augmented Lagrange method one has to solve subproblems of the type

$$ \underset{u_{\rho }}{\text {minimize}} \,\,f_{AL}(u_{\rho },\mu ,\rho ):=f(u_\rho )+\frac{1}{2\rho }\left\Vert \left( \mu +\rho (S(u_{\rho })-\psi )\right) _+\right\Vert _{L^2(\Omega )}^2 \qquad {(P_{AL}^{\rho ,\mu })} $$

where $(\cdot )_+:=\max (0,\cdot )$ in the pointwise sense, subject to the control constraints

$$ u_{\rho }\in U_{\mathrm {ad}}. $$

3.1 Analysis of the augmented Lagrange subproblem

Local solutions of the augmented Lagrange subproblem $(P_{AL}^{\rho ,\mu })$ are defined analogously to (P). In the following, existence of an optimal control and existence of a corresponding adjoint state will be proven.

Definition 3.1

(Local solution) A control ${{\bar{u}}}_\rho \in U_{\mathrm {ad}}$ is a local solution of the augmented Lagrange subproblem $(P_{AL}^{\rho ,\mu })$ if there exists a $\zeta >0$ such that

$$ f_{AL}({{\bar{u}}}_\rho ) \le f_{AL} (u),\quad \text { for all } u\in U_{\mathrm {ad}}\text { with } \left\Vert u-{{\bar{u}}}_\rho \right\Vert _{L^2(\Omega )}\le \zeta . $$

Theorem 3.1

(Existence of solutions of the augmented Lagrange subproblem) For every $\rho >0$, $\mu \in L^2(\Omega )$ with $\mu \ge 0$ the augmented Lagrange subproblem $(P_{AL}^{\rho ,\mu })$ admits at least one global solution ${{\bar{u}}}_{\rho }\in U_{\mathrm {ad}}$.

Proof

The proof follows standard arguments, see [37]. $\square$

Since the problem $(P_{AL}^{\rho ,\mu })$ has no state constraints, the first-order optimality system is fulfilled without any further regularity assumptions.

Theorem 3.2

(First-order necessary optimality conditions) For given $\rho >0$ and $0\le \mu \in L^2(\Omega )$ let $({\bar{y}}_{\rho },{{\bar{u}}}_{\rho })$ be a solution of $(P_{AL}^{\rho ,\mu })$. Then for every given $({\bar{y}}_{\rho },{{\bar{u}}}_{\rho })$ there exists a unique adjoint state ${\bar{p}}_{\rho }\in H^1(\Omega )$ satisfying the following system

$$ \begin{array}{ll} A{\bar{y}}_{\rho }+d({\bar{y}}_{\rho }) = {{\bar{u}}}_{\rho } &{}\text {in } \Omega ,\\ \quad \quad \;\;\partial _{\nu _A} {\bar{y}}_{\rho } = 0 &{}\text {on } \Gamma , \end{array} $$

(7a)

$$ \begin{array}{ll} A^*{\bar{p}}_{\rho } + d_y({\bar{y}}_{\rho }){\bar{p}}_{\rho } = {\bar{y}}_{\rho }-y_d +{\bar{\mu }}_{\rho } &{}\text {in } \Omega ,\\ \quad \quad \quad \quad \partial _{\nu _{A^*}}{\bar{y}}_{\rho } = 0 &{}\text {on } \Gamma , \end{array} $$

(7b)

$$ ({\bar{p}}_{\rho } +\alpha {{\bar{u}}}_{\rho },u-{{\bar{u}}}_{\rho })\ge 0,\qquad \forall u\in U_{\mathrm {ad}} $$

(7c)

$$ {\bar{\mu }}_{\rho }=\left( \mu +\rho ({\bar{y}}_{\rho }-\psi )\right) _+. $$

(7d)

Proof

For the existence of an adjoint state ${\bar{p}}_\rho \in H^1(\Omega )$ that satisfies the KKT system we refer to [18, Cor. 1.3, p.73]. By construction we get a unique ${\bar{\mu }}_\rho$ for each given $({\bar{y}}_\rho ,{{\bar{u}}}_\rho )$. Due to Theorem 2.4 the adjoint equation admits a unique solution. Thus, the adjoint state ${\bar{p}}_\rho$ is unique for every $({\bar{y}}_\rho ,{{\bar{u}}}_\rho )$. $\square$

Finally, in Algorithm 1 we present the augmented Lagrange algorithm, which is based on the algorithm that has been developed in [23].

The definition of a successful step is a variant of the strategy used in [11, 12].

In the following, we will use the notation $(a,b)_+:= \left( \int _\Omega (a,b)\right) _+$.We will call the step k successful if the quantity

$$ R_k:= \left\Vert ({\bar{y}}_{k}-\psi )_+\right\Vert _{C({\overline{\Omega }})}+ ( {\bar{\mu }}_{k},\psi -{\bar{y}}_{k})_+ $$

shows sufficient decrease (see step 4 of the algorithm). Otherwise we will call the step not successful. The first part of $R_k$ measures the maximal constraint violation while the second term quantifies the fulfilment of the complementarity condition in the second part. Since $({\bar{\mu }}_{k}(x),\psi (x)-{\bar{y}}_{k}(x))$ is nonnegative for every feasible ${\bar{y}}_k$ it is enough to check on the smallness of $( {\bar{\mu }}_{k},\psi -{\bar{y}}_{k})_+$ in the second term for quantifying whether or not the complementarity condition is satisfied.

From now on let $(P_{AL}^k)$ denote the augmented Lagrange subproblem $(P_{AL}^{\rho ,\mu })$ for given penalty parameter $\rho :=\rho _k$ and multiplier $\mu :=\mu _k$. We will denote its solution by $({\bar{y}}_k,{{\bar{u}}}_k)$ with adjoint state ${\bar{p}}_k$ and updated multiplier ${\bar{\mu }}_k$.

3.2 Successful steps and feasibility of limit points

The question of convergence of the algorithm is linked to the question of feasibility of limit points of the iterates $({{\bar{u}}}_k)_k$. Here, it turns out that the feasibility of limit points is tightly linked with the occurrence of infinitely many successful steps.

Let us emphasize that for non-convex optimization problems the feasibility of limit points of augmented Lagrange methods is not guaranteed. Typically, the feasibility of limit points is an additional assumption in convergence results [11, 12, 21]. Or the feasibility is the consequence of a constraint qualification assumed to hold in the limit point [3, 22].

Theorem 3.3

Let $({{\bar{u}}}_k)_k$ denote the sequence that is generated by Algorithm 1. Then $({{\bar{u}}}_k)_k$ has a feasible weak limit point if and only if infinitely many steps in the execution of Algorithm 1 were successful.

Proof

First, suppose that infinitely many steps were successful. Let $(y_n^+,u_n^+,p_n^+,\mu _n^+)_n$ denote the sequence of successful iterates generated by Algorithm 1. By the boundedness of $(u_{n}^+)_{n}\in U_{\mathrm {ad}}$ we get existence of a subsequence $u_{n'}^+\rightharpoonup u^*$ in $L^2(\Omega )$ and $y_{n'}^+\rightarrow y^*$ in ${H^1(\Omega )\cap {C({\overline{\Omega }})}}$ by Theorem 2.1. Due to the definition of successful steps, we have that $\left\Vert (y_n^+-\psi )_+\right\Vert _{C({\overline{\Omega }})}\le R_n^+ \rightarrow 0$ and $u^*$ is a feasible control of (P).

Suppose now that only finitely many steps were successful. Let m be the largest index of a successful step. Hence, all steps k with $k>m$ are not successful. According to Algorithm 1 it holds $\mu _k=\mu _m$ for all $k>m$. We will prove $\limsup _{k\rightarrow \infty }\ ({\bar{\mu }}_k,\psi -{\bar{y}}_k)_+\le 0$ first. Let

$$ \Omega _k:=\left\{ x\in \Omega :({\bar{\mu }}_k(x),\psi (x)-{\bar{y}}_k(x))\ge 0 \right\} . $$

Then the desired estimate follows easily by pointwise evaluation of the contributing quantities in

$$\begin{aligned} ({\bar{\mu }}_k,\psi -{\bar{y}}_k)_+&= ({\bar{\mu }}_k,-\frac{\mu _m}{\rho _k}+\psi -{\bar{y}}_k+\frac{\mu _m}{\rho _k})_+\le -\frac{1}{\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega _k)}+\frac{1}{\rho _k}({\bar{\mu }}_k,\mu _m)_{L^2(\Omega _k)}\\&\le -\frac{1}{2\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega _k)} +\frac{1}{2\rho _k}\left\Vert \mu _m\right\Vert ^2_{L^2(\Omega _k)}\le \frac{1}{2\rho _k}\left\Vert \mu _m\right\Vert ^2_{L^2(\Omega )}, \end{aligned}$$

where we applied Young’s inequality. The algorithm only makes $l\ge 0$ successful steps, which implies $R_k >\tau R_l^+$ for all $k>m$. This proves with $\mu _k = \mu _l^+$

$$ \begin{aligned} \liminf _{k\rightarrow \infty } \left\Vert ({\bar{y}}_k-\psi )_+\right\Vert _{C({\overline{\Omega }})}&= \liminf _{k\rightarrow \infty }\big (R_k - ({\bar{\mu }}_k,\psi -{\bar{y}}_k)_+ \big ) \\&\ge \tau R_l^+ - \limsup _{k\rightarrow \infty }\ ({\bar{\mu }}_k,\psi -{\bar{y}}_k)_+ \ge \tau R_l^+>0. \end{aligned}$$

Let $u^*$ be a weak limit of the subsequence $(u_{k'})_{k'}$ with associated state $y^*$. Then, arguing as in the first part of the proof, we have

$$ \left\Vert (y^*-\psi )_+\right\Vert _{C({\overline{\Omega }})}= \lim _{k'\rightarrow \infty } \left\Vert ({\bar{y}}_{k'}-\psi )_+\right\Vert _{C({\overline{\Omega }})}\ge \tau R_l^+>0, $$

and $u^*$ is not feasible. $\square$

The proof of the previous theorem shows that if the algorithm performs infinitely many successful steps then every limit point of $(u_n^+)_n$ is feasible for the original problem. In case that only finitely many steps are successful, we have the following additional result.

Theorem 3.4

Let us assume that Algorithm 1 does a finite number of successful steps only. Let $({{\bar{u}}}_k)_k$ denote the sequence that is generated by the algorithm and let $u^*$ be a weak limit point of $({{\bar{u}}}_k)_k$. Then, $u^*$ is infeasible for (P), and it is a stationary point of the minimization problem

$$ \underset{u\in U_{\mathrm {ad}}}{\min } \quad \left\Vert (S(u^*)-\psi )_+\right\Vert ^2_{L^2(\Omega )}. $$

(8)

Proof

The infeasibility of $u^*$ is a consequence of Theorem 3.3. Let m be the index of the last successful step. Dividing the first-order optimality condition of the augmented Lagrange subproblem by $\rho _k$

$$ \left( S'({{\bar{u}}}_k)^*\left( \frac{S({{\bar{u}}}_k)-y_d}{\rho _k}+\left( \frac{\mu _m}{\rho _k}+S({{\bar{u}}}_k)-\psi \right) _+\right) +\alpha \frac{{{\bar{u}}}_k}{\rho _k},v-{{\bar{u}}}_k \right) \ge 0 \quad \forall v\in U_{\mathrm {ad}} $$

and taking the limit $k\rightarrow \infty$ yields

$$ (S'(u^*)^*(S(u^*)-\psi )_+),v-u^*)\ge 0 \quad \forall v\in U_{\mathrm {ad}}, $$

which is exactly the optimality condition for (8). $\square$

In [3, 22] such a stationarity property together with a suitable constraint qualification was used to prove feasibility of limit points.

Another way to obtain feasibility of $u^*$ is to assume the boundedness of the sequence $(\frac{1}{\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )})_k$. Assumptions of this kind are common for augmented Lagrange methods. The multiplier update of [12, Algorithm 2] is constructed such that a related boundedness result holds. In safeguarded augmented Lagrange methods, see, e.g., [2, 21], a bounded sequence of safeguarded multipliers is used to define the multiplier update. In our situation, this would amount to choosing a bounded sequence $(w_k)_k$ in $L^2(\Omega )$ and computing stationary points of $\min _{u\in U_{\mathrm {ad}}} f_{AL}(u,w_k,\rho _k)$ instead of $\min _{u\in U_{\mathrm {ad}}} f_{AL}(u,\mu _k,\rho _k)$, which results in the safe-guarded multiplier update $\mu _{k+1}:=\left( w_k+\rho _k({\bar{y}}_k-\psi )\right) _+$.

Theorem 3.5

Assume that in step 1 of Algorithm 1, the solutions $({\bar{y}}_k,{{\bar{u}}}_k,{\bar{p}}_k)$ of (3.2) are chosen such that

$$ \frac{1}{\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )}=\frac{1}{\rho _k}\left\Vert (\mu _k+\rho _k({\bar{y}}_k-\psi ))_+\right\Vert ^2_{L^2(\Omega )} $$

is uniformly bounded. Then every weak limit point $u^*$ of $(u_k)_k$ is feasible.

Proof

Suppose first, that $(\rho _k)_k$ is bounded. Then the algorithm performs only finitely many unsuccessful steps. Consequently, the tails of the sequence of iterates $(u_k)_k$ and of the sequence of successful iterates $(u_n^+)_n$ coincide. By Theorem 3.3, all weak limit points of $(u_n^+)_n$ and thus of $(u_k)_k$ are feasible.

Now, consider the case $\rho _k\rightarrow +\infty$. Due to the assumption, there is $M>0$ such that

$$ \frac{1}{\rho _k}\left\Vert (\mu _k+\rho _k({\bar{y}}_k-\psi ))_+\right\Vert ^2_{L^2(\Omega )} = \rho _k \left\Vert \left( \frac{\mu _{k}}{\rho _{k}}+{\bar{y}}_{k}-\psi \right) _+\right\Vert ^2_{L^2(\Omega )} \le M, $$

which yields with $\mu _k\ge 0$ the estimate

$$ \frac{M}{\rho _k} \ge \left\Vert \left( \frac{\mu _{k}}{\rho _{k}}+{\bar{y}}_{k}-\psi \right) _+\right\Vert ^2_{L^2(\Omega )} \ge \left\Vert \left( {\bar{y}}_{k}-\psi \right) _+\right\Vert ^2_{L^2(\Omega )}. $$

This proves $\lim _{k\rightarrow \infty } \left\Vert \left( {\bar{y}}_{k}-\psi \right) _+\right\Vert ^2_{L^2(\Omega )}=0$. By the compactness result of Theorem 2.1, the claim follows. $\square$

Under the assumptions of the previous theorem, Algorithm 1 makes infinitely many successful steps by Theorem 3.3. In the case that Algorithm 1 chooses $({\bar{y}}_k,{{\bar{u}}}_k)$ to be global minimizers of the augmented Lagrange subproblem the boundedness assumption of Theorem 3.5 is satisfied.

Theorem 3.6

Let the feasible set $F_{\mathrm {ad}}$ be non-empty. Assume that in step 1 of Algorithm 1, ${{\bar{u}}}_k$ is chosen to be a global minimizer of the augmented Lagrange subproblem. Then the augmented Lagrange algorithm makes infinitely many successful steps.

Proof

Let ${{\bar{u}}}$ be a global solution of the original problem. Assume that algorithm performs only finitely many successful steps. Let $k>m$, where m is the largest index of a successful step. This implies $\mu _k=\mu _m$. Then we obtain

$$\begin{aligned} \frac{1}{2\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )}&\le f({{\bar{u}}}_k) + \frac{1}{2\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )}\\&\le f({{\bar{u}}}) + \frac{1}{2\rho _k}\left\Vert (\mu _k+\rho _k(S({{\bar{u}}})-\psi ))_+\right\Vert ^2_{L^2(\Omega )}\\&= f({{\bar{u}}}) + \frac{1}{2\rho _k}\left\Vert (\mu _m+\rho _k(S({{\bar{u}}})-\psi ))_+\right\Vert ^2_{L^2(\Omega )}\le f({{\bar{u}}}) + \frac{1}{2\rho _k}\left\Vert \mu _m\right\Vert ^2_{L^2(\Omega )}. \end{aligned}$$

Hence, all assumptions of Theorem 3.5 are satisfied, and all weak limit points of $(u_k)_k$ are feasible. As this sequence is bounded, there exists such weak limit points. This contradicts Theorem 3.3, and the algorithm performs infinitely many successful steps. $\square$

Note that this strategy is only viable if the original problem and thus the augmented Lagrange subproblems are convex. Then computing stationary points is equivalent to computing global minima. In practice, solutions of the augmented Lagrange subproblems are obtained by iterative methods. Naturally, these methods use the previous iterate as starting point. Thus, it is a realistic scenario that the iterates stay in a neighbourhood of a local solution of the original problem. One main result of this paper is to prove that such a situation can occur. To this end, let ${{\bar{u}}}$ be a strict local solution of (P). For some radius $r>0$, let us consider the auxiliary problem

$$ \begin{array}{ll} \underset{u^r_{\rho }\in L^2(\Omega )}{\text {minimize}}\quad &{}f_{AL}^r(u^r_{\rho },\mu ,\rho ):=f(u^r_\rho )+\frac{1}{2\rho }\left\Vert \left( \mu +\rho (S(u^r_{\rho })-\psi )\right) _+\right\Vert ^2_{L^2(\Omega )}\\ \text {subject to} \quad &{} u^r_{\rho }\in U_{\mathrm {ad}},\qquad \left\Vert u^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}\le r. \end{array} $$

(9)

The radius r is chosen sufficiently small such that a quadratic growth condition is satisfied. This auxiliary problem will be analysed in detail in Sect. 4. We will show that global solutions of the auxiliary problem are local solutions of the augmented Lagrange subproblem, provided the penalty parameter $\rho$ is sufficiently large. In addition, we will prove that if the iterates of Algorithm 1 are chosen as such a solution then the algorithm performs infinitely many successful steps. We refer to Theorems 4.8 and 4.9.

Let us close this section with an example demonstrating that augmented Lagrange methods will not deliver feasible limit points in general. The example is taken from [22]: Consider the minimization problem in ${\mathbb {R}}$ given by

$$ \min x \quad \text{ subject } \text{ to } \quad 1-x^3\le 0. $$

Clearly, $x^*=1$ is the global solution. Note that the inequality constraint is defined by a non-convex function, while the feasible set is the interval $[1,+\infty )$. For penalty parameter $\rho >0$ and multiplier estimate $\mu \ge 0$, the augmented Lagrangian is defined by

$$ L(x,\mu ,\rho ):= x + \frac{1}{2\rho } \left( (\mu + \rho (1-x^3))_+\right) ^2. $$

As argued in [22], the augmented Lagrange function admits for all possible values of $\rho$ and $\mu$ a local minimum $x_{\rho ,\mu }<0$. If the method chooses these minima as iterates, then limit points are clearly not feasible. This applies equally well to the classical quadratic penalty method, which corresponds to the choice $\mu =0$.

3.3 Convergence towards KKT points

In the previous section we have investigated several cases and conditions under which Algorithm 1 generates infinitely many successful steps. In the following, we will always assume that this is the case, i.e., the method produces an infinite sequence of successful iterates $(y_n^+, u_n^+, p_n^+)_n$. By Theorem 3.3, we know that $(u_n^+)_n$ has a feasible weak limit point.

However, we do not know yet, if $u^*$ is a stationary point, i.e., if $(p_n^+,\mu _n^+)_n$ converges in some sense to $(p^*,\mu ^*)$ such that $(y^*,u^*,p^*,\mu ^*)$ satisfies the optimality system (6). To achieve this aim, we have to suppose additional properties of the weak limit point $u^*$. In the rest of this section, we will prove convergence of the dual quantities $(p_n^+,\mu _n^+)_n$ under the assumption that the weak limit point $u^*$ satisfies the linearized Slater condition Assumption 2. We start with several auxiliary results.

Lemma 3.7

Let $(u_k)_k,(h_k)_k$ denote sequences in $L^2(\Omega )$ that converge weakly to the limits $u^*,h^*$, respectively. Then for $k\rightarrow \infty$ we have

$$ \left\Vert S'(u_k)h_k - S'(u^*)h^*\right\Vert _{{C({\overline{\Omega }})}}\rightarrow 0 . $$

Proof

From Theorem 2.1 we know that $y_k:=S(u_k)$ is the unique weak solution of the state equation

$$ \begin{array}{ll} A y_k +d(y_k) = u_k &{}\text { in }\Omega ,\\ \quad \quad \;\;\partial _{\nu _A}y_k = 0 &{}\text { on }\Gamma . \end{array} $$

Further, for $u_k\rightharpoonup u^*$ in $L^2(\Omega )$ we get $y_k\rightarrow y^*$ in ${H^1(\Omega )\cap {C({\overline{\Omega }})}}$. Let now $z_k$ denote the linearized state $z_k:= S'(u_k)h_k$. Then by Theorem 2.2 we know that $z_k$ is the unique solution of

$$ \begin{array}{ll} A z_k +d_y(y_k)z_k = h_k &{}\text { in }\Omega ,\\ \quad \quad \quad \;\;\partial _{\nu _A}z_k = 0 &{}\text { on }\Gamma . \end{array} $$

Further, let $z^*:=S'(u^*)h^*$ solve the equation

$$ \begin{array}{llll} A z^* +d_y(y^*)z^* &{}= h^* &{}\quad &{}\text { in }\Omega ,\\ \quad \quad \quad \;\;\partial _{\nu _A}z^* &{}= 0 &{}&{}\text { on }\Gamma . \end{array} $$

We subtract both PDEs and set $e_k:=S'(u_k)h_k-S'(u^*)h^*$

$$ \begin{array}{llll} A e_k +d_y(y_k)z_k-d_y(y^*)z^* &{}= h_k-h^* &{}\quad &{}\text { in }\Omega ,\\ \quad \quad \quad \quad \quad \quad \quad \;\;\partial _{\nu _A} e_k &{}= 0 &{}&{}\text { on }\Gamma . \end{array} $$

Inserting the identity $d_y(y_k)z_k-d_y(y^*)z^*= \left( d_y(y_k)-d_y(y^*)\right) z_k + d_y(y^*)(z_k-z^*)$ we obtain

$$ \begin{array}{llll} A e_k+d_y(y^*)e_k &{}= (h_k-h^*) - (d_y(y_k)-d_y(y^*))z_k&{}\quad &{}\text { in }\Omega ,\\ \quad \quad \quad\;\;\partial _{\nu _A} e_k &{}= 0 &{}&{}\text { on }\Gamma . \end{array} $$

From Assumption 1 we know that $d_y(y)$ is locally Lipschitz continuous, i.e.,

$$ \left\Vert d_y(y_1)-d_y(y_2)\right\Vert _{L^\infty (\Omega )}\le L(M)\left\Vert y_1-y_2\right\Vert _{L^\infty (\Omega )}. $$

Concluding, for $y_{k}\rightarrow y^*$ in $L^\infty (\Omega )$ we have $d_y(y_k)\rightarrow d_y(y^*)$ in $L^\infty (\Omega )$. Due to $h_k\rightharpoonup h^*$ in $L^2(\Omega )$ and the boundedness of $z_k$ in $L^2(\Omega )$ we gain $e_k\rightarrow 0$ in ${H^1(\Omega )\cap {C({\overline{\Omega }})}}$. Hence,

$$ \left\Vert S'(u_k)h_k-S'(u^*)h^*\right\Vert _{{C({\overline{\Omega }})}}\rightarrow 0 $$

and the proof is done. $\square$

Let us recall that $(y_n^+,u_n^+,p_n^+,\mu _n^+)$ denotes the solution of the n-th successful iteration of Algorithm 1. We want to investigate the convergence properties of the algorithm for a weak limit point $u^*$ of $(u_n^+)_n$. A point $u^*\in U_{\mathrm {ad}}$ satisfies the linearized Slater condition if there exists a ${\hat{u}}\in U_{\mathrm {ad}}$ and $\sigma >0$ such that

$$ S(u^*)(x)+S'(u^*)({\hat{u}}-u^*)(x)\le \psi (x) -\sigma \quad \forall x\in {\overline{\Omega }}. $$

(10)

Lemma 3.8

Let $u^*$ denote a weak limit point of $(u_n^+)_n$ that satisfies the linearized Slater condition (10). Then there exists an $N\in {\mathbb {N}}$ such that for all $n'>N$ the control $u_{n'}^+$ satisfies

$$ S(u_{n'}^+)+S'(u_{n'}^+)({\hat{u}}-u_{n'}^+) \le \psi -\frac{\sigma }{2}. $$

(11)

Proof

By Theorem 2.2 we have strong convergence $S(u_{n'}^+)\rightarrow S(u^*)$ in ${H^1(\Omega )\cap {C({\overline{\Omega }})}}$. By Theorem 3.7 we get $S'(u_{n'}^+)({\hat{u}}-u_{n'}^+) \rightarrow S'(u^*)({\hat{u}} - u^*)$ in ${H^1(\Omega )\cap {C({\overline{\Omega }})}}$. Using the identity

$$\begin{aligned} S(u_{n'}^+)+S'(u_{n'}^+)({\hat{u}}-u_{n'}^+)&= S(u^*)+S'(u^*)({\hat{u}}-u^*)\\&\quad + S(u_{n'}^+)-S(u^*)\\&\quad + S'(u_{n'}^+)({\hat{u}}-u_{n'}^+)-S'(u^*)({\hat{u}}-u^*) \end{aligned}$$

and exploiting the specified convergence results, we conclude the existence of an $N\in {\mathbb {N}}$ such that

$$ S(u_{n'}^+)+S'(u_{n'}^+)({\hat{u}}-u_{n'}^+) \le \psi - \frac{\sigma }{2},\quad \forall {n'}>N. $$

$\square$

We recall an estimate for the second term of the update rule, see [23, Lem. 3.9], that is necessary to state $L^1$-boundedness of the Lagrange multiplier. This estimate does not require any additional assumption, it just results from the structure of the update rule.

Lemma 3.9

Let $y_n^+,\mu _n^+$ be given as defined in Algorithm 1. Then for all $n>1$ it holds

$$ ( \mu _n^+,\psi -y_n^+)_+\le \tau ^{n-1}\left( \left\Vert (y_1^+-\psi )_+\right\Vert _{C({\overline{\Omega }})}+\left\Vert \mu _1^+\right\Vert _{L^2(\Omega )}\left\Vert (\psi -y_1^+)_+\right\Vert _{L^2(\Omega )}\right) . $$

Lemma 3.10

(Boundedness of the Lagrange multiplier) Let $(y_n^+,u_n^+,p_n^+,\mu _n^+)_n$ denote the sequence that is generated by Algorithm 1. Let $(u_{n'}^+)_{n'}$ denote a subsequence of $(u_n^+)_n$ that converges weakly to $u^*$. If $u^*$ satisfies the linearized Slater condition from (10), then the corresponding sequence of multipliers $(\mu _{n'}^+)_{n'}$ is bounded in $L^1(\Omega )$, i.e., there is a constant C> 0 independent of $n'$ such that for all $n'$ it holds

$$ \left\Vert \mu _{n'}^+\right\Vert _{L^1(\Omega )} \le C. $$

Proof

Writing (7c) in variational form we see

$$ (p_{n'}^+ +\alpha u_{n'}^+,u-u_{n'}^+)\ge 0 \qquad \forall u\in U_{\mathrm {ad}}. $$

Using the identity

$$ p_{n'}^+=S'(u_{n'}^+)^*(y_{n'}^+ -y_d+\mu _{n'}^+) $$

we obtain

$$ (S'(u_{n'}^+)^*(y_{n'}^+ -y_d+\mu _{n'}^+)+\alpha u_{n'}^+,u-u_{n'}^+)\ge 0, \qquad \forall u\in U_{\mathrm {ad}}. $$

Rearranging terms yields

$$ (\mu _{n'}^+,S'(u_{n'}^+)(u_{n'}^+-u))\le (y_{n'}^+-y_d, S'(u_{n'}^+)(u-u_{n'}^+))+(\alpha u_{n'}^+,u-u_{n'}^+). $$

Testing the left hand side of the previous inequality with the test function $u:={\hat{u}}\in U_{\mathrm {ad}}$ we get

$$\begin{aligned} (\mu _{n'}^+,S'(u_{n'}^+)(u_{n'}^+-{\hat{u}}))&= (\mu _{n'}^+,S'(u_{n'}^+)(u_{n'}^+-{\hat{u}})) +(\mu _{n'}^+,S(u_{n'}^+)-\psi ) -(\mu _{n'}^+,S(u_{n'}^+)-\psi )\\&= - (\mu _{n'}^+,S(u_{n'}^+)+S'(u_{n'}^+)({\hat{u}}-u_{n'}^+)-\psi ) +(\mu _{n'}^+,S(u_{n'}^+)-\psi ). \end{aligned}$$

By Lemma 3.8 we know that there exists an N such that for all $n'>N$ the control $u_{n'}^+$ satisfies (11). Hence for all $n'>N$ we obtain

$$ \frac{\sigma }{2}\left\Vert \mu _{n'}^+\right\Vert _{L^1(\Omega )}\le - (\mu _{n'}^+,S(u_{n'}^+)+S'(u_{n'}^+)({\hat{u}}-u_{n'}^+)-\psi ). $$

Thus, we estimate

$$\begin{aligned} \frac{\sigma }{2}\left\Vert \mu _{n'}^+\right\Vert _{L^1(\Omega )} \le&(\mu _{n'}^+,\psi - S(u_{n'}^+))+(y_{n'}^+-y_d, S'(u_{n'}^+)({\hat{u}}-u_{n'}^+))+(\alpha u_{n'}^+,{\hat{u}}-u_{n'}^+)\\ \le&(\mu _{n'}^+,\psi -y_{n'}^+)_+ +\left\Vert y_{n'}^+-y_d\right\Vert _{L^2(\Omega )}\left\Vert S'(u_{n'}^+)({\hat{u}}-u_{n'}^+)\right\Vert _{L^2(\Omega )} \\&+\alpha \left\Vert u_{n'}^+\right\Vert _{L^2(\Omega )} +\left\Vert {\hat{u}}-u_{n'}^+\right\Vert _{L^2(\Omega )}. \end{aligned}$$

From Theorem 2.2 we know, that $y_h:= S'(u_{n'}^+)({\hat{u}}-u_{n'}^+)$ is the weak solution of a uniquely solvable partial differential equation with right-hand side ${\hat{u}}-u_{n'}^+$. Hence, it is norm bounded by $c\left\Vert {\hat{u}}-u_{n'}^+\right\Vert _{L^2(\Omega )}$ with $c>0$ independent of n. Further, exploiting Theorem 2.1 and Lemma 3.9, the boundedness of the terms on the right-hand side now follows directly from the boundedness of the admissible set $U_{\mathrm {ad}}$. This yields the assertion. $\square$

Let us conclude this section with the following result on convergence.

Theorem 3.11

(Convergence towards KKT points) Let $(y_n^+,u_n^+,p_n^+,\mu _n^+)_n$ denote the sequence that is generated by Algorithm 1. Let $u^*$ denote a weak limit point of $(u_n^+)_n$. If $u^*$ satisfies the linearized Slater condition from (10), then there exist subsequences $(y_{n'}^+,u_{n'}^+,p_{n'}^+,\mu _{n'}^+)_{n'}$ of $(y_n^+,u_n^+,p_n^+,\mu _n^+)_n$ such that

$$\begin{aligned} \begin{array}{llllllll} u_{n'}^+ &{}\rightarrow u^* &{}\quad &{}\text { in }L^2(\Omega ),&{} \qquad &{}y_{n'}^+ \rightarrow y^* &{}\quad &{} \text { in } H^1(\Omega )\cap {C({\overline{\Omega }})},\\ p_{n'}^+&{}\rightharpoonup p^* &{}&{} \text { in } W^{1,s}(\Omega ),\ s\in [1,N/(N-1)) &{}&{}\mu _{n'}^+ \rightharpoonup ^* \mu ^* &{}&{} \text { in } {{\mathcal {M}}({\overline{\Omega }})}\end{array} \end{aligned}$$

and $(y^*,u^*,p^*,\mu ^*)$ is a KKT point of the original problem (P).

Proof

Since $(u_n^+)_n$ is bounded in $L^2(\Omega )$ we can extract a weak convergent subsequence $u_{n'}^+\rightharpoonup u^*$ in $L^2(\Omega )$, thus $y_{n'}^+\rightarrow y^*$ in $H^1(\Omega )\cap {C({\overline{\Omega }})}$ due to Theorem 2.1. Hence, (6a) ist satisfied. Since $u_{n'}^+$ satisfies a linearized Slater condition by Lemma 3.8 for $n'$ sufficiently large, Lemma 3.10 yields $L^1(\Omega )$-boundedness of $(\mu _{n'}^+)_{n'}$. Hence, we can extract a weak-* convergent subsequence in ${{\mathcal {M}}({\overline{\Omega }})}$ denoted w.l.o.g. by $\mu _{n'}\rightharpoonup ^* \mu ^*$, see [17]. Convergence of $p_{n'}^+ \rightharpoonup p^*$ in $W^{1,s}(\Omega ),s\in [1,N/(N-1))$ can now be shown as in [25, Lem. 11]. Thus, the adjoint equation (6b) is satisfied. The space $W^{1,s}(\Omega )$, is compactly embedded in $L^2(\Omega )$. Hence $p_{n'}^+ \rightarrow p^*$ in $L^2(\Omega )$ and we get

$$\begin{aligned} 0&\le \underset{n\rightarrow \infty }{\lim \inf }(p_{n'}^+ +\alpha u_{n'}^+,u-u_{n'}^+) \le (p^*,u-u^*) - \underset{k\rightarrow \infty }{\lim \inf } (\alpha u_{n'}^+,u_{n'}^+-u)\\&\le (p^*,u-u^*) - (\alpha u^*,u^*-u)= (p^* + \alpha u^*,u-u^*), \end{aligned}$$

where we exploited the weak lower semicontinuity of $(\alpha u_{n'}^+,u-u_{n'}^+)$, $u\in L^2(\Omega )$. Hence, (6c) is satisfied. Due to the structure of the update rule we have

$$\begin{aligned} \lim _{n'\rightarrow \infty }R_{n'}^+ = \lim _{n'\rightarrow \infty }\left\Vert (y_{n'}^+-\psi )_+\right\Vert _{C({\overline{\Omega }})}+ (\mu _{n'}^+,\psi -y_{n'}^+)_+ = 0. \end{aligned}$$

This implies $y^*\le \psi$ and $\langle \mu ^*,\psi -y^*\rangle _+ =0$. In addition, $y^*\le \psi$ and $\mu ^*\ge 0$ implies $\langle \mu ^*,\psi -y^*\rangle \ge 0$, and we get $\langle \mu ^*,\psi -y^*\rangle = 0$. Thus (6d) is satisfied. We have proven that $(y^*,u^*,p^*,\mu ^*)$ is a KKT point of (P), i.e., $(y^*,u^*,p^*,\mu ^*)$ solves (6). It remains to show strong convergence of $u_{n'}^+\rightarrow u^*$ in $L^2(\Omega )$. Testing (6c) with $u_{n'}^+$ and (7c) with $u^*$ and adding both inequalities we get

$$\begin{aligned} (p^*-p_{n'}^++\alpha (u^*-u_{n'}^+),u_{n'}^+-u^*)\ge 0. \end{aligned}$$

Hence

$$\begin{aligned} \alpha \left\Vert u_{n'}^+-u^*\right\Vert _{L^2(\Omega )}^2\le (p^*-p_{n'}^+,u_{n'}^+-u^*). \end{aligned}$$

Since we already know that $p_{n'}^+\rightarrow p^*$ in $L^2(\Omega )$ and $u_{n'}^+\rightharpoonup u^*$ in $L^2(\Omega )$ this directly yields $u_{n'}^+\rightarrow u^*$ in $L^2(\Omega )$. $\square$

Remark 1

The proof of Theorem 3.11 above requires $R_n^+\rightarrow 0$ only. This opens up the possibility to modify the decision about successful steps in Algorithm 1. We report about such a modification in Sect. 6.

4 Convergence towards local solutions

So far, we have been able to show that a weak limit point that has been generated by Algorithm 1 is a stationary point of the original problem (P) if it satisfies the linearized Slater condition. If a weak limit point satisfies a second-order condition, we gain convergence to a local solution. However, the convergence result from Theorem 3.11 yields convergence of a subsequence of $(u_n^+)_n$ only. Accordingly, during all other steps the algorithm might choose solutions of the KKT system (3.2) that are far away from a desired local minimum ${{\bar{u}}}$. Here the following questions arise:

• 1. For every fixed $\mu$ does there exist a KKT point of the arising subproblem that satisfies ${{\bar{u}}}_k\in B_r({{\bar{u}}})$?

  and

• 2. Is an infinite number of steps successful if the algorithm chooses these KKT points in step 1?

Indeed these questions can be answered positively. We will show in this section that for every fixed $\mu$ there exists a KKT point of the augmented Lagrange subproblem such that for $\rho$ sufficiently large ${{\bar{u}}}_k\in B_r({{\bar{u}}})$. One should keep in mind, that also in this case there is no warranty that forces the algorithm to choose exactly these solutions. However, if the previous iterates are used in numerical computations as a starting point for the computation of the next iterate, the remaining iterates are likely located in $B_r({{\bar{u}}})$. In order to reach this result we need the following assumption which is rather standard.

Assumption 3

(Quadratic growth condition (QGC)) Let ${{\bar{u}}}\in U_{\mathrm {ad}}$ be a control satisfying the first-order necessary optimality conditions (6). We assume that there exist $\beta >0$ and $r_{{{\bar{u}}}}>0$ such that the quadratic growth condition

$$\begin{aligned} f(u)\ge f({{\bar{u}}})+\beta \left\Vert u-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2 \end{aligned}$$

(12)

is satisfied for all feasible $u\in U_{\mathrm {ad}}$, $S(u)\le \psi$ with $\left\Vert u-{{\bar{u}}}\right\Vert _{L^2(\Omega )} \le r_{{{\bar{u}}}}$. Hence, ${{\bar{u}}}$ is a local solution in the sense of $L^2(\Omega )$ for problem (P).

Let us mention that the quadratic growth condition can be implied by some well known second-order sufficient condition (SSC). We refer the reader to Sect. 5 for more details.

Our idea now is the following: In order to show that in every iteration of the algorithm there exists ${{\bar{u}}}_k\in B_r({{\bar{u}}})$ we want to estimate the error norm $\left\Vert {{\bar{u}}}_k-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2$. Here we want to exploit the quadratic growth condition from Assumption 3. However, this condition requires a control $u\in U_{\mathrm {ad}}$ that is feasible for the original problem (P), which has explicit state constraints. Since the solutions of the augmented Lagrange subproblems cannot be expected to be feasible for the original problem in general, we consider an auxiliary problem. Due to the special construction of this problem one can construct an auxiliary control that is feasible for the original problem (P). This idea has been presented for instance in [9] for a finite-element approximation as well as in [25] for regularizing a semilinear elliptic optimal control problem with state constraints by applying a virtual control approach.

4.1 The auxiliary problem

Let ${{\bar{u}}}$ be a local solution of (P) that satisfies the first-order necessary optimality conditions (6) of Theorem 2.5 and the quadratic growth condition from Assumption 3. Following the idea from [9, 25] we consider the following auxiliary problem

$$\begin{aligned} \underset{u^r_{\rho }}{\min }\,f_{AL}^r(u^r_{\rho },\mu ,\rho ):=f(u^r_\rho )+\frac{1}{2\rho }\left\Vert \left( \mu +\rho (S(u^r_{\rho })-\psi )\right) _+\right\Vert ^2_{L^2(\Omega )} \qquad {({P_{AL}^r})} \end{aligned}$$

such that

$$\begin{aligned} u^r_{\rho }\in U_{\mathrm {ad}},\qquad \left\Vert u^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}\le r. \end{aligned}$$

We choose $r<r_{{{\bar{u}}}}$ such that the quadratic growth condition from Assumption 3 is satisfied. In the following we define the set of admissible controls of $({P_{AL}^r})$ by

$$\begin{aligned} U_{\mathrm {ad}}^r:=\lbrace u\in U_{\mathrm {ad}}\ |\ \left\Vert u-{\bar{u}}\right\Vert _{L^2(\Omega )}\le r\rbrace . \end{aligned}$$

Since the set $U_{\mathrm {ad}}^r$ is closed, convex and bounded, the auxiliary problem admits at least one (global) solution. Moreover, replacing $U_{\mathrm {ad}}$ with $U_{\mathrm {ad}}^r$, first-order necessary optimality conditions can be derived as for the augmented Lagrange subproblem, see Theorem 2.5.

4.2 Construction of a feasible control

In this section we want to construct a control $u^{r,\delta }\in U_{\mathrm {ad}}^r$ that is feasible for the original problem (P), i.e., $u^{r,\delta }\in U_{\mathrm {ad}}$ and $S(u^{r,\delta })\le \psi$. Based on a Slater point assumption controls of this type have already been constructed in [31] for obtaining error estimates of finite element approximation of linear elliptic state constrained optimal control problems. In [25] these techniques were combined with the idea of the auxiliary problem presented for nonlinear optimal control problems in [9].

We follow the strategy from [25]. This work applied the virtual control approach in order to solve (P). This means, that the state constraints are relaxed in a suitable way. To obtain optimality conditions for the corresponding auxiliary problem the authors showed that the linearized Slater condition of the original problem can be carried over to feasible controls of the auxiliary problem. This transferred linearized Slater condition is also the main ingredient for the construction of feasible controls of the original problem. In our case, the state constraints have been removed from the set of explicit constraints by augmentation. Thus it is not necessary to establish a linearized Slater condition for the auxiliary problem in order to establish optimality conditions. However the Slater-type inequality that is deduced in the following lemma is still needed for our analysis, see Lemma 4.2.

Lemma 4.1

Let ${{\bar{u}}}$ satisfy Assumption 2with $\sigma >0$ and associated linearized Slater point ${\hat{u}}$. For $r>0$ let us define

$$\begin{aligned} {\hat{u}}^r := {{\bar{u}}}+ t({\hat{u}}-{{\bar{u}}}),\qquad t:=\frac{r}{\max (r,\left\Vert {\hat{u}}-{{\bar{u}}}\right\Vert _{L^2(\Omega )})},\qquad \sigma _r:=t\sigma . \end{aligned}$$

Then it holds $\left\Vert {\hat{u}}^r-{{\bar{u}}}\right\Vert _{L^2(\Omega )}\le r$ and there exists an ${\bar{r}}>0$ such that for all $r\in (0,{\bar{r}})$ and all ${{\bar{u}}}_\rho ^r\in U_{\mathrm {ad}}^r$ the following inequality is satisfied

$$\begin{aligned} S({{\bar{u}}}^r_{\rho })+S'({{\bar{u}}}^r_{\rho })({\hat{u}}^r-{{\bar{u}}}^r_{\rho })\le \psi - \frac{\sigma _r}{2}. \end{aligned}$$

(13)

Proof

By definition of ${\hat{u}}^r$ and t it holds $\left\Vert {\hat{u}}^r-{{\bar{u}}}\right\Vert _{L^2(\Omega )}\le r$. Inserting the definition of ${\hat{u}}^r$ we obtain

$$\begin{aligned} S({{\bar{u}}}) +S'({{\bar{u}}})({\hat{u}}^r-{{\bar{u}}})&= S({{\bar{u}}}) + tS'({{\bar{u}}})({\hat{u}}-{{\bar{u}}})\\&=(1-t)S({{\bar{u}}}) + t \left( S({{\bar{u}}})+ S'({{\bar{u}}})({\hat{u}}-{{\bar{u}}})\right) \\&\le \psi -t\sigma =: \psi -\sigma _r. \end{aligned}$$

Note, that we exploited the feasibility of $S({{\bar{u}}})$ and the linearized Slater condition in the last step. Hence, ${\hat{u}}^r$ is a linearized Slater point of the original problem (P) in the neighborhood of ${{\bar{u}}}$. We have $\left\Vert {\hat{u}}^r-{{\bar{u}}}\right\Vert \le r, \left\Vert {{\bar{u}}}-{{\bar{u}}}^r_\rho \right\Vert \le r$ and hence $\left\Vert {\hat{u}}^r-{{\bar{u}}}^r_{\rho }\right\Vert \le 2r$. Since S and $S'$ are Lipschitz we obtain (if r sufficiently small) $\left\Vert S({{\bar{u}}}^r_{\rho })-S({{\bar{u}}})\right\Vert _{{C({\overline{\Omega }})}}\le \sigma _r/6$, $\left\Vert S'({{\bar{u}}})({{\bar{u}}}-{{\bar{u}}}^r_{\rho })\right\Vert _{C({\overline{\Omega }})}\le \sigma _r/6$ and $\left\Vert (S'({{\bar{u}}}^r_{\rho })-S'({{\bar{u}}}))({\hat{u}}^r -{{\bar{u}}}^r_{\rho }) \right\Vert _{C({\overline{\Omega }})}\le \sigma _r/6$ . Hence,

$$\begin{aligned} S({{\bar{u}}}^r_{\rho }) + S'({{\bar{u}}}^r_{\rho })({\hat{u}}^r-{{\bar{u}}}^r_{\rho })&= S({{\bar{u}}}) + S'({{\bar{u}}})({\hat{u}}^r - {{\bar{u}}})\\&\quad + S({{\bar{u}}}^r_{\rho })-S({{\bar{u}}})\\&\quad +(S'({{\bar{u}}}^r_{\rho })-S'({{\bar{u}}}))({\hat{u}}^r -{{\bar{u}}}^r_{\rho }) + S'({{\bar{u}}})({{\bar{u}}}-{{\bar{u}}}^r_{\rho })\\&\le \psi -\frac{\sigma _r}{2}. \end{aligned}$$

Thus, ${\hat{u}}^r$ satisfies (13) and the proof is done. $\square$

In the following lemma we will construct feasible controls for (P) to be used in the sequel for our convergence analysis. The construction of an admissible control $u^{r,\delta }\in U_{\mathrm {ad}}^r$ that is also feasible for (P) is based on the fact that ${{\bar{u}}}^r_{\rho }$ satisfies Lemma 4.1.

We define the maximal violation of ${{\bar{u}}}^r_{\rho }$ with respect to the state constraints ${\bar{y}}^r_\rho \le \psi$ by

$$\begin{aligned} d[{{\bar{u}}}^r_{\rho },(P)]:=\left\Vert ({\bar{y}}^r_{\rho }-\psi )_+\right\Vert _{C({\overline{\Omega }})}, \end{aligned}$$

(14)

where ${\bar{y}}^r_{\rho }=S({{\bar{u}}}^r_{\rho })$.

Lemma 4.2

Let all assumptions from Lemma 4.1be satisfied and define $\delta _\rho \in (0,1)$ via

$$\begin{aligned} \delta _{\rho }:=\frac{d[{{\bar{u}}}^r_{\rho },(P)]}{d[{{\bar{u}}}^r_{\rho },(P)]+\frac{\sigma _r}{4}}. \end{aligned}$$

Then there exists ${\bar{r}}>0$ such that for all $r\in (0,{{\bar{r}}})$ and ${{\bar{u}}}_\rho ^r\in U_{\mathrm {ad}}^r$ the auxiliary control

$$\begin{aligned} u^{r,\delta }:={{\bar{u}}}^r_{\rho }+\delta ({\hat{u}}^r-{{\bar{u}}}^r_{\rho }) \end{aligned}$$

is feasible for the original problem (P), i.e., $S(u^{r,\delta })\le \psi$ for all $\delta \in [\delta _{\rho },1]$.

Proof

Applying (13) the proof follows the argumentation from [25, Lem. 7].

$\square$

The error between the auxiliary control $u^{r,\delta }$ and the global solution ${{\bar{u}}}^r_{\rho }$ of $({P_{AL}^r})$ is bounded by the maximal constraint violation.

Lemma 4.3

The constructed feasible control $u^{r,\delta }$ from Lemma 4.2satisfies the estimate

$$\begin{aligned} \left\Vert {{\bar{u}}}^r_{\rho }-u^{r,\delta }\right\Vert _{L^2(\Omega )} \le c d[{{\bar{u}}}^r_{\rho },(P)]. \end{aligned}$$

Proof

We estimate $\delta _{\rho }$ from Lemma 4.2 by

$$\begin{aligned} \delta _{\rho } =\frac{d[{{\bar{u}}}^r_{\rho },(P)]}{d[{{\bar{u}}}^r_{\rho },(P)]+\frac{\sigma _r}{4}}\le 4\frac{d[{{\bar{u}}}^r_{\rho },(P)]}{\sigma _r}. \end{aligned}$$

Together with $\left\Vert {\hat{u}}^r-{{\bar{u}}}^r_{\rho }\right\Vert _{L^2(\Omega )}\le 2r$ and the definition of $\sigma _r$ from Lemma 4.1 we arrive at

$$\begin{aligned} \begin{aligned} \left\Vert {{\bar{u}}}^r_{\rho }-u^{r,\delta }\right\Vert _{L^2(\Omega )}&=\left\Vert {{\bar{u}}}^r_{\rho }-({{\bar{u}}}^r_{\rho }+\delta _\rho ({\hat{u}}^r-{{\bar{u}}}^r_{\rho }))\right\Vert _{L^2(\Omega )}=\left\Vert \delta _\rho ( {\hat{u}}^r-{{\bar{u}}}^r_{\rho })\right\Vert _{L^2(\Omega )}\\&\le \left\Vert \delta _{\rho }({\hat{u}}^r-{{\bar{u}}}^r_{\rho })\right\Vert _{L^2(\Omega )} \le 8 \frac{\max \lbrace r,\left\Vert {\hat{u}}^r-{\bar{u}}\right\Vert _{L^2(\Omega )}\rbrace }{\sigma }d[{{\bar{u}}}^r_{\rho },(P)] \\&\le c d[{{\bar{u}}}^r_{\rho },(P)] \end{aligned} \end{aligned}$$

and the proof is done. $\square$

Finally we are able to apply the quadratic growth condition from Assumption 3.

Lemma 4.4

Let ${{\bar{u}}}$ be a local solution of (P) that satisfies the quadratic growth condition Assumption 3and the linearized Slater condition Assumption 2. Let $\mu \in L^2(\Omega )$ be fixed. Then there exists ${{\bar{r}}}\in (0,r_{{\bar{u}}})$ such that for all $r\in (0,{\bar{r}})$, the global solution ${{\bar{u}}}^r_{\rho }$ of the auxiliary problem $({P_{AL}^r})$ satisfies

$$\begin{aligned} \begin{aligned} \beta \left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert ^2_{L^2(\Omega )} +\frac{1}{2\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^2 \le c \left\Vert ({\bar{y}}^r_{\rho }-\psi )_+\right\Vert _{C({\overline{\Omega }})}+\frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2, \end{aligned} \end{aligned}$$

(15)

with a constant $c>0$ that is independent of $\rho$ and $\mu$.

Proof

As has been shown in Lemma 4.2 there exists ${{\bar{r}}}\in (0,r_{{\bar{u}}})$ such that for all $r\in (0,{\bar{r}})$ the control $u^{r,\delta }$ is feasible for (P). We insert the special choice $u=u^{r,\delta }$ in the quadratic growth condition (12) and get

$$\begin{aligned} f(u^{r,\delta })&\ge f({{\bar{u}}})+\beta \left\Vert u^{r,\delta }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2 \nonumber \\&=f({{\bar{u}}})+\beta \left\Vert u^{r,\delta }-{{\bar{u}}}^r_{\rho }+{{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2 \nonumber \\&\ge f({{\bar{u}}})+\beta \left( \left\Vert u^{r,\delta }-{{\bar{u}}}^r_{\rho }\right\Vert _{L^2(\Omega )}^2-2|(u^{r,\delta }-{{\bar{u}}}^r_{\rho },{{\bar{u}}}^r_{\rho }-{{\bar{u}}})|+\left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2\right) \nonumber \\&\ge f({{\bar{u}}})+\beta \left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2-c\left\Vert {{\bar{u}}}^r_{\rho }-u^{r,\delta }\right\Vert _{L^2(\Omega )}, \end{aligned}$$

(16)

where we exploited that $\left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2\le r^2$ and $\left\Vert {{\bar{u}}}^r_{\rho }-u^{r,\delta }\right\Vert _{L^2(\Omega )}$ is bounded by the maximal constraint violation (Lemma 4.3). Rearranging the terms of (16) and applying Lemma 4.3 we get

$$\begin{aligned} \beta \left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2&\le f(u^{r,\delta } )-f({{\bar{u}}})+c\left\Vert u^{r,\delta } -{{\bar{u}}}^r_{\rho }\right\Vert _{L^2(\Omega )}\\&\le f(u^{r,\delta } )-f({{\bar{u}}}^r_{\rho })+f({{\bar{u}}}^r_{\rho })-f({{\bar{u}}}) +cd[{{\bar{u}}}^r_{\rho },(P)]. \end{aligned}$$

We recall the definition of the reduced cost functional of the auxiliary problem $({P_{AL}^r})$

$$\begin{aligned} f_r({{\bar{u}}}^r_{\rho }) :=f({{\bar{u}}}_\rho ^r)+\frac{1}{2\rho }\left\Vert {\bar{\mu }}_\rho ^r\right\Vert ^2_{L^2(\Omega )}, \quad {\bar{\mu }}_\rho ^r=(\mu +\rho (S({{\bar{u}}}_\rho ^r)-\psi ))_+. \end{aligned}$$

Exploiting $u_a,u_b\in L^\infty (\Omega )$, the Lipschitz continuity of the norm and the solution operator S for the estimate

$$\begin{aligned} | f(u^{r,\delta } )-f({{\bar{u}}}^r_{\rho })|\le c\left\Vert u^{r,\delta }-{{\bar{u}}}^r_{\rho }\right\Vert _{L^2(\Omega )}, \end{aligned}$$

and exploiting the optimality of ${{\bar{u}}}^r_{\rho }$ for $({P_{AL}^r})$ as well as applying the definition of the reduced cost functional and the feasibility of ${{\bar{u}}}$ for the auxiliary problem, we get

$$\begin{aligned} \beta&\left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2\le f({{\bar{u}}}^r_{\rho })-f({{\bar{u}}}) +cd[{{\bar{u}}}^r_{\rho },(P)]\\&\quad \le f_r({{\bar{u}}}^r_{\rho })-f_r({{\bar{u}}}) -\frac{1}{2\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^2+\frac{1}{2\rho }\left\Vert (\mu +\rho (S({{\bar{u}}})-\psi ))_+\right\Vert _{L^2(\Omega )}^2+cd[{{\bar{u}}}^r_{\rho },(P)]\\&\quad \le -\frac{1}{2\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^2 +\frac{1}{2\rho }\left\Vert (\mu +\rho (S({{\bar{u}}})-\psi ))_+\right\Vert _{L^2(\Omega )}^2 + cd[{{\bar{u}}}^r_{\rho },(P)]. \end{aligned}$$

Noting that it holds

$$\begin{aligned} \frac{1}{2\rho }\left\Vert (\mu +\rho (S({{\bar{u}}})-\psi ))_+\right\Vert _{L^2(\Omega )}^2\le \frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2 \end{aligned}$$

we get with (14)

$$\begin{aligned} \beta \left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{L^2(\Omega )}^2+\frac{1}{2\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^2&\le cd[{{\bar{u}}}^r_{\rho },(P)] +\frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2 \\&= c\left\Vert ({\bar{y}}^r_{\rho }-\psi )_+\right\Vert _{C({\overline{\Omega }})}+\frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2 \end{aligned}$$

which yields the claim. $\square$

4.3 An estimate of the maximal constraint violation

In this section we will derive an estimate on the maximal constraint violation. We recall an estimate from [26, Lem. 4].

Lemma 4.5

Let $f\in C^{0,1}({\overline{\Omega }})$ be given with $\left\Vert f\right\Vert _{C^{0,1}(\Omega )}\le L$. Then there exists a constant $c_L>0$, which is only dependent on L, such that the following estimate is satisfied

$$\begin{aligned} \left\Vert f\right\Vert _{C({\overline{\Omega }})}\le c_L\left\Vert f\right\Vert _{L^2(\Omega )}^\frac{2}{2+N}. \end{aligned}$$

Lemma 4.6

Let $\mu \in L^2(\Omega )$ be fixed and ${\bar{r}}$ be given as in Lemma 4.4. Further, let ${{\bar{u}}}^r_{\rho }$ be an optimal control of the auxiliary problem $({P_{AL}^r})$ with $r\in (0,{\bar{r}})$. Then the maximal violation $d[{{\bar{u}}}^{r}_{\rho },(P)]$ of ${{\bar{u}}}^r_{\rho }$ with respect to (P) can be estimated by

$$\begin{aligned} d[{{\bar{u}}}^r_{\rho },(P)]\le c\left( \frac{1}{\rho }\right) ^{1/(2+N)}\left( 1 + \frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2\right) ^{1/(2+N)}, \end{aligned}$$

where $c>0$ is independent of $r,\rho ,\mu$.

Proof

Since ${{\bar{u}}}^r_{\rho }\in L^\infty (\Omega )$ we get with a regularity result [24, Thm. 5] that ${\bar{y}}^r_{\rho }\in W^{2,q}(\Omega )$ for all $1<q<\infty$. Due to the embedding $W^{2,q}(\Omega )\hookrightarrow C^{0,1}(\Omega )$ for $q>N$ we can apply Lemma 4.5 and get the following estimate

$$\begin{aligned} \begin{aligned} d[{{\bar{u}}}^r_{\rho },(P)]&=\left\Vert (S({{\bar{u}}}^r_{\rho })-\psi )_+\right\Vert _{{C({\overline{\Omega }})}}\le c_L\left\Vert ({\bar{y}}^r_{\rho }-\psi )_+\right\Vert _{L^2(\Omega )}^{2/(2+N)}\\&\le c_L\left\Vert \frac{1}{\rho }\left( \mu +\rho ({\bar{y}}^r_{\rho }-\psi )\right) _+\right\Vert _{L^2(\Omega )}^{2/(2+N)} \le c_L\left( \frac{1}{\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}\right) ^{2/(2+N)}. \end{aligned} \end{aligned}$$

(17)

From Lemma 4.4 we obtain

$$\begin{aligned} \frac{1}{2\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^2 \le c \left\Vert ({\bar{y}}^r_{\rho }-\psi )_+\right\Vert _{C({\overline{\Omega }})}+\frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Since $\left\Vert y^r_{\rho '}\right\Vert _{{C({\overline{\Omega }})}}$ is uniformly bounded by Theorem 2.1 and $u^r_{\rho '}\in U_{\mathrm {ad}}^r$, there is $c>0$ independent of $r,\rho ,\mu$ such that

$$\begin{aligned} \frac{1}{2\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^2 \le c +\frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2. \end{aligned}$$

Straight forward calculations now yield

$$\begin{aligned} \left( \frac{1}{\rho }\left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}\right) ^{2/(2+N)}&=\left( \frac{1}{\rho }\right) ^{1/(2+N)}\left[ \frac{1}{\rho } \left\Vert {\bar{\mu }}^r_{\rho }\right\Vert _{L^2(\Omega )}^{2}\right] ^{1/(2+N)}\\&\le c\left( \frac{1}{\rho }\right) ^{1/(2+N)} \left( 1 + \frac{1}{2\rho }\left\Vert \mu \right\Vert _{L^2(\Omega )}^2\right) ^{1/(2+N)}, \end{aligned}$$

which is the desired estimate. $\square$

4.4 Main results

We can now formulate our main results of this section. Let us start with a result that shows that a local solution ${{\bar{u}}}$ of the original problem (P) can be approximated by a sequence of successful iterates $(u_n^+)_n$, which are KKT points of the augmented Lagrange subproblem in an arbitrary small neighborhood of a local solution ${{\bar{u}}}$ of (P). Since the successful iterates basically are found by fixing $\mu$ and letting $\rho _k$ tend to infinity, this investigation basically reduces to the investigation of a quadratic penalty method with a fixed shift.

Throughout this section we assume that ${{\bar{u}}}$ is a local solution of (P) satisfying the QGC from Assumption 3 and the linearized Slater condition from Assumption 2.

Theorem 4.7

Let $\mu \in L^2(\Omega )$ be fix, ${\bar{r}}$ be given as in Lemma 4.4, and let ${{\bar{u}}}^r_{\rho }$ denote a global solution of the auxiliary problem $({P_{AL}^r})$.

Then we have:

• (a) For every $r\in (0,{\bar{r}})$ there is a ${{\bar{\rho }}}$, which is dependent on $\mu$, such that for all $\rho >{{\bar{\rho }}}$ it holds $\left\Vert {{\bar{u}}}^r_{\rho }-{{\bar{u}}}\right\Vert _{{L^2(\Omega )}}< r$.

• (b) For every $r\in (0,{\bar{r}})$ the points ${{\bar{u}}}^r_{\rho }$ are local solutions of the augmented Lagrange subproblem $(P_{AL}^k)$, provided that $\rho >{\bar{\rho }}$.

Proof

(a) The first statement follows directly from Lemma 4.4, the estimate of the maximal constraint violation from Lemma 4.6 and the Lipschitz continuity of the solution operator (5). (b) Let $u\in U_{\mathrm {ad}}$ be chosen arbitrarily such that $\left\Vert u-{{\bar{u}}}_\rho ^r\right\Vert _{L^2(\Omega )}\le \frac{r}{2}$. Applying statement (a) we obtain

$$\begin{aligned} \left\Vert u-{{\bar{u}}}\right\Vert _{L^2(\Omega )}\le \left\Vert u-{{\bar{u}}}_\rho ^r\right\Vert _{L^2(\Omega )}+\left\Vert {{\bar{u}}}_\rho ^r-{{\bar{u}}}\right\Vert _{L^2(\Omega )}\le \frac{r}{2}+\frac{r}{2}=r \end{aligned}$$

for $\rho$ sufficiently large. Thus, $u\in U_{\mathrm {ad}}^r$. Since ${{\bar{u}}}_\rho ^r$ is the global solution of the auxiliary problem we obtain $f_{AL}(u)\ge f_{AL}({{\bar{u}}}_\rho ^r)$ for all $u\in U_{\mathrm {ad}}$ with $\left\Vert u-{{\bar{u}}}_\rho ^r\right\Vert _{L^2(\Omega )}\le \frac{r}{2}$. $\square$

In Theorem 4.7 we have accomplished to prove that it is at least possible to approximate a local solution of the original problem (P) by a sequence of stationary points of the augmented Lagrange subproblem. Moreover, Theorem 4.7 is the basis of the further analysis of the behavior of Algorithm 1 if in step 1 $({\bar{y}}_k,{{\bar{u}}}_k,{\bar{p}}_k)$ is chosen as a global solution of the auxiliary problem $({P_{AL}^r})$.

Theorem 4.8

Assume that in step 1 of Algorithm 1 $({\bar{y}}_k,{{\bar{u}}}_k,{\bar{p}}_k)$ is chosen as a global solution of the auxiliary problem $({P_{AL}^r})$ if this global solution solves the optimality system of the augmented Lagrange subproblem (3.2). Then Algorithm 1 makes infinitely many successful steps.

Proof

Theorem 4.7 justifies that global solutions of the auxiliary problem $({P_{AL}^r})$ are local solutions and hence KKT points of the augmented Lagrange subproblem. The remaining part of the proof follows the proof strategy of Theorem 3.6. $\square$

Moreover, if the penalty parameter remains bounded, the resulting multiplier ${\bar{\mu }}$ is a function in $L^2(\Omega )$ and $(\frac{1}{\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )})_k$ is uniformly bounded.

Theorem 4.9

Assume that the sequence of penalty parameters $(\rho _k)_k$ is bounded. Suppose further that $({\bar{y}}_k,{{\bar{u}}}_k,{\bar{p}}_k)$ is chosen as a global solution of the auxiliary problem $({P_{AL}^r})$ for all k large enough. Then the sequences $(\left\Vert {\bar{\mu }}_k\right\Vert _{L^2(\Omega )})_k$ and $(\frac{1}{\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )})_k$ are bounded. The multiplier ${\bar{\mu }}$ given by Theorem 3.11belongs to $L^2(\Omega )$.

Proof

By assumption, the algorithm makes only finitely many unsuccessful steps, and $\rho _k = {{\bar{\rho }}}$ holds for all k large enough. In addition, for all k large enough the iterates are global solutions of the auxiliary problem $({P_{AL}^r})$. Rearranging the terms from Lemma 4.4, we obtain for large k

$$\begin{aligned} \frac{1}{2{{\bar{\rho }}}}\left\Vert {\bar{\mu }}_k\right\Vert _{L^2(\Omega )}^2 - \frac{1}{2{{\bar{\rho }}}}\left\Vert {\bar{\mu }}_{k-1}\right\Vert _{L^2(\Omega )}^2\le c \left\Vert ({\bar{y}}_k-\psi )_+\right\Vert _{C({\overline{\Omega }})}\le c\ R_k. \end{aligned}$$

By definition of successful steps, we have $\sum _k R_k <+\infty$. Hence, summing the above inequality yields the boundedness of $({\bar{\mu }}_k)_k$ in $L^2(\Omega )$. Since $\rho _k\ge \rho _0$, the sequence $(\frac{1}{\rho _k}\left\Vert {\bar{\mu }}_k\right\Vert ^2_{L^2(\Omega )})_k$ is bounded as well. $\square$

One has to keep in mind that the quadratic growth condition is only a local condition. Hence, the result of Theorem 4.7 is actually the best we can expect. In particular, the subproblems $(P_{AL}^k)$ may have solutions arbitrarily far from ${{\bar{u}}}$ and we cannot exclude the possibility that these solutions are chosen in the subproblem solution process from Algorithm 1. However, one can prevent this kind of scenario by using the previous iterate ${{\bar{u}}}_k$ as a starting point for the computation of ${{\bar{u}}}_{k+1}$. In this way it is reasonable to expect that as soon as one of the iterates ${{\bar{u}}}_k$ lies in $B_r({{\bar{u}}})$ (with r as above) and the penalty parameter is sufficiently large, the remaining iterates will stay in $B_r({{\bar{u}}})$ and converge to ${{\bar{u}}}$. In practice, the occurring subproblems will be solved with a semi-smooth Newton method, see Sect. 6, which is only locally superlinear convergent. In order to obtain convergence of the overall method, it is necessary to assume that the initial value of the augmented Lagrange method is close enough the solution of the penalized subproblem. As soon as as the algorithm has once computed a KKT point of this subproblem, which is sufficiently close to a local solution ${{\bar{u}}}$, it is reasonable to expect the whole method to converge.

5 Second-order sufficient conditions

We take up the quadratic growth condition from Assumption 3. This condition is implied by a second-order sufficient condition, see [6]. We define the Lagrangian function

$$\begin{aligned} \underset{u\in U_{\mathrm {ad}}}{\min } {\mathcal {L}}(u,\mu )=f(u)+\int _{{\overline{\Omega }}} \left( S(u)-\psi \right) \,\mathrm {d}\mu \end{aligned}$$

where $y=S(u)$ and assume that for all $({\bar{y}},{\bar{p}},{\bar{\mu }})$ satisfying the first-order necessary optimality conditions (6) to ${{\bar{u}}}$ it holds

$$\begin{aligned} \frac{\partial ^2 {\mathcal {L}}}{\partial u^2}({{\bar{u}}},{\bar{\mu }})[h,h]\ge 0,\qquad \forall h \in C_{{{\bar{u}}}}\backslash \lbrace 0\rbrace , \end{aligned}$$

(18)

where $C_{{{\bar{u}}}}$ denotes the cone of critical directions as defined in [6]. Since the solution operator S (Theorem 2.2) and the cost functional $J:L^2(\Omega )\rightarrow {\mathbb {R}}$ are of class $C^2$ (see [6, 7]), inequality (18) together with the first-order necessary conditions implies the quadratic growth condition from Assumption 3, see [6, Thm. 4.1, Remark 4.2] and [37]. Note, that the multiplier ${\bar{\mu }}$ does not need to be unique. That is why (18) is imposed for every multiplier.

Let us return to the convergence analysis of Algorithm 1. If in addition to the assumptions of Theorem 3.11, $u^*$ satisfies the QGC from Assumption 3, then $u^*$ obviously is a local solution.

Second-order sufficient conditions not only allow us to prove convergence to a local solution but also to show local uniqueness of stationary points of the augmented Lagrange subproblem. This is an important issue for numerical methods. In [24] the authors proved that the Moreau–Yosida regularization without additional shift parameter is equivalent to the virtual control problem for a specific choice of therein appearing parameters. This equivalence can be transferred to the augmented Lagrange subproblem $(P_{AL}^{\rho ,\mu })$.

Remark 2

Let ${{\bar{u}}}\in U_{\mathrm {ad}}$ be a control that satisfies the first-order necessary optimality conditions (6) and let ${\bar{\mu }}$ be the unique Lagrange multiplier w.r.t. the state constraints. We assume that there exists a constant $\delta >0$ such that

$$\begin{aligned} \frac{\partial ^2 {\mathcal {L}}}{\partial u^2}({{\bar{u}}},{\bar{\mu }})[h,h]\ge \delta \left\Vert h\right\Vert ^2_{L^2(\Omega )},\qquad \forall h\in {L^2(\Omega )}. \end{aligned}$$

(19)

One can prove that the SSC (19) can be carried over to the augmented Lagrange subproblems. Let $\mu \in L^2( \Omega )$ and $\rho >0$ be fixed. Let ${{\bar{u}}}_\rho \in U_{\mathrm {ad}}$ be a control that satisfies ${{\bar{u}}}_\rho \in B_r({{\bar{u}}})$ and the first-order necessary optimality conditions (3.2). Let the SSC (19) be satisfied. Then there exists a constant $\delta '>0$, which is independent of $\mu$ such that for all $h\in L^2(\Omega )$ the following condition

$$\begin{aligned} f''({{\bar{u}}}_\rho )h^2+((\mu +\rho (S({{\bar{u}}}_\rho )-\psi )_+,S''({{\bar{u}}}_\rho )h^2)\ge \delta '\left\Vert h\right\Vert _{L^2(\Omega )}^2 \end{aligned}$$

or equivalently

$$\begin{aligned} \int _{\Omega }(y^2_{h}-{\bar{p}}_\rho d_{yy}(x,{\bar{y}}_\rho )y^2_{h}+\alpha h^2)\ \,\mathrm {d}x\ge \delta '\left\Vert h\right\Vert _{L^2(\Omega )}^2 \end{aligned}$$

is fulfilled for all $(h,y_{h})\in L^2(\Omega )\times H^1(\Omega )$ provided that $\rho$ is sufficiently large. Here, $y_{h}=S'({{\bar{u}}}_\rho )h$ and ${\bar{p}}_\rho$ is the solution of the adjoint equation of the augmented Lagrange subproblem.

Moreover, then there exists a constant $\beta >0$ and $\gamma >0$ such that the quadratic growth condition

$$\begin{aligned} f_{AL}(u)\ge f_{AL}({{\bar{u}}}_\rho )+\beta \left\Vert u-{{\bar{u}}}_\rho \right\Vert ^2_{L^2(\Omega )} \end{aligned}$$

holds for all $u\in U_{\mathrm {ad}}$ with $\left\Vert u-{{\bar{u}}}_\rho \right\Vert _{L^2(\Omega )}\le \gamma$ and ${{\bar{u}}}_\rho$ is a local solution with corresponding state ${\bar{y}}_\rho$ of the augmented Lagrange subproblem. Here, Theorem 13 from [25] yields the carried over version of the second-order condition for a virtual control problem. In [24, Prop. 3] it is proved that this condition implies a quadratic growth condition for the virtual control problem. Further, following the arguments as in [24, Thm. 5] this results can be adapted to the augmented Lagrange subproblem.

6 Numerical tests

In this section we report on numerical results for the solution of a semilinear elliptic pointwise state constrained optimal control problem in two dimensions. All optimal control problems have been solved using the above stated augmented Lagrange algorithm implemented with FEniCS [29] using the DOLFIN [30] Python interface.

In every outer iteration of the augmented Lagrange algorithm the KKT system (3.2) has to be solved for given $\mu$ and $\rho$. This is done by applying a semi-smooth Newton method. We define the sets

$$\begin{aligned} \begin{aligned} {\mathcal {A}}^{a}_{\rho }:=\bigg \lbrace x\in \Omega :-&\frac{1}{\alpha }{\bar{p}}_\rho \le u_a \bigg \rbrace ,\qquad {\mathcal {A}}^{b}_{\rho }:= \left\{ x\in \Omega :-\frac{1}{\alpha }{\bar{p}}_\rho \ge u_b\right\} ,\\&{\mathcal {Y}}_{\rho }:=\left\{ x\in \Omega :(\mu +\rho ({\bar{y}}_\rho -\psi ))(x) > 0 \right\} . \end{aligned} \end{aligned}$$

(20)

Then system (3.2) can be stated as

$$\begin{aligned} A{\bar{y}}_{\rho }+d({\bar{y}}_{\rho })&= {{\bar{u}}}_{\rho } \nonumber \\ A^*{\bar{p}}_{\rho } + d_y({\bar{y}}_{\rho }){\bar{p}}_{\rho }&= {\bar{y}}_{\rho }-y_d +\chi _{{\mathcal {Y}}_{\rho }}\left( \mu +\rho ({\bar{y}}_{\rho }-\psi )\right) \nonumber \\ {{\bar{u}}}_\rho + (1-\chi _{{\mathcal {A}}^{a}_{\rho }}-\chi _{{\mathcal {A}}^{b}_{\rho }}) \frac{1}{\alpha }{\bar{p}}_\rho&= \chi _{{\mathcal {A}}^{a}_{\rho }} u_a + \chi _{{\mathcal {A}}^{b}_{\rho }} u_b. \end{aligned}$$

(21)

The semi-smooth Newton method for solving (3.2) is given in Algorithm 2. In our numerical test we solved the system arising in step 4 of Algorithm 2 with the direct solver spsolve of the Python scipy linear algebra package.

Since the linear parts of the system can be solved exactly we choose the error that arises during the linearization of the discretized system (21) as a stopping criterion. We terminate the semi-smooth Newton method as soon as

$$\begin{aligned}\max ( r_1, r_2 ,r_3) \le 10^{-6},\end{aligned}$$

where

$$\begin{aligned} r_1&:= \left\Vert d(y_{k})-\left( d_y(y_{k-1})(y_{k}-y_{k-1})+d(y_{k-1}) \right) \right\Vert _{L^2(\Omega )},\\ r_2&:=\left\Vert d_y(y_{k}) - (d_y(y_{k-1})p_{k} + d_{yy}(y_{k-1})p_{k-1}(y_{k}-y_{k-1})) + (\chi _{{\mathcal {Y}}_{k}}-\chi _{{\mathcal {Y}}_{k-1}})(\mu +\rho (y_{k}-\psi )\right\Vert _{L^2(\Omega )},\\ r_3&:=\left\Vert u_k-P_{U_{\mathrm {ad}}}\left( -\frac{1}{\alpha }p_k\right) \right\Vert _{L^2(\Omega )} \end{aligned}$$

is satisfied. In the following, $(y_h , u_h , p_h, \mu _h )$ denote the calculated solutions after the stopping criterion is reached. We consider optimal control problems like

$$\begin{aligned} \min \ J(y,u):&=\frac{1}{2}||y-y_d||_{L^2(\Omega )}^2+\frac{\alpha }{2}||u||_{L^2(\Omega )}^2\\ \text {s.t.}\quad&y=Su,\qquad y\le \psi ,\qquad u\in U_{\mathrm {ad}}\end{aligned}$$

where $\Omega = [0,1]\times [0,1]$. As not mentioned otherwise, we initialize $({\bar{y}}_0,{{\bar{u}}}_0,{\bar{p}}_0,\mu _1)$ equal to zero, the penalty parameter with $\rho _0:=1.0$. The parameter in the decision concerning successful steps $\tau$ is chosen dependent on the example. If a step has not been successful, the penalization parameter is increased by the factor $\theta :=10$. We stopped the algorithm as soon as

$$\begin{aligned} R_n^+:=\left\Vert (y_n^+-\psi )_+\right\Vert _{C({\overline{\Omega }})} + ( \mu _n^+,\psi -y_n^+)_+ \le 10^{-4} \end{aligned}$$

(22)

was satisfied. Since the stopping criterion from Algorithm 2 yields $(y_h,u_h,p_h)$ that satisfies (6a)–(6c) with the desired accuracy this is a suitable stopping criterion.

We compare our method to the plain penalty method. In order to do so, we penalize the state constraint via the standard Moreau–Yosida regularization $(\rho /2)\left\Vert (y-\psi )_+\right\Vert ^2$ and increase the penalty parameter in every iteration of the arising algorithm via the factor $\theta$, which is the same as for the augmented Lagrange method. The algorithm is stopped as soon as (22) is satisfied. In this situation, all iterates are successful iterates corresponding to the notation $y_n^+,u_n^+,p_n^+,\mu _n^+$ and the approximation of the multiplier $\mu _n^+$ is computed via $\mu _n^+:= \rho (y_n^+-\psi )_+$. We will refer to this method as the MY method.

Moreover, we will examine the behavior of the algorithm, in particular the behavior of the penalty parameter $\rho$, dependent on the different choices of $\tau$. The natural choice of $\tau <1$ as a constant, postulates a linear increase of the quantity $R_n^+$. We will refer to this choice of $\tau$ as the method AL I. Additionally, we want to investigate the case that the choice of $\tau$ is modified such that no linear decrease is required any more. In this way, due to construction of the algorithm, one would expect more successful steps, hence, more updates of the multiplier and less increase of the penalty parameter. In the following we set

$$\begin{aligned} \tau _k:={\left\{ \begin{array}{ll} \tau _0 \in (0,1),\quad &{} \text {if } k=0,\\ \tau _{k-1}, \quad &{}\text {if the step { k} been successful,} \\ \frac{s}{s + \frac{1-\tau _0}{\tau _0}}, &{} \text {if the step { k} has not been successful.} \end{array}\right. } \end{aligned}$$

Thus, $\tau$ remains unchanged, if the step has been successful, otherwise, we increase its value according to the third case, where s is the number of successful steps until the k-th iteration. Clearly, this sequence is monotonically increasing with limit 1. Note, that this choice of $\tau$ entails a slight change in Lemma 3.9, where the factor $\tau ^n$ has to be replaced by a product of $\tau _n^+$, which are the parameters $\tau _k$ corresponding to the successful iterates. Since $\tau _n^+ \le n/(n + (1-\tau _0)/\tau _0)$, it follows $\lim _{n\rightarrow \infty }\prod _{j=1}^n\tau _j^+=0$. Note that this property is needed in the proof of Theorem 3.3, where we exploited $R_n^+\rightarrow 0$. The remaining convergence analysis, in particular Lemma 3.10, is not influenced. We will indicate this choice of $\tau$ as the AL II method.

Let us briefly comment on the influence of the tuning parameter $\tau$ on the number of successful updates. For a constant choice of $\tau$, one would naturally expect a higher number of successful steps and a smaller value of the final penalty parameter $\rho$ for a large value of $\tau$. We checked all of our numerical examples for different values of $\tau$. As expected, a larger value of $\tau$ leads to more successful updates. However, enlarging $\tau$ had no influence on the final penalty parameter. Thus, for the subsequent comparison of the different numerical methods in our examples we rely on the choice of $\tau$ that yields the best results concerning low iteration numbers and final value of $\rho$.

6.1 Example 1

Let us first consider an optimal control problem that is governed by the following partial differential equation

$$\begin{aligned} \begin{array}{llll} -\Delta y +y+ \exp (y) &{}= u &{}\quad &{}\text { in } \Omega ,\\ \quad \quad \quad \quad \quad\;\; \partial _{\nu } y &{}= 0 &{}&{}\text { on } \Gamma . \end{array} \end{aligned}$$

Clearly $d(y):=\exp (y)$ satisfies the required assumptions from Assumption 1. We set

$$\begin{aligned} y_d(x) := 8\sin (\pi x_1)\sin (\pi x_2)-4, \end{aligned}$$

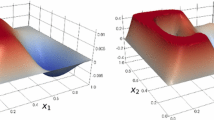
$\psi (x):=1.0$ and $U_{\mathrm {ad}}:= \left\{ u\in L^\infty (\Omega ) :-100\le u(x)\le 200\right\}$. We choose $\alpha := 10^{-5}$. Figures 1 and 2 illustrate the computed results for the augmented Lagrange method with constant $\tau :=0.4$ for a degree of freedom of $10^4$.

Table 1 shows iterations numbers for the Moreau–Yosida method compared with the augmented Lagrange method for two different choices of $\tau$. For the constant choice of $\tau$ in AL I the augmented Lagrange method converges nearly as fast as the Moreau–Yosida regularization method, however the penalty parameter is smaller. The value of the final penalty parameter can even be decreased more for AL II. Figure 3 depicts the behavior of the penalty parameter for AL I and AL II for a degree of freedom of $10^5$. While the penalty parameter tends towards infinity pretty fast for the constant choice of $\tau$ in AL I, it can be more controlled for AL II. However, the large percentage of successful steps results in high iteration numbers compared to the other two methods.

Fig. 1

(Example 1) Computed discrete optimal state $y_h$ (left) and optimal control $u_h$ (right)

Fig. 2

(Example 1) Computed discrete multiplier $\mu _h$ (left) and the adjoint state $p_h$ (right)

Table 1 (Example 1) Iteration numbers and final value of the penalty parameter $\rho$ with the parameters $\theta = 10$, $\tau := 0.4$ for AL I and $\tau _0:= 0.5$ for AL II

Fig. 3

(Example 1) $L^1(\Omega )$-norm of discrete multipliers $\mu _k$, penalty parameters $\rho _k$ versus iteration number for a degree of freedom of $10^5$

6.2 Example 2

Next, we consider the following partial differential equation

$$\begin{aligned} \begin{array}{llll} -\Delta y + y^3 &{}= u+f &{}\quad &{}\text { in } \Omega ,\\ \quad \quad\; \partial _{\nu } y &{}= 0 &{}&{}\text { on } \Gamma \end{array} \end{aligned}$$

and construct $({\bar{y}},{{\bar{u}}},{\bar{p}},{\bar{\mu }})$ that satisfy the KKT system (6). Let $\Omega :=B_2(0)$. We consider box constraints and set $u_a := -5$, $u_b := 5$. For clarity and to shorten our notation we set $r := r(x_1,x_2) := \sqrt{x_1^2 + x_2^2}$ and define the following functions

$$\begin{aligned} {{\bar{y}}}(x_1,x_2)&:= {\left\{ \begin{array}{ll} 1 &{} \text {if } r< 1\\ 32 - 120 \cdot r + 180 \cdot r^2 - 130 \cdot r^3 + 45 \cdot r^4 - 6 \cdot r^5 &{} \text {if } r \ge 1 \end{array}\right. },\\ {{\bar{p}}}(x_1,x_2)&:= 2\cos \left( \frac{3}{4}\pi x_1\right) \cos \left( \frac{3}{4}\pi x_2\right) \cdot \left( 1 - \frac{5}{4}r^3 + \frac{15}{16} r^4 - \frac{3}{16} r^5 \right) ,\\ {{\bar{u}}}(x_1,x_2)&:= P_{U_{\mathrm {ad}}}\left( -\frac{1}{\alpha }{\bar{p}}(x_1,x_2)\right) ,\\ {{\bar{\mu }}}(x_1,x_2)&:= {\left\{ \begin{array}{ll} \exp \left( - \frac{1}{1-r^2} \right) &{} \text {if } r < 1\\ 0 &{} \text {if } r \ge 1 \end{array}\right. },\\ \psi (x_1,x_2)&:= 1. \end{aligned}$$

Some calculation show that ${\bar{y}}, {{\bar{p}}} \in C^2({\overline{\Omega }})$ and $\bar{\mu }\in {C({\overline{\Omega }})}$. Furthermore $\partial _\nu {\bar{y}}= \partial _\nu {\bar{p}}= 0$ on $\Gamma$. We now set

$$\begin{aligned} f(x_1,x_2)&:= - \Delta {{\bar{y}}}(x_1,x_2) +{\bar{y}}^3(x_1,x_2)- {{\bar{u}}}(x_1,x_2),\\ y_d(x_1,x_2)&:= \Delta {{\bar{p}}}(x_1,x_2) -3{\bar{y}}^2(x_1,x_2){\bar{p}}(x_1,x_2)+ {{\bar{y}}}(x_1,x_2) + {{\bar{\mu }}}(x_1,x_2). \end{aligned}$$

We start the algorithm with $\alpha :=0.1$, $\rho _0:=1$ and $\tau := 0.5$. The Figs. 4 and 5 depict the computed result for constant $\tau := 0.1$ and a degree of freedom of $10^5$.

The iteration numbers given in Table 2 indicate once more that the augmented Lagrange method is a suitable method to solve state constrained optimal control problems with a resulting low value of the final penalty parameter $\rho$ compared to the quadratic penalty method. Moreover, in this example the iteration numbers scale well with increasing dimension. This might be due to the case that the multiplier enjoys a higher regularity. In fact ${\bar{\mu }}$ is an $L^2(\Omega )$-function. Furthermore, Fig. 6 supports Theorem 4.9 by emphasizing the likely boundedness of the penalty parameter for AL II.

Fig. 4

(Example 2) Computed discrete optimal state $y_h$ (left) and multiplier $\mu _h$ (right)

Fig. 5

(Example 2) Computed discrete optimal control $u_h$ (left) and the adjoint state $p_h$ (right)

Table 2 (Example 2) Iteration numbers and final value of the penalty parameter $\rho$ with the parameters $\theta = 10.0$, $\tau := 0.1$ for AL I and $\tau _0:= 0.5$ for AL II

Fig. 6

(Example 2) penalty parameters $\rho _k$ versus iteration number for different choices of $\theta$ for a degree of freedom of $10^5$

6.3 Example 3

We adapt an example from [23] which can also be found in [35] for state constraints given by $y\ge \psi$. In this case $\Omega := [-1,2]\times [-1,2]$. This example does not include constraints on the control. The optimal control problem is governed by the semilinear partial differential equation

$$\begin{aligned} \begin{array}{llll} -\Delta y + y^5 &{}= u+f &{}\quad &{}\text { in } \Omega ,\\ \quad \quad \; \partial _{\nu } y &{}= 0 &{}&{}\text { on } \Gamma \end{array} \end{aligned}$$

which satisfies Assumption 1. We set $r:= r(x_1,x_2):= \sqrt{x_1^2+x_2^2}$. The state constraint is given by $\psi (r) := -\frac{1}{2\pi \alpha }\left( \frac{1}{4}-\frac{r}{2}\right)$. Further, we have

$$\begin{aligned}&{\bar{y}}(r) := -\frac{1}{2\pi \alpha }\chi _{r\le 1}\left( \frac{r^2}{4}(\log r-2)+\frac{r^3}{4}+\frac{1}{4}\right) ,\qquad {{\bar{u}}}(r) := \frac{1}{2\pi \alpha }\chi _{r\le 1}(\log r +r^2-r^3), \\&\quad \qquad \qquad \quad {\bar{p}}(r) := -\alpha {{\bar{u}}}(r),\qquad {\bar{\mu }}(r) := \delta _0(r). \end{aligned}$$

It can be checked easily that ${\bar{y}}$ and ${\bar{p}}$ satisfy the Neumann boundary. We consider the auxiliary functions

$$\begin{aligned} {\tilde{y}}_d(r)&:= {\bar{y}}(r)-\frac{1}{2\pi }\chi _{r\le 1}(4-9r),\quad {\tilde{f}}(r) := -\frac{1}{8\pi }\chi _{r\le 1}(4-9r+4r^2-4r^3) \end{aligned}$$

and set

$$\begin{aligned} y_d(r) := {\tilde{y}}_d(r) - 5{\bar{y}}^4{\bar{p}}, \quad f(r):= {\tilde{f}}(r)-{\bar{y}}^5. \end{aligned}$$

We start the algorithm with $\alpha := 1.0$, $\rho _0:= 0.5$ and $\tau := 0.3$. The computed results can be seen in Figs. 7 and 8 for the choice of constant $\tau :=0.3$ and a degree of freedom of $10^4$. Concerning the performance of the algorithm, all methods behave very similarly, see Table 3. While the Moreau–Yosida method holds an advantage concerning iteration numbers, the augmented Lagrange method requires a smaller value of the penalty parameter at the expense of higher iteration numbers. In this example, the multiplier ${\bar{\mu }}$ is only a function in ${{\mathcal {M}}({\overline{\Omega }})}$, i.e., compared to Example 1 and Example 2 it is the most challenging example. This becomes apparent in the larger values of the final penalty parameter $\rho$ as well as the higher iteration numbers that are needed to solve the problem numerically. Moreover, it is surprising that Fig. 9 indicates the boundedness of the penalty parameter, which we would not expect in general from Theorem 4.9.

Let us emphasize that for all three examples the proposed augmented Lagrangian method yields the lowest value of the penalty parameter $\rho$. Even though the AL method might need slightly more inner iterations in comparison to the MY method this aspect is not to underestimate since a higher penalty parameter might cause numerical instability during the solution process of the subproblem.

Fig. 7

(Example 3) Computed discrete optimal state $y_h$ with state constraint $\psi$ (left) and multiplier $\mu _h$ (right)

Fig. 8

(Example 3) Computed discrete optimal control $u_h$ (left) and the adjoint state $p_h$ (right)

Table 3 (Example 3) Iteration numbers and final value of the penalty parameter $\rho$ with the parameters $\theta = 10.0$, $\tau := 0.3$ for AL I and $\tau _0:= 0.4$ for AL II

Fig. 9

(Example 1) $L^1(\Omega )$-norm of discrete multipliers $\mu _k$, penalty parameters $\rho _k$ versus iteration number for a degree of freedom of $10^5$