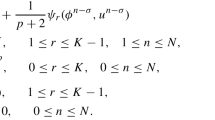1 Introduction

In the last few decades, fractional differential equations have been widely applied in various fields of science and engineering to model many phenomena [1–11]. The current applications of fractional differential equations make it important to find efficient methods to solve them. Though many analytic methods have been proposed, the solutions of most fractional differential equations cannot be easily obtained due to the nonlocality and complexity of fractional differential operators. Hence, numerical algorithms for fractional differential equations have been studied extensively by many researchers, which mainly cover finite difference methods [12–14], finite element methods [15], spectral methods[16], local fractional series expansion methods[17], and other methods[18–20]. In particular, operator-based approach[20] was proposed and developed to deal with nonlinear fractional order differential equations.

In this paper, we consider the following time fractional convection–diffusion equation with variable coefficients:

$$ \begin{aligned} &\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}-\epsilon \frac{\partial ^{2}u(x,t)}{\partial x^{2}}+p_{1}(x) \frac{\partial u(x,t)}{\partial x}+p_{2}(x)u(x,t)=f(x,t), \\ & 0< x < 1, \qquad 0< t \leq T, \end{aligned} $$
(1)

with the initial condition

$$ u(x,0)=h(x), \quad 0< x< 1, $$

and the boundary conditions

$$ u(a,t)=u(b,t)=0,\quad 0< t\leq T, $$

where \(0<\alpha < 1 \), ϵ is a known positive constant, \(p_{1}(x)\in C^{1}([0,1])\), \(p_{2}(x),h(x)\in C([0,1])\), and \(f(x,t)\in C(\Omega )\), \(\Omega =(0,1)\times (0,T]\). The time fractional derivative is defined in the Caputo sense as follows:

$$ \frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}= \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t} \frac{\partial u(x,\xi )}{\partial \xi } \frac{d\xi }{(t-\xi )^{\alpha }}, $$

where \(\Gamma (\cdot )\) is the gamma function.

The convection–diffusion equations widely occur in the mathematical modeling of various physical phenomena that arise in oil reservoir simulations, transport of mass and energy, global weather production, and dispersion of chemicals in reactors. Time fractional convection–diffusion equations can be utilized to simulate time-related abnormal diffusion processes. It is a generalization of the classical convection diffusion by replacing the integer order time derivative with a fractional order time derivative.

Sinc methods have been proposed and studied by Stenger [21]. The sinc method has been increasingly used for solving ordinary differential equations[22–25], partial differential equations[26–29], and integral equations[30–33]; it not only has exponential convergence rate, but also can deal with singular problems well. In recent years, the sinc method has been also frequently employed for the numerical solution of fractional partial differential equations. In [34], Nagy applied the sinc-Chebyshev collocation method for numerical investigation of the time fractional nonlinear Klein–Gordon equation. In [35], Saadatmandi et al. proposed the sinc-Legendre collocation method for a class of fractional convection–diffusion equations with variable coefficients. In [36], Mao et al. developed the sinc-Chebyshev collocation method to solve a class of fractional diffusion-wave equations. In [37], Pirkhedri et al. adopted the sinc-Haar collocation method for the time fractional diffusion equation. In [38], a new reliable algorithm based on the sinc function is employed for the time fractional diffusion equation. In [18], Sweilam et al. investigated the numerical solution of the time fractional order telegraph equation by means of the sinc-Legendre collocation method. In [39], Jalilian et al. adopted an algorithm based on sinc basis functions for the numerical solution of the nonlinear fractional integro-differential equation of pantograph type. In this paper, we apply the sinc-Galerkin method to solve the time fractional convection–diffusion equation with variable coefficients.

The remainder of this paper is organized as follows. In Sect. 2, some preliminaries are presented. In Sect. 3, the time fractional derivative is discretized and the sinc-Galerkin method is applied to find the approximate solution at each step. In Sect. 4, convergence analysis is presented for this method and an exponential convergence is obtained as well. In Sect. 5, illustrative examples are carried out to justify the theoretical results.

2 Preliminaries

In this section, we recall notations and definitions of the sinc function and state some known lemmas that are necessary for this paper. These are discussed thoroughly in [21].

For all \(x\in \mathbb{R}\), the sinc function is basically defined as

$$ \operatorname{sinc}(x)=\textstyle\begin{cases} \frac{\sin (\pi x)}{\pi x}, & x\neq 0, \\ 1, & x = 0. \end{cases} $$

For \(h>0\), the translated sinc basis functions are given as

$$ S(j,h) (x)=\operatorname{sinc} \biggl(\frac{x-jh}{h} \biggr), \quad j=0,\pm 1,\pm 2,\ldots $$

Let f be a function defined on \(\mathbb{R}\), then for \(h>0\) the series

$$ C(f,h) (x)=\sum_{j=-\infty }^{\infty } f(jh) S(j,h) (x) $$

is called the Whittaker cardinal expansion of f whenever this series converges. The properties of Whittaker cardinal expansions have been extensively studied in [40]. The properties are derived in the infinite strip \(D_{d}\) of the complex plane where \(d>0\)

$$ D_{d} = \biggl\{ w=u+iv: \vert v \vert < d \leq \frac{\pi }{2} \biggr\} . $$

To extend the approximation on \(\mathbb{R}\) to the finite interval \((0,1)\), we consider the conformal map

$$ \phi (z)=\log \biggl(\frac{z}{1-z} \biggr), $$

which maps the eye-shaped domain

$$ D_{E}= \biggl\{ z=x+iy: \biggl\vert \arg \biggl( \frac{z}{1-z} \biggr) \biggr\vert < d \leq \frac{\pi }{2} \biggr\} $$

onto the infinite strip \(D_{d}\).

The basis functions on \((0,1)\) for \(z\in D_{E}\) are taken to be the composite translated sinc functions

$$ S_{j}(z)=S(j,h)\circ \phi (z)=\operatorname{sinc} \biggl(\frac{\phi (z)-jh}{h} \biggr), \quad j=0, \pm 1, \pm 2,\ldots . $$
(2)

The inverse map of \(w=\phi (z)\) is

$$ z=\phi ^{-1}(w)=\frac{e^{w}}{1+e^{w}}. $$

Let ψ denote the inverse map of ϕ, so we define the range of \(\phi ^{-1}\) on \(\mathbb{R}\) as

$$ (0,1)=\bigl\{ \psi (u)=\phi ^{-1}(u)\in D_{E}: -\infty < u < \infty \bigr\} . $$

For the uniform grid \(\{kh\}^{\infty }_{k=-\infty }\) on \(\mathbb{R}\), the sinc points which correspond to these nodes are denoted by

$$ x_{k}=\psi (kh)=\frac{e^{kh}}{1+e^{kh}},\quad k=0,\pm 1, \pm 2, \ldots . $$
(3)

Definition 1

Let \(B(D_{E})\) be the class of functions f which are analytic in \(D_{E}\) and satisfy

$$ \int _{\psi (t+\Sigma )} \bigl\vert f(z) \bigr\vert \,\mathrm{d}z \rightarrow 0, \quad \mbox{as } t \rightarrow \pm \infty , $$

where \(\Sigma = \{\mathrm{i}\eta : |\eta |< d \leq \frac{\pi }{2} \}\), and satisfy

$$ N(f)= \int _{\partial D_{E}} \bigl\vert f(z)\,\mathrm{d}z \bigr\vert < \infty , $$

where \(\partial D_{E}\) represents the boundary of \(D_{E}\).

Definition 2

Let \(L_{\beta }(D_{E})\) be the set of all analytic function f in \(D_{E}\), for which there exists a constant C such that

$$ \bigl\vert f(z) \bigr\vert \leq C \frac{ \vert \mathrm{e}^{\phi (z)} \vert ^{\beta }}{(1+ \vert \mathrm{e}^{\phi (z)} \vert )^{2\beta }}, \quad z \in D_{E}, 0< \beta \leq 1. $$

Lemma 1

([40])

If \(f \phi ' \in B(D_{E}) \), then for all \(x \in (0,1)\)

$$ \Biggl\vert f(x)-\sum_{j=-N}^{N}f(x_{j})S_{j}(x) \Biggr\vert \leq \frac{2N(f\phi ')}{\pi d}\mathrm{e}^{-\pi d/h}. $$

Moreover, if \(|f(x)|\leq ce^{-\beta |\phi (x)|} \), \(x\in (0,1)\), for some positive constants c and β, and if we select \(h=\sqrt{\pi d/\beta N}\), then

$$ \mathop{\sup }_{x\in (0,1)} \Biggl\vert f(x)- \biggl( \frac{\mathrm{d}}{\mathrm{d}x} \biggr)^{l}\sum_{j=-N}^{N}f(x_{j})S_{j}(x) \Biggr\vert \leq C_{1}N^{(l+1)/2}\mathrm{e}^{-\sqrt{\pi d\beta N}}, $$

where \(C_{1}\)depends only on f, d, and β.

Lemma 2

([41])

Let \(F\in B(D_{E})\)and ϕ be a conformal map with constants β and \(C_{2}\)so that

$$ \biggl\vert \frac{F(x)}{\phi '(x)} \biggr\vert \leq C_{2}e^{-\beta \vert \phi (x) \vert }, \quad x \in (0,1), $$

by selecting \(h=\sqrt{\pi d/\beta N}\), then the sinc trapezoidal quadrature rule is

$$ \int _{0}^{1}F(x)\,dx=h\sum _{j=-N}^{N} \frac{F(x_{j})}{\phi '(x_{j})}+ o \bigl(e^{-\sqrt{\pi d\beta N}} \bigr). $$
(4)

Lemma 3

([41])

Let ϕ be the conformal one-to-one mapping of the simply connected domain \(D_{E}\)onto \(D_{d}\). Then

$$\begin{aligned}& \delta _{jk}^{(0)}=\bigl[S(j,h)\circ \phi (x)\bigr]|_{x=x_{k}}=\textstyle\begin{cases} 1, & j=k, \\ 0, & j\neq k, \end{cases}\displaystyle \end{aligned}$$
(5)
$$\begin{aligned}& \delta _{jk}^{(1)}=h \frac{d}{d\phi }\bigl[S(j,h)\circ \phi (x)\bigr]|_{x=x_{k}}= \textstyle\begin{cases} 0, & j=k, \\ \frac{(-1)^{k-j}}{k-j}, & j\neq k, \end{cases}\displaystyle \end{aligned}$$
(6)
$$\begin{aligned}& \delta _{jk}^{(2)}=h^{2} \frac{d^{2}}{d\phi ^{2}}\bigl[S(j,h)\circ \phi (x)\bigr]|_{x=x_{k}}= \textstyle\begin{cases} \frac{-\pi ^{2}}{3}, & j=k, \\ \frac{-2(-1)^{k-j}}{(k-j)^{2}}, & j\neq k. \end{cases}\displaystyle \end{aligned}$$
(7)

In relations (5)–(7), h is the step size and \(x_{k}\) is the sinc grid given by (3). For the assembly of the discrete system, it is convenient to define the following matrices:

$$ I^{(i)}=\bigl[\delta _{jk}^{(i)} \bigr], \quad i=0,1,2, $$
(8)

where \(\delta _{jk}^{(i)}\) denotes the \((j,k)\) the element of the matrix \(I^{(i)}\). The matrix \(I^{(0)}\) is the \(m\times m\) identity matrix. The matrix \(I^{(1)}\) is the skew symmetric Toeplitz matrix and \(I^{(2)}\) is the symmetric Toeplitz matrix.

3 Derivation of numerical method

3.1 Temporal discretization

In order to discretize equation (1) in time direction, let \(t_{n}=n\tau \), \(n=0,1,\ldots \) , where τ is the time step size. Denote \(u^{n}(x)=u(x,t_{n})\), \(u^{n}_{x}(x)= \frac{\partial u(x,t_{n})}{\partial x}\), \(u^{n}_{xx}(x)= \frac{\partial ^{2} u(x,t_{n})}{\partial x^{2}}\), and \(f^{n}(x)=f(x,t_{n})\). The time Caputo derivative is replaced by the \(L_{1}\)-approximation, and the approximation order can be given in the following lemma.

Lemma 4

([42])

Suppose \(0< \alpha < 1\)and \(f(t)\in C^{2}[0,t_{k}]\), it holds that

$$ \begin{aligned} & \Biggl\vert \frac{1}{\Gamma (1-\alpha )} \int ^{t_{k}}_{0} \frac{f'(t)}{(t_{k}-t)^{\alpha }}\,dt \\ &\qquad {}- \frac{\tau ^{-\alpha }}{\Gamma (2-\alpha )} \Biggl[b_{0}f(t_{k})- \sum^{k-1}_{m=1}(b_{k-m-1}-b_{k-m})f(t_{m})-b_{k-1}f(t_{0}) \Biggr] \Biggr\vert \\ &\quad \leq \frac{1}{\Gamma (2-\alpha )} \biggl[\frac{1-\alpha }{12}+ \frac{2^{2-\alpha }}{2-\alpha }-\bigl(1+2^{-\alpha }\bigr) \biggr]\max _{0 \leq t\leq t_{k}} \bigl\vert f''(t) \bigr\vert \tau ^{2-\alpha }, \end{aligned} $$
(9)

where \(b_{m}=(m+1)^{1-\alpha }-m^{1-\alpha }\), \(m\geq 0\).

Based on Lemma 4, we can approximate the Caputo fractional derivative as follows:

$$\begin{aligned} \frac{\partial ^{\alpha }u^{n}(x)}{\partial t^{\alpha }}=\mu \Biggl[b_{0}u^{n}(x)- \sum^{n-1}_{m=1}(b_{n-m-1}-b_{n-m})u^{m}(x)-b_{n-1}u^{0}(x) \Biggr]+O\bigl(\tau ^{2-\alpha }\bigr), \end{aligned}$$
(10)

where \(\mu =\frac{\tau ^{-\alpha }}{\Gamma (2-\alpha )}\).

Substituting (10) into (1), we have

$$ \begin{aligned} &\mu \Biggl[b_{0}u^{n}(x)- \sum^{n-1}_{m=1}(b_{n-m-1}-b_{n-m})u^{m}(x)-b_{n-1}u^{0}(x) \Biggr] \\ &\quad =\varepsilon u^{n}_{xx}(x)-p_{1}(x)u^{n}_{x}(x)-p_{2}(x)u^{n}(x)+f^{n}(x)+R_{n,1}, \end{aligned} $$
(11)

where \(R_{n,1}=O(\tau ^{2-\alpha })\).

Omitting the small error term \(R_{n,1}\), we reach the following semi-discrete scheme of equation (1):

$$ Lu^{n}=-\epsilon u^{n}_{xx}(x)+p_{1}(x)u^{n}_{x}(x)+ \bigl(\mu +p_{2}(x)\bigr)u^{n}(x)=g(x), \quad 0< x< 1, $$
(12)

subjected to the initial and boundary conditions

$$\begin{aligned}& u^{0}(x)=h(x), \\& u^{n}(0)=u^{n}(1)=0, \end{aligned}$$

where

$$ g(x)=f^{n}(x)+\mu \Biggl[\sum^{n-1}_{m=1}(b_{n-m-1}-b_{n-m})u^{m}(x)+b_{n-1}u^{0}(x) \Biggr]. $$

3.2 Space discretization

Next we consider space discretization to (12) by the sinc-Galerkin method. The approximation solution of (12) can be given by

$$ u^{n}(x)\approx u_{M}^{n}= \sum_{j=-N}^{N}c_{j}^{n}S_{j}(x), \quad M=2N+1, $$
(13)

where \(S_{j}(x) \) is the function \(S(j,h)\circ \phi (x)\) for some fixed step size h. The unknown coefficients \(c_{j}^{n}\) in (13) are determined by orthogonalizing the residual \(Lu^{n}-g(x)\) with respect to the basis function \(\{S_{k}(x)\}_{k=-N}^{N}\). Taking the inner product on both sides of (12), we have

$$ \begin{aligned} & \bigl( -\epsilon u^{n}_{xx}(x),S_{k}(x) \bigr)+ \bigl(p_{1}(x)u^{n}_{x}(x),S_{k}(x) \bigr) + \bigl(\bigl(\mu +p_{2}(x)\bigr)u^{n}(x),S_{k}(x) \bigr) \\ &\quad = \bigl(g(x),S_{k}(x) \bigr), \end{aligned} $$
(14)

where the inner product of functions f and η is defined by

$$ ( f,\eta )= \int _{0}^{1}f(x)\eta (x)\omega (x)\,dx. $$

Equation (14) can be rewritten as

$$ \begin{aligned} & { \int _{0}^{1}p_{1}(x)u^{n}_{x}(x)S_{k}(x) \omega (x)\,dx}- { \int _{0}^{1}\epsilon u^{n}_{xx}(x)S_{k}(x) \omega (x)\,dx} \\ &\quad {}+ { \int _{0}^{1}\bigl(\mu +p_{2}(x) \bigr)u^{n}(x)S_{k}(x)\omega (x)\,dx}= \int _{0}^{1}g(x)S_{k}(x)\omega (x) \,dx. \end{aligned} $$
(15)

Integrating by parts for the first two integral terms on the left-hand side of (15), we have

$$ \begin{aligned} & { \int _{0}^{1}p_{1}(x)u^{n}_{x}(x)S_{k}(x) \omega (x)dx}=B_{1}- \int _{0}^{1}u^{n}(x) \bigl( p_{1}(x)S_{k}(x)\omega (x) \bigr)'dx, \\ & { \int _{0}^{1}\epsilon u^{n}_{xx}(x)S_{k}(x) \omega (x)dx}=B_{2}- \int _{0}^{1}u^{n}(x) \bigl( \epsilon S_{k}(x)\omega (x) \bigr)''dx, \end{aligned} $$
(16)

where

$$ \begin{aligned} &B_{1}=\bigl\{ u^{n}(x) p_{1}(x)S_{k}(x)\omega (x)\bigr\} |_{0}^{1}, \\ &B_{2}=\bigl\{ u_{x}^{n}(x)\epsilon S_{k}(x)\omega (x)-u^{n}(x) \bigl(\epsilon S_{k}(x) \omega (x)\bigr)'\bigr\} |_{0}^{1}. \end{aligned} $$

We can choose the weight function \(\omega (x)=\frac{1}{\phi '(x)}\) such that \(B_{1}=B_{2}=0\), then we apply the sinc quadrature rule (4) in Lemma 1 to (15) and obtain the following approximations:

$$\begin{aligned}& { \int _{0}^{1}p_{1}(x)u^{n}_{x}(x)S_{k}(x) \omega (x)\,dx} \approx -h\sum_{j=-N}^{j=N} \sum_{l=0}^{1} \frac{u^{n}(x_{j})}{\phi '(x_{j})h^{l}} \delta _{kj}^{(l)}g_{1,l}(x_{j}), \end{aligned}$$
(17)
$$\begin{aligned}& { \int _{0}^{1}\epsilon u^{n}_{xx}(x)S_{k}(x) \omega (x)\,dx} \approx -h\sum_{j=-N}^{j=N} \sum_{l=0}^{2} \frac{u^{n}(x_{j})}{\phi '(x_{j})h^{l}} \delta _{kj}^{(l)}g_{2,l}(x_{j}), \end{aligned}$$
(18)
$$\begin{aligned}& { \int _{0}^{1}\bigl(\mu +p_{2}(x) \bigr)u^{n}(x)S_{k}(x)\omega (x)\,dx} \approx h \frac{(\mu +p_{2}(x_{k}))u^{n}(x_{k})\omega (x_{k})}{\phi '(x_{k})}, \end{aligned}$$
(19)
$$\begin{aligned}& { \int _{0}^{1}g(x)S_{k}(x)\omega (x) \,dx} \approx h \frac{g(x_{k})\omega (x_{k})}{\phi '(x_{k})}, \end{aligned}$$
(20)

where

$$ \begin{aligned} &g_{2,2}=-\epsilon \omega (x) \bigl(\phi '(x)\bigr)^{2}, \qquad g_{2,1}=- \epsilon \omega (x)\phi ''(x)-2\epsilon \omega '(x)\phi '(x), \qquad g_{2,0}=- \epsilon \omega ''(x), \\ &g_{1,1}=p_{1}(x)\omega (x)\phi '(x), \qquad g_{1,0}=\bigl(p_{1}(x)\omega (x)\bigr)'. \end{aligned} $$

Substituting (17)–(20) into (15) and replacing \(u^{n}(x_{j})\) with \(c_{j}^{n}\), we obtain the discrete sinc-Galerkin system for determination of the unknown coefficients \(\{c_{j}^{n}\}_{j=-N}^{N}\) as follows:

$$ \begin{aligned} &\sum _{j=-N}^{N}\sum_{l=0}^{2} \frac{\delta _{kj}^{(l)}g_{2,l}(x_{j})}{\phi '(x_{j})h^{l}}c_{j}^{n}- \sum _{j=-N}^{N}\sum_{l=0}^{1} \frac{\delta _{kj}^{(l)}g_{1,l}(x_{j})}{\phi '(x_{j})h^{l}}c_{j}^{n}+ \frac{(\mu +p_{2}(x_{k}))\omega (x_{k})}{\phi '(x_{k})}c_{k}^{n} \\ &\quad = \frac{f^{n}(x_{k})\omega (x_{k})}{\phi '(x_{k})}+\mu \Biggl[\sum^{n-1}_{m=1}(b_{n-m-1}-b_{n-m}) \frac{\omega (x_{k})}{\phi '(x_{k})}c_{k}^{m}+b_{n-1} \frac{\omega (x_{k})}{\phi '(x_{k})}c_{k}^{0} \Biggr] \end{aligned} $$
(21)

for \(k=-N, -N+1, \ldots , N\).

We define the diagonal matrix as follows:

$$ \mathbf{D}\bigl(g(x)\bigr)_{ij}= \textstyle\begin{cases} g(x_{i}), & i=j, \\ 0, & i\neq j. \end{cases} $$
(22)

Based on (8) and (22), system (21) can be represented by the following matrix form:

$$ \mathbf{M}\mathbf{C^{n}}=\mathbf{R}, $$
(23)

where C and R are \(2N+1\)-vectors and M is \((2N+1)\times (2N+1) \) matrix as

$$\begin{aligned}& \mathbf{C}^{n}= \bigl(c_{-N}^{n}, c_{-N+1}^{n}, \ldots , c_{N}^{n} \bigr)^{T}, \\& \mathbf{R}=\mathbf{D} \biggl(\frac{1}{(\phi '(x))^{2}} \biggr)\mathbf{F}^{n} \\& \hphantom{\mathbf{R}=}{}+ \mu \Biggl[\sum^{n-1}_{m=1}(b_{n-m-1}-b_{n-m}) \mathbf{D} \biggl( \frac{1}{(\phi '(x))^{2}} \biggr)\mathbf{C}^{m} +b_{n-1}\mathbf{D} \biggl(\frac{1}{(\phi '(x))^{2}} \biggr) \mathbf{C}^{0} \Biggr], \\& \mathbf{M}=\epsilon \mathbf{B}-\frac{1}{h}\mathbf{I}^{(1)} \mathbf{D} \biggl(\frac{p_{1}(x)}{\phi '(x)} \biggr) +\mathbf{D} \biggl( \frac{-1}{\phi '(x)} \biggl(\frac{p_{1}(x)}{\phi '(x)} \biggr)'+ \frac{d}{(\phi '(x))^{2}} \biggr), \end{aligned}$$

in which

$$\begin{aligned}& \mathbf{B}=\frac{-1}{h^{2}}\mathbf{I}^{(2)}+ \frac{1}{h}\mathbf{I}^{(1)} \mathbf{D} \biggl( \frac{\phi ''(x)}{(\phi '(x))^{2}} \biggr) +\mathbf{D} \biggl(\frac{-1}{\phi '(x)}\biggl( \frac{1}{\phi '(x)}\biggr)'' \biggr), \\& \mathbf{F}^{n}=\bigl(\mathbf{F}^{n}(x_{-N}), \mathbf{F}^{n}(x_{-N+1}), \ldots , \mathbf{F}^{n}(x_{N}) \bigr)^{T}. \end{aligned}$$

By solving the system of linear algebraic equations (23), we can obtain an approximate solution \(u_{M}^{n}\) of equation (12) from (13).

4 Convergence analysis

In this section, we show that the approximate solution \(u_{M}^{n}(x)\) converges to the exact solution \(u^{n}(x)\) of (12) at an exponential rate. In order to establish a bound of \(|u^{n}(x)-u_{M}^{n}(x)|\), we first need to get a bound of \(\|MU^{n}-R\|_{2}\) where

$$ U^{n}= \bigl(u^{n}(x_{-N}),u^{n}(x_{-N+1}), \ldots ,u^{n}(x_{N}) \bigr)^{\mathrm{T}}, $$

where components \(u^{n}(x_{j})\), \(j=-N,\ldots ,N\), are the values of the exact solution of (12) at the sinc points.

Lemma 5

Assume that (12) has a unique solution \(u^{n}(x)\in L_{\beta }(D_{E})\). If \(G \in L_{\beta }(D_{E})\)where

$$ G=\frac{g(x)}{\phi '(x)},\frac{\mu +p_{2}(x)}{\phi '(x)}, \frac{\phi ''(x)}{(\phi '(x))^{2}}, \frac{p_{1}(x)}{\phi '(x)}, - \frac{1}{\phi '(x)} \biggl(\frac{1}{\phi '(x)} \biggr)'', - \frac{1}{\phi '(x)} \biggl( \frac{p_{1}(x)}{\phi '(x)} \biggr)', $$

then there exists a constant \(C_{3}\)independent of N such that

$$ \bigl\Vert MU^{n}-R \bigr\Vert _{2} \leq C_{3}N^{\frac{3}{2}}\mathrm{e}^{-\sqrt{\pi d \beta N}}. $$
(24)

Proof

For simplicity, we denote \(r_{k}= (MU^{n}-R )_{k}\) for \(k=-N,\ldots ,N\). By orthogonalizing the residual \(Lu^{n}-g(x)\) with respect to the basis function \(\{S_{k}(x)\}_{k=-N}^{N}\) and using Theorem 4.4 of Lund et al. [41], we get

$$ 0=h \int _{0}^{1}\frac{(Lu^{n}(x)-g(x))S_{k}(x)}{\phi '(x)} \, \mathrm{d}x=r_{k}+C_{4}N\mathrm{e}^{-\sqrt{\pi d\beta N}}, $$

where \(C_{4}\) is a constant independent of N, then

$$ \vert r_{k} \vert \leq C_{4}N\mathrm{e}^{-\sqrt{\pi \beta dN}}. $$

Utilizing Euclidean norm, we obtain

$$ \bigl\Vert MU^{n}-R \bigr\Vert _{2}= \Biggl(\sum _{k=-N}^{k=N} \vert r_{k} \vert ^{2} \Biggr)^{ \frac{1}{2}} \leq C_{3}N^{\frac{3}{2}} \mathrm{e}^{-\sqrt{\pi d\beta N}}. $$

 □

Theorem 1

Let \(u^{n}(x)\)be the exact solution of (12) and \(u_{M}^{n}(x)\)be its sinc approximation defined by (13), then under the assumptions of Lemma 2and Lemma 5, there exists a constant C independent of N such that

$$ \sup_{x\in (0,1)} \bigl\vert u^{n}(x)-u^{n}_{M}(x) \bigr\vert \leq C N^{ \frac{3}{2}}\mathrm{e}^{-\sqrt{\pi d\beta N}}. $$

Proof

Suppose that exact solution of (12) at sinc points \(x_{j}\) (\(j=-N,\ldots ,N\)) is denoted by \(U_{N}^{n}(x)\) defined by

$$ U_{N}^{n}(x)=\sum_{j=-N}^{N}u^{n}(x_{j})S_{j}(x). $$

Then, by making use of the triangular inequality, we have

$$ \bigl\vert u^{n}(x)-u^{n}_{M}(x) \bigr\vert \leq \bigl\vert u^{n}(x)-U_{N}^{n}(x) \bigr\vert + \bigl\vert U_{N}^{n}(x)-u^{n}_{M}(x) \bigr\vert . $$
(25)

According to Lemma 1, there exists a constant \(C_{5}\) independent of N such that

$$ \sup_{x\in (0,1)} \bigl\vert u^{n}(x)-U_{N}^{n}(x) \bigr\vert \leq C_{5} N^{ \frac{1}{2}}\mathrm{e}^{-\sqrt{\pi d\beta N}}. $$
(26)

The second term on the right-hand side of (25) satisfies

$$ \begin{aligned} \bigl\vert U_{N}^{n}(x)-u^{n}_{M}(x) \bigr\vert &\leq \Biggl\vert {\sum_{j=-N}^{N}} \bigl(u^{n}(x_{j})-c_{j}^{n} \bigr)S_{j}(x) \Biggr\vert \\ & \leq \Biggl( {\sum_{j=-N}^{N}} \bigl\vert u^{n}(x_{j})-c_{j}^{n} \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \Biggl( {\sum _{j=-N}^{N}} \bigl\vert S_{j}(x) \bigr\vert ^{2} \Biggr)^{\frac{1}{2}}. \end{aligned} $$
(27)

We know that \(({\sum_{j=-N}^{N}}|S_{j}(x)|^{2} )^{\frac{1}{2}}\leq C_{6}\), where \(C_{6}\) is a constant, then by using (22) and (24) we get

$$ \begin{aligned} & \Biggl( {\sum _{j=-N}^{N}} \bigl\vert u^{n}(x_{j})-c_{j}^{n} \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \Biggl( {\sum _{j=-N}^{N}} \bigl\vert S_{j}(x) \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \\ &\quad \leq C_{6} \bigl\Vert U^{n}-C^{n} \bigr\Vert _{2} \\ &\quad =C_{6} \bigl\Vert M^{-1}\bigl(MU^{n}-R \bigr) \bigr\Vert _{2} \\ &\quad \leq C_{2}C_{6} \bigl\Vert M^{-1} \bigr\Vert _{2}N^{\frac{3}{2}}\mathrm{e}^{-\sqrt{\pi d \beta N}}. \end{aligned} $$
(28)

Finally, by applying relations (25)–(28), we conclude

$$ \sup_{x\in (0,1)} \bigl\vert u^{n}(x)-u^{n}_{M}(x) \bigr\vert \leq C N^{ \frac{3}{2}}\mathrm{e}^{-\sqrt{\pi d\beta N}}, $$

where \(C=\max \{C_{5},C_{2}C_{6}\|M^{-1}\|_{2} \}\). □

5 Numerical experiments

In this section, we give some numerical examples to confirm our analysis. In all the examples considered in this paper, we set parameters \(\beta =1\) and \(d=\frac{\pi }{2}\) which yield \(h=\frac{\pi }{\sqrt{2N}}\).

Example 1

Consider the following fractional convection–diffusion equation:

$$ \frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}- \frac{\partial ^{2}u(x,t)}{\partial x^{2}}+x \frac{\partial u(x,t)}{\partial x}=f(x,t), \quad 0< x < 1, 0< t \leq 1, $$
(29)

with the initial condition

$$ u(x,0)=0, \quad 0< x< 1, $$

and the boundary conditions

$$ u(0,t)=u(1,t)=0, \quad 0< t\leq 1, $$

where

$$ f(x,t)=\frac{2t^{2-\alpha }}{\Gamma (3-\alpha )}\bigl(x^{2}-x^{3}\bigr)+ t^{2}\bigl(2x^{2}-2x^{3}+6x-2\bigr). $$

The exact solution of (29) is given by

$$ u(x,t)=t^{2}\bigl(x^{2}-x^{3}\bigr). $$

To illustrate the accuracy of our method, the maximum absolute error at sinc grid points is taken as

$$ e_{\infty }(h,\tau )=\max_{i,j} \bigl\vert u(x_{i},t_{j})-u_{M}(x_{i},t_{j}) \bigr\vert , $$

where \(x_{i}=\frac{e^{ih}}{1+e^{ih}}\).

Furthermore, the temporal convergence order of presented method is denoted by

$$ rate_{1}=\log _{2} \biggl( \frac{e_{\infty }(h,2\tau )}{e_{\infty }(h,\tau )} \biggr) $$

for sufficiently small h.

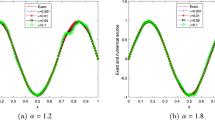
Table 1 shows the maximum absolute errors and temporal convergence order for \(\alpha =0.2,0.4,0.6,0.8\) and \(N=64\) with different values of time step size. Convergence curves of our method and the finite difference method with upwind strategy for the convection term are plotted in Fig. 1. It is clearly observed that the spatial errors appear in an exponential decay for our method. Figure 2 presents the graph of the numerical solution and the exact solution with \(\alpha =0.5\), \(N=128\), and \(\tau =\frac{1}{1000}\). From these diagrams, it can be seen that our scheme gives a good approximation to the exact solution at mesh points.

Figure 1
figure 1

Convergence of the sinc-Galerkin and FDM-upwind methods for various values of N with \(\alpha =0.8\), \(\tau =1/4000\)

Full size image
Figure 2
figure 2

Comparison of numerical solution and analytical solution for \(\alpha =0.5\), \(N=128\), \(\tau =1/1000\)

Full size image
Table 1 The maximum absolute errors and temporal convergence orders with \(N=64\)
Full size table

Example 2

Consider the following fractional convection–diffusion equation:

$$ \begin{aligned} &\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}-\epsilon \frac{\partial ^{2}u(x,t)}{\partial x^{2}}+ \bigl(2-x^{2}\bigr) \frac{\partial u(x,t)}{\partial x}+xu(x,t) \\ &\quad =f(x,t) \quad 0< x < 1, 0< t \leq 1, \end{aligned}$$
(30)

with the initial condition

$$ u(x,0)=0, \quad 0< x< 1, $$

and the boundary conditions

$$ u(0,t)=u(1,t)=0, \quad 0< t\leq 1, $$

where

$$ f(x,t)=10t^{2}\mathrm{e}^{-t}x(1-x). $$

As the exact solution \(u(x,t)\) of (30) is unknown, therefore for each ϵ the maximum absolute error at the sinc grid points is taken as

$$ e_{\infty }(h,\tau )=\max_{i,j} \bigl\vert u_{M}(x_{i},t_{j})-u_{2M}(x_{i},t_{j}) \bigr\vert , $$

where \(x_{i}=\frac{e^{ih}}{1+e^{ih}}\).

Table 2 shows the maximum absolute errors and temporal convergence order for \(\alpha =0.8\) and \(N=128\) with different values of ϵ and time step size. It is observed that the scheme generates temporal convergence order, which is consistent with our theoretical analysis. Convergence curves of our method and the finite difference method with upwind strategy for the convection term are plotted in Figs. 3 and 4. The two figures clearly show that the proposed method converges at the exponential rate with increasing N in space. Numerical solution profiles for \(\epsilon =2^{-8}\) and \(\epsilon =2^{-12}\) are plotted in Figs. 5 and 6. The two figures show that the boundary layer is located on the right-hand side of the rectangular domain.

Figure 3
figure 3

Convergence of the sinc-Galerkin and FDM-upwind methods for various values of N with \(\alpha =0.5\), \(\epsilon =2^{-5}\), \(\tau =1/500\)

Full size image
Figure 4
figure 4

Convergence of the sinc-Galerkin and FDM-upwind methods for various values of N with \(\alpha =0.5\), \(\epsilon =2^{-12}\), \(\tau =1/500\)

Full size image
Figure 5
figure 5

Numerical solutions with \(\alpha =0.2\), \(\epsilon =2^{-8}\), \(N=32\), \(\tau =1/100\)

Full size image
Figure 6
figure 6

Numerical solutions with \(\alpha =0.2\), \(\epsilon =2^{-12}\), \(N=32\), \(\tau =1/100\)

Full size image
Table 2 The maximum absolute errors and temporal convergence orders with \(\alpha =0.8\) and \(N=128\)
Full size table

6 Conclusion

In this paper, we have developed and analyzed an efficient numerical scheme for the time fractional convection–diffusion equations with variable coefficients. The problem is reduced to the solution of a system of linear algebraic equations at each time step. The convergence analysis of the proposed method is proven, and it is shown that the sinc-Galerkin method converges to the solution at the exponential rate in space. Two examples are tested and the obtained numerical results confirm the theoretical analysis.