Abstract
In the current paper, a review of the Homotopy perturbation method is offered thoroughly to fetch the analytical solution of coupled 1D non-linear Burgers' equation. The exact solution of the coupled 1D Burgers' equation is attained in the system of a power series, (convergent in nature). A suitable optimal of the initial condition leads towards the vital exact solution after some iterative phases.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
1.1. Coupled 1D Burgers' equation
The conception of coupled 1D Burgers' equation was offered by Esipov [1] to get information about the poly-dispersive sedimentation model. The coupled Burgers' equation system is a very modest model of the evolution or the sedimentation of the scaled volume having two categories of particles in the suspension of fluids or in the collision under the gravity effect. Burgers' [2] and Cole [3] presented the belief that this system of equations is correlated with a number of phenomena such as the approximation theory of flow through a shock wave travel in the viscous fluid, mathematical model regarding turbulence, and any more. Srivastava et al [4] presented the notion of a fully implicit FD scheme for the solution of coupled 1D Burgers' equation. Srivastava et al [5] contributed the numerical solution of an implicit logarithmic FD outline for the coupled 1D Burgers' equation. Mittal and Jiwari [6] offered the numerical solution of coupled viscous Burgers' equation. Nee and Duan [7] gave the perception of limit set trajectories for the coupled viscous Burgers' equation. Kaya [8] signified an explicit explanation of coupled viscous Burgers' equation by employing the decomposition method. Mittal and Arora [9] presented the numerical solution of coupled viscous Burgers' equation. Rashid et al [10] provided the perception of a Fourier Pseudo Spectral scheme for dealing with coupled viscous Burgers' equation. Khater et al [11] presented the conception of a Chebyshev spectral collocation scheme for the solution of different Burgers' type equations. Mokhtari et al [12] gave the knowledge of generalized DQM for the numerical solution of coupled Burgers' equation. He [13] contributed the notion of variational principle for solving the 'Generalized KdV-Burgers' equation' along with the fractal derivatives. In that paper, a semi-inverse scheme is used for the founding of a fractal variational system of the problem. Hayot and Jaya Prakash [14] discussed the different facets of the 'Stochastic Burgers' equation and it's connection with turbulence'. Scotti and Meneveau [15] offered a 'fractal model for large eddy simulation of the turbulent flow'.
1.2. Homotopy perturbation method
For any non-linear differential equation, the practice of HPM is discussed as follows by He (1999) [16, 17]. Bizar and Ghazvini [18] employed the notion of HPM in order to fetch the precise solution of the non-linear Schrodinger equation. Biazar and Ghazvini [19] employed the notion of HPM and presented the exact solution of non-linear Burgers' equation. Biazar and Eslami [20] provided the notion of a new Homotopy perturbation method for the solution of partial differential equations. Yildirim [21] presented the solution of the KdV equation by using the notion of HPM. Agirseven and Ozis [22] employed the notion of HPm for getting the analytical solution of Fisher's type equations. Yildirim [23] presented the conception of HPM for solving the fractional partial differential equation in the analytical aspect. HPM has it's role in developing effective schemes in fractional calculus also, like, He [24] gave a comprehensive review on the development of non-linear integral B.V.P. of fourth-order with fractal derivative. He and Ain [25] presented the ' New promise of future challenge' in their paper about fractal calculus. Anjum and Ain [26] presented the study of He's fractional derivative for time-fractional Camassa-Holm equation. in order to transform the mentioned fractional equation into a differential equation, the fractional complex transform was implemented and HPM was used to solve the equation. Two scale fractal theory was used for a physical understanding of fractional and complex transform. Yang and Wang [27] implemented the notion of 'A local fractional Homotopy Perturbation Method for the solution of the local fractional Korteweg-De Vries equation with the non-homogeneous term'.
2. Method description
Homotopy perturbation method is associated with the notion of the sum of an infinite series term, which commonly converges speedily towards the exact solution. The homotopy perturbation method diminishes the intricated equation into a simple equation, which is easy to solve. To define the elementary knowledge of the Homotopy perturbation method, considered the following differential equation.
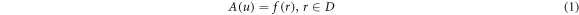
along with

Where A is known as the general operator, B is recognized as the boundary operator, f(r) is considered as an analytic function, Γ is the boundary of given domain D. In general, the operator A can be condensed into two operators, L and N, where L is the linear operator and N is the non-linear operator. Equation (1) can be inscribed as;
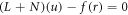


Coupled 1D Burgers' equation is given as follows:


Creating homotopy for equation (2),

which satisfies the following condition;
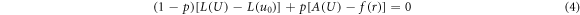
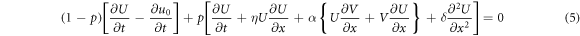
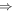
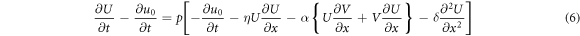
Considering that
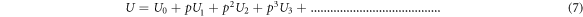
and
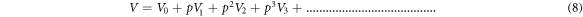
By using equations (7) and (8) in equation (6),

On making comparisons of diverse powers of p in both sides of equation (9),
p0:
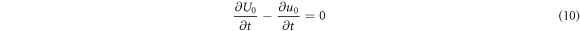
p1:
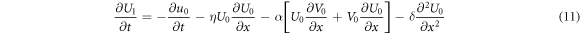
p2:
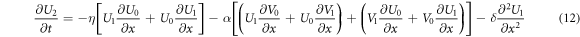
In general:
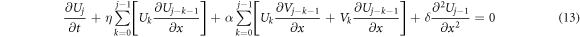
From equation (13), a recurrence relation for Uj will be obtained;

Creating homotopy for equation (3), as follows

which satisfies the following condition;

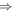

By using equation (7) and (8) in equation (17), the following equation will be obtained;
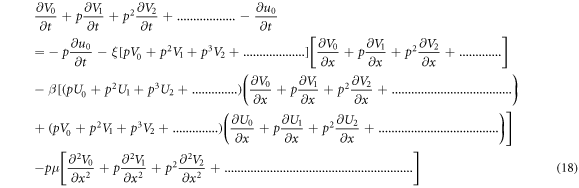
On comparing the powers of p in equation (18), the following system of equations will be obtained;
p0:
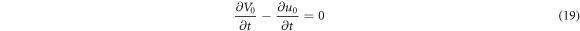
p1:
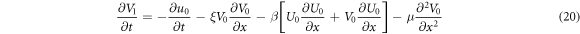
p2:
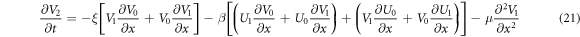
In general; pj :
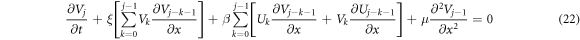
From (22), a recurrence relation for Vj will be obtained,
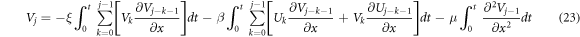
3. Numerical examples
Example 1. By setting  and
and  in equations (2) and (3), the following set of equations will be obtained and considered initial conditions are also provided,
in equations (2) and (3), the following set of equations will be obtained and considered initial conditions are also provided,
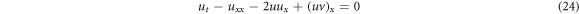
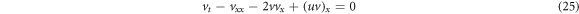
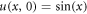
and

Where Domain is ![$=\,[-\pi ,\pi ],t\gt 0$](https://content.cld.iop.org/journals/2399-6528/4/9/095017/revision4/jpcoabb218ieqn8.gif) . For equation (24) and (25), by using the method of Homotopy perturbation method, following recurrence relations will be obtained,
. For equation (24) and (25), by using the method of Homotopy perturbation method, following recurrence relations will be obtained,
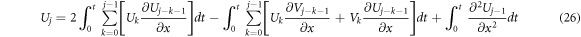
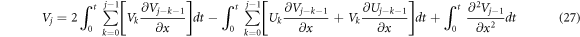
From the recurrence relations, (26) and (27), the values of U1, U2, U3, ........ and V1, V2, V3, ....... will be obtained. The exact solution will be obtained as follows;

and
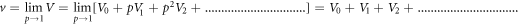


and

Example 2. By using  and
and 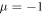 in equations (2) and (3) respectively. The following equations will be obtained;
in equations (2) and (3) respectively. The following equations will be obtained;
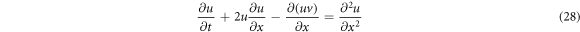

along with initial conditions as:


and corresponding recurrence relations for the values of Uj and Vj are given as follows;

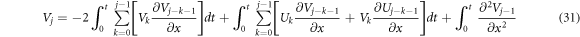
From equations (30) and (31), values of U1, U2, U3, ................... and V1, V2, V3,............ will be obtained,
Exact solution will be obtained as follows;
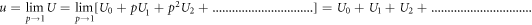
and
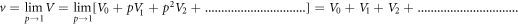


4. Conclusion
In the present paper, review of the exact solution of coupled 1D Burgers' equation is provided by using HPM. General formulae in the form of recurrence relations are established for coupled 1D Burgers' equation, with the aid of these formulae analytical solution of coupled 1D Burgers' equation can be effortlessly attained. Two numerical examples are discussed, in order to find the analytical solution of coupled 1D Burgers' equation.

