1 Introduction and motivations

In near-fault (NF) conditions, as opposed to far-field (FF) ones, the relative position of a site with respect to the fault and the rupture propagation can favour the constructive interference of seismic waves. This phenomenon, which does not affect all the ground motions recorded in NF conditions, is called forward-directivity. It leads to ground motions characterised by a large, full-cycle velocity pulse at the beginning of the record, concentrating most of the radiated seismic energy; the resulting ground motions are labelled as “pulse-like”. Hereinafter, the term “pulse-like” is adopted to refer exclusively to forward-directivity effects.

In the past, extensive damage observed on structures located in NF regions has been associated to pulse-like ground motions. Examples include events such as the 1999 M7.6 Chi–Chi earthquake (Shin and Teng 2001), the 1994 M6.7 Northridge earthquake (Jones et al. 1994), and most recently, the 2009 M6.3 L’Aquila (De Luca et al. 2015), and the 2011 M6.1 Christchurch (Bannister and Gledhill 2012) earthquakes. The distinct features of these ground motions and their (potentially) devasting impact on structures have boosted various studies addressing the effects of pulse-like ground motions both on the seismic demands and the capacity of various structural systems; a comprehensive overview of these past research is outside the scope of this paper, but some key findings are briefly reviewed here.

Many studies addressed the characterisation of pulse-like ground motions (e.g., Bray and Rodriguez-Marek 2004; Baker and Cornell 2008), considering their main describing parameters (such as the period of the pulse). Baker (2007), among others, proposed an algorithm for identifying large velocity pulses in ground-motion records, which are generally stronger in the direction orthogonal to the strike of the fault. Out of the 3500 strong ground motions contained in the Next Generation Attenuation (NGA) project library (Chiou et al. 2008), the study found 91 records containing strong velocity pulses and identified the associated pulse period.

Most of the conventional ground motion models (GMMs) used in probabilistic seismic hazard analysis (PSHA) do not explicitly account for the occurrence of pulse-like ground motions and resulting pulse features. This could lead to an under-prediction of the seismic hazard (e.g. in terms of spectral accelerations) in NF conditions, and could impact the subsequent seismic demand/damage/loss assessment. Some researchers have proposed modifications to the conventional PSHA framework to model the pulse-occurrence probability, the pulse period distribution, and the spectral amplification induced by forward-directivity effects (Shahi and Baker 2011; Chioccarelli and Iervolino 2013; Spudich et al. 2013). Among various research studies, Iervolino and Cornell (2008), based on the previous work of Somerville et al. (1997) and the pulse-like ground motions identified by Baker (2007), proposed a set of models to estimate the probability of pulse occurrence for strike–slip and dip–slip events, depending on the relative location of the site with respect to the source. Based on the same set of ground motions, Chioccarelli and Iervolino (2013) proposed a model relating the pulse period to the moment magnitude of the event, following the approach proposed by other authors (Somerville 2003; Baker 2007). Baker (2008) proposed a narrow-band amplification function to account for the increased spectral accelerations (around the pulse period) for pulse-like ground motions. This was combined with the Boore and Atkinson GMM (Boore and Atkinson 2008) and it can be readily used in PSHA.

Similarly, a number of studies have addressed the impact of the characteristics of pulse-like ground motions on structural response and consequent damage, in the context of fragility assessment. Chopra and Chintanapakdee (2001) highlighted that NF pulse-like records tend to increase the displacement demand in both elastic and inelastic single degree of freedom systems relatively to ordinary motions. Alavi and Krawinkler (2004) stated that generic moment resisting frames with a fundamental period longer than the pulse period behave in a considerably different way with respect to those with a shorter period, since the pulse may excite higher modes in the former case and may produce period elongation in the latter case. Champion and Liel (2012) investigated the problem in relation to ductile and non-ductile reinforced concrete (RC) moment-resisting frames, highlighting that the collapse risk of the considered frames can be significantly higher due to pulse-like ground motions. Similar findings (using the same methodology and ground-motion records of Champion and Liel 2012) can be found in Tzimas et al. (2016) for self-centering steel frames with viscous dampers, and in Song and Galasso (2020) in terms of fracture risk of pre-Northridge welded column splices. Kohrangi et al. (2019) stated that the response of structures to pulse-like ground motions is governed by both spectral shape and the ratio of the pulse period over the fundamental period of the structure (\(T_{p} /T_{1}\)). According to such study, the geometrical mean of spectral acceleration over a period range (AvgSA) together with \(T_{p} /T_{1}\), form an efficient and sufficient intensity measure for response prediction to pulse-like ground motions.

Most of the existing studies focus on structural response/performance assessment for a given set of pulse-like ground-motion records or on the estimation of fragility in conditions of total collapse. To the best of the authors’ knowledge, no study investigated the effect of pulse-like ground motions on the seismic fragility for damage states (DSs) prior to collapse (i.e. probability of exceeding damage states defined in terms of a finite-valued engineering demand parameter, EDP, conditional on an intensity measure, IM). In fact, although the collapse DS is expected to be the most affected one, the life-safety and near-collapse DSs may be equally affected, thus significantly impacting the overall losses. Moreover, no previous studies investigated the effects of pulse-like ground motions on vulnerability relationships (i.e. distribution of repair-to-replacement ratio given IM) or on the explicit calculation of direct economic losses, at building- nor at portfolio-level. In fact, quantifying the potential impact of earthquakes-induced pulse-like ground motions on portfolios of properties located in seismically prone regions, and especially in NF regions, can be of interest to property owners, (re-)insurance companies, local government agencies, and structural engineers. Each is likely to have a different viewpoint and different (refinement) requirements and can cope with seismic risk using a variety of strategies (e.g. proactive seismic retrofit, earthquake insurance coverage). Regardless of which risk reduction or risk transfer mechanism is ultimately chosen, it is critical that the estimates of potential loss on which these decisions are based are as accurate as possible given the available information.

This study aims to fill these gaps by investigating the influence of pulse-like ground motions on the estimation of seismic losses for building portfolios. The main specific objectives are: (1) to describe a simulation-based risk assessment framework including pulse-like effects on both the hazard and fragility/vulnerability estimates, thus enhancing the state-of-practice catastrophe risk modelling (Mitchell-Wallace et al. 2017); (2) to demonstrate how to derive building-level fragility relationships for a set of DSs, explicitly accounting for the pulse occurrence; (3) to investigate the influence of pulse-like ground motions on the direct economic losses of building portfolios, depending on their size and composition, together with the relative position of the portfolios with respect to an earthquake fault.

The study starts with an overview of the simulation-based risk assessment framework, giving more emphasis to the aspects related to pulse-like effects. The proposed methodology relies on near-fault PSHA (accounting for pulse-occurrence probability, pulse period, and the resulting amplification of earthquake-induced ground-motion IMs), cloud analysis-based fragility relationship derivation (Jalayer and Cornell 2009), and simulation-based loss estimation. The methodology is applied to 24 synthetic portfolios with size ranging from approximately 200 to 6800 km2, located in a fault-normal or fault-parallel relative position with respect to a case-study fault. Different proportions of building types are also considered in each portfolio, including gravity-designed reinforced concrete buildings, and seismically-designed RC or steel frames. The results are critically discussed considering the effects of pulse-like ground motions on the expected annual loss (EAL) of the different portfolios, together with a discussion and some practical guidance on considering the effects of pulse-like ground motions on the hazard and fragility modules of the framework.

2 Simulation-based seismic loss assessment

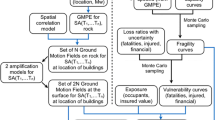
The implemented Monte Carlo-based risk assessment framework is schematically illustrated in Fig. 1, while Sects. 2.1 to 2.3 describe in detail the relevant probabilistic models considered for the hazard, fragility and loss modules of the framework. Various building portfolios in the vicinity of a causative fault are considered; each portfolio consists of a number of equally-spaced locations (i.e. sites) and in each location a group of buildings of different typologies is collocated (i.e. the exposure is “lumped” at the considered locations).

Fig. 1
figure 1

Simulation-based risk assessment framework including directivity-induced pulse-like effects. IM intensity measure, MAF mean annual frequency of exceedance, LR loss ratio, Tp pulse period, M magnitude

Full size image

Event-based PSHA (Silva 2018) is used to simulate seismicity in the considered region as described by a source model and to simulate the resulting ground shaking at the considered set of locations by using a GMM. An ad-hoc Matlab (MATLAB 2018) code is created by the authors to perform the calculations involved in this study. For a given time span \(T_{cat}\), a stochastic event set (also known as synthetic catalogue) is generated which includes \(N_{e}\) events; \(T_{cat}\) is dependent on the minimum rate of exceedance of interest (in terms of hazard intensities or loss values). The number of occurrences in \(T_{cat}\) is simulated by sampling the corresponding probability distribution for rupture occurrence for the considered sources (a single fault in this specific study). In general, for a given source, the main parameters are the geometry, constraining the earthquake rupture locations, and the magnitude-frequency distribution, defining the average annual occurrence rate over a magnitude range.

For each event in the stochastic catalogue, the related magnitude is first simulated from the magnitude-frequency distribution. Each event is associated with \(N_{sim}\) realisations of the rupture length, the position of the rupture length on the considered fault and the position of the epicentre on the rupture length. For each realisation of these parameters, and for each location of interest, the probability of pulse occurrence is calculated. A pulse-like ground motions is assumed to occur if a random number in the range [0,1] is smaller than the calculated pulse probability (i.e. a Bernoulli distribution is assumed); for the realisations characterised by a pulse-like ground motion, the pulse period is also simulated. For each simulation, ground-motions IMs are sampled from the probability distribution defined by the GMM. Such IMs are amplified according to a relevant model if pulse-like conditions occur. This is only possible if a relationship for such amplification is available, which is in turn compatible with the adopted GMM. The simulation of ground-shaking values at a set of locations forms a ground-motion field; \(N_{sim}\) ground-motion fields are generated here. The use of a set of ground-motion fields is necessary so that the aleatory variability (both inter- and intra-event) in the GMM is captured.

Given two suites of spectrally-equivalent, site-independent ground-motion records (ordinary and pulse-like), sets of fragility and vulnerability relationships are derived for each considered building type making the considered portfolios. For each location of interest, building type and simulated IMs, the loss ratio is calculated using the appropriate vulnerability model depending on the simulated ordinary or pulse-like conditions. For each simulation, the total loss for the entire portfolio is calculated by summation over all the locations and all the buildings.

Loss exceedance curves (mean annual frequency, MAF, of exceedance vs loss ratio/loss value) for specific buildings/locations and for the portfolio can be easily computed using all the simulated ground-motion fields, leading to lists of events and associated loss ratios/loss values. These lists can be sorted from the highest loss ratio/loss value to the lowest. The rate of exceedance of each loss ratio/loss value is calculated by dividing the number of exceedances of that loss ratio by the length of the event set (eventually multiplied by the number of stochastic event sets, if more than one set are generated). By assuming a Poisson distribution of the occurrence model, the probability of exceedance of each loss ratio/loss value can also be calculated. The portfolio EAL is finally calculated by averaging over all the simulations and events.

2.1 Hazard analysis

A Poisson model is used here to simulate the earthquake occurrence of \(N_{e}\) events on the considered fault; time-dependent earthquake-recurrence models may be more appropriate for fault-based PSHA (e.g. Faure Walker et al. 2019), but their investigation is outside the scope of this study. For each of those, the characteristic earthquake-recurrence model by Convertito et al. (2006) is adopted to simulate the related moment magnitude (\(M_{w}\)). It considers a log linear recurrence relationship (i.e. frequency of occurrence vs \(M_{w}\)) for moderate (non-characteristic) events (\(M_{min} \le M_{w} < m_{c}\), where \(M_{min}\) is the minimum considered magnitude and \(m_{c}\) is the characteristic earthquake magnitude for the given fault), and a constant probability branch of occurrence for events with \(m_{c} \le M_{w} \le M_{max}\), where \(M_{max}\) is the maximum magnitude of interest. The characteristic-earthquake model is based on the observation that during repeated ruptures occurring on the same fault (or fault system), some characteristics, like fault geometry, source mechanism, and seismic moment, remain approximately constant over a large timescale. The magnitude-dependent length of the rupture is obtained using the equations proposed by Wells and Coppersmith (1994). The position of the rupture length over the fault, and the epicentre over the rupture, are simulated uniformly at random.

Among various models (e.g. Shahi and Baker 2011), the model by Chioccarelli and Iervolino (2013) is adopted here to estimate the probability of pulse. Specifically, for strike–slip faults, Eq. 1 is used, where \(R\) is the minimum distance between the considered site and the fault rupture, \(s\) is the distance of the site to the epicentre measured along the rupture direction, and \(\theta\) is the angle between the fault strike and the path from epicentre to the site (Fig. 2). The parameters \(\alpha\) and \(\beta_{1,2,3}\) correspond to regression coefficients, depending on the rupture type.

$$P\left( {pulse |R,s,\theta } \right) = \frac{{e^{{\alpha + \beta_{1} R + \beta_{2} s + \beta_{3} \theta }} }}{{1 + e^{{\alpha + \beta_{1} R + \beta_{2} s + \beta_{3} \theta }} }}$$
(1)
Fig. 2
figure 2

Strike-slip fault: a definition of the site-to-rupture geometrical parameters required for the computation of the pulse probability; b variation of the R parameter with respect to the site position

Full size image

The model by Chioccarelli and Iervolino (2013) is chosen for the pulse period distribution, although other options are available (e.g. Baker 2007). In particular, \(T_{p}\) is assumed to follow a lognormal distribution for which the median is calculated through Eq. 2 while the logarithmic standard deviation is equal to 0.59.

$${ \ln }\left( {T_{p} } \right) = - 6.19 + 1.07M_{w}$$
(2)

The considered ground-motion IM (AvgSA) is finally simulated for each seismic event contained in the stochastic catalogue by using the indirect approach presented in Minas and Galasso (2019). The AvgSA realisations are drawn by using the Boore and Atkinson GMM (Boore and Atkinson 2008) for 5% damped spectral accelerations (\(S_{a}\)) at different periods of interest since a related model to derive the IM amplification due to pulse-like effects is available (Baker 2008), as discussed above. In particular, a multivariate lognormal distribution is adopted, for which the median and standard deviation are defined according to the considered GMM, while the correlation coefficients among accelerations at different vibration periods are defined according to Baker and Jayaram (2008). Although this model was developed for ordinary ground motions, its validity for pulse-like ones has been demonstrated (Tarbali 2017).

Specifically, the mean prediction \(\mu_{{\ln \left( {Sa} \right)GMM}}\) from the GMM (the “baseline” component) is incremented by the gaussian function that depends on \(T_{p}\) (Eq. 3); while the dispersion from the GMM is kept unchanged (Eq. 4), although other literature approaches (e.g. Shahi and Baker 2011) also modify the GMM standard deviation.

$$\mu_{{\ln \left( {S_{a} } \right)}} = \mu_{{\ln(Sa)_{GMM}}} + e^{{ - \left( {\ln \left( {\frac{{{\text{T}}_{\text{p}} }}{\text{T}}} \right)} \right)^{2} }}$$
(3)
$$\sigma_{{\ln \left( {S_{a} } \right)}} = \sigma_{{\ln(Sa)_{GMM}}}$$
(4)

It is worth noting that to accurately consider the epistemic uncertainties involved in the framework, different models for all the relevant hazard components (e.g. GMM, probability of pulse, \({\text{T}}_{\text{p}}\) distribution, IM amplification) should be considered and combined in a logic tree. For simplicity, only one set of models is used herein, since the study mainly focuses on relative loss results (pulse-like vs ordinary); future research efforts will address this current limitation. For instance, the effect of GMM-related epistemic uncertainties on portfolio losses has been investigated in Silva (2016, 2018).

It is also worth mentioning that only the combined (intra- and inter-event) GMM uncertainty is considered in this study, with no consideration of ground-motion spatial correlation (among the locations of the portfolio). Yet, a full correlation for the buildings pertaining to one single location is implicitly assumed, since ground shaking is herein simulated for each location (rather than for each building). Several studies (e.g. Weatherill et al. 2015) have shown that the spatial correlation in ground motion IMs has important implications on probabilistic seismic hazard and loss estimates of spatially distributed engineering systems, including building portfolios. In fact, inclusion of spatial cross-correlation of IMs into the seismic risk analysis may often result in the likelihood of observing larger (and in certain cases smaller) losses for a portfolio distributed over a typical city scale, when compared against simulations in which spatial correlation is neglected. However, to the best of the authors’ knowledge, no spatial correlation model explicitly calibrated for pulse-like events is available in the literature. As an alternative, a spatial correlation model for ordinary ground motions may still be used. Nevertheless, disregarding near-fault effects in the correlation model may mask the actual spatial distribution of ground motions in the vicinity of a fault (Akkar et al. 2018). This should be kept in mind while implementing the proposed approach. More in general, it is worth highlighting that this study is more focused on presenting a general methodology and perform a comparative analysis rather than providing absolute loss results for the considered portfolios.

2.2 Fragility/vulnerability derivation

As discussed above, compared with ordinary ground motions, pulse-like records tend to cause higher spectral accelerations around the period of the pulse, which is generally moderate-to-long (e.g. the \(T_{p}\) is equal to 0.43 s, 1.25 s and 3.67 s for \(M_{w}\) equal to 5, 6 and 7, according to Eq. 2). In particular, the ratio \(T_{p} /T_{1}\) of the pulse period in the ground-motion velocity time history to the first-mode period of the building has a critical effect on structural response (e.g. Chopra and Chintanapakdee 2001; Alavi and Krawinkler 2004; Champion and Liel 2012; Kohrangi et al. 2019). For structures responding in the elastic range, the highest demands will be experienced if \(T_{p} \cong T_{1}\); for non-linear responding structures, the effective fundamental period of the building elongates as damage accumulates. Accordingly, ground-motion pulses with \(T_{p} \cong 2T_{1}\) may be the most damaging for highly nonlinear systems. For \(T_{p} < T^{*}\), ground-motion pulses may excite higher modes (if significant for the given structure) and cause a travelling wave effect over the height of the building, resulting in large displacement and shear force demands in the upper stories.

It is argued that, by using an ideal, perfect IM—in terms of its (absolute) sufficiency and efficiency, would allow one to characterise structural fragility/vulnerability embedding both ordinary and pulse-like conditions in a single mathematical formulation/model, without the need of differentiating between the fragility/vulnerability relationships for the two scenarios. However, this may not be possible using conventional IMs. Therefore, different sets of fragility relationships for ordinary and pulse-like conditions may be preferable. Also, according to previous research (e.g. Kohrangi et al. 2019), AvgSA is herein adopted as an IM. This IM is characterised by high (absolute) sufficiency also in the case of pulse-like ground motions. As discussed above, directivity-induced pulse-like ground motions are characterized by a peculiar spectra shape (around the pulse period) with respect to ordinary ground motions; indeed, AvgSA is a very good proxy for the ground-motion spectral shape in a range of periods of interest.

A cloud-based non-linear time-history analysis (Jalayer and Cornell 2009) with two suites of ordinary and pulse-like natural (i.e. recorded) ground motions is used. This analysis method does not require a site-specific, hazard-consistent selection of records (e.g. according to Tarbali et al. 2019), and it is therefore deemed appropriate if the derived fragility relationships are used for portfolio-type applications. Using cloud analysis also allows one to adopt none-to-low scaling factors for the selected records. Two suites of records (ordinary and pulse-like) assembled by Kohrangi et al. (2019) are adopted. The authors firstly identified 192 pulse-like ground motions from the NGA-West2 database (Ancheta et al. 2014) by means of the above-mentioned algorithm based on wavelet theory (Baker 2007). Subsequently, 192 spectrally-equivalent ordinary records were chosen matching the spectral shape in the period range 0.05–6.00 s. This was done selecting the ordinary records for which the sum of squared error differences (with respect each pulse-like one) is minimum. Amplitude scale factors up to 5 were allowed in the process for the ordinary records. Using sets of spectrally-equivalent ordinary and pulse like records, enables one to separate the effect of spectral shape from that of the time domain pulse and to show the significance of both.

Each suite of records is used an input for time-history analysis of case-study non-linear models of selected index buildings representative of the considered building typologies. This results in pairs of IM vs engineering demand parameter (EDP) values (herein chosen as AvgSA and maximum inter-storey drift, respectively). Fragility relationships are finally defined according to Eq. 5 for a given set of damage states, each corresponding to an EDP threshold, \(EDP_{DS}\). Such thresholds are quantified in Sect. 3.1.1 with references to the specific case-study structures.

$$P(EDP \ge EDP_{DS} |IM) = P(EDP \ge EDP_{DS} |IM,NoC)(1 - P(C|IM)) + P(C|IM)$$
(5)

Consistently with (Jalayer et al. 2017), the obtained IM-EDP pairs are partitioned in two sets: the “Collapse (C)” and “Non-Collapse (NoC)”cases. Collapse herein corresponds to a global dynamic instability (i.e. non-convergence) of the numerical analysis, likely corresponding to a plastic mechanism (i.e. the structure is under-determined) or exceeding a 10% maximum inter-storey drift (conventional threshold). The total probability theorem is adopted to consider both “C” and “NoC” cases. In Eq. 5, \(P(EDP \ge EDP_{DS} |IM,NoC)\) is the conditional probability that the EDP threshold (\(EDP_{DS}\)) is exceeded given that collapse does not occur, and \(P(C|IM)\) is the probability of collapse. It is implicitly assumed that (\(EDP_{DS}\)) is exceeded for collapse cases, i.e. \(P(EDP \ge EDP_{DS} |IM,C) = 1\).

The linear least square method is applied to the “NoC” pairs in order to estimate the conditional mean and standard deviation of EDP given IM and derive the commonly-used power-law model \(EDP = aIM^{b}\) (Jalayer and Cornell 2009), where \(a\) and \(b\) are the parameters of the regression. The derived probabilistic seismic demand model is used to define the median and logarithmic standard deviation of the lognormal distribution representing \(P(EDP \ge EDP_{DS} |IM,NoC)\) for each DS. The probability of collapse \(P(C|IM)\) can be represented by a generalised regression model with a “logit” link function (logistic regression), which is appropriate for cases in which the response variable is binary (in this case, “collapse” or “no collapse”).

Vulnerability curves are finally derived using a building-level consequence model relating the repair-to-reconstruction cost to structural and non-structural damage states. Such model requires the definition of the expected building-level damage-to-loss ratios (DLRs) for each DS. The (mean) loss ratio (LR) for a given value of the IM is defined according to Eq. (2), for both sets of fragility relationships, \(F_{ds} \left( {IM} \right)\), and considering that \(F_{0} = 1\) for any value of the IM.

$$LR\left( {IM} \right) = \mathop \sum \limits_{ds} \left( {F_{ds - 1} \left( {IM} \right) - F_{ds} \left( {IM} \right)} \right)DLR_{ds}$$
(6)

It is worth mentioning that building-level DLRs are generally deemed appropriate for assessing earthquake-induced losses of building portfolios consisting of various building typologies. More advanced, component-based loss-estimation procedures are now available for building-specific applications, e.g. (Federal Emergency Management Agency 2012). Such approaches are generally deemed unfeasible for large portfolio applications due to the scarcity of input data and the high computational burden. The uncertainty of the DLRs (e.g. Dolce et al. 2006) may strongly affect the loss estimation, particularly in terms of its variability (Silva 2019). Since for this particular study the loss results are expressed in relative terms (NF vs FF), such uncertainty is neglected for simplicity.

2.3 Loss assessment

For each event and each IM simulation (i.e. ground-motion field), the mean LR is calculated using the relevant vulnerability relationships depending on the simulated conditions (ordinary or pulse-like ground motion). This process is repeated for each location within the portfolio, and for each considered building typology, \(t\). For each computed LR, the ground-up loss at each of the \(n_{loc}\) locations is calculated through Eq. 7, assuming \(N_{b,t}\) buildings of typology \(t\) for which the cost of reconstruction is equal to \(CR_{b,t}\). Such cost (which can include structural/non-structural component and/or contents) is generally given in the exposure model. Therefore, the loss ratio of each location for a given IM value is calculated with Eq. 8.

$$L_{loc} \left( {IM} \right) = \mathop \sum \limits_{t} LR_{b,t} \left( {IM} \right)N_{b,t} CR_{b,t}$$
(7)
$$LR_{loc} \left( {IM} \right) = \frac{{L_{loc} \left( {IM} \right)}}{{CR_{loc} }} = \frac{{\mathop \sum \nolimits_{t} LR_{b,t} \left( {IM} \right)N_{b,t} CR_{b,t} }}{{\mathop \sum \nolimits_{t} N_{b,t} CR_{b,t} }}$$
(8)

In the hypothesis that \(CR_{b,t} = CR\) for each \(b\), the Eq. 8 is simplified into Eq. 9, in which \(n_{b,t} = N_{b,t} /\mathop \sum \limits_{t} N_{b,t}\) is the proportion of buildings of typology \(t\). By further assuming that the distribution of buildings \(n_{b}\) is uniform in the portfolio, the LR of the portfolio is calculated as the mean of the loss ratios of each location (Eq. 10). Consistently with the scope of this work and given such simplified assumptions, there is no need to assume any \(CR\) nor the number of buildings at the given location for each building typology, without jeopardising the generality of the results.

$$LR_{loc} \left( {IM} \right) = \frac{{\mathop \sum \nolimits_{t} LR_{b,t} \left( {IM} \right)N_{b,t} }}{{\mathop \sum \nolimits_{t} N_{b,t} }} = \mathop \sum \limits_{t} LR_{b,t} \left( {IM} \right)n_{b,t}$$
(9)
$$LR_{loc} \left( {IM} \right) = \frac{{\mathop \sum \nolimits_{loc} L_{loc} }}{{CR_{port} }} = \frac{{\mathop \sum \nolimits_{loc} LR_{loc} CR_{loc} }}{{\mathop \sum \nolimits_{loc} CR_{loc} }} = \frac{{\mathop \sum \nolimits_{loc} LR_{loc} }}{{n_{loc} }}$$
(10)

The final result of the analysis is expressed in terms of loss exceedance curves introduced above and EAL, representing the expected loss per year (statistical mean loss) and used as an estimate of the annual insurance premiums to cover the peril (Mitchell-Wallace et al. 2017). This is obtained by averaging the portfolio LR for each event and each simulation in the stochastic catalogue. Besides the ground-up losses, it is also possible to calculate insured losses (i.e. economic value that can be covered by the insurance industry according to a certain policy). To do so, both a deductible and a limit for each type of cost (structural, non-structural or contents) needs to be defined.

3 Illustrative application

3.1 Considered building typologies

Three building typologies representative of distinct vulnerability classes in the Mediterranean region are considered: non-ductile moment-resisting RC infilled frames, mainly designed to sustain gravity loads (i.e. pre-code frame—RCp hereinafter); two types of ductile moment-resisting frames designed according to modern seismic standards and high-ductility capacity (i.e. special-code RC infilled frame—RCs; special-code steel bare frame—Ss). The considered building classes refer to mid-rise buildings; for each class, a four-storey index building is defined.

The two RC uniformly-infilled buildings share the same geometry, for which the total height is equal to 13.5 m with a first storey of 4.5 m, upper storeys of 3 m and a bay width of 4.5 m in both directions. This gravity-designed structure does not conform to modern seismic requirements and it is characterised by a non-ductile behaviour due to the lack of capacity design considerations. The RCs frame is designed and detailed according to modern seismic provisions and high-ductility capacity. These two frames are fully consistent with those used by Aljawhari et al. (2019, 2020). In such references, a detailed description of those case studies is given, including the detailing of each RC member and the material characteristics.

The Ss frame is adapted from a case study in the SAC steel project (Gupta and Krawinkler 1999) (i.e. same floor plans and elevations, while having four rather than three storeys). This frame is designed according to modern seismic provisions and high ductility capacity. This is consistent with a case study used by Song et al. (2020) and Galasso et al. (2015), where all the relevant details of the design are given (such as materials properties and member detailing).

3.1.1 Modelling strategies

The response of the case-study structures is simulated via 2D numerical models developed using the software OpenSees (McKenna et al. 2000). For all the case studies, gravity loads, and masses are uniformly distributed on the beams and concentrated at the beam-column intersections, respectively. Moreover, elastic damping is modelled through the Rayleigh model (Zareian and Medina 2010), using a 5% damping ratio for the first two vibration modes. However, different modelling strategies are adopted for each case study to capture specific characteristics of their behaviour.

A lumped plasticity approach is used for both the RCp and RCs frames, using zero-length rotational springs for beams and columns. Both beam-column joints and floor diaphragms are modelled as rigid. Geometric non-linearities are deemed negligible for such RC structures and not included in the model. The moment-drift constitutive relationship for beams and columns is consistent with the model by Panagiotakos and Fardis (2001), while the Ibarra-Medina-Krawinkler model (Ibarra et al. 2005) is used to describe hysteresis and strength degradation (both within-cycle and cyclic). For the RCp frame only, non-linear shear springs consistent with the model by Setzler and Sezena (2008) are added in series to the rotational ones.

Masonry infills are modelled as equivalent struts consistently with the force–deformation relationship developed by Liberatore and Mollaioli (2015). Single diagonal struts connecting the nodes at the beam-column intersections are modelled for the RCs frame. Conversely, to better capture possible column shear failures due to infill-frame interaction, a double strut approach (Burton and Deierlein 2014) is chosen for the RCp frame. The detailed assumptions for the hysteresis and strength degradation parameters of all the RC and infill members are given in Aljawhari et al. (2020). The numerical models (both in terms of capacity curve and plastic mechanism) are validated via analytical calculations according to the Simple Lateral Mechanism Analysis (Gentile et al. 2019a, b, c, d).

For the Ss frame, force-based fibre sections are chosen for the steel beams and columns, with the purpose of simulating axial load–moment interaction and to spread plasticity through the whole length of each structural member. Reduced beam sections are also modelled to control the location of plastic hinge formation. Finite-length joint panels are modelled as rigid. Geometric nonlinearities are explicitly simulated. A leaning column is also added in each model.

A bilinear kinematic hardening relationship is utilized to model the cyclic response of steel in the fibre sections. Such modelling strategy is consistent with the assumptions by Song et al. (2020), where more details are available. It is worth mentioning that the Simple Lateral Mechanism Analysis is not adopted for the Ss frame, since it is not yet available for steel structures.

Based on eigenvalue analysis, the fundamental periods of the considered case studies are equal to 0.27 s, 0.20 s and 0.96 s respectively for the RCp, RCs and Ss. Such large differences allow investigating the susceptibility different types of low-to-moderate period frames to pulse-like effects. Figure 3 shows the considered index buildings for each building typology, together with the results of pushover analyses represented in terms of the roof drift vs base shear coefficient (base shear normalised with respect to the total weight). Such displacement-control analyses allow the quantification of structure-specific damage states. Four DSs are assumed in this case: slight, moderate, extensive and complete damage. Those are defined according to HAZUS, HAZard United States (Kircher et al. 2006), and correspond to the dots in Fig. 3b.

Fig. 3
figure 3

Modified after Gentile et al. (2019c), Aljawhari et al. (2020) and Song et al. (2020)

a Considered building typologies. b Pushover curves with definition damage states.

Full size image

3.2 Considered portfolios

24 synthetic building portfolios are considered in this study. As shown in Fig. 4a, a fault-parallel and a fault-normal “zone” are first defined with respect to a case-study fault. The zones are defined such that the closest sites are located at a 5 km minimum distance from the fault while the furthermost ones are located at a distance equal to twice the fault length. It is worth mentioning that having a single line fault controlling the hazard for a given portfolio may represent a ‘perfect’ condition to maximise directivity effects in the loss assessment. A generic site may be affected by many faults (or area sources) and this may reduce the directivity effects. Nonetheless, the presented results may be considered as an upper bound for regions whose hazard is driven by one or very few seismic sources (e.g. the Marmara region, Istanbul, Turkey; the New Madrid fault, in the Southern and Midwestern United States).

Fig. 4
figure 4

Considered portfolios: a geometrical features; b composition in terms of building types. FP fault parallel, FN fault normal, RCp RC pre code, RCs RC special code, Ss steel special code

Full size image

In each of the considered zone, the centroid of each location in the portfolio is distributed on a uniform lattice approximately 3 km-spaced. Therefore, a 9 km2 area pertains to each location. Since uniform site conditions are considered (Sect. 3.3), such choice allows achieving a trade-off between computational burden and accuracy of the results, and it is based on a sensitivity analysis of the hazard results (with particular reference to the spatial resolution of the adopted GMM). In general, the spatial resolution of the lattice should be linked to the spatial variation of the soil conditions (Bal et al. 2010).

Three different portfolio sizes are considered: those are equal to 1/16 and 1/4 of the total zone area and the total zone area, respectively. As shown in Fig. 4b, those dimensions may be representative of a city up to a county or region. Four different exposure configurations are considered, assuming that each location has the same building composition. The first three configurations involve a single building typology (RCp, RCs, Ss). The fourth case represents a mixed composition: 60%RCp + 32%RCs + 8%Ss. This is based on the Italian 2011 (Istituto nazionale di STATistica ISTAT 2011) census to obtain a plausible assumption. The census data is given in disaggregated form with respect to each decade and three construction materials: RC, masonry and other. The above assumption is obtained by aggregating the RC data before and after the year 2001 (the post-2001 cases are assigned to the special-code typology), disregarding the masonry buildings (which are not included in the considered building typologies) and assigning the steel typology to the category “other”. Considering all the combinations of zone, size and composition, 24 synthetic portfolios are obtained.

3.3 Assumptions for the stochastic catalogue generation

It is assumed that the considered case-study strike-slip fault can generate \(m_{c} = 6.5\). The other parameters required by the characteristic earthquake-recurrence model of Convertito et al. (2006) are assumed as follows:\(b = 1\) (\(b\) is the \(b\)-value of the Gutenberg–Richter law); \(M_{min} = 5\); \(M_{max} = 7.0\); and \(\Delta_{m1} = 1\) (this parameter represent an interval below the magnitude level \(m_{c}\), required in the considered probabilistic model). A rock soil type is assumed for simplicity for each location in the portfolios (with shear wave velocity in the first 30 m of soil \(V_{s30} = 800 \;{\text{m/s}}\)).

A 10,000-year stochastic catalogue is considered; for each event, 500 realisations of the rupture length, rupture position, epicentre, \(T_{p}\), and IMs are generated. These values of \(T_{cat}\) and \(N_{sim}\) are selected based on the current catastrophe risk modelling practice and represent a good trade-off in terms of statistical validity of the loss estimates and computational burden. Modelling issues related to convergence in probabilistic event-based analysis (i.e. choice of \(T_{cat}\) and \(N_{sim}\)) are thoroughly investigated in Silva (2018).

As discussed above, AvgSA is selected as the IM and it is calculated in the period bandwidth [0.2T1:1.5T1] for the Ss (consistently with EC8), and [0.3T1:4T1] for the RCp and RCs (Aljawhari et al. 2020).

The hazard and loss amplifications due to pulse-like effects are appropriately isolated for a detailed discussion. For convenience only, the results are named “far field (FF)”, for which pulse-like effects are neglected (even in NF conditions), and “near-fault (NF)”, for which pulse-like effects are modelled as discussed above. Such results are also shown in relative terms, i.e. (NF-FF)/FF.

4 Results and discussions

4.1 Effects of pulse-like ground motions on hazard estimates

Figure 5a–c show the relative hazard amplification considering 2500-year mean return period (50% percentile) due to pulse-like effects considering the appropriate AvgSA (in terms of period ranges) for the three index buildings. As expected, the hazard amplification decreases with the distance from the fault. For all the considered building typologies, such increase is approximately equal to 1% at approximately 20 km from the fault (both in the fault-parallel and fault-normal zones), and it completely vanishes 30 km away from the fault. Such results are consistent with previous studies (e.g. Chioccarelli and Iervolino 2014; Akkar et al. 2018). The main difference among the three considered typologies is the maximum recorded hazard increment, which is somehow proportional to the fundamental period of the structures. The results indeed confirm that pulse-like effects are mainly a long-period phenomenon, and therefore the maximum hazard relative amplification is equal to 5% for the RCs (\(T_{1} = 0.2\;{\text{s}}\)), increases to 15% for the RCp (\(T_{1} = 0.27\;{\text{s}}\)), and it’s equal to 20% for the Ss (\(T_{1} = 0.94\;{\text{s}}\)).

Fig. 5
figure 5

Near-fault to far-field ground motion amplification (NF-FF)/FF in terms of AvgSA for 2500-year mean return period (50% percentile): a pre-code RC, b special code RC, c special code steel. d Uniform hazard spectra for a selected site (far-field vs. near-fault conditions)

Full size image

Using AvgSA as the selected IM, as opposed to \(S_{a}\) at the fundamental period, has a strong influence on the registered hazard increment. This can be seen in Fig. 6d, that shows the 50% percentile uniform hazard spectrum (2500-year mean return period) for the fault-parallel site 5 km away from the fault. The hazard increment in terms of SA is equal to 3%, 8% and 45% for the RCp, RCs and Ss respectively. Such differences (with respect to the above values) are governed by the portion of the period bandwidth for AvgSA that overlaps with the “bump” in the spectrum caused by the pulse-like effects. Since the overlap depends both on the fundamental period and the extremes of the bandwidth, this effect has non-trivial consequences on the hazard estimation.

Fig. 6
figure 6

Cloud analyses considering the ordinary and pulse-like ground motions: a pre-code RC, b special-code RC, c special code steel, d pulse period of the considered pulse-like records

Full size image

4.2 Pulse-like effects on fragility and vulnerability relationships

Figure 6a–c show the results of the cloud analyses conducted using both the ordinary and the pulse-like suites of ground motions. A filtering of the ordinary records is first performed, by excluding the ones classified as pulse-like (Baker 2008) when the scale factor adopted by Kohrangi et al. (2019) is applied. This reduces the number of records to 171 (the spectral-equivalent pulse-like ones are also removed). It is worth mentioning that, only for the Ss case study, the selected records are scaled up with an additional factor ranging from two to five. A similar pulse-like check confirms that no record should be removed due to the further scaling. Due to the particular modelling strategy adopted for this steel frame, its behaviour is particularly stable, and it is only affected by the “nominal” collapse criterion (exceeding 10% drift).

As mentioned above, the pulse-like effects are much stronger if the period of the pulse of a given ground-motion record is close enough to the fundamental period of the considered structure (elongated period, for the inelastic response). However, as confirmed by Fig. 6d, directivity-affected ground motions are characterised by long-period pulses. Since this study involves low-to-moderate period structures, filtering the records depending on the pulse period (for example partitioning them in bins depending on \(T_{p} /T_{1}\)) results in an insufficient number of records that would in turn lead to statistically-insignificant results in terms of fragility relationships. Therefore, it is decided to include the entire suite of records in the cloud analysis, defining the fragility relationships with a binary variable (ordinary vs pulse like). On the one hand, this means accepting a bias in the fragility results. On the other hand, since the hazard calculations are defined based on \(T_{p}\), the overall loss results would still explicitly depend on the pulse period. It is worth noting that such a shortcoming of existing empirical ground-motion databases in terms of pulse-like ground motions could be addressed by using various types of validated synthetic ground-motion signals (e.g. Galasso et al. 2013; Tsioulou et al. 2018, 2019).

The pulse-like ground motions consistently impose a higher demand on the case study frames, as shown by the probabilistic seismic demand models in Fig. 6a–c. However, given the fairly low period of the structures, such demand increase is minimal. This effect is propagated on the fragility relationships (Fig. 7a, c, e), which also depend on the ground motions that caused collapse (which are assigned a 10% drift in Fig. 6a–c for illustration purposes). In this regard, a considerable number of collapse cases (circa 40 GMs, both ordinary and pulse-like) is registered for the RCp due to dynamic instability, while only five ground motions cause collapse for the RCs. Due to its particularly stable behaviour, the Ss frame is essentially elastic-responding and it is only affected by nominal cases of collapse (exceeding 10% drift).

Fig. 7
figure 7

Fragility and vulnerability relationships for the considered building types: a, b pre-code RC, c, d special code RC, e, f special code steel

Full size image

As expected, the effects of pulse-like ground motions on the fragility of such short-period structures are not particularly significant. This may also relate to the high sufficiency of AvgSA in embedding the effect of the pulse. However, clear trends can be identified with regard to the considered DSs and the ductility capacity of each case study. Generally speaking, pulse-like ground motions reduce the median fragility, while having a negligible on the fragility dispersion. For all the case studies, pulse-like ground motions are practically not affecting the DS1 and DS2 fragility relationships. Indeed, at this stage an essentially-elastic behaviour is expected, and the maximum reduction in the median fragility is equal to 10%. Considering that, for example, the DS1 median fragility is on the order of 0.2 g, a 0.02 g variation can be neglected for all practical purposes.

For the DSs involving non-linear behaviour (DS3 and DS4), the effect of the pulse-like ground motions is somehow proportional to the ductility capacity of the case-study frame. By considering DS4 as an example (often related to near-collapse issues), the median fragility is practically unchanged for the RCp (1% reduction), which exhibits a particularly low ductility capacity. Such reduction is equal to 13% and 25% for the RCs and Ss frames, respectively, for which the ductility capacity is much larger. It is worth mentioning that a robust statistical analysis (e.g. statistical hypothesis testing) based on larger datasets (out of scope herein) is needed to determine if the observed fragility shifts are statistically significant. If the observed differences are not statistically significant, a single set of fragility relationships may be used for both ordinary and pulse-like conditions. Moreover, the highlighted effect of pulse-like conditions on seismic fragility may not hold for long-period structures. In fact, since directivity-induced pulses are generally long-period phenomena, their effect on the seismic demands and resulting fragility of high-rise structures may be more significant (e.g. Song and Galasso 2020).

The above-mentioned effects are obviously reflected on the vulnerability relationships (Fig. 7b, d, f), calculated using 0.01, 0.10, 055 and 1.00 as DLRs for DS1 to DS4. This choice is consistent with the assumptions in Aljawhari et al. (2020), which is in turn an adaptation of the model by Di Pasquale et al. (2005). Such DLRs are defined under the assumption that the repair process reinstates the original conditions of buildings before the occurrence of seismic events. No considerations are made to account for possible increase in the replacement cost due to retrofitting and upgrading of the building seismic resistance. Although DLRs are both dependent on the considered building type and region, their careful calibration is deemed less relevant for this specific study, since only relative loss results are discussed (NF vs FF).

4.3 Pulse-like effects on losses

Based on the two sets of fragility relationships, and the simulated ground-motion IM fields, the building-level EAL is calculated, and the NF-to-FF amplification is mapped in Fig. 8a–c. As an example, Fig. 8d also shows the simulated loss curves (MAF of exceedance vs loss ratio) for the Ss frame in the fault-parallel zone closest to the fault.

Fig. 8
figure 8

Near-fault to far-field EAL amplification: a pre-code RC, b special code RC, c special code steel, d simulated loss curves for a selected Special code steel building

Full size image

The shape of the EAL relative amplification mapping reflects the hazard amplification. Therefore, the EAL amplification is dependent on the period of the structures and the distance from the fault. The maximum amplification can be as high as 35% for the RCp (\(T_{1} = 0.2\;{\text{s}}\)), 40% for the RCs (\(T_{1} = 0.27\;{\text{s}}\)) and 50% for the Ss (\(T_{1} = 0.94\,{\text{s}}\)). Clearly, this is also affected by the higher effect of the pulse-like ground motions on the vulnerability relationship of the Ss, if compared to both the RC cases studies (Fig. 7). The EAL relative amplification rapidly decreases with distance and it is negligible at 30 km away from the fault.

The simulated losses are aggregated to derive portfolio-level estimates. Figure 9 shows the loss curves (50% percentile) of the medium-size portfolios, with the four considered exposure configurations. The medium-size portfolios are chosen because, both in the fault-parallel (Fig. 9a) and fault-normal zones (Fig. 9b), they are almost entirely overlapping with the area affected by the loss amplification (approximately 30 km away from the fault). Since the distribution of building is uniform in each building location, similar trends are identified regardless of the exposure composition.

Fig. 9
figure 9

Sensitivity of the loss curves on the exposure composition of the of the medium-size portfolios: a fault-parallel zone; b fault-normal zone

Full size image

Similar trends are identified both in the fault-parallel and fault-normal zones. The loss amplification is higher for events with lower frequency of exceedance, for which the simulated IM amplification is higher, together with a higher shift in vulnerability (which is higher for higher IM values). For a MAF equal to 0.0001 (10,000 years return period), the LR increases by 6.5%, 5.5% and 22.2% respectively for the portfolios composed of RCp, RCs or Ss only. The absolute value of the LR is driven by the overall vulnerability (rather than the hazard amplification), and therefore the losses of the 100% RCp portfolio are the highest. These two effects counterbalance each other in such a way that the loss amplification for the mixed exposure portfolio (60%RCp + 32%RCs + 8%Ss) is close to the 100%RCp one, and it is equal to 6.7%. Such effects are not expected for realistic exposure configurations, for which the hazard amplification may play a major role due to the considerably higher variability in the building vulnerability.

Considering the mixed exposure configuration, Fig. 10 shows a sensitivity analysis with respect to the size of the considered portfolios. Clearly, the absolute values of the portfolio-level LRs decrease as their size increase, since larger portfolios have a larger number of buildings affected by lower hazard levels. However, the amplification of the portfolio loss ratio is inversely proportional to the size of the portfolio. In the fault-normal zone (for MAF = 0.0001), this is equal to 9.0%, 6.7% and 5.0% for the small, medium and large portfolios. Indeed, the area proportion of these portfolios overlapping with the region surrounded by contour line corresponding to 0.001 amplification in the 2500-year mean return period IM is respectively equal to 100%, 89% and 39% respectively. Such region can be approximated considering the area around the fault for which the Joyner-Boore distance (i.e. the shortest distance from a site to the surface projection of the rupture surface) is smaller than \(r_{jb} = 30\;{\text{km}}\). In the fault-parallel zone, such amplification is equal to 8.3%, 3.9% and 2.5%, respectively corresponding to 100%, 52% and 15% area overlap. This result is the first indication that the overlapping area may be a reasonable discriminant to determine if, for a given portfolio, explicitly accounting for pulse-like effects has a non-negligible impact on the computed losses.

Fig. 10
figure 10

Sensitivity of the loss curves on the size of the portfolios (assuming 60%RCp + 32%RCs + 8%Ss): a fault-parallel zone; b fault-normal zone

Full size image

The parameters most suitable to represent the portfolio losses is the EAL (normalised with respect to the total reconstruction cost of the portfolio, in this case). Figure 11a shows the calculated EAL for the 24 considered portfolios, considering both zones and all the combinations of portfolio size and exposure configuration. Figure 11b shows the amplification of EAL due to pulse-like effects. The same results are also reported in Table 1.

Fig. 11
figure 11

Expected annual loss of all the considered portfolios. p1: 100%RCp; p2: 100%RCs; p3: 100%Ss; p4: 60%RCp + 32%RCs + 8%Ss; d1: small; d2: medium; d3: large

Full size image
Table 1 Expected annual loss of all the considered portfolios
Full size table

The absolute results confirm the trends discussed above. The normalised EAL decreases with the size of the portfolios, since, according to their particular definition, larger portfolios have a higher number of locations affected by lower levels of hazard. Moreover, due the uniform composition of each portfolio location, the exposure composition does not change the overall trends. The relative EAL amplification is inversely proportional to the portfolio size. Exception are the large portfolios in the fault-normal zone, which have approximately the same EAL amplification as the medium-size ones. Indeed, when moving from the medium- to the large-size portfolio in the fault-normal zone, a considerable portion of the “added” buildings fall within the zone for which \(r_{jb} \le 30\;{\text{km}}\), thus more affected by the pulse-like effects. This is not true for the fault-parallel zone, for which the “added” buildings when moving from the medium- to the large-size portfolio fall outside the above-mentioned region. This confirms that the portfolio area overlapping with the \(r_{jb} \le 30\;{\text{km}}\) zone can be considered as a proxy for the influence of the pulse-like effects on the portfolio EAL.

Based on these results, although referring to simplified assumptions, portfolios with 15% (or less) overlapping area with the \(r_{jb} \le 30\;{\text{km}}\) zone show a 5% (or less) increase in the portfolio EAL. Such a small variation is deemed to be negligible with respect to the expected variability of portfolio loss estimations, which can be rather large (Silva 2019). For this reason, it could be practical to neglect pulse-like effects if the total area of a given portfolio overlapping with the \(r_{jb} \le 30\;{\text{km}}\) zone is smaller than 15% of the total portfolio area. Applying the derived threshold for faults shorter than the length considered herein (42 km) will likely result in higher conservativism.

5 Concluding remarks

This study investigated the influence of pulse-like ground motions on the estimation of seismic losses for building portfolios. A simulation-based risk assessment framework that includes pulse-like effects has been presented, providing more focus on the aspects related to the pulse-like effects. The proposed methodology relies on near-fault PSHA (accounting for pulse-occurrence probability, pulse period, and the related increase in earthquake-induced ground-motion intensity measures). A cloud analysis-based fragility relationship derivation is included, providing guidance on adopting different suites of ground-motion records to derive fragility relationships for ordinary and pulse-like conditions. A simulation-based estimation of the losses is finally discussed.

The methodology has been applied to 24 synthetic portfolios with size ranging from approximately 200 to 6800 km2, located in a fault-normal or fault-parallel relative position with respect to a case-study fault. Different proportions of building types are also considered for the portfolios, including gravity-designed, pre-code reinforced concrete buildings and seismically-designed, special-code reinforced concrete or steel frame.

The main results can be summarised as follows:

  • As expected, the hazard amplification decreases with the distance from the fault. Such amplification completely vanishes 30 km away from the fault. The main difference among the three considered typologies is the maximum recorded hazard increment, which is somehow proportional to the fundamental period of the structures;

  • Using average spectral acceleration as the selected intensity measure, as opposed to the spectral acceleration at the fundamental structural period, has a strong influence on the registered hazard increment. This is governed by the portion of the period bandwidth for the average spectral acceleration that overlaps with the “bump” in the spectrum caused by the pulse-like effects. Since the overlap depends both on the fundamental period and the extremes of the bandwidth, this effect has non-trivial consequences on the hazard estimation and should be carefully considered while interpreting the overall results;

  • When deriving pulse-like dependent fragility/vulnerability relationships for structures with fundamental period smaller than one second, an important problem to face is the scarcity of records with period of the pulse smaller than twice the fundamental period. Filtering the records depending on the pulse period is likely to result in an insufficient number, likely leading to statistically-insignificant results in terms of fragility/vulnerability. Therefore, it is proposed to include in the analysis also the records with higher pulse period. It is proposed to define fragility relationships based on a binary variable (ordinary vs pulse like). On the one hand, this means accepting a bias in the fragility results. On the other hand, since the hazard calculations are defined based on the pulse period, the overall loss results would still explicitly depend on the pulse period;

  • Pulse-like ground motions consistently impose a higher demand on the case study frames, although this is not particularly higher for the considered short-period structures. This is reflected on the fragility relationships, with a slight reduction of the median, and a negligible effect on the dispersion It is worth mentioning that a robust statistical analysis based on larger datasets is needed to determine if the observed fragility shifts are statistically significant. If this is not the case, a single set of fragility relationships (based on AvgSA) may be used for both ordinary and pulse-like conditions;

  • Pulse-like ground motions are practically not affecting the slight and moderate damage fragility relationships, for which an essentially-elastic behaviour is expected. Instead, for the damage states involving non-linear behaviour (extensive and complete damage), such effect is somehow proportional to the ductility capacity of the case study;

  • The expected annual loss (normalised with respect to the reconstruction cost of the portfolio) decreases with the size of the considered portfolios, since, according to their particular definition, larger portfolios have a higher number of locations affected by lower levels of hazard;

  • The influence of pulse-like effects is significant when estimating the losses of individual building or small portfolios located very close to a fault. The relative amplification of the expected annual loss is inversely proportional to the size of the considered portfolios. In particular, the pulse-like effects are proportional to the portion of portfolio area that overlaps with area around the fault for which the Joyner-Boore distance is smaller than \(r_{jb} = 30\;{\text{km}}\).

  • Based on these results, although referring to simplified portfolios, portfolios with 15% (or less) overlapping area with the \(r_{jb} \le 30\;{\text{km}}\) zone show a 5% (or less) increase in the portfolio expected annual loss. Such a small variation is deemed to be negligible with respect to the expected variability of portfolio loss estimations, which can be rather large. For this reason, it could be proposed to neglect pulse-like effects if the area of a given portfolio overlapping with the \(r_{jb} \le 30\;{\text{km}}\) zone is smaller than 15% of the total portfolio area. Applying the derived threshold for faults shorter than the length considered herein (42 km) will likely result in higher conservativism.