1 Introduction

Laminated plates and shells are the quite important parts of engineering structures (e.g., ship body, car bodywork, helmets, pressure vessels) [1,2,3,4,5,6]. The heterogeneous nature of laminated composite materials makes them susceptible to many types of damage modes. Delamination or interlaminar fracture is one of the primary failure modes in such materials [7,8,9]. Delamination physically means that the neighboring layers partially or entirely get separated from each other reducing significantly the stiffness and strength of the laminate [10], respectively. Apart from that even the dynamic properties of the structure alter significantly [11,12,13]. It is therefore very important to develop models which are able to capture adequately the mechanical behavior of delaminated composite structures.

The literature offers numerous classic and improved models for the computational analysis of laminated plates and shells. The so-called equivalent single layer (ESL) theories are two-dimensional theories based on suitable assumptions of kinematics and stress state along the thickness direction compared to those of three-dimensional models. Obviously, the classical laminated plate and shell theories (CLPT and CST) [14, 15] are quite essential in this field. Eventually, the CLPT and CST theories are useful only if the structure does not contain imperfections at all. On the contrary, if material defects, such as cracks and delaminations, appear in the structure, then higher-order theories are indispensable [14]. The basic idea of the first-order shear deformation plate (FSDT) and shell theories (FST) [16,17,18,19] is to involve cross section rotations given by parameters, which are independent of the deflection. This model is able to provide the sufficient accuracy in most of the cases. If further improvement is required, such as the more accurate description of interlaminar shear or normal stresses, then the second- (SSDT and SST) [20, 21] and third-order shear deformation (TSDT and TST) [16, 17, 22] theories might be taken into consideration, as well as other higher-order theories (HSDT) [23,24,25,26,27,28]. Further developments can be achieved by adding the transverse stretching term to the displacement field [12, 29,30,31,32,33].

As a final word of this short introduction, the three-dimensional methods are mentioned. The so-called elasticity solution [34, 35] and the layerwise theories [36,37,38,39,40,41,42] are able to provide more accurate solutions for thick laminates and strain and stress fields at the ply level.

The application of plate and shell theories to standard problems is well documented in the literature [14, 43, 44]. On the other hand, if the structure contains interlaminar cracks and delaminations, then the problem becomes significantly more complicated and its size increases considerably as well [45, 46]. The related literature offers several analytical [47,48,49,50] and numerical [51, 52] methodologies, respectively. One of the analytical solutions was developed by the current author, and the major works are briefly mentioned in the sequel.

The through-width delamination means that the delamination passes through the whole width of the shell with delamination front parallel to the width. In contrast, the expression of through-thickness is related to the thicknesswise or normal direction perpendicularly to shell midsurface. The basic idea to model plates with a through-width delamination is to apply a semi-layerwise modeling technique [53]. This means that the plate or shell is divided by the surface of the delamination and the obtained sublaminates (the top and bottom parts) are further divided into subparts by interface or perturbation surfaces. If only two ESLs are utilized (above and below the delamination), then the method of 2ESLs is involved [53,54,55]. If there are two additional interface (or perturbation) surfaces, then the method of 4ESLs is proposed [56] as shown in Fig. 1. Apparently, Fig. 1 introduces cases I-IV through shell elements by varying the location of delamination surface. The kinematic continuity of the adjacent layers can be ensured by using the system of exact kinematic conditions (SEKC) developed primarily for the first-order plates [57]. The latter work was followed by the extension of the basic idea to the second- and third-order plates [57] as well as thick sandwich plates [21, 32].

The main purpose of the mentioned series of works was to find an optimal candidate for a possible shell finite element for the delamination analysis of laminated structures. This element could make it possible to provide high accuracy in the calculation of energy release rates and to replace the computationally expensive 3D finite element models. In this work, the first-, second and third-order shell theories are applied together with the method of 4ESLs to delaminated composite shells. The extension of the former models is a challenge, because shells are significantly more complex structures than plates. Thus, the models are extended and applied to elliptic and hyperbolic shells with constant radii of curvature including a through-width delamination. Many of the existing works deals with shells having constant radii of curvatures. Shells with variable radii of curvatures can be analyzed by beam function method and Galerkin method [58] or extended Kantorovich-Ritz method [59] using differential quadrature method [60] and the finite element method [14]. An important aspect of this work is the determination of the mode-II and mode-III energy release rates (ERR) and their distributions along the delamination front performed by the three-dimensional J-integral [61, 62]. Finally, the results are compared to 3D finite element calculations, and a discussion is given as well as some conclusions.

Fig. 1
figure 1

Shell elements with orthotropic plies and the position of delamination over the shell thickness for cases I–IV

Full size image

2 Partial semi-layerwise displacement field and continuity conditions

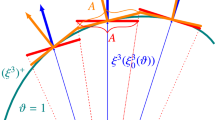
The proposed modeling technique belongs to the partial semi-layerwise theories, i.e., the transverse normal stress is neglected [14]. Figure 1 shows differential shell elements with delamination. In Fig. 1, \(\xi _1\) and \(\xi _2\) are curvilinear coordinates, \(\zeta \) is the through-thickness coordinate, respectively. The whole laminate is captured by four ESLs, and two ESLs are applied below and above the delamination. The surfaces between the adjacent ESLs are called interface surfaces or perturbation surfaces. Figure 2a shows the \(\xi _1\)-\(\zeta \) plane of the cross section of a delaminated shell. The lines crossing the section through the thickness represent the in-surface displacements by the different theories and different regions. The distribution is linear by FST, quadratic by SST and cubic in accordance with the TST. Figure 2b shows how the transverse shear strains are distributed over the thickness of shell. The \(\xi _2\)-\(\zeta \) plane of the problem is shown in Fig. 3a, and the shear strains are plotted in Fig. 3b. In the sequel, the equations of undelaminated and delaminated regions are presented separately and are based on an assumed displacement field. To clarify the assumptions of the models, the strain–displacement relation of doubly curved shells is applied and can be written as [14]:

Fig. 2
figure 2

Cross sections and deformation of the top and bottom elements of a delaminated composite shell in the \(\xi _1\)-\(\zeta \) plane (a). Distribution of the transverse shear strains by FST and SST (b)

Full size image
$$\begin{aligned} \varepsilon _{1(i)}= & {} \frac{1}{{A_1 }}\left( {\frac{{\partial u_{(i)} }}{{\partial \xi _1 }} + \frac{1}{{a_2 }}\frac{{\partial a_1 }}{{\partial \xi _2 }}v_{(i)} + \frac{{a_1 }}{{R_1 }}w} \right) , \nonumber \\ \varepsilon _{2(i)}= & {} \frac{1}{{A_2 }}\left( {\frac{{\partial v_{(i)} }}{{\partial \xi _2 }} + \frac{1}{{a_1 }}\frac{{\partial a_2 }}{{\partial \xi _1 }}u_{(i)} + \frac{{a_2 }}{{R_2 }}w} \right) , \nonumber \\ \gamma _{12(i)}= & {} \frac{{A_2 }}{{A_1 }}\frac{\partial }{{\partial \xi _1 }}\left( {\frac{{v_{(i)} }}{{A_2 }}} \right) + \frac{{A_1 }}{{A_2 }}\frac{\partial }{{\partial \xi _2 }}\left( {\frac{{u_{(i)} }}{{A_2 }}} \right) , \end{aligned}$$
(1)
$$\begin{aligned} \gamma _{2\zeta (i)}= & {} \frac{1}{{A_2 }}\frac{{\partial w}}{{\partial \xi _2 }} + A_2 \frac{\partial }{{\partial \zeta ^{(i)} }}\left( {\frac{{v_{(i)} }}{{A_2 }}} \right) , \nonumber \\ \gamma _{1\zeta (i)}= & {} \frac{1}{{A_1 }}\frac{{\partial w}}{{\partial \xi _1 }} + A_1 \frac{\partial }{{\partial \zeta ^{(i)} }}\left( {\frac{{u_{(i)} }}{{A_1 }}} \right) , \end{aligned}$$
(2)

where \(\varepsilon _1\) and \(\varepsilon _2\) are the normal strains, \(\gamma \) denotes the shear strains, \(A_1 = a_1 (1 + \zeta ^{(i)} /R_1 ), A_2 = a_2 (1 + \zeta ^{(i)} /R_2 )\) are the Lamé parameters, u, v and w are the displacement parameters, index i refers to the actual ESL, \(a_1\) and \(a_2\) are the scale factors, \(R_1\) and \(R_2\) are principal radii of curvatures in both directions. If the shell is shallow, then \(1 + \zeta ^{(i)} /R_1 \cong 1\) and \(1 + \zeta ^{(i)} /R_2 \cong 1\). Also, in this paper, doubly curved shells with constant curvature are considered only, i.e., \(a_1\)=const. and \(a_2\)=const. In accordance with Eqs. (1) and (2), it is clear that the strain field depends upon the displacement components. Moreover, the strain field equations can be obtained in Cartesian coordinate system through \(\partial / \partial x = \partial /(a_1 \partial \xi _1)\) and \(\partial / \partial y = \partial /(a_2 \partial \xi _2)\). The primary field parameter is the displacement; thus, it is formulated separately for the undelaminated and delaminated parts of the shell.

Fig. 3
figure 3

Cross sections and deformation of the top and bottom elements of a delaminated composite shell in the \(\xi _2\)-\(\zeta \) plane (a). Distribution of the transverse shear strains by FST and SST (b)

Full size image

2.1 Undelaminated part

The general third-order Taylor-expansion of the in-surface displacement functions results in the following displacement field components [63]:

$$\begin{aligned} u_{(i)} (\xi _1,\xi _2,\zeta ^{(i)} )= & {} u_0 (\xi _1,\xi _2) + u_{0i} (\xi _1,\xi _2) + \theta _{(\xi _1)i} (\xi _1,\xi _2)\zeta ^{(i)} + \phi _{(\xi _1)i} (\xi _1,\xi _2)[\zeta ^{(i)} ]^2 \nonumber \\&+ \lambda _{(\xi _1)i} (\xi _1,\xi _2)[\zeta ^{(i)} ]^3, \nonumber \\ v_{(i)} (\xi _1,\xi _2,\zeta ^{(i)} )= & {} v_0 (\xi _1,\xi _2) + v_{0i} (\xi _1,\xi _2) + \theta _{(\xi _2)i} (\xi _1,\xi _2)\zeta ^{(i)} + \phi _{(\xi _2)i} (\xi _1,\xi _2)[\zeta ^{(i)} ]^2 \nonumber \\&+ \lambda _{(\xi _2)i} (\xi _1,\xi _2)[\zeta ^{(i)} ]^3, \nonumber \\ w_{(i)} (\xi _1,\xi _2)= & {} w(\xi _1,\xi _2), \end{aligned}$$
(3)

where \(i = 1..4\) is the index of the actual ESL, \(\zeta ^{(i)}\) is the local through thickness coordinate of the \(i^{th}\) ESL and always coincides with the local midplane, \(u_0\) and \(v_0\) are the global, \(u_{0i}\) and \(v_{0i}\) are the local membrane displacements; moreover, \(\theta \) means the rotations of cross sections about the \(\xi _1\) and \(\xi _2\) axes, \(\phi \) denotes the second-order, and \(\lambda \) represents the third-order terms in the displacement functions. Finally \(w_{(i)}\) is the transverse deflection function. Equation (1), which is the basic idea behind the third-order shear deformable shell theory (TST), will be applied equally to the undelaminated and delaminated portions, and the continuity between these parts will be established. In this work, only shear deformable shell models are developed, and in other words, the deflection is inextensible in the through-thickness direction involving that \(w_{(i)}(\xi _1,\xi _2)=w(\xi _1,\xi _2)\). The displacement functions of the first-order (FST) and second-order shear deformable shell theory (SST) can be obtained by reducing Eq. (3) and setting \(\phi _{(\xi _1)i}=\phi _{(\xi _2)i}=0\) and \(\lambda _{(\xi _1)i}=\lambda _{(\xi _2)i}=0\), respectively [64, 65]. The displacement field given by Eq. (3) is associated with each ESL.

The displacement vector field for the \(i^{th}\) ESL is \({\mathbf {u}}_{(i)}=\left( {\begin{array}{*{20}c} {u_{(i)} } &{} {v_{(i)} } &{} {w_{(i)} } \\ \end{array} } \right) ^\text {T}\). The layerwise kinematic continuity between the displacement fields of adjacent ESLs is established by the system of exact kinematic conditions (SEKC), which was originally developed in [20, 53, 55,56,57]. The SEKC is the set of continuity conditions against the displacement and shear strain components. Similar conditions have been applied by others too, e.g., [14, 42, 51]. The first set of conditions formulates the continuity of the in-surface (\(\xi _1, \xi _2\)) and transverse (\(\zeta \)) displacements between the neighboring plies as (refer to Figs. 2 and 3):

$$\begin{aligned} \left. {(u_{(1)} ,v_{(1)} ,w_{(1)} )} \right| _{\zeta ^{(1)} = t_1 /2}= & {} \left. {(u_{(2)} ,v_{(2)} ,w_{(2)} )} \right| _{\zeta ^{(2)} = - t_2 /2}, \nonumber \\ \left. {(u_{(2)} ,v_{(2)} ,w_{(2)} )} \right| _{\zeta ^{(2)} = t_2 /2}= & {} \left. {(u_{(3)} ,v_{(3)} ,w_{(3)} )} \right| _{\zeta ^{(3)} = - t_3 /2}, \nonumber \\ \left. {(u_{(3)} ,v_{(3)} ,w_{(3)} )} \right| _{\zeta ^{(3)} = t_3 /2}= & {} \left. {(u_{(4)} ,v_{(4)} ,w_{(4)} )} \right| _{\zeta ^{(4)} = - t_4 /2}, \end{aligned}$$
(4)

where \(t_i\), \(i=1..4\) are the thicknesses of ESLs. The second set of conditions defines the global membrane displacements (\(u_0, v_0\)) at the reference surface of the actual region. The reference surface belongs to the second ESL (see Fig. 2); therefore, the following condition is imposed:

$$\begin{aligned} \left. {(u_{(2)} ,v_{(2)} )} \right| _{\zeta ^{(2)} = \zeta _R^{(2)} } = (u_0 (\xi _1,\xi _2),v_0 (\xi _1,\xi _2)), \end{aligned}$$
(5)

where \(\zeta _R^{(2)} = 1/2(t_3 + t_4 - t_1 )\) is the position of the global midsurface of the model with respect to ESL2 (see Fig. 2). The next set of conditions imposes the continuous shear strains at the interface surfaces [66]:

$$\begin{aligned} \left. {(\gamma _{1\zeta (1)} ,\gamma _{2\zeta (1)} )} \right| _{\zeta ^{(1)} = t_1 /2}= & {} \left. {(\gamma _{1\zeta (2)} ,\gamma _{2\zeta (2)} )} \right| _{\zeta ^{(2)} = - t_2 /2}, \nonumber \\ \left. {(\gamma _{1\zeta (2)} ,\gamma _{2\zeta (2)} )} \right| _{\zeta ^{(2)} = t_2 /2}= & {} \left. {(\gamma _{1\zeta (3)} ,\gamma _{2\zeta (3)} )} \right| _{\zeta ^{(3)} = - t_3 /2}, \nonumber \\ \left. {(\gamma _{1\zeta (3)} ,\gamma _{2\zeta (3)} )} \right| _{\zeta ^{(3)} = t_3 /2}= & {} \left. {(\gamma _{1\zeta (4)} ,\gamma _{2\zeta (4)} )} \right| _{\zeta ^{(4)} = - t_4 /2}, \end{aligned}$$
(6)

where the shear strains are determined by Eq. (2). This equation set is applicable only to the second- and third-order shells, refer to Figs. 2b and 3b. Although the continuity of shear strains seems to be wrong, if the shear moduli of the neighboring layers are relatively close to each other, then this condition works perfectly. Moreover, it makes it possible to reduce the number of displacement parameters and the mathematical size of the problem. It should be mentioned that if the mismatch between the shear moduli of adjacent layers is relatively large, as it is in the case of softcore sandwich plates, then this condition should be ignored [21]. The oscillations in the shear strain distribution can be reduced by ensuring continuous shear strain derivatives at interface surfaces 1-2 and 3-4:

$$\begin{aligned} \left. {\left( {\frac{{\partial \gamma _{1\zeta (1)} }}{{\partial \zeta ^{(1)} }}, \frac{{\partial \gamma _{2\zeta (1)} }}{{\partial \zeta ^{(1)} }}} \right) } \right| _{\zeta ^{(1)} = t_1 /2}= & {} \left. {\left( {\frac{{\partial \gamma _{1\zeta (2)} }}{{\partial \zeta ^{(2)} }}, \frac{{\partial \gamma _{2\zeta (2)} }}{{\partial \zeta ^{(2)} }}} \right) } \right| _{\zeta ^{(2)} = - t_2 /2}, \nonumber \\ \left. {\left( {\frac{{\partial \gamma _{1\zeta (3)} }}{{\partial \zeta ^{(3)} }}, \frac{{\partial \gamma _{2\zeta (3)} }}{{\partial \zeta ^{(3)} }}} \right) } \right| _{\zeta ^{(3)} = t_3 /2}= & {} \left. {\left( {\frac{{\partial \gamma _{1\zeta (4)} }}{{\partial \zeta ^{(4)} }}, \frac{{\partial \gamma _{2\zeta (4)} }}{{\partial \zeta ^{(4)} }}} \right) } \right| _{\zeta ^{(4)} = - t_4 /2} , \end{aligned}$$
(7)

furthermore, by imposing continuous second derivatives of shear strains in the same surfaces by using the conditions below:

$$\begin{aligned} \left. {\left( {\frac{{\partial ^2 \gamma _{1\zeta (1)} }}{{\partial (\zeta ^{(1)} )^2 }}, \frac{{\partial ^2 \gamma _{2\zeta (1)} }}{{\partial (\zeta ^{(1)} )^2 }}} \right) } \right| _{\zeta ^{(1)} = \frac{t_1}{2}}= & {} \left. {\left( {\frac{{\partial ^2 \gamma _{1\zeta (2)} }}{{\partial (\zeta ^{(2)} )^2 }}, \frac{{\partial ^2 \gamma _{2\zeta (2)} }}{{\partial (\zeta ^{(2)} )^2 }}} \right) } \right| _{\zeta ^{(2)} = - \frac{t_2}{2} }, \nonumber \\ \left. {\left( {\frac{{\partial ^2 \gamma _{1\zeta (3)} }}{{\partial (\zeta ^{(3)} )^2 }}, \frac{{\partial ^2 \gamma _{2\zeta (3)} }}{{\partial (\zeta ^{(3)} )^2 }}} \right) } \right| _{\zeta ^{(3)} = \frac{t_3}{2} }= & {} \left. {\left( {\frac{{\partial ^2 \gamma _{1\zeta (4)} }}{{\partial (\zeta ^{(4)} )^2 }}, \frac{{\partial ^2 \gamma _{2\zeta (4)} }}{{\partial (\zeta ^{(4)} )^2 }}} \right) } \right| _{\zeta ^{(4)} = - \frac{t_4}{2} }. \end{aligned}$$
(8)

Obviously the latter two sets of conditions are again applicable only for the second- and third-order shells in accordance with Figs. 2b and 3b. To further reduce the number of parameters in the displacement field and to obtain more accurate results, the so-called shear strain control condition (SSCC, [56]) is applied at the top and bottom boundaries of the undelaminated part:

$$\begin{aligned} \left. {(\gamma _{1\zeta (1)} ,\gamma _{2\zeta (1)} )} \right| _{\zeta ^{(1)} = - t_1 /2} = \left. {(\gamma _{1\zeta (4)} ,\gamma _{2\zeta (4)} )} \right| _{\zeta ^{(4)} = t_4 /2} . \end{aligned}$$
(9)

In Eq. (3), the displacement functions are modified in order to satisfy Eqs. (4)–(9). In the general sense, by applying the FST, SST and TST theories the in-surface displacement functions can be written as:

$$\begin{aligned} u_{(i)} (\xi _1 ,\xi _2 ,\zeta )= & {} u_0 (\xi _1 ,\xi _2 ) + \left( {K_{(u)ij}^{(0)} + K_{(u)ij}^{(1)} \zeta ^{(i)} + K_{(u)ij}^{(2)} \left[ {\zeta ^{(i)} } \right] ^2 + K_{(u)ij}^{(3)} \left[ {\zeta ^{(i)} } \right] ^3 } \right) \psi _{(1)j}, \end{aligned}$$
(10)
$$\begin{aligned} v_{(i)} (\xi _1 ,\xi _2 ,\zeta )= & {} v_0 (\xi _1 ,\xi _2 ) + \left( {K_{(v)ij}^{(0)} + K_{(v)ij}^{(1)} \zeta ^{(i)} + K_{(v)ij}^{(2)} \left[ {\zeta ^{(i)} } \right] ^2 + K_{(v)ij}^{(3)} \left[ {\zeta ^{(i)} } \right] ^3 } \right) \psi _{(2)j}, \end{aligned}$$
(11)
$$\begin{aligned} w_{(i)} (\xi _1 ,\xi _2 ,\zeta )= & {} w(\xi _1 ,\xi _2 ) , \end{aligned}$$
(12)

where \(K_{(p)ij}, (p = u\) or v) is the displacement multiplicator matrix and related exclusively to the geometry (ESL thicknesses and radii of curvatures), i refers to the ESL number, the summation index j defines the component in \(\varvec{\psi }\), which is the vector of primary parameters. Subscript u and v indicates the corresponding direction (\(\xi _1\) or \(\xi _2\)); finally, \(w_{(i)}(\xi _1,\xi _2)=w(\xi _1,\xi _2)\) for each ESLs, i.e., the transverse normal of each ESL is inextensible [14]. Equations (10)–(11) can be obtained by parameter elimination [21]. It is important to note that the size and the elements of \(\varvec{\psi }\) depend on the applied theory, the number of ESLs and the number of conditions applied. Tables 1 and 2 collect a possible choice of primary parameters for the undelaminated and delaminated parts as well. The parameters in circle are the so-called autocontinuity parameters [57]. The corresponding \(K_{(p)ij}\) multiplicator matrix elements (in Cartesian coordinate system) are presented in “Appendix A” for the FST and SST theories assuming shallow shell geometry. The multiplicator matrix elements of TST theory are so lengthy that these are not presented in this work at all.

Table 1 Primary parameters of the different shell theories, undelaminated part, \(p=\xi _1\) or \(\xi _2\). The parameter in the circle is an autocontinuity parameter [57]
Full size table

2.2 Delaminated part

In the delaminated region (refer to Fig. 1), the top and bottom surfaces are equally modeled by two ESLs, and thus, the first and third of Eq. (4) still hold in each theory. In accordance with Eq. (2), the transverse deflections of the top and bottom shells of the delaminated region are identical (constrained mode model, [55]). The main aim of the analysis was to develop a shell model to capture the delamination effect with good accuracy and to verify the analytical model by FE calculations under the same conditions, i.e., without the contact mechanics. The contact conditions—which would make the problem nonlinear—are not considered in this work being a linear analysis; however, this should be one of the next future steps. The definition of the top and bottom reference surfaces involves:

$$\begin{aligned} \left. {(u_{(1)} ,v_{(1)} )} \right| _{\zeta ^{(1)} = t_2 /2}= & {} (u_{0b} (\xi _1,\xi _2),v_{0b} (\xi _1,\xi _2)), \nonumber \\ \left. {(u_{(3)} ,v_{(3)} )} \right| _{\zeta ^{(3)} = t_4 /2}= & {} (u_{0t} (\xi _1,\xi _2),v_{0t} (\xi _1,\xi _2)), \end{aligned}$$
(13)

where \(u_{0b}\) and \(u_{0t}\) are the global membrane displacements of the bottom and top shells (refer to Figs. 2 and 3). This implies that in Eq. (3) \(u_0\) and \(v_0\) should be replaced by \(u_{0b}\) and \(v_{0b}\) for ESL1 and ESL2, moreover by \(u_{0t}\) and \(v_{0t}\) for ESL3 and ESL4, respectively. Furthermore, the first and third of Eq. (4) apply again, as well as Eqs. (5)–(6). Three other equations are formulated by using the shear strain control conditions:

$$\begin{aligned} \left. {(\gamma _{1\zeta (1)} ,\gamma _{2\zeta (1)} )} \right| _{\zeta ^{(1)} = - t_1 /2}= & {} \left. {(\gamma _{1\zeta (2)} ,\gamma _{2\zeta (2)} )} \right| _{\zeta ^{(2)} = t_2 /2} , \nonumber \\ \left. {(\gamma _{1\zeta (3)} ,\gamma _{2\zeta (3)} )} \right| _{\zeta ^{(3)} = - t_3 /2}= & {} \left. {(\gamma _{1\zeta (4)} ,\gamma _{2\zeta (4)} )} \right| _{\zeta ^{(4)} = t_4 /2} , \nonumber \\ \left. {(\gamma _{1\zeta (1)} ,\gamma _{2\zeta (1)} )} \right| _{\zeta ^{(1)} = - t_1 /2}= & {} \left. {(\gamma _{1\zeta (4)} ,\gamma _{2\zeta (4)} )} \right| _{\zeta ^{(4)} = t_4 /2} , \end{aligned}$$
(14)

Using the equations above, the displacement field can be given by the following equations:

$$\begin{aligned} u_{(i)}(\xi _1,\xi _2,\zeta )= & {} \left( {K_{(u)ij}^{(0)} + K_{(u)ij}^{(1)} \zeta ^{(i)} + K_{(u)ij}^{(2)} [\zeta ^{(i)} ]^2 + K_{(u)ij}^{(3)} [\zeta ^{(i)} ]^3 } \right) \psi _{(1)j}, \; i=1..2, \nonumber \\ v_{(i)}(\xi _1,\xi _2,\zeta )= & {} \left( {K_{(v)ij}^{(0)} + K_{(v)ij}^{(1)} \zeta ^{(i)} + K_{(v)ij}^{(2)} [\zeta ^{(i)} ]^2 + K_{(v)ij}^{(3)} [\zeta ^{(i)} ]^3 } \right) \psi _{(2)j}, \; i=1..2, \end{aligned}$$
(15)
$$\begin{aligned} u_{(i)}(\xi _1,\xi _2,\zeta )= & {} \left( {K_{(u)ij}^{(0)} + K_{(u)ij}^{(1)} \zeta ^{(i)} + K_{(u)ij}^{(2)} [\zeta ^{(i)} ]^2 + K_{(u)ij}^{(3)} [\zeta ^{(i)} ]^3 } \right) \psi _{(1)j}, \; i=3..4, \nonumber \\ v_{(i)}(\xi _1,\xi _2,\zeta )= & {} \left( {K_{(v)ij}^{(0)} + K_{(v)ij}^{(1)} \zeta ^{(i)} + K_{(v)ij}^{(2)} [\zeta ^{(i)} ]^2 + K_{(v)ij}^{(3)} [\zeta ^{(i)} ]^3 } \right) \psi _{(2)j}, \; i=3..4, \nonumber \\ w_{(i)}(\xi _1,\xi _2,\zeta )= & {} w(\xi _1,\xi _2), \quad i=1..4, \end{aligned}$$
(16)
Table 2 Primary parameters of the different shell theories, delaminated part, \(p=\xi _1\) or \(\xi _2\)
Full size table

where the \(K_{(p)ij}\) multiplicator matrix elements can be obtained by applying the above-mentioned equations to Eq. (1). The \(K_{(p)ij}\) elements are collected in “Appendix A” for the FST and SST theories. Quite similar to the undelaminated part, Table 2 collects the primary parameters chosen for the delaminated part. It may be surprising that even the membrane displacements are treated as primary parameters in Table 2, in contrast to Table 1. This can be perceived by considering the conditions against the transverse shear strains (e.g., Eq. (14)) and the fact that according to Eq. (2) shear strains depend on the membrane displacements too.

3 The strain and stress fields

Applying Eqs. (1)–(2) to the displacement field by Eqs. (10)–(12) for the undelaminated part or Eq. (15) for the delaminated part yields:

$$\begin{aligned} \left( {\begin{array}{*{20}c} {\varepsilon _1 } \\ {\varepsilon _2 } \\ {\gamma _{12} } \\ \end{array} } \right) _{(i)} = \left( {\begin{array}{*{20}c} {\varepsilon _1^{(0)} } \\ {\varepsilon _2^{(0)} } \\ {\gamma _{12}^{(0)} } \\ \end{array} } \right) + \zeta ^{(i)} \left( {\begin{array}{*{20}c} {\varepsilon _1^{(1)} } \\ {\varepsilon _2^{(1)} } \\ {\gamma _{12}^{(1)} } \\ \end{array} } \right) + \left[ {\zeta ^{(i)} } \right] ^2 \left( {\begin{array}{*{20}c} {\varepsilon _1^{(2)} } \\ {\varepsilon _2^{(2)} } \\ {\gamma _{12}^{(2)} } \\ \end{array} } \right) + \left[ {\zeta ^{(i)} } \right] ^3 \left( {\begin{array}{*{20}c} {\varepsilon _1^{(3)} } \\ {\varepsilon _2^{(3)} } \\ {\gamma _{12}^{(3)} } \\ \end{array} } \right) . \end{aligned}$$
(17)

The vector of transverse shear strains is:

$$\begin{aligned} \left( {\begin{array}{*{20}c} {\gamma _{1\zeta } } \\ {\gamma _{2\zeta } } \\ \end{array} } \right) _{(i)} = \left( {\begin{array}{*{20}c} {\gamma _{1\zeta }^{(0)} } \\ {\gamma _{2\zeta }^{(0)} } \\ \end{array} } \right) _{(i)} + \zeta ^{(i)} \cdot \left( {\begin{array}{*{20}c} {\gamma _{1\zeta }^{(1)} } \\ {\gamma _{2\zeta }^{(1)} } \\ \end{array} } \right) _{(i)} + \left[ {\zeta ^{(i)} } \right] ^2 \cdot \left( {\begin{array}{*{20}c} {\gamma _{1\zeta }^{(2)} } \\ {\gamma _{2\zeta }^{(2)} } \\ \end{array} } \right) _{(i)} . \end{aligned}$$
(18)

To determine the stress field, we apply the constitutive equation for orthotropic materials under plane stress state, which is \(\varvec{\sigma } _{(i)}^{(m)} = \overline{\mathbf{C }} _{(i)}^{(m)} \varvec{\varepsilon } ^{(m)}\) [14, 15], leading to:

$$\begin{aligned} \left( {\begin{array}{*{20}c} {\sigma _{1} } \\ {\sigma _{2} } \\ {\tau _{2\zeta } } \\ {\tau _{1\zeta } } \\ {\tau _{12 } } \\ \end{array} } \right) _{(i)}^{(m)} = \left( {\begin{array}{*{20}c} {{\overline{C}} _{11} } &{} {{\overline{C}} _{12} } &{} 0 &{} 0 &{} 0 \\ {{\overline{C}} _{12} } &{} {{\overline{C}} _{22} } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {{\overline{C}} _{44} } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {{\overline{C}} _{55} } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {{\overline{C}} _{66} } \\ \end{array} } \right) _{(i)}^{(m)} \left( {\begin{array}{*{20}c} {\varepsilon _1 } \\ {\varepsilon _2 } \\ {\gamma _{2\zeta } } \\ {\gamma _{1\zeta } } \\ {\gamma _{12} } \\ \end{array} } \right) _{(i)}, \end{aligned}$$
(19)

where \(\overline{\mathbf{C }} _{(i)}^{(m)}\) is the stiffness matrix of the \(m^{th}\) layer within the \(i^{th}\) ESL.

For the delaminated part, the form of the strain and stress fields is the same as those by Eqs. (17)–(18); however, Eqs. (15)–(16) have to be involved when Eqs. (1)- (2) are applied.

4 Governing partial differential equations

To derive the governing equations of the shell system, we apply the virtual work principle [14, 67]:

$$\begin{aligned} \int \limits _{T_0} ^{T_1} (\delta {\mathcal {U}} - \delta {\mathcal {W}}_F) \mathrm{d}t =0, \quad \delta {\mathcal {U}} = \sum _ i \delta {\mathcal {U}}_{(i)}, \delta {\mathcal {W}}_F = \sum _ i \delta {\mathcal {W}}_{F(i)} \end{aligned}$$
(20)

where \({\mathcal {U}}\) is the strain energy, \({\mathcal {W}}_F\) is the work of external forces, and t is the time (\({\mathcal {L}} = {\mathcal {U}}-\mathcal {W_F}\) is the Lagrange function). To derive the equilibrium equations of the shell system in a compact and invariant form, we define the following vectors:

$$\begin{aligned} \mathbf{N }_i^{(1,12)}= & {} \left( {\begin{array}{*{20}c} {N_1 } &{} {N_{12} } \\ \end{array} } \right) _{(i)}^T , \quad \mathbf{N }_i^{(12,2)} = \left( {\begin{array}{*{20}c} {N_{12} } &{} {N_2 } \\ \end{array} } \right) _{(i)}^T , \nonumber \\ \mathbf{M }_i^{(1,12)}= & {} \left( {\begin{array}{*{20}c} {M_1 } &{} {M_{12} } \\ \end{array} } \right) _{(i)}^T , \quad \mathbf{M }_i^{(12,2)} = \left( {\begin{array}{*{20}c} {M_{12} } &{} {M_2 } \\ \end{array} } \right) _{(i)}^T, \end{aligned}$$
(21)

where it was assumed that \(N_{12} = N_{21}\), etc. The vectors of higher-order stress resultants become:

$$\begin{aligned} \mathbf{L }_i^{(1,12)}= & {} \left( {\begin{array}{*{20}c} {L_1 } &{} {L_{12} } \\ \end{array} } \right) _{(i)}^T , \quad \mathbf{L }_i^{(12,2)} = \left( {\begin{array}{*{20}c} {L_{12} } &{} {L_2 } \\ \end{array} } \right) _{(i)}^T, \quad \nonumber \\ \mathbf{P }_i^{(1,12)}= & {} \left( {\begin{array}{*{20}c} {P_1 } &{} {P_{1} } \\ \end{array} } \right) _{(i)}^T , \quad \mathbf{P }_i^{(12,2)} = \left( {\begin{array}{*{20}c} {P_{12} } &{} {P_2 } \\ \end{array} } \right) _{(i)}^T. \end{aligned}$$
(22)

Finally, the vector of shear forces becomes:

$$\begin{aligned} \mathbf{Q }_i = \left( {\begin{array}{*{20}c} {Q_1 } &{} {Q_2 } \\ \end{array} } \right) _{(i)}^T . \end{aligned}$$
(23)

In the sequel, the equilibrium equations are derived separately for the undelaminated and delaminated regions.

4.1 Undelaminated region

The application of virtual work principle [14] to the undelaminated region of the shell leads to three sets of equations. The first set is related to the in-surface equilibrium of the following stress resultants:

$$\begin{aligned}&\delta u_0: \sum \limits _{i = 1}^4 {{\hat{\nabla }} \cdot \mathbf{N }^{(1,12)} + \frac{{a_1 a_2 }}{{R_1 }}Q_{1(i)} + } \frac{{a_1 }}{2}\left( {\frac{1}{{R_1 }} - \frac{1}{{R_2 }}} \right) M_{12(i),2} = 0, \nonumber \\&\delta v_0 : \sum \limits _{i = 1}^4 {{\hat{\nabla }} \cdot \mathbf{N }^{(12,2)} + \frac{{a_1 a_2 }}{{R_2 }}Q_{2(i)} - } \frac{{a_2 }}{2}\left( {\frac{1}{{R_1 }} - \frac{1}{{R_2 }}} \right) M_{12(i),1} = 0 , \end{aligned}$$
(24)

where \({\hat{\nabla }} = a_2 (..)_{,1} \mathbf{e }_1 + a_1 (..)_{,2} \mathbf{e }_2\) (\(\mathbf{e }_1\) and \(\mathbf{e }_2\) are shown in Fig. 1). The second set of equations is related to the elements of the vector of primary parameters:

$$\begin{aligned}&\left. {\begin{array}{*{20}c} {\delta \psi _{(1)j} :} \\ {\delta \psi _{(2)j} :} \\ \end{array} } \right\} \sum _{i=1} ^4 \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(0)}{\hat{\nabla }} \cdot \mathbf{N }^{(1,12)} } \\ {K_{(v)ij}^{(0)}{\hat{\nabla }} \cdot \mathbf{N }^{(12,2)} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(1)}{\hat{\nabla }} \cdot \mathbf{M }^{(1,12)} } \\ {K_{(v)ij}^{(1)}{\hat{\nabla }} \cdot \mathbf{M }^{(12,2)} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(2)}{\hat{\nabla }} \cdot \mathbf{L }^{(1,12)} } \\ {K_{(v)ij}^{(2)}{\hat{\nabla }} \cdot \mathbf{L }^{(12,2)} } \\ \end{array} } \right) \nonumber \\&\quad + \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(3)}{\hat{\nabla }} \cdot \mathbf{P }^{(1,12)} } \\ {K_{(v)ij}^{(3)}{\hat{\nabla }} \cdot \mathbf{P }^{(12,2)} } \\ \end{array} } \right) - a_1 a_2 \left( {\begin{array}{*{20}c} {(R_1 K_{(u)ij}^{(1)} - K_{(u)ij}^{(0)} )/R_1 \cdot Q_{1(i)} } \\ {(R_2 K_{(v)ij}^{(1)} - K_{(v)ij}^{(0)} )/R_2 \cdot Q_{2(i)} } \\ \end{array} } \right) \nonumber \\&\quad - 2a_1 a_2 \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(2)}R_{1(i)} } \\ {K_{(v)ij}^{(2)}R_{2(i)} } \\ \end{array} } \right) - a_1 a_2 \left( {\begin{array}{*{20}c} {(3R_1 K_{(u)ij}^{(3)} + K_{(u)ij}^{(2)} )/R_1 \cdot S_{1(i)} } \\ {(3R_2 K_{(v)ij}^{(3)} + K_{(v)ij}^{(2)} )/R_2 \cdot S_{2(i)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right) . \end{aligned}$$
(25)

The last equation represents the equilibrium of shear and membrane forces:

$$\begin{aligned} \sum \limits _{i = 1}^4 {{\hat{\nabla }} \cdot \mathbf{Q }_i - a_1 a_2 \sum \limits _{i = 1}^4 {\left( {\frac{{N_{1(i)} }}{{R_1 }} + \frac{{N_{2(i)} }}{{R_2 }}} \right) } + } q = 0, \end{aligned}$$
(26)

where q is the function of external load. As a next step we write the equilibrium equations in Cartesian coordinate system (x, y and \(\zeta \)) by [14]:

$$\begin{aligned} \frac{\partial }{{\partial x}} = \frac{1}{{a_1 }}\frac{\partial }{{\partial \xi _1 }}, \quad \frac{\partial }{{\partial y}} = \frac{1}{{a_2 }}\frac{\partial }{{\partial \xi _2 }}. \end{aligned}$$
(27)

Applying Eq. (27) and dividing Eqs. (24)–(26) by \(a_1 a_2\), it is possible to obtain:

$$\begin{aligned}&\delta u_0 :\sum \limits _{i = 1}^4 \bigg ( {\nabla \cdot \mathbf{N }^{(1,12)} + \frac{{Q_{1(i)} }}{{R_1 }} + } C_0 M_{12(i),y} \bigg ) = 0, \nonumber \\&\delta v_0 :\sum \limits _{i = 1}^4 \bigg ( {\nabla \cdot \mathbf{N }^{(12,2)} + \frac{{Q_{2(i)} }}{{R_2 }} - C_0 } M_{12(i),x} \bigg ) = 0, \end{aligned}$$
(28)

where [14]:

$$\begin{aligned} C_0 = \frac{{1 }}{2}\left( {\frac{1}{{R_1 }} - \frac{1}{{R_2 }}} \right) . \end{aligned}$$
(29)

Moreover, we have:

$$\begin{aligned}&\left. {\begin{array}{*{20}c} {\delta \psi _{(1)j} :} \\ {\delta \psi _{(2)j} :} \\ \end{array} } \right\} \sum _{i=1}^4 \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(0)}\nabla \cdot \mathbf{N }^{(1,12)} } \\ {K_{(v)ij}^{(0)}\nabla \cdot \mathbf{N }^{(12,2)} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(1)}\nabla \cdot \mathbf{M }^{(1,12)} } \\ {K_{(v)ij}^{(1)}\nabla \cdot \mathbf{M }^{(12,2)} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(2)}\nabla \cdot \mathbf{L }^{(1,12)} } \\ {K_{(v)ij}^{(2)}\nabla \cdot \mathbf{L }^{(12,2)} } \\ \end{array} } \right) \nonumber \\&\quad + \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(3)}\nabla \cdot \mathbf{P }^{(1,12)} } \\ {K_{(v)ij}^{(3)}\nabla \cdot \mathbf{P }^{(12,2)} } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} {(R_1 K_{(u)ij}^{(1)} - K_{(u)ij}^{(0)} )/R_1 \cdot Q_{1(i)} } \\ {(R_2 K_{(v)ij}^{(1)} - K_{(v)ij}^{(0)} )/R_2 \cdot Q_{2(i)} } \\ \end{array} } \right) \nonumber \\&\quad - 2 \left( {\begin{array}{*{20}c} {K_{(u)ij}^{(2)}R_{1(i)} } \\ {K_{(v)ij}^{(2)}R_{2(i)} } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} {(3R_1 K_{(u)ij}^{(3)} + K_{(u)ij}^{(2)} )/R_1 \cdot S_{1(i)} } \\ {(3R_2 K_{(v)ij}^{(3)} + K_{(v)ij}^{(2)} )/R_2 \cdot S_{2(i)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right) . \end{aligned}$$
(30)

The equation of shear and in-surface forces reduces to:

$$\begin{aligned} \sum \limits _{i = 1}^4 {\nabla \cdot \mathbf{Q }_i - \sum \limits _{i = 1}^4 {\left( {\frac{{N_{1(i)} }}{{R_1 }} + \frac{{N_{2(i)} }}{{R_2 }}} \right) } + } q = 0. \end{aligned}$$
(31)

The stress resultants in Eqs. (28)–(31) are determined based on the assumption of shallow shells by considering that \(1+ \zeta /R_1 \cong 1\) and \(1+ \zeta /R_2 \cong 1\) [14]. Thus, in this case the stress resultants are approximated as:

$$\begin{aligned}&\left( {\begin{array}{*{20}c} {N_{\alpha \beta } } \\ {M_{\alpha \beta } } \\ {L_{\alpha \beta } } \\ {P_{\alpha \beta } } \\ \end{array} } \right) _{(i)} = \int \limits _{ - t_i /2}^{t_i /2{\text { }}} {\sigma _{\alpha \beta } } \left( {\begin{array}{*{20}c} 1 \\ \zeta \\ {\zeta ^2 } \\ {\zeta ^3 } \\ \end{array} } \right) _{(i)} \mathrm{d}\zeta ^{(i)} , \nonumber \\&\left( {\begin{array}{*{20}c} {Q_\alpha } \\ {R_\alpha } \\ {S_\alpha } \\ \end{array} } \right) _{(i)} = \int \limits _{ - t_i /2}^{t_i /2{\text { }}} {\tau _{\alpha \zeta } } \left( {\begin{array}{*{20}c} 1 \\ \zeta \\ {\zeta ^2 } \\ \end{array} } \right) _{(i)} \mathrm{d}\zeta ^{(i)} , \end{aligned}$$
(32)

where \(\alpha \) and \(\beta \) take 1 or 2. Taking the constitutive law by Eq. (19) back into Eq. (32) yields [14, 21]:

$$\begin{aligned} \left( {\begin{array}{*{20}c} {\{ N\} } \\ {\{ M\} } \\ {\{ L\} } \\ {\{ P\} } \\ \end{array} } \right) _{(i)}= & {} \left[ {\begin{array}{*{20}c} {{\text {[}}A{\text {]}}} &{} {{\text {[}}B{\text {]}}} &{} {{\text {[}}D{\text {]}}} &{} {{\text {[}}E{\text {]}}} \\ {{\text {[}}B{\text {]}}} &{} {{\text {[}}D{\text {]}}} &{} {{\text {[}}E{\text {]}}} &{} {{\text {[}}F{\text {]}}} \\ {{\text {[}}D{\text {]}}} &{} {{\text {[}}E{\text {]}}} &{} {{\text {[}}F{\text {]}}} &{} {{\text {[}}G{\text {]}}} \\ {{\text {[}}E{\text {]}}} &{} {{\text {[}}F{\text {]}}} &{} {{\text {[}}G{\text {]}}} &{} {{\text {[}}H{\text {]}}} \\ \end{array} } \right] _{(i)} \left( {\begin{array}{*{20}c} {\{ \varepsilon ^{(0)} \} } \\ {\{ \varepsilon ^{(1)} \} } \\ {\{ \varepsilon ^{(2)} \} } \\ {\{ \varepsilon ^{(3)} \} } \\ \end{array} } \right) _{(i)} , \end{aligned}$$
(33)
$$\begin{aligned} \left( {\begin{array}{*{20}c} {\left\{ Q \right\} } \\ {\left\{ R \right\} } \\ {\left\{ S \right\} } \\ \end{array} } \right) _{(i)}= & {} \left[ {\begin{array}{*{20}c} {{\text {[}}A{\text {]}} } &{} {{\text {[}}B{\text {]}} } &{} {{\text {[}}D{\text {]}} } \\ {{\text {[}}B{\text {]}} } &{} {{\text {[}}D{\text {]}} } &{} {{\text {[}}E{\text {]}} } \\ {{\text {[}}D{\text {]}} } &{} {{\text {[}}E{\text {]}} } &{} {{\text {[}}F{\text {]}} } \\ \end{array} } \right] _{(i)} \left( {\begin{array}{*{20}c} {\{ \gamma ^{(0)} \} } \\ {\{ \gamma ^{(1)} \} } \\ {\{ \gamma ^{(2)} \} } \\ \end{array} } \right) _{(i)}, \end{aligned}$$
(34)

where \(A_{pq}\) is the extensional, \(B_{pq}\) is coupling, \(D_{pq}\) is the bending, \(E_{pq}\), \(F_{pq}\), \(G_{pq}\) and \(H_{pq}\) are higher-order stiffnesses defined as [21]:

$$\begin{aligned}&\left( {A_{pq} ,B_{pq} ,D_{pq} ,E_{pq} ,F_{pq} ,G_{pq} ,H_{pq} } \right) _{(i)} \nonumber \\&\quad =\sum \limits _{m = 1}^{N_{l(i)} } {\int \limits _{\zeta ^{(i)}_m }^{\zeta ^{(i)}_{m + 1} } {{\overline{C}} _{pq}^{(m)} (1,\zeta ,\zeta ^2 ,\zeta ^3 ,\zeta ^4 ,\zeta ^5 ,\zeta ^6 )^{(i)} \mathrm{d}\zeta ^{(i)} } }, \end{aligned}$$
(35)

The equations of the delaminated part can be obtained similarly.

4.2 Delaminated region

Taking Eqs. (15)–(16) into consideration while formulating Eq. (20) (similarly to the undelaminated region) results in identical equilibrium equations with those given by Eqs. (30)–(31) in accordance with Table 2.

5 Lévy method and state space solution

Analytical solution of the presented system of PDEs is possible under Lévy type boundary conditions [68]. Figure 4 shows simply supported elliptic (a) and hyperbolic (b) delaminated shells built-up by layers made out of orthotropic material. The shells are divided into four parts: , and are the parts of the delaminated region, is the undelaminated region. Region is the delaminated region subjected to the uniform line load. The region denoted by is a delaminated region, and finally, region is the delaminated part between the undelaminated part and . The concentrated force was captured by a uniformly distributed line load over a finite length. In accordance with Fig.4, the line load was distributed over the length of \(2 d_0\) and \(x_Q\) is the point of action of the resultant force, F. For each region, the models presented in Sects. 2–4 should be applied.

Fig. 4
figure 4

Simply supported doubly curved elliptic (a) and hyperbolic (b) delaminated composite shells subjected to a concentrated force

Full size image

The basic idea of Lévy formulation is that the primary displacement parameters (presented in Tables 1 and 2), the external load parameter, q in Eq. (31), the deflection, w(x, y) and the membrane displacements are expressed by trial functions in the form of:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\psi _{(1)i} (x,y)} \\ {\psi _{(2)i} (x,y)} \\ \end{array} } \right\}= & {} \sum \limits _{n = 1}^\infty {\left\{ {\begin{array}{*{20}c} {\varPhi _{(1)in} (x)\sin \beta y} \\ {\varPhi _{(2)in} (x)\cos \beta y} \\ \end{array} } \right\} } , \nonumber \\ \left\{ {\begin{array}{*{20}c} {u(x,y)} \\ {v(x,y)} \\ {q(x,y)} \\ {w(x,y)} \\ \end{array} } \right\}= & {} \sum \limits _{n = 1}^\infty {\left\{ {\begin{array}{*{20}c} {U_n (x)\sin \beta y} \\ {V_n (x)\cos \beta y} \\ {Q_n (x)\sin \beta y} \\ {W_n (x)\sin \beta y} \\ \end{array} } \right\} }, \end{aligned}$$
(36)

where \(\beta = n \pi / b\), b is the shell width (see Fig. 4), \(Q_n\) is defined in [56, 57]. In the next step, we take the trial functions in Eq. (37) back into the strain field (Eqs. (17)–(18)). This is followed by expressing the stress resultants in accordance with Eqs. (33)–(34). Finally, to reduce the system of PDEs to system of ODEs, we can employ the equilibrium equations given by Eqs. (28)–(31). The system of ODEs can be solved by the state-space approach [44], and the state-space model of the shell system takes the form below: [14, 44]:

$$\begin{aligned} \mathbf {Z'} = {\mathbf {T}} {\mathbf {Z}} + {\mathbf {F}}, \end{aligned}$$
(37)

where \({\mathbf {Z}}\) is the state vector, \({\mathbf {T}}\) is the system matrix, \({\mathbf {F}}\) is the vector related to the external load, and the comma means differentiation with respect to x. The general solution of Eq. (37) becomes [44]:

$$\begin{aligned} {\mathbf {Z}} (x) = e^{{\mathbf {T}} x} \left( {{\mathbf {K}} + \int \limits _{x^* }^x {e^{ - {\mathbf {T}} \xi } } {\mathbf {F}} (\xi )\mathrm{d}\xi } \right) = {\mathbf {G}} (x){\mathbf {K}} + {\mathbf {H}} (x), \end{aligned}$$
(38)

where \({\mathbf {K}}\) is the vector of constants, \(x^{*}\) is the lower integration bound for the different regions of the problems in Fig. 4. The parameters of the state vector can be expressed through:

$$\begin{aligned} Z_i^{(d)} = \sum \limits _{j = 1}^r {G_{ij}^{(d)} K_j^{(d)} } + H_j^{(d)} ,\;Z_i^{(ud)} = \sum \limits _{j = 1}^s {G_{ij}^{(ud)} K_j^{(ud)} } + H_j^{(ud)} , \end{aligned}$$
(39)

where subscript or refers to the delaminated, while refers the undelaminated shell portion, r and s are the size of vectors and matrices of these parts, respectively.

5.1 Generalized continuity conditions

The generalized continuity conditions between regions and in Fig. 4 can be written as:

$$\begin{aligned} \left. {\left( {\begin{array}{*{20}c} {g_\alpha } \\ {h_\alpha } \\ {m_\alpha } \\ {n_\alpha } \\ {p_\alpha } \\ \end{array} } \right) } \right| _{x = + 0}^{(1)} = \left. {\left( {\begin{array}{*{20}c} {g_\alpha } \\ {h_\alpha } \\ {m_\alpha } \\ {n_\alpha } \\ {p_\alpha } \\ \end{array} } \right) } \right| _{x = - 0}^{(2)} , \end{aligned}$$
(40)

where g, h, m, n and p denote parameter sets or functions defined in the sequel.

  • The continuity of deflection, its derivatives and the primary parameters can be defined by a parameter set given by:

    $$\begin{aligned} g_\alpha ^{(l)} = (w,\frac{{\partial w}}{{\partial x}},.....,\psi _{(p)j} ;j = 1..\text {Min}(q_l) ), \end{aligned}$$
    (41)

    where l denotes the actual region ( or ) and \(q_l\) is the number of parameters in \(\psi _{(p)j}\) in both regions. We note that \(q_l\) is the total number of parameters in \(\psi _{(p)j}\). As an example, for the TST model in Table 1, there are four parameters, and on the other hand, in Table 2, we have three, (excluding the membrane displacements) and thus for the TST theory with 4ESLs \(\text {Min}(q_l)=3\).

  • The continuity condition of membrane displacement parameters can be imposed by using the following functions: [21]:

    $$\begin{aligned} h_\alpha ^{(1)}= & {} \left. \sum \limits _{j = 1}^{q_1 } \left( {\begin{array}{*{20}c} {{K_{(u)1j}^{(0)} }\psi _{(1)j} } \\ {{K_{(u)1j}^{(0)} }\psi _{(2)j} } \\ \end{array} } \right) \right| ^{(1)}, \nonumber \\ h_\alpha ^{(2)}= & {} \left. {\left( {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ \end{array} } \right) + \sum \limits _{j = 1}^{q_2 } \left( {\begin{array}{*{20}c} {{K_{(u)1j}^{(0)} }\psi _{(1)j} } \\ {{K_{(u)1j}^{(0)} }\psi _{(2)j} } \\ \end{array} } \right) } \right| ^{(2)}, \nonumber \\ m_\alpha ^{(1)}= & {} \left. \sum \limits _{j = 1}^{q_1 } \left( {\begin{array}{*{20}c} {{K_{(u)3j}^{(0)} }\psi _{(1)j} } \\ {{K_{(v)3j}^{(0)} }\psi _{(2)j} } \\ \end{array} } \right) \right| ^{(1)} , \nonumber \\ m_\alpha ^{(2)}= & {} \left. {\left( {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ \end{array} } \right) + \sum \limits _{j = 1}^{q_2 } \left( {\begin{array}{*{20}c} {{K_{(u)3j}^{(0)} }\psi _{(1)j} } \\ {{K_{(v)3j}^{(0)} }\psi _{(2)j} } \\ \end{array} } \right) } \right| ^{(2)} . \end{aligned}$$
    (42)

    In accordance with Eq. (42), the membrane displacement continuity requires the imposition of the conditions above for a single layer in the bottom and a single one in the top shell.

  • Since \(q_l\) is not always the same number for the delaminated and undelaminated parts of the shell, it is required to define the so-called autocontinuity (AC) condition by [56, 57]:

    $$\begin{aligned} n_\alpha ^{(l)} = \left. {\sum \limits _{j = 1}^{q_l } \left( {\begin{array}{*{20}c} {{K_{(u)\kappa j}^{(\vartheta )} }\psi _{(1)j} } \\ {{K_{(v)\kappa j}^{(\vartheta )} }\psi _{(2)j} } \\ \end{array} } \right) } \right| ^{(l)} , \end{aligned}$$
    (43)

    where \(\vartheta =1,2,3\) depending on the order of multiplicator matrix, \(\kappa \) is the ESL number that the AC parameter is associated with (see Tables 1 and 2). The AC is not required for the FST, but it is for the SST and TST models. The application of Eq. (43) to the latter two theories involves the following. In accordance with Table 1, the AC parameter is \(\phi _{(p)2}\) in the undelaminated part, and this is a second-order parameter in Eq. (3); thus, \(\vartheta =2\). Moreover, it belongs to the second ESL, and therefore, \(\kappa =2\) as well. This results in the following:

    $$\begin{aligned} \left. \left( {\begin{array}{*{20}c} {\phi _{(1)2} } \\ {\phi _{(2)2} } \\ \end{array} } \right) \right| ^{(2)}_{x=-0} = \left. {\sum \limits _{j = 1}^{q_1=5 } \left( {\begin{array}{*{20}c} {{K_{(u)2 j}^{(2 )} }\psi _{(1)j} } \\ {{K_{(v)2 j}^{(2 )} }\psi _{(2)j} } \\ \end{array} } \right) } \right| ^{(1)}_{x=+0} . \end{aligned}$$
    (44)

  • The continuity conditions of stress resultants can be defined by:

    $$\begin{aligned} p_\alpha ^{(l)} = \left. {\left( {\sum \limits _{i = 1..k} {\mathbf{N }_i^{(1,12)} ,} \hat{\mathbf{M }}_1^{(1,12)} ...,\hat{\mathbf{L }}_1^{(1,12)} ...,\hat{\mathbf{P }}_1 ^{(1,12)} ,...} \right) } \right| ^{(l)}, \end{aligned}$$
    (45)

    where the vectors including the hat mean equivalent stress resultants. Since Eq. (45) plays a key role in the accuracy of the solution, the equations sets are detailed for each theory. In the case of the FST theory, the rotations are primary parameters; thus, the continuity of bending moments should be imposed by:

    $$\begin{aligned} \left. {\left( {\begin{array}{*{20}c} {{\hat{M}}_1 } \\ {{\hat{M}}_{12} } \\ \end{array} } \right) _{(j)}^{(1)} } \right| _{x = + 0} \left. { = \left( {\begin{array}{*{20}c} {{\hat{M}}_1 } \\ {{\hat{M}}_{12} } \\ \end{array} } \right) _{(j)}^{(2)} } \right| _{x = - 0} , \end{aligned}$$
    (46)

    where:

    $$\begin{aligned} \left( {\begin{array}{*{20}c} {{\hat{M}}_1 } \\ {{\hat{M}}_{12} } \\ \end{array} } \right) _{(j)}^{(l)} = \left( {\begin{array}{*{20}c} {M_1 } \\ {M_{12} } \\ \end{array} } \right) _{(j)}^{(l)} + \sum \limits _{i = 1}^4 {\left( {\begin{array}{*{20}c} {K_{(u)ij}^{(0)(l = 2)} N_{1(i)}^{(l)} } \\ {K_{(v)ij}^{(0)(l = 2)} N_{12(i)}^{(l)} } \\ \end{array} } \right) } ,\quad j = 1..4, \end{aligned}$$
    (47)

    where it is important to highlight that the multiplicator matrices of the undelaminated region (\(l=2\)) are equally involved for both sides of the equation [69]. Equation (46) means eight conditions. If the SST or TST theories are considered, then six conditions are formulated against the equivalent stress resultants:

    $$\begin{aligned} \left. {\left( {\begin{array}{*{20}c} {{\hat{M}}_{(u)12} } \\ {{\hat{M}}_{(u)34} } \\ {{\hat{M}}_{(v)12} } \\ {{\hat{M}}_{(v)34} } \\ {{\hat{L}}_{(u)1234} } \\ {{\hat{L}}_{(v)1234} } \\ \end{array} } \right) _{(j)}^{(1)} } \right| _{x = + 0} \left. { = \left( {\begin{array}{*{20}c} {{\hat{M}}_{(u)12} } \\ {{\hat{M}}_{(u)34} } \\ {{\hat{M}}_{(v)12} } \\ {{\hat{M}}_{(v)34} } \\ {{\hat{L}}_{(u)1234} } \\ {{\hat{L}}_{(v)1234} } \\ \end{array} } \right) _{(j)}^{(2)} } \right| _{x = - 0} \end{aligned}$$
    (48)

    where:

    $$\begin{aligned} {\hat{M}}_{(u)12}^{(l)}= & {} \sum \limits _{i = 1}^2 {\left( {\begin{array}{*{20}c} {K_{(u)i1}^{(0)} + K_{(u)i3}^{(0)} } \\ {K_{(u)i1}^{(1)} + K_{(u)i3}^{(1)} } \\ {K_{(u)i1}^{(2)} + K_{(u)i3}^{(2)} } \\ {K_{(u)i1}^{(3)} + K_{(u)i3}^{(3)} } \\ \end{array} } \right) ^{(l = 2)} \left( {\begin{array}{*{20}c} {N_{1(i)} } &{} {M_{1(i)} } &{} {L_{1(i)} } &{} {P_{1(i)} } \\ \end{array} } \right) ^{(l)}} \end{aligned}$$
    (49)
    $$\begin{aligned} {\hat{M}}_{(u)34}^{(l)}= & {} \sum \limits _{i = 3}^4 {\left( {\begin{array}{*{20}c} {K_{(u)i1}^{(0)} + K_{(u)i3}^{(0)} } \\ {K_{(u)i1}^{(1)} + K_{(u)i3}^{(1)} } \\ {K_{(u)i1}^{(2)} + K_{(u)i3}^{(2)} } \\ {K_{(u)i1}^{(3)} + K_{(u)i3}^{(3)} } \\ \end{array} } \right) ^{(l = 2)} \left( {\begin{array}{*{20}c} {N_{1(i)} } &{} {M_{1(i)} } &{} {L_{1(i)} } &{} {P_{1(i)} } \\ \end{array} } \right) ^{(l)} } \end{aligned}$$
    (50)
    $$\begin{aligned} {\hat{M}}_{(v)12}^{(l)}= & {} \sum \limits _{i = 1}^2 {\left( {\begin{array}{*{20}c} {K_{(v)i1}^{(0)} + K_{(v)i3}^{(0)} } \\ {K_{(v)i1}^{(1)} + K_{(v)i3}^{(1)} } \\ {K_{(v)i1}^{(2)} + K_{(v)i3}^{(2)} } \\ {K_{(v)i1}^{(3)} + K_{(v)i3}^{(3)} } \\ \end{array} } \right) ^{(l = 2)} \left( {\begin{array}{*{20}c} {N_{12(i)} } &{} {M_{12(i)} } &{} {L_{12(i)} } &{} {P_{12(i)} } \\ \end{array} } \right) ^{(l)} } \end{aligned}$$
    (51)
    $$\begin{aligned} {\hat{M}}_{(v)34}^{(l)}= & {} \sum \limits _{i = 3}^4 {\left( {\begin{array}{*{20}c} {K_{(v)i1}^{(0)} + K_{(v)i3}^{(0)} } \\ {K_{(v)i1}^{(1)} + K_{(v)i3}^{(1)} } \\ {K_{(v)i1}^{(2)} + K_{(v)i3}^{(2)} } \\ {K_{(v)i1}^{(3)} + K_{(v)i3}^{(3)} } \\ \end{array} } \right) ^{(l = 2)} \left( {\begin{array}{*{20}c} {N_{12(i)} } &{} {M_{12(i)} } &{} {L_{12(i)} } &{} {P_{12(i)} } \\ \end{array} } \right) ^{(l)} } \end{aligned}$$
    (52)
    $$\begin{aligned} {\hat{L}}_{(u)1234}^{(l)}= & {} \sum \limits _{i = 1}^4 {\left( {\begin{array}{*{20}c} {K_{(u)i2}^{(0)} + K_{(u)i4}^{(0)} } \\ {K_{(u)i2}^{(1)} + K_{(u)i4}^{(1)} } \\ {K_{(u)i2}^{(2)} + K_{(u)i4}^{(2)} } \\ {K_{(u)i2}^{(3)} + K_{(u)i4}^{(3)} } \\ \end{array} } \right) ^{(l = 2)} \left( {\begin{array}{*{20}c} {N_{1(i)} } &{} {M_{1(i)} } &{} {L_{1(i)} } &{} {P_{1(i)} } \\ \end{array} } \right) ^{(l)} } \end{aligned}$$
    (53)
    $$\begin{aligned} {\hat{L}}_{(v)1234}^{(l)}= & {} \sum \limits _{i = 1}^4 {\left( {\begin{array}{*{20}c} {K_{(v)i2}^{(0)} + K_{(v)i4}^{(0)} } \\ {K_{(v)i2}^{(1)} + K_{(v)i4}^{(1)} } \\ {K_{(v)i2}^{(2)} + K_{(v)i4}^{(2)} } \\ {K_{(v)i2}^{(3)} + K_{(v)i4}^{(3)} } \\ \end{array} } \right) ^{(l = 2)} \left( {\begin{array}{*{20}c} {N_{12(i)} } &{} {M_{12(i)} } &{} {L_{12(i)} } &{} {P_{12(i)} } \\ \end{array} } \right) ^{(l)} } \end{aligned}$$
    (54)

    where \(l=1\) or 2 but again \(l=2\) is fixed for the multiplicator matrices and refers to the undelaminated region.

The continuity conditions between regions - and - for the problems in Fig. 4 are imposed by :

$$\begin{aligned} \begin{array}{*{20}l} {\left. {g_\beta ^{(1)} } \right| _{x = x_Q - d_0 } = \left. {g_\beta ^{(1q)} } \right| _{x = x_Q - d_0 } ,} \\ {\left. {g_\gamma ^{(1)} } \right| _{x = x_Q - d_0 } = \left. {g_\gamma ^{(1q)} } \right| _{x = x_Q - d_0 } ,} \\ {\left. {g_\beta ^{(1q)} } \right| _{x = x_Q + d_0 } = \left. {g_\beta ^{(1a)} } \right| _{x = x_Q + d_0 } ,} \\ {\left. {g_\gamma ^{(1q)} } \right| _{x = x_Q + d_0 } = \left. {g_\gamma ^{(1a)} } \right| _{x = x_Q + d_0 } ,} \\ \end{array} \end{aligned}$$
(55)

where the parameter sets are [21]:

$$\begin{aligned} g_\beta ^{(l)}= & {} (w,\frac{{\partial w}}{{\partial x}},.....,u_{0b} ,u_{0t} ,v_{0b} ,v_{0t} ,\psi _{(p)j} ;j = 1..q_l ), \quad p=1,2, \nonumber \\ g_\gamma ^{(l)}= & {} \left. {\left( {\sum \limits _{i = 1} ^{2 } {\mathbf{N }_i^{(1,12)} } , \sum \limits _{i = 3} ^{4} {\mathbf{N }_i^{(1,12)} } ,\mathbf{M }_i^{(1,12)}..,\mathbf{L }_i^{(1,12)}..,\mathbf{P }_i^{(1,12)}..} \right) } \right| ^{(l)}, \end{aligned}$$
(56)

where \(i = 1..4\) if not fixed. It is important to note that Eqs.(55) and (56) depend on the applied theory. As a matter of fact, for the FST model the conditions against \(\mathbf{N }\) and \(\mathbf{M }\) should be imposed, for the SST and TST even the condition with respect to \(\mathbf{L }\) is required.

5.2 Boundary conditions

The boundary conditions of the problems in Fig. 4 for the SST and TST models are detailed here. The boundary conditions are imposed at region in Fig. 4 as:

$$\begin{aligned}&{\left. {(w,v_{0b} ,v_{0t} ,\theta _{(\xi _2)2} ,\theta _{(\xi _2)4} , \phi _{(\xi _2)4} )} \right| _{x = a}^{(1a)} = 0}, \nonumber \\&\quad {\left. {\left( \sum \limits _{i = 1}^2 {N_{1(i)} } ,\sum \limits _{i = 3}^4 {N_{1(i)}}\right) } \right| _{x = a}^{(1a)} = 0}, \nonumber \\&{\quad \left. {(M_{1(1)}+M_{1(2)} ,M_{1(3)} +M_{1(4)} ,L_{1(4)}) } \right| _{x = a}^{(1a)} = 0}. \end{aligned}$$
(57)

For region , the conditions are:

$$\begin{aligned}&{\left. (w,v_0 ,\theta _{ (\xi _2)1},\phi _{(\xi _2)2} ,\theta _{(\xi _2)4} ,\phi _{(\xi _2)4}) \right| _{x = - c}^{(2)} = 0}, \nonumber \\&\quad {\left. {\bigg (\sum \limits _{i = 1}^4 {N_{1(i)} } ,M_{1(1)}+M_{1(2)} ,M_{1(3)}+M_{1(4)} ,L_{1(2)},L_{1(4)} \bigg ) } \right| _{x = - c}^{(2)} = 0}. \end{aligned}$$
(58)

For the SST and FST theories, the boundary conditions can be obtained similarly (refer to [21]).

6 Finite element model

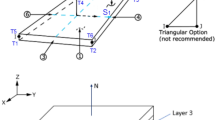
In the next subsections, the solution of the problems in Fig. 4 is presented. The lay-up of the shell is given by Fig. 1, and the elastic properties of layers are listed in Table 3. The finite element models of the delaminated elliptic and hyperbolic shells were also created in ANSYS environment using 3D isoparametric SOLID elements with linear interpolation, and the mechanical fields were calculated. The FE model employed to determine the transverse displacement and energy release rates is shown in Fig. 5. In the vicinity of the delamination, tip mesh refinement was done, as it can be seen in Fig. 5. The energy release rates are determined by the virtual crack closure technique (VCCT) [70, 71]. The crack tip element sizes were: \(\Delta \xi _1\)=0.25 mm, \(\Delta \xi _2\)=1.015 mm and \(\Delta \zeta \)=0.25 mm. mm, respectively. These values were determined in accordance with the recommendations of the literature meaning that \(\Delta \xi _1\) and \(\Delta \zeta \) should be between one quarter and one half of the thickness of one layer, which is 0.5 mm (refer to Fig. 1). [70, 72] . To determine the distribution of displacements and stresses over the thickness, the mesh shown in Fig. 4 was refined and the number of elements was twice of the original mesh in each direction. The two different meshes resulted in essentially the same transverse displacements.

The geometrical data are: \(a=105\) mm, \(b=100\) mm, \(c=45\) mm and \(x_Q = 31\) mm. The load is \(F=1000\) N. The lay-up of the plate is \([\pm 45^{f}/ 0 /\pm 45^{f}_2/ {\bar{0}} ]_S\), which is shown in Fig. 1. The radii of curvatures were \(R_1=300\), \(R_2=200\) for the elliptic shell and \(R_1=300\), \(R_2=-200\) for the hyperbolic shell ([mm]), respectively.

Table 3 Elastic properties of single carbon/epoxy composite laminates
Full size table
Fig. 5
figure 5

3D FE model of an elliptic composite shell with delamination

Full size image

7 Results and discussions

Results are presented for the mechanical fields (displacement and stress) as well as for the ERRs and mode mixities. The effect of shell geometry and delamination position on the results is demonstrated.

Fig. 6
figure 6

Comparison of deflections at \(Y=b/2\) determined by FE analysis FST, SST and TST for elliptic shells, case I (a) and case III (b)

Full size image

7.1 Displacement and stress fields

In this subsection, the results of the developed analytical model and those of the 3D FE model are compared to each other. The main aspect is the verification of the analytical model. The deflection of the middle curve (\(y=b/2\)) of the mid-surface of the shell is plotted in Fig. 6 for the elliptical shell (\(R_1=300\) mm, \(R_2 =200\) mm) including cases I and III (refer to Fig. 1). The agreement with the numerical results is undeniably good. Out of the three theories, the highest displacement is provided by the TST model, it is followed by the SST and the FST is placed third for both cases I and III. If the shell mid-surface is hyperbolic (\(R_1=300\) mm, \(R_2 =-200\) mm), then the results for cases II and IV presented in Fig. 7 were obtained. The agreement between analytical and numerical results is again quite good. However, the ranking of the theories turns about, and this time the FST theory gives the highest deflection at each point, the runner-up is the SST theory, and finally, the TST is placed third, respectively.

In many previous works, the deflection function was a primary indicator to assess the accuracy of a plate theory [56, 57]. Following this concept, each theory seems definitely to have sufficient accuracy compared to the FE model. The next stage is to elaborate how the in-surface displacements, the normal and shear stresses are distributed over the thickness of shell. For this aim, some specified points are assigned on the mid-surface of the shell.

Fig. 7
figure 7

Comparison of deflections at \(Y=b/2\) determined by FE analysis FST, SST and TST for hyperbolic shells, case I (a) and case III (b)

Full size image
Fig. 8
figure 8

Distribution of in-surface displacements (u, v) and normal stresses (\(\sigma _1\), \(\sigma _2\)) over the thickness, case I, elliptic shell

Full size image

The in-surface displacements and the normal stresses are shown in Fig. 8 for case I if the shell is elliptic. The location of the points the distributions are created in the vicinity of can be found by reading the coordinates of the horizontal axis labels. The left fragment of the figure indicates the lay-up and the location of delamination as well. The analytical model follows very well the set of points by FE solution (u displacement) in Fig. 8. Also, the normal stress (\(\sigma _1\)) is captured excellently by each theory, which is piecewise continuous, as expected. The v displacement is shown in the bottom of Fig. 8 indicating that there is no difference between the results by three shell theories; however, the membrane displacement (or simply the value at the mid-surface) is apparently higher by FE solution than it is predicted by the shell theories. The distributions of the normal stress, \(\sigma _2\), are placed again in the bottom of the figure including good agreement between the different solutions. Figure 9 brings the shear stresses, \(\tau _{1\zeta }\) and \(\tau _{2\zeta }\) into the stage. The peak by the FE solution takes place at the delamination tip, this cannot be reproduced by the analytical models, and what is more, the latter is essentially a non-singular solution [56, 57].

Fig. 9
figure 9

Distribution of shear stresses (\(\tau _{1\zeta }\), \(\tau _{2\zeta }\)) over the thickness, case I, elliptic shell

Full size image
Fig. 10
figure 10

Distribution of in-surface displacements (u, v) and normal stresses (\(\sigma _1\), \(\sigma _2\)) over the thickness, case III, elliptic shell

Full size image

The distributions for case III are shown in Figs. 10 and 11. Considering the in-surface u displacement, the FST theory seems to follow the FE solution better than the SST and TST. The latter two theories result in a significant perturbation at ESL3 and ESL4. Similarly to case I in Fig. 8, the membrane part of the v displacement component is notably smaller than that by FE solution. Finally, the approximation of both normal stresses in Fig. 10 is apparently good, and the difference between the FST, SST and TST is negligible. Figure 11 presents the shear stresses along the thickness at some specified locations of the mid-surface. The agreement between the analysis and numerical model is bad again.

Fig. 11
figure 11

Distribution of shear stresses (\(\tau _{1\zeta }\), \(\tau _{2\zeta }\)) over the thickness, case III, elliptic shell

Full size image
Fig. 12
figure 12

Distribution of in-surface displacements (u, v) and normal stresses (\(\sigma _1\), \(\sigma _2\)) over the thickness, case II, hyperbolic shell

Full size image

To elaborate how the radii of curvatures influence the field parameters, a hyperbolic shell is analyzed as well (\(R_1=300\) mm, \(R_2=-200\) mm). Cases II and IV are chosen to demonstrate the results. Taking Fig. 12 and case II into consideration, the overall agreement is essentially very good between the analysis and FE calculation results from the standpoint of each parameter. The shear stresses shown by Fig. 13 provide again bad agreement. At this stage, the ability of the proposed models to capture the shear stresses accurately seems to be insufficient, and this will be commented later. To finalize this subsection, Figs. 14 and 15 for case IV are brought to the scene and these figures emphasize the accuracy of the models in describing the displacements and normal stresses. The shear stresses demonstrated in Fig. 15 seem to fit better the FE solution; however, the outstanding peak by the SST and TST taking place in ESL4 is significant.

Fig. 13
figure 13

Distribution of shear stresses (\(\tau _{1\zeta }\), \(\tau _{2\zeta }\)) over the thickness, case II, hyperbolic shell

Full size image
Fig. 14
figure 14

Distribution of in-surface displacements (u, v) and normal stresses (\(\sigma _1\), \(\sigma _2\)) over the thickness, case IV, hyperbolic shell

Full size image
Fig. 15
figure 15

Distribution of shear stresses (\(\tau _{1\zeta }\), \(\tau _{2\zeta }\)) over the thickness, case IV, hyperbolic shell

Full size image

7.2 Energy release rates and mode-mixity

The energy release rate is equivalent to the J-integral under quasi-static conditions and linear elastic material [73]. Because of the constrained mode model \(G_I =0\) and mixed mode II/III fracture conditions are involved. The required calculation can be performed based on the previous works of the author [56, 57], and thus, no details are given here. The mode-II J-integral becomes:

$$\begin{aligned} \begin{array}{*{20}c} {J_{II} = \frac{1}{2}\sum \limits _{i = 1}^k {\left\{ \right. } } &{} {(}N_{1(i)} \left. {\varepsilon _{1(i)}^{(0)} } \right| _{x = + 0}^{(1)} &{} { - N_{1(i)} \left. {\varepsilon _{1(i)}^{(0)} } \right| _{x = - 0}^{(2)} )} - \\ &{}{ (N_{2(i)} \left. {\varepsilon _{2(i)}^{(0)} } \right| _{x = + 0}^{(1)} } &{} { - N_{2(i)} \left. {\varepsilon _{2(i)}^{(0)} } \right| _{x = - 0}^{(2)} )} + \\ {} &{} {(M_{1(i)} \left. {\varepsilon _{1(i)}^{(1)} } \right| _{x = + 0}^{(1)} } &{} { - M_{1(i)} \left. {\varepsilon _{1(i)}^{(1)} } \right| _{x = - 0}^{(2)} )} - \\ &{} {(M_{2(i)} \left. {\varepsilon _{2(i)}^{(1)} } \right| _{x = + 0}^{(1)} } &{} { - M_{2(i)} \left. {\varepsilon _{2(i)}^{(2)} } \right| _{x = - 0}^{(2)} )} + \\ {} &{} {(L_{1(i)} \left. {\varepsilon _{1(i)}^{(2)} } \right| _{x = + 0}^{(1)} } &{} { - L_{1(i)} \left. {\varepsilon _{1(i)}^{(2)} } \right| _{x = - 0}^{(2)} )} - \\ &{} {(L_{2(i)} \left. {\varepsilon _{2(i)}^{(2)} } \right| _{x = + 0}^{(1)} } &{} { - L_{2(i)} \left. {\varepsilon _{2(i)}^{(2)} } \right| _{x = - 0}^{(2)} )} + \\ {} &{} {(P_{1(i)} \left. {\varepsilon _{1(i)}^{(3)} } \right| _{x = + 0}^{(1)} } &{} { - P_{1(i)} \left. {\varepsilon _{1(i)}^{(3)} } \right| _{x = - 0}^{(2)} )} - \\ &{} {(P_{2(i)} \left. {\varepsilon _{2(i)}^{(3)} } \right| _{x = + 0}^{(1)} } &{} { - P_{2(i)} \left. {\varepsilon _{2(i)}^{(3)} } \right| _{x = - 0}^{(2)} )} \left. \right\} , \\ \end{array} \end{aligned}$$
(59)

where \(k=4\) because the method of 4ESLs is applied. The stress resultants are determined by Eqs. (33)–(34). The mode-III J-integral is:

$$\begin{aligned} \begin{array}{*{20}c} {J_{III} = - \frac{1}{2}\sum \limits _{i = 1}^k {\left\{ {} \right. } } &{} { (N_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(0)} } \right| _{x = + 0}^{(1)} } &{} { - N_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(0)} } \right| _{x = - 0}^{(2)} ) + } \\ &{} {(M_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(1)} } \right| _{x = + 0}^{(1)} } &{} { - M_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(1)} } \right| _{x = - 0}^{(2)} ) + } \\ {} &{} {(L_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(2)} } \right| _{x = + 0}^{(1)} } &{} { - L_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(2)} } \right| _{x = - 0}^{(2)} ) + } \\ {} &{} {(P_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(3)} } \right| _{x = + 0}^{(1)} } &{} { - P_{12(i)} \left. {{\hat{\gamma }} _{12(i)}^{(3)} } \right| _{x = - 0}^{(2)} )} \left. \right\} , \\ \end{array} \end{aligned}$$
(60)

where \(k=4\) and:

$$\begin{aligned} {\hat{\gamma }} _{12(i)}^{(q)} = \frac{{\partial u_{(i)}^{(q)} }}{{\partial y}} - \frac{{\partial v_{(i)}^{(q)} }}{{\partial x}},\quad q = 0,1,2,3, \end{aligned}$$
(61)

are the so-called conjugate shear strains. Equations (59)–(61) are valid up to the third-order shells and plates; however, it is easy to generalize for nth order shells and plates as well. Previously, the deflection and the comparison stage with FE computation results was assigned to be the primary indicator to assess the accuracy and sufficiency of the theories. The secondary indicator is the distribution of ERRs along the delamination front and its relation to the FE calculations performed by the VCCT. It is reasonable to mention that other path invariant integrals are available to characterize singularities in electromagnetic and hydrodynamic fields [74, 75].

Fig. 16
figure 16

Distribution of ERRs and mode mixity along the delamination front, case I, elliptic shell

Full size image
Fig. 17
figure 17

Distribution of ERRs and mode mixity along the delamination front, case II, elliptic shell

Full size image

In the sequel, the results for elliptic and hyperbolic shells are presented. Figure 16 plots the results for case I and when the shell is elliptic. The analytical models fit well the numerical set of points, and there are only minor differences between the different theories. The mode ratios are also calculated, and in each figure, \(G_T = G_{II} + G_{III}\) is the total ERR. It is seen that the agreement between analytical and numerical solutions decreases significantly near the edges and it is around the middle the solutions agree at. Case II is summarized in Fig. 17 providing an excellent agreement between the different methods. Very briefly, the results for cases III and IV are shown in Figs. 18 and 19 proving again the suitability of the proposed models for the solution of shell problems with delamination.

Fig. 18
figure 18

Distribution of ERRs and mode mixity along the delamination front, case III, elliptic shell

Full size image
Fig. 19
figure 19

Distribution of ERRs and mode mixity along the delamination front, case IV, elliptic shell

Full size image
Fig. 20
figure 20

Distribution of ERRs and mode mixity along the delamination front, case I, hyperbolic shell

Full size image
Fig. 21
figure 21

Distribution of ERRs and mode mixity along the delamination front, case II, hyperbolic shell

Full size image

The hyperbolic shells are also taken into account. In accordance with Figs. 20 and 21, the results are promising again and they match excellently with the FE results from each point of view (ERR and mode mixity). However, looking at Fig. 22, it is clear that the accuracy of the models declines from the point of view of mode-II ERR. In this respect, the SST and TST theories are better than the FST. At the same time, the mode-III ERR is correctly determined by each theory. Continuing with Fig. 23, it is again the mode-II component that is captured by less correctly compared to the mode-III component, which is still well captivated. The possible reasons for the bad agreement experienced through cases III and IV for the hyperbolic shell are difficult to figure out. On the one hand, the FE mesh and crack tip element size were the same for the elliptic and hyperbolic shells; thus, it is likely not a FE convergence problem. This can be admitted by especially considering the fact that the ERR oscillates with the crack tip element size and the literature recommendations were met in this work [70, 72]. On the other hand, the mismatch was not observed in the case of mode-III ERR at all, and this implies again that the local FE mesh is probably not the crucial factor causing the disagreement. Apparently, more work is required to resolve this discrepancy. Finally, it can also be concluded that although the transverse shear stresses by numerical and analytical solutions did not agree, the two methods are based on very different considerations [56, 57]. In the FE models, the shear stress distribution is governed by two major aspects. First, the delamination tip is a singular-type point involving significant stress concentration. Second, the dynamic boundary condition is approximately satisfied at the top and bottom surfaces, and the higher the number of elements is, the rather the dynamic boundary condition (zero shear stress) satisfied is. In contrast, the analytical solution is non-singular, and the shear stress distribution is governed by the fact that the areas under the shear stress distributions are equal to the shear forces. Thus, no correlation can be established between the accuracy of ERRs and shear stresses.

Fig. 22
figure 22

Distribution of ERRs and mode mixity along the delamination front, case III, hyperbolic shell

Full size image
Fig. 23
figure 23

Distribution of ERRs and mode mixity along the delamination front, case IV, hyperbolic shell

Full size image

8 Conclusions

In this work, the first-, second- and third-order shell theories were applied to delaminated elliptic and hyperbolic shells made out of composite material. The mathematical model was derived for the undelaminated and delaminated parts as well using the principle of virtual work. The set of equilibrium equations was solved by the Lévy formulation and the state space method involving simply supported edges. In the next step, the generalized boundary and continuity conditions were also provided and some important improvements were done as compared to some previous works dealing with delaminated composite plates. The mechanical fields, namely the displacement and stress, were determined, and the results were compared to spatial finite element calculations.

Based on the work carried out in this paper, the following conclusions can be drawn. The deflection of the shell was captured accurately by the proposed models; thus, it is considered to be a primary indicator to assess the accuracy of a possible model. Moreover, there were only negligible differences among the different shell theories in capturing the deflection independently of whether the shell was elliptic or hyperbolic. The in-surface displacements were calculated with sufficient accuracy. Nevertheless, it is important to note that the displacement distributions were significantly perturbated by the delamination front. From the point of view of stresses, the agreement was very good for the normal stresses, but it was less satisfactory for the transverse shear stresses. In the final stage, the energy release rates and mode mixities were computed and the ERR was assigned to be the secondary indicator to assess the accuracy of the proposed models. Out of the four cases investigated, each provided very good agreement with the finite element solution if the shell was elliptic. If the shell was hyperbolic, then a moderate reduction in the accuracy was found in case III, and a significant one was experienced for case IV; however, this effect was recognized only regarding the mode-II component and not the mode-III one at all. The main outcome of this work is the following. The solution by the developed models can be accurate even if the transverse shear stresses do not agree with the FE results. Out of the three shell theories, the second-order model seems to be reasonable to be the candidate for a possible shell finite element. This statement can be justified by the facts that the size of mathematical model is smaller than that of the first-order theory, it is the same as that of third-order model, and in the crucial cases (case II and IV for the hyperbolic shell), its performance was a little bit better than that of the first-order theory. The possible application field of the presented models is to model plated fracture specimens [76,77,78].