Abstract
This paper introduces the paired lasso: a generalisation of the lasso for paired covariate settings. Our aim is to predict a single response from two high-dimensional covariate sets. We assume a one-to-one correspondence between the covariate sets, with each covariate in one set forming a pair with a covariate in the other set. Paired covariates arise, for example, when two transformations of the same data are available. It is often unknown which of the two covariate sets leads to better predictions, or whether the two covariate sets complement each other. The paired lasso addresses this problem by weighting the covariates to improve the selection from the covariate sets and the covariate pairs. It thereby combines information from both covariate sets and accounts for the paired structure. We tested the paired lasso on more than 2000 classification problems with experimental genomics data, and found that for estimating sparse but predictive models, the paired lasso outperforms the standard and the adaptive lasso. The R package palasso is available from cran.
Similar content being viewed by others
1 Background
Lasso regression has become a popular method for variable selection and prediction. Among other things, it extends generalised linear models to settings with more covariates than samples. The lasso shrinks the coefficients towards zero, setting some coefficients equal to zero. Compared to the standard lasso, the adaptive lasso shrinks large coefficients less. In high-dimensional spaces, most coefficients are set to zero, since the number of non-zero coefficients is bounded by the sample size (Zou and Hastie 2005). It is possible to decrease the maximum number of non-zero coefficients, and estimate the coefficients given this sparsity constraint. By including fewer covariates, the resulting model may be less predictive but more practical and interpretable. Given an efficient algorithm that produces the regularisation path, we can extract models of different sizes without increasing the computational cost.
Paired covariates arise in many applications. Possible origins include two measurements of the same attributes, and two transformations of the same measurements. The covariates are then in two sets, with each covariate in one set forming a pair with a covariate in the other set. These covariate sets may be strongly correlated. Naively, we could either exclude one of the two sets or ignore the paired structure. However, we want to include both sets, and account for the paired structure. Such a compromise potentially improves predictions.
Our motivating example is to predict a binary response from microrna isoform (isomir) expression quantification data. Micrornas help to regulate gene expression and are dysregulated in cancer. Typically, most raw counts from such sequencing experiments equal zero. Different transformations of rna sequencing data lead to different predictive abilities (Zwiener et al. 2014), and knowledge about the presence or absence of an isomir might be more predictive than its actual expression level (Telonis et al. 2017). We hypothesise that combining two transformations of isomir data, namely a count and a binary representation, improves predictions. We also analysed other molecular profiles to show the generality of our approach.
The paired lasso, like the group lasso (Yuan and Lin 2006) and the fused lasso (Tibshirani et al. 2005), is an extension of the lasso for a specific covariate structure. If the covariates are split into groups, we could use the group lasso to select groups of covariates. If the covariates have a meaningful order, we could use the fused lasso to estimate similar coefficients for close covariates. And if there are paired covariates, we recommend the paired lasso to weight among and within the covariate pairs.
Our aim is to create a sparse model for paired covariates. The paired lasso exploits not only both covariate sets but also the structure between them. We demonstrate that it outperforms the standard and the adaptive lasso in a number of settings, while also showing its limitations.
In the following, we introduce paired covariate settings and the paired lasso (Sect. 2), classify cancer types based on two transformations of the same molecular data (Sect. 3), discuss sparsity constraints and potential applications to other paired settings (Sect. 4), and predict survival from gene expression in tumour and normal tissue (see appendix).
2 Method
2.1 Setting
Data are available for n samples, one response and twice p covariates. We allow for continuous, discrete, binary and survival responses. We assume all covariates are standardised, and the setting is high-dimensional (\({p \gg n}\)). Let the \({n \times 1}\) vector \({\varvec{y}}\) represent the response, the \({n \times p}\) matrix  the first covariate set, and the \({n \times p}\) matrix
the first covariate set, and the \({n \times p}\) matrix  the second covariate set:
the second covariate set:

The one-to-one correspondence between  and
and  gives rise to paired covariates. In practice, the two covariate sets may represent different transformations of the same data. For each j in \(\{1,\ldots ,p\}\), the \({n \times 1}\) covariate vectors
gives rise to paired covariates. In practice, the two covariate sets may represent different transformations of the same data. For each j in \(\{1,\ldots ,p\}\), the \({n \times 1}\) covariate vectors  and
and  represent one covariate pair.
represent one covariate pair.
We relate the response to the covariates through a generalised linear model. The linear predictor for any sample i in \(\{1,\ldots ,n\}\) equals

where \(\alpha \) is the unknown intercept, and  and
and  are the unknown regression coefficients. We want to estimate a model with a limited number of non-zero coefficients (e.g.
are the unknown regression coefficients. We want to estimate a model with a limited number of non-zero coefficients (e.g.  ). Our ambition is to select the most predictive model given such a sparsity constraint. Although additional covariates could improve predictions, many applications require small model sizes.
). Our ambition is to select the most predictive model given such a sparsity constraint. Although additional covariates could improve predictions, many applications require small model sizes.
Such models can be estimated by penalised maximum likelihood, i.e. by finding

where  is the likelihood which depends on the regression model (e.g. linear, logistic) and
is the likelihood which depends on the regression model (e.g. linear, logistic) and  is a penalty function, which we denote shortly by \(\rho (\lambda )\) in the remainder. Unlike ridge regularisation, lasso regularisation implies variable selection. The standard lasso (Tibshirani 1996) and the adaptive lasso (Zou 2006) have the penalty terms
is a penalty function, which we denote shortly by \(\rho (\lambda )\) in the remainder. Unlike ridge regularisation, lasso regularisation implies variable selection. The standard lasso (Tibshirani 1996) and the adaptive lasso (Zou 2006) have the penalty terms

respectively, where the parameter \(\lambda \) and all estimates  and
and  are non-negative. The regularisation parameter \(\lambda \) makes a compromise between the unpenalised model (\({\lambda =0}\)) and the intercept-only model (\({\lambda \rightarrow \infty }\)). Increasing \(\lambda \) decreases the number of non-zero coefficients. The purpose of the adaptive lasso is consistent variable selection and optimal coefficient estimation (Zou 2006). It requires the initial estimates
are non-negative. The regularisation parameter \(\lambda \) makes a compromise between the unpenalised model (\({\lambda =0}\)) and the intercept-only model (\({\lambda \rightarrow \infty }\)). Increasing \(\lambda \) decreases the number of non-zero coefficients. The purpose of the adaptive lasso is consistent variable selection and optimal coefficient estimation (Zou 2006). It requires the initial estimates  and
and  (see below) for weighting the covariates. In high-dimensional settings, the adaptive lasso can have a similar predictive performance to the standard lasso while including less covariates (Huang et al. 2008). This makes the adaptive lasso promising for estimating sparse models.
(see below) for weighting the covariates. In high-dimensional settings, the adaptive lasso can have a similar predictive performance to the standard lasso while including less covariates (Huang et al. 2008). This makes the adaptive lasso promising for estimating sparse models.
2.2 Paired lasso
For the standard and the adaptive lasso, we have to decide whether the model should exploit  ,
,  , or both. If we included only one covariate set, we would loose the information in the other covariate set. If we included both covariate sets, we would double the dimensionality and still ignore the paired structure. In contrast, the paired lasso exploits both covariate sets, and accounts for the paired structure.
, or both. If we included only one covariate set, we would loose the information in the other covariate set. If we included both covariate sets, we would double the dimensionality and still ignore the paired structure. In contrast, the paired lasso exploits both covariate sets, and accounts for the paired structure.
We achieve this by choosing among four different weighting schemes: (1) within covariate set  , (2) within covariate set
, (2) within covariate set  , (3) among all covariates, or (4) among and within covariate pairs. The tuning parameter
, (3) among all covariates, or (4) among and within covariate pairs. The tuning parameter  determines the weighting scheme. Each
determines the weighting scheme. Each  in
in  leads to different weights
leads to different weights  and
and  for covariates
for covariates  and
and  , for any pair j:
, for any pair j:

where  and
and  are some initial estimates (see below). Figure 1 illustrates the four weighting schemes, by showing the sets of weights emanating from some initial estimates. The first three schemes are fallbacks to the adaptive lasso based on
are some initial estimates (see below). Figure 1 illustrates the four weighting schemes, by showing the sets of weights emanating from some initial estimates. The first three schemes are fallbacks to the adaptive lasso based on  (
( ),
),  (
( ), or both (
), or both ( ). The pairwise-adaptive scheme (
). The pairwise-adaptive scheme ( ) is novel: it weights among and within covariate pairs. It depends on the data which weighting scheme leads to the most predictive model.
) is novel: it weights among and within covariate pairs. It depends on the data which weighting scheme leads to the most predictive model.
Weighting schemes. The marginal effects of the covariates on the response determine the four weighting schemes. Each covariate pair (y-axis) receives weights for both parts (x-axis), here for simulated data. The first two schemes exclude one of the covariates sets, the third scheme treats them equally, and the fourth scheme weights among and within covariate pairs. The paired lasso chooses the most suitable weighting scheme for the data
Leaving the weighting scheme  free, we weight the covariates in the penalty term
free, we weight the covariates in the penalty term

where \(\lambda \ge 0\) and  . All weights
. All weights  and
and  are in the unit interval. The inverse weights serve as penalty factors. Covariate
are in the unit interval. The inverse weights serve as penalty factors. Covariate  has the penalty factor
has the penalty factor  , and covariate
, and covariate  has the penalty factor
has the penalty factor  . By receiving infinite penalty factors, covariates with zero weight are automatically excluded. While methods like GRridge (van de Wiel et al. 2016) and ipflasso (Boulesteix et al. 2017) adapt penalisation to covariate sets, our penalty factors are covariate-specific. The penalty increases with both coefficients
. By receiving infinite penalty factors, covariates with zero weight are automatically excluded. While methods like GRridge (van de Wiel et al. 2016) and ipflasso (Boulesteix et al. 2017) adapt penalisation to covariate sets, our penalty factors are covariate-specific. The penalty increases with both coefficients  and
and  , but more with the one that has a larger penalty factor. We can thereby penalise the covariates asymmetrically: less if presumably important, and more if presumably unimportant.
, but more with the one that has a larger penalty factor. We can thereby penalise the covariates asymmetrically: less if presumably important, and more if presumably unimportant.
Exploiting the efficient procedure for penalised maximum likelihood estimation from glmnet (Friedman et al. 2010), we use internal cross-validation to select \(\lambda \) from 100 candidates, and to select  from four candidates. To avoid overfitting, we estimate the weights in each internal cross-validation iteration. The tuning parameter
from four candidates. To avoid overfitting, we estimate the weights in each internal cross-validation iteration. The tuning parameter  governs the type of weighting, and the tuning parameter \(\lambda \) determines the amount of regularisation. Despite the covariate-specific penalty factors, the paired lasso is only four times as computationally expensive as the standard lasso. Unlike cross-validating the weighting scheme, cross-validating all weights in
governs the type of weighting, and the tuning parameter \(\lambda \) determines the amount of regularisation. Despite the covariate-specific penalty factors, the paired lasso is only four times as computationally expensive as the standard lasso. Unlike cross-validating the weighting scheme, cross-validating all weights in  and
and  would be computationally infeasible and likely prone to overfitting.
would be computationally infeasible and likely prone to overfitting.
2.3 Initial estimators
Inspired by the adaptive lasso (Zou 2006), we estimate the effects of the covariates on the response in two steps, obtaining the initial and the final estimates from the same data. Suggested initial estimates for the adaptive lasso in high-dimensional settings include absolute coefficients from ridge (Zou 2006), lasso (Bühlmann and van de Geer 2011) and simple (Huang et al. 2008) regression. Marginal estimates have several advantages over conditional estimates. First, estimating conditional effects is hard in high-dimensional settings with strongly correlated covariates. Conditional estimation strongly depends on the type of regularisation. Second, estimating marginal effects is computationally more efficient than estimating conditional effects. Third, we can easily improve the quality of the marginal estimates by empirical Bayes, because standard errors are available (Dey and Stephens 2018).
We can obtain marginal estimates from simple correlation or simple regression. Even if the covariates are standardised, logistic regression on binary covariates sometimes leads to extreme coefficients. Instead of adjusting regression coefficients for different standard errors, we use correlation coefficients. Their absolute values are between zero and one, and thus interpretable as weights. Fan and Lv (2008) also use correlation for screening covariates. For linear, logistic and Poisson regression, we calculate the absolute Pearson correlation coefficients between the response and the standardised covariates:

For Cox regression, we calculate the rescaled concordance indices between the right-censored survival time and the standardised covariates (\(C \rightarrow | 2 C - 1 |\)), which are interpretable as absolute correlation coefficients. To stabilise noisy estimates, we shrink  and
and  separately towards zero, using the adaptive correlation shrinkage from CorShrink (Dey and Stephens 2018). This procedure Fisher-transforms the correlation coefficients to standard scores (\(\rho \rightarrow \text {artanh}(\rho )\)), uses an asymptotic normal approximation, performs the shrinkage by empirical Bayes, and transforms the shrunken standard scores back (\(z \rightarrow \text {tanh}(z)\)). Empirical Bayes implies that the data determine the amount of shrinkage. We denote the shrunken estimates by
separately towards zero, using the adaptive correlation shrinkage from CorShrink (Dey and Stephens 2018). This procedure Fisher-transforms the correlation coefficients to standard scores (\(\rho \rightarrow \text {artanh}(\rho )\)), uses an asymptotic normal approximation, performs the shrinkage by empirical Bayes, and transforms the shrunken standard scores back (\(z \rightarrow \text {tanh}(z)\)). Empirical Bayes implies that the data determine the amount of shrinkage. We denote the shrunken estimates by  and
and  .
.
Although marginal and conditional effects of covariates may differ strongly, we conjecture covariates with strong marginal effects tend to be conditionally more important than those with weak marginal effects. Using the same hypothesis, Fan and Lv (2008) showed that reducing dimensionality by screening out covariates with weak marginal effects can improve model selection. For each combination of two covariates, we conjecture the one with the greater absolute correlation coefficient is conditionally more important than the other. Instead of comparing all coefficients at once, we compare them within the first covariate set, within the second covariate set, among all covariates, and simultaneously among and within the covariate pairs. These comparisons correspond to the four weighting schemes.
3 Results
We tested the paired lasso in 2048 binary classification problems. In each classification problem, we used one molecular profile to classify samples into two cancer types. Our paired covariates consist of two representations of the same molecular profile. We compared the paired lasso with the standard and the adaptive lasso.
3.1 Classification problems
Molecular tumour markers may improve cancer diagnosis, cancer staging and cancer prognosis. One may analyse blood or urine samples to detect cancer, classify cancer subtypes, predict disease progression, or predict treatment response. Because too few liquid biopsy data are available for reliably evaluating prediction models, we analyse tissue samples to classify cancer types, as a proof of concept. This is less clinically relevant, but allows a comprehensive comparison of models. The challenge is to select a small subset of features with high predictive power.
The Cancer Genome Atlas (tcga) provides genomic data for more than 11,000 patients. From the harmonised data, we retrieved gene expression quantification, microrna isoform (isomir) expression quantification, microrna (mirna) expression quantification, and “masked” copy number segments with TCGAbiolinks (Colaprico et al. 2016). Data are available for 19,602 protein-coding genes, 197,595 isomirs, and 1881 mirnas. The transcriptome profiling data are counts, and the copy number variation (cnv) data are segment mean values. We extracted the segment mean values at 10,000 evenly spaced chromosomal locations. The samples come from different types of material. We included primary solid tumour samples for all cancer types available, except in the case of leukaemia, where we included peripheral blood samples. For patients with replicate samples, we randomly chose one sample.
Analysing one molecular profile at a time, we classified the samples into cancer types. Depending on the molecular profile, the samples come from 32 or 33 cancer types, leading to \(\left( {\begin{array}{c}32\\ 2\end{array}}\right) = 496\) or \(\left( {\begin{array}{c}33\\ 2\end{array}}\right) = 528\) binary classification problems, respectively. In each classification problem, we classified samples from two cancer types, ignoring samples from other cancer types (Fig. 2).
We used double cross-validation with 10 internal and 5 external folds to tune the parameters and to estimate the prediction accuracy, respectively. In the outer cross-validation loop, we repeatedly \((5\times )\) split the samples into four external folds for training and validation \((80\%)\), and one external fold for testing \((20\%)\). In the inner cross-validation loop, we repeatedly \((10\times )\) split the samples for training and validation into nine inner folds for training \((72\%)\) and one inner fold for validation \((8\%)\). Training samples serve for estimating the coefficients  and
and  , validation samples for tuning the parameters \(\lambda \) and
, validation samples for tuning the parameters \(\lambda \) and  , and testing samples for measuring the predictive performance. As a loss function for logistic regression, we chose the deviance \(-2 \sum _{i=1}^n \{ y_i \log {(p_i)} + {(1-y_i)} {\log (1-p_i)} \}\), where \(y_i\) and \(p_i\) are the observed response and the predicted probability for individual i, respectively. Although we minimised the deviance to tune the parameters, we also calculated the area under the receiver operating characteristic curve (auc) and the misclassification rate to estimate the prediction accuracy. Since indirect maximisation might lead to suboptimal aucs (Cortes and Mohri 2004), we prefer the deviance as a primary evaluation metric.
, and testing samples for measuring the predictive performance. As a loss function for logistic regression, we chose the deviance \(-2 \sum _{i=1}^n \{ y_i \log {(p_i)} + {(1-y_i)} {\log (1-p_i)} \}\), where \(y_i\) and \(p_i\) are the observed response and the predicted probability for individual i, respectively. Although we minimised the deviance to tune the parameters, we also calculated the area under the receiver operating characteristic curve (auc) and the misclassification rate to estimate the prediction accuracy. Since indirect maximisation might lead to suboptimal aucs (Cortes and Mohri 2004), we prefer the deviance as a primary evaluation metric.
3.2 Paired covariates
Transcriptome profiling data require some preprocessing. We preprocessed the expression counts for each cancer–cancer combination separately, using the same procedure for genes, isomirs and mirnas. The total raw count for an individual is its library size, and the total raw count for a transcript is its abundance. We used the trimmed mean normalisation method from edgeR (Robinson and Oshlack 2010) to adjust for different library sizes, and filtered out all transcripts with an abundance smaller than the sample size. This filtering removes non-expressed transcripts and lets the dimensionality increase with the sample size. Furthermore, we Anscombe-transformed the normalised expression counts (\(x \rightarrow {2\sqrt{x + 3/8}}\)).
Then we converted each molecular profile to paired covariates. The covariate matrix  contains the “original” data, and the covariate matrix
contains the “original” data, and the covariate matrix  contains a compressed version, obtained in the following way:
contains a compressed version, obtained in the following way:
-
Gene expression: Shmulevich and Zhang (2002) binarise microarray gene expression data by separating low and high expression values with an edge detection algorithm. For each gene j, we sorted the normalised counts in ascending order
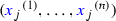 , and calculated the differences between consecutive values
, and calculated the differences between consecutive values 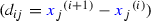 . Maximising \({H(i/n)} d_{ij}\) with respect to i, where \(H(\cdot )\) is the binary entropy function, we obtained the cutoff
. Maximising \({H(i/n)} d_{ij}\) with respect to i, where \(H(\cdot )\) is the binary entropy function, we obtained the cutoff 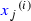 . The binary covariate
. The binary covariate 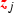 indicates whether the continuous covariate
indicates whether the continuous covariate 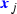 is above this cutoff
is above this cutoff 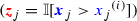 .
. -
Isomir and mirna expression: Telonis et al. (2017) binarise isomir data by labelling the bottom \({80\%}\) and top \({20\%}\) most expressed isomirs of a sample as “absent” or “present”, respectively. Because we analysed samples from only two cancer types at a time, and filtered out low-abundance transcripts, this binarisation procedure would be unstable. Instead, we let the binary covariate matrix
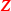 indicate non-zero expression counts.
indicate non-zero expression counts. -
Copy number variation: If c is a copy number, the corresponding segment mean value equals \({\log _2 (c/2)}\). Negative and positive values indicate deletions or amplifications, respectively. Without introducing lower and upper bounds, we only assigned values equalling zero to the diploid category. Accordingly, the ternary covariate matrix
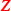 indicates the signs of the segment mean values.
indicates the signs of the segment mean values.
Thus, we obtained two transformations of the same data: the continuous  and the binary or ternary
and the binary or ternary  . Attribute j is represented by both
. Attribute j is represented by both  and
and  . Preparing for penalised regression, we transformed all covariates to mean zero and unit variance.
. Preparing for penalised regression, we transformed all covariates to mean zero and unit variance.
3.3 Predictive performance
Natural competitors for the paired lasso are the standard and the adaptive lasso. We compared the paired lasso, exploiting both  and
and  , with six competing models: the standard and the adaptive lasso exploiting either
, with six competing models: the standard and the adaptive lasso exploiting either  ,
,  , or both. We strive for very sparse models, as often desired in clinical practice. For now, each model may include up to 10 covariates.
, or both. We strive for very sparse models, as often desired in clinical practice. For now, each model may include up to 10 covariates.
We compared the predictive performance of the paired lasso and the competing models based on the cross-validated deviance. We speak of an improvement if the paired lasso decreases the deviance, and of a deterioration if the paired lasso increases the deviance. Compared to each competing model, the paired lasso leads to more improvements than deteriorations, for all molecular profiles (Fig. 3). According to the median deviance, the best competing model is the adaptive lasso based on  for genes and isomirs, and the adaptive lasso based on
for genes and isomirs, and the adaptive lasso based on  for mirnas and cnvs. But the paired lasso is better in \({57\%}\), \({69\%}\), \({61\%}\) and \({54\%}\) of the cases, respectively. We also calculated the difference in deviance between the paired lasso and the competing models. The improvements tend to exceed the deteriorations (Fig. 3).
for mirnas and cnvs. But the paired lasso is better in \({57\%}\), \({69\%}\), \({61\%}\) and \({54\%}\) of the cases, respectively. We also calculated the difference in deviance between the paired lasso and the competing models. The improvements tend to exceed the deteriorations (Fig. 3).
In addition to the deviance, we also examined the more interpretable auc and misclassification rate. For example, cnvs reliably separate testicular cancer (tgct) and ovarian cancer (ov) from most cancer types, but not ovarian from uterine cancer (ucec and ucs) (Fig. 4). Despite the sparsity constraint, the paired lasso achieves a median auc above 0.99 for genes, isomirs and mirnas, and a median auc of 0.94 for cnvs. The misclassification rates are \({0.4\%}\), \({0.6\%}\), \({0.4\%}\) and \({10.0\%}\), respectively. The reason for the extremely good separation is that the samples are not only from different cancer types, but also from different tissues. Comparisons are most meaningful for cnvs, for which the paired lasso indeed tends to greater aucs and smaller misclassification rates than the competing models (Fig. 5).
The next step is to test whether the paired lasso is significantly better than the competing models. For each molecular profile and each competing model, we calculated the difference in deviance between the paired lasso and the competing model. A setting with k cancer types leads to \({k \atopwithdelims ()2}\) differences in deviance. However, these values are mutually dependent because of the overlapping cancer types. We therefore cannot directly test whether they are significantly different from zero. Instead, we accounted for their dependencies.
We split the dependent values into groups of independent values. To increase power, we minimised the number of groups and maximised the group sizes. Given 32 cancer types, we split the 496 dependent values into 31 groups of 16 independent values (Fig. 6). Given 33 cancer types, we split the 528 dependent values into 33 groups of 16 independent values. After conducting the one-sided Wilcoxon signed-rank test within each group, we combined the 31 or 33 dependent p values with Simes combination test (Westfall 2005). This combination leads to one p value for each molecular profile and each competing model (Table 1). At the \({5\%}\) level, 22 out of 24 combined p values are significant. The insignificant improvements occur for gene expression with the adaptive lasso based on  , and cnv with the adaptive lasso based on
, and cnv with the adaptive lasso based on  . We conclude that for these data the paired lasso is significantly better than the competing models.
. We conclude that for these data the paired lasso is significantly better than the competing models.
Group assignment for isomirs. Given 32 cancer types, this matrix shows the assignment of 496 dependent pairs to 31 groups of 16 independent pairs. The row and column names indicate cancer types, each cell represents one cancer–cancer combination, and each symbol represents one group of cancer–cancer combinations. Within each group, no cancer type appears more than once
3.4 Weighting schemes
After cross-validation, we trained the paired lasso with the full data sets. The paired lasso exploits all four weighting schemes, often including both covariate sets (\({46\%}\) for genes, \({49\%}\) for isomirs, \({55\%}\) for mirnas, and \({54\%}\) for cnvs) (Table 2). When including both covariate sets, it tends to weight among all covariates for genes ( ), but among and within covariate pairs for isomirs, mirnas and cnvs (
), but among and within covariate pairs for isomirs, mirnas and cnvs ( ). When including one covariate set, it tends to weight within
). When including one covariate set, it tends to weight within  for genes (
for genes ( ), but within
), but within  for isomirs, mirnas and cnvs (
for isomirs, mirnas and cnvs ( ). On average, the covariates in
). On average, the covariates in  receive a larger proportion of the total weight than those in
receive a larger proportion of the total weight than those in  (\({63\%}\) for genes, \({64\%}\) for isomirs, \({79\%}\) for mirnas, and \({60\%}\) for cnvs). Except for genes,
(\({63\%}\) for genes, \({64\%}\) for isomirs, \({79\%}\) for mirnas, and \({60\%}\) for cnvs). Except for genes,  receives a larger proportion of the non-zero coefficients than
receives a larger proportion of the non-zero coefficients than  (\({36\%}\) for genes, \({58\%}\) for isomirs, \({82\%}\) for mirnas, and \({71\%}\) for cnvs). Often, the paired lasso does not merely select the most informative covariate set, but combines information from both covariate sets.
(\({36\%}\) for genes, \({58\%}\) for isomirs, \({82\%}\) for mirnas, and \({71\%}\) for cnvs). Often, the paired lasso does not merely select the most informative covariate set, but combines information from both covariate sets.
Subject to at most 10 non-zero coefficients, the paired lasso has a better predictive performance than the standard and the adaptive lasso based on  and/or
and/or  . We repeated cross-validation with tighter and looser sparsity constraints. As the maximum number of non-zero coefficients increases, the differences between the paired lasso and the competing models decrease (Fig. 7). Alleviating the sparsity constraint allows the competing models to include more or all relevant predictors. This improves classifications, leaves less room for further improvements, and makes the pairwise-adaptive weighting less important. Nevertheless, without a sparsity constraint, the paired lasso leads to much sparser models than the standard lasso (Table 3).
. We repeated cross-validation with tighter and looser sparsity constraints. As the maximum number of non-zero coefficients increases, the differences between the paired lasso and the competing models decrease (Fig. 7). Alleviating the sparsity constraint allows the competing models to include more or all relevant predictors. This improves classifications, leaves less room for further improvements, and makes the pairwise-adaptive weighting less important. Nevertheless, without a sparsity constraint, the paired lasso leads to much sparser models than the standard lasso (Table 3).
The elastic net (Zou and Hastie 2005) is an alternative method for handling the strong correlation between the two covariate sets. Without a sparsity constraint, the elastic net might render much larger models than the paired lasso, and thereby lead to a better predictive performance. We fix the elastic net mixing parameter at \(\alpha =0.95\) (close to lasso) to obtain sparse and stable solutions (Friedman et al. 2010). Compared to the paired lasso, the elastic net includes more non-zero coefficients (Table 3), and thereby decreases the logistic deviance for \({67\%}\) of the genes, \({68\%}\) of the isomirs, \({83\%}\) of the mirnas, and \({83\%}\) of the cnvs. Given the same resolution in the solution path, the elastic net has more and larger jumps in the sequence of non-zero coefficients, because it renders larger models. We doubled the resolution for the elastic net to facilitate approaching sparsity constraints as close as possible. At the sparsity constraint 10, the paired lasso leads to a lower logistic deviance for more than \({95\%}\) of the genes, isomirs, mirnas, and cnvs. This confirms that the elastic net is good for estimating relatively dense models, and the paired lasso is good for estimating sparse models.
4 Discussion
We developed the paired lasso for estimating sparse models from paired covariates. It handles situations where it is unclear whether one covariate set is more predictive than the other covariate set, or whether both covariate sets together are more predictive than one covariate set alone.
Under a sparsity constraint, the paired lasso can have a better predictive performance than the standard and the adaptive lasso based on  and/or
and/or  . In our comparisons, the standard and the adaptive lasso each have three chances to beat the paired lasso: exploiting
. In our comparisons, the standard and the adaptive lasso each have three chances to beat the paired lasso: exploiting  ,
,  , or both. Nevertheless, the paired lasso, automatically choosing from
, or both. Nevertheless, the paired lasso, automatically choosing from  and
and  , improves the best standard and the best adaptive lasso.
, improves the best standard and the best adaptive lasso.
This improvement stems from introducing a pairwise-adaptive weighting scheme and choosing among multiple weighting schemes. A super learner (van der Laan et al. 2007) would combine predictions from multiple weighting schemes, improving predictions at the cost of interpretability. In contrast, the paired lasso attempts to select the most predictive combination of covariate sets, and the most predictive covariates.
Sparsity constraints should be employed regardless of whether the underlying effects are sparse or not. Their purpose is to make models as sparse as desired. Even if numerous covariates influence the response, we might still be interested in the top few most influential covariates. For example, a cost-efficient clinical implementation may require a limited number of markers. But if the standard lasso without a sparsity constraint returns a sufficiently sparse model, the sparsity constraint is redundant.
The paired lasso uses the response twice, first for weighting the covariates, and then for estimating their coefficients. This two-step procedure increases the weight of presumably important covariates, and decreases the weight of presumably unimportant covariates. Therefore, without an effective sparsity constraint, the paired lasso tends to sparser models than the standard lasso, and with an effective sparsity constraint, the paired lasso tends to more predictive models than the standard lasso.
Paired covariates arise in many genomic applications:
-
Molecular profiles with meaningful thresholds also include exon expression and dna methylation. Exons can have different types of effects on a clinical response. Some exons are retained for some samples, but spliced out for other samples. Other exons are retained for all samples, but with different expression levels. Both the change from “non-expressed” to “expressed” and the expression level might have an effect. We could match zero-indicators with count covariates to account for both types of effects. Similarly, beyond considering cpg islands as unmethylated or methylated, we could also account for methylation levels.
-
Some molecular profiles lead to categorical variables with three or more levels. Single nucleotide polymorphism (snp) genotype data take the values zero, one and two minor alleles. Depending on the effect of interest, we would normally construct indicators for “one or two minor alleles” to analyse dominant effects, indicators for “two minor alleles” to analyse recessive effects, or quantitative variables to analyse additive effects. Instead, we could include both indicator groups to account for all three types of effects. Similarly, we could represent cnv data as two sets of ternary covariates, the first indicating losses and gains, and the second indicating great losses and great gains.
-
Another source of paired covariates are repeated measures. If the same molecular profile is measured twice under the same conditions, the average might be a good choice. But less so if the same molecular profile is measured under different conditions. Then it might be better to match the repeated measures. An interesting application is to predict survival from gene expression in tumour (
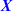 ) and normal (
) and normal (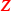 ) tissue collected from the vicinity of the tumour (Huang et al. 2016). We compared the paired lasso with the standard and the adaptive lasso based on
) tissue collected from the vicinity of the tumour (Huang et al. 2016). We compared the paired lasso with the standard and the adaptive lasso based on 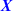 and/or
and/or 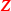 (see appendix). For at least five out of six cancer types, the paired lasso fails to improve the cross-validated predictive performance. We argue that sparsity might be a wrong assumption for these data, in particular for the survival response, which may be better accommodated by dense predictors like ridge regression (van Wieringen et al. 2009). Indeed, the standard lasso generally selects few or no variables for four cancer types. Moreover, adaptation fails to improve the standard lasso for another cancer type, leaving little room for improvement to the paired lasso, which is essentially a bag of adaptive lasso models. Finally, for one cancer type, the paired lasso is competitive with the adaptive lasso based on tumour tissue, both performing relatively well. The paired lasso has the practical advantage of automatically selecting from the covariate sets.
(see appendix). For at least five out of six cancer types, the paired lasso fails to improve the cross-validated predictive performance. We argue that sparsity might be a wrong assumption for these data, in particular for the survival response, which may be better accommodated by dense predictors like ridge regression (van Wieringen et al. 2009). Indeed, the standard lasso generally selects few or no variables for four cancer types. Moreover, adaptation fails to improve the standard lasso for another cancer type, leaving little room for improvement to the paired lasso, which is essentially a bag of adaptive lasso models. Finally, for one cancer type, the paired lasso is competitive with the adaptive lasso based on tumour tissue, both performing relatively well. The paired lasso has the practical advantage of automatically selecting from the covariate sets. -
An omnipresent challenge is the integration of multiple molecular profiles (Gade et al. 2011; Bergersen et al. 2011; Aben et al. 2016; Boulesteix et al. 2017; Rodríguez-Girondo et al. 2017). The paired lasso is not directly suitable for analysing multiple molecular profiles simultaneously. However, for two molecular profiles with a one-to-one correspondence, the paired lasso can be used as an integrative model. A well-known example is messenger rna expression and matched dna copy number.
-
Paired main and interaction effects have the same paired structure as paired covariates. Since the paired lasso would treat the two sets of effects as two sets of covariates, it would violate the hierarchy principle. In this context, the group lasso was shown to be beneficial (Ternès et al. 2017). Although the paired lasso might also improve predictions, an adaptation would be required to enforce the hierarchy principle.
In paired covariate settings, there are two types of groups: covariate pairs and covariate sets. From each covariate pair, the paired lasso selects zero, one, or two covariates. Alternatively, the group lasso (Yuan and Lin 2006) would select either zero or two covariates, the exclusive lasso (Campbell and Allen 2017) at least one covariate, and the protolasso (Reid and Tibshirani 2016) at most one covariate. Although these methods were not designed for paired covariates, they might improve interpretability in some applications with paired covariates. However, it would be challenging to account for covariate pairs and covariate sets, because these are overlapping groupings.
We focussed on binary responses, but our approach also works with other univariate responses. Currently, our implementation supports linear, logistic, Poisson and Cox regression. Although it allows for \(L_1\) regularisation (lasso), \(L_2\) regularisation (ridge) and combinations thereof (elastic net), sparsity constraints require an \(L_1\) penalty, and the performance under an \(L_2\) penalty requires further research.
Data availability
All results are based upon data produced by The Cancer Genome Atlas (tcga) Research Network, publicly available from the National Cancer Institute (nci) Genomic Data Commons (gdc) Data Portal.
References
Aben N, Vis DJ, Michaut M, Wessels LF (2016) TANDEM: a two-stage approach to maximize interpretability of drug response models based on multiple molecular data types. Bioinformatics 32(17):i413–i420. https://doi.org/10.1093/bioinformatics/btw449
Bergersen LC, Glad IK, Lyng H (2011) Weighted lasso with data integration. Stat Appl Genet Mol Biol 10(1):39. https://doi.org/10.2202/1544-6115.1703
Boulesteix AL, De Bin R, Jiang X, Fuchs M (2017) IPF-LASSO: Integrative \(L_1\)-penalized regression with penalty factors for prediction based on multi-omics data. Comput Math Methods Med 2017:7691937. https://doi.org/10.1155/2017/7691937 (ipflasso)
Bühlmann P, van de Geer S (2011) Statistics for high-dimensional data: methods, theory and applications. Springer, Berlin. https://doi.org/10.1007/978-3-642-20192-9
Campbell F, Allen GI (2017) Within group variable selection through the exclusive lasso. Electron J Stat 11(2):4220–4257. https://doi.org/10.1214/17-EJS1317
Colaprico A, Silva TC, Olsen C, Garofano L, Cava C, Garolini D, Sabedot TS, Malta TM, Pagnotta SM, Castiglioni I et al (2016) TCGAbiolinks: an R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res 44(8):e71. https://doi.org/10.1093/nar/gkv1507
Cortes C, Mohri M (2004) AUC optimization vs. error rate minimization. In: Thrun S, Saul LK, Schölkopf B (eds) Advances in neural information processing systems 16. MIT Press, Cambridge, pp 313–320
Dey KK, Stephens M (2018) CorShrink: empirical Bayes shrinkage estimation of correlations, with applications. bioRxiv https://doi.org/10.1101/368316
Fan J, Lv J (2008) Sure independence screening for ultrahigh dimensional feature space. J R Stat Soc Ser B (Stat Methodol) 70(5):849–911. https://doi.org/10.1111/j.1467-9868.2008.00674.x
Friedman J, Hastie T, Tibshirani R (2010) Regularization paths for generalized linear models via coordinate descent. J Stat Softw. https://doi.org/10.18637/jss.v033.i01 (glmnet)
Gade S, Porzelius C, Fälth M, Brase JC, Wuttig D, Kuner R, Binder H, Sültmann H, Beißbarth T (2011) Graph based fusion of miRNA and mRNA expression data improves clinical outcome prediction in prostate cancer. BMC Bioinform 12(1):488. https://doi.org/10.1186/1471-2105-12-488
Huang J, Ma S, Zhang CH (2008) Adaptive lasso for sparse high-dimensional regression models. Stat Sin 18(4):1603–1618
Huang X, Stern DF, Zhao H (2016) Transcriptional profiles from paired normal samples offer complementary information on cancer patient survival-evidence from TCGA pan-cancer data. Sci Rep 6:20567. https://doi.org/10.1038/srep20567
Reid S, Tibshirani R (2016) Sparse regression and marginal testing using cluster prototypes. Biostatistics 17(2):364–376. https://doi.org/10.1093/biostatistics/kxv049
Robinson MD, Oshlack A (2010) A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol 11(3):R25. https://doi.org/10.1186/gb-2010-11-3-r25 (edgeR)
Rodríguez-Girondo M, Kakourou A, Salo P, Perola M, Mesker WE, Tollenaar RA, Houwing-Duistermaat J, Mertens BJ (2017) On the combination of omics data for prediction of binary outcomes. In: Datta S, Mertens BJ (eds) Statistical analysis of proteomics, metabolomics, and lipidomics data using mass spectrometry. Springer, Cham, pp 259–275. https://doi.org/10.1007/978-3-319-45809-0_14
Shmulevich I, Zhang W (2002) Binary analysis and optimization-based normalization of gene expression data. Bioinformatics 18(4):555–565. https://doi.org/10.1093/bioinformatics/18.4.555
Telonis AG, Magee R, Loher P, Chervoneva I, Londin E, Rigoutsos I (2017) Knowledge about the presence or absence of miRNA isoforms (isomiRs) can successfully discriminate amongst 32 TCGA cancer types. Nucleic Acids Res 45(6):2973–2985. https://doi.org/10.1093/nar/gkx082
Ternès N, Rotolo F, Heinze G, Michiels S (2017) Identification of biomarker-by-treatment interactions in randomized clinical trials with survival outcomes and high-dimensional spaces. Biom J 59(4):685–701. https://doi.org/10.1002/bimj.201500234
Tibshirani R (1996) Regression shrinkage and selection via the lasso. J R Stat Soc Ser B (Methodol) 58(1):267–288
Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K (2005) Sparsity and smoothness via the fused lasso. J R Stat Soc Ser B (Stat Methodol) 67(1):91–108. https://doi.org/10.1111/j.1467-9868.2005.00490.x
van de Wiel MA, Lien TG, Verlaat W, van Wieringen WN, Wilting SM (2016) Better prediction by use of co-data: adaptive group-regularized ridge regression. Stat Med 35(3):368–381. https://doi.org/10.1002/sim.6732 (GRridge)
van der Laan MJ, Polley EC, Hubbard AE (2007) Super learner. Stat Appl Genet Mol Biol 6(1):25. https://doi.org/10.2202/1544-6115.1309
van Wieringen WN, Kun D, Hampel R, Boulesteix AL (2009) Survival prediction using gene expression data: a review and comparison. Comput Stat Data Anal 53(5):1590–1603. https://doi.org/10.1016/j.csda.2008.05.021
Westfall PH (2005) Combining \(P\) values. In: Armitage P, Colton T (eds) Encyclopedia of biostatistics. Wiley, Hoboken. https://doi.org/10.1002/0470011815.b2a15181
Yuan M, Lin Y (2006) Model selection and estimation in regression with grouped variables. J R Stat Soc Ser B (Stat Methodol) 68(1):49–67. https://doi.org/10.1111/j.1467-9868.2005.00532.x
Zou H (2006) The adaptive lasso and its oracle properties. J Am Stat Assoc 101(476):1418–1429. https://doi.org/10.1198/016214506000000735
Zou H, Hastie T (2005) Regularization and variable selection via the elastic net. J R Stat Soc Ser B (Stat Methodol) 67(2):301–320. https://doi.org/10.1111/j.1467-9868.2005.00503.x
Zwiener I, Frisch B, Binder H (2014) Transforming RNA-Seq data to improve the performance of prognostic gene signatures. PLoS ONE 9(1):e85150. https://doi.org/10.1371/journal.pone.0085150
Acknowledgements
This research was funded by the Department of Epidemiology and Biostatistics, Amsterdam umc, vu University Amsterdam.
Author information
Authors and Affiliations
Contributions
The authors contributed to this research by developing the method (ar, maw), preparing the manuscript (ar) or the appendix (ict), and revising the manuscript critically (ict, maj, rxm, maw). All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no potential conflicts of interest.
Reproducibility
The R package palasso contains a vignette for reproducing all results.
Software
The R package palasso runs on any operating system equipped with R-3.5.0 or later. It is available from cran under a free software license: https://CRAN.R-project.org/package=palasso.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rauschenberger, A., Ciocănea-Teodorescu, I., Jonker, M.A. et al. Sparse classification with paired covariates. Adv Data Anal Classif 14, 571–588 (2020). https://doi.org/10.1007/s11634-019-00375-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-019-00375-6







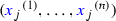 , and calculated the differences between consecutive values
, and calculated the differences between consecutive values 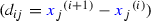 . Maximising
. Maximising 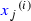 . The binary covariate
. The binary covariate 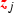 indicates whether the continuous covariate
indicates whether the continuous covariate 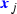 is above this cutoff
is above this cutoff 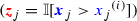 .
.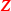 indicate non-zero expression counts.
indicate non-zero expression counts.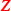 indicates the signs of the segment mean values.
indicates the signs of the segment mean values.




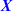 ) and normal (
) and normal (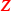 ) tissue collected from the vicinity of the tumour (Huang et al.
) tissue collected from the vicinity of the tumour (Huang et al. 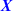 and/or
and/or 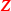 (see appendix). For at least five out of six cancer types, the paired lasso fails to improve the cross-validated predictive performance. We argue that sparsity might be a wrong assumption for these data, in particular for the survival response, which may be better accommodated by dense predictors like ridge regression (van Wieringen et al.
(see appendix). For at least five out of six cancer types, the paired lasso fails to improve the cross-validated predictive performance. We argue that sparsity might be a wrong assumption for these data, in particular for the survival response, which may be better accommodated by dense predictors like ridge regression (van Wieringen et al.