Non-tracial Free Graph von Neumann Algebras

Abstract

Given a finite, directed, connected graph $\Gamma$ equipped with a weighting $\mu$ on its edges, we provide a construction of a von Neumann algebra equipped with a faithful, normal, positive linear functional $(\mathcal {M}(\Gamma ,\mu ),\varphi )$. When the weighting $\mu$ is instead on the vertices of $\Gamma$, the first author showed the isomorphism class of $(\mathcal {M}(\Gamma ,\mu ),\varphi )$ depends only on the data $(\Gamma ,\mu )$ and is an interpolated free group factor equipped with a scaling of its unique trace (possibly direct sum copies of $\mathbb {C}$). Moreover, the free dimension of the interpolated free group factor is easily computed from $\mu$. In this paper, we show for a weighting $\mu$ on the edges of $\Gamma$ that the isomorphism class of $(\mathcal {M}(\Gamma ,\mu ),\varphi )$ depends only on the data $(\Gamma ,\mu )$, and is either as in the vertex weighting case or is a free Araki–Woods factor equipped with a scaling of its free quasi-free state (possibly direct sum copies of $\mathbb {C}$). The latter occurs when the subgroup of ${\mathbb {R}}^+$ generated by $\mu (e_1)\cdots \mu (e_n)$ for loops $e_1\cdots e_n$ in $\Gamma$ is non-trivial, and in this case the point spectrum of the free quasi-free state will be precisely this subgroup. As an application, we give the isomorphism type of some infinite index subfactors considered previously by Jones and Penneys.

Appendix

1.1 Some infinite index subfactors

Let $\mathcal {T}\mathcal {L}_{\bullet }$ denote the Temperley Lieb planar algebra with parameter $\delta \in [2, \infty )$. In [GJS10], one considers ${{\,\mathrm{Gr}\,}}(\mathcal {T}\mathcal {L}) = \oplus _{n=1}^{\infty } \mathcal {T}\mathcal {L}_{n}$. Recall from [GJS10] that ${{\,\mathrm{Gr}\,}}(\mathcal {T}\mathcal {L})$ has the structure of a graded algebra with graded multiplication $\wedge$ and normalized Voiculescu trace $\tau$:

Moreover, this graded algebra acts on itself by left and right multiplication, which is bounded with respect to the $\Vert \cdot \Vert _2$-norm induced by this trace. Let $\mathcal {N}= ({{\,\mathrm{Gr}\,}}(\mathcal {T}\mathcal {L}), \tau )''$. It was shown in [Har13] that $\mathcal {N}\cong L({\mathbb {F}}_{\infty })$.

Jones and Penneys in [JP19, Section 6.4] studied a directed graph $\Gamma =(V, E)$ with edge-weighting $\mu$ as in Section 2 with the additional requirement that $(\Gamma ,\mu )$ is balanced:

$$\begin{aligned} \displaystyle \sum _{e:s(e) = v} \mu (e) = \delta \qquad \forall v \in V. \end{aligned}$$

Fixing $v \in V$, they studied the loop algebra $\mathbf{A }_{v}$ which is spanned by formal linear combinations of loops based at v. It comes equipped with the following $*$-algebra structure and state $\phi$:

• $(e_{1}\cdots e_{n}) \cdot (f_{1}\cdots f_{m}) = e_{1}\cdots e_{n}f_{1}\cdots f_{m}$

• $(e_{1}\cdots e_{n})^{*} = \sqrt{\mu (e_{1})\cdots \mu (e_{n})}e_{n}\cdots e_{1}$

• With $NC_{2}([n])$ the set of non-crossing pair partitions on $\{1, \ldots , n\}$,

  

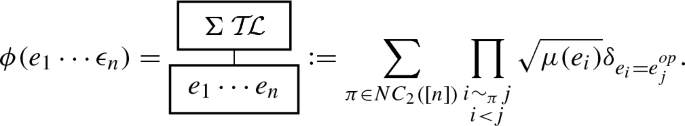
The following proposition is a standard combinatorial argument involving the elements $Y_{e} \in (\mathcal {M}(\Gamma , \mu ), \varphi )$.

Proposition

The map $p_{v}{\mathbb {C}}\langle Y_{e} : e \in E\rangle p_{v} \rightarrow \mathbf{A }_{v}$ given by $Y_{e_{1}}\cdots Y_{e_{n}} \mapsto e_{1}\cdots e_{n}$ for every loop based at v is a $*$-algebra isomorphism statisfying $\phi (e_{1}\cdots e_{n}) = \varphi (Y_{e_{1}}\cdots Y_{e_{n}})$.

This proposition allows us to conclude that $(\mathcal {M}, \phi ) := (\mathbf{A }_{v}, \phi )'' \cong (T_{H}, \varphi _{H})$ for $H = H(\Gamma , \mu )$. (Note that $\delta \ge 2$, and so requiring that $\mu$ is balanced ensures $\mathcal {M}(\Gamma ,\mu )$ is a factor.) Section 6.4 of [JP19] studied an inclusion of $i : \mathcal {N}\hookrightarrow \mathcal {M}$ as follows. Identifying each diagram $x\in {{\,\mathrm{Gr}\,}}(\mathcal {T}\mathcal {L})$ with a partition $\pi \in NC_{2}([2n])$ in the natural way, one has

$$\begin{aligned} i(x) = \sum _{\begin{array}{c} e_{1}\cdots e_{2n}: \\ i \sim _{\pi } j, \, i< j \Rightarrow e_{i} = e_{j}^{{{\,\mathrm{op}\,}}} \end{array}} \left( \prod _{ \begin{array}{c} i \sim _{\pi } j \\ i < j \end{array}} \mu (e_{i}) \right) e_{1}\cdots e_{2n} \end{aligned}$$

This inclusion preserves the tracial state $\tau$ on $\mathcal {N}$, and so $\mathcal {N}\hookrightarrow \mathcal {M}^{\phi }$.

Jones and Penneys showed that the subfactor $\mathcal {N}\subset \mathcal {M}$ is of infinite index, irreducible ($\mathcal {N}' \cap \mathcal {M}= {\mathbb {C}}$), discrete ($L^{2}(\mathcal {M})$ decomposes as a direct sum of irreducible, finite index $\mathcal {N}-\mathcal {N}$ bimodules), and that the subfactor $\mathcal {N}\subset \mathcal {M}$ is determined by $(\Gamma , \mu )$. Our work shows that the inclusion $\mathcal {N}\subset \mathcal {M}$ can be realized as an inclusion $L({\mathbb {F}}_{\infty }) \subset (T_{H}, \varphi _{H}),$ where $L({\mathbb {F}}_{\infty })$ lies inside $T_{H}^{\varphi _{H}}$.