Skip to main content
SpringerLink
Log in

Vibrational analysis of Love waves in a viscoelastic composite multilayered structure

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

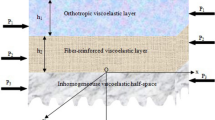
A unified procedure is presented to investigate the dispersion and damping behavior of Love waves in a double-layered structure. The double-layered structure is comprised of a viscoelastic fiber-reinforced medium (Medium I) embedded between a viscoelastic sandy layer (Medium II) and a viscoelastic porous semi-infinite medium (Medium III). The displacement vectors for the respective medium have been obtained using analytical techniques. Using the separation of variables method and admissible boundary conditions at the free surface and the interfaces, the complex frequency equation is obtained in closed form. The substantial impact of all material parameters involved in the considered model on the phase velocity as well as damped velocity has been observed numerically and shown by graphical illustrations. The outcomes from this analysis may serve as a dynamic tool in various fields including geophysics, geotechnical, and earthquake engineering.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Abd-Alla, A., Abo-Dahab, S., Al-Mullise, A.: Effects of rotation and gravity field on surface waves in fibre-reinforced thermoelastic media under four theories. J. Appl. Math. 2013, 20 (2013). https://doi.org/10.1155/2013/562369

    Article  MATH  Google Scholar 

  2. Abd-Alla, A., Khan, A., Abo-Dahab, S.: Rotational effect on Rayleigh, Love and Stoneley waves in fibre-reinforced anisotropic general viscoelastic media of higher and fraction orders with voids. J. Mech. Sci. Tech. 29(10), 4289–4297 (2015)

    Article  Google Scholar 

  3. Acharya, D., Roy, I.: Magnetoelastic surface waves in electrically conducting fibre-reinforced media. Bull. Instit. Math. Acad. Sinica New Series 4(3), 333–352 (2009)

    MathSciNet  MATH  Google Scholar 

  4. Alam, P., Kundu, S., Badruddin, I., Khan, T.: Dispersion and attenuation characteristics of Love-type waves in a fiber-reinforced composite over a viscoelastic substrate. Phys. Wave Phenom. 27(4), 281–289 (2019)

    Article  Google Scholar 

  5. Alam, P., Kundu, S., Gupta, S.: Dispersion and attenuation of torsional wave in a viscoelastic layer bonded between a layer and a half-space of dry sandy media. Appl. Math. Mech. 38(9), 1313–1328 (2017)

    Article  MathSciNet  Google Scholar 

  6. Alam, P., Kundu, S., Gupta, S.: Dispersion and attenuation of Love-type waves due to a point source in magneto-viscoelastic layer. J. Mech. 34(6), 801–816 (2018)

    Article  Google Scholar 

  7. Alam, P., Kundu, S., Gupta, S.: Dispersion study of sh-wave propagation in an irregular magneto-elastic anisotropic crustal layer over an irregular heterogeneous half-space. J. King Saud University-Sci. 30(3), 301–310 (2018)

    Article  Google Scholar 

  8. Alam, P., Kundu, S., Gupta, S.: Love-type wave propagation in a hydrostatic stressed magneto-elastic transversely isotropic strip over an inhomogeneous substrate caused by a disturbance point source. J. Intell. Mater. Syst. Struct. 29(11), 2508–2521 (2018)

    Article  Google Scholar 

  9. Alam, P., Kundu, S., Gupta, S., Saha, A.: Study of torsional wave in a poroelastic medium sandwiched between a layer and a half-space of heterogeneous dry sandy media. Waves in Random and Complex Media 28(1), 182–201 (2018)

    Article  MathSciNet  Google Scholar 

  10. Belfield, A., Rogers, T., Spencer, A.: Stress in elastic plates reinforced by fibres lying in concentric circles. J. Mech. Phys. Solids 31(1), 25–54 (1983)

    Article  Google Scholar 

  11. Biot, M.: Theory of elastic waves in a fluid-saturated porous solid. 1. low frequency range. J. Acoust. Soc. Am. 28, 168–178 (1956)

    Article  MathSciNet  Google Scholar 

  12. Biot, M.A.: Mechanics of Incremental Deformations: Theory of Elasticity and Viscoelasticity of Initially Stressed Solids and Fluids, Including Thermodynamic Foundations and Applications to Finite Strain. Wiley, New York (1965)

    Book  Google Scholar 

  13. Boxberg, M.S., Prévost, J.H., Tromp, J.: Wave propagation in porous media saturated with two fluids. Transp. Porous Med. 107(1), 49–63 (2015)

    Article  MathSciNet  Google Scholar 

  14. Chattopadhyay, A., Choudhury, S.: Propagation, reflection and transmission of magnetoelastic shear waves in a self-reinforced medium. Int. J. Eng. Sci. 28(6), 485–495 (1990)

    Article  Google Scholar 

  15. Deresiewicz, H.: The effect of boundaries on wave propagation in a liquid-filled porous solid: Vi. Love waves in a double surface layer. Bull. Seismol. Soc. Am. 54(1), 417–423 (1964)

    Google Scholar 

  16. Deresiewicz, H.: The effect of boundaries on wave propagation in a liquid-filled porous solid: Ix. Love waves in a porous internal stratum. Bull. Seismol. Soc. Am. 55(5), 919–923 (1965)

    Google Scholar 

  17. Dey, S., Gupta, A.K., Gupta, S.: Effect of gravity and initial stress on torsional surface waves in dry sandy medium. J. Eng. Mech. 128(10), 1115–1118 (2002)

    Article  Google Scholar 

  18. Ewing, W.M., Jardetzky, W.S., Press, F., Beiser, A.: Elastic waves in layered media. Phys. Today 10, 27 (1957)

    Article  Google Scholar 

  19. Gubbins, D.: Seismology and Plate Tectonics. Cambridge University Press, Cambridge (1990)

    Google Scholar 

  20. Gupta, S., Ahmed, M.: On propagation of Love waves in dry sandy medium sandwiched between fiber-reinforced layer and prestressed porous half-space. Earthq. Struct. 12(6), 619–628 (2017)

    Google Scholar 

  21. Gupta, S., Ahmed, M., Misra, J.C.: Effects of periodic corrugated boundary surfaces on plane sh-waves in fiber-reinforced medium over a semi-infinite micropolar solid under the action of magnetic field. Mech. Res. Commun. 95, 35–44 (2019)

    Article  Google Scholar 

  22. Hashin, Z., Rosen, B.W.: Erratum:“the elastic moduli of fiber-reinforced materials”(J. Appl. Mech., 1964, 31, pp. 223-232). J. Appl. Mech. 32, 219 (1965)

  23. Ke, L.-L., Wang, Y.-S., Zhang, Z.-M.: Love waves in an inhomogeneous fluid saturated porous layered half-space with linearly varying properties. Soil Dyn. Earthq. Eng. 26(6–7), 574–581 (2006)

    Article  Google Scholar 

  24. Kiełczyński, P., Szalewski, M., Balcerzak, A.: Effect of a viscous liquid loading on Love wave propagation. Int. J. Solids Struct. 49(17), 2314–2319 (2012)

    Article  Google Scholar 

  25. Kumari, P., Sharma, V.: Propagation of torsional waves in a viscoelastic layer over an inhomogeneous half space. Acta Mech. 225(6), 1673–1684 (2014)

    Article  MathSciNet  Google Scholar 

  26. Kundu, S., Alam, P., Gupta, S.: Shear waves in magneto-elastic transversely isotropic (mti) layer bonded between two heterogeneous elastic media. Mech. Adv. Mater. Struct. 26(5), 407–415 (2019)

    Article  Google Scholar 

  27. Love, A.: Mathematical Theory of Elasticity. Cambridge University Press, Cambridge (1920)

    MATH  Google Scholar 

  28. Love, A.: A Treatise on the Mathematical Theory of Elasticity. Cambridge University Press, Cambridge (1927)

    MATH  Google Scholar 

  29. Maity, M., Kundu, S., Pandit, D., Gupta, S.: Characteristics of torsional wave profiles in a viscous fiber-reinforced layer resting over a sandy half-space under gravity. Int. J. Geomech. 18(7), 06018015 (2018)

    Article  Google Scholar 

  30. Manna, S., Kundu, S., Gupta, S.: Effect of reinforcement and inhomogeneity on the propagation of Love waves. Int. J. Geomech. 16(2), 04015045 (2015)

    Article  Google Scholar 

  31. Pal, A., Kalyani, V., Kar, B.: Energy partitions at a solid-sandy bilateral interface due to an incident antiplane shear wave. Proc. Indian Natl. Sci. Acad. 52, 1390–1397 (1986)

    Google Scholar 

  32. Pal, J., Ghorai, A.P.: Propagation of Love wave in sandy layer under initial stress above anisotropic porous half-space under gravity. Transp. Porous Med. 109(2), 297–316 (2015)

    Article  MathSciNet  Google Scholar 

  33. Pandit, D.K., Kundu, S., Gupta, S.: Propagation of Love waves in a prestressed voigt-type Viscoelastic orthotropic functionally graded layer over a porous half-space. Acta Mech. 228(3), 871–880 (2017)

    Article  MathSciNet  Google Scholar 

  34. Samal, S.K., Chattaraj, R.: Surface wave propagation in fiber-reinforced anisotropic elastic layer between liquid saturated porous half space and uniform liquid layer. Acta Geophys. 59(3), 470–482 (2011)

    Article  Google Scholar 

  35. Sengupta, P., Nath, S.: Surface waves in fibre-reinforced anisotropic elastic media. Sadhana 26(4), 363–370 (2001)

    Article  Google Scholar 

  36. Sethi, M., Gupta, K., Gupta, D., et al.: Surface waves in fibre-reinforced anisotropic solid elastic media under the influence of gravity. Int. J. Appl. Mech. Eng. 18(1), 177–188 (2013)

    Article  Google Scholar 

  37. Wang, Y.-S., Zhang, Z.-M.: Propagation of Love waves in a transversely isotropic fluid-saturated porous layered half-space. J. Acoust. Soc. Am. 103(2), 695–701 (1998)

    Article  Google Scholar 

  38. Weiskopf, W.H.: Stresses in soils under a foundation. J. Frankl. Instit. 239(6), 445–465 (1945)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors convey their sincere thanks to DST-SERB for funding by the research project no. DST-SERB/2018-2019/599/AM entitled “Analytical modelling of surface waves in fiber-reinforced and micro-polar media”.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computing, Indian Institute of Technology (Indian School of Mines), Dhanbad, Jharkhand, 826004, India

    Dharmendra Kumar, Santimoy Kundu, Raju Kumhar & Shishir Gupta

Authors
  1. Dharmendra Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Santimoy Kundu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Raju Kumhar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shishir Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dharmendra Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$\begin{aligned} \alpha _1= & {} (\mu _t +i \omega \mu _t^{\prime }) = \mu _t(1 + i \epsilon _2),\\ \alpha _2= & {} (\mu _l +i \omega \mu _l^{\prime }-\mu _t -i \omega \mu _t^{\prime })\\= & {} \mu _t\left( \frac{\mu _l}{\mu _t} + i \epsilon _1 -1 - i \epsilon _2\right) ,\\ D_1= & {} (2 i k a_1 + P_1 a_3) =X_1 + i X_2,\\ D_2= & {} ({P_1}^{2} + 4 {\phi _2}^{2}) = X_3 + i X_4,\\ D_3= & {} (P_1 \alpha _1 + a_3 \alpha _2 D_1 -2 \phi _3 {\overline{L}}) = Y_5 + i Y_6,\\ D_4= & {} (a_3 \alpha _2 (2 i k P_1 a_1 + a_3 D_2) = Y_7 + i Y_8,\\ D_5= & {} (a_3 \alpha _2 (a_3 \alpha _2 {D_1}^{2} + 4 {a_3}^{2} {\phi _2}^{2}) = Y_9 + i Y_{10}, \end{aligned}$$
$$\begin{aligned} \epsilon _1= & {} \omega \frac{\mu _l' }{{\mu _t }},\quad \epsilon _2 =\omega \frac{\mu _t' }{{\mu _t }},\\ \epsilon _3= & {} \omega \frac{{N}^{*}}{{N }}, \quad \epsilon _4 = \omega \frac{{L}^{*}}{{L }},\\ X_1= & {} (Y_1 a_3 - 2 k_1 a_1 \delta ), X_2 = (2 k_1 a_1 + a_3 y_2),\\ X_3= & {} ({Y_1}^2 - {Y_2}^2 + 4 {x_2}^2 - 4 {y_2}^2), X_4 = (2 Y_1 Y_2 + 8 x_2 y_2),\\ X_5= & {} (1+(\frac{\mu _l}{\mu _t}-1){a_1}^2)(1-{\delta }^2)-2 \delta (\epsilon _2+(\epsilon _1-\epsilon _2){a_1}^2),\\ X_6= & {} (\epsilon _2 + (\epsilon _1-\epsilon _2){a_1}^2)(1-{\delta }^2)+2 \delta \left( 1+\left( \frac{\mu _l}{\mu _t}-1\right) {a_1}^2\right) ,\\ X_7= & {} (Y_1 a_3 - 2 k_1 a_1 \delta ), X_8 = (2 k_1 a_1 + a_3 Y_2),\\ Y_1= & {} \frac{a_1 a_3 k_1 \left( (1 - \frac{\mu _l}{\mu _t}) \delta - (\epsilon _1-\epsilon _2)-{(\frac{\mu _l}{\mu _t} - 1)}^2 {a_3}^2 \delta +\left( \frac{\mu _l}{\mu _t}-1\right) \epsilon _2- \epsilon _2 \delta ( \epsilon _1 -\epsilon _2)-{( \epsilon _1 - \epsilon _2)}^2 {a_3}^2\delta \right) }{{\left( 1+(\frac{\mu _l}{\mu _t}-1){a_3}^2\right) }^2 + {\left( \epsilon _2 + (\epsilon _1 - \epsilon _2){a_3}^2\right) }^2},\\ Y_2= & {} \frac{a_1 a_3 k_1 \left( ( \frac{\mu _l}{\mu _t} - 1) - \delta (\epsilon _1 - \epsilon _2) +{( \frac{\mu _l}{\mu _t} - 1)}^2 {a_3}^2 + \epsilon _2 (\frac{\mu _l}{\mu _t} - 1) \delta + \epsilon _2 (\epsilon _1 - \epsilon _2) + {(\epsilon _1 - \epsilon _2)}^2 {a_3}^2\right) }{{{\left( 1 + (\frac{\mu _l}{\mu _t} - 1){a_3}^2\right) }^2 + {\left( \epsilon _2 + (\epsilon _1 - \epsilon _2){a_3}^2\right) }^2}},\\ Y_3= & {} \frac{\rho _2 {\omega }^2(1+(\frac{\mu _l}{\mu _t}-1){a_3}^2)-\mu _t {k_1}^2\left( (1+(\frac{\mu _l}{\mu _t}-1){a_3}^2) X_5 + (\epsilon _2+(\epsilon _1-\epsilon _2){a_3}^2) X_6 \right) }{\mu }_t{\left( 1+(\frac{\mu _l}{\mu _t}-1){a_3}^2\right) }^2\\&+{\left( \epsilon _2+(\epsilon _1-\epsilon _2){a_3}^2\right) }^2,\\ Y_4= & {} \frac{\left( \mu _t {k_1}^2 \left( X_5 \right) (\epsilon _2 +(\epsilon _1 - \epsilon _2){a_3}^2) - (1 + (\frac{\mu _l}{\mu _t}-1){a_3}^2)\left( X_6 \right) \right) -\rho _2 {\omega }^2(\epsilon _2+(\epsilon _1-\epsilon _2){a_3}^2)}{\mu _t{\left( 1+(\frac{\mu _l}{\mu _t}-1){a_3}^2\right) }^2 + {\left( \epsilon _2+(\epsilon _1-\epsilon _2){a_3}^2\right) }^2}, \end{aligned}$$
$$\begin{aligned} x_1= & {} \sqrt{r_1}\cos \frac{\theta _1}{2},\quad y_1 = \sqrt{r_1}\sin \frac{\theta _1}{2},\\ r_1 \cos \theta _1= & {} \frac{\omega ^2}{{\beta _1}^2 \eta _1\left( \frac{1}{{\eta _1}^2}+{\varpi }^2\right) }-(1-{\delta }^2){k_1}^2,\\ r_1 \sin \theta _1= & {} - \frac{{\omega }^2 \varpi }{{\beta _1}^2 \left( \frac{1}{{\eta _1}^2}+{\varpi }^2 \right) }- 2\delta {k_1}^2,\\ x_2= & {} \sqrt{r_2}\cos \frac{\theta _2}{2}, \quad y_2 = \sqrt{r_2}\sin \frac{\theta _2}{2},\\ r_2 \cos \theta _2= & {} \frac{4 Y_3 - {Y_1}^2 + {Y_2}^2}{4},\quad r_2 \sin \theta _2 = \frac{2 Y_4 - Y_1 Y_2}{2},\\ x_3= & {} \sqrt{r_3}\cos \frac{\theta _3}{2}, \quad y_3 = \sqrt{r_3}\sin \frac{\theta _3}{2},\\ r_3 \cos \theta _3= & {} \frac{N {k_1}^2 (1-{\delta }^2)+ \epsilon _3 \epsilon _4 N {k_1}^2 (1-{\delta }^2)-{\omega }^2 d_1-2 \epsilon _3 N {k_1}^2 \delta + 2 \epsilon _4 N {k_1}^2 \delta }{L(1+{\epsilon _4}^2)},\\ r_3 \sin \theta _3= & {} \frac{\epsilon _3 N {k_1}^2 (1-{\delta }^2)-\epsilon _4 N {k_1}^2 (1-{\delta }^2)+\epsilon _4 {\omega }^2 d_1 + 2 N {k_1}^2 \delta + 2 \epsilon _3 \epsilon _4 N {k_1}^2 \delta }{L(1+{\epsilon _4}^2)},\\ Y_5= & {} \left( \mu _t\left( (Y_1 - Y_2 \epsilon _2)+ a_3((\frac{\mu _l}{\mu _t}-1)(Y_1 a_3 -2 k_1 a_1 \delta )- (\epsilon _1-\epsilon _2)(2 k_1 a_1 + a_3 Y_2))\right) -2 L (x_3 - y_3 \epsilon _4)\right) ,\\ Y_6= & {} \left( \mu _t \left( (Y_2 + Y_1 \epsilon _2)+ a_3 ((\epsilon _1-\epsilon _2)(Y_1 a_3 - 2 k_1 a_1 \delta )+ (\frac{\mu _l}{\mu _t}-1)(2 k_1 a_1 + a_3 Y_2))\right) -2 L (y_3 + x_3 \epsilon _4)\right) ,\\ Y_7= & {} a_3 \mu _t \left( (\frac{\mu _l}{\mu _t}-1)\left( a_3 ({Y_1}^2 - {Y_2}^2 + 4 {x_2}^2 - 4 {y_2}^2)- 2 a_1 k_1 (Y_1 \delta + Y_2)\right) \right. \\&\left. - (\epsilon _1-\epsilon _2)\left( a_3 (2 Y_1 Y_2 + 8 x_2 y_2)+ 2 a_1 k_1 (Y_1 - Y_2 \delta )\right) \right) ,\\ Y_8= & {} a_3 \mu _t\left( (\frac{\mu _l}{\mu _t}-1)\left( a_3 (2 Y_1 Y_2 + 8 x_2 y_2)+ 2 a_1 k_1 (Y_1 - Y_2 \delta )\right) \right. \\&\left. + (\epsilon _1 - \epsilon _2)\left( a_3 ({Y_1}^2 - {Y_2}^2 + 4 {x_2}^2 - 4 {y_2}^2)-2 a_1 k_1 (Y_1 \delta + Y_2)\right) \right) ,\\ Y_9= & {} {a_3}^2 \mu _t (\frac{\mu _l}{\mu _t}-1)\left( \mu _t \left( (\frac{\mu _l}{\mu _t}-1)((X_7)^2 -(X_8)^2)- 2 (\epsilon _1 - \epsilon _2)( X_7)(X_8)\right) + 4 a_3 ({x_2}^2 - {y_2}^2)\right) \\&- {a_3}^2 \mu _t (\epsilon _1 - \epsilon _2) \left( \mu _t \left( 2 (\frac{\mu _l}{\mu _t}-1)(X_7)(X_8) + (\epsilon _1 - \epsilon _2)((X_7)^2 - (X_8)^2)\right) + 8 a_3 x_2 y_2\right) ,\\ Y_{10}= & {} (\epsilon _1 - \epsilon _2) {a_3}^2 \mu _t \left( \mu _t \left( (\frac{\mu _l}{\mu _t}-1)((X_7)^2 - (X_8)^2) - 2 (\epsilon _1 - \epsilon _2)(X_7)(X_8)\right) + 4 a_3 ({x_2}^2 - {y_2}^2)\right) \\&+ {a_3}^2 \mu _t (\frac{\mu _l}{\mu _t}-1)\left( \mu _t \left( 2 (\frac{\mu _l}{\mu _t}-1)(X_7)(X_8) + (\epsilon _1 - \epsilon _2)((X_7)^2 - (X_8)^2)\right) + 8 a_3 x_2 y_2 \right) ,\\ \end{aligned}$$
$$\begin{aligned} T_1= & {} 4 \mu _t \left( x_2 (1 + {a_3}^2 (\frac{\mu _l}{\mu _t} - 1)) - y_2 (\epsilon _2 + {a_3}^2 (\epsilon _1 - \epsilon _2))\right) ,\\ T_2= & {} 4 \mu _t \left( y_2 (1 + {a_3}^2 (\frac{\mu _l}{\mu _t} - 1)) + x_2 (\epsilon _2 + {a_3}^2 (\epsilon _1 - \epsilon _2))\right) , \\ T_3= & {} \mu _1 \left( (\frac{x_1 S_3 - y_1 S_4}{\eta _1}) - \varpi (y_1 S_3 + x_1 S_4 )\right) - L (x_3 - y_3 \epsilon _4),\\ T_4= & {} \varpi (x_1 S_3 - y_1 S_4) + (\frac{y_1 S_3 + x_1 S_4}{\eta _1}) - L (y_3 + x_3 \epsilon _4),\\ T_5= & {} - 2 \mu _1 \left( (\frac{x_1}{\eta _1} - y_1 \varpi )(S_3 Y_5 - S_4 Y_6) - (\frac{y_1}{\eta _1}+ x_1 \varpi )(S_4 Y_5 + S_3 Y_6)\right) , \\ T_6= & {} - 2 \mu _1 \left( (\frac{y_1}{\eta _1} + x_1 \varpi )(S_3 Y_5 - S_4 Y_6) + (\frac{x_1}{\eta _1}- y_1 \varpi )(S_4 Y_5 + S_3 Y_6)\right) ,\\ T_7= & {} {\mu _t}^2 \left( (1 - {\epsilon _2}^2) X_3 - 2 \epsilon _2 X_4 \right) + \left( 2 \mu _t (Y_7 - \epsilon _2 Y_8) + Y_9 \right) ,\\ T_8= & {} {\mu _t}^2 \left( 2 \epsilon _2 X_3 + (1 - {\epsilon _2}^2) X_4\right) + \left( 2 \mu _t (\epsilon _2 Y_7 + Y_8) + Y_{10}\right) ,\\ T_9= & {} - 2 L \left( (X_1 x_3 - X_2 y_3) - \epsilon _4 (X_2 x_3 + X_1 y_3)\right) - L \left( (Y_1 x_3 - Y_2 y_3) - \epsilon _4 (Y_2 x_3 + Y_1 y_3)\right) ,\\ T_{10}= & {} - 2 L \left( (X_2 x_3 + X_1 y_3) + \epsilon _4 (X_1 x_3 - X_2 y_3)\right) - L \left( (Y_2 x_3 + Y_1 y_3) + \epsilon _4 (Y_1 x_3 - Y_2 y_3)\right) ,\\ T_{11}= & {} \left( (\frac{x_1}{\eta _1} - y_1 \varpi )( S_3 (x_3 - y_3 \epsilon _4) - S_4 (y_3 + x_3 \epsilon _4)) - (\frac{y_1}{\eta _1} + x_1 \varpi )( S_4 (x_3 - y_3 \epsilon _4) + S_3 (y_3 + x_3 \epsilon _4))\right) ,\\ T_{12}= & {} \left( (\frac{y_1}{\eta _1} + x_1 \varpi )( S_3 (x_3 - y_3 \epsilon _4) - S_4 (y_3 + x_3 \epsilon _4)) + (\frac{x_1}{\eta _1} - y_1 \varpi )( S_4 (x_3 - y_3 \epsilon _4) + S_3 (y_3 + x_3 \epsilon _4))\right) ,\\ T_{13}= & {} \mu _2 \left( \sqrt{\frac{c^2}{{\beta _2}^2}-1}\right) \left( \mu _1 \sqrt{\frac{c^2}{{\beta _1}^2}-1} \; \tan \left( \sqrt{\frac{c^2}{{\beta _1}^2}-1}\right) H_2 - \mu _3 k_1 \left( \sqrt{1 - \frac{c^2}{{\beta _4}^2}}\right) \right) ,\\ T_{14}= & {} \mu _1 \mu _3 \left( \sqrt{\frac{c^2}{{\beta _1}^2}-1}\; \tan \left( \sqrt{\frac{c^2}{{\beta _1}^2}-1}\right) H_2 \sqrt{1-\frac{c^2}{{\beta _4}^2}}\right) + {\mu _2}^2 k_1 \left( \frac{c^2}{{\beta _2}^2}-1\right) ,\\ T_{15}= & {} a_1 k_1 \mu _3 \sqrt{1 - \frac{c^2}{{\beta _4}^2}},\\ S_3= & {} \frac{\tan (x_1 H_2)(1 - \tanh ^2 (y_1 H_2))}{1 + \tan ^2 (x_1 H_2) \tanh ^2 (y_1 H_2)},\\ S_4= & {} \frac{\tanh (y_1 H_2)(1 + \tan ^2 (x_1 H_2))}{1 + \tan ^2 (x_1 H_2) \tanh ^2 (y_1 H_2)}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, D., Kundu, S., Kumhar, R. et al. Vibrational analysis of Love waves in a viscoelastic composite multilayered structure. Acta Mech 231, 4199–4215 (2020). https://doi.org/10.1007/s00707-020-02767-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-020-02767-8

Search

Navigation